4.3 势能 势能曲线
合集下载
4.3 势能 势能曲线
势能具有相对性，势能大小与势能零点的选取有关 . 势能是属于系统的 .
2、势能曲线
Ep mgy
Ep
1 2 Ep kx 2
Mm Ep G r
Ep
O
Ep
r
O
y
O
x
弹性势能曲线 引力势能曲线
重力势能曲线
y 0, Ep 0
x 0, Ep 0
r , Ep 0
a
b
取地面 yb 0 处为重力势能零点；取 弹簧原长 xb 0 处为弹性势能零点；取无 穷远 rb 处为引力势能零点，则 重力势能：
Ep重 mgy
Mm E p引 -G r
弹性势能： E p弹 引力势能：
1 2 kx 2
讨论
势能是状态函数
Ep Ep ( x, y, z )
4.3 势能 势能曲线
1、势能(potential energy) 重力的功： A mgya mgyb
1 1 2 2 弹性力的功： A kxa kxb 2 2 万有引力的功： A (G Mm ) (G Mm ) ra rb
A保 Ep (a) Ep (b)
或
A保 [Ep (b) Ep (a)] Ep
E p 势能函数或位能函数(简称为势能或位能)
保守力的功等于系统始末位置势能之差， 或保守力的功等于系统势能增量的负值。
Ep (a) A保 Ep (b)
或
E p (a) F保 dr E p (b)
a
b
——势能的定义式
若取 Ep (b) 0 ，则
E p (a) F保 dr
势能与势能曲线的求解
势能与势能曲线的求解一、引言在物理学中，势能是描述物体在力场中所具有的能量。
势能的概念在研究物体的运动、相互作用以及力的性质等方面起着重要的作用。
势能曲线则是描述势能随位置变化的图形，通过势能曲线可以更好地理解物体的运动规律和相互作用。
二、势能的定义和计算势能是一个相对概念，它依赖于物体所处的位置和相互作用的力。
在经典力学中，我们常常使用重力势能和弹性势能作为例子来说明势能的概念。
重力势能是指物体由于位置的高低而具有的能量。
当物体处于高处时，具有较高的重力势能；当物体处于低处时，具有较低的重力势能。
计算重力势能的公式为：势能 = 质量 ×重力加速度 ×高度。
弹性势能是指物体由于受到弹性力而具有的能量。
当物体被压缩或拉伸时，弹性势能会增加。
计算弹性势能的公式为：势能 = 0.5 ×弹性系数 ×变形长度的平方。
除了重力势能和弹性势能，还有其他形式的势能，如电势能、化学势能等。
它们的计算方式各不相同，但都可以通过物体的位置和相互作用力来求解。
三、势能曲线的求解势能曲线是描述势能随位置变化的图形。
在物理学中，我们经常使用势能曲线来研究物体的运动和相互作用。
对于重力势能和弹性势能，它们的势能曲线可以通过绘制势能与位置的关系来得到。
在重力势能的情况下，随着物体高度的增加，势能也会增加，所以势能曲线是一个递增的曲线。
在弹性势能的情况下，随着物体变形长度的增加，势能也会增加，所以势能曲线也是一个递增的曲线。
对于其他形式的势能，其势能曲线的求解方法各不相同。
例如，电势能的曲线可以通过绘制电势与位置的关系来得到，化学势能的曲线可以通过绘制化学反应能量与反应进度的关系来得到。
通过势能曲线的求解，我们可以更好地理解物体的运动和相互作用。
例如，在重力势能曲线中，我们可以确定物体在不同高度处具有的势能大小，从而预测物体的运动轨迹。
在弹性势能曲线中，我们可以确定物体在不同变形长度处具有的势能大小，从而研究物体的弹性性质。
势能曲线与一维运动
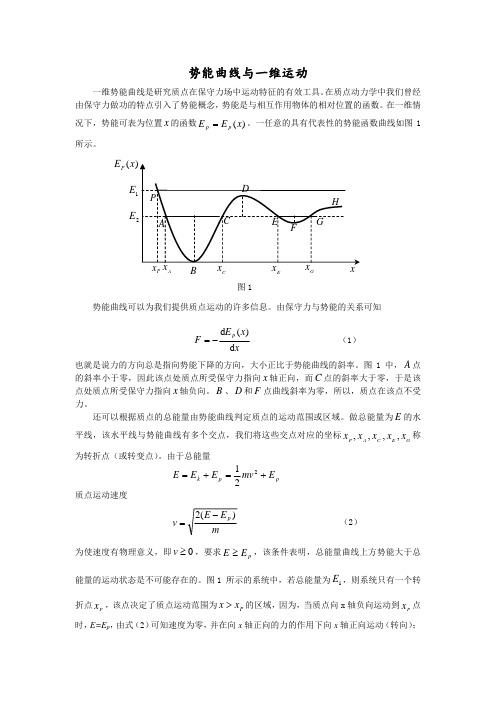
体。面上的凹坑就是一个直观的重力势阱。许多宏观和微观的物理现象都与势阱有关。
如图 2 所示为一倒摆装置,螺旋弹簧将它支撑在 0 的平衡位置处。摆锤在重力和弹性
力作用下运动。设弹簧服从胡克定律，力矩为 M ，则其弹性势能为
E p弹
d
1 2
0Байду номын сангаас
2
倒摆的重力势能为
（10）
d2Ep dx 2
d ( dE p ) dx dx
dF dx
0
（3）
该结果说明，该两点附近质点受力与位移正比反向，即为回复力。通常将这种位置称为稳定
平衡位置。这是因为回复力的存在总是将质点拉回到平衡位置。而 D 点的情况则有所不同， 该点附近质点受力总是指向远离 D 点的方向，因此质点的运动将远离该点而去，这样的位 置称为不稳定平衡位置。在势能曲线为常数的 H 点，平衡被称为随遇平衡。
E p重 mgl(cos 1) （11）
总能量为
Ep
E p弹
E p重
1 2 2
mgl (cos
1) （12）
势能极小值处有
dE p mgl sin 0
（13）
图2
d
为分析平衡位置的稳定性问题，我们求势能函数的二阶导数，
d 2 E p mgl cos d 2
势能曲线与一维运动
一维势能曲线是研究质点在保守力场中运动特征的有效工具。在质点动力学中我们曾经 由保守力做功的特点引入了势能概念，势能是与相互作用物体的相对位置的函数。在一维情
况下，势能可表为位置 x 的函数 E p E p (x) 。一任意的具有代表性的势能函数曲线如图 1
最新教科版高中物理必修二4.3《势能》优质课件.pptx
A.重力做功为 1.8J B.重力做了 0.55J 的负功 C.球的重力势能一定减少 0.55J D.球的重力势能一定增加 1.25J 解析:整个过程重力对球做正功,其大小为
W=mgΔh=mg(h1-h2)=0.55J,A、B 错误;重力做正功,重力势能减少,且重力做
多少正功,重力势能就减少多少,因此球的重力势能减少 0.55J,C 正确,D 错
关 系
知 (1)重力(弹性)势能的正、负不表示方向,只表示相对大小 识 (2)重力势能是地球和物体组成的系统共有的,弹性势能是弹簧和物体组 要 成的系统共有的,都不是物体单独具有的.通常说物体具有多少重力势 点 能(弹性势能),只是一种简略的说法
探究一
探究二
探究一 对重力势能的理解
因为 Ep=mgh,高度 h 的相对性决定了重力势能具有相对性.如图所示,若选 择桌面为参考平面,物体的重力势能为 0;若选择地面为参考平面,物体的重 力势能为正值;若选择物体重心上方的某一高度为参考平面,物体的重力 势能为负值
误. 答案:C
探究一
探究二
题后反思:两种方法求重力做的功: (1)先求初末位置的高度差,再求出重力与此高度差的乘积即为重力做的功. (2)根据重力势能的变化与重力做功的关系来求重力做的功.
12345
1 某游客领着孩子游泰山时,孩子不小心将手中的皮球滑落,球从 A 点滚到 了山脚下的 B 点,高度标记如图所示,则下列说法正确的是( ) A.从 A 到 B 的曲线轨迹长度不知道,无法求出此过程中重力做的功 B.从 A 到 B 过程中阻力大小不知道,无法求出此过程中重力做的功 C.从 A 到 B 重力做功 mg(H+h) D.从 A 到 B 重力做功 mgH 解析:重力做功与物体的运动路径无关,只与初末状态物体的高度差有关,从 A 到 B 的高度是 H,故从 A 到 B 重力做功 mgH,D 正确. 答案:D
W=mgΔh=mg(h1-h2)=0.55J,A、B 错误;重力做正功,重力势能减少,且重力做
多少正功,重力势能就减少多少,因此球的重力势能减少 0.55J,C 正确,D 错
关 系
知 (1)重力(弹性)势能的正、负不表示方向,只表示相对大小 识 (2)重力势能是地球和物体组成的系统共有的,弹性势能是弹簧和物体组 要 成的系统共有的,都不是物体单独具有的.通常说物体具有多少重力势 点 能(弹性势能),只是一种简略的说法
探究一
探究二
探究一 对重力势能的理解
因为 Ep=mgh,高度 h 的相对性决定了重力势能具有相对性.如图所示,若选 择桌面为参考平面,物体的重力势能为 0;若选择地面为参考平面,物体的重 力势能为正值;若选择物体重心上方的某一高度为参考平面,物体的重力 势能为负值
误. 答案:C
探究一
探究二
题后反思:两种方法求重力做的功: (1)先求初末位置的高度差,再求出重力与此高度差的乘积即为重力做的功. (2)根据重力势能的变化与重力做功的关系来求重力做的功.
12345
1 某游客领着孩子游泰山时,孩子不小心将手中的皮球滑落,球从 A 点滚到 了山脚下的 B 点,高度标记如图所示,则下列说法正确的是( ) A.从 A 到 B 的曲线轨迹长度不知道,无法求出此过程中重力做的功 B.从 A 到 B 过程中阻力大小不知道,无法求出此过程中重力做的功 C.从 A 到 B 重力做功 mg(H+h) D.从 A 到 B 重力做功 mgH 解析:重力做功与物体的运动路径无关,只与初末状态物体的高度差有关,从 A 到 B 的高度是 H,故从 A 到 B 重力做功 mgH,D 正确. 答案:D
高中物理必修二课件-4.3 势能7-教科版
即：物体的重力势能等于物体的重量和它的高 度的乘积．
m — 物体的质量， 单位：千克（kg）
g — 重力加速度， 单位：米／秒2（m／s2）
h —物体的高度， 单位：米（m） Ep — 物体的重力势能， 单位：焦耳（J）
②标矢性：标量 （正、负号不代表方向）
12
例题：请同学们估算一下课桌上物理教科书 的重力势能？（书的质量约为0.2千克，桌子高
mgh1 mgh2
②理论定量推导
例2、物体沿斜面运动从A到B，
求重力做功？
mA
θ
△h
h1
l
B
h2
讨论：
（1）若物体沿高度相同的 不同斜 面下滑，重力做 功是否发生变化？ （2）斜面是否光滑对”重 力做功“有影响吗？
6
WG mgl cos mgh
mgh1 mgh2
例3、物体沿曲线运动从A到B，求重力做功？
3. 势能
一、重力势能
定义：
地球上的物体由于处于一定的高度而具有
的能量，我们把这种能量叫做重力势能。 表示。
用EP
（1）打桩机的重锤从高处落下时，为什么能把 水泥打进地里?
（2）水力发问题： 重力势能的大小与什么因素有关？
▲建立假设： 与质量和高度都有关系。
总结：重力做功是重力势能变化的量度
物体下落，重力做正m功gh ，重力势能减E少p mgh 物体上升，重力做负功mgh ，重力势能增加E p mgh
WG E p
重力是物体与地球之间 的相互作用
mg
重力势能是物体与地球 组成的系统共同具有的
任何形式的势能，都是相应 的物体组成的系统具有的
说明：平常所说的“物体”的重力势能,只是习惯简化的说法。
m — 物体的质量， 单位：千克（kg）
g — 重力加速度， 单位：米／秒2（m／s2）
h —物体的高度， 单位：米（m） Ep — 物体的重力势能， 单位：焦耳（J）
②标矢性：标量 （正、负号不代表方向）
12
例题：请同学们估算一下课桌上物理教科书 的重力势能？（书的质量约为0.2千克，桌子高
mgh1 mgh2
②理论定量推导
例2、物体沿斜面运动从A到B，
求重力做功？
mA
θ
△h
h1
l
B
h2
讨论：
（1）若物体沿高度相同的 不同斜 面下滑，重力做 功是否发生变化？ （2）斜面是否光滑对”重 力做功“有影响吗？
6
WG mgl cos mgh
mgh1 mgh2
例3、物体沿曲线运动从A到B，求重力做功？
3. 势能
一、重力势能
定义：
地球上的物体由于处于一定的高度而具有
的能量，我们把这种能量叫做重力势能。 表示。
用EP
（1）打桩机的重锤从高处落下时，为什么能把 水泥打进地里?
（2）水力发问题： 重力势能的大小与什么因素有关？
▲建立假设： 与质量和高度都有关系。
总结：重力做功是重力势能变化的量度
物体下落，重力做正m功gh ，重力势能减E少p mgh 物体上升，重力做负功mgh ，重力势能增加E p mgh
WG E p
重力是物体与地球之间 的相互作用
mg
重力势能是物体与地球 组成的系统共同具有的
任何形式的势能，都是相应 的物体组成的系统具有的
说明：平常所说的“物体”的重力势能,只是习惯简化的说法。
4.3重力势能和弹性势能
三、势能是系统所共有的！
注: 重力势能与弹性势能都是由相互作用物体的相 对位置决定的能；势能,也称为位能.
答案：105J；重力势能增加105J
二、弹性势能EP ——由于物体发生弹性形变而具有的能量
弹性势能EP 其大小与哪些因素有关？
F F
* EP
1 kx2 2
(J，焦耳)
• 如图所示，物体和弹簧组成的体统，物体由A位 置经平衡位置O运动到B位置的过程中
AOB
• AO段：弹力做正功，弹性势能减小， • 减小的弹性势能等于弹力对外做的功 。 • OB段：弹力做负功，弹性势能增加， • 增加的弹性势能等于物体克服弹力做的功。
重力势能
物体由于位于高处而具有的能量叫做重力势能。
猜想：重力势能与哪些因素有关？
一、重力势能
θ’
• 1、重力做功
• ①沿AB直线路径
D
• ②沿ACB折线路径
• ③沿ADB折线路径
• ④沿APB曲线路径
• 重力做功与路径无关，只与物体的重力和始、末 • 位置的高度差有关。
WG = mg（h1－h2）= mgh1－mgh2
h1=1.2m的A点落到地面的B点，桌面高 h2=0.8m．请按要求填写下表．(g=10m/s2)
参考 小球在 小球在 下落过程 下落过程
平面 A点重 B点重 小球重力 小球重力
Aቤተ መጻሕፍቲ ባይዱ
力势能 力势能 做功 势能变化
h1 桌面 6J
-4J
10J
10J
地面 10J
0
10J
10J
h2 B
选取不同的参考平面,物体的重力势能的数值不同 对一个确定的过程，WG和△EP与参考面的选择无关
重力势能曲线引力势能曲线弹性势能曲线
(1) 对沙箱, 应用动能定理：
(2) 对弹丸，应用动能定理：
s s+l
(3) 机械能变化：
s 一对非保守内力(耗散力)做 负功，使系统动能减少。 s+l
3 -- 5
功能原理 能量守恒定律
一、质点系动能定理
二、功能原理
保守内力的总功
内力做的总功
非保守内力的总功
注： 1、取好系统及初、末状态。 2、惯性系。 3、If
b A ( Fi ) dr Fi dr Ai i a i
直角坐标系： 单位：N· m or J
b b 自然坐标系： A F dr Ft dr Ft ds
b a a a
A P t A dA F dr P lim F v dt dt t 0 t
第三章 机械能和功
3-1 功 动能定理 空间上的累积
力的累积效应 时间上的累积 恒力之功：
F
功
冲量
r
A F cos r F r
变力之功：
Ai Fi cosi ri
A Fi cos i ri
b( xb , yb , zb )
ri
i
例：
三、已知势能函数确定保守力场
而
故：
力沿某方向分力等于势能函数沿该方向空间变化率负值！
式中
称为矢量微分算子
称为势能函数的梯度
例：
则重力
例：
四、势能曲线
Ｏ Ｚ Ｏ 重力势能曲线 ｒ x Ｏ 弹性势能曲线
引力势能曲线
双原子分子的势能曲线
Ｏ
ｒ
[例3-5] 已知地球半径 R，物体质量 m，处在地面 2R 处。 求势能:（1）地面为零势能点；（2）无限远处为零势 能点。
(2) 对弹丸，应用动能定理：
s s+l
(3) 机械能变化：
s 一对非保守内力(耗散力)做 负功，使系统动能减少。 s+l
3 -- 5
功能原理 能量守恒定律
一、质点系动能定理
二、功能原理
保守内力的总功
内力做的总功
非保守内力的总功
注： 1、取好系统及初、末状态。 2、惯性系。 3、If
b A ( Fi ) dr Fi dr Ai i a i
直角坐标系： 单位：N· m or J
b b 自然坐标系： A F dr Ft dr Ft ds
b a a a
A P t A dA F dr P lim F v dt dt t 0 t
第三章 机械能和功
3-1 功 动能定理 空间上的累积
力的累积效应 时间上的累积 恒力之功：
F
功
冲量
r
A F cos r F r
变力之功：
Ai Fi cosi ri
A Fi cos i ri
b( xb , yb , zb )
ri
i
例：
三、已知势能函数确定保守力场
而
故：
力沿某方向分力等于势能函数沿该方向空间变化率负值！
式中
称为矢量微分算子
称为势能函数的梯度
例：
则重力
例：
四、势能曲线
Ｏ Ｚ Ｏ 重力势能曲线 ｒ x Ｏ 弹性势能曲线
引力势能曲线
双原子分子的势能曲线
Ｏ
ｒ
[例3-5] 已知地球半径 R，物体质量 m，处在地面 2R 处。 求势能:（1）地面为零势能点；（2）无限远处为零势 能点。
4.3势能(用).ppt
A、物体的位置一旦确定，它的重力势能大小 也随之确定
B、物体与零势能面间的距离越大，它的重力 势能也越大
C、一个物体的重力势能由-5J变化到-3J，重 力势能变大了
D、重力势能的减小量等于重力对物体做的功
四、弹性势能 （详见课本P66）
同理：
即弹性势能的变化仅由 决定，与其他 力是否做功无关。
五、势能是系统所共有的 （详见课本P66）
一、功和能 1.做功的过程就是能量转化的过程
功是能量转化的量度
2.功和能都是标量； 3.功是过程量，能是状态量； 4.功不是能。
高处的巨 石为什么 总让人望 而生畏？
§ 4.3 势 能
二、重力势能
1.概念：物体由于处于高处而具有的能量叫 重力势能。
那么重力势能的大小与什么有关，又 如何定量表示呢?
〖讨论交流〗
设想你由一座 高楼的17层下到 第8层，你可以 乘电梯，也可以 沿楼梯走下去， 两种方式下楼， 重力对人做的功 有何特点？
①物体m沿折线ACB
WG＝ mg∆h ＝mg（h1－h2） ＝ mgh1－mgh2
②物体m沿直线AB
WG＝ mgxsinθ＝mg∆h
＝ mgh1－mgh2
③物体m沿曲线APB
WG＝mgΔh1＋mgΔh2 ＋ ··· ＝mg(Δh1 ＋Δh2 ＋ ···) ＝mg∆h
＝mgh1－mgh2
x ∆h
同理可以证 明物体沿其他任 意路径，重力做 功均相同。
2.重力做功特点：
重力做功与物体运动的路径无关，只与 初末位置的高度差∆h有关。
Hale Waihona Puke WG=±mg∆h∆h为初末位置高度差
∆h
WG = ＋mg∆h
WG= － mg∆h
B、物体与零势能面间的距离越大，它的重力 势能也越大
C、一个物体的重力势能由-5J变化到-3J，重 力势能变大了
D、重力势能的减小量等于重力对物体做的功
四、弹性势能 （详见课本P66）
同理：
即弹性势能的变化仅由 决定，与其他 力是否做功无关。
五、势能是系统所共有的 （详见课本P66）
一、功和能 1.做功的过程就是能量转化的过程
功是能量转化的量度
2.功和能都是标量； 3.功是过程量，能是状态量； 4.功不是能。
高处的巨 石为什么 总让人望 而生畏？
§ 4.3 势 能
二、重力势能
1.概念：物体由于处于高处而具有的能量叫 重力势能。
那么重力势能的大小与什么有关，又 如何定量表示呢?
〖讨论交流〗
设想你由一座 高楼的17层下到 第8层，你可以 乘电梯，也可以 沿楼梯走下去， 两种方式下楼， 重力对人做的功 有何特点？
①物体m沿折线ACB
WG＝ mg∆h ＝mg（h1－h2） ＝ mgh1－mgh2
②物体m沿直线AB
WG＝ mgxsinθ＝mg∆h
＝ mgh1－mgh2
③物体m沿曲线APB
WG＝mgΔh1＋mgΔh2 ＋ ··· ＝mg(Δh1 ＋Δh2 ＋ ···) ＝mg∆h
＝mgh1－mgh2
x ∆h
同理可以证 明物体沿其他任 意路径，重力做 功均相同。
2.重力做功特点：
重力做功与物体运动的路径无关，只与 初末位置的高度差∆h有关。
Hale Waihona Puke WG=±mg∆h∆h为初末位置高度差
∆h
WG = ＋mg∆h
WG= － mg∆h
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
a
b
取地面 yb 0 处为重力势能零点；取 弹簧原长 xb 0 处为弹性势能零点；取无 穷远 rb 处为引力势能零点，则 重力势能：
Ep重 mgy
Mm E p引 -G r
弹性势能： E p弹 引力势能：
1 2 kx 2
讨论
势能是状态函数
Ep Ep ( x, y, z )
势能具有相对性，势能大小与势能零点的选取有关 . 势能是属于系统的 .
2、势能曲线
Ep mgyEp来自1 2 Ep kx 2
Mm Ep G r
Ep
O
Ep
r
O
y
O
x
弹性势能曲线 引力势能曲线
重力势能曲线
y 0, Ep 0
x 0, Ep 0
r , Ep 0
4.3 势能 势能曲线
1、势能(potential energy) 重力的功： A mgya mgyb
1 1 2 2 弹性力的功： A kxa kxb 2 2 万有引力的功： A (G Mm ) (G Mm ) ra rb
A保 Ep (a) Ep (b)
或
A保 [Ep (b) Ep (a)] Ep
E p 势能函数或位能函数(简称为势能或位能)
保守力的功等于系统始末位置势能之差， 或保守力的功等于系统势能增量的负值。
Ep (a) A保 Ep (b)
或
E p (a) F保 dr E p (b)
a
b
——势能的定义式
若取 Ep (b) 0 ，则
E p (a) F保 dr
b
取地面 yb 0 处为重力势能零点；取 弹簧原长 xb 0 处为弹性势能零点；取无 穷远 rb 处为引力势能零点，则 重力势能：
Ep重 mgy
Mm E p引 -G r
弹性势能： E p弹 引力势能：
1 2 kx 2
讨论
势能是状态函数
Ep Ep ( x, y, z )
势能具有相对性，势能大小与势能零点的选取有关 . 势能是属于系统的 .
2、势能曲线
Ep mgyEp来自1 2 Ep kx 2
Mm Ep G r
Ep
O
Ep
r
O
y
O
x
弹性势能曲线 引力势能曲线
重力势能曲线
y 0, Ep 0
x 0, Ep 0
r , Ep 0
4.3 势能 势能曲线
1、势能(potential energy) 重力的功： A mgya mgyb
1 1 2 2 弹性力的功： A kxa kxb 2 2 万有引力的功： A (G Mm ) (G Mm ) ra rb
A保 Ep (a) Ep (b)
或
A保 [Ep (b) Ep (a)] Ep
E p 势能函数或位能函数(简称为势能或位能)
保守力的功等于系统始末位置势能之差， 或保守力的功等于系统势能增量的负值。
Ep (a) A保 Ep (b)
或
E p (a) F保 dr E p (b)
a
b
——势能的定义式
若取 Ep (b) 0 ，则
E p (a) F保 dr