多电平逆变器主要控制策略综述
多电平逆变器的控制策略及应用研究

多电平逆变器的控制策略及应用研究多电平逆变器是一种用于将直流电能转换为交流电能的重要电力电子设备。
其控制策略直接影响了逆变器的性能和应用效果。
本文将从多电平逆变器的控制策略以及相关应用方面展开研究,以期对该领域的研究和应用产生一定的推动作用。
多电平逆变器的控制策略主要包括PWM(脉宽调制)控制和MPWM(多电平脉宽调制)控制两种。
PWM控制通过控制逆变器中IGBT开关管的导通时间实现输出电压的宽度调制,从而获得所需的输出波形。
然而,由于PWM控制仅能获得两个离散化电平的输出波形,无法满足高功率和高精度的应用需求。
而MPWM控制则通过调整多个电平的导通时间,可获得多个离散化电平的输出波形,提高了输出波形的质量和精度。
近年来,随着电力电子技术的发展,MPWM控制成为了多电平逆变器中常用的控制策略。
多电平逆变器的应用非常广泛,涉及到电力系统稳定控制、交流传动控制、电力质量控制以及新能源发电等领域。
在电力系统稳定控制方面,多电平逆变器可用于提供无电池储能系统,以实现电力系统的频率和电压平衡调节,从而改善电网的稳定性。
在交流传动控制方面,多电平逆变器可用于驱动大功率交流电机,提高传动效率和稳定性。
在电力质量控制方面,多电平逆变器可用于消除电力系统中的谐波和干扰,提高电力质量。
在新能源发电方面,多电平逆变器可应用于风力发电和光伏发电等领域,提高发电效率和能源利用率。
此外,多电平逆变器还具有多级结构、能量分流和故障容错等特点,这些特点也为其在电力电子设备领域的应用提供了更多选择和优化空间。
例如,多电平逆变器可以通过增加级数来提高输出波形的质量,从而适应更复杂和敏感的应用环境。
同时,多电平逆变器还可以通过能量分流来减小单个器件的功率损耗,提高整个系统的能量利用效率。
此外,在故障容错方面,多电平逆变器能够通过调整导通时间和增加备份开关管等措施来实现故障切换,提高系统的可靠性和容错能力。
综上所述,多电平逆变器的控制策略和应用研究是当前电力电子领域的一个重要研究方向。
多电平逆变器的工作原理、控制方法以及仿真

目录第一章绪论 (1)1.1多电平逆变器的背景 (1)1.2多电平逆变器的研究现状 (2)1.3多电平逆变器的应用 (3)第二章多电平逆变器的种类介绍 (6)2.1二极管箝位式多电平逆变器及其优缺点 (6)2.2电容箝位式多电平逆变器及其优缺点 (6)2.3H桥级联式多电平逆变器及其优缺点 (7)第三章多电平变换器PWM调制策略 (8)3.1多电平变换器PWM调制策略的分类 (8)3.2多电平SPWM调制策略 (9)3.2.1 SPWM调制策略 (9)3.2.2 载波垂直分布多电平调制策略 (9)3.2.3 载波水平移相多电平调制策略 (10)3.2.4多载波SPWM调制策略谐波分析 (10)3.3多电平SVPWM调制策略 (46)3.3.1 SVPWM调制策略 (46)第四章多电平逆变器中的电压平衡技术 (48)第五章三电平中点箝位型逆变器SPWM控制策略与仿真 (53)5.1三电平NPC逆变器SPWM方法 (53)5.2基于MATLAB的三电平NPC逆变器SPWM仿真 (54)5.2.1仿真系统整体框图 (54)5.2.2 基于载波反向SPWM带电机负载的仿真模块 (54)5.3基于载波同向SPWM带电机负载的仿真模块 (56)5.3.1 SPWM开关信号的发生模块 (56)5.3.2仿真结果与分析 (56)5.4基于注入三次谐波的SPWM带电机负载的仿真模块 (57)5.4.1 SFOPWM开关信号的发生模块 (57)5.4.2仿真结果与分析 (58)5.5三电平NPC逆变器SPWM的实验结果 (58)5.6小结 (59)第六章总结展望 (60)第一章绪论1.1 多电平逆变器的背景电力电子技术自二十世纪50年代诞生以来,经过近半个世纪的飞速发展,至今已被广泛应用于需要电能变换的各个领域。
在低压小功率的用电领域,电力电子技术的各个方面己渐趋成熟,将来研究的目标是高功率密度、高效率、高性能;而在高压大功率的工业和输配电领域,各个方面的技术正成为当今电力电子技术的研究重点。
多电平逆变器

多电平逆变器摘要多电平逆变器及其相关技术的研究与应用,是现代电力电子技术的最新发展之一,它主要面向高压大容量的应用场合近年来,多电平逆变器的研究受到广泛重视,并得到了一定的应用。
多电平逆变器输出端可以有更多级的输出电压波形,谐波含量小,波形更接近正弦波,逆变器性能更好,更适用于高压大容量的电力电子变换。
总结和比较了多电平逆变器各种基本拓扑结构的特点,它们主要包括了:二极管钳位式、飞跨电容钳位式,电容电压自平衡式和联型式拓扑,并且分析了它们的优缺点。
本文介绍了几种多电平逆变器调制方式。
关键字多电平逆变器拓扑结构调制策略1引言1.1 多电平逆变器的产生和发展背景电力电子技术自20世纪50年代诞生以来,经过半个多世纪的飞速发展,至今已被广泛应用于电力系统、电机调速系统及各种电源系统等需要电能变换的领域。
在低压小功率的用电领域,电力电子技术的各个方面己渐趋成熟,将来的研究目标则是高功率密度、高效率和高性能;而在高压大功率的工业和输配电领域,各个方面的技术正成为当今电力电子技术的研究重点。
大功率电力电子装置如电力系统中的高压直流输电(HVDC),以静止同步补偿器(STATCOM)和有源电力滤波器(APF)为代表的柔性交流输电技术(FACTS),以及以高压变频为代表的大电机驱动和大功率电源等需要能够处理越来越高的电压等级和容量等级,同时,为了满足输出电压谐波含量的要求,这些大功率电力电子装置还要能够工作在高开关频率下,并且尽量减少电磁干扰(EMI)问题。
电力电子器件是电力电子装置的核心。
在过去几十年里,以GTO、BJT、MOSFET为代表的自关断器件得到长足的发展,尤其是以IGBT、IGCI,为代表的双极性复合器件的惊人进步,使得电力电子器件向大容量、高频、易驱动、低损耗、智能模块化的方向发展。
即便如此,在某些应用场合,传统的两电平电压源变换器拓扑,仍然不能满足人们对高压、大功率的要求。
并且,以现有的电力电子器件的工艺水平,其功率处理能力和开关频率之间是矛盾的,往往功率越大,开关频率越低。
第3章 多电平变换器PWM调制策略1
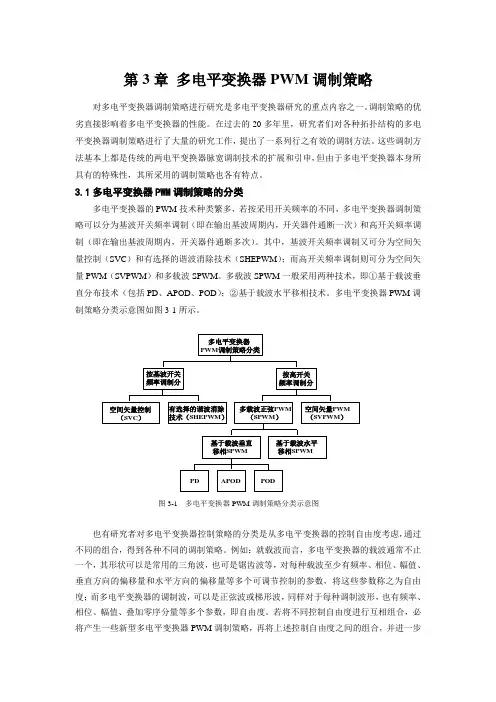
第3章 多电平变换器PWM 调制策略对多电平变换器调制策略进行研究是多电平变换器研究的重点内容之一。
调制策略的优劣直接影响着多电平变换器的性能。
在过去的20多年里,研究者们对各种拓扑结构的多电平变换器调制策略进行了大量的研究工作,提出了一系列行之有效的调制方法。
这些调制方法基本上都是传统的两电平变换器脉宽调制技术的扩展和引申,但由于多电平变换器本身所具有的特殊性,其所采用的调制策略也各有特点。
3.1多电平变换器PWM 调制策略的分类多电平变换器的PWM 技术种类繁多,若按采用开关频率的不同,多电平变换器调制策略可以分为基波开关频率调制(即在输出基波周期内,开关器件通断一次)和高开关频率调制(即在输出基波周期内,开关器件通断多次)。
其中,基波开关频率调制又可分为空间矢量控制(SVC )和有选择的谐波消除技术(SHEPWM );而高开关频率调制则可分为空间矢量PWM (SVPWM )和多载波SPWM 。
多载波SPWM 一般采用两种技术,即①基于载波垂直分布技术(包括PD 、APOD 、POD );②基于载波水平移相技术。
多电平变换器PWM 调制策略分类示意图如图3-1所示。
也有研究者对多电平变换器控制策略的分类是从多电平变换器的控制自由度考虑,通过不同的组合,得到各种不同的调制策略。
例如:就载波而言,多电平变换器的载波通常不止一个,其形状可以是常用的三角波,也可是锯齿波等,对每种载波至少有频率、相位、幅值、垂直方向的偏移量和水平方向的偏移量等多个可调节控制的参数,将这些参数称之为自由度;而多电平变换器的调制波,可以是正弦波或梯形波,同样对于每种调制波形,也有频率、相位、幅值、叠加零序分量等多个参数,即自由度。
若将不同控制自由度进行互相组合,必将产生一些新型多电平变换器PWM 调制策略,再将上述控制自由度之间的组合,并进一步多电平变换器PWM 调制策略分类按基波开关频率调制分按高开关频率调制分空间矢量控制 (SVC )有选择的谐波消除技术(SHEPWM )多载波正弦PWM (SPWM )空间矢量PWM (SVPWM )基于载波垂直 移相SPWM 基于载波水平 移相SPWMPD APOD POD图3-1 多电平变换器PWM 调制策略分类示意图与各种多电平变换器的基本拓扑相结合,将产生数量庞大的多电平变换器PWM调制策略[84]。
多电平变换器拓扑及控制技术的发展综述

5
1
质,电压利用率高,易于数字实现
V14(-110)
V5(010) V6(110)
(-10-1) 6 (00-1)
等,不足之处在于当电平数超过5 V18(10-1) 时 , 算 法 过 于 复 杂 。
V15(-11-1) V16(01-1) V17(11-1)
图8 三电平逆变器空间电压矢量图
2. APEC’2002-2003中提出的新拓扑和控制方法
思想:拓扑存在着多种开关状态组合,当器件发生断路故障 时,改变开关状态组合,使发生故障的器件处于关断状态; 当器件发生短路故障时,改变开关状态组合,使发生故障的 器件处于导通状态。
图17 消谐波调制方法
(a) sp1断路故障时输出电压
(b) sp2短路故障时输出电压
图18 器件故障时的实验结果
3.4 提出基于控制自由度组合的载波PWM控制方法
图10 混合多电平变换器原理图
新的控制方法
❖一种通用的空间矢量PWM控制算法:解决了空间矢量计算的复杂性,并且该法可以 应用于任意电平的H-桥级联型多电平拓扑。(APEC’2003) ❖用于级联型多电平变换器的错时采样的空间矢量调制方法,大大减小了谐波分量。 (APEC’2003) ❖减少电流纹波的空间矢量混合PWM技术。(级联型)(APEC’2003)
3.3 提出一种具有冗余功能的多电平变换器拓扑
sp4
Dp4
Sp1 Vo
Sn1
Sp2
Sc1 Dp 1
C1 Sc2
Dn 1
Sn2
2 -Lev el
Sp3
Sc3 Dp 2
C2 Sc4
Dc1
Sc5 Dc2
C3 Sc6
Dn 2
多电平功率变换器的PWM控制策略综述

mo e c mp e e sv , mo e d f c l t l p e c nr la ms a d t i i h i i ci n o e eo me to W M t o s fr r o r h n ie r i u t wi mu t l o t i , n h s s t e man d r t f d v lp n f P i y h i o e o me 的 P 对 WM控制策略进行了较为详 细的综述 研究 , 对其发展趋势进行 了展望。多电平变换器的拓 扑结构 的丰 富性 和多电平 P WM控制 自由度的增加, 决定 了多 电平逆变器 P WM控制方法的灵活性 和多样性, 以可能存在全新 的、 所 更加有
效的 P WM 控 制 方 法 , 制 方 案 的增 加 使 得 控 制 方 案 的 优 化 问 题 显 得 非 常 重要 , 将 是 多 电 平 P 控 这 WM 的一 个 必 然 的发 展 方 向; 每
南 京 师 范 大 学 ( 苏 南 京 2 04 ) 张艳 莉 费 万 民 江 10 2 ( aj gN r a nv sy J nsuN ni 10 2 hn ) Z agY n F i n i N ni om l ir t i gh aj g20 4 ,C i n U ei, a n a h n al i e Wam n 浙 江 大 学 ( 江 杭 州 30 2 ) 吕征 宇 浙 1 0 7 ( h i g U i r t, Z e in a gh u3 0 2 ,C ia L h ny Z e a nv s y h i g H n zo 0 7 hn ) uZ e gu jn ei ja 1
一
种 主电路拓扑结构都有不 同的中间变量控制任务, 导致 了多电平功率变换 器的 P WM控制 目标 多、 任务大 、 难度大 、 综合性强,
多电平逆变电路的三种控制方法
多电平逆变电路的三种控制方法多电平变换器PWM控制方法可分为两大类:三角载波PWM技术和直接数字技术(空间电压矢量法SVPWM),它们都是2电平P WM在多电平中的扩展。
1. 三角载波PWM方法①消谐波PWM(SHPWM)法消谐波PWM法的原理是电路的每一相使用一个正弦调制波和几个三角波进行比较,在正弦波与三角波相交的时刻,如果正弦波的幅值大于某个三角波的值,则开通相应的开关器件,否则,则关断该器件。
为了使M-1个三角载波所占的区域是连续的,它们在空间上是紧密相连且对称地分布在零参考量的正负两侧。
消谐波PWM是2电平三角载波PWM在多电平中的扩展。
②开关频率最优PWM(SFOPWM)法开关频率最优法是由2电平三角载波PWM扩展而来。
它的载波要求与SHPWM法相同,不同的是它在正弦调制波中注入了零序分量。
对于一个三相系统,这个零序分量是三相正弦波瞬态最大值和最小值的平均值,所以SFOPWM的调制波是三相正弦波减去零序分量后所得到的波形。
这种方法通过在调制波中注入零序分量而使得电压调制比达到1.15。
但是该方法只能用于三相系统。
因为在单相系统中注入的零序分量无法互相抵消,从而在输出波形中存在三次谐波,而在三相系统中就不会有这种问题。
实际上,这种零序分量注入的方法在本质上与电压空间矢量法是一致的,它相当于零矢量在半开关周期始末两端均匀分布的空间电压矢量法。
所以,SFOPWM法可以看成是2电平空间电压矢量法在多电平变换器控制中的推广。
③三角波移相PWM(PSPWM)法三角载波移相PWM法是一种专门用于级联型多电平变换器的P WM方法。
这种控制方法与SHPWM方法不同,每个模块的SPWM 信号都是由一个三角载波和一个正弦波比较产生,所有模块的正弦波都相同,但每个模块的三角载波与它相邻模块的三角载波之间有一个相移,这一个相移使得各模块所产生的SPWM脉冲在相位上错开,从而使得各模块最终叠加输出的SPWM波的等效开关率提高到原来的Keff倍,在不提高开关频率的条件下大大减小了输出谐波。
多电平逆变器的工作原理、控制方法以及仿真
目录第一章绪论 (1)1.1多电平逆变器的背景 (1)1.2多电平逆变器的研究现状 (2)1.3多电平逆变器的应用 (3)第二章多电平逆变器的种类介绍 (6)2.1二极管箝位式多电平逆变器及其优缺点 (6)2.2电容箝位式多电平逆变器及其优缺点 (6)2.3H桥级联式多电平逆变器及其优缺点 (7)第三章多电平变换器PWM调制策略 (8)3.1多电平变换器PWM调制策略的分类 (8)3.2多电平SPWM调制策略 (9)3.2.1 SPWM调制策略 (9)3.2.2 载波垂直分布多电平调制策略 (9)3.2.3 载波水平移相多电平调制策略 (10)3.2.4多载波SPWM调制策略谐波分析 (10)3.3多电平SVPWM调制策略 (46)3.3.1 SVPWM调制策略 (46)第四章多电平逆变器中的电压平衡技术 (48)第五章三电平中点箝位型逆变器SPWM控制策略与仿真 (53)5.1三电平NPC逆变器SPWM方法 (53)5.2基于MATLAB的三电平NPC逆变器SPWM仿真 (54)5.2.1仿真系统整体框图 (54)5.2.2 基于载波反向SPWM带电机负载的仿真模块 (55)5.3基于载波同向SPWM带电机负载的仿真模块 (57)5.3.1 SPWM开关信号的发生模块 (57)5.3.2仿真结果与分析 (57)5.4基于注入三次谐波的SPWM带电机负载的仿真模块 (58)5.4.1 SFOPWM开关信号的发生模块 (58)5.4.2仿真结果与分析 (58)5.5三电平NPC逆变器SPWM的实验结果 (59)5.6小结 (59)第六章总结展望 (60)第一章绪论1.1 多电平逆变器的背景电力电子技术自二十世纪50年代诞生以来,经过近半个世纪的飞速发展,至今已被广泛应用于需要电能变换的各个领域。
在低压小功率的用电领域,电力电子技术的各个方面己渐趋成熟,将来研究的目标是高功率密度、高效率、高性能;而在高压大功率的工业和输配电领域,各个方面的技术正成为当今电力电子技术的研究重点。
多电平逆变器技术及其原理综述
收稿日期:2011-06-21作者简介:蔡兴(1987-),男,江西新建人,学士,主要研究方向:电气自动化。
0引言自20世纪50年代电力电子技术诞生以来,经过几十年的飞速发展,至今已被广泛应用于电力系统、电机调速等需要电能变换的领域。
日本学者南波江章(A.Naba )于1980年提出三电平中点钳位逆变器以来,引起人们的普遍关注。
由于在节能、可靠性和性能指标等方面的巨大优势,使得它越来越多地被人们所采用。
经过近30年的研发,很多学者相继提出了具有实际意义的多电平逆变器电路及多种多电平逆变器的调制控制方法。
当前的多电平逆变器的主要结构有:H 桥级联式(Cascaded H-bridge )、电容箝位式(Capacitor-Clamped )、二极管箝位式(Diode-Clamped )、飞跨电容嵌位式(Flying-Capacitors )。
为了更好地利用这项技术,许多研究人员提出了一些改进:在拓扑的研究方面,改进的主要方向是减少器件使用数量,并解决电容电压的不平衡等问题;在控制方面,改进的主要方向是优化输出波形和算法等[1](p5-13)。
1多电平逆变器种类及优缺点分析1.1二极管箝位式多电平逆变器及其优缺点二极管钳位式多电平逆变器是研究最早和应用最多的一种多电平逆变器。
二极管钳位式多电平逆变器是通过串连的一系列电容将较高电压分成一系列较低的电压。
一个M 电平的二极管钳位多电平逆变器在直流侧需要M-1个电容。
例如一个三相五电平二极管钳位式逆变器的一相,在其直流侧含有4个大小相同的电容C 1,C 2,C 3和C 4。
若直流侧的总电压为1V ,那么每个电容上分得的电压为V/4,并且通过钳位二极管的作用,每个开关器件上的电压应就限制在一个电容的电压V/4上,这样逆变器合成的输出电压就可以相对地提高了。
二极管钳位多电平逆变器只需要一个公共的直流电源,这使它的整流侧设计比较简单。
虽然开关器件被钳位在V/4电压上,但是钳位二极管却要承受不同倍数的V/4反向电压。
多电平电压源逆变器控制策略研究
式中b 为 :
b 一÷ [ on l Vcs a 十 … 十J cs a十 - sa 十2 o nz Vc V o n,
多 电平变换器 是通过 多个 直流 电平来合成逼 近 正 弦输 出的阶梯 波 电压 , 这种 变换 器用 容 量小 的器 件 输 出大 容量 、 高质 量 的电能 , 因此得 到越来越广泛
的应 用 。多 电平变换 器 拓 扑结 构种 类较 多 , 涌现 也 出多 种控制策 略和 方法 , 文介 绍 多 电平变 换器 的 本
墨 Q ! 墨 :!
CN 21 2 / 2 — 3 3 N
多 电平 电压 源逆 变 器控 制策略 研 究
侯 丽 华 , 爽 昕 王 晓 曦 刘 ,
(. 1 长春工程学 院教务处 , 长春 1 0 1 ; . 3 0 2 2 大连理 工大学 电子信 息与 电气 工程学 部 , 大连 1 6 2 ) 1 0 3
2 当 和 。 ; 导通 , 和 。 断时 , O 电位差 关 U 间
为0 。该 电路 特点 是 被 V 和 V D D 两 只二 极 管箝
制 开 关 电压 为 直 流 侧 电 压 的 一 半 , 3个 输 出 、 2 0 一 / 。用 与三 电平 电路 类 似 的方 2
, 儿 f
…
十n c sa] V o n
() 2
电源 哪一点相 连 , 作 状 态也 间 接 地反 映 了逆 变器 工
输 出端 的 电位 状 态 , 0表 示 一 / 1表 示 0电 位 , 2, 2
收 稿 日期 :O O 7 O 2 1 —O —2 基 金项 目 : 林 省教 育 厅 科研 计 划 项 目(0 0 1 ) 吉 2 1 44 作 者 简介 : 丽华 (9 6 )女 ( ) 吉林 伊 通 , 授 侯 16 一 , 满 , 教
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多电平逆变器主要控制策略综述( 本站提供应用行业:阅读次数:1082) 【字体:大中小】1 引言多电平逆变器具有谐波小、共模电压小、电压变化率小、电磁干扰小、开关频率低、系统效率高、适合中高压大容量变频器应用等特点,近十年得到广泛的研究[1]。
研究主要集中在拓扑结构、控制策略两方面。
图1是多电平逆变器的主要研究内容。
图1 多电平逆变器主要研究内容由于多电平逆变器拓扑结构的多样性,且涉及到直流电压的均衡、开关频率的合理分配、冗余状态的利用等特殊要求,使得对多电平逆变器的控制具有一定的挑战性。
2 载波调制方法(Carrier-based Modulation)载波调制是最常用的多电平控制方法之一,其特点是通过载波和调制波(或参考波)间的比较而获得器件的开关状态。
载波调制按其采样方法可分为:自然采样和规则采样,自然采样一般用于模拟电路实现,规则采样用于数字实现。
规则采样又分对称和不对称采样。
在载波调制中,对于m电平逆变器,常定义幅度调制比ma和频率调制比mf分别为:其中Ac为载波峰峰值,fc为载波频率,Am为调制波峰值,fm为调制波频率。
多电平载波调制由于载波个数的增加,而变得较复杂,但也给控制提供了更多的自由度。
2.1 子谐波脉宽调制SHPWM(SubHarmonic PWM)由Carrara[2]提出的SHPWM的基本原理是:对m电平逆变器,将m-1个具有相同频率fc和峰峰值Ac的三角载波集连续分布。
频率为fm、幅值为Am的正弦调制波置于载波集的中间。
将调制波与各载波信号进行比较,得到逆变器的开关状态。
在载波间的相位关系方面,Carrara考虑了三种典型配置方案:(1) PD—所有载波具有相同相位;(2) POD—正、负载波间相位相反;(3) APOD—相邻载波间相位相反。
图2是SHPWM采用PD配置的波形图。
SHPWM的最大线性幅度调制比ma为1。
对SHPWM的研究有如下一些重要结论[3]:·对于三相系统,频率比mf应为取3的倍数;·单相逆变器,APOD配置电压谐波最小;·三相逆变器,PD配置线电压谐波最小。
图2 5电平SHPWM-PD波形(ma=0.9,mf=21)2.2 开关频率最优脉宽调制SFOPWM(Switching Frequency Optimal PWM)由Steinke[4]提出的SFOPWM与SHPWM基本原理相同,只是前者在三相正弦调制波中叠加了一定的零序电压(三次谐波电压)。
设三相均衡参考电压分别为va,vb,vc,叠加零序电压vn,后三相参考电压分别为varef,vbrdf,vcref,具体叠加方法为:图3是采用SFOPWM的波形图,其中包括零序电压vn的波形。
SFOPWM只适用于三相逆变器,其优点是可以提高线性调制范围,其最大线性幅度调制比ma可以达到1.15,比SHPWM提高15%。
图3 5电平SFOPWM波形(ma=0.9,mf=21)2.3 载波相移脉宽调制CPSPWM(Carrier Phase Shifting PWM)CPSPWM[5]的基本原理是:多电平逆变器的各单元模块均采用低开关频率的单相SPWM,各单元模块具有相同的幅度调制比、频率调制比,但各单元模块的载波间存在一定的相位差θc,逆变器的总输出为各单元模块输出的线性叠加,使其等效开关频率提高。
各单元模块调制方法可以采用单极性、双极性、单极倍频SPWM调制,研究表明[6],单元模块采用单极倍频SPWM调制时,可获得最小谐波输出电压,这时单元模块两臂的调制信号相位相反,且载波间相位差θc=π/n(n为级联单元数)。
图4为单元模块采用单极倍频SPWM调制时CPSPWM的波形。
理论分析和实验结果表明[3],在总开关频率相同的条件下,CPSPWM与SHPWM的APOD配置方案具有相似的性能。
图4 5电平单极倍频CPSPWM波形(ma=0.9,mf=6)2.4 其它载波调制方法在SHPWM中,不同载波对应单元的开关频率不等,且随幅度调制比的改变而不同。
在考虑载波间相位关系时,Carrara只考虑了三种典型的配置方案。
Tolbert[7]对载波间相位关系对各单元开关频率的影响进行了全面的研究,并提出了一种使各单元开关频率相等、不同载波的频率不等且随幅度调制比ma而变化的载波调制方法。
载波调制可得到谐波含量较小的输出电压, 但不能消除共模电压。
Zhang[8]提出了一种利用中间变量消除共模电压的载波调制方法, 但其最大线性幅度调制比ma只能达到0.87。
从控制自由度[9]的角度来看,多电平载波调制方法的变化很多。
在载波方面,存在载波类型、幅值、频率、相位、偏移量以及载波间相位关系等自由度;在调制波方面,也存在调制波类型、幅值、频率、是否叠加零序分量以及多相系统中调制波间的相位关系等自由度;还有载波和调制波相互间的相位等自由度。
通过这些自由度的选择可以产生各种适合于特定拓扑结构、实现特定控制目标的载波调制方法。
例如,Hammond[10]采用故障单元旁路和中性点平移技术,可以采用不对称三相载波调制实现。
3 空间矢量调制SVM(Space Vector Modulation)空间矢量调制具有线性调制范围宽,直流电压利用率高,无须大量的存储空间,结构简单,控制方便,易于数字实现等优点,所以得到广泛的研究和应用。
多电平SVM和两电平SVM一样,是一种基于矢量合成调制方法。
如图5所示,在V1,V2,V3三角形中的任意矢量V0均可由矢量V1,V2,V3根据电压伏秒等效原则合成。
即:图5 空间矢量合成基础SVM算法一般由:(1)将参考矢量在选定坐标系中投影;(2)投影分量的取整处理;(3)邻近矢量识别及开通比计算;(4)开关状态映射等四步构成。
m电平逆变器,共有m3个开关状态,3m(m-1)+1个基本矢量,随电平数m的增加,常规SVM算法的计算量会急剧增加,因此,快速算法是多电平SVM的研究重点之一。
目前,已经提出一些有效的快速算法[11]~[14],这些算法的关键在于选择一个特殊坐标系,使得SVM的上述四步在该坐标系得到简化。
SVM算法中常用的坐标系统有如下几种。
3.1 线电压坐标系分析图5所示的矢量合成,可以得到如下关系[11]:式(5)中,Aijk为ViVjVk三角形的面积,di→jk为Vi到VjVk直线距离。
上式最后一步说明,如果三个矢量V1V2V3为等边三角形,且边长为,则合成矢量V0时每个矢量的开通比就等于V0到另外两个矢量连线的距离。
选择如图6所示的ab、bc和ca为参考坐标系[11],该坐标系的特点是所有小三角形的边都垂直于三个坐标轴中的一个。
在多数应用中,参考矢量通常是在dqo坐标系内给出,如果dqo坐标系也按图6选取,即d轴和ab轴重合,则算法将进一步简化,其SVM算法在表1中给出。
3.2 六边形坐标系如果选择图6中的g、h为参考坐标系[12][13],则称为六边形坐标系。
该坐标系的特点是所有小三角形均有两条边平行于坐标轴,因此问题同样可以得到简化,其具体算法同样在表1中给出。
图6 空间矢量调制用坐标系统表1 两种坐标系统中的空间矢量调制算法3.3 扁平坐标系Prats[14]提出了一种扁平坐标系,在该坐标系中,同样可以避免复杂三角函数的计算,而由简单的逻辑判断和加减运算实现SVM算法。
Rodriguez[15]提出了空间矢量控制(SVC)方法,它不采用矢量合成技术,而是直接采用与参考矢量最接近的基本矢量代替,该方法只适用于电平级数较多的拓扑结构中。
多电平逆变器中输出同一基本矢量的开关状态存在冗余,前面提到的SVM算法中的第4步,只给出了所有的冗余状态,并没有解决状态选择及状态顺序问题。
Zhang[8]从消除共模电压角度,McGrath[16]从降低开关频率和减小谐波角度分别研究了这些问题。
Wei[17]研究了单元故障情况下的SVM方法。
Li[18]将5电平SVM分解为两个3电平SVM,并利用移相方法实现谐波的消除。
Kang[19]提出了基于载波的SVM方法,并研究了如何利用冗余状态降低开关频率。
研究表明[16],适当的选择空间矢量的开关顺序,SVM和SFOPWM 的PD配置方案具有相似的性能。
4 波形逼近方法(waveform approximation modulation)波形逼近方法是利用一系列宽度可调的正负脉冲按照某种优化准则进行叠加,逼近参考波方法。
常用的优化准则有:(1) 选择性谐波消除;(2) 总谐波失真最小;(3) 总谐波电流最小等。
其中选择性谐波消除最为常用,对应的方法常称为选择性谐波消除脉宽调制SHEPWM。
根据叠加方式的不同,波形逼近方法主要有如下几种。
4.1 阶梯波形脉宽调制图7是由k对正负脉冲按阶梯波形逼近方法合成的(2k+1)电平逆变器的输出波形,由于波形的对称性,输出电压中不含偶次谐波分量,奇次谐波的幅值hn为:图7 (2k+1)电平逆变器阶梯调制输出波形式中,n为谐波次数,α1,α2,…,αk为对应脉冲的开关角。
从图7可知,α1,α2,…,αk必须满足条件0<α1,α2,…,αk<π/2。
为了获得最小的谐波失真,同时使得基波幅值可调,可以通过选择α1,α2,…,αk消除最多(k-1)个谐波分量。
通常选择消除次数最低的(k-1)个谐波,因为高次谐波相对比较容易采用附加滤波电路消除。
对于三相无中线系统,由于不会产生零序电流,因此可以不用消除三的倍数次谐波。
4.2 分区逼近方法阶梯波调制的开关角必须满足0<α1,α2,…,αk<π/2,否则该方法不存在,因此其调制范围通常较窄。
Sirisukprasert[20]提出了一种提高调制范围的方法,其基本思想是:由k对脉冲波合成的输出,可将其调制范围分为k个区间,在不同的区间采用不同的波形叠加方式。
图8是k=3时,在不同调制区合成的输出波形的正半波。
该方法输出波形的各奇次谐波的一般表达式为:图8 7电平逆变器不同调制系数下正半周期波形其中,正号表示对应开关角产生上升沿,负号表示对应开关角产生下降沿。
4.3 虚拟级数脉宽调制VSPWM(Virtual Stage PWM)上面两种方法的开关频率都是基波频率,能消除的谐波个数受逆变器电平级数的限制。
为了消除更多次数的谐波,提出了一种更一般的波形叠加方法[21]。
由k个直流电压相等的H桥构成的逆变器,其输出可以由p个正脉冲和q个负脉冲合成(p-q=k),如图9所示。
该方法输出波形的各奇次谐波的一般表达式为:VSPWM可通过选择正、负脉冲的个数,消除更多的谐波,不受逆变器电平数的限制,但开关频率也提高。
图9 VSPWM正半波输出波形(k=2,p=4,n=2)无论采用上述何种方法,必须事先通过求解一组超越方程,确定切换角等,应用时采用查表或和插值等方法获得开关切换时间。
