2020届高考数学总复习第四章三角函数、解三角形 4-7 解三角形的应用举例课时作业文(含解析)新人教A版

合集下载

第4章第四章三角函数、解三角形第4节二倍角公式及应用课件(共35张PPT) 高考数学一轮复习

内容索引
＝12－co2s2α＋12＋14cos2α－ 43sin2α＋ 43sin2α－12sin2α＝1－14cos2α－12 sin2α
＝1－14(1－2sin2α)－12sin2α＝34.
内容索引
思考1►►► 如何利用二倍角公式进行三角函数式的化简及恒等式的证明？要注意什么？
内容索引
要充分观察角与角之间的联系，看角是否有倍数关系？能否用二倍角公式化简？有切有弦要弦切互化．
sin15°cos15°＝12sin30°＝14，故 D 不正确．
【答案】 C
内容索引
2. 已知角α的顶点为坐标原点，始边与x轴的非负半轴重合，且
P(8,3cosα)为α终边上一点，则cos2α等于( )
A. －79
B. －89
7
8
C. 9
D. 9
【分析】根据三角函数定义和同角三角函数关系求出sinα，再由二
＝cos2αcsoinsαα2cosα2＝cosαsinα2cosα2＝12sinαcosα＝14sin2α＝右边，所以原式成立．
内容索引
某同学在一次研究性学习中发现，以下四个式子的值都等于同一个常数：
①sin212°＋cos242°＋sin12°cos42°； ②sin215°＋cos245°＋sin15°cos45°； ③sin220°＋cos250°＋sin20°cos50°； ④sin230°＋cos260°＋sin30°cos60°. (1) 试从上述式子中选择一个，求出这个常数； (2) 根据(1)的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．
倍角公式可求cos2α.
内容索引
【解析】由三角函数定义可知 tanα＝3c8osα＝csoinsαα，则 3cos2α＝8sinα ＝3－3sin2α，解得 sinα＝13或 sinα＝－3(舍去)，则 cos2α＝1－2sin2α＝79.

高中数学知识点总结(第四章三角函数、解三角形第八节解三角形的实际应用)

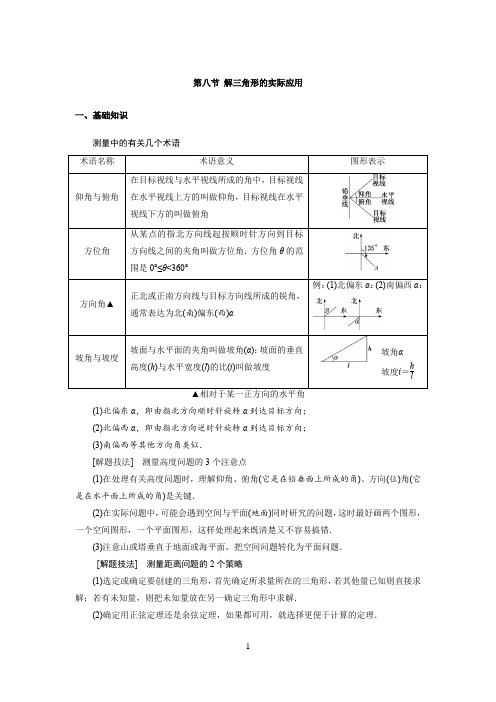
第八节解三角形的实际应用一、基础知识测量中的有关几个术语术语名称术语意义图形表示仰角与俯角在目标视线与水平视线所成的角中，目标视线在水平视线上方的叫做仰角，目标视线在水平视线下方的叫做俯角方位角从某点的指北方向线起按顺时针方向到目标方向线之间的夹角叫做方位角．方位角θ的范围是0°≤θ<360°方向角▲正北或正南方向线与目标方向线所成的锐角，通常表达为北(南)偏东(西)α例：(1)北偏东α：(2)南偏西α：坡角与坡度坡面与水平面的夹角叫做坡角(α)；坡面的垂直高度(h)与水平宽度(l)的比(i)叫做坡度坡角α坡度i＝hl(1)北偏东α，即由指北方向顺时针旋转α到达目标方向；(2)北偏西α，即由指北方向逆时针旋转α到达目标方向；(3)南偏西等其他方向角类似．[解题技法]测量高度问题的3个注意点(1)在处理有关高度问题时，理解仰角、俯角(它是在铅垂面上所成的角)、方向(位)角(它是在水平面上所成的角)是关键．(2)在实际问题中，可能会遇到空间与平面(地面)同时研究的问题，这时最好画两个图形，一个空间图形，一个平面图形，这样处理起来既清楚又不容易搞错．(3)注意山或塔垂直于地面或海平面，把空间问题转化为平面问题．[解题技法]测量距离问题的2个策略(1)选定或确定要创建的三角形，首先确定所求量所在的三角形，若其他量已知则直接求解；若有未知量，则把未知量放在另一确定三角形中求解．(2)确定用正弦定理还是余弦定理，如果都可用，就选择更便于计算的定理．[解题技法]测量角度问题的基本思路测量角度问题的关键是在弄清题意的基础上，画出表示实际问题的图形，并在图形中标出有关的角和距离，再用正弦定理或余弦定理解三角形，最后将解得的结果转化为实际问题的解．。

2025年高考数学总复习课件36第四章第七节解三角形应用举例

必备知识
落实“四基”
自查自测
知识点测量中的几个有关术语
1．判断下列说法的正误，正确的画“√”，错误的画“×”．
(1)东南方向与南偏东45˚方向相同．( √ ) (2)方位角与方向角其实质是一样的，均是确定观察点与目标点之间的位置关
系．( √ ) (3)从A处望B处的仰角为α，从B处望A处的俯角为β，则α，β的关系为α＋β＝
在△ACM中，由正弦定理得sinA6C0˚＝siAnM45˚，所以AC＝siAnM45˚·sin 60˚，
所以BC＝AC·sin 60˚＝siAnM45˚·sin260˚＝1002 2 × 34＝150(m)．
2
第七节解三角形应用举例
必备知识落实“四基”
核心考点提升“四能”
课时质量评价
测量高度问题的求解策略 (1)理解仰角、俯角、方向(位)角是关键． (2)在实际问题中，若遇到空间与平面(地面)同时研究的问题，最好画两个图形，一个空间图形，一个平面图形． (3)注意山或塔垂直于地面或海平面，把空间问题转化为平面问题．
(2)若b2＋c2＝8，求b，c. 解：(方法一)在△ABD与△ACD中，
必备知识落实“四基”
核心考点提升“四能”
课时质量评价
c2=
由余弦定理得൞
b2=
1 4 1 4
a2+1－2×
1 2
a2
+1－2×
1 2
a×1× cos a×1× cos
π－∠ADC ∠ADC，
，
整理得12a2＋2＝b2＋c2，而b2＋c2＝8，则a＝2 3.
△ABC中，若AD是边BC上的中线，则AB2＋AC2＝2(BD2＋AD2)，AD2＝14(b2＋c2

2020版高考数学大一轮复习第四章三角函数、解三角形第8讲解三角形的应用举例课件文

【解析】由题可得，在△ABC 中， AB2＝AC2＋BC2－2AC·BCcos ∠ACB，所以 AB2＝4002＋6002－2×400×600cos 60°＝280 000. 所以 AB＝200 7 m．即 A，B 两点间的距离为 200 7 m.
【答案】 200 7
角度三两点间可视但有一点不可到达如图所示，A，B 两点在一条河的两
在某次测量中，在 A 处测得同一半平面方向的 B 点的仰角是
60°，C 点的俯角为 70°，则∠BAC 等于( )
A．10°
B．50°
C．120°
D．130°
答案：D
若点 A 在点 C 的北偏东 30°，点 B 在点 C 的南偏东 60°，且
．11.4 km C．6.5 km
B．6.6 km D．5.6 km
解析：选 B．因为 AB＝1 000×610＝530(km)．所以 BC＝sinAB45°·sin 30°＝3502(km)．所以航线离山顶 h＝3502×sin 75° ＝3502×sin(45°＋30°)≈11.4(km)．所以山高为 18－11.4＝6.6(km)．
[典例引领]
角度一两点都不可到达
如图，A，B 两点在河的同侧，且 A，
B 两点均不可到达，要测出 A，B 的距离，
测量者可以在河岸边选定两点 C，D，测
得 CD＝a，同时在 C，D 两点分别测得∠BCA＝α，∠ACD＝β，
∠CDB＝γ，∠BDA＝δ.在△ADC 和△BDC 中，由正弦定理分
别计算出 AC 和 BC，再在△ABC 中，应用余弦定理计算出 AB．
岸，测量者在 A 的同侧，且 B 点不可到达，要测出 A，B 的距离，其方法为：在 A 所在的岸边选定一点 C，可以测出 A，C 的距离 m，再借助仪器，测出∠ACB＝α，∠CAB＝β，在△ABC 中，运用正弦定理就可以

2024年高考数学总复习第四章三角函数与解三角形真题分类18解三角形

(1)求∠A；
(2)求 AC 边上的高．解：(1)在△ ABC 中，因为 cos B＝－17 ，
所以 sin B＝ 1－cos2B ＝473 .
由正弦定理，得
sinA＝a
sin b
B
＝
3 2
.
由题设知π2 <∠B<π，所以 0<∠A<π2 .
所以∠A＝π3 .
第12页
返回层目录
返回目录
真题分类18 解三角形
＝sin [π－(∠C＋∠BDC)]
＝sin (∠C＋∠BDC)
＝sin ∠C·cos ∠BDC＋cos ∠C·sin ∠BDC
＝45
×
2 2
＋35
×
2 2
＝7102
.
第8页
高考·数学
返回层目录返回目录
真题分类18 解三角形
高考·数学
4.(2016·课标全国Ⅱ，13,5分)△ABC的内角A，B，C的对边分别为a，b，c，若cos A＝
又 A，B，C 为锐角，则 sin A≠0.
故
sin
B＝
3 2
，所以 B＝π3
.
第10页
返回层目录返回目录
真题分类18 解三角形
高考·数学
(2)由 A＋B＋C＝π，得 C＝23π －A，
由△ ABC 是锐角三角形，得 A∈(π6 ，π2 ).
由
cos
C＝cos
2π (3
－A)＝－12
cos A＋
3 2
sin A，得
cos
A＋cos
B＋cos
C＝
3 2
sin A＋12
cos A＋12
＝sin (A＋π6

高三数学课件：第四章三角函数解三角形 4-7

(7)△ABC 为正三角形的充要条件是 A，B，C 成等差数列，且 a，b，c 成等比数列．
(8)在△ABC 中，最大内角的取值范围是3π，π，最小内角的取值范围是0，π3.
(9)在锐角△ABC 中，sinA>cosB，sinB>cosC，sinC>cosA 等．
第
四
三角函数解三角形
章
第七节
正弦定理和余弦定理
高考概览掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题.
吃透教材夯双基
填一填记一记厚积薄发
[知识梳理] 1．正弦定理和余弦定理
[温馨提示] (1)利用余弦定理求边长，实质是解一元二次方程，得到方程的根即边长，然后根据已知条件对方程的根进行取舍。如：若 a＝2 3，b＝ 6，A＝45°，则 c＝ 3＋3.
[答案] D
2．(2016·天津卷)在△ABC 中，若 AB＝ 13，BC＝3，∠C＝
120°，则 AC＝( )
A．1
B．2
C．3
D．4
[解析] 由余弦定理得 13＝9＋AC2＋3AC⇒AC＝1.故选 A.
[答案] A
3．在△ABC 中，B＝60°，b2＝ac，则三角形一定是( ) A．直角三角形 B．等边三角形 C．等腰直角三角形 D．钝角三角形
角度 2：余弦定理解三角形 (2016·山东卷)在△ABC 中，角 A，B，C 的对边分
别是 a，b，c.已知 b＝c，a2＝2b2(1－sinA)，则 A＝( )
3π
π
A. 4
B.3
π
π
C.4
D.6
[思路引导] 所给条件中边的关系多 → 考虑余弦定理
[解析] ∵b＝c，a2＝2b2(1－sinA)，∴2b2－a2＝2b2sinA.由余弦定理知 cosA＝b2＋2cb2c－a2＝2b22－b2 a2＝sinA.

超实用高考数学专题复习：第四章三角函数解三角形三角函数与解三角形热点问题

【尝试训练】 (2020·郑州质检)在△ABC 中，内角 A，B，C 的对边分别为 a，b，c，若向量 m＝2cos2C2 ，cos A－2 B，n＝58，cos A－2 B，m·n＝98. (1)求 tan Atan B 的值； (2)求c2a－bsai2n－Cb2的最小值. 解 (1)由题意可得 m·n＝54cos2C2＋cos2A－2 B＝98，即－58cos(A＋B)＋12cos(A－B)＝0，展开可得 cos Acos B＝9sin Asin B，
所以 f(x)的最小正周期 T＝22π＝π.
(2)由－π2＋2kπ≤2x－π3≤π2＋2kπ(k∈Z)，得－1π2＋kπ≤x≤51π2＋kπ(k∈Z). 设 A＝－4π，π4，B＝x－1π2＋kπ≤x≤51π2＋kπ，k∈Z，易知 A∩B＝－1π2，π4.
所以当 x∈－π4，π4时，f(x)在区间－1π2，π4上单调递增，在区间－π4，－1π2上单调递减.
6＋ 4
2 .
两角差正弦公式的应用
12′
[高考状元满分心得]
❶写全得步骤分：对于解题过程中得分点的步骤有则给分，无则没分，所以得分点
步骤一定要写全，如第(1)问中只要写出 0°<A<180°就有分，没写就扣 1 分，第(2)
问中 0°<C<120°也是如此.
❷写明得关键分：对于解题过程中的关键点，有则给分，无则没分，所以在答题时
教你如何审题——三角函数与平面向量
【例题】 (2020·湘赣十四校联考)已知向量 m＝(sin x，－1)，n＝( 3，cos x)，且函
数 f(x)＝m·n. (1)若 x∈0，2π，且 f(x)＝23，求 sin x 的值；
(2)在锐角三角形 ABC 中，内角 A，B，C 的对边分别为 a，b，c.若 a＝ 7，△ABC

高中数学高考25第四章三角函数、解三角形 4 7 解三角形的实际应用

A.10 km
B.10 3 km
C.10 5 km
√D.10 7 km
解析如图所示，由余弦定理可得AC2＝100＋400－2×10×20×cos 120°＝
700，
∴AC＝10 7.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
2.如图所示，在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°，向山顶前进100 m到达B处，又测得C对于山坡的斜度为45°，若CD＝50 m，山坡对于地平面的坡度为θ，则cos θ等于
平视线下方的叫做俯角
图形表示
从某点的指北方向线起按顺时针方向方位角到目标方向线之间的夹角叫做方位角.
方位角θ的范围是0°≤θ<360°
正北或正南方向线与目标方向线所成例：(1)北偏东α：方向角的锐角，通常表达为北(南)偏东
(西)α
(2)南偏西α：
坡角与坡比
坡面与水平面所成二面角的度数叫坡
3.一艘海轮从A处出发，以每小时40海里的速度沿南偏东40°的方向直线航行，
30分钟后到达B处，在C处有一座灯塔，海轮在A处观察灯塔，其方向是南偏
东70°，在B处观察灯塔，其方向是北偏东65°，那么B，C两点间的距离是
√A.10 2 海里
B.10 3 海里
解析如图所示，易知，
ቤተ መጻሕፍቲ ባይዱ
C.20 3 海里
D.20 2 海里
又∠PBC＝γ＝60°，
∴∠BPA＝90°－α－90°－γ＝γ－α＝30°，
∴在△PAB 中，sina30°＝sinPB15°，∴PB＝
6－ 2
2 a，
∴PQ＝PC＋CQ＝PB·sin γ＋asin β＝

高中数学高考20第四章三角函数、解三角形 4 3 三角函数的图象与性质

又 x∈0，π2，∴函数的单调递增区间为0，π6.
命题点2 根据单调性求参数
例 4 已知 ω>0，函数 f(x)＝sinωx＋π4在π2，π上单调递减，则 ω 的取值范围是 12，45 .
引申探究
本例中，若已知 ω>0，函数 f(x)＝cosωx＋π4在π2，π上单调递增，则 ω 的取值范围是 32，47 .
2 题型分类深度剖析
PART TWO
自主演练
题型一三角函数的定义域
1.函数 f(x)＝－2tan2x＋π6的定义域是
A.xx≠π6
B.xx≠－1π2
C.xx≠kπ＋π6k∈Z
√D.xx≠k2π＋π6k∈Z
解析由正切函数的定义域，得 2x＋π6≠kπ＋π2，k∈Z，即 x≠k2π＋π6(k∈Z)，
(3)函数
y＝12sin
x＋
3 2 cos
xx∈0，2π的单调递增区间是
0，π6
.
解析
∵y＝12sin
x＋
3 2 cos
x＝sinx＋π3，
由 2kπ－π2≤x＋π3≤2kπ＋π2(k∈Z)，
解得 2kπ－56π≤x≤2kπ＋π6(k∈Z).
∴函数的单调递增区间为2kπ－56π，2kπ＋π6(k∈Z)，
解析函数 y＝cos x 的单调递增区间为[－π＋2kπ，2kπ]，k∈Z，
则ωω2ππ＋＋4π4π≤≥2－kππ，＋2kπ，
k∈Z，解得 4k－52≤ω≤2k－14，k∈Z，
又由 4k－52－2k－14≤0，k∈Z 且 2k－14>0，k∈Z，
师生共研
题型三三角函数的周期性与对称性
例2 (1)若函数f(x)＝2tan kx＋π3 的最小正周期T满足1<T<2，则自然数k的值为 2或3 .

2024年高考数学总复习第四章《三角函数解三角形》任意角弧度制及任意角的三角函数

2024年高考数学总复习第四章《三角函数、解三角形》§4.1任意角、弧度制及任意角的三角函数最新考纲1.了解任意角的概念和弧度制，能进行弧度与角度的互化.2.借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义．1．角的概念(1)任意角：①定义：角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形；②分类：角按旋转方向分为正角、负角和零角．(2)所有与角α终边相同的角，连同角α在内，构成的角的集合是S ＝{β|β＝k ·360°＋α，k ∈Z }．(3)象限角：使角的顶点与原点重合，角的始边与x 轴的非负半轴重合，那么，角的终边在第几象限，就说这个角是第几象限角；如果角的终边在坐标轴上，就认为这个角不属于任何一个象限．2．弧度制(1)定义：把长度等于半径长的弧所对的圆心角叫做1弧度的角，用符号rad 表示，读作弧度．正角的弧度数是一个正数，负角的弧度数是一个负数，零角的弧度数是0.(2)角度制和弧度制的互化：180°＝πrad,1°＝π180rad ，1rad(3)扇形的弧长公式：l ＝|α|·r ，扇形的面积公式：S ＝12lr ＝12|α|·r 2.3．任意角的三角函数任意角α的终边与单位圆交于点P (x ，y )时，则sin α＝y ，cos α＝x ，tan α＝yx (x ≠0)．三个三角函数的性质如下表：三角函数定义域第一象限符号第二象限符号第三象限符号第四象限符号sin αR＋＋－－cos αR＋－－＋tan α{α|α≠k π＋π2，k ∈Z }＋－＋－4.三角函数线如下图，设角α的终边与单位圆交于点P ，过P 作PM ⊥x 轴，垂足为M ，过A (1,0)作单位圆的切线与α的终边或终边的反向延长线相交于点T .三角函数线有向线段MP 为正弦线；有向线段OM 为余弦线；有向线段AT 为正切线概念方法微思考1．总结一下三角函数值在各象限的符号规律．提示一全正、二正弦、三正切、四余弦．2．三角函数坐标法定义中，若取点P (x ，y )是角α终边上异于顶点的任一点，怎样定义角α的三角函数？提示设点P 到原点O 的距离为r ，则sin α＝y r ，cos α＝x r ，tan α＝yx(x ≠0)．题组一思考辨析1．判断下列结论是否正确(请在括号中打“√”或“×”)(1)锐角是第一象限的角，第一象限的角也都是锐角．(×)(2)角α的三角函数值与其终边上点P 的位置无关．(√)(3)不相等的角终边一定不相同．(×)(4)若α为第一象限角，则sin α＋cos α>1.(√)题组二教材改编2．角－225°＝弧度，这个角在第象限．答案－5π4二3．若角α的终边经过点－22，sin α＝，cos α＝.答案22－224．一条弦的长等于半径，这条弦所对的圆心角大小为弧度．答案π3题组三易错自纠5|k π＋π4≤α≤k π＋π2，k ∈Z(阴影部分)是()答案C解析当k ＝2n (n ∈Z )时，2n π＋π4≤α≤2n π＋π2，此时α表示的范围与π4≤α≤π2表示的范围一样；当k ＝2n ＋1(n ∈Z )时，2n π＋π＋π4≤α≤2n π＋π＋π2，此时α表示的范围与π＋π4≤α≤π＋π2表示的范围一样，故选C.6．已知点Pθ的终边上，且θ∈[0,2π)，则θ的值为()A.5π6B.2π3C.11π6D.5π3答案C解析因为点P所以根据三角函数的定义可知tan θ＝－1232＝－33，又θθ＝11π6.7．在0到2π范围内，与角－4π3终边相同的角是．答案2π3解析与角－4π3终边相同的角是2k πk ∈Z )，令k ＝1，可得与角－4π3终边相同的角是2π3.8．(2018·济宁模拟)函数y ＝2cos x －1的定义域为．答案2k π－π3，2k π＋π3(k ∈Z )解析∵2cos x －1≥0，∴cos x ≥12.由三角函数线画出x 满足条件的终边范围(如图阴影部分所示)，∴x ∈2k π－π3，2k π＋π3(k ∈Z )．题型一角及其表示1．下列与角9π4的终边相同的角的表达式中正确的是()A ．2k π＋45°(k ∈Z )B ．k ·360°＋9π4(k ∈Z )C ．k ·360°－315°(k ∈Z )D ．k π＋5π4(k ∈Z )答案C解析与角9π4的终边相同的角可以写成2k π＋9π4(k ∈Z )，但是角度制与弧度制不能混用，所以只有答案C 正确．2．设集合M |x ＝k2·180°＋45°，k ∈ZN |x ＝k4·180°＋45°，k ∈Z()A ．M ＝NB ．M ⊆NC ．N ⊆MD ．M ∩N ＝∅答案B解析由于M 中，x ＝k2·180°＋45°＝k ·90°＋45°＝(2k ＋1)·45°，2k ＋1是奇数；而N 中，x ＝k4·180°＋45°＝k ·45°＋45°＝(k ＋1)·45°，k ＋1是整数，因此必有M ⊆N ，故选B.3．(2018·宁夏质检)终边在直线y ＝3x 上，且在[－2π，2π)内的角α的集合为．答案－53π，－23π，π3，43π解析如图，在坐标系中画出直线y ＝3x ，可以发现它与x 轴的夹角是π3，在[0,2π)内，终边在直线y ＝3x 上的角有两个：π3，43π；在[－2π，0)内满足条件的角有两个：－23π，－53π，故满足条件的角α构成的集合为－53，－23π，π3，43π4．若角α是第二象限角，则α2是第象限角．答案一或三解析∵α是第二象限角，∴π2＋2k π<α<π＋2k π，k ∈Z ，∴π4＋k π<α2<π2＋k π，k ∈Z .当k 为偶数时，α2是第一象限角；当k 为奇数时，α2是第三象限角．综上，α2是第一或第三象限角．思维升华(1)利用终边相同的角的集合可以求适合某些条件的角，方法是先写出与这个角的终边相同的所有角的集合，然后通过对集合中的参数k (k ∈Z )赋值来求得所需的角．(2)确定kα，αkk ∈N *)的终边位置的方法先写出kα或αk 的范围，然后根据k 的可能取值确定kα或αk的终边所在位置．题型二弧度制及其应用例1已知一扇形的圆心角为α，半径为R ，弧长为l .若α＝π3，R ＝10cm ，求扇形的面积．解由已知得α＝π3，R ＝10cm ，∴S 扇形＝12α·R 2＝12·π3·102＝50π3(cm 2)．引申探究1．若例题条件不变，求扇形的弧长及该弧所在弓形的面积．解l ＝α·R ＝π3×10＝10π3(cm)，S 弓形＝S 扇形－S 三角形＝12·l ·R －12·R 2·sin π3＝12·10π3·10－12·102·32＝50π－7533(cm 2)．2．若例题条件改为：“若扇形周长为20cm ”，当扇形的圆心角α为多少弧度时，这个扇形的面积最大？解由已知得，l ＋2R ＝20，则l ＝20－2R (0<R <10)．所以S ＝12lR ＝12(20－2R )R ＝10R －R 2＝－(R －5)2＋25，所以当R ＝5cm 时，S 取得最大值25cm 2，此时l ＝10cm ，α＝2rad.思维升华应用弧度制解决问题的方法(1)利用扇形的弧长和面积公式解题时，要注意角的单位必须是弧度．(2)求扇形面积最大值的问题时，常转化为二次函数的最值问题．(3)在解决弧长问题和扇形面积问题时，要合理地利用圆心角所在的三角形．跟踪训练1(1)(2018·湖北七校联考)若圆弧长度等于圆内接正三角形的边长，则其圆心角的弧度数为()A.π6B.π3C ．3D.3答案D解析如图，等边三角形ABC 是半径为r 的圆O 的内接三角形，则线段AB 所对的圆心角∠AOB ＝2π3，作OM ⊥AB ，垂足为M ，在Rt △AOM 中，AO ＝r ，∠AOM ＝π3，∴AM ＝32r ，AB ＝3r ，∴l ＝3r ，由弧长公式得α＝l r ＝3rr＝ 3.(2)一扇形是从一个圆中剪下的一部分，半径等于圆半径的23，面积等于圆面积的527，则扇形的弧长与圆周长之比为．答案518解析设圆的半径为r ，则扇形的半径为2r3，记扇形的圆心角为α，由扇形面积等于圆面积的527，可得12α2r 3πr 2＝527，解得α＝5π6.所以扇形的弧长与圆周长之比为l C ＝5π6·2r 32πr ＝518.题型三三角函数的概念命题点1三角函数定义的应用例2(1)(2018·青岛模拟)已知角α的终边与单位圆的交点为－12，sin α·tan α等于()A ．－33B ．±33C ．－32D ．±32答案C解析由OP 2＝14＋y 2＝1，得y 2＝34，y ＝±32.当y ＝32时，sin α＝32，tan α＝－3，此时，sin α·tan α＝－32.当y ＝－32时，sin α＝－32，tan α＝3，此时，sin α·tan α＝－32.所以sin α·tan α＝－32.(2)设θ是第三象限角，且|cosθ2|＝－cos θ2，则θ2是()A ．第一象限角B ．第二象限角C ．第三象限角D ．第四象限角答案B解析由θ是第三象限角知，θ2为第二或第四象限角，∵|cos θ2|＝－cos θ2，∴cos θ2<0，综上可知，θ2为第二象限角．命题点2三角函数线例3(1)满足cos α≤－12的角的集合是．答案|2k π＋23π≤α≤2k π＋43π，k ∈Z 解析作直线x ＝－12交单位圆于C ，D 两点，连接OC ，OD ，则OC 与OD 围成的区域(图中阴影部分)即为角α终边的范围，故满足条件的角α的集合为|2k π＋23π≤α≤2k π＋43π，k ∈Z(2)若－3π4<α<－π2，从单位圆中的三角函数线观察sin α，cos α，tan α的大小关系是．答案sin α<cos α<tan α解析如图，作出角α的正弦线MP ，余弦线OM ，正切线AT ，观察可知sin α<cos α<tan α.思维升华(1)利用三角函数的定义，已知角α终边上一点P 的坐标可求α的三角函数值；已知角α的三角函数值，也可以求出点P 的坐标．(2)利用三角函数线解不等式要注意边界角的取舍，结合三角函数的周期性写出角的范围．跟踪训练2(1)(2018·济南模拟)已知角α的终边经过点(m ，－2m )，其中m ≠0，则sin α＋cosα等于()A ．－55B ．±55C ．－35D ．±35答案B解析∵角α的终边经过点(m ，－2m )，其中m ≠0，∴m >0时，sin α＝－2m 5m ＝－25cos α＝m 5m ＝15，∴sin α＋cos α＝－55；m <0时，sin α＝－2m －5m ＝25，cos α＝m －5m ＝－15，∴sin α＋cos α＝55；∴sin α＋cos α＝±55，故选B.(2)在(0,2π)内，使得sin x >cos x 成立的x 的取值范围是()答案C解析当x ∈π2，sin x >0，cos x ≤0，显然sin x >cos x 成立；当x ，π4时，如图，OA 为x 的终边，此时sin x ＝|MA |，cos x ＝|OM |，sin x ≤cos x ；当xOB 为x 的终边，此时sin x ＝|NB |，cos x ＝|ON |，sin x >cos x ．同理当x ∈πsin x >cosx ；当x ∈5π4，sin x ≤cos x ，故选C.1．下列说法中正确的是()A ．第一象限角一定不是负角B ．不相等的角，它们的终边必不相同C ．钝角一定是第二象限角D ．终边与始边均相同的两个角一定相等答案C解析因为－330°＝－360°＋30°，所以－330°角是第一象限角，且是负角，所以A 错误；同理－330°角和30°角不相等，但它们终边相同，所以B 错误；因为钝角的取值范围为(90°，180°)，所以C 正确；0°角和360°角的终边与始边均相同，但它们不相等，所以D 错误．2．已知扇形的周长是6，面积是2，则扇形的圆心角的弧度数是()A ．1B ．4C ．1或4D ．2或4答案C解析设扇形的半径为r ，弧长为l ，＋l ＝6，＝2，＝1，4＝2，2.从而α＝l r ＝41＝4或α＝l r ＝22＝1.3．(2018·石家庄调研)已知角θ的终边经过点P (4，m )，且sin θ＝35，则m 等于()A ．－3B ．3C.163D ．±3答案B 解析sin θ＝m16＋m 2＝35，且m >0，解得m ＝3.4．点P 从(1,0)出发，沿单位圆逆时针方向运动2π3弧长到达Q 点，则Q 点的坐标为()－12，－32，－－12，－－32，答案A解析点P 旋转的弧度数也为2π3，由三角函数定义可知Q 点的坐标(x ，y )满足x ＝cos 2π3＝－12，y ＝sin 2π3＝32.5．若sin θ·cos θ>0，sin θ＋cos θ<0，则θ在()A ．第一象限B ．第二象限C ．第三象限D ．第四象限答案C解析∵sin θ·cos θ>0，∴sin θ>0，cos θ>0或sin θ<0，cos θ<0.当sin θ>0，cos θ>0时，θ为第一象限角，当sin θ<0，cos θ<0时，θ为第三象限角．∵sin θ＋cos θ<0，∴θ为第三象限角．故选C.6．sin 2·cos 3·tan 4的值()A ．小于0B ．大于0C ．等于0D ．不存在答案A解析∵sin 2>0，cos 3<0，tan 4>0，∴sin 2·cos 3·tan 4<0.7．已知角α的终边过点P (－8m ，－6sin 30°)，且cos α＝－45，则m 的值为()A ．－12B ．－32C.12D.32答案C解析由题意得点P (－8m ，－3)，r ＝64m 2＋9，所以cos α＝－8m64m 2＋9＝－45，解得m ＝±12，又cos α＝－45<0，所以－8m <0，即m >0，所以m ＝12.8．给出下列命题：①第二象限角大于第一象限角；②三角形的内角是第一象限角或第二象限角；③不论是用角度制还是用弧度制度量一个角，它们与扇形的半径的大小无关；④若sin α＝sin β，则α与β的终边相同；⑤若cos θ<0，则θ是第二或第三象限的角．其中正确命题的个数是()A ．1B ．2C ．3D ．4答案A解析举反例：第一象限角370°不小于第二象限角100°，故①错；当三角形的内角为90°时，其既不是第一象限角，也不是第二象限角，故②错；③正确；由于sinπ6＝sin 5π6，但π6与5π6的终边不相同，故④错；当cos θ＝－1，θ＝π时，其既不是第二象限角，也不是第三象限角，故⑤错．综上可知，只有③正确．9．若圆弧长度等于该圆内接正方形的边长，则其圆心角的弧度数是．答案2解析设圆半径为r ，则圆内接正方形的对角线长为2r ，∴正方形边长为2r ，∴圆心角的弧度数是2rr＝ 2.10．若角α的终边与直线y ＝3x 重合，且sin α<0，又P (m ，n )是角α终边上一点，且|OP |＝10，则m －n ＝.答案2解析由已知tan α＝3，∴n ＝3m ，又m 2＋n 2＝10，∴m 2＝1.又sin α<0，∴m ＝－1，n ＝－3.故m －n ＝2.11．已知角α的终边上一点P 2π3，cos α的最小正值为．答案11π6解析由题意知，点r ＝1，所以点P 在第四象限，根据三角函数的定义得cos α＝sin2π3＝32，故α＝2k π－π6(k ∈Z )，所以α的最小正值为11π6.12．函数y ＝sin x －32的定义域为．答案2k π＋π3，2k π＋23π，k ∈Z 解析利用三角函数线(如图)，由sin x ≥32，可知2k π＋π3≤x ≤2k π＋23π，k ∈Z .13．已知角α的终边在如图所示阴影表示的范围内(不包括边界)，则角α用集合可表示为．答案α|2k π＋π4<α<2k π＋56π，k ∈Z 解析∵在[0,2π)内，终边落在阴影部分角的集合为π4，56π∴α|2k π＋π4<α<2k π＋56π，k ∈Z14．若角α的终边落在直线y ＝3x 上，角β的终边与单位圆交于点12，m，且sin α·cos β<0，则cos α·sin β＝.答案±34解析由角β12，m cos β＝12sin α·cos β<0知，sin α<0，因为角α的终边落在直线y ＝3x 上，所以角α只能是第三象限角．记P 为角α的终边与单位圆的交点，设P (x ，y )(x <0，y <0)，则|OP |＝1(O 为坐标原点)，即x 2＋y 2＝1，又由y ＝3x 得x ＝－12，y ＝－32，所以cos α＝x ＝－12，因为点12，m 12＋m 2＝1，解得m ＝±32，所以sin β＝±32，所以cos α·sin β＝±34.15．《九章算术》是我国古代数学成就的杰出代表作，其中“方田”章给出了计算弧田面积时所用的经验公式，即弧田面积＝12×(弦×矢＋矢2)．弧田(如图1)由圆弧和其所对弦围成，公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差，现有圆心角为2π3，半径为3米的弧田，如图2所示．按照上述经验公式计算所得弧田面积大约是平方米．(结果保留整数，3≈1.73)答案5解析如题图2，由题意可得∠AOB ＝2π3，OA ＝3，所以在Rt △AOD 中，∠AOD ＝π3，∠DAO ＝π6，OD ＝12AO ＝12×3＝32，可得CD ＝3－32＝32，由AD ＝AO ·sin π3＝3×32＝332，可得AB ＝2AD ＝2×332＝3 3.所以弧田面积S ＝12(弦×矢＋矢2)＝12×33×32＋＝943＋98≈5(平方米)．16．如图，A ，B 是单位圆上的两个质点，点B 的坐标为(1,0)，∠BOA ＝60°.质点A 以1rad /s 的角速度按逆时针方向在单位圆上运动，质点B 以2rad/s 的角速度按顺时针方向在单位圆上运动．(1)求经过1s 后，∠BOA 的弧度；(2)求质点A ，B 在单位圆上第一次相遇所用的时间．解(1)经过1s 后，质点A 运动1rad ，质点B 运动2rad ，此时∠BOA 的弧度为π3＋3.(2)设经过t s 后质点A ，B 在单位圆上第一次相遇，则t (1＋2)＋π3＝2π，解得t ＝5π9，即经过5π9s后质点A ，B 在单位圆上第一次相遇．。

【北师大版】高三数学一轮复习：4-7解三角形的实际应用举例

－∠CAB＝180°－45°－105°＝30°，
则由正弦定理得sin∠ABACB＝sin∠ACCBA，
∴AB＝ACsi·nsi∠n∠CBAACB＝50×1
2 2 ＝50
2(m)．
2
答案：A
高三总复习 ·北师大版 ·数学（理）
进入导航
第四章第七节
系列丛书
4．要测量底部不能到达的电视塔AB的高度，在C点测得塔顶A的仰角是45°，在D点测得塔顶A的仰角是30°，并测得水平面上的∠BCD＝120°，CD＝40m，则电视塔的高度为( )
自主回顾·打基础突破考点·速通关
答题模板·提素能课时作业
高三总复习 ·北师大版 ·数学（理）
进入导航
第四章第七节
系列丛书
自主回顾·打基础01
夯实基础·厚积薄发
高三总复习 ·北师大版 ·数学（理）
进入导航
第四章第七节
系列丛书
1．用正弦定理和余弦定理解三角形的常见题型测量距离问题、高度问题、角度问题、计算面积问题、航海问题、物理问题等． 2．实际应用中的常用术语
解析：∵sin∠BAC＝sin(90°＋∠BAD)＝cos∠BAD＝
2 3
2，
∴BD2＝AB2＋AD2－2AB·ADcos∠BAD
＝18＋9－2×9 2×232＝3，∴BD＝ 3.
答案： 3
高三总复习 ·北师大版 ·数学（理）
进入导航
第四章第七节
系列丛书
突破考点·速通关02
互动探究·各个击破
范围是(________)
图形表示
高三总复习 ·北师大版 ·数学（理）
进入导航
第四章第七节
系列丛书
方向角

2020高考文科数学(人教A版)总复习课件：第四章三角函数、解三角形4.7

-11-
(设因2)△为由A正bB2+C弦c的2定-a外理2=接8及>圆条 0,所半件以径,得为cobscR+A,c则>b0=si,4��n0��a<��=bAs2i<Rnπ2,C,所因,所以为以sai=��ns��i��R��n��=��.��2=R2a, , 所以 sin A=12,A=30°,所以 cos A=��2+2��2��-��2 = √23,所以 bc=8√33, 所以 S△ABC=12bcsin A=2√33.
第四章
知识梳理考点自诊
4.7 解三角形
必必备备知知识识··预预案案自自诊诊
关键能力·学案突破
-6-
1.判断下列结论是否正确,正确的画“√”,错误的画“×”.
(1)在△ABC中,已知a,b和角B,能用正弦定理求角A;已知a,b和角C, 能用余弦定理求边c. ( √ )
(2)在三角形中,已知两角和一边或已知两边和一角都能解三角形. (√)
2.已知两边和它们的夹角、已知两边和一边的对角或已知三边都能直接运用余弦定理解三角形,在运用余弦定理时,要注意整体思想的运用.
3.已知两角和一边,该三角形是确定的,其解是唯一的;已知两边和一边的对角,该三角形具有不唯一性,通常根据三角函数值的“有界性”和“大边对大角”进行判断.
考点1
第四章
D.不确定
(2)设△ABC的内角A,B,C所对的边分别为a,b,c,若a2+b2-c2=ab,且
2cos Asin B=sin C,则△ABC的形状为等边三角形 .
解析: (1)由正弦定理得sin Bcos C+sin Ccos B=sin2A,

2020届高考数学一轮复习讲义第四章《三角函数、解三角形》

2020届高考数学一轮复习讲义第四章《三角函数、解三角形第一节任意角和弧度制及任意角的三角函数1．角的概念的推广(1)定义：角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形．(2)按旋转方向不同分为正角、负角、零角.按终边位置不同分为象限角和轴线角.(3)终边相同的角：所有与角α终边相同的角，连同角α在内，可构成一个集合S ＝{β|β＝α＋k ·360°，k ∈Z }．2．弧度制的定义和公式(1)定义：把长度等于半径长的弧所对的圆心角叫做1弧度的角，弧度记作rad.(2)公式：3.任意角的三角函数三角函数正弦余弦正切定义设α是一个任意角，它的终边与单位圆交于点P (x ，y )，那么y 叫做α的正弦，记作sin αx 叫做α的余弦，记作cos αyx 叫做α的正切，记作tan α各象限符号一＋＋＋二＋－－三－－＋四－＋－三角函数线有向线段MP 为正弦线有向线段OM 为余弦线有向线段AT 为正切线[小题体验]1．若θ是第二象限角，且满足sin θ2＜0，则θ2的终边在第________象限．答案：三2．若角α的终边过点sin5π6，tan α＝________.答案：－33．α为第一象限角，则sin α＋cos α________1.(填“＞”“＜”“＝”)答案：＞1．注意易混概念的区别：象限角、锐角、小于90°的角是概念不同的三类角．第一类是象限角，第二、第三类是区间角．2．角度制与弧度制可利用180°＝πrad 进行互化，在同一个式子中，采用的度量制度必须一致，不可混用．3．已知三角函数值的符号确定角的终边位置不要遗漏终边在坐标轴上的情况．4．三角函数的定义中，当P (x ，y )是单位圆上的点时有sin α＝y ，cos α＝x ，tan α＝yx ，但若不是单位圆时，如圆的半径为r ，则sin α＝y r ，cos α＝x r ，tan α＝yx.[小题纠偏]1．－1000°是第________象限角，α＝3是第________象限角，72°＝________rad.答案：一二2π52．如图所示，在直角坐标系xOy 中，射线OP 交单位圆O 于点P ，若∠AOP ＝θ，则点P 的坐标是____________．答案：(cos θ，sin θ)考点一角的集合表示及象限角的判定(基础送分型考点——自主练透)[题组练透]1.下列命题中，真命题是()A ．第一象限角是锐角B ．直角不是任何象限角C ．第二象限角比第一象限角大D ．三角形的内角一定是第一或第二象限角解析：选B390°是第一象限角，但不是锐角，A 错；135°是第二象限角，390°＞135°，C 错；直角不是任何象限角，D 错，B 对．2．若α＝k π－π4(k ∈Z )，则α在()A ．第一象限或第三象限B ．第一象限或第二象限C ．第二象限或第四象限D ．第三象限或第四象限解析：选C当k ＝2m ＋1(m ∈Z )时，α＝2m π＋3π4，所以α在第二象限；当k ＝2m (m ∈Z )时，α＝2m π－π4，所以α在第四象限．故选C.3．设集合M |x ＝k 2·180°＋45°，k N |x ＝k 4·180°＋45°，k 那么M ________N ．(填“＝”“⊆”“⊇”)解析：法一：由于M |x ＝k2·180°＋45°，k ∈＝{…，－45°，45°，135°，225°，…}，N |x ＝k4·180°＋45°，k ∈＝{…，－45°，0°，45°，90°，135°，180°，225°，…}，显然有M ⊆N .法二：由于M 中，x ＝k2·180°＋45°＝k ·90°＋45°＝(2k ＋1)·45°，2k ＋1是奇数；而N 中，x ＝k4·180°＋45°＝k ·45°＋45°＝(k ＋1)·45°，k ＋1是整数，因此必有M ⊆N .答案：⊆4．终边在直线y ＝3x 上的角的集合为__________________．解析：在坐标系中画出直线y ＝3x ，可以发现它与x 轴正半轴的夹角是π3，终边在直线y ＝3x |α＝k π＋π3，k ∈.答案|α＝k π＋π3，k 5．(2018·嘉兴七校联考)设角α是第三象限角，且满足|sinα2|＝－sin α2，则α2是第________象限角．解析：因为角α是第三象限角，所以2k π＋π＜α＜2k π＋3π2(k ∈Z )，所以k π＋π2＜α2＜k π＋3π4(k ∈Z )，所以α2是第二或第四象限角．又因为|sin α2|＝－sin α2，所以sin α2＜0，所以α2是第四象限角．答案：四[谨记通法]1．终边在某直线上角的求法4步骤(1)数形结合，在平面直角坐标系中画出该直线；(2)按逆时针方向写出[0,2π)内的角；(3)再由终边相同角的表示方法写出满足条件角的集合；(4)求并集化简集合．2．确定kα，αk (k ∈N *)的终边位置3步骤(1)用终边相同角的形式表示出角α的范围；(2)再写出kα或αk的范围；(3)然后根据k 的可能取值讨论确定kα或αk 的终边所在位置．考点二扇形的弧长及面积公式(基础送分型考点——自主练透)[题组练透]1．若一扇形的圆心角为72°，半径为20cm ，则扇形的面积为()A ．40πcm 2B ．80πcm 2C ．40cm 2D ．80cm 2解析：选B∵72°＝2π5，∴S 扇形＝12|α|r 2＝12×2π5×202＝80π(cm 2)．2．若扇形的圆心角是α＝120°，弦长AB ＝12cm ，则弧长l 等于()A.433πcm B.833πcm C.43cm D ．83cm解析：选B设扇形的半径为r cm ，如图．由sin 60°＝6r ，得r ＝43cm ，∴l ＝|α|·r ＝2π3×43＝833πcm.3．(2019·瑞安模拟)设扇形的周长为8，面积为4，则扇形的圆心角的弧度数为________．解析：＋l ＝8，＝4.＝2，4，所以扇形的圆心角的弧度数为|α|＝l r ＝42＝2.答案：24．若扇形的圆心角α＝60°，半径R ＝10cm ，求扇形的弧长l 及扇形的弧所在的弧形的面积．解：∵α＝60°＝π3，R ＝10cm ，∴l ＝Rα＝10×π3＝10π3cm.设弧形的面积为S ，则S ＝12R 2α－12R 2sin π3＝12×102×π3－12×102×32＝2.[谨记通法]弧度制下有关弧长、扇形面积问题的解题策略(1)明确弧度制下弧长公式l ＝|α|r ，扇形的面积公式是S ＝12lr ＝12|α|r 2(其中l 是扇形的弧长，α是扇形的圆心角)．(2)求扇形面积的关键是求得扇形的圆心角、半径、弧长三个量中的任意两个量．考点三三角函数的定义(题点多变型考点——多角探明)[锁定考向]任意角的三角函数(正弦、余弦、正切)的定义属于理解内容．在高考中多以选择题、填空题的形式出现．常见的命题角度有：(1)三角函数定义的应用；(2)三角函数值的符号判定．[题点全练]角度一：三角函数定义的应用1．已知角α的终边经过点P (－x ，－6)，且cos α＝－513，则1sin α＋1tan α＝________.解析：∵角α的终边经过点P (－x ，－6)，且cos α＝－513，∴cos α＝－xx 2＋36＝－513，即x ＝52或x ＝－52(舍去)，∴－52，－sin α＝－1213，∴tan α＝sin αcos α＝125，则1sin α＋1tan α＝－1312＋512＝－23.答案：－232．已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线y ＝2x 上，则cos 2θ＝________.解析：设P (t,2t )(t ≠0)为角θ终边上任意一点，则cos θ＝t 5|t |.当t ＞0时，cos θ＝55；当t ＜0时，cos θ＝－55.因此cos 2θ＝2cos 2θ－1＝25－1＝－35.答案：－35角度二：三角函数值的符号判定3．(2019·湖州六校联考)已知sin 2θ＜0，且|cos θ|＝－cos θ，则点P (tan θ，sin θ)在()A ．第一象限B ．第二象限C ．第三象限D ．第四象限解析：选B由|cos θ|＝－cos θ可知cos θ＜0，由sin 2θ＝2sin θcos θ＜0可知sinθ＞0，所以tan θ＜0.所以点P (tan θ，sin θ)在第二象限．4．已知点P (sin θcos θ，2cos θ)位于第三象限，则角θ是第________象限角．解析：因为点P (sin θcos θ，2cos θ)位于第三象限，所以sin θ·cos θ＜0,2cos θ＜0θ＞0，θ＜0，所以θ为第二象限角．答案：二[通法在握]定义法求三角函数的3种情况(1)已知角α终边上一点P 的坐标，可求角α的三角函数值．先求P 到原点的距离，再用三角函数的定义求解．(2)已知角α的某三角函数值，可求角α终边上一点P 的坐标中的参数值，可根据定义中的两个量列方程求参数值．(3)已知角α的终边所在的直线方程或角α的大小，根据三角函数的定义可求角α终边上某特定点的坐标．[演练冲关]1．已知角α的终边经过点(3，－4)，则sin α＋1cos α＝()A ．－15B.3715C.3720D.1315解析：选D ∵角α的终边经过点(3，－4)，∴sin α＝－45，cos α＝35，∴sin α＋1cos α＝－45＋53＝1315.2.如图，在平面直角坐标系xOy 中，角α的终边与单位圆交于点A ，点A 的纵坐标为45，则cos α的值为()A.45B ．－45C.35D ．－35解析：选D因为点A 的纵坐标y A ＝45，且点A 在第二象限，又因为圆O 为单位圆，所以A 点横坐标x A ＝－35，由三角函数的定义可得cos α＝－35.一抓基础，多练小题做到眼疾手快1．已知点P (tan α，sin α)在第三象限，则角α的终边在()A ．第一象限B ．第二象限C ．第三象限D ．第四象限解析：选D因为点P α＜0，α＜0，所以α的终边在第四象限，故选D.2．(2018·舟山五校联考)若tan α＜0，则()A ．sin α＜0B ．cos α＞0C ．sin αcos α＜0D ．2cos 2α－1＜0解析：选C因为tan α＜0，所以α是第二或第四象限角，所以sin α，cos α的符号不确定，故排除A 、B ；当α是第二象限角时，sin α，cos α符号相反，所以sin αcos α＜0；当α是第四象限角时，sin α，cos α符号相反，所以sin αcos α＜0，故选C.3．若一圆弧长等于其所在圆的内接正三角形的边长，则其圆心角α(0＜α＜π)的弧度数为()A ．π3B ．π2C ．3D ．2解析：选C 设圆半径为r ，则其内接正三角形的边长为3r ，所以3r ＝αr ，所以α＝ 3.4．在直角坐标系中，O 是原点，A (3，1)，将点A 绕O 逆时针旋转90°到B 点，则B 点坐标为__________．解析：依题意知OA ＝OB ＝2，∠AOx ＝30°，∠BOx ＝120°，设点B 坐标为(x ，y )，所以x ＝2cos 120°＝－1，y ＝2sin 120°＝3，即B (－1，3)．答案：(－1，3)5．(2019·丽水模拟)已知角α的终边经过点(2，－2)，则sin α＝________，sin αcos α＝________.解析：因为角α的终边经过点(2，－2)，所以sin α＝－22，cos α＝22，sin αcos α＝－12.答案：－22－12二保高考，全练题型做到高考达标1．将表的分针拨快10分钟，则分针旋转过程中形成的角的弧度数是()A ．π3B ．π6C ．－π3D ．－π6解析：选C 将表的分针拨快应按顺时针方向旋转，为负角．故A 、B 不正确，又因为拨快10分钟，故应转过的角为圆周的16，即为－16×2π＝－π3.2．(2019·台州模拟)已知点P (sin(－30°)，cos(－30°))在角θ的终边上，且θ∈[－2π，0)，则角θ的大小为()A ．－π3B ．2π3C ．－2π3D ．－4π3解析：选D 因为P (sin(－30°)，cos(－30°))，所以－12，θ是第二象限角，又θ∈[－2π，0)，所以θ＝－4π3.3．已知角α终边上一点P 的坐标是(2sin 2，－2cos 2)，则sin α等于()A ．sin 2B ．－sin 2C ．cos 2D ．－cos 2解析：选D因为r ＝(2sin 2)2＋(－2cos 2)2＝2，由任意三角函数的定义，得sin α＝yr＝－cos 2.4．已知角α＝2k π－π5(k ∈Z )，若角θ与角α的终边相同，则y ＝sin θ|sin θ|＋cos θ|cos θ|＋tan θ|tan θ|的值为()A ．1B ．－1C ．3D ．－3解析：选B由α＝2k π－π5(k ∈Z )及终边相同的概念知，角α的终边在第四象限，又角θ与角α的终边相同，所以角θ是第四象限角，所以sin θ＜0，cos θ＞0，tan θ＜0.所以y ＝－1＋1－1＝－1.5．点A (sin 2018°，cos 2018°)在直角坐标平面上位于()A．第一象限B．第二象限C．第三象限D．第四象限解析：选C由2018°＝360°×5＋(180°＋38°)可知，2018°角的终边在第三象限，所以sin2018°＜0，cos2018°＜0，即点A位于第三象限．6．已知角α的终边经过点(3a－9，a＋2)，且cosα≤0，sinα＞0，则实数a的取值范围是________．解析：∵cosα≤0，sinα＞0，∴角α的终边落在第二象限或y轴的正半轴上．a－9≤0，＋2＞0，∴－2＜a≤3.答案：(－2,3]7．已知α是第二象限的角，则180°－α是第________象限的角．解析：由α是第二象限的角可得90°＋k·360°＜α＜180°＋k·360°(k∈Z)，则180°－(180°＋k·360°)＜180°－α＜180°－(90°＋k·360°)(k∈Z)，即－k·360°＜180°－α＜90°－k·360°(k∈Z)，所以180°－α是第一象限的角．答案：一8．(2017·北京高考)在平面直角坐标系xOy中，角α与角β均以Ox为始边，它们的终边关于y轴对称．若sinα＝13，则sinβ＝________.解析：当角α的终边在第一象限时，取角α终边上一点P1(22，1)，其关于y轴的对称点(－22，1)在角β的终边上，此时sinβ＝13；当角α的终边在第二象限时，取角α终边上一点P2(－22，1)，其关于y轴的对称点(22，1)在角β的终边上，此时sinβ＝13.综上可得sinβ＝13.答案：139．已知角θ的终边上有一点(a，a)，a∈R且a≠0，则sinθ的值是________．解析：由已知得r＝a2＋a2＝2|a|，sinθ＝ar＝a2|a|＝＞0，a＜0.所以sinθ的值是22或－22.答案：22或－2210．已知扇形AOB的周长为8.(1)若这个扇形的面积为3，求圆心角的大小；(2)求这个扇形的面积取得最大值时圆心角的大小和弦长AB .解：设扇形AOB 的半径为r ，弧长为l ，圆心角为α，(1)＋l ＝8，＝3，＝3，2＝1，6，∴α＝l r ＝23或α＝l r ＝6.(2)法一：∵2r ＋l ＝8，∴S 扇＝12lr ＝14l ·2r＝14×＝4，当且仅当2r ＝l ，即α＝lr ＝2时，扇形面积取得最大值4.∴圆心角α＝2，弦长AB ＝2sin 1×2＝4sin 1.法二：∵2r ＋l ＝8，∴S 扇＝12lr ＝12r (8－2r )＝r (4－r )＝－(r －2)2＋4≤4，当且仅当r ＝2，即α＝lr ＝2时，扇形面积取得最大值4.∴弦长AB ＝2sin 1×2＝4sin 1.11．角α终边上的点P 与A (a,2a )关于x 轴对称(a ＞0)，角β终边上的点Q 与A 关于直线y ＝x 对称，求sin αcos α＋sin βcos β＋tan αtan β的值．解：由题意得，点P 的坐标为(a ，－2a )，点Q 的坐标为(2a ，a )．所以sin α＝－2a a 2＋(－2a )2＝－25，cos α＝a a 2＋(－2a )2＝15，tan α＝－2aa＝－2，sin β＝a (2a )2＋a 2＝15，cos β＝2a (2a )2＋a 2＝25，tan β＝a 2a ＝12，故sin αcos α＋sin βcos β＋tan αtan β＝－25×15＋15×25＋(－2)×12＝－1.三上台阶，自主选做志在冲刺名校(2019·衢州模拟)已知角α的终边经过点P(x，－2)(x≠0)，且cosα＝36x.(1)求x的值；(2)求sinα＋1tanα的值．解：(1)因为角α的终边经过点P(x，－2)，且cosα＝36 x，所以有xx2＋2＝36x.因为x≠0，所以x2＋2＝12，解得x＝±10.(2)若x＝10，则P(10，－2)，所以sinα＝－212＝－66，tanα＝－210＝－55，所以sinα＋1tanα＝－66－ 5.若x＝－10，则P(－10，－2)，所以sinα＝－212＝－66，tanα＝210＝55，所以sinα＋1tanα＝－66＋ 5.第二节同角三角函数的基本关系与诱导公式_1．同角三角函数的基本关系式(1)平方关系：sin2α＋cos2α＝1；(2)商数关系：tanα＝sinαcosα.2．诱导公式组序一二三四五六角2k π＋α(k ∈Z )π＋α－απ－απ2－απ2＋α正弦sin α－sin α－sin αsin αcos αcos_α余弦cos α－cos αcos α－cos_αsin α－sin α正切tan αtan α－tan α－tan_α口诀函数名不变符号看象限函数名改变符号看象限记忆规律奇变偶不变，符号看象限[小题体验]1．已知＝35，αsin(π＋α)＝______.答案：－452．若tan θ＝12，则2cos α－3sin α3cos α＋4sin α的值为________．答案：1103．化简sin(－1071°)sin 99°＋sin(－171°)sin(－261°)的结果为________．解析：原式＝(－sin 1071°)sin 99°＋sin 171°sin 261°＝－sin(3×360°－9°)sin(90°＋9°)＋sin(180°－9°)·sin(270°－9°)＝sin 9°cos 9°－sin 9°cos 9°＝0.答案：01．利用诱导公式进行化简求值时，先利用公式化任意角的三角函数为锐角三角函数，其步骤：去负—脱周—化锐．特别注意函数名称和符号的确定．2．在利用同角三角函数的平方关系时，若开方，要特别注意判断符号．3．注意求值与化简后的结果一般要尽可能有理化、整式化．[小题纠偏]1．已知α是第二象限角，sin α＝513，则cos α＝________.答案：－12132．________，________.答案：(1)22(2)3考点一三角函数的诱导公式(基础送分型考点——自主练透)[题组练透]1．(2018·宁波模拟)sin 210°cos 120°的值为()A ．14B ．－34C ．－32D ．34解析：选Asin 210°cos 120°＝－sin 30°(－cos 60°)＝12×12＝14.2．(2019·嵊州模拟)已知sin(π＋α)＝－12，则cos ()A ．12B ．－12C ．32D ．－32解析：选B因为sin(π＋α)＝－12＝－sin α，所以sin α＝－12.3．已知＝33，则________.解析：－π6＋＝tan π＝－＝－33.答案：－334．(易错题)设f (α)αf解：∵f (α)＝(－2sin α)(－cos α)＋cos α1＋sin 2α＋sin α－cos 2α＝2sin αcos α＋cos α2sin 2α＋sin α＝cos α(1＋2sin α)sin α(1＋2sin α)＝1tan α，∴＝114π＝1tan π6＝ 3.5．已知π＜α＜2π，cos(α－7π)＝－35，求sin(3π＋α)·tan 解：∵cos(α－7π)＝cos(7π－α)＝cos(π－α)＝－cos α＝－35，∴cos α＝35.∴sin(3π＋α＝sin(π＋α)·－sin α＝sin αsin α·cos αsin α＝cos α＝35.[谨记通法]1．利用诱导公式把任意角的三角函数转化为锐角三角函数的步骤也就是：“负化正，大化小，化到锐角就好了．”2．利用诱导公式化简三角函数的要求(1)化简过程是恒等变形；(2)结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值．考点二同角三角函数的基本关系(重点保分型考点——师生共研)[典例引领]1．已知sin α＋3cos α3cos α－sin α＝5，则sin 2α－sin αcos α的值为()A ．－15B ．－25C ．15D ．25解析：选D 依题意得：tan α＋33－tan α＝5，∴tan α＝2.∴sin 2α－sin αcos α＝sin 2α－sin αcos αsin 2α＋cos 2α＝tan 2α－tan αtan 2α＋1＝22－222＋1＝25.2．已知sin θ＝m －3m ＋5，cos θ＝4－2mm ＋5(m ≠0)，则tan(k π＋θ)(k ∈Z)的值为________．解析：因为sin θ＝m －3m ＋5，cos θ＝4－2mm ＋5，所以sin 2θ＋cos 2θ＝1，解得m ＝8，所以sin θ＝513，cos θ＝－1213，所以tan θ＝sin θcos θ＝－512.所以tan(k π＋θ)(k ∈Z )＝tan θ＝－512.答案：－5123．已知sin θ＋cos θ＝43，θsin θ－cos θ的值为________．解析：因为(sin θ＋cos θ)2＝sin 2θ＋cos 2θ＋2sin θ·cos θ＝1＋2sin θcos θ＝169，所以2sin θcos θ＝79，则(sin θ－cos θ)2＝sin 2θ＋cos 2θ－2sin θcos θ＝1－2sin θcosθ＝29.又因为θsin θ＜cos θ，即sin θ－cos θ＜0，所以sin θ－cos θ＝－23.答案：－23[由题悟法]同角三角函数基本关系式的应用技巧技巧解读适合题型切弦互化主要利用公式tan θ＝sin θcos θ化成正弦、余弦，或者利用公式sin θcos θ＝tan θ化成正切表达式中含有sin θ，cos θ与tan θ“1”的变换1＝sin 2θ＋cos 2θ＝cos 2θ(1＋tan 2θ)＝tanπ4＝(sin θ±cos θ)2∓2sin θcos θ表达式中需要利用“1”转化和积转换利用(sin θ±cos θ)2＝1±2sin θcos θ的关系进行变形、转化表达式中含有sin θ±cos θ或sin θcos θ[即时应用]1．若sin α＝－513，且α为第四象限角，则tan α的值等于()A ．125B ．－125C ．512D ．－512解析：选D法一：因为α为第四象限的角，故cos α＝1－sin 2α＝＝1213，所以tan α＝sin αcos α＝－5131213＝－512.法二：因为α是第四象限角，且sin α＝－513，所以可在α的终边上取一点P (12，－5)，则tan α＝yx＝－512.故选D.2．(2019·缙云模拟)设sin α＋sin β＝13，则sin α－cos 2β的最大值为()A ．－35B ．－23C ．－1112D ．49解析：选D因为sin α＋sin β＝13，所以sin α＝13－sin β.因为－1≤sin α≤1，所以－23≤sin β≤1.所以sin α－cos 2β＝13－sin β－1＋sin 2ββ－1112，当sin β＝－23时，sin α－cos 2β有最大值49.3．已知sin αcos α＝18，且5π4＜α＜3π2，则cos α－sin α的值为()A ．－32B ．32C ．－34D ．34解析：选B∵5π4＜α＜3π2，∴cos α＜0，sin α＜0且|cos α|＜|sin α|，∴cos α－sin α＞0，又(cos α－sin α)2＝1－2sin αcos α＝1－2×18＝34，∴cos α－sin α＝32.4．已知sin(π－α)－cos(π＋α)α＜sin α－cos α＝________.解析：由sin(π－α)－cos(π＋α)＝23，得sin α＋cos α＝23，①将①两边平方得1＋2sin αcos α＝29，故2sin αcos α＝－79.∴(sin α－cos α)2＝1－2sin αcos α＝1＝169.又∵π2＜α＜π，∴sin α＞0，cos α＜0.∴sin α－cos α＝43.答案：43一抓基础，多练小题做到眼疾手快1．(2018·嘉兴七校联考)已知＝32，且|α|＜π2，则tan α＝()A ．－33B ．33C ．－3D ．3解析：选C 因为sin α＝32，所以sin α＝－32.因为|α|＜π2，所以α＝－π3，所以tan α＝＝－3.2．已知sin(π＋θ)＝－3cos(2π－θ)，|θ|＜π2，则θ等于()A ．－π6B ．－π3C ．π6D ．π3解析：选D ∵sin(π＋θ)＝－3cos(2π－θ)，∴－sin θ＝－3cos θ，∴tan θ＝ 3.∵|θ|＜π2，∴θ＝π3.3．(2019·嘉兴模拟)已知sin α，cos α是方程3x 2－2x ＋a ＝0的两个根，则实数a 的值为()A ．56B ．－56C ．43D ．34解析：选B由题可得，sin α＋cos α＝23，sin αcos α＝a3.所以sin 2α＋cos 2α＝(sin α＋cos α)2－2sin αcos α＝49－2a 3＝1，解得a ＝－56.4．1－2sin (π＋2)cos (π＋2)＝()A ．sin 2－cos 2B ．cos 2－sin 2C ．±(sin 2－cos 2)D ．sin 2＋cos 2解析：选A1－2sin (π＋2)cos (π＋2)＝1－2sin 2·cos 2＝sin 22－2sin 2·cos 2＋cos 22＝|sin 2－cos 2|.又∵π2＜2＜π，∴sin 2＞0，cos 2＜0.∴|sin 2－cos 2|＝sin 2－cos 2.5．如果sin(π＋A )＝12，那么cos ________．解析：∵sin(π＋A )＝12，∴－sin A ＝12.∴sin A ＝12.答案：12二保高考，全练题型做到高考达标1．已知tan(α－π)＝34，且α()A ．45B ．－45C ．35D ．－35解析：选B因为tan(α－π)＝34，所以tan α＝34.又因为α所以α为第三象限的角，cos α＝－45.2．已知f (x )＝a sin(πx ＋α)＋b cos(πx ＋β)＋4，若f (2018)＝5，则f (2019)的值是()A ．2B ．3C ．4D ．5解析：选B∵f (2018)＝5，∴a sin(2018π＋α)＋b cos(2018π＋β)＋4＝5，即a sin α＋b cos β＝1.∴f (2019)＝a sin(2019π＋α)＋b cos(2019π＋β)＋4＝－a sin α－b cos β＋4＝－1＋4＝3.3．(2018·宁波五校联考)已知倾斜角为α的直线l 与直线x ＋2y －3＝0垂直，则cos (1009π－2α)的值为()A ．－35B ．35C ．2D ．－12解析：选B由题意可得tan α＝2，所以cos (1009π－2α)＝－cos 2α＝－cos 2α－sin 2αsin 2α＋cos 2α＝－1－tan 2αtan 2α＋1＝35.4．当θ为第二象限角，且＝13时，1－sin θcos θ2－sin θ2的值是()A ．1B ．－1C ．±1D ．0解析：选B ∵＝13，∴cos θ2＝13，∴θ2在第一象限，且cos θ2＜sin θ2，∴1－sin θcos θ2－sin θ2＝cos θ2－sinθ21.5．若sin α是5x 2－7x －6＝0的根，则(π＋α)()A ．35B ．53C ．45D ．54解析：选B由5x 2－7x －6＝0，得x ＝－35或x ＝2.则sin α＝－35.故原式＝cos α(－cos α)·tan 2αsin α·(－sin α)·(－sin α)＝1－sin α＝53.6．若sin θ，cos θ是方程4x 2＋2mx ＋m ＝0的两根，则m 的值为()A ．1＋5B ．1－5C ．1±5D ．－1－5解析：选B由题意知sin θ＋cos θ＝－m 2，sin θcos θ＝m 4.∵(sin θ＋cos θ)2＝1＋2sin θcos θ，∴m 24＝1＋m2，解得m ＝1±5，又Δ＝4m 2－16m ≥0，∴m ≤0或m ≥4，∴m ＝1－ 5.7．已知a (|a |≤1)，则sin ________．解析：由题意知，cos π＝－a .sin π2＋a ，所以0.答案：08．(2019·义乌模拟)已知tan(π－α)＝－2，则1sin 2α－2cos 2α＝________.解析：因为tan(π－α)＝－tan α＝－2，所以tan α＝2.所以1sin 2α－2cos 2α＝sin 2α＋cos 2αsin 2α－2cos 2α＝tan 2α＋1tan 2α－2＝4＋14－2＝52.答案：529．(2018·嘉兴七校联考)已知cos(75°＋α)＝513，α是第三象限角．求sin(195°－α)＋cos(α－15°)的值．解：因为cos(75°＋α)＝513，且α是第三象限角，所以75°＋α是第四象限角，所以sin(75°＋α)＝－1－cos 2(75°＋α)＝－1213.所以sin(195°－α)＋cos(α－15°)＝sin(α－15°)＋cos(α－15°)＝sin [(α＋75°)－90°]＋cos [(α＋75°)－90°]＝－cos(α＋75°)＋sin(α＋75°)＝－513－1213＝－1713.10．已知sin(3π＋θ)＝13，求cos (π＋θ)cos θ[cos (π－θ)－1]＋cos (θ－2π)(θ－π)－解：∵sin(3π＋θ)＝－sin θ＝13，∴sin θ＝－13.∴原式＝－cos θcos θ(－cos θ－1)＋cos θcos θ·(－cos θ)＋cos θ＝11＋cos θ＋cos θ－cos 2θ＋cos θ＝11＋cos θ＋11－cos θ＝21－cos 2θ＝2sin 2θ＝21＝18.三上台阶，自主选做志在冲刺名校1．sin 21°＋sin 22°＋…＋sin 290°＝________.解析：sin 21°＋sin 22°＋…＋sin 290°＝sin 21°＋sin 22°＋…＋sin 244°＋sin 245°＋cos 244°＋cos 243°＋…＋cos 21°＋sin 290°＝(sin 21°＋cos 21°)＋(sin 22°＋cos 22°)＋…＋(sin 244°＋cos 244°)＋sin 245°＋sin 290°＝44＋12＋1＝912.答案：9122．已知f (x )＝cos 2(n π＋x )·sin 2(n π－x )cos 2[(2n ＋1)π－x ](n ∈Z)．(1)化简f (x )的表达式；(2)求f 解：(1)当n 为偶数，即n ＝2k (k ∈Z )时，f (x )＝cos 2(2k π＋x )·sin 2(2k π－x )cos 2[(2×2k ＋1)π－x ]＝cos 2x ·sin 2(－x )cos 2(π－x )＝cos 2x ·(－sin x )2(－cos x )2＝sin 2x ；当n 为奇数，即n ＝2k ＋1(k ∈Z )时，f (x )＝cos 2[(2k ＋1)π＋x ]·sin 2[(2k ＋1)π－x ]cos 2{[2×(2k ＋1)＋1]π－x }＝cos 2[2k π＋(π＋x )]·sin 2[2k π＋(π－x )]cos 2[2×(2k ＋1)π＋(π－x )]＝cos 2(π＋x )·sin 2(π－x )cos 2(π－x )＝(－cos x )2sin 2x (－cos x )2＝sin 2x ，综上得f (x )＝sin 2x .(2)由(1)得＝sin 2π2018＋sin 21008π2018＝sin 2π2018＋sin＝sin 2π2018＋cos 2π2018＝1.第三节三角函数的图象与性质1．用五点法作正弦函数和余弦函数的简图正弦函数y ＝sin x ，x ∈[0,2π]的图象上，五个关键点是：(0,0)(π，0)(2π，0)．余弦函数y ＝cos x ，x ∈[0,2π]的图象上，五个关键点是：(0,1)，(π，－1)，(2π，1)．2．正弦、余弦、正切函数的图象与性质(下表中k ∈Z).[小题体验]1．①y ＝cos 2x;②y ＝sin 2x;③y ＝tan 2x;④y ＝|sin x |四个函数中，最小正周期为π的奇函数是________．答案：②2．(教材习题改编)函数y ＝－2的定义域为________________．|x ≠k π＋π3，k1．闭区间上最值或值域问题，首先要在定义域基础上分析单调性，含参数的最值问题，要讨论参数对最值的影响．2．要注意求函数y ＝A sin(ωx ＋φ)的单调区间时ω的符号，尽量化成ω＞0时的情况．3．三角函数存在多个单调区间时易错用“∪”联结．[小题纠偏]1．函数y ＝4sin(－x )，x ∈[－π，π]的单调性是()A ．在[－π，0]上是增函数，在[0，π]上是减函数B ．在－π2，π2上是增函数，在－π，－π2和π2，π上是减函数C ．在[0，π]上是增函数，在[－π，0]上是减函数D ．在π2，π和－π，－π2上是增函数，在－π2，π2上是减函数答案：D2．函数f (x )＝sin x 在区间0，π2上的最小值为________．解析：由已知x ∈0，π2，得2x －π4∈－π4，3π4，所以x ∈－22，1，故函数f (x )＝sin x 在区间0，π4上的最小值为－22.答案：－2 2考点一三角函数的定义域(基础送分型考点——自主练透)[题组练透] 1．函数y＝log21sin x－1的定义域为________．解析：21sin x－1≥0，x＞0，所以有0＜sin x≤12，解得2kπ＜x≤2kπ＋π6或2kπ＋5π6≤x＜2kπ＋π，k∈Z，|2kπ＜x≤2kπ＋π6或2kπ＋5π6≤x＜2kπ＋π，k∈.|2kπ＜x≤2kπ＋π6或2kπ＋5π6≤x＜2kπ＋π，k2．函数y＝lg(sin2x)＋9－x2的定义域为______________．解析：2x＞0，－x2≥0，π＜x＜kπ＋π2，k∈Z，3≤x≤3.∴－3≤x＜－π2或0＜x＜π2.∴函数y＝lg(sin2x)＋9－x2的定义域为－3答案：－3[谨记通法]三角函数定义域的求法求三角函数定义域实际上是构造简单的三角不等式(组)，常借助三角函数图象来求解．考点二三角函数的值域或最值(重点保分型考点——师生共研)[典例引领]1．函数y＝≤x≤9)的最大值与最小值之和为()A．2－3B．0C．－1D．－1－3解析：选A∵0≤x≤9，∴－π3≤π6x－π3≤7π6，∴∈－32，1.∴y ∈[－3，2]，∴y max ＋y min ＝2－3.2．(2018·浙北联考)函数f (x )＝2cos 2x ＋5sin x －4的最小值为________，最大值为________．解析：f (x )＝2cos 2x ＋5sin x －4＝－2sin 2x ＋5sin x －2＝－x ＋98.因为－1≤sin x ≤1，所以当sin x ＝－1时，f (x )有最小值－9；当sin x ＝1时，f (x )有最大值1.答案：－913．函数y ＝sin x －cos x ＋sin x cos x ，x ∈[0，π]的值域为________________．解析：设t ＝sin x －cos x ，则t 2＝sin 2x ＋cos 2x －2sin x cos x ，即sin x cos x ＝1－t 22，且－1≤t ≤ 2.∴y ＝－t 22＋t ＋12＝－12(t －1)2＋1.当t ＝1时，y max ＝1；当t ＝－1时，y min ＝－1.∴函数的值域为[－1,1]．答案：[－1,1]4．(2019·平阳模拟)已知函数f (x )＝2a x a ＋b (a ＜0)的定义域为0，π2，值域为[－5,1]，则a＋b ＝________.解析：因为x ∈0，π2，所以2x ＋π6∈π6，7π6，所以x ∈－12，1.因为a ＜0，所以f (x )∈[3a ＋b ，b ]．因为函数的值域为[－5,1]，所以3a ＋b ＝－5，b ＝1，所以a ＝－2，所以a ＋b ＝－1.答案：－1[由题悟法]三角函数最值或值域的3种求法(1)直接法：直接利用sin x 和cos x 的值域求解．(2)化一法：把所给三角函数化为y ＝A sin(ωx ＋φ)＋k 的形式，由正弦函数单调性写出函数的值域．(3)换元法：把sin x 、cos x 、sin x cos x 或sin x ±cos x 换成t ，转化为二次函数．[即时应用]求函数y ＝cos 2x ＋sin x|解：令t ＝sin x ，∵|x |≤π4，∴t ∈－22，22.∴y ＝－t 2＋t ＋1＋54，∴当t ＝12时，y max ＝54，当t ＝－22时，y min ＝1－22.∴函数y ＝cos 2x ＋sin x |的最大值为54，最小值为1－22.考点三三角函数的性质(题点多变型考点——多角探明)[锁定考向]三角函数的性质主要包括单调性、奇偶性、周期性、对称性，而三角函数的对称性多与奇偶性、周期性结合．常见的命题角度有：(1)三角函数的周期性；(2)三角函数的对称性；(3)三角函数的单调性．[题点全练]角度一：三角函数的周期性1．(2019·湖州期末)函数y ＝5sin －π3x()A ．6B ．－6C ．2π3D ．23解析：选A函数的最小正周期为T ＝2π|－π3|＝6.2．(2017·天津高考)设函数f (x )＝2sin(ωx ＋φ)，x ∈R，其中ω＞0，|φ|＜π.若2，0，且f (x )的最小正周期大于2π，则()A ．ω＝23，φ＝π12B ．ω＝23，φ＝－11π12C ．ω＝13，φ＝－11π24D ．ω＝13，φ＝7π24解析：选A∵2，0，∴11π8－5π8＝T4(2m ＋1)，m ∈N ，∴T ＝3π2m ＋1，m ∈N ，∵f (x )的最小正周期大于2π，∴T ＝3π，∴ω＝2π3π＝23，∴f (x )＝＋由×5π8＋2，得φ＝2k π＋π12，k ∈Z .又|φ|＜π，∴取k ＝0，得φ＝π12.角度二：三角函数的对称性3．(2018·嘉兴期末)函数f (x )＝sin x ()A ．x ＝π12B ．x ＝5π12C ．x ＝π3D ．x ＝π6解析：选A由题可得，令2x ＋π3＝k π＋π2，k ∈Z ，得x ＝k π2＋π12，k ∈Z .所以当k ＝0时，函数f (x )的图象的一条对称轴方程为x ＝π12.4．函数y ＝cos(3x ＋φ)的图象关于原点成中心对称图形，则φ＝________.解析：由题意，得y ＝cos(3x ＋φ)是奇函数，故φ＝k π＋π2(k ∈Z )．答案：k π＋π2(k ∈Z )角度三：三角函数的单调性5．(2019·浦江模拟)已知函数f (x )＝2sin ＋φ＞0，|φ|π，且是偶函数，则()A ．f (x )B ．f (x )C ．f (x )D ．f (x )解析：选A 因为函数f (x )的最小正周期为π，所以ω＝2.因为函数f (x )是偶函数，且|φ|＜π2，所以φ＝π4.所以f (x )＝2sinx ＝2cos 2x ，所以函数f (x )[通法在握]1．函数f (x )＝A sin(ωx ＋φ)的奇偶性、周期性和对称性(1)若f (x )＝A sin(ωx ＋φ)为偶函数，则当x ＝0时，f (x )取得最大或最小值；若f (x )＝A sin(ωx ＋φ)为奇函数，则当x ＝0时，f (x )＝0.(2)对于函数y ＝A sin(ωx ＋φ)，其对称轴一定经过图象的最高点或最低点，对称中心一定是函数的零点，因此在判断直线x ＝x 0或点(x 0,0)是否是函数的对称轴或对称中心时，可通过检验f (x 0)的值进行判断．2．求三角函数单调区间的2种方法(1)代换法：就是将比较复杂的三角函数含自变量的代数式整体当作一个角u (或t )，利用基本三角函数的单调性列不等式求解．(2)图象法：画出三角函数的正、余弦曲线，结合图象求它的单调区间．[演练冲关]1．(2019·舟山模拟)若函数f (x )＝sin(φ－x )是奇函数，则φ的值可能是()A ．π6B ．π3C ．π2D ．π解析：选D因为函数f (x )是奇函数，所以φ＝k π(k ∈Z )．对比选项可知，φ的值可能是π.故选D.2．若函数f (x )＝sin ωx (ω＞0)相邻两对称轴之间的距离为2，则ω＝________.解析：f (x )＝sin ωx ＝12sin ωx ＋32cos ωx ＋sin ωx ＝32sin ωx ＋32cos ωx ＝3sin 又因为f (x )相邻两条对称轴之间的距离为2，所以T ＝4，所以2πω＝4，即ω＝π2.答案：π23．函数y ＝|tan x |－π2，_______．解析：如图，观察图象可知，y ＝|tan x |－π2，减区间为－π2，0和π.－π2，0和π一抓基础，多练小题做到眼疾手快1．下列函数中，周期为π的奇函数为()A ．y ＝sin x cos xB ．y ＝sin 2xC ．y ＝tan 2xD ．y ＝sin 2x ＋cos 2x解析：选A y ＝sin 2x 为偶函数；y ＝tan 2x 的周期为π2；y ＝sin 2x ＋cos 2x 为非奇非偶函数，B 、C 、D都不正确，选A.2．函数y ＝sin x ＝2处取得最大值，则正数ω的最小值为()A.π2B.π3C.π4D.π6解析：选D 由题意得，2ω＋π6＝π2＋2k π(k ∈Z )，解得ω＝π6＋k π(k ∈Z )，∵ω＞0，∴当k ＝0时，ωmin＝π6，故选D.3．函数y ＝cos x －32的定义域为()A.－π6，π6B.k π－π6，k π＋π6(k ∈Z )C.2k π－π6，2k π＋π6(k ∈Z )D ．R 解析：选C∵cos x －32≥0，得cos x ≥32，∴2k π－π6≤x ≤2k π＋π6，k ∈Z .4．(2018·浙江六校联考)函数y ＝3sin x ＋3cos x ∈0________．解析：化简可得y ＝23sin 由2k π－π2≤x ＋π6≤2k π＋π2(k ∈Z )，得－2π3＋2k π≤x ≤π3＋2k π(k ∈Z )，又x ∈0，π2，∴函数的单调递增区间是0，π3.答案：0，π35．函数f (x )＝sin x 在0，π2上的值域是________．解析：∵x ∈0，π2，∴2x ＋π3∈π3，4π3，∴当2x ＋π3＝π2，即x ＝π12时，f (x )max ＝1.当2x ＋π3＝4π3，即x＝π2时，f (x )min ＝－32，∴f (x )∈－32，1.答案：－32，1二保高考，全练题型做到高考达标1．(2019·诸暨模拟)若函数f (x )＝sin ωx (ω＞0)在区间0，π3上单调递增，在区间π3，π2上单调递减，则ω＝()A ．3B ．2C ．32D ．23解析：选C 因为函数f (x )在区间0，π3上单调递增，在区间π3，π2上单调递减，所以f (x )max ＝sinωπ3＝1.又因为2πω≥2×π2，所以0＜ω≤2，所以ωπ3＝π2，解得ω＝32.2．关于函数y ＝x ()A ．是奇函数BD ．最小正周期为π解析：选C函数y ＝tanx A 错；函数y ＝tan x 增，B 错；最小正周期为π2，D 错；由2x －π3＝k π2，k ∈Z ，得x ＝k π4＋π6，k ∈Z .当k ＝0时，x ＝π6，所以它的3．函数f (x )＝2sin(ωx ＋φ)(ω＞0)对任意x 都有f ()A ．2或0B ．－2或2C ．0D ．－2或0解析：选B因为函数f (x )＝2sin(ωx ＋φ)对任意x 都有x＝π6对称，因为在对称轴处对应的函数值为最大值或最小值，所以选B.4．已知函数f (x )＝2sin(ωx ＋φ)，x ∈R，其中ω＞0，－π＜φ≤π.若f (x )的最小正周期为6π，且当x ＝π2时，f (x )取得最大值，则()A ．f (x )在区间[－2π，0]上是增函数B ．f (x )在区间[－3π，－π]上是增函数C ．f (x )在区间[3π，5π]上是减函数D ．f (x )在区间[4π，6π]上是减函数解析：选A∵f (x )的最小正周期为6π，∴ω＝13.∵当x ＝π2时，f (x )有最大值，∴13×π2＋φ＝π2＋2k π(k ∈Z )，φ＝π3＋2k π(k ∈Z )，∵－π＜φ≤π，∴φ＝π3.∴f (x )＝令－π2＋2k π≤x 3＋π3≤π2＋2k π，k ∈Z ，得－5π2＋6k π≤x ≤π2＋6k π，k ∈Z ，故f (x )的单调增区间为－5π2＋6k π，π2＋6k π，k ∈Z ，令k ＝0，得x ∈－5π2，π2，∵[－2π，0]⊆－5π2，π2，故A 正确．5．已知ω＞0，函数f (x )＝sinω的取值范围是()A ．12，54B ．12，34C ，12D ．(0,2]解析：选A由π2＜x ＜π得π2ω＋π4＜ωx ＋π4＜πω＋π4，＋π4，πω⊆π2，3π2，＋π4≥π2，＋π4≤3π2，∴12≤ω≤54，故选A.6．若函数f (x )＝2tanT 满足1＜T ＜2，则自然数k 的值为________．解析：由题意知，1＜πk ＜2，即k ＜π＜2k .又k ∈N ，所以k ＝2或k ＝3.答案：2或37．已知函数f (x )＝x ∈－π3，a ，若f (x )的值域是－12，1，则实数a 的取值范围是________．解析：∵x ∈－π3，a ，∴x ＋π6∈－π6，a ＋π6，∵当x ＋π6∈－π6，π2时，f (x )的值域为－12，1，∴结合函数的图象知π2≤a ＋π6≤7π6，∴π3≤a ≤π.答案：π3，π8．若函数f (x )＝ω＞0)的图象的相邻两条对称轴之间的距离为π2，且该函数图象关于点(x 0,0)成中心对称，x 0∈0，π2，则x 0＝________.解析：由题意得T 2＝π2，T ＝π，ω＝2.又2x 0＋π6＝k π(k ∈Z )，x 0＝k π2－π12k ∈Z )，而x 0∈0，π2，所以x 0＝5π12.答案：5π129．已知函数f (x )＝sin(ωx ＋φ＜φπ.(1)求当f (x )为偶函数时φ的值；(2)若f (x )f (x )的单调递增区间．解：∵f (x )的最小正周期为π，则T ＝2πω＝π，∴ω＝2.∴f (x )＝sin(2x ＋φ)．(1)当f (x )为偶函数时，φ＝π2＋k π，k ∈Z ，∴cos φ＝0，∵0＜φ＜2π3，∴φ＝π2.(2)f (x )×π6＋＝32，即＝32.又∵0＜φ＜2π3，∴π3＜π3＋φ＜π.∴π3＋φ＝2π3，φ＝π3.∴f (x )＝x 令2k π－π2≤2x ＋π32k π＋π2，k ∈Z ，得k π－5π12≤x ≤k π＋π12，k ∈Z .∴f (x )的单调递增区间为k π－5π12，k π＋π12，k ∈Z .10．已知函数f (x )＝2sinx (1)求函数f (x )图象的对称轴方程；(2)求函数f (x )的单调递增区间；(3)当x ∈π4，3π4时，求函数f (x )的最大值和最小值．解：(1)令2x ＋π4＝k π＋π2，k ∈Z ，得x ＝k π2＋π8，k ∈Z .所以函数f (x )图象的对称轴方程是x ＝k π2＋π8，k ∈Z .(2)令2k π－π2≤2x ＋π4≤2k π＋π2，k ∈Z ，得k π－3π8≤x ≤k π＋π8，k ∈Z .故函数f (x )的单调递增区间为k π－3π8，k π＋π8，k ∈Z .(3)当x ∈π4，3π4时，3π4≤2x ＋π4≤7π4，所以－1≤x ≤22，所以－2≤f (x )≤1，所以当x ∈π4，3π4时，函数f (x )的最大值为1，最小值为－2.三上台阶，自主选做志在冲刺名校1．若存在实数a ，使函数y ＝sin 2x ＋a cos x ＋58a －32在闭区间0，π2上取到最大值1，则实数a 等于()A ．1B ．52C ．32D ．2解析：选Cy x －12a ＋a 24＋58a －12.当0≤x ≤π2时，0≤cos x ≤1，令t ＝cos x ，则0≤t ≤1，所以y －12a ＋a 24＋58a －12，0≤t ≤1.①当0≤a 2≤1，即0≤a ≤2时，则当t ＝a 2cos x ＝a 2时，y max ＝a 24＋58a －12＝1，解得a ＝32或a ＝－4(舍去)，故a ＝32；②当a2＜0，即a ＜0时，则当t ＝0，即cos x ＝0时，y max ＝58a －12＝1，解得a ＝125，由于a ＜0，故这种情况不存在满足条件的a 值；③当a2＞1，即a ＞2时，则当t ＝1，即cos x ＝1时，y max ＝a ＋58a －32＝1，解得a ＝2013.由于2013＜2，故这种情况下不存在满足条件的a 值．综上知，存在a ＝32符合题意．故选C.2．设函数f (x )＝sin(ωx ＋φ＞0，|φ|①它的最小正周期为π；②它的图象关于直线x ＝π12成轴对称图形；④在区间－π6，以其中两个论断作为条件，另两个论断作为结论，写出你认为正确的一个命题________(用序号表示即可)．解析：若①②成立，则ω＝2ππ＝2.令2×π12＋φ＝k π＋π2，k ∈Z ，且|φ|＜π2，故k ＝0，则φ＝π3.此时f (x )＝x 当x ＝π3时，x sin π＝0，所以f (x )f (x )在－5π12，π12上是增函数，则f (x )在－π6，⇒③④.用类似的分析可求得①③⇒②④.。

2020届高考数学总复习 第四章 三角函数、解三角形 4-7 解三角形的应用举例课时作业 文(含解析)新人教A版