计算方法中的Lagrange插值
计算方法 插值法Lagrange插值

的n次插值基函数
以n+1个n次基本插值多项式lk(x)(k 0,1, … , n) 为基础,可直接写出满足插值条件
P(xi ) f(x i ) (i 0,1,2, … , n)
的n次代数插值多项式:
P(x) l0(x)y 0 l1(x)y1 … ln(x)yn
B(x1, f(x1))
x0
x1
由解析几何知道,这条直线用点斜式表示为
改写为
p(x)
y0
y1 x1
y0 x0
(x
x0)
p(x)
x x1 x0 x1
y0
x x0 x1 x0
y1
为了便于推广,记
推导
l0(x)
x x1 , x0 x1
l1(x )
x x0 x1 x0
线性插值 基函数
或者写成:
(i 0,1,2)
其几何意义是用经过3个点
(x0, y0 ), (x1, y1), (x2, y2 )
的抛物线 y P(x) 用以近似计算 y f(x)
y=f(x)
y
y = L 2 (x)
y0
y1
x0
x1
y2 x
x2
P(x)的系数 a0 , a1, a2 直接由插值条件决定,即
a0 , a1, a2 满足代数方程组:
(x 0 x1)(x 0 x2 )
从而导出 l0(x)
(x (x 0
x1)(x x2 ) x1)(x 0 x2 )
类似地可以构造出插值多项式 l1(x )和l2 (x )
于是确定了3个抛物插值的基函数:
l0(x)
(x (x 0
x1)(x x1)(x
第5章 实四Lagrange插值多项式

第5章 实验四Lagrange 插值多项式实验目的:理解Lagrange 插值多项式的基本概念,熟悉Lagrange 插值多项式的公式及源代码,并能根据所给条件求出Lagrange 插值多项式,理解龙格现象。
5.1 Lagrange 插值多项式 Lagrange 插值多项式的表达式: 1,,2,1,)()()(,)()(1111+=--==∏∑+≠=+=n i x x x x x l x l y x L n ij j j i j i n i i i 。
其中)(x l i 被称为插值基函数,实际上是一个n 次多项式。
)(x l i 的这种表示具有较好的对称性。
公式具有两大优点:(1)求插值多项式,不需要求解线性方程组,当已知数据点较多时,此公式更能显示出优越性。
(2)函数值可以用符号形式表示,数据点未确定的纵坐标可用多项式表示。
5.2 Lagrange 插值多项式源代码I% 功能: 对一组数据做Lagrange 插值 % 调用格式:yi=Lagran_(x,y,xi) % x,y 数组形式的数据表 % xi:待计算y 值的横坐标数组 % yi 用Lagrange 插值算出的y 值数组 function fi=Lagran_(x,f,xi)fi=zeros(size(xi)); np1=length(f); for i=1:np1z=ones(size(xi)); for j=1:np1if i~=j,z=z.*(xi-x(j))/(x(i)-x(j));end endfi=fi+z*f(i); end return例5.1 已知4对数据(1.6,3.3),(2.7,1.22),(3.9,5.61),(5.6,2.94)。
写出这4个数据点的Lagrange 插值公式,并计算出横坐标xi=[2.101,4.234]时对应的纵坐标。
解:4个数据点的Lagrange 插值公式为:)9.36.1(*)7.26.5(*)6.16.5()9.3(*)7.2)(6.1(*94.2)6.59.3(*)7.29.3(*)6.19.3()6.5(*)7.2(*)6.1(*9.3)6.57.2(*)9.37.2(*)6.17.2()6.5(*)9.3(*)6.1(*22.4)6.56.1(*)9.36.1(*)7.26.1()6.5(*)9.3(*)7.2(*3.3)(3------+------+------+------=x x x x x x x x x x x x x L清单5.1 clearx=[1.6, 2.7, 3.9, 5.6]; y=[3.3, 1.22, 5.61, 2.94]; xi=[2.101,4.234]; yi=Lagran_(x,y,xi); xx=1.5:0.05:6.5; yy=Lagran_(x,y,xx); plot(xx,yy,x,y,'o')其结果为:yi =1.0596 6.6457xg (x ):-, d a t a p o i n t s :o图5.1 插值多项式曲线图5.3 Lagrange插值多项式源代码II% 输入:x是插值节点横坐标向量;y是插值节点对应纵坐标向量。
Lagrange插值法学习教程
ID 疗法 12 12 12 12 12
年龄 36.4271 36.4271 36.4271 36.4271 36.4271
时间 Log(CD4 count+1)
0
3.1355
7.5714
3.0445
15.5714 2.7726
23.5714 2.8332
第35页2./共57601页4
3.2189 ………….
第21页/共60页
令L1(x)=l0(x)y0+l1(x)y1 由L1(x0)=y0 , L1(x1)=y1得
l0(x0)=1, l0(x1)=0,
l1(x0)=0, l1(x1)=1.
即l0(x)含有因子x-x1, l1(x)含有因子(x-x0), 令 l0(x)=λ0 (x-x1) , l1(x)=λ1 (x-x0),利用 l0(x0)=1 和 l1(x1)=1确定其中的系数λ0, λ1得:
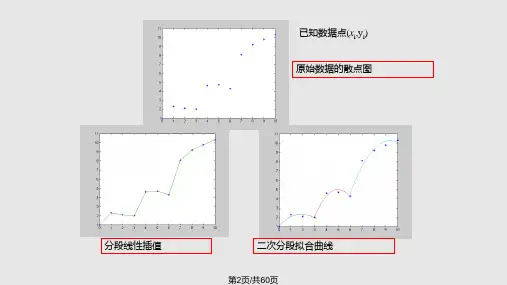
生长阻滞模型
第12页/共60页
高等教育学费问题探讨
年份 1989 1990 1991 1992 1993 1994
平均学费 187.06 190.64 205.09 396.56 592.99 871.13
缺少数据
缺少数据是用样条插值函数求 出来的
年份 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006
PtID CD4Date CD4Count RNADate
23424
0
178
0
23424
4
228
4
23424
8
126
8
23424
25 171
25
lagrange插值定理在高等代数中的不同解读

Lagrange插值定理在数学中有着重要的地位,特别是在高等代数中起着至关重要的作用。
它可以用来解决复杂的多项式函数的插值问题,为我们理解和应用数学领域的知识提供了有力的工具。
在不同的学术领域,人们对于Lagrange插值定理有着不同的解读,从而衍生出不同的应用和研究方向。
本文将从几个不同的角度来探讨Lagrange插值定理在高等代数中的不同解读。
一、数学领域中的Lagrange插值定理解读Lagrange插值定理最基本的形式可以描述为:给定一个次数为n的多项式函数,通过n+1个互异的插值点,可以确定该多项式函数的系数,并进而插值计算出其他点的函数值。
从数学的角度来看,Lagrange插值定理是关于多项式插值的一个重要定理。
1. 从数学原理角度解读从数学原理角度来看,Lagrange插值定理是建立在对多项式插值理论的深入研究之上的。
它涉及到多项式插值的基本概念和方法,通过对于插值点的选取和多项式函数的构造来实现对未知函数值的估计。
在数学原理角度下,人们可以进一步研究多项式插值的稳定性、误差估计和收敛性等问题,从而深化对Lagrange插值定理的理解,并且将其应用于更广泛的数学领域。
2. 从数值计算角度解读与数学原理角度不同,Lagrange插值定理也可以从数值计算的角度来解读。
在数值计算中,我们常常需要利用已知的数据点来估计未知函数值,在这种情况下,Lagrange插值定理就可以发挥出极大的作用。
通过构造插值多项式,我们可以利用插值多项式来进行数值计算,从而得到我们所需要的结果。
从数值计算的角度来看,Lagrange插值定理是一个非常实用的工具和方法。
二、Lagrange插值定理在高等代数中的应用除了在数学领域中有着重要的理论意义之外,Lagrange插值定理在高等代数中还有着广泛的应用。
在高等代数课程中,Lagrange插值定理不仅可以帮助学生更深入地理解多项式插值的原理,还可以通过实际案例来展示插值多项式的具体应用。
第一章 第一节 Lagrange插值公式.

Rn
x
M n+1 n +1
max ! axb
n+1
x
Lagrange余项定理在理论上有重要价值,它刻画了 Lagrange插值的某些基本特征。
n
注1 余项中含有因子n+1 x x xi ,如果插值点x 偏离插 i0
值节点xi 比较远,插值效果可能不理想。如何选择节点xi ,
可以证明,插值问题1.1、1.2 的解是存在且唯一的。为了
得到 Lagrange 公式的一般形式,我们先从最简单的一次插 值入手。
二、线性插值
已知:
x
x0
x1
y
y0
y1
求一个一次多项式P1(x) ,使满足
P1(xi ) yi ,i 0,1.
即求过点 x0, y0 , x1, y1 的一次曲线
使
Rn x
f x Pn x
f n+1
n +
1!
n+1
x
1.9
记 M n+1
max
a xb
f n+1 x ,于是由1.9 式可得
或者
Rn
x
M n+1
n +1!
n+1 x
,
1.10
max axb
简单才行。如果仅仅给出了一系列节点上的函数值
f xi yi ,i 0,1, 2,L , n ,则应采用 Lagrange 插值。
如果只提供了 f x 的一些离散值,并没给出具体的分析式 子, 就无法利用公式1.9 估计误差了。下面介绍另一种误差
拉格朗日插值多项式推导

拉格朗日插值多项式是一种近似函数,它可以通过给定一组离散数据点,来估算出其他数据点的值。
拉格朗日插值多项式是由18世纪法国数学家Joseph-Louis Lagrange提出的,他是一位杰出的数学家和物理学家。
拉格朗日插值多项式的推导可以从一个简单的例子开始。
假设我们有一组离散的数据点{(x1, y1), (x2, y2), …, (xn, yn)},我们想要通过这些点来拟合一个函数,使得在这些点上的函数值与给定的数据点相等。
首先,我们假设要拟合的函数是一个n-1次多项式:P(x) = a0 + a1x + a2x^2 + … + an-1x^n-1我们的目标是找到多项式中的系数a0, a1, …, an-1,使得在给定的数据点上函数值与数据点的y值相等。
根据插值的思想,我们希望在每个数据点上函数值与给定的数据点相等,即对于每个数据点(xi, yi)都满足:P(xi) = yi我们可以将这个条件用一个方程表示出来。
将插值多项式代入方程中,我们得到:a0 + a1xi + a2xi^2 + … + an-1xi^n-1 = yi现在我们有n个方程,通过解这个方程组,我们可以求解出多项式的系数。
为了方便求解,我们引入拉格朗日基函数。
拉格朗日基函数Li(x)的定义是一个n 次多项式,它可以满足以下条件:1.对于所有的i≠j,Li(xj) = 02.Li(xi) = 1根据拉格朗日基函数,我们可以将插值多项式表示为:P(x) = L0(x)y0 + L1(x)y1 + … + Ln-1(x)yn-1其中Li(x)可以表示为:Li(x) = (x - x0)(x - x1)…(x - xi-1)(x - xi+1)…(x - xn-1) / (xi - x0)(xi - x1)…(xi - xi-1)(xi - xi+1)…(xi - xn-1)现在我们可以使用拉格朗日基函数来表示插值多项式,并求解多项式的系数。
数值分析Lagrange插值
分别利用x 分别利用 0, x1 以及 x1, x2 计算
π
6 , x1 =
π
4
5π ⇒ sin 50 ≈ L1 ( ) ≈ 0.77614 18 (2) f (ξ x ) π π 1
R1 ( x ) = 2!
L1(x) = x −π / 4 × 1 + x −π / 6 × 1 π / 6−π / 4 2 π / 4−π / 6 2
f (n+1) (ξ ) n Rn ( x) = f ( x) − Ln ( x) = ∏(x − xi ) (n + 1)! i =0
Rolle’s Theorem的推论 若 ϕ (x )充分光滑,且 的推论: 充分光滑, 的推论 存在 ξ ∈ (a , b) 使得 ϕ ( n ) (ξ ) = 0 ϕ ( x0 ) = L = ϕ ( xn ) = 0
...
n n
x x
i −1
= ∏∏ ( x i − x j )
i =1 j = 0
由于x 互异,所以(4)右端不为零, (4)右端不为零 由于xi互异,所以(4)右端不为零,从而方程组 (3)的解 (3)的解 a0 ,a1 ,…an 存在且唯一。 a 存在且唯一。
通过解上述方程组(3)求得插值多项式 通过解上述方程组 求得插值多项式pn(x)的方法并 求得插值多项式 的方法并 不可取.这是因为当 较大时解方程组的计算量较大, 这是因为当n较大时解方程组的计算量较大 不可取 这是因为当 较大时解方程组的计算量较大, 而且方程组系数矩阵的条件数一般较大(可能是 而且方程组系数矩阵的条件数一般较大(可能是 病态方程组) 当阶数 当阶数n越高时,病态越重。 病态方程组),当阶数 越高时,病态越重。 为此我们必须从其它 途径来求P 途径来求 n(x): : 不通过求解方程组而 获得插值多项式
拉格朗日(Lagrange)插值算法
拉格朗⽇(Lagrange)插值算法拉格朗⽇插值(Lagrange interpolation)是⼀种多项式插值⽅法,指插值条件中不出现被插函数导数值,过n+1个样点,满⾜如下图的插值条件的多项式。
也叫做拉格朗⽇公式。
这⾥以拉格朗⽇3次插值为例,利⽤C++进⾏实现:1//利⽤lagrange插值公式2 #include<iostream>3using namespace std;45double Lx(int i,double x,double* Arr)6 {7double fenzi=1,fenmu=1;8for (int k=0;k<4;k++)9 {10if (k==i)11continue;12 fenzi*=x-Arr[k];13 fenmu*=Arr[i]-Arr[k];14 }15return fenzi/fenmu;16 }1718int main()19 {20double xArr[4]={};21double yArr[4]={};22//输⼊4个节点坐标23 cout<<"请依次输⼊4个节点的坐标:"<<endl;24for (int i=0;i<4;i++)25 cin>>xArr[i]>>yArr[i];2627//输⼊要求解的节点的横坐标28 cout<<"请输⼊要求解的节点的横坐标:";29double x;30 cin>>x;31double y=0;32for (int i=0;i<4;i++)33 y+=Lx(i,x,xArr)*yArr[i];34 printf("x=%lf时,y=%lf\n",x,y);3536//分界,下⾯为已知y求x37 cout<<"请输⼊要求解的节点的纵坐标:";38 cin>>y;39 x=0;40for (int i=0;i<4;i++)41 x+=Lx(i,y,yArr)*xArr[i];42 printf("y=%lf时,x=%lf\n",y,x);4344 system("pause");45return0;46 }作者:耑新新,发布于转载请注明出处,欢迎邮件交流:zhuanxinxin@。
拉格朗日(Lagrange)插值
li ( x) = Ci ( x x0 )...(x xi )...(x xn ) = Ci ( x x j ) ji j =0 1 li ( xi ) = 1 Ci = j i ( xi xj )
l ( x) y
i =0 i
1
i
l0(x)
l1(x)
称为拉格朗日插值基函数 , 满足条件 li(xj)=ij /* Kronecker Delta */
n1
希望找到li(x),i = 0, …, n 使得 li(xj)=ij ;然后令
Pn ( x ) =
l (x) y
i=0 i
n
i
,则显然有Pn(xi) = yi 。
§4.2 拉格朗日(Lagrange)插值
n 求 n 次多项式 Pn ( x) = a0 a1 x an x 使得
Pn ( x i ) = y i ,
i = 0 , ... , n
条件:无重合节点,即 i j
xi x j
一. 插值多项式的存在唯一性 定理4.2.1 : 在 n 1 个互异节点 xk 处满足插值条件 Pn ( xk ) = yk
n
f
( n 1)
( n 1 ) ( x0 ) = = ( xn ) = 0( n 1 ) ( x ) Ln ( x ) K ( x )( n 1) ! = Rn ( x ) K ( x ) ( n 1) ! ( n) 存在 (a, b) 使得 ( ) = 0 ( n 1 ) n ( n 1 ) f ( ) x f ( x) Rn ( x ) = ( x xi ) = K ( x) (n 1) ! i =0 ( n 1) !
数值分析实验报告Lagrange插值法
2) 选取插值节点为 x1 0.50,x 2 0.70, x 3 0.80 作抛物线插值
运行结果和总结 运行结果 例一: 设 y ln x 且给出函数表 x lnx 0.40 -0.916291 0.50 -0.693147 0.70 -0.356675 0.80 -0.223144
试计算 f(0.6)=ln0.6 近似值。 1)选取插值节点为 x1 0.50,x 2 0.70 作线性插值
>> X=[0.50 0.70 0.80;-0.693147 -0.356675 -0.223144]; >> x=0.60; >> format long >> f=Lagrange(X,x) f= -0.513342666666667
总结 ( 1 )线性插值与抛物线插值都是 Lagrange 插值的特殊形式,两者可以用 Lagrange 插值算法进行计算; (2)并不是给出的插值节点越多越精确,要看步长的大小。 指导教师意见
山东师范大学数学科学学院实验报告
实验课程: 数值分析引论 实验项目: 拉格朗日插值多项式
姓名: XXX 学号: 2015XXXXXX2 班级: XXX 班 专业: 数学与应用数学 指导教师: 实验目的 1、Lagrange 插值法的 matlab 实现; 2、用 Lagrange 插值程序进行插值计算。 实验内容: 问题分析和算法设计 Lagrange 插值 已知 y f(x )函数表(xi ,y i ) ,(a x 0 xi x n b ),给定 xx [a,b ] 及 表示选取 x i , ,x i n 作为插值节点作 n0 次插值多项式 Ln (xx ), 计算 f(xx )近 i0、n0 ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
举例
已经测得在某处海洋不同深度处的水温如下: 深度(M) 466 741 水温(oC)7.04 4.28 950 3.40 1422 1634 2.54 2.13
根据这些数据,希望合理地估计出其它深度(如 500米,600米,1000米…)处的水温
5 sin 50 L2 ( ) 0.76543 18
0
cos x R2 ( x ) ( x )( x )( x ) ; 3! 6 4 3
5 0.00044 R2 0.00077 18 sin 50 = 0.7660444…
1 V( x 0, x1,..., x n) 1 ... 1
n
x x x x
0 1
2 0 2 1
... ... ... ...
x x x
n 0 n 1
...
n
...
2 n
...
n n
x x
i 1Biblioteka ( x i x j )
i 1 j 0
由于xi互异,所以(4)右端不为零,从而方程组 (3)的解 a0 ,a1 ,…an 存在且唯一。
3.2 代数插值问题解的存在惟一性
给定区间[a,b]上互异的n+1个点{xj}nj=0的一 组函数值f(xj),j =0,…, n,求一个n次多项式 pn(x)∈Pn,使得 pn(xj)=f(xj),j=0,1,…,n. …... (1) 令 pn(x)=a0+a1x+…+anxn, …... (2) 只要证明Pn(x)的系数a0 ,a1,…, an存在唯一即可
1 cos 3 x 2 2
2次插值的实际误差 0.00061
的n+1个互异的点,对 f(x)所作的n次Lagrange插 值多项式Ln (x) 有误差估计
f ( ) n Rn ( x) f ( x) Ln ( x) ( x xi ) (n + 1) ! i 0
( n +1)
Rolle’s Theorem的推论: 若 ( x )充分光滑,且 ( n) 存在 使得 ( ) 0 ( a , b) ( x0 ) ( xn ) 0
这就是本章要讨论的“插值问题”
插值问题的定义
当精确函数 y = f(x) 非常复杂或未知时,在区 间[a,b]上一系列节点 x0 … xm 处测得函数值 y0 = f(x0), …, ym = f(xm),由此构造一个简单易算的 近似函数 g(x) f(x),满足条件 g(xj) = f(xj) (j = 0, … m) (*) 这个问题称为“插值问题” 这里的 g(x) 称为f(x) 的插值函数。 节点 x0 … xm称为插值节点,
i 0 i j n
x x
j
x xi
j=0,1,…,n
i
(1)
这里每个lj(x)都是n次多项式,且由(1)式容易验证 lj(x)满足
0, i j l j ( xi) 1, i j
(2 )
可以证明函数组l0(x),l1(x),…, ln(x) 在插 值区间[a,b]上线性无关,所以这n+1个函数可 作为Pn的一组基函数,称为Lagrange插值基函数 对任意的pn(x)∈Pn,都有 pn(x)=c0 l0(x)+c1 l1(x)+…+cn ln(x) 其中c0 ,c1 ,…,cn 为组合系数
l0 ( x0 ) l1 ( x0 ) l ( x ) l ( x ) 0 1 1 1 l0 ( xn ) l1 ( xn )
ln ( x0 ) c0 f ( x0 ) ln ( x1 ) c1 f ( x1 ) ln ( xn ) cn f ( xn )
为此由插值条件(1)知Pn(x)的系数满足下列n+1个 代数方程构成的线性方程组 a0+a1x0+…+anx0n=f(x0) a0+a1x1+…+anx1n= f(x1) ……………………. a0+a1xn+…+anxnn= f(xn)
……(3)
而ai(i=0,1,2,…,n)的系数行列式是Vandermonde行列式
sin 50 = 0.7660444… 利用x0, x1 作为插值节点的实际误差 0.01001 利用x1, x2作为插值节点的实际误差 0.00596
n=2
(x )( x ) ( x )( x 1 1 4 3 6 3) L2 ( x) + ( 6 4 )( 6 3 ) 2 ( 4 6 )( 4 3 ) 2 (x )( x 3 6 4) + ( 3 6 )( 3 4 ) 2
L1 ( x ) x / 4 1 + x / 6 1 / 6 / 4 2 / 4 / 6 2
5 0.01319 R1 ( ) 0.00762 18
利用
x1 , x2 4 3
计算得:sin 50 0.76008,
5 0.00538 R1 0.00660 18
i 0 i 0
n
n
(t)有 n+2 个不同的根 x0 … xn x
( n+1)
( x ) 0, x (a, b)
f ( n+1) ( ) u ( x) (n + 1) !
例:已知 sin 1 , sin 1 , sin 3 6 2 4 2 3 2 分别利用 sin x 的1次、2次 Lagrange 插值计算
sin 50, 并估计误差。
解: n = 1 分别利用x0, x1 以及 x1, x2 计算
6 , x1
利用 x0
0
4
5 sin 50 L1 ( ) 0.77614 18 (2) f ( x ) 1 3 R1 ( x) ( x )( x ), sin x 2! 6 4 2 2
由Lagrange插值基函数满足(2)式可知,方程组变成
1 0 0
0 1 0
0 c0 f ( x0 ) 0 c1 f ( x1 ) 1 cn f ( xn )
证明:由于Rn(xi) =0 ,i=0,1,…,n
n R ( x) u ( x) ( x x ) n i i0
任意固定 x xi (i = 0, …, n), 考察
(t ) Rn (t ) u ( x) (t xi ) f (t ) Ln (t ) u ( x) (t xi )
条件(*)称为插值条件,区间[a,b]称为插值区间
g(x)
f(x)
x0
x1
x2
x
x3
x4
插值函数的类型有很多种
最常用的插值函数是代数多项式 …? 用代数多项式作插值函数的插值称为代数插值
本章主要讨论的内 容
插值法 插值问题 插值函数
代 数 插 值
• 一、插值问题解的存在唯一性? • 二、插值多项式的常用构造方法? • 三、插值函数的误差如何估计?
因此得到插值多项式 pn(x)= f(x0)l0(x)+f(x1) l1(x)+…+ f(xn) ln(x)
称Ln(x)为n次Lagrange插值多项式
记为Ln(x)= f(xj)lj(x)
插值余项 /* Remainder */
( n +1) f ( x) 在[a , b]内存在, 则在[a , b]上 定理4.3.1 若
通过解上述方程组(3)求得插值多项式pn(x)的方法并 不可取.这是因为当n较大时解方程组的计算量较大, 而且方程组系数矩阵的条件数一般较大(可能是 病态方程组),当阶数n越高时,病态越重。 为此我们必须从其它 途径来求Pn(x): 不通过求解方程组而 获得插值多项式
基本思想:在n次多项式空间Pn中找一组合适的基函数 0(x),1(x),…, n(x),使 pn(x)=a0 0(x) +a1 1(x) +…+an n(x) 不同的基函数的选取导致不同的插值方法
Lagrange插值 Newton插值
3.3 Lagrange插值
求 n 次多项式 Pn ( x) a0 + a1 x + + an x n 使得
Pn ( xi ) yi , i 0,1,, n
n=1 已知 x0 , x1 ; y0 , y1 ,求
使得
P 1 ( x) a0 + a1 x 使得P 1 ( x0 ) y0 , P 1 ( x1 ) y1
可见 P1(x) 是过 ( x0 , y0 ) 和 ( x1, y1 ) 两点的直线。
P1 ( x ) y 0 + y1 y0 x1 x 0 ( x x0 )
x x0 x1 x 0
=
x x1 y0 + x 0 x1
y1
1
i 0
li ( x ) y
i
l0(x)
l1(x)
与 节点有关,而与f 无关
• 构造基函数 ( x x0 )( x x1 ) ( x x j 1 )(x x j +1 ) (x xn ) l j ( x) ( x j x0 )( x j x1 ) ( x j x j 1 )( x j x j +1) (x j xn )
