2019-2020年七年级数学上册 4.3.3 余角和补角练习 (新版)新人教版
人教版七年级数字上册:4.3.3《余角与补角》基础巩固题及答案

4.3 角4.3.3 余角和补角基础稳固1.(知识点 1)以下图形中互为补角的两个角是()A.①和②B.①和③C.①和④D.②和④2.(题型二)假如从甲船看乙船,乙船在甲船的北偏东30°方向,那么从乙船看甲船,甲船在乙船的()A.南偏西30°方向B.南偏西60°方向C.南偏东30°方向D.南偏东60°方向3.(题型三)以下选项是将一副三角尺按不一样地点摆放的,∠α与∠β互余的是()4.(题型二)一艘海上搜救船借助雷达探测仪找寻到事故船的地点,雷达表示图如图 4-3.3-1,搜救船位于图中圆心 O 处,事故船位于距点O 40 海里的 A 处,雷达操作员要用方向角把事故船相关于搜救船的地点报告给船长,以便调整航向,以下四种表述方式正确的选项是()图 4-3.3-1A.事故船在搜救船的北偏东60°方向B.事故船在搜救船的北偏东30°方向C.事故船在搜救船的北偏西60°方向D.事故船在搜救船的南偏东30°方向5.(题型三)如图 4-3.3-2,∠AOC=∠BOD=90°,四位同学察看图形后分别说了自己的看法 .甲:∠ AOB=∠COD;乙:∠ BOC+∠AOD=180°;丙:∠ AOB+∠COD=90°;丁:图中小于平角的角有 6 个.此中看法正确的选项是()图 4-3.3-2A. 甲、乙、丙B.甲、丙、丁C.乙、丙、丁D.甲、乙、丁6.(题型一)已知∠ A=35°10′48″,则∠ A 的补角是 _____.7.(题型一)如图 4-3.3-3, A, B,C 三点在同一条直线上,若∠ECD=90°,∠ 1=23°30′,则∠ 2 的度数是 ______°.图 4-3.3-38.(题型一)若∠ 1 和∠ 2 互为余角,则∠ 1 和∠ 2 的补角之和是 ______.9.(题型一)一个角的补角加上 10°后,等于这个角的余角的 3 倍,求这个角以及它的余角和补角的度数 .能力提高10.(题型二)如图 4-3.3-4,货轮 O 在航行过程中,发现灯塔 A 在它南偏东 60°的方向上,同时,在它北偏东 30°、西北(即北偏西 45°)方向上又分别发现了客轮 B 和海岛 C.(1)模仿表示灯塔方向的方法,分别画出表示客轮 B 和海岛 C 方向的射线 OB,OC(不写作法);(2)若图中有一艘渔船 D,且∠ AOD 的补角是它的余角的 3 倍,画出表示渔船 D 方向的射线 OD,则渔船 D 在货轮 O 的 ______方向上 .(写出方向角)图 4-3.3-411.(题型三)如图 4-3.3-5,O 为直线 AB 上一点,过点 O 作射线OC 使∠ BOC=120°,将有一 30°角的直角三角尺的直角极点放在点处,一边 OM 在射线 OB 上,另一边ON 在直线 AB 的下方 .(中∠OMN=30°,∠ NOM=90°)(1)(2)(3)图 4-3.3-5(1)将图 4-3.3-5(1)中的三角尺绕点 O 逆时针旋转至图 4-3.3-5(2),使 OM 在∠ BOC 的内部,且恰巧均分∠ BOC.问:直线 ON能否均分∠ AOC?请说明原因 .(2)将图 4-3.3-5(1)中的三角尺绕点 O 按每秒 6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t 秒时,直线 ON 恰巧均分∠AOC,求 t.(3)将图 4-3.3-5(1)中的三角尺绕点 O 顺时针旋转至图 4-3.3-5(3),使 ON 在∠ AOC 的内部 .请研究:∠ AOM 与∠ NOC 之间的数目关系,并说明原因 .答案基础稳固1.C 分析:由于①和④两个角的和为 180°,因此①和④互为补角 .应选 C.2.A 分析:由图 D4-3.3-1 可知,∠1=30°.由于从甲船看乙船,乙船在甲船的北偏东30°方向,因此从乙船看甲船,甲船在乙船的南偏西30°方向 .应选 A.图 D4-3.3-123.A 分析: A.∠α与∠ β互余,故此选项切合题意; B.∠α=∠β,故此选项不切合题意; C.∠α=∠β,故此选项不切合题意; D.∠α与∠β互补,故此选项不切合题意 .应选 A.4.B 分析:由题图可知,事故船在搜救船的北偏东30°方向 .应选B.5. D分析:由于∠AOC=∠BOD=90°,因此∠AOC-∠BOC=∠BOD-∠BOC,即∠AOB= ∠COD,因此甲同学的看法正确;由于∠BOC+∠AOD= ∠ AOC+ ∠ COD+ ∠ BOC= ∠ AOC+ ∠ BOD=90 ° +90 °=180°,因此乙同学的看法正确;由于∠AOB+ ∠BOC= ∠AOC=90°,∠B OC 和∠ COD 不必定相等,因此丙同学的看法不正确;由于图中小于平角的角有∠ AOB,∠AOC,∠AOD,∠BOC,∠BOD,∠COD,共 6 个,因此丁同学的看法正确.应选 D.6.144°49′12″分析:由于∠ A=35°10′48″,因此∠ A 的补角为180°-35°10′48″=144°49′12″.7.66.5 分析:由于∠ ECD=90°,∠ACB=180°,因此∠ 2+∠1=90°. 由于∠ 1=23°30′,因此∠ 2=90°-23°30′=66°30′=66.5°.8. 270°分析:设∠ 2=x,则∠ 1=90°-x.由题意,得180°-(90°-x)+180°-x=270°.9.解:设这个角为 x° .由题意,得 180-x+10=3(90-x),解得 x=40.即这个角是 40°,它的余角是50°,补角是 140°.能力提高10. 解:(1)如图 D4-3.3-2.图 D4-3.3-2图 D4-3.3-3(2)由∠ AOD 的补角是它的余角的 3 倍,得180°-∠AOD=3(90°-∠AOD),解得∠ AOD=45°.如图 D4-3.3-3,故渔船 D 在货轮 O 南偏东 15°或北偏东 75°方向上 .11.解:(1)直线ON 均分∠AOC.原因以下:设 ON 的反向延伸线为 OD.由于 OM 均分∠ BOC,∠ BOC=120°,因此∠ MOC=∠MOB= 1∠BOC=60°. 2又由于∠ MON=90°,因此∠ BON=30°,因此∠ CON=120°+30°=150°,因此∠ COD=30°.又由于∠ AOC=180° - ∠ BOC=60 °,因此∠ DOA= ∠ AOC- ∠COD=30°,因此∠ COD=∠AOD,因此 OD 均分∠ AOC,即直线 ON 均分∠ AOC.(2)由(1)可知,当ON 绕点O 沿逆时针方向旋转60°时,直线ON 均分∠ AOC,当 ON 绕点 O 沿逆时针方向旋转 240°[即( 1)中OD 的地点]时,直线 ON 均分∠ AOC.由题意,得 6t=60 或 6t=240,解得 t=10 或 t=40.(3)由于∠ MON=90°,∠ AOC=60°,因此∠ AOM=90°-∠AON,∠ NOC=60°-∠ AON,因此∠ AOM-∠NOC=(90°-∠AON)-(60°-∠AON)=30°.。
人教版七年级上数学试题:4.3.3余角和补角 练习题(含答案)

4.3.3余角和补角1.如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据(C)A.直角都相等B.等角的余角相等C.同角的余角相等D.同角的补角相等2.如图,一艘轮船在O处同时测得小岛A,B的方向分别为北偏西30°和东北方向,则∠AOB 的度数是(D)A.135°B.115°C.105°D.75°3.已知岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,符合条件的示意图是(D)A BC D4.一个锐角的补角比它的余角大(C)A.45°B.60°C.90°D.120°5.若∠A=64°,则它的余角等于(B)A.116°B.26°C.64°D.50°6.下列能与60°的角互余的角是(A)A BC D7.如图所示,∠1>∠2,那么∠2与12(∠1-∠2)之间的关系是(B)A .互补B .互余C .和为45°D .和为22.5°8.已知∠A =60°,则它的补角的度数是120°.9.若∠1=∠2,且∠1与∠2互余,则∠1=∠2=45°.10.已知∠α=59°20′,若∠α与∠β互余,且∠β与∠γ互余,则∠γ的度数为59°20′.11.若∠α=∠β,且∠α+∠1=180°,∠β+∠2=180°,则∠1与∠2的大小关系是相等.12.一个角的余角比它的补角的13还少20°,则这个角的大小是75°. 13.如图,根据点A 、B 、C 、D 、E 在图中的位置填空.(1)射线OA 表示东北方向;(2)射线OB 表示北偏西30°;(3)射线OC 表示南偏西60°;(4)射线OD 表示正南方向;(5)射线OE 表示南偏东50°.14.如图,∠AOB =124°,OC 是∠AOB 的平分线,∠1与∠2互余,求∠1和∠BOD 的度数.解:因为∠AOB =124°,OC 是∠AOB 的平分线,所以∠BOC =∠2=12∠AOB =62°. 因为∠1与∠2互余,所以∠1+∠2=90°.所以∠1=90°-∠2=28°.所以∠BOD =∠BOC -∠1=34°.15.如图,O 点是学校所在位置,A 村位于学校南偏东42°方向,B 村位于学校北偏东25°方向,C 村位于学校北偏西65°方向,在B 村和C 村间的公路OE(射线)平分∠BOC.(1)求∠AOE 的度数;(2)公路OE 上的车站D 相对于学校O 的方位是什么?(以正北、正南方向为基准)解:(1)如图所示:因为A村位于学校南偏东42°方向,所以∠1=42°.因为B村位于学校北偏东25°方向,所以∠4=25°.所以∠AOB=180°-∠1-∠4=113°.因为C村位于学校北偏西65°方向,所以∠COM=65°.所以∠BOC=∠COM+∠4=90°.因为OE平分∠BOC,所以∠COE=∠BOE=45°.所以∠AOE=∠AOB+∠BOE=113°+45°=158°.(2)∠EOM=∠BOE-∠4=20°,所以车站D相对于学校O的方位是北偏西20°.16.如图1所示,将一副三角尺的直角顶点重合在点O处.(1)①∠AOD和∠BOC相等吗?说明理由;②∠AOC和∠BOD在数量上有何关系?说明理由;(2)若将等腰的三角尺绕点O旋转到如图2的位置.①∠AOD和∠BOC相等吗?说明理由;②∠AOC和∠BOD的以上关系还成立吗?说明理由.解:(1)①∠AOD=∠BOC.理由略.②∠AOC和∠BOD互补.理由略.(2)①∠AOD=∠BOC.理由略.②∠AOC和∠BOD互补.理由略.。
2020年七年级数学上册第四章几何图形初步4.3角4.3.3余角和补角知能演练提升新版新人教版
1
9.
如图,∠2 是∠1 的 4 倍,∠2 的补角比∠1 的余角大 45°. (1)求∠1,∠2 的度数; (2)若∠AOD=90°,试问 OC 平分∠AOB 吗?为什么?
10.
如图,已知小明家在商场南偏东 60°方向,小华家在商场的东北方向. (1)若王亮家在商场的北偏西 19°20'的方向,则∠AOB 和∠AOC 的度数分别是多少? (2)若∠BOC=67°20',试求∠AOC 的度数,并说明王亮家在商场的什么方向.
4.3.3 余角和补角
知能演练提升 能力提升
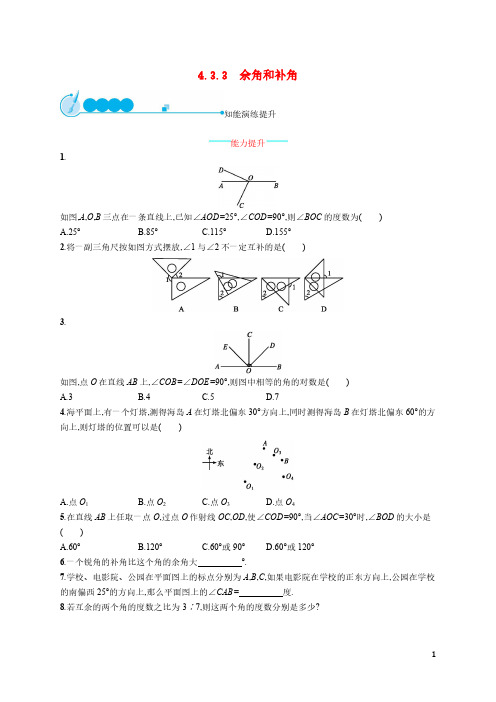
1.
如图,A,O,B 三点在一条直线上,已知∠AOD=25°,∠COD=90°,则∠BOC 的度数为( )
A.25°
B.85°
C.115°
D.155°
2.将一副三角尺按如图方式摆放,∠1 与∠2 不一定互补的是( )
3.
如图,点 O 在直线 AB 上,∠COB=∠DOE=90°,则图中相等的角的对数是( )
A.3
B.4
C.5
D.7
4.海平面上,有一个灯塔,测得海岛 A 在灯塔北偏东 30°方向上,同时测得海岛 B 在灯塔北偏东 60°的方
向上,则灯塔的位置可以是( )
A.点 O1
B.点 O2
C.点 O3
D.点 O4
5.在直线 AB 上任取一点 O,过点 O 作射线 OC,OD,使∠COD=90°,当∠AOC=30°时,∠BOD 的大小是
创新应用 3
★13.先按图示折纸,再回答问题:
(1)∠2 是多少度的角?为什么? (2)∠1 与∠3 有何关系? (3)∠1 与∠AEC,∠3 和∠BEF 分别有何关系?
★14.
已知∠AOB=20°,∠AOE=100°,OB 平分∠AOC,OD 平分∠AOE.
2019-2020年七年级数学上册 4.3角同步练习1 人教新课标版

DABC 2019-2020年七年级数学上册 4.3角同步练习1 人教新课标版一、选择:1.下列关于角的说法正确的个数是( )①角是由两条射线组成的图形;②角的边越长,角越大; ③在角一边延长线上取一点D;④角可以看作由一条射线绕着它的端点旋转而形成的图形. A.1个 B.2个 C.3个 D.4个2.下列4个图形中,能用∠1,∠AOB,∠O 三种方法表示同一角的图形是( )AA1BO BA1B OCA B OCDA 1BOD3.图中,小于平角的角有( )A.5个B.6个C.7个D.8个 二、填空:4.将一个周角分成360份,其中每一份是______°的角, 直角等于____°,平角等于______°.5.30.6°=_____°_____′=_______′;30°6′=_______′______°. 三、解答题:6.计算:(1)49°38′+66°22′; (2)180°-79°19′; (2)22°16′×5; (4)182°36′÷4.7.根据下列语句画图:(1)画∠AOB=100°;(2)在∠AOB的内部画射线OC,使∠BOC=50°;(3)在∠AOB的外部画射线OD,使∠DOA=40°;(4)在射线OD上取E点,在射线OA上取F,使∠OEF=90°.8.任意画一个三角形,估计其中三个角的度数,再用量角器检验你的估计是否准确.9.分别确定四个城市相应钟表上时针与分钟所成的角的度数.10.九点20分时,时钟上时钟与分钟的夹角a等于多少度?11.马路上铺的地砖有很多种图案,如图所示的图案是某街面方砖铺设的示意图,请你用量角器量一下其中出现的所有的角度?12.如图,在∠AOB的内部引一条射线OC,可得几个小于平角的角? 引两条射线OC、OD呢?引三条射线OC、OD、OE呢?若引十条射线一共会有多少个角?ABO13.请用直线、线段、角等图形设计成表示客观事物的图画,如图, 并为你的图画命名.一盏吊灯一帆风顺答案:1.A2.B3.D4.1,90,1805.30,36,1836;1806,30.16.(1)116°;(2)100°41′;(3)111°20′;(4)45°39′.9.30°;0°;120°;90°10.160°12. 引1条射线有2+1=3个角;引2条射线有3+2+1=6个角;引3条射线有4+3+2+1=10个角;引10条射线有11+10+9+……+3+2+1=66个角.4.3 角的比较一、填空:1.如图1,∠AOB______∠AOC,∠AOB_______∠BOC(填>,=,<); 用量角器度量∠BOC=____°,∠AOC=______°,∠AOC______∠BOC.OC(1)AB O DC(2)ABOD C (3)A B2.如图2,∠AOC=______+______=______-______;∠BOC=______-______= _____-________.3.OC 是∠AOB 内部的一条射线,若∠AOC=12________,则OC 平分∠AOB;若OC 是∠AOB 的角平分线,则_________=2∠AOC. 二、选择:4.下列说法错误的是( )A.角的大小与角的边画出部分的长短没有关系;B.角的大小与它们的度数大小是一致的;C.角的和差倍分的度数等于它们的度数的和差倍分;D.若∠A+∠B>∠C,那么∠A 一定大于∠C 。
人教版七年级上册数学 4.3.3余角和补角 同步练习(含解析)

4.3.3余角和补角同步练习一.选择题1.若∠A与∠B互为补角,∠A=40°,则∠B=()A.50°B.40°C.140°D.60°2.下列叙述正确的是()A.一个钝角和一个锐角一定互为补角B.每一个锐角都有余角C.两个锐角一定互为余角D.一个钝角的余角是锐角3.如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC的度数为()A.43°B.34°C.56°D.50°4.下列说法中,正确的是()①已知∠A=40°,则∠A的余角是50°.②若∠1+∠2=90°,则∠1和∠2互为余角.③若∠1+∠2+∠3=180°,则∠1、∠2和∠3互为补角.④一个角的补角必为钝角.A.①,②B.①,②,③C.③,④,②D.③,④5.已知锐角α,那么∠α的补角与∠α的余角的差是()A.90°B.120°C.60°+αD.180°﹣α6.若α=27°25',则α的余角等于()A.62°25'B.62°35'C.152°25'D.152°35'7.如果∠1与∠2互补,∠2与∠3互余,那么∠1与∠3的关系是()A.∠1=90°+∠3B.∠3=90°+∠1C.∠1=∠3D.∠1=180°﹣∠3 8.如图,∠AOC和∠BOD都是直角.如果∠DOC=58°,则下列判断错误的是()A.∠AOD=∠BOCB.∠AOB=132°C.∠AOB+∠DOC=180°D.若∠DOC变小,则∠AOB变大9.将一副三角尺按不同位置摆放,下列摆放中∠1与∠2互为余角的是()A.B.C.D.10.如图,点A,O,B在一条直线上,OE⊥AB于点O,如果∠1与∠2互余,那么图中相等的角有()A.5对B.4对C.3对D.2对二.填空题11.若两个角互补,且度数之比为3:2,求较大角度数为.12.一个角的补角与它的余角的3倍的差是40°,则这个角为.13.已知:如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,图形中相等的角有对,互余的角有对.14.若一个角的补角与这个角的余角之和为200°,则这个角的度数为度.15.如图,将一副三角尺的直角顶点O重合在一起.若∠COB与∠DOA的比是5:13,OE 平分∠DOA,则∠EOC=度.三.解答题16.如图,已知∠AOB=128°,OC平分∠AOB,请你在∠COB内部画射线OD,使∠COD 和∠AOC互余,并求∠COD的度数.17.如图,在直线AD上任取一点O,过点O做射线OB,OE平分∠DOB,OC平分∠AOB,∠BOC=26°时,求∠BOE的度数.18.如图①,点O为直线AB上一点,过点O作射线OC,使∠BOC=60°,将一直角三角板的直角顶点放在点O处,一边ON在射线OB上,另一边OM在直线AB的上方.(1)在图①中,∠COM=度;(2)将图①中的三角板绕点O按逆时针方向旋转,使得ON在∠BOC的内部,如图②,若∠NOC=∠MOA,求∠BON的度数;(3)将图①中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,当直线ON恰好平分锐角∠BOC时,旋转的时间是秒.(直接写出结果)参考答案一.选择题1.解:∵∠A与∠B互为补角,∴∠A+∠B=180°,∵∠A=40°,∴∠B=180°﹣40°=140°.故选:C.2.解:A.一个锐角与一个钝角不一定互为补角,故本选项错误;B.每一个锐角都有余角,故本选项正确;C.只有两个锐角的和为90°时,这两个角才互余,故原说法错误;D.钝角的没有余角,故此选项错误;故选:B.3.解:∠AOB=∠COD=90°,∠AOD=146°则∠BOC=360°﹣2×90°﹣146°=34°则∠BOC=34°.故选:B.4.解:①已知∠A=40°,则∠A的余角是50°,原说法正确;②若∠1+∠2=90°,则∠1和∠2互为余角,原说法正确;③若∠1+∠2+∠3=180°,则∠1、∠2和∠3不能互为补角,原说法错误;④一个角的补角不一定是钝角,原说法错误.说法正确的是①②,故选:A.5.解:(180°﹣∠α)﹣(90°﹣∠α)=180°﹣∠α﹣90°+∠α=90°.故选:A.6.解:α的余角=90°﹣α=90°﹣27°25'=62°35'.故选:B.7.解:∵∠1+∠2=180°∴∠1=180°﹣∠2又∵∠2+∠3=90°∴∠3=90°﹣∠2∴∠1﹣∠3=90°,即∠1=90°+∠3.故选:A.8.解:A、∵∠AOC和∠BOD都是直角,∴∠AOD+∠DOC=∠DOC+∠BOC=90°,∴∠AOD=∠BOC,故A正确,不符合题意;B、∵∠DOC=58°,∴∠AOD=32°,∴∠AOB=32°+90°=122°,故B错误,符合题意,C、∵∠AOD+∠DOC=∠DOC+∠BOC=90°,∴∠AOD+∠DOC+∠DOC+∠BOC=180°,∴∠AOB+∠DOC=180°,故C正确,不符合题意;D、∵∠AOD+∠DOC+∠DOC+∠BOC=180°,∴∠AOB+∠DOC=180°,∴∠DOC变小,则∠AOB变大,故D正确,不符合题意.故选:B.9.解:A、∠1与∠2不互余,故本选项错误;B、∠1与∠2不互余,故本选项错误;C、∠1与∠2不互余,故本选项错误;D、∠1与∠2互余,故本选项正确.故选:D.10.解:∵OE⊥AB,∴∠AOE=∠BOE=90°,∵∠1与∠2互余,∴∠1+∠2=90°,∴∠1=∠AOC,∠2=∠BOD,∠AOE=∠COD,∴图中相等的角有5对.故选:A.二.填空题11.解:因为两个角的度数之比为3:2,所以设这两个角的度数分别为(3x)°和(2x)°.根据题意,列方程,得3x+2x=180,解这个方程,得x=36,所以3x=108.即较大角度数为108°.故答案为108°.12.解:设这个角为x°,则其余角为(90﹣x)°,补角为(180﹣x)°,依题意有180﹣x﹣3(90﹣x)=40,解得x=65.故这个角是65°.故答案为:65°.13.解:图形中相等的角有∠A=∠BCD,∠B=∠ACD,∠ACB=∠BDC,∠ACB=∠CDA,∠BDC=∠CDA,一共5对,互余的角有∠A和∠B,∠A和∠ACD,∠B和∠BCD,∠ACD和∠BCD,一共4对.故答案为:5;4.14.解:设这个角为x°,由题意得:90﹣x+180﹣x=200,解得:x=35,故答案为:35.15.解:∵∠COB+∠DOA=∠COB+∠COA+∠COB+∠DOB=∠AOB+∠COD=180°,又∵∠COB与∠DOA的比是5:13,∴∠DOA=180°×=130°,∵OE平分∠DOA,∴∠DOE=65°,故答案为:25.三.解答题16.解:作OD⊥OA,则∠COD和∠AOC互余,如图所示.∵∠AOB=128°,OC平分∠AOB,∴∠AOC=∠AOB=64°,∵∠COD和∠AOC互余,∴∠COD=90°﹣∠AOC=26°.17.解:∵OC平分∠AOB,∠BOC=26°,∴∠AOB=2∠BOC=52°.∴∠BOD=180°﹣52°=128°.∵OE平分∠DOB,∴∠BOE=∠DOB=×128°=64°.18.解:(1)∵将一直角三角板的直角顶点放在点O处,一边ON在射线OB上,另一边OM在直线AB的上方,∴∠MON=90°,∴∠COM=∠MON﹣∠BOC=90°﹣60°=30°,故答案为:30(2)设∠NOC=x,那么∠MOA=6x,∠BON=60°﹣x.由题意,可知6x+90°+60°﹣x=180°,即5x=180°﹣90°﹣60°,即5x=30°,所以x=6°.所以∠BON=60°﹣x=60°﹣6°=54°.(3)∵直线ON平分∠BOC,∠BOC=60°,∴∠BON=30°或∠BON=210°,∵三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,∴直线ON平分∠BOC时,旋转的时间是3或21秒,故答案为:3或21。
2019年秋人教版七年级上册数学4.3.3余角和补角 检测练习(含答案)

2019年秋人教版七年级上册数学4.3.3余角和补角 检测练习一、单选题1.如果一个角的余角是50°,那么这个角的度数是( )A .30°B .40°C .50°D .130°2.如图,将一副三角板的直角顶点重合摆放在在桌面上,下列各组角一定能互补的是( )A .∠BCD 和∠ACFB .∠ACD 和∠ACFC .∠ACB 和∠DCBD .∠BCF 和∠ACF3.1∠、2∠互为补角,且12∠>∠,则2∠的余角是( )A .12∠+∠B .12∠-∠C .190∠-︒D .901︒-∠4.若∠1与∠2互余,∠2与∠3互补,则∠1与∠3的关系是( )A .∠1=∠3B .∠1与∠3互余C .∠1与∠3互补D .∠3﹣∠1=90°5.如图,O 为直线AB 上一点,OM 平分∠AOC ,ON 平分∠BOC ,则图中互余的角有( )A .4对B .3对C .2对D .1对6.已知一个角的补角等于这个角的余角的4倍,则这个角的度数是( )A .30°B .60°C .90°D .120°7.已知∠α=140°﹣5m ,∠β=5m ﹣50°,∠α和∠β关系一定成立的是( )A .互余B .互补C .∠α=∠βD .∠α=2∠β8.如图,∠AOC 和∠BOC 互补,∠AOB =α,OM 是∠AOC 的平分线,ON 是∠BOC 的平分线,∠MON 的度数是( )A .1802α-B .12aC .1902a +D .1902a -o 9.如图,将三个直角三角形的直角顶点重合放置,下列关系式一定成立的是( )A .∠1=∠3B .∠1=∠2C .∠1+∠2+∠3=90°D .∠1+∠3=2∠2二、填空题 10.已知∠A =34°47′.则∠A 的补角的度数是_____.11.若3842α'∠=︒,则α∠的余角等于_______.12.已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β﹣∠γ=_______ ___.13.一个角的对顶角比它的邻补角的3倍还大20°,则这个角的补角的度数为_____.14.若∠1+∠2=90°,∠2+∠3=90°,则∠1与∠3的关系是 .,理由是 . 15.如图,AB ,CD 相交于点O ,∠BOE =90°,有以下结论:①∠AOC 与∠COE 互为余角;②∠BOD 与∠COE 互为余角;③∠AOC =∠BOD ;④∠COE 与∠DOE 互为补角;⑤∠AOC 与∠DOE 互为补角;⑥∠AOC =∠COE其中错误的有_____(填序号).16.如图将一副三角板的直角顶点重合,摆放在桌面上,若110AOC ∠=︒,则BOD ∠=_________°.三、解答题17.如图,直线AB 、CD 相交于点O ,OF ⊥CD ,OF 平分∠BOE ,垂足为O .(1)直接写出图中所有与∠BOC 互补的角;(2)若∠BOE =110°,求∠AOC 的度数.18.设∠α、∠β的度数分别为(2n +5)°和(65﹣n )°,且∠α、∠β都是∠γ的补角(1)求n 的值;(2)∠α与∠β能否互余,请说明理由.19.一副直角三角板按照如图所示放置,注意观察AOC ∠和BOD ∠的数量关系.(1)如图①,AOC ∠和BOD ∠的数量关系是______;(2)如图②,将两个直角三角板的直角顶点置于一点O ,无论如何旋转其中一个直角三角板(两直三角板无重叠),AOC ∠和BOD ∠的数量关系是______;(3)如图③,将两个直角三角板的直角顶点置于一点O ,旋转后使两直三角板有重叠,请直接写出AOC ∠和BOD ∠的数量关系,并说明理由.20.已知∠ABC =∠DBE ,射线BD 在∠ABC 的内部.(1)如图1,已知∠ABC ═90°,当BD 是∠ABC 的平分线时,求∠ABE 的度数.(2)如图2,已知∠ABE 与∠CBE 互补,∠DBC :∠CBE =1:3,求∠ABE 的度数;(3)如图3,若∠ABC =45°时,直接写出∠ABE 与∠DBC 之间的数量关系.21.已知O为直线AB上的一点,∠COE是直角,OF平分∠AOE.(1)如图1,若∠COF=34°,则∠BOE=______;(2)如图1,若∠BOE=80°,则∠COF=______;(3)若∠COF=m°,则∠BOE=______度;∠BOE与∠COF的数量关系为______.(4)当∠COE绕点O逆时针旋转到如图2的位置时,(3)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.答案1.B 2.A 3.C 4.D 5.A 6.B 7.A 8.B 9.C 10.145°13′11.5118'︒12.90°13.40°14.∠1=∠3 同角的余角相等15.⑥16.7017.(1)∠AOC,∠BOD,∠COE;(2)35°.18.(1)n=20;(2)∠α与∠β互余,19.(1)90AOC BOD∠+∠=︒,.AOC BOD∠+∠=︒;(3)180AOC BOD∠+∠=︒;(2)18020.(1)∠ABE=135°;(2)∠ABE=126°;(3)∠ABE+∠DBC=90°.. 21.(1)68° (2) 40°(3)2m∠BOE=2∠COF;(4)成立,。
2020-2021学年人教版七年级数学上学期《4.3.3 余角和补角》测试卷及答案解析

2020-2021学年人教版七年级数学上学期《4.3.3 余角和补角》测试卷一.选择题(共10小题)1.若α=29°45′,则α的余角等于()A.60°55′B.60°15′C.150°55′D.150°15′2.与30°的角互为余角的角的度数是()A.30°B.60°C.70°D.90°3.已知∠α=60°32′,则∠α的余角是()A.29°28′B.29°68′C.119°28′D.119°68′4.如果∠1和∠2互补,且∠1>∠2,则下列表示∠2的余角的式子中:①90°﹣∠1;②∠1﹣90°;③(∠1+∠2);④(∠1﹣∠2).正确的有()A.1个B.2个C.3个D.4个5.下列说法:①射线AB和射线BA是同一条射线;②锐角和钝角互补;③若一个角是钝角,则它的一半是锐角;④一个锐角的补角比这个角的余角大90度.其中正确的个数是()A.1个B.2个C.3个D.4个6.如果∠1与∠2互余,∠2与∠3互余,那么∠1与∠3的关系为()A.互余B.互补C.相等D.无法确定7.如果∠1的余角是∠2,并且∠1=2∠2,则∠1的补角为()A.30°B.60°C.120°D.150°8.如图,在△ABC中,∠BAC=90°,点D,E分别在BC,CA边的延长线上,EH⊥BC 于点H,EH与AB交于点F.则∠1与∠2的数量关系是()A.∠1=∠2B.∠1与∠2互余C.∠1与∠2互补D.∠1+∠2=100°9.∠1、∠2互为补角,且∠1>∠2,则∠2的余角是()A.∠1+∠2B.∠1﹣∠2C.∠1﹣90°D.90°﹣∠1 10.如图,一副三角板按不同的位置摆放,摆放位置中∠1≠∠2的是()A.B.C.D.二.填空题(共9小题)11.如果∠α=35°,那么∠α的余角等于°.12.如图,∠AOB与∠BOD互为余角,OB是∠AOC的平分线,∠AOB=25°,则∠COD 的度数是.13.已知∠α和∠β互为余角,且∠β比∠α大40°,则∠β=°.14.一个角的余角的度数为30°,则这个角的补角的度数为.15.如图,∠AOC与∠BOD都是直角,且∠AOD:∠AOB=7:2,则∠AOB等于度.16.已知∠α+∠β=90°,且∠α=35°41′,则∠β=.17.如图,将一副直角三角尺的直角顶点C叠放在一起,若∠ECD比∠ACB的小6°,则∠BCD的度数为.18.如图将一副三角板的直角顶点重合,摆放在桌面上,若∠AOC=110°,则∠BOD=°.19.如图,将一副三角板按不同位置摆放,∠α与∠β互余的是,∠α与∠β互补的是,∠α与∠β相等的是.三.解答题(共8小题)20.如图,O是直线AB上一点,OD平分∠BOC,∠COE=90°.若∠AOC=40°.(1)求∠DOE的度数;(2)图中互为余角的角有.21.一个角的余角比它的补角的还少15°,求这个角的度数.22.如图,O为直线AB上一点,OM是∠AOC的角平分线,ON是∠COB的平分线(1)指出图中所有互为补角的角.(2)求∠MON的度数.(3)指出图中所有互为余角的角.23.如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE=;(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;(3)如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.24.将一副三角板中的两块直角三角板按如图的方式叠放在一起,直角顶点重合.(1)若∠ACB=115°时,则∠DCE的度数等于;(2)当CE平分∠ACD时,求∠ACB的度数;(3)猜想并直接写出∠ACB与∠DCE的数量关系(不必说明理由).25.设∠α、∠β的度数分别为(2n+5)°和(65﹣n)°,且∠α、∠β都是∠γ的补角(1)求n的值;(2)∠α与∠β能否互余,请说明理由.26.如图①,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一直角边OM在射线OB上,另一直角边ON在直线AB 的下方,(1)将图①中的三角板绕点O逆时针方向旋转至图②,使边OM在∠BOC的内部,且恰好平分∠BOC,求∠BON大小;(2)将图①中的三角板绕点O逆时针方向旋转至图③.①如果ON恰好是∠AOC的角平分线,则∠AOM﹣∠NOC的度数为;②如果ON始终在∠AOC的内部,∠AOM﹣∠NOC的度数不会变化,请猜测出∠AOM﹣∠NOC的度数并说明理由.27.如图,若O是直线AB上一点,∠COD=90°,OE平分∠BOC,∠AOC=40°,求∠DOE的度数.2020-2021学年人教版七年级数学上学期《4.3.3 余角和补角》测试卷参考答案与试题解析一.选择题(共10小题)1.若α=29°45′,则α的余角等于()A.60°55′B.60°15′C.150°55′D.150°15′【解答】解:∵α=29°45′,∴α的余角等于:90°﹣29°45′=60°15′.故选:B.2.与30°的角互为余角的角的度数是()A.30°B.60°C.70°D.90°【解答】解:与30°的角互为余角的角的度数是:60°.故选:B.3.已知∠α=60°32′,则∠α的余角是()A.29°28′B.29°68′C.119°28′D.119°68′【解答】解:∵∠α=60°32′,∠α的余角是为:90°﹣60°32′=29°28′,故选:A.4.如果∠1和∠2互补,且∠1>∠2,则下列表示∠2的余角的式子中:①90°﹣∠1;②∠1﹣90°;③(∠1+∠2);④(∠1﹣∠2).正确的有()A.1个B.2个C.3个D.4个【解答】解:∵∠1和∠2互补,∴∠1+∠2=180°.因为90°﹣∠2=∠1﹣90°,所以①错误,②正确;(∠1+∠2)+∠2=×180°+∠2=90°+∠2≠90°,所以③错误;(∠1﹣∠2)+∠2=(∠1+∠2)=×180°=90°,所以④正确.综上可知,②④均正确.故选:B.5.下列说法:①射线AB和射线BA是同一条射线;②锐角和钝角互补;③若一个角是钝角,则它的一半是锐角;④一个锐角的补角比这个角的余角大90度.其中正确的个数是()A.1个B.2个C.3个D.4个【解答】解:①射线AB和射线BA表示的方向不同,不是同一条射线,故原说法错误;②锐角和钝角是相对于直角的大小而言,没有一定的数量关系,不一定构成互补关系故原说法错误;③一个角是钝角,则这个角大于90°小于180°,它的一半大于45°小于90°,是锐角,正确;④锐角为x°,它的补角为(180﹣x°),它的余角为(90﹣x°),相差为90°,正确.故正确的说法有③④共2个.故选:B.6.如果∠1与∠2互余,∠2与∠3互余,那么∠1与∠3的关系为()A.互余B.互补C.相等D.无法确定【解答】解:∵∠1与∠2互余,∠2与∠3互余,∴∠1+∠2=90°,∠2+∠3=90°,∴∠1=∠3,故选:C.7.如果∠1的余角是∠2,并且∠1=2∠2,则∠1的补角为()A.30°B.60°C.120°D.150°【解答】解:∵∠1的余角是∠2,∴∠1+∠2=90°,∵∠1=2∠2,∴2∠2+∠2=90°,∴∠2=30°,∴∠1=60°,∴∠1的补角为180°﹣60°=120°.故选:C.8.如图,在△ABC中,∠BAC=90°,点D,E分别在BC,CA边的延长线上,EH⊥BC 于点H,EH与AB交于点F.则∠1与∠2的数量关系是()A.∠1=∠2B.∠1与∠2互余C.∠1与∠2互补D.∠1+∠2=100°【解答】解:∵EH⊥BC,∴∠1+∠B=90°,∵∠BAC=90°,∴∠BCE+∠B=90°,∴∠1=∠BCE.∵∠BCE+∠2=180°,∴∠1+∠2=180°,即∠1与∠2互补,故选:C.9.∠1、∠2互为补角,且∠1>∠2,则∠2的余角是()A.∠1+∠2B.∠1﹣∠2C.∠1﹣90°D.90°﹣∠1【解答】解:∵∠1,∠2互为补角∴∠1+∠2=180°∴∠2的余角是90°﹣∠2=∠1﹣90°,故选:C.10.如图,一副三角板按不同的位置摆放,摆放位置中∠1≠∠2的是()A.B.C.D.【解答】解:A.∠1=45°,所以∠1=∠2=45°,故本选项不合题意;B.根据等角的补角相等可得∠1=∠2=135°,故本选项不合题意;C.图中∠1≠∠2,故本选项符合题意;D.根据同角的补角相等可得∠1=∠2,故本选项不合题意.故选:C.二.填空题(共9小题)11.如果∠α=35°,那么∠α的余角等于55°.【解答】解:∵∠α=35°,∴∠α的余角等于90°﹣35°=55°故答案为:55.12.如图,∠AOB与∠BOD互为余角,OB是∠AOC的平分线,∠AOB=25°,则∠COD 的度数是40°.【解答】解:∵OB是∠AOC的平分线,∴∠BOC=∠AOB=25°,∵∠AOB与∠BOD互为余角,∴∠BOD=90°﹣∠AOB=90°﹣25°=65°,∴∠COD=∠BOD﹣∠BOC=65°﹣25°=40°.故答案为:40°13.已知∠α和∠β互为余角,且∠β比∠α大40°,则∠β=65°.【解答】解:设∠α为x,则∠β为90°﹣x,由题意得,90°﹣x=x+40°,解得x=65°.故答案为:65.14.一个角的余角的度数为30°,则这个角的补角的度数为120°.【解答】解:∵一个角的余角的度数是30°,∴这个角的补角的度数是90°+30°=120°,故答案为:120°.15.如图,∠AOC与∠BOD都是直角,且∠AOD:∠AOB=7:2,则∠AOB等于36度.【解答】解:设∠AOB=x,则∠AOD=90°+x,∵∠AOD:∠AOB=7:2,∴,解得:x=36°.故答案为:36.16.已知∠α+∠β=90°,且∠α=35°41′,则∠β=54°19′.【解答】解:∵∠α+∠β=90°,∠α=35°41′,∴∠β=90°﹣35°41′=54°19′,故答案为:54°19′.17.如图,将一副直角三角尺的直角顶点C叠放在一起,若∠ECD比∠ACB的小6°,则∠BCD的度数为65°.【解答】解:∵∠ACE=90°﹣∠ECD,∴∠ACB=90°+∠ACE=90°+90°﹣∠ECD=180°﹣∠ECD,∴∠ECD=(180°﹣∠ECD)﹣6°,解得:∠ECD=25°,∴∠BCD=90°﹣∠ECD=90°﹣25°=65°,故答案为:65°.18.如图将一副三角板的直角顶点重合,摆放在桌面上,若∠AOC=110°,则∠BOD=70°.【解答】解:∵∠AOB=∠COD=90°,∴∠AOD=∠AOC﹣∠COD=110°﹣90°=20°,∴∠BOD=∠AOB﹣∠AOD=90°﹣20°=70°.故答案为:70.19.如图,将一副三角板按不同位置摆放,∠α与∠β互余的是(1),∠α与∠β互补的是(4),∠α与∠β相等的是(2)(3).【解答】解:(1)根据平角的定义得:∠α+90°+∠β=180°,∴∠α+∠β=90°,即∠α与∠β互余;(2)根据两个直角的位置得:∠α=∠β;(3)根据三角尺的特点和摆放位置得:∠α+45°=180°,∠β+45°=180°,∴∠α=∠β;(4)根据图形可知∠α与∠β是邻补角,∴∠α+∠β=180°;综上所述:(1)中∠α与∠β互余;(4)中∠α与∠β互补;(2)(3)中,∠α=∠β.故答案为:(1),(4),(2)(3).三.解答题(共8小题)20.如图,O是直线AB上一点,OD平分∠BOC,∠COE=90°.若∠AOC=40°.(1)求∠DOE的度数;(2)图中互为余角的角有∠AOC和∠BOE,∠COD和∠DOE,∠BOD和∠DOE.【解答】解:(1)∵∠AOC=40°,∴∠BOC=180°﹣∠AOC=140°,∵OD平分∠BOC,∴∠COD=∠BOC=70°,∵∠COE=90°,∴∠DOE=90°﹣70°=20°.(2)∵∠COE=90°,∴∠AOC+∠BOE=90°,∠COD+∠DOE=90°,∵OD平分∠BOC,∴∠COD=∠BOD,∴∠BOD+∠DOE=90°,∴图中互为余角的角有∠AOC和∠BOE,∠COD和∠DOE,∠BOD和∠DOE;故答案为:∠AOC和∠BOE,∠COD和∠DOE,∠BOD和∠DOE.21.一个角的余角比它的补角的还少15°,求这个角的度数.【解答】解:设这个角的度数为x,根据题意得:90°﹣x=(180°﹣x)﹣15°,解得:x=30°.答:这个角的度数为30°.22.如图,O为直线AB上一点,OM是∠AOC的角平分线,ON是∠COB的平分线(1)指出图中所有互为补角的角.(2)求∠MON的度数.(3)指出图中所有互为余角的角.【解答】解:(1)∠AOM与∠MOB,∠AOC与∠BOC,∠AON与∠BON,∠COM与∠MOB,∠CON与∠AON;(2)∵∠AOC的平分线是OM,∠BOC的平分线是ON,∴∠COM=∠AOC,∠CON=∠BOC,∵∠AOB=∠AOC+∠BOC=180°,∴∠MON=∠COM+∠CON=(∠AOC+∠BOC)=×180°=90°,(3)∠AOM与∠BON,∠COM与∠BON,∠CON与∠AOM,∠CON与∠COM.23.如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE=25°;(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;(3)如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.【解答】解:(1)∠COE=∠DOE﹣∠AOC=90°﹣65°=25°,故答案为:25°.(2)∵OC恰好平分∠AOE,∠AOC=65°,∴∠AOC=EOC=65°,∴∠COD=∠DOE﹣∠EOC=90°﹣65°=25°,答:∠COD=25°,(3)∠COE﹣∠AOD=25°,理由如下:当OD始终在∠AOC的内部时,有∠AOD+∠COD=65°,∠COE+∠COD=90°,∴∠COE﹣∠AOD=90°﹣65°=25°,24.将一副三角板中的两块直角三角板按如图的方式叠放在一起,直角顶点重合.(1)若∠ACB=115°时,则∠DCE的度数等于65°;(2)当CE平分∠ACD时,求∠ACB的度数;(3)猜想并直接写出∠ACB与∠DCE的数量关系(不必说明理由).【解答】解:(1)∵∠ACE+∠DCE=∠ACD=90°,∠BCD+∠DCE=∠BCE=90°,∴∠ACE=∠BCD=∠ACB﹣90°=25°,∴∠DCE═∠ACB﹣∠ACE﹣∠BCD=115°﹣25°﹣25°=65°;故答案为:65°(2)由CE平分∠ACD可得CE平分∠ACD=∠DCE=45°,由(1)可知∠ACE=∠BCD=45°,∴∠ACB=∠ACE+∠BCD+∠DCE=135°;(3)猜想:∠ACB+∠DCE=180°理由如下:∵∠ACE=90°﹣∠DCE又∵∠ACB=∠ACE+90°∴∠ACB=90°﹣∠DCE+90°=180°﹣∠DCE即∠ACB+∠DCE=180°.25.设∠α、∠β的度数分别为(2n+5)°和(65﹣n)°,且∠α、∠β都是∠γ的补角(1)求n的值;(2)∠α与∠β能否互余,请说明理由.【解答】解:(1)由∠α、∠β都是∠γ的补角,得∠α=∠β,即(2n+5)°=(65﹣n)°.解得n=20;(2)∠α与∠β互余,理由如下:∠α=(2n+5)°=45°,∠β=(65﹣n)°=45°,∵∠α+∠β=90°,∴∠α与∠β互为余角.26.如图①,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一直角边OM在射线OB上,另一直角边ON在直线AB 的下方,(1)将图①中的三角板绕点O逆时针方向旋转至图②,使边OM在∠BOC的内部,且恰好平分∠BOC,求∠BON大小;(2)将图①中的三角板绕点O逆时针方向旋转至图③.①如果ON恰好是∠AOC的角平分线,则∠AOM﹣∠NOC的度数为30°;②如果ON始终在∠AOC的内部,∠AOM﹣∠NOC的度数不会变化,请猜测出∠AOM﹣∠NOC的度数并说明理由.【解答】解:(1)∵OM平分∠BOC,∠BOC=120°,∴∠BOM=∠MON=60°,∵∠MON=90°,∴∠BON=∠MON﹣∠BOM=90°﹣60°=30°;(2)①∠AOM﹣∠NOC=30°;故答案为:30°②∠AOM﹣∠NOC=30°,理由如下:∵∠AOM=∠MON﹣∠AON=90°﹣∠AON,∠NOC=∠AOC﹣∠AON=60°﹣∠AON,∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°.27.如图,若O是直线AB上一点,∠COD=90°,OE平分∠BOC,∠AOC=40°,求∠DOE的度数.【解答】解:∵∠AOC=40°,∴∠BOC=180°﹣∠AOC=180°﹣40°=140°.∵OE平分∠BOC,∴∠COE=∠BOE=∠BOC=×140°=70°,∴∠DOE=∠COD﹣∠COE=90°﹣70°=20°.。
2019-2020学年七年级数学上册 4.3.3《余角和补角》课时练习(新版)新人教版

2019-2020学年七年级数学上册 4.3.3《余角和补角》课时练习(新版)新人教版一、选择题1.52°24'的余角和补角分别是( )A .37°36',127°36'B .127°36',37°36'C .38°24',128°24'D .128°24',38°24'答案:A知识点:余角和补角 角的计算解析:解答:52°24'的余角为:90°-52°24'=89°60'-52°24'=37°36',它的补角为:180°-52°24'=179°60'-52°24'=127°36'.分析:和为90°的两个角互为余角,和为180°的两个角互为补角.2.一个角比它的余角大25°,那么这个角的补角是( )A .67.5° B.22.5° C.57.5° D.122.5°答案:D知识点:余角和补角 一元一次方程的应用解析:解答:设这个角的度数为x °,根据题意得:x -(90-x )=25,解得x =57.5,所以这个角为57.5°,所以这个角的补角为180°-57.5°=122.5°.分析:先根据题意利用一元一次方程求的这个角,再根据补角的定义求这个角的补角.3.∠α的补角与∠β的余角相等,则∠α与∠β的关系是( )A .互为余角B .互为补角C .∠α比∠β大90°D .∠β比∠α大90°答案:C知识点:余角和补角 等式的性质解析:解答:因为∠α的补角与∠β的余角相等,所以180°-∠α=90°-∠β,等式两边都减90°同时加∠α得90°=∠α-∠β,所以∠α比∠β大90°.分析:根据余角和补角的定义列等式,再利用等式的性质对所列的等式进行变形,最后找到正确的答案.4.若∠1和∠2互补,且∠1<∠2,则∠1的余角是( )A .221∠ B .121∠ C .∠2—∠1 D .()1221∠-∠ 答案:D知识点:余角和补角解析:解答:因为∠1和∠2互补即∠1+∠2=180°,所以()112902∠+∠=o ,所以∠1的余角为()()119011212122-∠=∠+∠-∠=∠-∠o . 分析:互为补角的两个角有∠1<∠2即∠1为锐角,因为只有直角和锐角有余角,钝角没有余角.5.已知∠1=30°,则∠1的余角度数( )A .160°B .150°C .70°D .60°答案:D知识点:余角和补角解析:解答:因为90°-30°=60°,所以∠1的余角度数60°.分析:一个角的余角可以有多个,但是它们的度数是相同的.6.如果α∠和β∠互补,且αβ∠>∠,则下列表示β∠的余角的式子中正确的有( ) ①β∠-︒90 ②︒-∠90α ③()βα∠+∠21 ④()12βα∠-∠ A .①②③ B.①②④ C.①③④ D.②③④答案:B知识点:余角和补角解析:解答:因为∠α和∠β互补即∠α+∠β=180°,所以()1902αβ∠+∠=o ,所以∠β的余角为()()119022ααβαβα-∠=∠+∠-∠=∠-∠o ,所以④正确;根据余角的定义①正确;因为()90901809090βααα-∠=--∠=-+∠=∠-o o o o o,所以②正确. 分析:互为补角的两个角有αβ∠>∠即∠β为锐角,因为只有直角和锐角有余角,钝角没有余角.7.A 看B 的方向是北偏东21°,那么B 看A 的方向( )A .南偏东69°B .南偏西69°C .南偏东21°D .南偏西21° 答案:D知识点:钟面角、方位角解析:解答:由题意作图,在图中可知B看A的方向是南偏西21°.分析:先确定观察点,再确定方向.从A看B则点A是观察点,从B看A则点B是观察点.8.如果在点O北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则∠AOB 的度数是()A.100° B.70° C.180° D.140°答案:A知识点:钟面角、方位角解析:解答:由题意可作下图,在图中可看出∠AOB的度数是100°.分析:解此类题根据题意画出图后再结合相关知识比较容易解决.9.下列说法正确的是( )A.90°的角叫余角B.一个角的补角一定是钝角C.如果两个角互补,其中一个是钝角,那么另一个角一定是锐角D.已知∠A+∠B+∠C=180°,则∠A、∠B、∠C互补答案:C知识点:余角和补角解析:解答:和为90°的两个角互为余角,所以A的说法错误;锐角的补角是钝角,直角补角的是直角,钝角的补角是锐角,所以B的说法错误而C的说法正确;互补是两个角之间的数量关系,所以D的说法错误.分析:紧扣余角和补角的定义来解此类题.10.如果∠1与∠2互余,∠3与∠4互余,如果∠1=∠3,则∠2与∠4的数量关系是()A.∠2=∠4 B.∠2<∠4 C.∠2>∠4 D.无法判断答案:A知识点:余角和补角角的大小比较解析:解答:因为∠1与∠2互余,∠3与∠4互余,且∠1=∠3,即等角的余角相等,所以∠2=∠4.分析:余角的性质:同角(等角)的余角相等.11.一个锐角的余角加上90°,就等于( )A.这个锐角的余角 B.这个锐角的补角C.这个锐角的2倍 D.这个锐角的3倍答案:B知识点:余角和补角解析:解答:设这个锐角为∠α,那么根据题意有90°-∠α+90°=180°-∠α,即为∠α的补角.分析:根据余角与补角的定义列式即可解此题.12.一个角的余角比它本身小,这个角是( )A.大于45° B.小于45° C.大于0°小于45° D.大于45°小于90°答案:D知识点:余角和补角解析:解答:依据选项,可以选取度数大于45°的角,如60°的角,发现满足题意,但是只有锐角才有余角,所以必须同时小于90°,所以选择D.分析:对于单选题和填空题,有时我们可以采用取特殊值的方法解题.13.下列说法中正确的是( )A.一个角的补角只有一个B.一个角的补角必大于这个角C.若不相等的两个角互补,则这两个角一个是锐角,一个是钝角D.互余的两个角一定相等答案:C知识点:余角和补角解析:解答:一个角的补角可以有多个,但是它们的度数相同,所以A的说法错误;一个钝角的补角为锐角,那么它的补角小于这个角,所以B的说法错误;互余的两个角和90°,不一定相等,所以D的说法错误.分析:锐角的补角为钝角,直角的补角为直角,钝角的补角为锐角.14.如果一个角等于36°,那么它的余角等于( )A.64° B.54° C.144° D.36°答案:B知识点:余角和补角解析:解答:和为90°的两个角互为余角,所以36°的角的余角为54°.分析:和为90°的两个角互为余角.15.∠α=∠β,且∠α与∠β互余,则( )A.∠α=90° B.∠β=45° C.∠β=60° D.∠α=30°答案:B知识点:余角和补角解析:解答:因为∠α与∠β互余,所以∠α+∠β=90°,又因为∠α=∠β,所以2∠α=90°即∠α=∠β=45°.分析:互余的两个角和为90°.二、填空题1.40°的余角是,106°20'的补角是.答案:50°;73°40'知识点:余角和补角角的计算解析:解答:因为90°-40°=50°,所以40°的余角是50°;因为180°-106°20'=73°40',所以106°20'的补角是73°40'.分析:互余的两个角和为90°,互补的两个角和为180°.2.一个角为n°(n<90),则它的余角为,补角为.答案:90°-n°;180°-n°知识点:余角和补角解析:解答:因为互余的两个角和为90°,所以n °角的余角为90°-n °,又因为互补的两个角和为180°,所以n °角的补角为180°-n °.分析:互余的两个角和为90°,互补的两个角和为180°.3.α∠和β∠都是AOB ∠的余角,则α∠ β∠.答案:=知识点:余角和补角解析:解答:因为∠α和∠β都是∠AOB 的余角,又因为同角的余角相等,所以∠α=∠β. 分析:余角的性质:同角(等角)的余角相等.4.如果∠3+∠4=180°,∠5+∠3=180°,则∠4与∠5的关系是 ,理由是 .答案:∠4 =∠5;同角的补角相等知识点:余角和补角解析:解答:因为∠3+∠4=180°,∠5+∠3=180°,即∠3与∠4、∠5分别互补,所以∠4=∠5,理由为同角的补角相等.分析:补角的性质:同角(等角)的补角相等.5.看下图填空:∠AOB =∠AOD -( )=( )-∠BOC ;∠COD =∠BOD -( )=∠AOD -( ).答案:∠BOD ,∠AOC ;∠BOC ,∠AOC知识点:角的计算解析:解答:结合图形可解此题. 分析:在进行角的和、差运算时,一定要结合图形,只有先弄清角之间的位置关系,才能正确解题.三、解答题1.读句画图并填空:(1)画平角AOB ,画射线OC ,再分别画AOC ∠、BOC ∠的角平分线OD 、OE ;(2)图中,∵COE ∠= COB ∠,COD ∠= AOC ∠, ∴=∠+∠=∠COD COE DOE AOB ∠= ×︒180= . 答案:(1)见解析图;(2)1111;;;;902222o 知识点:角平分线的定义解析:解答:解:(1)如下图所示:(2)∵COE ∠=12COB ∠,=∠COD 12AOC ∠(角平分线的定义)∴DOE COE COD ∠=∠+∠12AOB =∠=1180902⨯︒=o (等量代换). 分析:角平分线即将一个分成两个相等角的射线.2.α∠和β∠互补,且50αβ∠-∠=︒,求α∠和β∠的度数.答案:115°,65°知识点:余角与补角 一元一次方程的应用解析:解答:解:设∠α的度数为x ,则∠β的度数为180°-x .因为∠α-∠β=50°,所以x -(180°-x )=50°,解得x =115°,所以∠β=65°,所以∠α和∠β的度数分别为115°和65°.分析:利用互余、互补的关系求角度,常用设未知数列方程的方法来求解.3.一个角的余角比它的补角的13还少20o ,求这个角的度数. 答案:75°知识点:余角与补角 一元一次方程的应用解析:解答:解:设这个角的度数为x .根据题意得90°-x =13(180°-x )-20°,解得x =75°,所以这个角的度数为75°. 分析:利用互余、互补的关系求角度,常用设未知数列方程的方法来求解.4.若α∠和β∠互余,且α∠:β∠=7:2,求α∠、β∠的度数.答案:70°,20°知识点:余角与补角 一元一次方程的应用解析:解答:解:因为∠α:∠β=7:2,所以可设∠α和∠β的度数分别为7x 与2x .因为∠α和∠β互余,所以7x +2x =90°,解得x =10°,所以∠α=70°,∠β=20°,所以∠α与∠β的度数分别为70°与20°.分析:在遇到比例时,我们一般设一份为x .5.如图,已知︒=∠90AOC ,COD ∠比DOA ∠大︒28,OB 是AOC ∠的平分线,求BOD ∠的度数.答案:14°知识点:余角和补角 角平分线的定义 一元一次方程的应用 角的计算解析:解答:解:设∠AOD 的度数为x ,则∠COD 的度数为x +28°.因为∠AOC =90°,所以可列方程x +x +28°=90°,解得x =31°,即∠AOD =31°,又因为OB 是∠AOC 的平分线,所以∠AOB =45°,所以∠BOD =∠BOA -∠AOD =45-31°=14°.分析:求∠BOD ,由图中可知∠BOD =∠BOA -∠AOD ,由题可知关键在于求∠AOD ,所以可设∠AOD 的度数为x ,则∠COD 的度数为x +28°,再结合题意与图形可知∠COD 与∠AOD 互余可列方程,进而求得∠AOD ,最后求得∠BOD .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020年七年级数学上册 4.3.3 余角和补角练习 (新版)新人
教版
1.下列说法正确的有( ) ①若∠1+∠2=90°,则∠1与∠2互为余角; ②若∠1+∠2=180°,则∠1与∠2互为补角; ③120°的角和60°的角都互为补角 ④同角的余角相等;
A.1个
B.2个
C.3个
D.4个 2.下列说法正确的是( ) A.一个角的补角一定大于它本身 B.一个角的余角一定小于它本身 C.若两个角的余角相等,则它们的补角也相等.
D.一个钝角减去一个锐角的差一定是一个锐角.
3.一个锐角的补角比这个角的余角大( ) A.30° B.45° C.60° D.90°
4.如图,∠AOB=150°,∠AOC=∠BOD=60°,有下列结论: ①∠COD=30°, ②∠AOD =∠BOC; ③BO⊥OC; 其中正确的是( )
A.只有①
B.只有①②
C.只有②③
D.①②③
5.一条船沿北偏东50°的方向航行到某地,然后沿原方向返回,船返回时航行的正确方向是( )
A.北偏西130°
B.南偏西50°
C.北偏西50°
D.南偏西130°
6.学校、电影院、公园在平面图上的标点分别是A 、B 、C ,电影院在学校的正东方向,公园在学校的南偏西25°方向,那么平面图上的∠CAB 等于( )
A.155°
B.115°
C.65°
D.25° 7.如果∠1的补角是∠2,且∠1>∠2,那么∠2的余角是( )
A.
121∠ B.22
1
∠ C.1900∠- D.()
1902
10
∠+
8.一个角的余角比它的补角的
3
1
还少20°,则这个角的度数为( )
A.75°
B.85°
C.95°
D.105°
9.已知∠A 与∠B 互余,且∠B=450
,则∠A=__________,∠A 与∠B 的大小关系是________.
10.如图所示,如果把三角形AD B 对折恰好能与三角形ADC 完全重合,那么∠B 与∠C 的关系是_________,∠ADB 与∠ADC 的关系是___________.
11.已知一个角是它的余角的三分之一,那么这个角的余角是______,补角是______. 12.已知三角形的内角和为180°,如图,∠A 与∠B 互余,∠1与∠A 互余,∠2与∠B 互余,请指出图中所有相等的角
.
13. 已知∠A 与∠B 互余,∠A 与∠C 互补,且∠B+∠C=120°,求∠A +∠B+∠C 的度数.
14.已知蚂蚁从点O 出发,沿北偏东60°方向爬行2cm ,碰到障碍物B ,又沿北偏西60°方向向西行2cm 到点C.
(1)请画出蚂蚁的爬行路线;
(2)点C 在点O 的什么位置?测量出点C 离点O 的长度(精确到1cm ).
4.3.3 余角和补角
1.D;
2.C;
3.D;
4.D;
5.B;
6.A;
7.C;
8.A;
9. 45°,相等;10.相等,相等;11. 67.5°,157.5°;12.解:∠A=∠2,∠1=∠B;13.解:由题意得,∠A+∠B=90°,所以∠B=90°-∠A,∠C=180°-∠A,因为∠B+∠C=120°,所以90°-∠A+180°-∠A=120°,解得∠A=75°,所以∠A+∠B+∠C=195°;14.(1)如图;(2)正北方,2cm;。
