重庆市九校联盟2019届高三数学12月联考试题文201901110319
重庆市九校联盟2019届高三上学期12月联合考试理综化学试题(附答案及解析)
重庆市九校联盟2019届高三上学期12月联合考试理综化学试题题号一二三总分得分评卷人得分一、选择题本大题共5道小题。
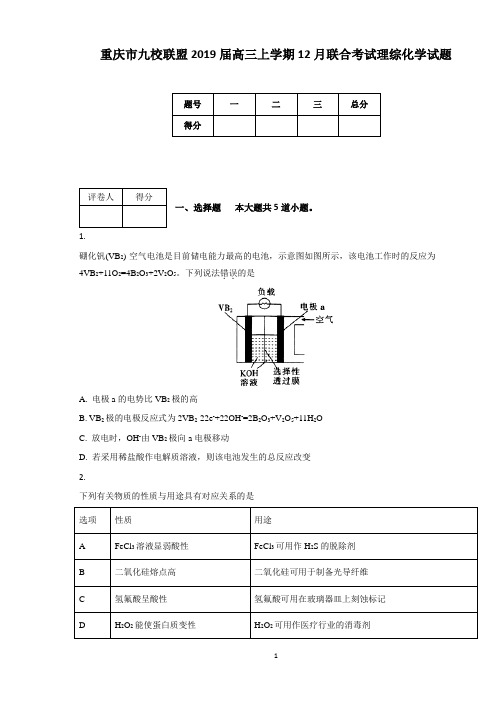
1.硼化钒(VB2)-空气电池是目前储电能力最高的电池,示意图如图所示,该电池工作时的反应为4VB2+11O2=4B2O3+2V2O5。
下列说法错误..的是A. 电极a的电势比VB2极的高B. VB2极的电极反应式为2VB2-22e-+22OH-=2B2O3+V2O5+11H2OC. 放电时,OH-由VB2极向a电极移动D. 若采用稀盐酸作电解质溶液,则该电池发生的总反应改变2.下列有关物质的性质与用途具有对应关系的是选项性质用途A FeCl3溶液显弱酸性FeCl3可用作H2S的脱除剂B 二氧化硅熔点高二氧化硅可用于制备光导纤维C 氢氟酸呈酸性氢氟酸可用在玻璃器皿上刻蚀标记D H2O2能使蛋白质变性H2O2可用作医疗行业的消毒剂3.设N A为阿伏加德罗常数的数值,下列有关说法正确的是A. 将1 mol NH4NO3溶于稀氨水中使溶液呈中性,溶液中NH4+的数目为N AB. 标准状况下,2.24 L甲醇中含有C—H键的数目为0.3N AC. 0.1 mol·L-1的Na2CO3溶液中,阳离子的总数为0.2N AD. 将1 mol Cl2通入水中,HClO、Cl-、ClO-的粒子数之和为2N A4.下列有关实验操作的叙述错误..的是A. 过滤操作中,漏斗的尖端应接触烧杯内壁B. 向容量瓶中转移液体时,引流用的玻璃棒可以接触容量瓶内壁C. 配制5%NaCl溶液时,必须用到的玻璃仪器是容量瓶、烧杯、胶头滴管、玻璃棒D. 配制氯化铁溶液时,将氯化铁溶解在较浓的盐酸中再加水稀释5.短周期主族元素W、X、Y、Z的原子序数依次增大,W的最简单氢化物是天然气的主要成分,W与Y 的最外层电子数之和等于X的最外层电子数,且W、X、Y、Z的最外层电子数均为偶数;向X、Y、Z组成的一种化合物中加入盐酸,产生的气体能使品红溶液褪色。
2019届重庆市 九校联盟 高三12月联合考试 数学(理)试卷(PDF版含答案与详细解析)

为
C
上一点,
uuur F1Q
=
uuur QP
,O
为坐标原点,若
|PF1|=10,则|OQ|=
A.9 B.10 C.1 D.1 或 9
10.△ABC 的内角 A,B,C 的对边分别为 a,b,c.若(sin B+sin C)2-sin2(B+C)=3sin Bsin C,且 a=2,则 △ABC 的面积的最大值是
=
x(ex
−1) + x ex −1
+1
=
x
+
x +1 有解. ex −1
令
g(x)
=
x
+
x +1 ex −1
,则
g ′( x )
=
−xex − 1 (ex − 1)2
+1=
ex(ex − x − (ex − 1)2
2)
.
设函数 h(x)=ex-x-2,h′(x)=ex-1>0,所以 h(x)在(0,+∞)上单调递增.
8.为了得到 y=-2cos 2x 的图象,只需把函数 y = 3 sin 2x − cos 2x 的图象
A.向左平移 π 个单位长度 B.向右平移 π 个单位长度
3
3
C.向左平移 π 个单位长度 D.向右平移 π 个单位长度
6
6
9.已知双曲线
C:
x2 16
−
y2 48
=
1 的左、右焦点分别为
F1,F2,P
2019 届重庆市九校联盟高三 12 月联合考试 高三数学考试(理科)
第Ⅰ卷
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
重庆市九校联盟2019届高三12月联合考试数学(文)试题(精品解析)

高三数学考试(文科)第Ⅰ卷一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={x|3-2x<-1},B={x|x(2x-5)≤0},则A∪B=A. B.C. [0,+∞)D.【答案】C【解析】【分析】解不等式化简集合,利用一元二次不等式的解法化简集合,然后利用并集的定义求解即可.【详解】,,,故选C.【点睛】研究集合问题,一定要抓住元素,看元素应满足的属性.研究两集合的关系时,关键是将两集合的关系转化为元素间的关系,本题实质求满足属于集合或属于集合的元素的集合.2.若复数满足,则的虚部为( )A. B. C. 1 D. -1【答案】D【解析】【分析】由复数的除法运算化简即可得解.【详解】由,可得.z的虚部为-1,故选D.【点睛】本题主要考查了复数的除法运算,属于基础题.3.函数的图象大致是( )A. B. C. D.【答案】C【解析】【分析】利用排除法,由排除选项;由排除选项,从而可得结果.【详解】,,排除选项;,排除选项,故选C.【点睛】函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势;(3)从函数的奇偶性,判断图象的对称性;(4)从函数的特征点,排除不合要求的图象.4.已知平面向量满足,且,则向量的夹角为A. B. C. D.【答案】A【解析】【分析】由,结合可得,利用平面向量的数量积公式可得结果. 【详解】,,所以,可得,即,,设两向量夹角为,则,,,即为,故选A.【点睛】本题主要考查向量的模、夹角及平面向量数量积公式,属于中档题.平面向量数量积公式有两种形式,一是,二是,主要应用以下几个方面:(1)求向量的夹角,(此时往往用坐标形式求解);(2)求投影,在上的投影是;(3)向量垂直则;(4)求向量的模(平方后需求).5.已知函数f(x)为R上的奇函数,当x<0时,,则xf(x)≥0的解集为( )A. [-1,0)∪[1,+∞)B. (-∞,-1]∪[1,+∞)C. [-1,0]∪[1,+∞)D. (-∞,-1]∪{0}∪[1,+∞)【答案】D【解析】【分析】由时,,可得在上递增,利用奇偶性可得在上递增,再求得,分类讨论,将不等式转化为不等式组求解即可.【详解】时,,,且在上递增,又是定义在上的奇函数,,且在上递增,等价于或或,解得或或,即解集为,故选D.【点睛】本题主要考查函数的奇偶性与单调性的应用,属于难题.将奇偶性与单调性综合考查一直是命题的热点,解这种题型往往是根据函数在所给区间上的单调性,根据奇偶性判断出函数在对称区间上的单调性(偶函数在对称区间上单调性相反,奇函数在对称区间单调性相同),然后再根据单调性列不等式求解.6.设x,y满足约束条件则z=4x+y的最小值为( )A. -3B. -5C. -14D. -16【答案】C【解析】【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,把最优解的坐标代入目标函数得结论.【详解】画出表示的可行域,如图,由可得,可得,将变形为,平移直线,由图可知当直经过点时,直线在轴上的截距最小,最小值为,故选C.【点睛】本题主要考查线性规划中,利用可行域求目标函数的最值,属于简单题.求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.7.某几何体的三视图如图所示(其中俯视图中的曲线是圆弧),则该几何体的表面积为A. 4π+6B. 6π+6C. 4π+3D. 6π+3【答案】A【解析】【分析】由三视图可知,该几何体为半个圆柱,圆柱的底面半圆的半径为1,半圆柱高为3,算出各表面的面积即可得结果.【详解】由三视图可知,该几何体为半个圆柱,圆柱的底面半圆的半径为1,半圆柱高为3,其表面积有四部分组成,上、下底面半圆面积为,轴截面矩形面积为,圆柱侧面积的一半为,几何体表面积为,故选A.【点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力,属于难题.三视图问题是考查学生空间想象能力最常见题型,也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键,不但要注意三视图的三要素“高平齐,长对正,宽相等”,还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响,对简单组合体三视图问题,先看俯视图确定底面的形状,根据正视图和侧视图,确定组合体的形状.8.为了得到y=−2cos 2x的图象,只需把函数的图象( )A. 向左平移个单位长度B. 向右平移个单位长度C. 向左平移个单位长度D. 向右平移个单位长度【答案】D【解析】【分析】逆用两角和的余弦公式,得=,再分析两个函数图象的变换.【详解】因为,要得到函数,只需将的图象向右平移个单位长度即可.故选D.【点睛】本题考查了三角函数的图象与变换,考查了两角和的余弦公式的应用;解决三角函数图象的变换问题,首先要把变换前后的两个函数化为同名函数.9.已知双曲线的左、右焦点分别为,,为上一点,,为坐标原点,若,则A. 10B. 9C. 1D. 1或9【答案】B【解析】【分析】连接,利用,可得是三角形的中位线,由,结合双曲线的定义可得,从而可求得的大小.【详解】连接,因为,所以是三角形的中位线,,由可得,,或,又因为,所以,,故选B.【点睛】本题主要考查双曲线的定义与简单性质、平面向量的线性运算,属于中档题.求解与双曲线性质有关的问题时要结合图形进行分析,即使不画出图形,思考时也要联想到图形,当涉及顶点、焦点、实轴、虚轴、渐近线等双曲线的基本量时,要理清它们之间的关系,挖掘出它们之间的内在联系.10.如图,△ABC和△DEF均为等边三角形,AF=BD=CE,DF=2AF=20 cm,若在△ABC中随机投入260粒芝麻,则落在△DEF外的芝麻粒数约为A. 100B. 130C. 150D. 180【答案】D【解析】【分析】利用余弦定理求出的值,从而可得两个正三角形的面积比,得到豆粒落在小正三角形内的概率,从而可得豆粒落在小三角形内的个数,再作差即可得结果.【详解】,为正三角形,,,,即芝麻粒落在内的概率为,粒芝麻落在内的有粒,落在外的有(粒),故选D.【点睛】本题主要考查“面积型”的几何概型的应用,属于中档题. 解决几何概型问题常见类型有:长度型、角度型、面积型、体积型,求与面积有关的几何概型问题关鍵是计算问题的总面积以及事件的面积;几何概型问题还有以下几点容易造成失分,在备考时要高度关注:(1)不能正确判断事件是古典概型还是几何概型导致错误;(2)基本事件对应的区域测度把握不准导致错误;(3)利用几何概型的概率公式时, 忽视验证事件是否等可能性导致错误.11.的内角的对边分别为,若,且,则的面积的最大值是()A. B. C. D. 4【答案】B【解析】【分析】由,根据三角形内角和定理,结合诱导公式可得,再由正弦定理可得,从而由余弦定理求得,再利用基本不等式可得,由三角形面积公式可得结果.【详解】,且,,由正弦定理可得,由余弦定理可得,,又,即,,即最大面积为,故选B.【点睛】本题主要考查正弦定理、余弦定理以及基本不等式的应用,属于难题.对余弦定理一定要熟记两种形式:(1);(2),同时还要熟练掌握运用两种形式的条件.另外,在解与三角形、三角函数有关的问题时,还需要记住等特殊角的三角函数值,以便在解题中直接应用.12.设0<m ≤2,已知函数,对于任意x 1,x 2∈[m -2,m ],都有|f (x 1)-f (x 2)|≤1,则实数m 的取值范围为A. B.C.D.【答案】B 【解析】 【分析】 设,函数,对于任意,都有,等价于在上,,利用导数判断函数在为减函数,由,解不等式可得结果.【详解】设,函数,对于任意,都有,等价于在上,,求导时,在为减函数, 因为,,在上为减函数,,,,得或,又,即实数的范围是,故选B.【点睛】本题主要考查利用导数研究函数的单调性、求函数的最值,以及转化与划归思想的应用,属于难题.转化与划归思想解决高中数学问题的一种重要思想方法,尤其在解决知识点较多以及知识跨度较大的问题发挥着奇特功效,运用这种方法的关键是将题设条件研究透,这样才能快速找准突破点.以便将问题转化为我们所熟悉的知识领域,进而顺利解答,希望同学们能够熟练掌握并应用于解题当中.解答本题的关键是将不等式恒成立问题转化为求函数最值问题.第Ⅱ卷二、填空题:把答案填在答题卡中的横线上.13.已知函数,则____.【答案】【解析】【分析】利用分段函数的解析式先求出,从而可得的值.【详解】,且,,,故答案为.【点睛】本题主要考查分段函数的解析式,属于中档题.对于分段函数解析式的考查是命题的动向之一,这类问题的特点是综合性强,对抽象思维能力要求高,因此解决这类题一定要层次清楚,思路清晰. 当出现的形式时,应从内到外依次求值.14.已知,,则cos 2α=____.【答案】【解析】【分析】由,,求得,再利用二倍角的余弦公式可得结果.【详解】,①,②①-②得,,故答案为.【点睛】三角函数求值有三类,(1)“给角求值”:一般所给出的角都是非特殊角,从表面上来看是很难的,但仔细观察非特殊角与特殊角总有一定关系,解题时,要利用观察得到的关系,结合公式转化为特殊角并且消除非特殊角的三角函数而得解.(2)“给值求值”:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题关键在于“变角”,使其角相同或具有某种关系.(3)“给值求角”:实质是转化为“给值求值”,先求角的某一函数值,再求角的范围,确定角.15.如图,在直四棱柱ABCD-A1B1C1D1中,已知四边形ABCD是直角梯形,∠BAD=90°,AB∥CD,AB=AD=AA1=1,CD=2,E为BB1的中点,则直线AD与直线CE所成角的正切值为____.【答案】【解析】【分析】设为中点,为中点,可得是平行四边形,,又有,由此是和所成角,先证明平面,,利用直角三角形的性质可得结果.【详解】如图,为中点,为中点,连结,则,可得是平行四边形,,又有,是和所成角,由直棱柱的性质可得,由已知可得,所以平面,可得平面,因为平面,所以,,,故答案为.【点睛】本题主要考查异面直线所成的角,属于中档题.求异面直线所成的角先要利用三角形中位线定理以及平行四边形找到异面直线所成的角,然后利用直角三角形的性质及余弦定理求解,如果利用余弦定理求余弦,因为异面直线所成的角是直角或锐角,所以最后结果一定要取绝对值.16.点在椭圆上,的右焦点为,点在圆上,则的最小值为__________.【答案】【解析】【分析】先求得椭圆的值,求得圆的圆心和半径.设左焦点为将所求的最小值,转化为来求解.当四点共线时,取得最小值,利用两点间的距离公式来求得这个最小值.【详解】依题意可知,椭圆的,设左焦点为.圆的方程配方得,故圆心为,半径为.根据椭圆的定义有:,故当时,上式取得最小值,即,即最小值为.【点睛】本小题主要考查椭圆的定义以及几何性质,考查圆的一般方程化为标准方程,考查与椭圆和圆有关的距离的最小值的求法,考查了化归与转化的数学思想方法.属于中档题.根据椭圆的定义,椭圆上的点到两个焦点的距离之和是常数,这个是本题中转化的关键.圆的方程化为标准方程主要是通过配方法.三、解答题:解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题17.已知数列{a n}的前n项和为S n,a1=3,a n+1=2S n+3(n∈N*).(1)求数列{a n}的通项公式;(2)设b n=log3a n,若数列的前n项和为T n,证明:T n<1.【答案】(1);(2)详见解析.【解析】【分析】(1)由,可得,两式相减得,即,为从第2项开始的等比数列,求得,验证首项是否适合即可得结果;(2)由(1)知,可得,利用裂项相消法求出,再由放缩法可得结果.【详解】(1)因为a n+1=2S n+3,①a n=2S n-1+3.②①-②得a n+1-a n=2a n,即a n+1=3a n(n≥2),所以{a n}为从第2项开始的等比数列,且公比q=3,又a1=3,所以a2=9,所以数列{a n}的通项公式a n=3n(n≥2).当n=1时,a1=3满足上式,所以数列{a n}的通项公式为a n=3n.(2)由(1)知b n=log3a n=log33n=n,所以,所以得证.【点睛】本题主要考查等比数列的定义与通项公式,以及裂项相消法求数列的和,属于中档题. 裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,常见的裂项技巧:(1);(2);(3);(4);此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.18.2018年4月全国青少年足球超级联赛火爆开启,这是体育与教育的强强联手,这是培养足球运动员的黄金摇篮,也是全国青少年足球的盛宴.组委会在某场联赛结束后,随机抽取了300名观众进行对足球“喜爱度”的调查评分,将得到的分数分成6段:[64,70),[70,76),[76,82),[82,88),[88,94),[94,100]后得到如图所示的频率分布直方图.(1)求a的值并估计这300名观众评分的中位数;(2)若评分在“88分及以上”确定为“足球迷”,现从“足球迷”中按区间[88,94)与[94,100]两部分按分层抽样抽取5人,然后再从中任意选取两人作进一步的访谈,求这两人中至少有1人的评分在区间[94,100]的概率.【答案】(1);(2).【解析】【分析】(1)根据所有小矩形的面积和为1,列方程求解可得,利用直方图左右两边面积相等处横坐标表示中位数;(2)列举出从5人中选取2人作进一步的访谈的所有事件共有10个,以及这两人中至少有1人的评分在区间的基本事件有7个,利用古典概型概率公式可得结果.【详解】(1)因为(a+0.025+0.035+0.050+0.030+0.020)×6=1,所以.设y为观众评分的中位数,由前三组的概率和为0.40,前四组的概率和为0.70,知82<y<88,所以0.4+(y-82)×0.05=0.5,则y=84.(2)以样本的频率作为概率,评分在“88分及以上”确定为“足球迷”,现从“足球迷”中按分层抽样抽取5人,则从评分在区间[88,94)的“足球迷”中抽取3人,记为A,B,C,从评分在区间[94,100]的“足球迷”中抽取2人,记为a,b.从5人中选取2人作进一步的访谈的所有事件为AB,AC,BC,Aa,Ba,Ca,Ab,Bb,Cb,ab,共10个基本事件,这两人中至少有1人的评分在区间[94,100]的基本事件有Aa,Ba,Ca,Ab,Bb,Cb,ab,共7个基本事件,则选取的2人中至少有1人的评分在区间[94,100]上的概率.【点睛】本题主要考查直方图与古典概型概率公式的应用,属于中档题,利用古典概型概率公式求概率时,找准基本事件个数是解题的关键,基本亊件的探求方法有(1) 枚举法:适合给定的基本事件个数较少且易一一列举出的;(2) 树状图法:适合于较为复杂的问题中的基本亊件的探求,在找基本事件个数时,一定要按顺序逐个写出:先,…. ,再,…..依次….… 这样才能避免多写、漏写现象的发生.19.如图,在五面体ABCDFE中,底面ABCD为矩形,EF∥AB,BC⊥FD,过BC的平面交棱FD于P,交棱FA于Q.(1)证明:PQ∥平面ABCD;(2)若CD⊥BE,EF=EC=1,,求五面体ABCDFE的体积.【答案】(1)详见解析;(2).【解析】【分析】(1)由矩形的性质可得,由线面平行的判定定理可得平面,再由线面平行的性质定理可得,进而可得结果;(2)由,证明平面,可得,由,证明平面,可得,即,两两垂直,利用分割法,根据锥体的体积公式,从而可得结果.【详解】(1)因为底面ABCD为矩形,所以AD∥BC.,,.(2)由CD⊥BE,CD⊥CB,易证CD⊥CE,由BC⊥CD,BC⊥FD,易证BC⊥平面CDFE,所以CB⊥CE,即CD,CE,CB两两垂直.连接FB,FC,则CD=2,BC=3,,,.【点睛】本题主要考查线面平行的判定定理,以及几何体体积的求解,属于中档题. 空间几何体体积问题的常见类型及解题策略:(1)求简单几何体的体积时若所给的几何体为柱体、锥体或台体,则可直接利用公式求解;(2)求组合体的体积时若所给定的几何体是组合体,不能直接利用公式求解,则常用转换法、分割法、补形法等进行求解;(3)求以三视图为背景的几何体的体积时应先根据三视图得到几何体的直观图,然后根据条件求解. 20.已知抛物线y2=2px(p>0)的焦点为F,过F且与x轴垂直的直线交该抛物线于A,B两点,|AB|=4.(1)求抛物线的方程;(2)过点F的直线l交抛物线于P,Q两点,若△OPQ的面积为4,求直线l的斜率(其中O为坐标原点).【答案】(1);(2).【解析】【分析】(1)根据抛物线的定义以及抛物线通径的性质可得,从而可得结果;(2)设直线的方程为,代入,得,利用弦长公式,结合韦达定理可得的值,由点到直线的距离公式,根据三角形面积公式可得,从而可得结果.【详解】(1)由抛物线的定义得到准线的距离都是p,所以|AB|=2p=4,所以抛物线的方程为y2=4x.(2)设直线l的方程为y=k(x-1),P(x1,y1),Q(x2,y2).因为直线l与抛物线有两个交点,所以k≠0,得,代入y2=4x,得,且恒成立,则,y1y2=-4,所以.又点O到直线l的距离,所以,解得,即.【点睛】本题主要考查直线与抛物线的位置关系的相关问题,意在考查综合利用所学知识解决问题能力和较强的运算求解能力,其常规思路是先把直线方程与圆锥曲线方程联立,消元、化简,然后应用根与系数的关系建立方程,解决相关问题.21.设函数.(1)求的单调区间;(2)若对于任意,都有,求的取值范围.【答案】(1)的单调递减区间是,单调递增区间是 (2)【解析】【分析】(1)对函数求导,由导函数的正负得到原函数的单调区间;(2)由第一问确定出函数在给定区间上的单调性,之后将任意的,恒成立转化为,即,再构造新函数,求导得到其单调性,结合其性质,求得最后的结果.【详解】(1)因为,所以,所以当时,;当时,.所以的单调递减区间是,单调递增区间是.(2)由(1)知,在上单调递减,在上单调递增,故在处取得最小值,且.所以对于任意的,的充要条件为,即①设函数,则.当时,;当时,,故在上单调递减,在上单调递增.又,,,所以当时,,即①式成立,综上所述,的取值范围是.【点睛】该题考查的是应用导数研究函数的问题,涉及到的知识点有应用导数研究函数的单调性,应用导数研究恒成立问题对应的参数的取值范围,在解题的过程中,需要正确理解题意,对问题正确转化,构造相应的新函数来解决问题.(二)选考题:请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.在直角坐标系中,曲线的参数方程为(为参数).M是曲线上的动点,将线段OM绕O 点顺时针旋转得到线段ON,设点N的轨迹为曲线.以坐标原点O为极点,轴正半轴为极轴建立极坐标系.(1)求曲线的极坐标方程;(2)在(1)的条件下,若射线与曲线分别交于A, B两点(除极点外),且有定点,求的面积.【答案】(1),;(2).【解析】【分析】(1)将曲线C1的参数方程转化为普通方程,然后由普通方程转化为极坐标方程;再用N表示出M,根据点M在曲线C1上,采用相关点法,求轨迹C2的极坐标方程;(2)根据已知条件,求得,通过求解.【详解】(1)由题设,得的直角坐标方程为,即,故的极坐标方程为,即.设点,则由已知得,代入的极坐标方程得,即.(2)将代入的极坐标方程得,又因为,所以,,所以.【点睛】本题考查了极坐标方程、直角坐标方程、参数方程的互化,考查了点的极坐标以及极坐标与直角坐标的关系,涉及了三角函数的诱导公式和三角形的面积公式,考查了推理论证能力、运算求解能力,以及化归与转化思想.23.已知函数(1)当时,求不等式的解集;(2)对于任意的实数,存在实数,使得不等式成立,求实数的取值范围。
重庆市九校联考2019届高三语文上学期12月试题及解析

重庆市九校联考2019届高三12月语文试卷一、现代文阅读(一)论述类文本阅读阅读下面的文字,完成1~3题。
性灵源于古代诗以言志之论,性指本性,性情,本真;灵有灵机、灵巧之意,侧重于情感表达的技巧,后来又加入了天赋、契机、生趣等含义。
自南朝刘勰、钟嵘之后很长时期内,性情、性灵、情性在文学批评中出现的时候,只是侧重点的不同,并不存在大的差别,都是在古典诗学性情论的语境中使用。
明代中期以来,王阳明心学盛行海内,主张“心者天地万物之主”,打破了程朱理学一统天下的格局和思想学术的僵化状态。
与此同时,传统伦理对人性的禁锢进一步加深,社会经济的发展和市民阶层的兴起又刺激了个人主体意识的觉醒。
明代社会随处可见“存天理,去人欲”的说教,又随处可见对金钱、美色的追求。
万历年间,王学左派尤其是其后期杰出的代表人物李贽,对程朱理学做了尖锐批判,提出保护和尊重人欲使其健康合理的发展,在文学上提倡“童心”,即“绝假纯真,最初一念之本心”。
汤显祖倡言“情有者理必无,理有者情必无”,都表现出以情反理的鲜明特征。
晚明公安派文学家袁宏道则将这股个性解放的思潮与古老的“性灵”相结合,提出了“独抒性灵,不拘格套”的宣言。
他们强调诗文创作当不受传统伦理以及古人陈法的禁锢与束缚,自由地抒发真情实感,即使言语拗口难工,也显示出作者自己的本色与独创,呼吁充分发挥自身的创造力,无所依傍、天真率直地创造属于自己时代的文学。
性灵追求创作个体的情感体验和生命本真,自然也就深入到了世俗、琐碎的社会生活,开始坦率地表达对世俗生活的热爱和“好货”等生活欲望的肯定和追求,注重创作主体在精神上的独立不倚,强调灵感触发的创作冲动,以童心、幽默、风趣以及冲决传统伦理之束缚的信念,荡涤了文坛抄袭剽窃丧失创造的卑弱文风。
然而,晚明性灵文学思潮在产生之初,助推个性解放以反抗传统伦理的同时,也存在鄙俚庸俗、狂放怪诞之失,公安末流的创作又导致了新的文坛流弊。
公安派自身的修正以及竟陵派钟惺、谭元春的另辟蹊径已经不可能力挽狂澜。
重庆市九校联盟2019届高三12月联合考试语文试题

高三语文考试阅读下面的文字,完成下列小题。
性灵源于古代诗以言志之论,性指本性,性情,本真;灵有灵机、灵巧之意,侧重于情感表达的技巧,后来又加入了天赋、契机、生趣等含义。
自南朝刘勰、钟嵘之后很长时期内,性情、性灵、情性在文学批评中出现的时候,只是侧重点的不同,并不存在大的差别,都是在古典诗学性情论的语境中使用。
明代中期以来,王阳明心学盛行海内,主张“心者天地万物之主”,打破了程朱理学一统天下的格局和思想学术的僵化状态。
与此同时,传统伦理对人性的禁锢进一步加深,社会经济的发展和市民阶层的兴起又刺激了个人主体意识的觉醒。
明代社会随处可见“存天理,去人欲”的说教,又随处可见对金钱、美色的追求。
万历年间,王学左派尤其是其后期杰出的代表人物李贽,对程朱理学做了尖锐批判,提出保护和尊重人欲使其健康合理的发展,在文学上提倡“童心”,即“绝假纯真,最初一念之本心”。
汤显祖倡言“情有者理必无,理有者情必无”,都表现出以情反理的鲜明特征。
晚明公安派文学家袁宏道则将这股个性解放的思潮与古老的“性灵”相结合,提出了“独抒性灵,不拘格套”的宣言。
他们强调诗文创作当不受传统伦理以及古人陈法的禁锢与束缚,自由地抒发真情实感,即使言语拗口难工,也显示出作者自己的本色与独创,呼吁充分发挥自身的创造力,无所依傍、天真率直地创造属于自己时代的文学。
性灵追求创作个体的情感体验和生命本真,自然也就深入到了世俗、琐碎的社会生活,开始坦率地表达对世俗生活的热爱和“好货”等生活欲望的肯定和追求,注重创作主体在精神上的独立不倚,强调灵感触发的创作冲动,以童心、幽默、风趣以及冲决传统伦理之束缚的信念,荡涤了文坛抄袭剽窃丧失创造的卑弱文风。
然而,晚明性灵文学思潮在产生之初,助推个性解放以反抗传统伦理的同时,也存在鄙俚庸俗、狂放怪诞之失,公安末流的创作又导致了新的文坛流弊。
公安派自身的修正以及竟陵派钟惺、谭元春的另辟蹊径已经不可能力挽狂澜。
加上明清鼎革,广大士人饱经动荡之苦和亡国之痛,一代知识人进行了深刻的反省,尤其是顾炎武等思想家严厉批判以李贽为代表的左派王学败坏了世道人心,甚至将其与“神州陆沉”“五胡窃据”相联系。
2019届重庆市九校联盟高三上学期12月联合考试理综化学试题(解析版)

2019届重庆市九校联盟高三上学期12月联合考试理综化学试题(解析版)第Ⅰ卷(选择题)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的。
1.化学与生产、生活密切相关,下列说法错误..的是A. 用K2FeO4处理自来水,既可杀菌消毒又可除去悬浮杂质B. NH4MgPO4·6H2O(鸟粪石)与草木灰混合施肥效果更好C. 将地沟油回收加工为生物柴油,既可获得能源物质又可防止水体污染D. 医院常用含碘2%~3%的酒精溶液用作医疗消毒剂,因为它能使蛋白质变性【答案】B【解析】【分析】A、K2FeO4处理自来水时,利用其强氧化性可杀菌消毒,同时生成氢氧化铁胶体能吸附杂质;B、NH4MgPO4·6H2O(鸟粪石)水解呈酸性,草木灰水解后呈碱性;C、将地沟油回收加工为生物柴油,符合绿色化学理念;D、碘能使蛋白质变性。
【详解】A、K2FeO4处理自来水时,利用其强氧化性可杀菌消毒,同时生成氢氧化铁胶体能吸附杂质,故A 正确;B、NH4MgPO4·6H2O(鸟粪石)电离出铵根离子,水解呈酸性,草木灰溶于水电离出碳酸根离子,水解后呈碱性,两者混合后发生双水解,肥效减小,故B错误;C、将地沟油回收加工为生物柴油,既可获得能源物质又可防止水体污染,符合绿色化学理念,故C正确;D、含碘2%~3%的酒精溶液用作医疗消毒剂,因为它能使蛋白质变性,故D正确;故选B。
【点睛】本题考查化学与生活、生产之间的关系,解题关键:对日常生活、生产中涉及的的基础知识的理解,难点A,K2FeO4处理自来水时,既能杀菌消毒,又能吸附杂质,氢氧化铁胶体能吸附杂质。
2.下列有关物质的性质与用途具有对应关系的是A. AB. BC. CD. D【答案】D【解析】【详解】A.FeCl3可用作H2S的脱除剂,是因为FeCl3中三价铁具有较强的氧化性,故A错误;B.二氧化硅制成的纤维具有良好的传导光信号的能力,可作光导纤维,故B错误;C.氢氟酸具有腐蚀性,与玻璃中的二氧化硅反应,故C错误;D.细菌是一种蛋白质,H2O2具有强氧化性能使蛋白质变性,可用作医疗行业的消毒剂,故D正确。
2018-2019学年重庆市九校联盟高三(上)12月联考数学试卷(文科)

2018-2019学年重庆市九校联盟高三(上)12月联考数学试卷(文科)一、选择题:(共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)若集合A={x|3﹣2x<﹣1},B={x|x(2x﹣5)≤0},则A∪B=()A.B.C.[0,+∞)D.2.(5分)若复数z满足(2+i)z=3﹣i,则z的虚部为()A.i B.﹣i C.1D.﹣13.(5分)函数的图象大致是()A.B.C.D.4.(5分)已知平面向量,满足||=2,||=1,且(4﹣)•(+3)=2,则向量,的夹角θ为()A.B.C.D.5.(5分)已知函数f(x)为R上的奇函数,当x<0时,,则xf(x)≥0的解集为()A.[﹣1,0)∪[1,+∞)B.(﹣∞,﹣1]∪[1,+∞)C.[﹣1,0]∪[1,+∞)D.(﹣∞,﹣1]∪{0}∪[1,+∞)6.(5分)设x,y满足约束条件,则z=4x+y的最小值为()A.﹣3B.﹣5C.﹣14D.﹣167.(5分)某几何体的三视图如图所示(其中俯视图中的曲线是圆弧),则该几何体的表面积为()A.4π+6B.6π+6C.4π+3D.6π+38.(5分)为了得到y=﹣2cos 2x的图象,只需把函数y=sin 2x﹣cos2x的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度9.(5分)已知双曲线C:﹣=1的左、右焦点分别为F1,F2,P为C上一点,=,O为坐标原点,若|PF1|=10,则|OQ|=()A.10B.1或9C.1D.910.(5分)如图,△ABC和△DEF均为等边三角形,AF=BD=CE,DF=2AF=20cm,若在△ABC中随机投入260粒芝麻,则落在△DEF外的芝麻粒数约为()A.100B.130C.150D.18011.(5分)△ABC的内角A,B,C的对边分别为a,b,c.若(sin B+sin C)2﹣sin2(B+C)=3sin B sin C,且a=2,则△ABC的面积的最大值是()A.B.C.D.412.(5分)设0<m≤2,已知函数,对于任意x1,x2∈[m﹣2,m],都有|f(x1)﹣f(x2)|≤1,则实数m的取值范围为()A.B.C.D.二、填空题:(共4个小题,每小题5分,共20分。
重庆市九校联盟2019届高三12月联合考试 数学(理)(含答案)

A.(1,2] B.
C.[0,1) D.(1,+∞)
【答案】B 【解析】解不等式得集合 A,B,利用集合的交集定义求解即可. 【详解】
由集合
,
所以
.
故选 B. 【点睛】 本题考查了集合的交集运算,属于基础题. 2.若复数 z 满足(2+i)z=3-i,则 z 的虚部为( ) A.i B.-i C.1 D.-1 【答案】D 【解析】由复数的除法运算化简即可得解. 【详解】
重庆市九校联盟 2019 届高三 12 月联合考试
数学(理)试题
一、单选题 1.若集合 A={x|3-2x<1},B={x|4x-3x2≥0},则 A∩B=( )
A.(1,2]
B.
C.[0,1)
2.若复数 z 满足(2+i)z=3-i,则 z 的虚部为( )
A.i
B.-i
C.1
3.已知
,
,则 cos 2α=( )
B.(-∞,-1]∪[1,+∞) D.(-∞,-1]∪{0}∪[1,+∞)
·1·
7.设 x,y 满足约束条件
则 z=4x+y 的最小值为( )
A.-3
B.-5
8.为了得到 y=-2cos 2x 的图象,只需把函数
C.-14
D.-16 的图象( )
A.向左平移 个单位长度
B.向右平移 个单位长度
C.向左平移 个单位长度
(2)在(1)的条件下,若射线 求 的面积.
与曲线 , 分别交于 两点(除极点外),且有定点 ,
23.已知函数
.
(1)当 时,求不等式
的解集;
(2)对于任意的实数 ,存在实数 ,使得不等式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)证明:PQ∥平面 ABCD; (2)若 CD⊥BE,EF=EC=1, CD 2 FF
2 BC ,求五面体 ABCDFE 的体积. 3
20. 已知抛物线 y2=2px(p>0)的焦点为 F, 过 F 且与 x 轴垂直的直线交该抛物线于 A, B 两点, |AB|=4. (1)求抛物线的方程; (2)过点 F 的直线 l 交抛物线于 P,Q 两点,若△OPQ 的面积为 4,求直线 l 的斜率(其中 O 为坐标原点).
2.若复数 z 满足(2+i)z=3-i,则 z 的虚部为 A.1 B.-1 C.i D.-i
3.函数 f ( x )
log 2 ( x 2 1) 的图象大致是 x
4.已知平面向量 a,b 满足|a|=2,|b|=1,且(4a-b)·(a+3b)=2,则向量 a,b 的夹角 θ 为 A.
2π 3
1 . 150
设 y 为观众评分的中位数, 由前三组的概率和为 0.40,前四组的概率和为 0.70,知 82<y<88, 所以 0.4+(y-82)×0.05=0.5,则 y=84. (2)以样本的频率作为概率,评分在“88 分及以上”确定为“足球迷” ,现从“足球迷”中 按分层抽样抽取 5 人,则从评分在区间[88,94)的“足球迷”中抽取 3 人,记为 A,B,C,从 评分在区间[94,100]的“足球迷”中抽取 2 人,记为 a,b. 从 5 人中选取 2 人作进一步的访谈的所有事件为 AB,AC,BC,Aa,Ba,Ca,Ab,Bb,Cb,ab, 共 10 个基本事件, 这两人中至少有 1 人的评分在区间[94,100]的基本事件有 Aa,Ba,Ca,Ab,Bb,Cb,ab, 共 7 个基本事件, 则选取的 2 人中至少有 1 人的评分在区间[94,100]上的概率 P 19.(1)证明:因为底面 ABCD 为矩形,所以 AD∥BC.
21.解:(1)因为 f ( x ) e x
x2 2x 2x x ,所以 f ( x ) e x 2 1 (e x 1) 2 , 2 m m m
所以当 x∈(-∞,0)时,ex-1<0, 当 x∈(0,+∞)时,ex-1>0,
2x 0 ,f′(x)<0; m2
-1-
A.4π+6 B.6π+6 C.4π+3 D.6π+3 8.为了得到 y=-2cos 2x 的图象,只需把函数 y 3 sin 2 x cos 2 x 的图象 A.向左平移 C.向左平移
π π 个单位长度 B.向右平移 个单位长度 3 3 π π 个单位长度 D.向右平移 个单位长度 6 6
2x 0 ,f′(x)>0. m2
所以 f(x)的单调递减区间是(-∞,0),单调递增区间是(0,+∞). (2)由(1)知,f(x)在[-m,0]上单调递减,在[0,m]上单调递增, 故 f(x)在 x=0 处取得最小值,且 f(0)=1. 所以对于任意的 x1,x2∈[-m,m],|f(x1)-f(x2)|≤e-1 的充要条件为
-4-
21.设函数 f ( x ) e x
x2 x. m2
(1)求 f(x)的单调区间; (2)若对于任意 x1,x2∈[-m,m](m>0),都有|f(x1)-f(x2)|≤e-1,求 m 的取值范围. (二)选考题:请考生在第 22、23 题中任选一题作答.如果多做,则按所做的第一题计分. 22.[选修 4-4:坐标系与参数方程]
A.100 B.130 C.150 D.180 11.△ABC 的内角 A,B,C 的对边分别为 a,b,c.若(sin B+sin C)2-sin2(B+C)=3sin Bsin
C,且 a=2,则△ABC 的面积的最大值是
-2-
A.
3 2
B. 3
C. 2 3
D.4
x 3 12 x 50 , 对于任意 x1, x2∈[m-2, m], 都有|f(x1)-f(x2)| 16m
1 2 y 3 x 3, 6.设 x,y 满足约束条件 y 2 x 1, 则 z=4x+y 的最小值为 1 y x 4, 2
A.-3 C.-14 B.-5 D.-16
7.某几何体的三视图如图所示(其中俯视图中的曲线是圆弧),则该几何体的表面积为
7 . 10
-6-
AD 平面ADF BC ∥平面ADF , BC 平面ADF AD ∥ BC
BC 平面BCPQ BC ∥ PQ , 平面BCPQ 平面ADF PQ BC ∥平面ADF
PQ 平面ABCD PQ ∥平面ABCD . BC 平面ABCD PQ ∥ BC
4 ,y1y2=-4, k
1 4( k 2 1) | y y | . 1 2 k2 k2
-7-
所以 | PQ | 1
又点 O 到直线 l 的距离 d
| k 0 | k 1
2
|k | k2 1
,
1 2 k2 1 1 3 所以 S△OPQ | PQ | d . 4 ,解得 k 2 ,即 k 2 |k | 3 3
重庆市九校联盟 2019 届高三数学 12 月联考试题 文
第Ⅰ卷 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若集合 A={x|3-2x<-1},B={x|x(2x-5)≤0},则 A∪B=
2 A. [ , 2) 5
C.[0,+∞)
5 B. (2, ] 2 5 D. [ , ) 2
-5-
高三数学考试参考答案(文科) 1.C 13.-1 2.B 14. 3.C 4.A 15.
5 2
5.D
6.C
7.A
8.D
9.B
10.D
11.B
12.B
7 25
16. 2 5 6 ①
17.(1)解:因为 an+1=2Sn+3,
an=2Sn-1+3. ②
①-②得 an+1-an=2an,即 an+1=3an(n≥2), 所以{an}为从第 2 项开始的等比数列,且公比 q=3, 又 a1=3,所以 a2=9,所以数列{an}的通项公式 an=3n(n≥2). 当 n=1 时,a1=3 满足上式,所以数列{an}的通项公式为 an=3n. (2)证明:由(1)知 bn=log3an=log33n=n, 所以
▲ .16.点 P 在椭圆 1:x2 y2 1 上,C1 的右焦点为 F,点 Q 在圆 C2:x2+y2+6x-8y+21=0 上, 4 3
则|PQ|-|PF|的最小值为
▲
.
三、解答题:解答应写出文字说明、证明过程或演算步骤.第 17-21 题为必考题,每个试题 考生都必须作答.第 22、23 题为选考题,考生根据要求作答. (一)必考题 17.已知数列{an}的前 n 项和为 Sn,a1=3,an+1=2Sn+3(n∈N*). (1)求数列{an}的通项公式; (2)设 bn=log3an,若数列 {
12. 设 0<m≤2, 已知函数 f ( x ) ≤1,则实数 m 的取值范围为
5 A. [ , 2] 3 1 C. [ ,1] 3
4 B. [ , 2] 3 2 D. [ ,1] 3
第Ⅱ卷
二、填空题:把答案填在答题卡中的横线上.
x 2, x 0 3 13.已知函数 f ( x ) ,则 f ( f ( )) 2 log 2 x, x 0
(2)解:由 CD⊥BE,CD⊥CB,易证 CD⊥CE, 由 BC⊥CD,BC⊥FD,易证 BC⊥平面 CDFE,所以 CB⊥CE, 即 CD,CE,CB 两两垂直.
1 连接 FB,FC,则 CD=2,BC=3, VF ABCD (2 3) 1 2 , 3 1 1 1 VF BCE ( 3 1) 1 , 3 2 2 VABCDEF VF ABCD VF BCE 2 1 5 . 2 2
x 5cos , 在直角坐标系 xOy 中,曲线 C1 的参数方程为 (α 为参数).M 是曲线 C1 上的动 y 5 5sin
点,将线段 OM 绕 O 点顺时针旋转 90°得到线段 ON,设点 N 的轨迹为曲线 C2.以坐标原点 O 为极点,x 轴的正半轴为极轴建立极坐标系. (1)求曲线 C1,C2 的极坐标方程; (2)在(1)的条件下,若射线
1 1 1 1 , bn bn1 n( n 1) n n 1
1 1 1 1 1 所以 Tn (1 ) ( ) … ( ) 2 2 3 n n 1 1 1 1 得证. n 1
18.解:(1)因为(a+0.025+0.035+0.050+0.030+0.020)×6=1, 所以 a
▲
.
7 2 14.已知 sin cos , 2sin cos ,则 cos 2α= 5 5
▲
.
15.如图,在直四棱柱 ABCD-A1B1C1D1 中,已知四边形 ABCD 是直角梯形,∠BAD=90°,AB∥
CD,AB=AD=AA1=1,CD=2,E 为 BB1 的中点,则直线 AD 与直线 CE 所成角的正切值为
B.
π 3
C.
π 2
D.
π 6 1 ,则 xf(x)≥0 的解集为 2
5.已知函数 f(x)为 R 上的奇函数,当 x<0 时, f ( x ) 2 x A.[-1,0)∪[1,+∞) C.[-1,0]∪[1,+∞) B.(-∞,-1]∪[1,+∞) D.(-∞,-1]∪{0}∪[1,+∞)
