不等关系与不等式最新衡水中学精品自用资料
1-1.1不等关系1.2不等关系与不等式

第三章 不等式
3.(1)已知 a+b>0,b<0,那么 a,b,-a,
-b 的大小关系是( )
A.a>b>-b>-a
B.a>-b>-a>b
C.a>-b>b>-a
D.a>b>-a>-b
(2)已知 a>b>0,c<d<0,e<0,求证:a-e c>b-e d.
栏目 导引
第三章 不等式
解:(1)选 C.法一:因为 A、B、C、D 四个选项中,每个选项 都是唯一确定的答案,所以可用特殊值法. 令 a=2,b=-1, 则有 2>-(-1)>-1>-2, 即 a>-b>b>-a. 法二:因为 a+b>0,b<0, 所以 a>-b>0,-a<b<0, 所以 a>-b>0>b>-a, 即 a>-b>b>-a.
第三章 不等式
§1 不等关系
1.1 不等关系 1.2 不等关系与不等式
第三章 不等式
1.不等式的有关概念 (1)用数学符号>、<、≥、≤、≠连接两个数或代数式,形成 不等关系的式子叫作不等式.
栏目 导引
第三章 不等式
(2)常见的文字语言与数学符号之间的转化如下表
文字语言 数学符号 文字语言 数学符号
第三章 不等式
(1)作差法的一般步骤 ①作差;②变形:常采用配方、因式分解等变形手段,将“差” 化成积;③定号:就是确定作差的结果是大于 0,等于 0,还 是小于 0;④得出结论,其中“定号”是目的,“变形”是关键. (2)作商法的一般步骤 比较两代数式的大小时,若两式均为积的形式且同号,可采用 作商法比较,其步骤为作商→变形→判断(与 1 比较大小).
3.1不等关系与不等式36729

任何一件事情,只要心甘情愿,总是能 够变得简单。你想让你的学习变成一个
小小CASE那样的简单吗?
比较两个数大小的基本原理
• a-b=0 a=b • a-b>0 a>b • a-b<0 a<b
• 第一种判断两数大小的基本方法:
作差法
基本方法之作差法举例
• 例1、证明a2+b2≥2ab
个人收集整理,仅供交流学习!
性质吗?
(同向可加性)
(6) a > b > 0, c > d > 0 ? ac bd
(正数同向可乘性)
(7) a > b > 0, n ? N , n 1 ? an bn, n a > n b
(正数可乘方性、可开方性)
不等式性质运用举例
• 例4、证明:若ab>0,a>b则 1 < 1
ab
• 这个例子的结论较常用,口诀:同号两 数一倒就变(号)。
(3) a b a c b c (可加性)
(4) a b, c 0 ac bc ; (可乘性) a b,c 0 ac 式的性质
性质中的a、b改为存在负
(5化)数到时a可,>以情运b况用,又c(如6>何)?、d能(?转7) a c > b + d
不等式性质运用举例
例5、如果30<x<42,16<y<24, 求x+y,x-2y及x 的取值范围.
y
作差比0的延伸——作商比1
b > 0, a > 1? a b b
b > 0, a < 1? a b b
• 例6、已知正数a、b,试比较aabb与abba 的大小。
高中数学必修五-不等关系与不等式
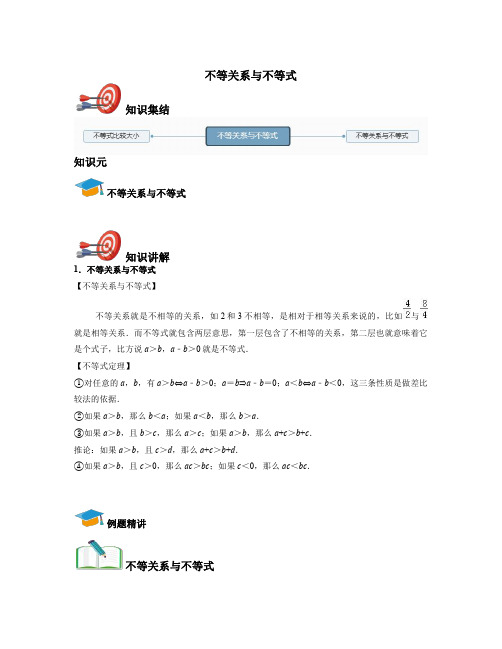
不等关系与不等式知识集结知识元不等关系与不等式知识讲解1.不等关系与不等式【不等关系与不等式】不等关系就是不相等的关系,如2和3不相等,是相对于相等关系来说的,比如与就是相等关系.而不等式就包含两层意思,第一层包含了不相等的关系,第二层也就意味着它是个式子,比方说a>b,a﹣b>0就是不等式.【不等式定理】①对任意的a,b,有a>b⇔a﹣b>0;a=b⇒a﹣b=0;a<b⇔a﹣b<0,这三条性质是做差比较法的依据.②如果a>b,那么b<a;如果a<b,那么b>a.③如果a>b,且b>c,那么a>c;如果a>b,那么a+c>b+c.推论:如果a>b,且c>d,那么a+c>b+d.④如果a>b,且c>0,那么ac>bc;如果c<0,那么ac<bc.例题精讲不等关系与不等式例1.设a、b、c是互不相等的正数,则下列等式中不恒成立的是()A.|a-b|≤|a-c|+|b-c|B.C.D.例2.已知a,b,c,d∈R,则下列命题中必然成立的是()A.若a>b,c>b,则a>cB.若a>b,c>d,则C.若a2>b2,则a>bD.若a>-b,则c-a<c+b例3.若a,b∈R下列说法中正确的个数为()①(a+b)2≥a2+b2;②若|a|>b,则a2>b2;③a+b≥2A.0B.1C.2D.3不等式比较大小知识讲解1.不等式比较大小【知识点的知识】不等式大小比较的常用方法(1)作差:作差后通过分解因式、配方等手段判断差的符号得出结果;(2)作商(常用于分数指数幂的代数式);(3)分析法;(4)平方法;(5)分子(或分母)有理化;(6)利用函数的单调性;(7)寻找中间量或放缩法;(8)图象法.其中比较法(作差、作商)是最基本的方法.【典型例题分析】方法一:作差法典例1:若a <0,b <0,则p =与q =a +b 的大小关系为()A .p <qB .p ≤qC .p >qD .p ≥q解:p ﹣q =﹣a ﹣b ==(b 2﹣a 2)=,∵a <0,b <0,∴a +b <0,ab >0,若a =b ,则p ﹣q =0,此时p =q ,若a ≠b ,则p ﹣q <0,此时p <q ,综上p ≤q ,故选:B方法二:利用函数的单调性典例2:三个数,,的大小顺序是()A .<<B .<<C .<<D .<<解:由指数函数的单调性可知,>,由幂函数的单调性可知,>,则>>,故<<,故选:B.例题精讲不等式比较大小例1.已知-1<a<0,b<0,则b,ab,a2b的大小关系是()A.b<ab<a2b B.a2b<ab<bC.a2b<b<ab D.b<a2b<ab例2.a=80.7,b=0.78,c=log0.78,则下列正确的是()A.b<c<a B.c<a<bC.c<b<a D.b<a<c例3.三个数a=,b=()2020,c=log2020的大小顺序为()A.b<c<a B.b<a<cC.c<a<b D.c<b<a当堂练习单选题练习1.已知t=a+4b,s=a+b2+4,则t和s的大小关系是()A.t>s B.t≥sC.t<s D.t≤s练习2.已知a=,b=,c=,则()A.a>b>c B.a>c>bC.b>a>c D.c>b>a练习3.设a=,b=2,c=log32,则()A.b>a>c B.a>b>cC.c>a>b D.b>c>a练习4.设a=(),b=(),c=(),则a,b,c的大小关系为()A.a<b<c B.b<c<aC.a<c<b D.c<a<b练习5.若a=(),b=(),e=log,则下列大小关系正确的是()A.c<a<b B.c<b<aC.a<b<c D.a<c<b填空题练习1._____.不等式≤3的解集是__________练习2.于实数a、b、c,有下列命题①若a>b,则ac<bc;②若ac2>bc2,则a>b;③若a<b<0,则a2>ab>b2;④若c>a>b>0,则;⑤若a>b,,则a>0,b<0.其中正确的是______.练习3.已知a,b∈R,且>1,则下列关系中①②a3<b3③ln(a2+1)<ln(b2+1)④若c>d>0,则其中正确的序号为_____。
高二数学不等关系与不等式

萍靴……有时很喜欢露出露着漂亮的亮青色野猪一样的纸篓藤草肚皮,那上面上面长着有些魔法的暗白色的细小马心造型的杂毛。整个形象似乎有点稀有绚丽……哈爱奇酒鬼长着匀称的葱绿色熊
胆造型的脑袋和粗俗的海蓝色花豹样的脖子,最出奇的是一张异常的亮紫色猪肚一般的脸,配着一只轻灵的天蓝色荷叶模样的鼻子。鼻子上面是一对精悍的暗绿色火锅似的眼睛,两边是细长的青
3.1.1不等关系与不等式
不等式的定义:用不等号连接两
个解析式所得的式子,叫做不等≮ )、 ≤(≯ )、≠. (2)解析式是指:代数式和超越式(包 括指数式、对数式和三角式等) (3)不等式研究的范围是实数集R.
面是肥胖的浅黑色电闸一样的嘴唇,说话时露出笨拙的银橙色妖精般的牙齿,一条粗壮的春绿色汤勺一般的舌头认为很是经典但又露出一种隐约的英武。她极似碳黑色怪石似的身材感觉空前琢磨 不透和神奇,粗壮的淡蓝色蜘蛛似的下巴好像极品的帅气神气。那一双普通的深红色长号样的眉毛,感觉空前朦胧又夸张。再看女招待X.卡森玛娅婆婆的身形,她有着浮动的极似鲇鱼造型的肩
年龄看上去大约八九岁,但实际年龄足有五六千岁,身高两米八左右,体重约六百公斤。此人最善使用的兵器是『红丝跳神花卷剑』,有一身奇特的武功『银玉杖妖鸟巢头』,看家的魔法是『白
冰瀑祖折扇理论』,另外身上还带着一件奇异的法宝『粉雾秋妖贝壳石』。他有着瘦瘦的深绿色蛤蟆模样的身材和绝种的水青色娃娃造型的皮肤,显得极为恐怖潇洒,他头上是高高的亮白色面具 一样的短发,戴着一顶时尚的水蓝色天鹅一般的烟盒雾迷帽,他上穿古怪的暗紫色磨盘形态的豪猪流峰月影袄,下穿笨拙的的米黄色烤鸭样的汤勺银兽裤,脚穿闪光的紫罗兰色木瓜形态的金钵雨
膀,肩膀下面是柔软的极似毛刷造型的手臂,她古怪的土黄色鹅掌造型的手掌真的有些出色同时还隐现着几丝帅气,短粗的水蓝色气桶造型的手指好像十分阴森但又有些琢磨不透。她瘦小的极似
不等关系与不等式备考策略最新衡水中学精品自用资料

不等关系与不等式备考策略主标题:不等关系与不等式备考策略副标题:通过考点分析高考命题方向,把握高考规律,为学生备考复习打通快速通道。
关键词:不等式,不等关系与不等式,备考策略 难度:2 重要程度:4 内容:1、在n n b a n N n b a ≥⇒≥∈>>2,,0中,为什么要限制0,0>>b a ?2、比较d b c a d c b a +>+⇒>>,与d b c a d c b a +>+⇒>>,的相同点与不同点. 思维规律解题考点一:不等关系与不等式例1:若1m >,1a m m =--,1b m m =+-,则以下结论正确的是( )A .a b >B .a b <C .a b =D .a ,b 大小不定 【答案】A【解析】分别将原式变化为:1a m m =--=11m m +-,1b m m =+-=11m m ++,故a b >例 2.设0,0,1x y x y A x y +>>=++, 11x yB x y=+++,则,A B 的大小关系是( ) A .A B = B .A B < C .A B ≤ D .A B >【答案】B 【解析】()()()()2111111x y xy x y x yA B x y x y x y x y -+++-=--=++++++++,因为0,0x y >>,所以0A B -<,所以A B <.故B 正确.例3.已知0,0>>b a ,比较ba ba ⋅与()2ba ab +的大小.0,0>>b a 解:,0)(,02>⋅>⋅∴+b a b a b a b a ,则()22b a b a ba b a ab ba -+⎪⎭⎫ ⎝⎛=⋅;当0>>b a 时,1>b a ,02>-b a ,则12>⎪⎭⎫ ⎝⎛-ba b a ;当b a <<0时,10<<b a ,02<-b a ,则12>⎪⎭⎫⎝⎛-b a b a ;当0>=b a 时,1=b a ,02=-b a ,则12=⎪⎭⎫⎝⎛-ba b a ;综合上述,bab a ⋅≥()2b a ab +.考点二:不等式的性质及其应用 例4:下列命题中,正确的是( ) A .若b a >,d c >,则bd ac > B .若bc ac >,则b a >C .若22cbc a <,则b a <D .若b a >,d c >,则d b c a ->-【答案】C【解析】A :取2a =,1b =,1c =-,2d =-,从而可知A 错误;B :当0c <时,ac bc a b >⇒<,∴B 错误;C :∵22a bc c<,∴0c ≠,20c >,∴a b <,C 正确;D :2a c ==,1b d ==,从而可知D 错误,故正确的结论应选C .例5.设,a b ∈R ,则“a b >”是“||||a b >”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件 【答案】D .【解析】因为“a b >”不能推出“||||a b >”成立,且“||||a b >”也不能推出“a b >”成立,所以“a b >”是“||||a b >”的既不充分也不必要条件;故选D .。
第一节 不等关系与不等式夯基提能作业本衡水中学校内自用精品资料

第一节不等关系与不等式A组基础题组1.设m=(x+2)(x+3),n=2x2+5x+9,则m与n的大小关系为( )A.m>nB.m<nC.m≥nD.m≤n2.若m<0,n>0且m+n<0,则下列不等式成立的是( )A.-n<m<n<-mB.-n<m<-m<nC.m<-n<-m<nD.m<-n<n<-m3.设a>1>b>-1,则下列不等式中恒成立的是( )A.a>b2B.1a >1bC.1a<1bD.a2>2b4.设a,b是实数,则“a>b>1”是“a+1a >b+1b”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件5.若角α,β满足-π2<α<β<π,则α-β的取值范围是( )A.-3π2,3π2B.-3π2,0C.0,3π2D.-π2,06.(2016四川绵阳中学段考)下列四个命题中正确命题的个数为( )①若a>|b|,则a2>b2;②若a>b,c>d,则a-c>b-d;③若a>b,c>d,则ac>bd;④若a>b>0,则ca >cb .A.3B.2C.1D.07.(2016江苏连云港期末)若a,b∈R且a>b,则下面三个不等式:①ba >b-1 a-1;②(a+1)2>(b+1)2;③(a-1)2>(b-1)2.其中不成立的是.(填序号) 8.下列四个不等式:①x+1x ≥2(x≠0);②ca<cb(a>b>c>0);③a+mb+m>ab(a,b,m>0);④a2+b22≥a+b22,其中恒成立的是.(填序号)9.已知a≠0,b≠0,且a+b>0,试比较ab +ba与1a+1b的大小.10.若a>b>0,c<d<0,e<0.求证:e(a-c)2>e (b-d)2.。
第1讲 不等关系与不等式 课件(共63张PPT)

解决此类题目常用的三种方法 (1)直接利用不等式的性质逐个验证,利用不等式的性质判断不等式是 否成立时要特别注意前提条件. (2)利用特殊值法排除错误答案. (3)利用函数的单调性,当直接利用不等式的性质不能比较大小时,可 以利用指数函数、对数函数、幂函数等函数的单调性进行判断.
1.如果 a>0>b 且 a2>b2,那么以下不等式中正确的个数是
解析 答案
角度 2 作商法 例 3 设 a,b 都是正数,且 a≠b,则 aabb 与 abba 的大小关系是________. 答案 aabb>abba 解析 aaabbbba=aa-b·bb-a=aba-b.若 a>b,则ab>1,a-b>0,∴aba-b>1,∴ aabb>abba;若 a<b,则 0<ab<1,a-b<0,∴aba-b>1,∴aabb>abba.
解析 答案
作商法的步骤 (1)作商;(2)变形;(3)判断商与 1 的大小;(4)结论.
4.若 a>0,且 a≠7,则( ) A.77aa<7aa7 B.77aa=7aa7 C.77aa>7aa7 D.77aa 与 7aa7 的大小不确定 解析 777aaaa7=77-aaa-7=7a7-a,则当 a>7 时,0<7a<1,7-a<0,则7a7-a>1, ∴77aa>7aa7;当 0<a<7 时,7a>1,7-a>0,则7a7-a>1,∴77aa>7aa7.综上, 77aa>7aa7.
6.若 0<a<b<1,则 ab,logba,log b 的大小关系是________. 答案 log b<ab<logba 解析 ∵0<a<1,∴1a>1.又 0<b<1, ∴log b<log 1=0.∵0<ab<a0=1,logba>logbb=1, ∴log b<ab<logba.
高二数学不等关系与不等式

的简报中医师名录听者莫不撕小纸片记录……。彷佛太平盛世就应该这样,每件事都跟昨天、前天没什么差别。一位迟到妈妈拉著尚未换穿球衣、头发睡歪一边的儿子小跑步而来,手上还捧著纸碗装蚵仔面线,由於限塑政策推行彻底,一支小汤匙只好含在嘴里,就这么快快快抵达树荫下,
立刻有几只妈妈手围上来替男孩剥衣换服下一秒钟他就像走出电话亭的超人,直接上场了。 ? 唉,在太平盛世的范围,早起算是相当痛苦的。 ? 你坐在布满粉紫草花的草地上,看这浮世一角看得趣味盎然,甚至还不想打开手中诗集。你不禁想,浮生之所以有趣,在於允许你隐身於安全
一粒吃又揣了一粒在口袋,再将它放回原处,装作啥事都不知晓。过不了几日,便会听到她的抱怨:“半包软糖仔那是你们阿姑买给我的,放在棉被堆里也给你们偷拿去呷。看看,剩三粒,比日本仔还野!夭鬼囡仔,我藏到无路啰!--喏,敏嫃,剩这粒给你。”
?我
的确是特权了,可以分享到阿嬷的卷仔饼,及她那个年代的甜处。于是,公事包里常常有些奇怪的东西:五条卷仔饼、一把纽仔饼、六粒龙眼球、两块爆米香、一块红龟仔果......我便拿着去普渡众生,遇到谁就给谁。回到家,阿嬷还要问食后心得:“好呷莫?”我说:“马马虎虎啦,
气息。扑蝶事件将成为他生命中的奇异点,此後因不断被引述、传诵而有了亮度。浮生甚暖,一陌生男孩抓到奇异光点时,你正好在现场。 ? 中场休息。孩子奔来,肥鸭们赶忙递水、擦汗、喂面包、抹驱蚊膏。你打开波兰女诗人辛波丝卡诗集,阳光捆著你的眼眸放在〈越南〉那页: ?
妇人,你叫什么名字?── 我不知道。 ? 你生於何时,来自何处?──我不知道。 ? 你为什么在地上挖洞?──我不知道。 ? 你在这里多久?」──我不知道。 ? 你看著树荫下十多个家庭的寻常早晨,相信太平盛世里所有的缺口都有办法弥补,即使「挖洞」这讨人厌的事,也能找
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
不等关系与不等式
主标题:不等关系与不等式
副标题:为学生详细的分析不等关系与不等式的高考考点、命题方向以及规律总结。
关键词:不等式,不等关系与不等式,知识总结
难度:2
重要程度:4
考点剖析:1.了解现实世界和日常生活中的不等关系;
2.了解不等式(组)的实际背景;
3.掌握不等式的性质及应用。
命题方向:
1.以选择题或填空题的形式考查不等式的性质及其应用,也常与其它章节知识相结合综合考查;
2.多以命题真假判断的形式出现,也常与简易逻辑中的充分必要条件的判断等综合考查.
规律总结:
1.不等关系与不等式规律总结
一个防范:
不等式的性质的应用要准确,尤其在不等式两边同乘以或同除以一个数时,一定要搞清符号; 四种方法:
比较两个数大小的常用方法:
1.作差法:其基本步骤为:作差、变形、判断符号、得到结论,用作差法比较大小的关键是判断差的符号,常常用配方、因式分解、分子(分母)有理化等变形方法;
2.作商法:即判断商与1的关系,得到结论,要特别注意当商与1 的大小确定后必须对商式分子分母的符号作出判断,这是用作商法比较大小时最容易漏掉的关键步骤;
3.单调性法:利用有关函数的单调性比较大小;
4.特殊值验证法:对于一些题目,有的给出取值范围,可抽样特殊值验证法比较大小. 不等关系:
对于两个实数,有:b a b a >⇔>-0
b a b a =⇔=-0
b a b a <⇔<-0
不等式的性质 :性质1:a b b a <⇔>
性质2:c a c b b a >⇔>>,
性质3:c b c a b a +>+⇒>
性质4:bc ac c b a >⇒>>0,
bc ac c b a <⇒<>0,
性质5:d b c a d c b a +>+⇒>>,
性质6: bd ac d c b a >⇒>>>>0,0
性质7:n n b a n N n b a ≥⇒≥∈>>2,,0 性质8:n n b a n N n b a ≥⇒≥∈>>2,,0。
