24.3 正多边形和圆(1) 同步练习
2020年九年级数学上册专题24.3正多边形和圆(讲练)【含解析】

2020年九年级数学上册专题24.3正多边形和圆(讲练)一、知识点1.正多边形与圆(1)正多边形的有关概念:边长(a)、中心(O)、中心角(∠AOB)、半径(R))、边心距(r),如图所示①.(2)特殊正多边形中各中心角、长度比:中心角=120° 中心角=90° 中心角=60°,△BOC 为等边△a:r:R=2:1:2 a:r:R=2::2 a:r:R=2:2二、标准例题:例1:如图,正六边形ABCDEF 内接于⊙O ,连接BD .则∠CBD 的度数是()A .30°B .45°C .60°D .90°【答案】A【解析】∵在正六边形ABCDEF 中,∠BCD ==120°,BC =CD,(62)1806-⨯∴∠CBD =(180°﹣120°)=30°,12故选:A .总结:本题考查的是正多边形和圆、等腰三角形的性质,三角形的内角和,熟记多边形的内角和是解题的关键.例2:如图中有两张型号完全一样的折叠式饭桌,将正方形桌面边上的四个弓形翻折起来后,就能形成一个圆形桌面(可以近似看作正方形的外接圆),正方形桌面与翻折成圆形桌面的面积之比最接近( )A .B .C .D .45342312【答案】C【解析】连接AC ,设正方形的边长为a ,∵四边形ABCD 是正方形,∴∠B=90°,∴AC 为圆的直径,a ,,223π=≈故选C.总结:本题考查的是正多边形和圆,掌握圆周角定理、正方形的性质是解题的关键.例3:如图,正六边形ABCDEF 内接于⊙O ,BE 是⊙O 的直径,连接BF ,延长BA ,过F 作FG ⊥BA ,垂足为G .(1)求证:FG是⊙O的切线;(2)已知FG =,求图中阴影部分的面积.【答案】(1)见解析;(2) 图中阴影部分的面积为.83π【解析】(1)证明:连接OF ,AO ,∵AB =AF =EF ,∴,AB AF EF ==∴∠ABF =∠AFB =∠EBF =30°,∵OB =OF ,∴∠OBF =∠BFO =30°,∴∠ABF =∠OFB ,∴AB ∥OF ,∵FG ⊥BA ,∴OF ⊥FG ,∴FG 是⊙O 的切线;(2)解:∵,AB AF EF ==∴∠AOF =60°,∵OA =OF ,∴△AOF 是等边三角形,∴∠AFO =60°,∴∠AFG =30°,∵FG =,∴AF =4,∴AO =4,∵AF ∥BE ,∴S △ABF =S △AOF ,∴图中阴影部分的面积=.260483603ππ⨯=总结:此题考查切线的判定,等边三角形的判定,扇形面积,解题关键在于利用等弧对等角三、练习1.如图,正六边形的边长为2,分别以点为圆心,以为半径作扇形,扇形ABCDEF ,A D ,AB DCABF .则图中阴影部分的面积是( )DCE A .B .C .D.43π83π-43π-43π【答案】B 【解析】解:∵正六边形的边长为2,ABCDEF ∴正六边形的面积是:,,ABCDEF ()22sin 606622︒⨯⨯=⨯=120FAB EDC ∠=∠=∴图中阴影部分的面积是:,21202823603ππ⨯⨯-⨯=故选:B .2.有一个正五边形和一个正方形边长相等,如图放置,则的值是()1∠A .B .C .D .15︒18︒20︒9︒【答案】B 【解析】解:正五边形的内角的度数是1(52)1801085︒︒⨯-⨯=正方形的内角是90°,则∠1=108°-90°=18°.故选:B .3.如图,已知正方形的顶点、在上,顶点、在内,将正方形绕点逆ABCD A B O C D O ABCD A 时针旋转,使点落在上.若正方形的边长和的半径均为,则点运动的路径长为D O ABCD O 6cm D ()A .B .C .D .2cmπ32cm πcm π12cm π【答案】C 【解析】解:设圆心为O ,连接AO ,BO , OF ,∵AB=6,AO=BO=6,∴AB=AO=BO,∴三角形AOB 是等边三角形,∴∠OAB=60°∵AF=AO=FO=6,∴△FAO 是等边三角形,∴∠OAF=60°∠FAB=∠OAB+∠OAF =120°,∴∠EAC=120°-90°=30°,∵AD=AB=AF=6,∴点D 运动的路径长为:=π.306180π⨯⨯故选:C .4.如图,在正五边形中,,的延长线交于点,则等于( ).ABCDE AE CD FF ∠A .B .C .D .30°32︒36︒38︒【答案】C 【解析】∵五边形ABCDE 是正五边形,∴∠AED =∠EDC =108°,∴∠FED =∠FDE =72°,由三角形的内角和定理得:∠F =180°﹣72°﹣72°=36°.故选C .5.如图,已知正五边形内接于,连结,则的度数是( )ABCDE O BD ABD ∠A .B .C .D .60︒70︒72︒144︒【答案】C 【解析】∵五边形为正五边形ABCDE ∴()1552180108ABC C ∠=∠=-⨯︒=︒∵CD CB =∴181(8326)010CBD ∠=︒-︒=︒∴72ABD ABC CBD ∠=∠-∠=︒故选:C .6.如图,正六边形的边长为2,分别以正六边形的六条边为直径向外作半圆,与正六边形的外接圆围成的6个月牙形的面积之和(阴影部分面积)是( )A .B .C .D .π-2π-π+2π+【答案】A【解析】解:6个月牙形的面积之和,2132622πππ⎛=--⨯⨯= ⎝故选:A .7.阅读理如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M 的位置可由∠MOx 的度数θ与OM 的长度m 确定,有序数对(θ,m)称为M 点的“极坐标”,这样建立的坐标系称为“极坐标系”。
2020年人教版九年级数学上册24.3《正多边形和圆》随堂练习(含答案)

2020年人教版九年级数学上册24.3《正多边形和圆》随堂练习基础题知识点1 认识正多边形1.下面图形中,是正多边形的是( )A.矩形 B.菱形C.正方形 D.等腰梯形2.如图,正六边形的每一个内角都相等,则其中一个内角α的度数是( )A.240° B.120° C.60° D.30°3.一个正多边形的一个外角等于30°,则这个正多边形的边数为.4.如图,AC是正五边形ABCDE的一条对角线,则∠ACB= .知识点2 与正多边形有关的计算5.如图,正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )A. 3 B.2 C.2 2 D.2 36.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )A.正三角形 B.正方形C.正五边形 D.正六边形7.若正方形的外接圆半径为2,则其内切圆半径为( )A. 2 B.2 2C.22D.18.边长为6 cm的等边三角形的外接圆半径是.9.如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合.若A点的坐标为(-1,0),则点C的坐标为( ).10.将一个边长为1的正八边形补成如图所示的正方形,这个正方形的边长等于 (结果保留根号).知识点3 画正多边形11.如图,甲:①作OD的中垂线,交⊙O于B,C两点;②连接AB,AC,△ABC即为所求的三角形.乙:①以D为圆心,OD长为半径作圆弧,交⊙O于B,C两点;②连接AB,BC,CA,△ABC即为所求的三角形.对于甲、乙两人的作法,可判断( )A.甲、乙均正确 B.甲、乙均错误C.甲正确,乙错误 D.甲错误,乙正确12.图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图2,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹).中档题13.正三角形内切圆半径r与外接圆半径R之间的关系为( )A.4R=5r B.3R=4rC.2R=3r D.R=2r14.如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是( )A.(2,-3) B.(2,3)C.(3,2) D.(3,-2)15.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )A.22B.32C. 2D. 316.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )A.2a2 B.3a2 C.4a2 D.5a217.如图,圆O与正八边形OABCDEFG的边OA,OG分别交于点M,N,则弧MN所对的圆心角∠MPN的大小为.18.如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10= .19.如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.(1)正方形ABCD与正六边形AEFCGH的边长之比为;(2)连接BE,BE是否为⊙O的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由.综合题20.如图1,2,3,…,m,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…正n边形ABCDEF…的边AB,BC上的点,且BM=CN,连接OM,ON.(1)求图1中∠MON的度数;(2)图2中∠MON的度数是,图3中∠MON的度数是;(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).参考答案01 基础题知识点1 认识正多边形1.下面图形中,是正多边形的是(C)A .矩形B .菱形C .正方形D .等腰梯形2.(柳州中考)如图,正六边形的每一个内角都相等,则其中一个内角α的度数是(B)A .240°B .120°C .60°D .30°3.(连云港中考)一个正多边形的一个外角等于30°,则这个正多边形的边数为12.4.(资阳中考)如图,AC 是正五边形ABCDE 的一条对角线,则∠ACB=36°.知识点2 与正多边形有关的计算5.(沈阳中考)如图,正六边形ABCDEF 内接于⊙O ,正六边形的周长是12,则⊙O 的半径是(B)A. 3B .2C .2 2D .2 3 6.(株洲中考)下列圆的内接正多边形中,一条边所对的圆心角最大的图形是(A) A .正三角形 B .正方形 C .正五边形 D .正六边形7.(滨州中考)若正方形的外接圆半径为2,则其内切圆半径为(A)A. 2 B .2 2C.22D .1 8.边长为6 cm 的等边三角形的外接圆半径是23.9.(宁夏中考)如图,将正六边形ABCDEF 放在直角坐标系中,中心与坐标原点重合.若A点的坐标为(-1,0),则点C 的坐标为(12,-32).10.(教材P109习题T6变式)将一个边长为1的正八边形补成如图所示的正方形,这个正方形的边长等于1+2(结果保留根号).知识点3 画正多边形甲:①作OD的中垂线,交⊙O于B,C两点;②连接AB,AC,△ABC即为所求的三角形.乙:①以D为圆心,OD长为半径作圆弧,交⊙O于B,C两点;②连接AB,BC,CA,△ABC即为所求的三角形.对于甲、乙两人的作法,可判断(A)A.甲、乙均正确B.甲、乙均错误C.甲正确,乙错误D.甲错误,乙正确12.(镇江中考改编)图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图2,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹).解:如图.02中档题13.正三角形内切圆半径r与外接圆半径R之间的关系为(D)A.4R=5r B.3R=4rC.2R=3r D.R=2r14.(滨州中考)如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是(C)A.(2,-3) B.(2,3)C.(3,2) D.(3,-2)15.(达州中考)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是(A)A.22B.32C. 2D. 316.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为(A)A.2a2 B.3a2 C.4a2 D.5a217.(山西中考命题专家原创)如图,圆O与正八边形OABCDEFG的边OA,OG分别交于点M,N,则弧MN所对的圆心角∠MPN的大小为67.5°.18.(连云港中考)如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10=75°.19.如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.(1)正方形ABCD与正六边形AEFCGH的边长之比为2∶1;(2)连接BE,BE是否为⊙O的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由.解:BE是⊙O的内接正十二边形的一边,理由:连接OA ,OB ,OE ,在正方形ABCD 中,∠AOB=90°,在正六边形AEFCGH 中,∠AOE=60°,∴∠BOE=30°.∵n=360°30°=12, ∴BE 是正十二边形的边.03 综合题20.如图1,2,3,…,m ,M ,N 分别是⊙O 的内接正三角形ABC ,正方形ABCD ,正五边形ABCDE ,…正n 边形ABCDEF …的边AB ,BC 上的点,且BM=CN ,连接OM ,ON.(1)求图1中∠MON 的度数;(2)图2中∠MON 的度数是90°,图3中∠MON 的度数是72°;(3)试探究∠MON 的度数与正n 边形边数n 的关系(直接写出答案).解:(1)连接OA ,OB.∵正三角形ABC 内接于⊙O ,∴OA=OB ,∠OAM=∠OBA=30°,∠AOB=120°.∵BM=CN ,AB=BC ,∴AM=BN.∴△AOM ≌△BON(SAS).∴∠AOM=∠BON.∴∠AOM +∠BOM=∠BON +∠BOM ,即∠AOB=∠MON.∴∠MON=120°.(3)∠MON=360°n.。
2024年人教版九年级数学上册教案及教学反思第24章24.3 正多边形和圆(第1课时)

24.3 正多边形和圆第1课时一、教学目标【知识与技能】了解正多边形和圆的关系,了解正多边形半径和边长,边心距,中心,中心角等概念.会应用正多边形的有关知识解决圆中的计算问题.【过程与方法】结合生活中的正多边形形状的图案,发现正多边形和圆的关系.【情感态度与价值观】学生经历观察、发现、探究等数学活动,感受到数学来源于生活、又服务于生活.二、课型新授课三、课时第1课时,共2课时。
四、教学重难点【教学重点】正多边形与圆的相关概念及其之间的运算.【教学难点】探索正多边形和圆的关系,正多边形半径,中心角、边心距,边长之间的关系.五、课前准备课件、图片、直尺等.六、教学过程(一)导入新课出示课件2,3:观察上边的美丽图案,思考下面的问题:(1)这些都是生活中经常见到的利用正多边形得到的物体,你能找出正多边形吗?(2)你知道正多边形和圆有什么关系吗?怎样做一个正多边形呢?学生通过观察美丽的图案,欣赏生活中正多边形形状的物体.让学生感受到数学来源于生活,并从中感受到数学美.(板书课题)(二)探索新知探究一正多边形的对称性教师问:什么叫做正多边形?(出示课件5)学生答:各边相等,各角也相等的多边形叫做正多边形.教师问:矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?学生答:矩形不是正多边形,因为矩形不符合各边相等;菱形不是正多边形,因为菱形不符合各角相等;教师强调:正多边形:①各边相等;②各角相等,两个条件,缺一不可.教师问:正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?(出示课件6,7)学生动手操作,交流,感受正多边形的对称性.教师归纳:正n边形都是轴对称图形,都有n条对称轴,只有边数为偶数的正多边形既是轴对称图形又是中心对称图形.探究二正多边形的有关概念教师问:以正四边形为例,根据对称轴的性质,你能得出什么结论?(出示课件8,9)师生结合图形共同探究:EF是边AB、CD的垂直平分线,∴OA=OB,OD=OC.GH是边AD、BC的垂直平分线,∴OA=OD,OB=OC.∴OA=OB=OC=OD.∴正方形ABCD有一个以点O为圆心的外接圆.AC是∠DAB及∠DCB的角平分线,BD是∠ABC及∠ADC的角平分线,∴OE=OH=OF=OG.∴正方形ABCD还有一个以点O为圆心的内切圆.出示课件10:教师问:所有的正多边形是不是也都有一个外接圆和一个内切圆?学生答:任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆.教师问:一个正多边形的各个顶点在同一个圆上?学生答:一个正多边形的各个顶点在同一个圆上,则这个正多边形就是这个圆的一个内接正多边形,圆叫做这个正多边形的外接圆.教师问:所有的多边形是不是都有一个外接圆和内切圆?学生答:多边形不一定有外接圆和内切圆,只有是正多边形时才有,任意三角形都有外接圆和内切圆.教师出示概念:(出示课件11)1.正多边形的外接圆和内切圆的公共圆心,叫做正多边形的中心.2.外接圆的半径叫做正多边形的半径.3.内切圆的半径叫做正多边形的边心距.4.正多边形每一条边所对的圆心角,叫做正多边形的中心角.正多边形的每个中心角都等于360.n练一练:(出示课件12)完成下面的表格:学生计算交流并填表.探究三 正多边形的有关计算出示课件13:如图,已知半径为4的圆内接正六边形ABCDEF :①它的中心角等于 度; ②OC BC(填>、<或=); ③△OBC 是 三角形;④圆内接正六边形的面积是△OBC 面积的 倍. ⑤圆内接正n 边形面积公式:_______________________. 学生计算交流后,教师抽学生口答.①60;②=;③等边;④6;⑤1=2S ⨯⨯正多边形周长边心距出示课件14:例 有一个亭子,它的地基是半径为4m 的正六边形,求地基的周长和面积(精确到0.1m 2).教师分析:根据题意作图,将实际问题转化为数学问题.师生共同解答:(出示课件15)解:过点O 作OM ⊥BC 于M.在Rt △OMB 中,OB =4,MB =4222BC ==,利用勾股定理,可得边心距r ==亭子地基的面积:2112441.6(m ).22S l r =⋅=⨯⨯≈ 巩固练习:(出示课件16)如图所示,正五边形ABCDE 内接于⊙O ,则∠ADE 的度数是( )A .60°B .45°C .36°D .30° 学生独立思考后自主解答:C.教师归纳:圆内接正多边形的辅助线(出示课件17)1.连半径,得中心角;2.作边心距,构造直角三角形. 巩固练习:(出示课件18)已知直角三角形两条直角边的和等于8,两条直角边各为多少时,这个直角三角形的面积最大,最大值是多少?学生独立思考后解答,一生板演.解:∵直角三角形两直角边之和为8,设一边长为x. ∴ 另一边长为8-x.则该直角三角形面积:S=(8-x )x ÷2,即214.2s x x =-+ 当x=2b a -=4,另一边为4时,S 有最大值244ac b a -=8.∴当两直角边都是4时,直角面积最大,最大值为8. (三)课堂练习(出示课件19-24)1.图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=______度.2.填表:3.若正多边形的边心距与半径的比为1:2,则这个多边形的边数是_____.4.如图是一枚奥运会纪念币的图案,其形状近似看作为正七边形,则一个内角为_____度.(不取近似值)5.要用圆形铁片截出边长为4cm的正方形铁片,则选用的圆形铁片的直径最小要____cm.6.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.7.如图,正六边形ABCDEF的边长为,点P为六边形内任一点.则点P 到各边距离之和是多少?8.如图,M,N分别是☉O内接正多边形AB,BC上的点,且BM=CN.(1)求图①中∠MON=_______;图②中∠MON=_______;图③中∠MON=_______;(2)试探究∠MON的度数与正n边形的边数n的关系.参考答案:1.360°解析:由多边形的外角和等于360°可知,∠1+∠2+∠3+∠4+∠5=360°.2.3.34.412875.6.解:∵正方形的面积等于4, ∴正方形的边长AB=2. 则圆的直径AC=2, ∴⊙O 的半径=.∴⊙O 的面积为22.ππ=7.解:过P 作AB 的垂线,分别交AB 、DE 于H 、K ,连接BD ,作CG ⊥BD 于G.22∵六边形ABCDEF 是正六边形, ∴AB ∥DE ,AF ∥CD ,BC ∥EF ,∴P 到AF 与CD 的距离之和,及P 到EF 、BC 的距离之和均为HK 的长. ∵BC=CD ,∠BCD=∠ABC=∠CDE=120°, ∴∠CBD=∠BDC=30°,BD ∥HK ,且BD=HK.∴CG=12BC=.∵CG ⊥BD ,∴BD=2BG=2×=2×3=6.∴点P 到各边距离之和=3BD=3×6=18. 8.解:⑴①120°;②90°;③72°;⑵360MON n ︒∠=.(四)课堂小结通过这节课的学习,你知道正多边形和圆有怎样的关系吗?你知道正多边形的半径、边心距、内角、中心角等概念吗?(五)课前预习22BG BC-预习下节课(24.3第2课时)的相关内容.七、课后作业配套练习册内容八、板书设计:九、教学反思:本节课通过创设问题情境,将正多边形与圆紧密联系,让学生发现它们之间的密切关系,并将结论由特殊推广到一般,符合学生的认识规律,通过学习正多边形中的一些基本概念,引导学生将实际问题转化为数学问题,体现了化归的思想.。
部编数学九年级上册24.3正多边形和圆(7大题型)2023考点题型精讲(解析版)含答案

24.3 正多边形和圆正多边形的概念 各边相等,各角也相等的多边形是正多边形.正多边形的有关概念 (1)一个正多边形的外接圆的圆心叫做这个正多边形的中心. (2)正多边形外接圆的半径叫做正多边形的半径. (3)正多边形每一边所对的圆心角叫做正多边形的中心角. (4)正多边形的中心到正多边形的一边的距离叫做正多边形的边心距.题型1:正多边形的相关概念1.下列关于正多边形的叙述,正确的是( )A.正九边形既是轴对称图形又是中心对称图形B.存在一个正多边形,它的外角和为720°C.任何正多边形都有一个外接圆D.不存在每个外角都是对应每个内角两倍的正多边形【答案】C【解析】【解答】解:正九边形是轴对称图形,不是中心对称图形,故选项A不正确;任何多边形的外角和都为360°,故选项B不正确;【变式1-1】已知:如图,四边形ABCD是⊙O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数是( )A.45° B.60° C.75° D.90°【答案】A.【解析】如图,连接OB、OC,则∠BOC=90°,根据圆周角定理,得:∠BPC=∠BOC=45°.故选A.【点评】本题主要考查了正方形的性质和圆周角定理的应用.【变式1-2】如图,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB等于( )A.30° B.45° C.55° D.60°【答案】连接OA,OB.根据正方形的性质,得∠AOB=90°.再根据圆周角定理,得∠APB=45°.故选B.正多边形的有关计算 (1)正n边形每一个内角的度数是; (2)正n边形每个中心角的度数是; (3)正n边形每个外角的度数是.注意:要熟悉正多边形的基本概念和基本图形,将待解决的问题转化为直角三角形题型2:正多边形与圆有关的计算-角度2.如图,正五边形ABCDE内接于⊙O,连接AC,则∠BAC的度数是( )A.45°B.38°C.36°D.30°【答案】C【解析】【解答】解:连接OC、OB,如下图:根据正多边形的性质可得:∠BOC=360°5=72°根据圆周角定理可得:∠BAC=12∠BOC=36°故答案为:C【分析】连接OC、OB,根据正多边形的性质可得∠BOC=360°5=72°,再根据圆周角定理求解即可。
人教版九年级数学上册24.3 正多边形和圆同步练习含答案【2021年新编版】

第24章 24.3《正多边形和圆》同步练习及答案 (1) 1.边长为a的正六边形的边心距是__________,周长是____________,面积是___________。
2.如图1,正方形的边长为a,以顶点B、D为圆心,以边长a为半径分别画弧,在正方形内两弧所围成图形的面积是___________。
(1) (2) (3)3.圆内接正方形ABCD的边长为2,弦AE平分BC边,与BC交于F,则弦AE的长为__________。
4.正六边形的面积是183,则它的外接圆与内切圆所围成的圆环面积为_________。
5.圆内接正方形的一边截成的小弓形面积是2π-4,则正方形的边长等于__________。
6.正三角形的内切圆半径、外接圆半径和高的比为___________。
7.在半径为R的圆中,内接正方形与内接正六边形的边长之比为___________。
8.同圆的内接正n边形与外切正n边形边长之比是______________。
9.正三角形与它的内切圆及外接圆的三者面积之比为_____________。
10.正三角形的外接圆半径为4cm,以正三角形的一边为边作正方形,则此正方形的外接圆半径长为___________。
B卷1.正方形的内切圆半径为r,这个正方形将它的外接圆分割出四个弓形,其中一个弓形的面积为_________。
2.如果正三角形的边长为a,那么它的外接圆的周长是内切圆周长的_______倍。
3.如图2,正方形边长为2a,那么图中阴影部分的面积是__________。
4.正多边形的一个内角等于它的一个外角的8倍,那么这个正多边形的边数是________。
5.半径为R的圆的内接正n边形的面积等于__________。
6.如果圆的半径为a,它的内接正方形边长为b,该正方形的内切圆的内接正方形的边长为c,则a,b,c间满足的关系式为___________。
7.如图3,正△ABC内接于半径为1cm的圆,则阴影部分的面积为___________。
人教版九年级数学上册《24.3正多边形和圆》同步测试题及答案
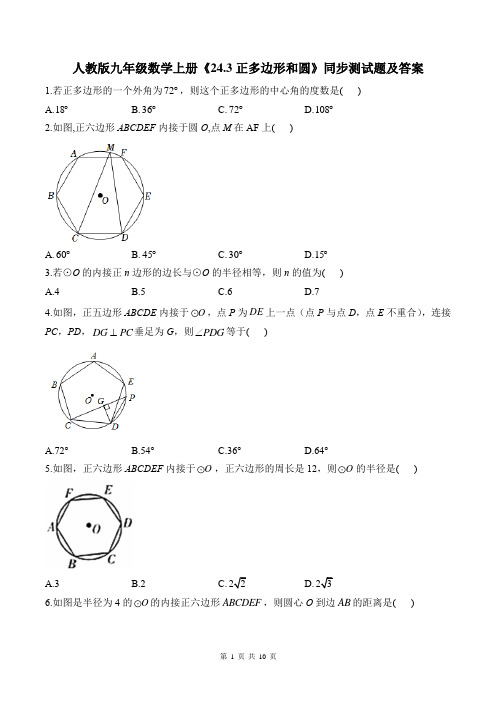
人教版九年级数学上册《24.3正多边形和圆》同步测试题及答案1.若正多边形的一个外角为72︒,则这个正多边形的中心角的度数是( )A.18︒B.36︒C.72︒D.108︒2.如图,正六边形ABCDEF内接于圆O,点M在AF上( )A.60︒B.45︒ C.30︒ D.15︒3.若⊙O的内接正n边形的边长与⊙O的半径相等,则n的值为( )A.4B.5C.6D.74.如图,正五边形ABCDE内接于O,点P为DE上一点(点P与点D,点E不重合),连接PC,PD,⊥DG PC垂足为G,则∠PDG等于( )A.72°B.54°C.36°D.64°5.如图,正六边形ABCDEF内接于,正六边形的周长是12,则的半径是( )A.3B.2C.22D.236.如图是半径为4的O的内接正六边形ABCDEF,则圆心O到边AB的距离是( )O OA.23B.3C.2D.37.如图,正六边形ABCDEF 内接于O ,O 的半径为6,则这个正六边形的边心距OM 和弧BC 的长分别为( )A.32 πB.332 πC.332 2π3D.33 π8.如图,正三角形ABC 和正六边形ADBECF 都内接于,O 连接,OC 则∠+∠=ACO ABE ( )A.90︒B.100︒C.110︒D.120︒9.如图,正五边形ABCDE 内接于O ,P 为DE 上的一点(点P 不与点D 重合),则∠=CPD ________°.10.如图,正六边形ABCDEF内接于O,若O的周长等于6π,则正六边形的边长为______.11.早在1800多年前,魏晋时期的数学家刘徽首创“割圆术”,用圆内接正多边形的面积去无限逼近圆面积,如图所示的圆的内接正十二边形,若该圆的半径为1,则这个圆的内接正十二边形的面积为_________________.12.如图,圆内接正六边形ABCDEF的半径为2,则该正六边形的面积是_________________.13.有一个亭子,它的地基是半径为8m的正六边形,求地基的面积.(结果保留根号)14.如图,O的周长等于8πcm,正六边形ABCDEF内接于O.(1)求圆心O 到AF 的距离.(2)求正六边形ABCDEF 的面积.参考答案及解析1.答案:C 解析:正多边形的一个外角为72︒∴正多边形的边数为360725︒÷︒=∴这个正多边形的中心角的度数是360572︒÷=︒故选:C.2.答案:C解析:连接OC ,OD多边形ABCDEF 是正六边形60∴∠=︒COD1302∴∠=∠=︒CMD COD故选:C.3.答案:C解析:内接正n 边形的边长与⊙O 的半径相等∴正n 边形的中心角为60︒360606︒÷︒=∴n 的值为6故选:C.4.答案:B解析:正五边形ABCDE 内接于O∠CPD 与所对的弧相同1362∴∠=∠=︒CPD COD故选:B.5.答案:B解析:如图,连结OA ,OBABCDEF 为正六边形1360606∴∠=︒⨯︒=AOB∴AOB △是等边三角形正六边形的周长是1211226∴=⨯=AB2∴===AO BO AB故选B.6.答案:A解析:如图,做⊥OM AB 于点M360725COD ︒∴∠==︒COD ∠180903654PDG ∠=︒-︒-︒=∴︒正六边形ABCDEF 外接半径为4的O4∴==OA OB 360606︒∠==︒AOB 1302∴∠=∠=∠=︒AOM BOM AOB122∴===AM BM OA2223∴=-=OM OA AM ∴圆心O 到边AB 的距离为23故选:A.7.答案:D解析:连接OB 、OC六边形ABCDEF 为正六边形360606︒∴∠==︒BOC 。
24.3正多边形和圆-人教版九年级数学上册练习

人教版九年级数学上册24.3正多边形和圆一.选择题(共6小题)1.如图,正六边形ABCDEF 内接于。
0, 连接BD.则ZCDB 的度数是()3.下列判断中正确的是()A.矩形的对角线互相垂直B.正八边形的每个内角都是145°C.三角形三边垂直平分线的交点到三角形三边的距离相等D. 一组对边平行,一组对角相等的四边形是平行四边形 4.正六边形的周长为6,则它的外接圆半径为()5.若一个正六边形的半径为2,则它的边心距等于()6.有一边长为2去的正三角形,则它的外接圆的而积为(二.填空题(共6小题)7. 如图,在同一平面内,将边长相等的正方形、正五边形的一边重合,那么匕1=60° C. 45° D. 30°2.若一个圆内接正多边形的中心角是36’ ,则这个多边形是(A.正五边形B.正八边形C.正十边形D. 正十八边形A. 1B. 2C. 3D.A. 2B. 1c. VsD.2^3C. 4nD. 12n8.如图,将边长相等的正六边形和正五边形拼接在一起,则ZABC的度数为9.我们把正多边形的一个内角与外角的比值叫做正多边形的内外比,内外比为3的正多边形的边数为.10.如果一个正〃边形的每个内角为108° ,那么这个正〃边形的边数为.11.正六边形的中心角为:当它的半径为1时,边心距为.12.已知。
过正方形ABCD顶点A、B,且与CO相切,若正方形边长为2,则圆的半径13.有一正六边形ABCDEF的内切圆半径为R,求R与这个正六边形ABCDEF的外接圆半径之比.14.如图,已知正六边形ABCDEF内接于。
,且边长为4.(1)求该正六边形的半径、边心距和中心角;(2)求该正六边形的外接圆的周长和面积.15.如图所示,在正五边形ABCDE中,A/是CD的中点,连接AC, BE, AM.求证:(1)AC=BE;(2)AMLCD.人教版九年级数学上册24.3正多边形和圆参考答案一. 选择题(共6小题)1.如图,正六边形ABCDEF 内接于。
九年级数学人教版上册24.3正多边形和圆优秀教学案例

在实际教学过程中,我将以知识与技能、过程与方法、情感态度与价值观为目标,设计丰富多样的教学活动和实例,引导学生积极参与,主动探究,使学生在掌握知识的同时,也能提高自身的综合素质和能力。同时,注重因材施教,关注每个学生的个体差异,充分调动学生的积极性和主动性,使每个学生都能在数学学科的学习中得到充分的发展和提高。
2.培养学生的动手操作能力,提高学生运用数学知识解决实际问题的能力。
3.引导学生运用归纳、推理等方法,总结正多边形的性质和规律,培养学生的创新思维能力。
(三)情感态度与价值观
1.培养学生对数学学科的兴趣和自信心,激发学生学习数学的内在动力。
2.培养学生独立思考、合作交流的习惯,提高学生的人际沟通能力和团队合作精神。
2.组织学生进行自我评价和同伴评价,让学生了解自己的学习成果和不足之处,提高学生的自我认知和评价能力。
3.教师对学生的学习情况进行总结和评价,关注学生的个体差异,给予有针对性的指导和鼓励,激发学生的学习动力和信心。
四、教学内容与过程
(一)导入新课
1.利用多媒体展示各种正多边形的实物图片,如正方形、正三角形等,引导学生关注正多边形在现实生活中的应用。
2.问题导向与小组合作相辅相成:在教学过程中,教师引导学生提出问题并自主探究,通过小组合作的形式进行研究讨论。这样的教学方式既培养了学生的提问意识和自主学习能力,又提高了学生的团队合作和交流沟通能力。
3.反思与评价注重个体差异:教师在教学过程中注重引导学生进行反思和评价,关注学生的个体差异,给予有针对性的指导和鼓励。这种教学方式既激发了学生的学习动力,又培养了学生的自我认知和评价能力。
2.设计一个正多边形的拼图游戏,让学生在游戏中体会正多边形的性质和特点,激发学生的学习兴趣。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014人教版九年级数学上册
第24章 24.3《正多边形和圆》同步练习及答案 (1) 1.边长为a的正六边形的边心距是__________,周长是____________,面积是___________。
2.如图1,正方形的边长为a,以顶点B、D为圆心,以边长a为半径分别画弧,在正方形内两弧所围成图形的面积是___________。
(1) (2) (3)
3.圆内接正方形ABCD的边长为2,弦AE平分BC边,与BC交于F,则弦AE的长为__________。
4.正六边形的面积是183,则它的外接圆与内切圆所围成的圆环面积为_________。
5.圆内接正方形的一边截成的小弓形面积是2π-4,则正方形的边长等于__________。
6.正三角形的内切圆半径、外接圆半径和高的比为___________。
7.在半径为R的圆中,内接正方形与内接正六边形的边长之比为___________。
8.同圆的内接正n边形与外切正n边形边长之比是______________。
9.正三角形与它的内切圆及外接圆的三者面积之比为_____________。
10.正三角形的外接圆半径为4cm,以正三角形的一边为边作正方形,则此正方形的外接圆半径长为___________。
B卷
1.正方形的内切圆半径为r,这个正方形将它的外接圆分割出四个弓形,其中一个弓形的面积为_________。
2.如果正三角形的边长为a,那么它的外接圆的周长是内切圆周长的_______倍。
3.如图2,正方形边长为2a,那么图中阴影部分的面积是__________。
4.正多边形的一个内角等于它的一个外角的8倍,那么这个正多边形的边数是________。
5.半径为R的圆的内接正n边形的面积等于__________。
6.如果圆的半径为a,它的内接正方形边长为b,该正方形的内切圆的内接正方形的边长
为c ,则a,b ,c 间满足的关系式为___________。
7.如图3,正△ABC 内接于半径为1cm 的圆,则阴影部分的面积为___________。
8.如果圆内接正六边形的边长为10cm ,则它的边心距为_______cm ,正六边形的一边在圆上截得的弓形面积是____________。
9.已知正方形的边长为a ,以各边为直径在正方形内画半圆,则所围成的阴影部分(如图)的面积为__________。
10.周长相等的正方形和正六边形的面积分别为4S 和6S ,则4S 和6S 的大小关系为__________。
答案
A 卷
1.22
33;6;23a a 2.222a a -π
3.点B 到弦AE 的垂线段长为
552,由勾股定理或射影定理,求得弦AE 的长为558。
4.由正六边形的面积为183,得正六边形的边长为23,边心距为3,从而正六边形的外接圆半径为23,内切圆半径为3,故所围成的圆环面积为3π。
5.设所求正方形的边长为x ,则外接圆的半径为
x 22,正方形的一边截成的小弓形面积为224181
x x ππ-,即224
181x x ππ- = 2π- 4,于是,得正方形的边长等于4。
6.设正三角形的边长为a ,则内切圆半径为
a 63,外接圆半径为a 33,高为a 23,故内切圆半径、外接圆半径和高的比为1:2:3。
7.内接正方形的边长为2R ,内接正六边形的边长为R ,其比为2:1。
8.设圆的半径为R ,则同圆的内接正π边形和外切正n 边形的边分别为2Rsin n ︒180和2Rtg n ︒180,其比为cos n
︒180。
9.设正三角形的边长为a ,则内切圆半径为
a 63,外接圆半径为a 33,其面积分别为243a 、2121a π和23
1a π,三者之比为33:π:4π。
10.求得正三角形的边长即所作正方形的边长为43,从而外接圆的半径长为26。
B 卷
1.由已知得正方形的边长为2r , 从而正方形的外接圆半径为2r ,所求弓形的面积为2)22
1
(r -π。
2.边长为a 的正三角形的外接圆半径和内切圆半径分别为a 33、a 6
3,其周长分别为332的πa 和a π3
3,故它的外接圆周长是内切圆周长的2倍。
3.阴影部分面积为2224
1)22(21)2(41
a a a πππ=- 4.设所求正多边形的边数为n ,则它的一个内角等于
︒⋅-180)2(n n , 相应的外角等于180°- ︒⋅-180)2(n
n , 则由已知,得︒⋅-180)2(n n =8×(180°-︒⋅-180)2(n
n ),解之,得n = 18。
5.半径为R 的圆的内接正n 边形的边长为2Rsin n ︒180,边长距为Rcos n
︒180, 则正n 边形的面积为= n
n nR n R n R n ︒⋅︒=︒⋅︒⋅⋅180cos 180sin 180cos 180sin 2212 6.半径为a 的圆的内接正方形的边长为2a ,即 b = 2a ;
边长为b 的正方形的内切圆的内接正方形的边长为
22b ,即 C = 22b , 从而得知 a = c ,故a,b,c 三者之间的关系为:222c a b +=
7.设正△ABC 的边长为a ,则a 3
3=1,a=3, 于是阴影部分的面积为π·))(4
33()3(431222cm -=⋅-π 8.边心距2
3×10=53(2cm ); 正六边的一边在圆上截得的弓形的面积减去三角形的面积, 即)(325350104310321222cm -=⋅-⋅⋅ππ
9.图中四个半圆都通过正方形的中心,用正方形的面积减去四隙的面积,剩下的就是阴影部分的面积,而正方形的面积减去两个半圆的面积就得两个空隙的面积,故所求阴影部分的面积为.22])2([22222a a a
a a -=⨯⋅--π
π
10.设周长为a ,则正方形的正六边形的边长分别为
a a 6141和,其面积分别为22224
3)61(436161a a a =⋅⋅和,故64S S <。
