热力学第一定理2014
热力学第一定律

热力学第一定律基本概念体系(system ):作为研究对象的部分物质及其空间环境(surrounding ):体系以外且与体系密切相关的物质及其所在空间 敞开体系,封闭体系,绝热体系,孤立体系 状态:体系宏观性质的总和状态性质:描述体系状态的宏观物理量。
广度性质,强度性质 状态函数:依赖其他状态变量的状态性质称为状态函数 状态函数的数学性质:单值,连续,可微的函数;在状态图上是连续变化的单值平滑曲线 若 Z = f (x, y) 为状态函数,则有全微分:Z Z dZ dx dy x y ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭ 0dZ =⎰ 22Z Zx y y x ∂∂=∂∂∂∂1y xZ Z x y x y Z ⎛⎫∂∂∂⎛⎫⎛⎫=- ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ 过程:发生状态变化的方式 途径:完成某一变化的具体步骤等温过程,等压过程,等容过程,绝热过程,节流过程,循环过程,卡诺循环 热力学平衡:力平衡,热平衡,相平衡,化学平衡 反应进度热力学第一定律U Q W ∆=+ 或 dU Q W δδ=+U 热力学能(内能):是体系的广度性质,它是体系中一切形式能量的总和。
如分子,原子的平动能、转动能、振动能,分子,原子,电子及原子核等相互作用的势能;但不包括力场中整体运动的动能、势能;绝对值不可知。
Q 热:体系与环境由于温度的差别所交换的能量。
是以分子无序运动相互碰撞传递能量的方式。
体系从环境吸热为正值,反之为负值。
W 功:体系与环境之间除热的形式以外所交换的能量,是体系和环境间以物质分子宏观有序运动传递能量的方式。
环境对体系作功为正值,反之为负值。
W 的计算:W p dV p dV δ=-≠-外体反抗恒外压:Wp V =-∆外理想气体等温可逆过程:W = nRTln(V 2/V 1) = nRTln(p 1/p 2)理想气体绝热可逆过程:W = nC v,m (T 2 -T 1) = (p 2 V 2-p 1V 1)/(γ-1)理想气体绝热不可逆过程:W = nC v,m (T 2 -T 1) = p 外(V 2-V 1)=nRp 外(T 2/p 2-T 1/p 1)Q 的计算:显热(封闭体系,无相变化,无化学反应),21()V V m Q nC T T =-,,21()p p m Q nC T T =-潜热(相变过程)恒压可逆相变:Q Qp H ==∆相变不可逆相变:Q U W =∆-化学反应热Hess 定律, 生成热, 燃烧热, 离子生成热,键焓 Kirchhoff 定律 p v Q Q nRT =+∆ 焓定义式: H = U + pV ∆H = ∆U + ∆(pV) 理想气体等温过程:∆H = ∆U =0 Joule — Thomson 效应1HT T H p Cp p μ⎛⎫⎛⎫∂∂==-⎪ ⎪∂∂⎝⎭⎝⎭卡诺热机效率:122122Q Q T T Q T η+-==热力学第二定律概念自发过程:不需外力帮助就能进行的过程,其显著特点就是它具有热力学的不可逆性。
热力学第一定律

热力学第一定律功:δW =δW e +δW f(1)膨胀功 δW e =p 外dV 膨胀功为正,压缩功为负。
(2)非膨胀功δW f =xdy非膨胀功为广义力乘以广义位移。
如δW (机械功)=fdL ,δW (电功)=EdQ ,δW (表面功)=rdA 。
热 Q :体系吸热为正,放热为负。
热力学第一定律: △U =Q —W 焓 H =U +pV 理想气体的内能和焓只是温度的单值函数。
热容 C =δQ/dT(1)等压热容:C p =δQ p /dT = (∂H/∂T )p (2)等容热容:C v =δQ v /dT = (∂U/∂T )v 常温下单原子分子:C v ,m =C v ,m t =3R/2常温下双原子分子:C v ,m =C v ,m t +C v ,m r =5R/2 等压热容与等容热容之差:(1)任意体系 C p —C v =[p +(∂U/∂V )T ](∂V/∂T )p (2)理想气体 C p —C v =nR 理想气体绝热可逆过程方程:pV γ=常数 TV γ-1=常数 p 1-γT γ=常数 γ=C p / C v 理想气体绝热功:W =C v (T 1—T 2)=11-γ(p 1V 1—p 2V 2) 理想气体多方可逆过程:W =1nR-δ(T 1—T 2) 热机效率:η=212T T T - 冷冻系数:β=-Q 1/W 可逆制冷机冷冻系数:β=121T T T -焦汤系数: μJ -T =H p T ⎪⎪⎭⎫⎝⎛∂∂=-()pT C p H ∂∂ 实际气体的ΔH 和ΔU :ΔU =dT T U V ⎪⎭⎫ ⎝⎛∂∂+dV V U T ⎪⎭⎫ ⎝⎛∂∂ ΔH =dT T H P ⎪⎭⎫ ⎝⎛∂∂+dp p H T⎪⎪⎭⎫ ⎝⎛∂∂ 化学反应的等压热效应与等容热效应的关系:Q p =Q V +ΔnRT 当反应进度 ξ=1mol 时, Δr H m =Δr U m +∑BB γRT化学反应热效应与温度的关系:()()()dT B C T H T H 21T T m p B1m r 2m r ⎰∑∆∆,+=γ热力学第二定律Clausius 不等式:0TQS BAB A ≥∆∑→δ—熵函数的定义:dS =δQ R /T Boltzman 熵定理:S =kln Ω Helmbolz 自由能定义:F =U —TS Gibbs 自由能定义:G =H -TS 热力学基本公式:(1)组成恒定、不作非膨胀功的封闭体系的热力学基本方程:dU =TdS -pdV dH =TdS +Vdp dF =-SdT -pdV dG =-SdT +Vdp (2)Maxwell 关系:T V S ⎪⎭⎫⎝⎛∂∂=V T p ⎪⎭⎫ ⎝⎛∂∂Tp S ⎪⎪⎭⎫ ⎝⎛∂∂=-p T V ⎪⎭⎫ ⎝⎛∂∂ (3)热容与T 、S 、p 、V 的关系:C V =T VT S ⎪⎭⎫⎝⎛∂∂ C p =T p T S ⎪⎭⎫ ⎝⎛∂∂Gibbs 自由能与温度的关系:Gibbs -Helmholtz 公式 ()pT /G ⎥⎦⎤⎢⎣⎡∂∆∂T =-2T H ∆ 单组分体系的两相平衡: (1)Clapeyron 方程式:dT dp=mX m X V T H ∆∆ 式中x 代表vap ,fus ,sub 。
2014-2015修订热力学第一定律
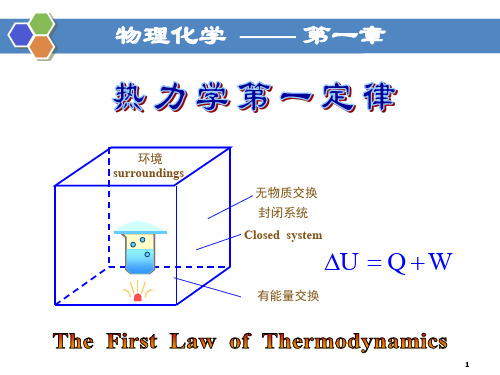
热力学第一定律的含义 (1) 说明了内能、热、功可以相互转 化; (2) 说明了转化时的数量关系。 功和热都是能量的传递形式,而不是系统自身的 属性,因此它不是状态函数,而是过程的属性,是过 程的产物。一个体系从同一个始态到同一个终态,可 以经历不同的途径。 Q 、 W 数值可能不同,但代数和 是相同的,即内能的变化都是相同的。
13
如图,判定下列为何种系统? 电阻丝+电池 密闭系统 密闭系统 密闭系统
水
电阻丝
电阻丝+电池+水 隔离系统
14
若一系统,其各项性质均具有确定的数值,则称该 系统处于一定的状态。状态是系统的物理性质和化学性 质的综合表现。 系统的性质只取决于系统目前所处的状态,而与过 去的历史无关。状态发生变化,系统的性质也发生相应 的变化,变化值只取决于系统的始态和终态,而与变化 的途径无关。无论多么复杂的变化,系统复原,所有的 性质也都复原。具有这种性质的物理量称为状态性质, 又称为状态函数。
状态函数的特性:
异途同归,值变相等;周而复始,数值还原。
15
状 态 性 质
强度性质 容量性质 (广度性质)
• 与系统中的物质的量无关 • 无加和性 • 与系统中物质的量有关 • 有加和性
体积 V总=V1+V2+… 质量 m总= m1+m2 +… 内能 U总=U1+U2+…
温度 T总=T1=T2=… 压力 p总=p1=p2=… 密度 ρ总=ρ1=ρ2=…
ห้องสมุดไป่ตู้
29
注意点
② 内能的绝对值无法测定,只能求出它的变化值。 内能的绝对值为什么无法确定?是否不利 于解决实际问题? 答:人类对物质运动形式的认识存在局限 。热力学是通过系统状态函数的改变量来 解决问题。
热力学第一定理及其应用

作业: 1、在汽车消耗的每100桶汽油中,大约 有多少桶实际上用来驱动一辆小车在路 上奔跑?
2、热机在一次循环中做100焦耳功,却 放出300焦耳热能,它的输入能量是多 少?效率是多少?
• 等温压缩阶段:
W 3 -Q L
• 绝热压缩阶段:
W4 Ui U f U D U A 0
• A 和 B 在同一条等温线:
UA UB
• C 和 D 在同一条等温线:
UC UD
• 整个循环中,总功为:
W W1 W 2 W3 W 4 Q H Q L
All storms are heat engines; they convert thermal energy into the mechanical energy of wind. A hurricane can be described, at least partly, as a heat engine that uses the ocean as its high temperature heat reservoir and the upper atmosphere as the low temperature reservoir. Using the atmosphere as its working substance, a hurricane does work by driving huge masses of air to speeds as high as 240 kilometers per hour.
P
T2 1 T1
A
Q1 T1
B
在相同的高温热源与相同 的低温热源之间工作的 • 一切可逆机,不论用什 么工作物质,效率相等。 • 一切不可逆机,效率不 可能高于可逆机的效率。
热力学第一定律热力学第二定律

★符号法则: 系统吸热, Q为正。 系统放热, Q为负。
★ 摩尔热容量Cm:一摩尔物质温度升高1K时系 统从外界吸取的热量。
1 dQ
Cm
( dT
)
7
四、内能
★特点:状态量 (只与始末两态有关,与中间 过程无关)
★气体的内能 E m i RT
1
是内能减少。 (温度减少)
内能变化: E cV T
22
(4)绝热线与等温线的比较
等温线 斜率
PV C
K等温
dP dV
P V
绝热线 斜率
PV C1
K绝热(P0,V0,T0)斜率之比
K绝热
K等温
K绝热
K等温
P0
V0 P0
V0
P
a 等温
结论:绝热线比等温线陡峭
2
(2)按过程的特性分类:
等容过程: dV = 0 等压过程: dP = 0
等温过程: 绝热过程: 循环过程:
dT = 0 dQ = 0,Q = 0
dE = 0 E终态 = E初态
3
3.过程曲线
P
PV 图上一种点,表达一种平衡状态。
PV 图上一条线,表达一种平衡过程。
V
非平衡态,非平衡过程不能在PV 图上表达!!
V1
V2
V
Q E A 意义: 系统吸取的热量,
dQ
dE
dA
一部分对外作功,一部分 增加本身的内能。
作功: dA PdV d(PV ) d( RT ) RdT
( A)P P(V2 V1 ) R(T2 T1 )
内能增量: dE CV dT
第一章热力学第一定律

第一章 热力学第一定律核心内容:能量守恒 ΔU=Q+W主要内容:三种过程(单纯pVT 变化、相变、化学反应)W 、Q 、ΔU 、ΔH 的计算一、内容提要1.热力学第一定律与状态函数(1)热力学第一定律: ΔU=Q+W (封闭系统) 用途:可由ΔU ,Q 和W 中的任意两个量求第三个量。
(2)关于状态函数(M )状态函数:p 、V 、T 、U 、H 、S 、A 、G ……的共性: ①系统的状态一定,所有状态函数都有定值;②系统的状态函数变化值只与始终态有关,而与变化的途径无关。
用途:在计算一定始终态间的某状态函数增量时,为了简化问题,可以撇开实际的复杂过程,设计简单的或利用已知数据较多的过程进行计算。
ΔM (实)=ΔM (设)。
这种方法称为热力学的状态函数法。
③对于循环过程,系统的状态函数变化值等于零,即ΔM =0。
此外,对于状态函数还有如下关系:对于组成不变的单相封闭系统,任一状态函数M 都是其他任意两个独立自变量(状态函数)x 、y 的单值函数,表示为M=M(x 、y),则注意:因为W 和Q 为途径函数,所以Q 和W 的计算必须依照实际过程进行。
⎰-=21V V a m bdV p W ,其中p amb 为环境压力。
Q 由热容计算或由热力学第一定律求得。
dy y M dx x M dM xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂=)(1循环关系式-=⎪⎭⎫⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂x M y M y y x x M )(22尤拉关系式xy M y x M ∂∂∂=∂∂∂1(p 1,V 1,T 1) (p'1,V 1,T 2)2(p 2,V 2,T 2) (p 1,V'1,T 2) VT 将热力学第一定律应用于恒容或恒压过程,在非体积功为零(即w'=0)的情况下有:Q V =ΔU ,Q p =ΔH (H 的定义:H=U+pV )。
此时,计算Q v 、Q p 转化为计算ΔU 、ΔH ,由于U 、H 的状态函数性质,可以利用上面提到的状态函数法进行计算。
热力学定理

热力学定理热力学第一定律也称热力学第零定律,它揭示了热力学系统与环境之间的关系。
内容是:不可能从单一热源吸收热量使之完全变为有用功而不引起其他变化,或把热量从温度较高的物体传到温度较低的物体而不引起其他变化。
热力学第一定律还表明,作为能源的一种形式,只有从周围环境中不断吸取热量才能向环境做功。
热力学第一定律指出:在任何封闭系统中,如果在不损失能量的情况下,系统中的任何一个过程都不可能转化为功,则该系统必定处于平衡状态,即热力学第一定律的表述方法是:在热力学系统和外界没有相互作用的情况下,系统的一切可逆过程总是自发地进行的。
这样,就可以从数学上将非自发过程区别开来。
由于熵是一个状态参数,所以它表征了一个系统无序、混乱的程度,它描述的是一个过程无序性或混乱程度的大小。
现在是上课时间,我在写作业,看见许多同学在那边说话,我就知道他们肯定没听讲,要不然怎么会这么无聊呢?我写了一会儿,就听见一些吵闹声,我气愤极了,就停下手中的笔,对他们说:“你们能安静一点吗?没看见老师正在上课吗?你们想被老师批评吗?”他们听了我的话,全都乖乖坐好,认真听讲。
我觉得很奇怪,就走到他们身边,看见他们各自拿着笔,快速地算题,过了一会儿,他们抬起头,都在埋怨刚才太吵了,害得他们心神不宁。
又过了一会儿,一个同学忽然站起来问:“老师,刚才是哪一章节啊?”老师回答说:“是《热力学》。
”这位同学接着说:“这章节我们已经学完了。
”老师满脸疑惑地说:“这才学了第一节啊,难道是第二节吗?”同学们立刻欢呼雀跃起来,异口同声地说:“不是第二节,是第一节!”老师十分生气,让同学们马上停下来。
同学们吓坏了,赶紧坐好。
通过这个实验,我觉得我们要认真学习,不懂就要问,不然就是“三只手”了。
比如,物理中的一些公式定律,就得让我们去思考。
比如,关于我们生活中的家电。
我们应该熟悉它们的结构,原理,构造等。
当然,我们更应该多做实验,遇到困难要多向老师请教,不然就得做“三只手”了。
热力学第一定律TheFirstLawofThermodynamics 共66页

热力学第一定律 (The First Law of Thermodynamics)
能量守恒与转换定律 能量之间数量的关系
A process must satisfy the first law of Thermodynamics to occur. (一个过程必须满足热力学第一定律才能发生)
能不能找出共同的规律性? 能不能找到一个判据?
热力学第二定律
研究过程的方向性和补偿限
§5.2 Statement and Essence of the Second Law of Thermodynamics (热力学第二定律的表述和实质)
热二律的表述有 60-70 种
传热
热功转换
1850年 克劳修斯表述
是否满足能量守恒与转换定律的过程一定都能自动发生?
Satisfying the first law alone does not ensure that the process will actually take place.
(但是,满足热力学第一定律的过程未必都能发生)
Chapter 5.The Second Law of Thermodynamics
This is thus in violation of the Kelvin-Planck statement of the second law.
Now suppose we have a heat engine which can convert heat into work without rejecting heat anywhere else.
空调,制冷
(Air-Conditioning, Refrigerating)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i E RT 2
当温度改度时,内能也改变:
E E (T )
i E R T 2
9/40
一、温度(从测量角度)
1、热平衡 在不受外界影响的条件下,两个热力学系 21.2 统相互传递能量(热传递),达到一个共同 的平衡态。 热 热平衡是能量的平衡,不是物质数量的平衡。 力 2、温度 处于同一平衡态的所有热力学系统都有 学 一个共同的宏观性质。 定义为:温度 第 处于热平衡的所有热力学系统的热力学温度相同
1 dQ 1 dE i CV ( )V R dT dT 2
0
摩尔理想气体内能的计算
2、定压摩尔热容量 Cp (迈耶公式) 设摩尔理想气体,经历等压过程
1 dQ 1 dE p V Cp dT p dT T p
5 2
Qacb 5.07 10 J
2
应用公式:热力学第一定律和理想气体状态方程。
23/40
五、绝热过程
理想气体状态方程
热力学第一定律
1、过程特征
pV RT 0 E A (1) (2)
系统和外界无热量交换进行的过程为绝热过程,dQ=0, Q = 0
(1)、(2)两式微分得: pdV Vdp RdT
表述:某系统从外界吸收热量其一部份用来增加系统 的内能,另一部份用来对外作功。 Q A E2 E1
+ 系统吸热 系统放热 内能增加 内能减少 系统对外界做功 外界对系统做功
物理意义
热现象的能量守恒定律。
14/40
积分形式
Q E2 E1 pdV E pdV
V1
V1
V2
第21章
热 力 学 第 一 定 律
21.1 基本概念 21.2 热力学第零定律 21.3 热力学第一定律 21.4 热力学第一定律对理想气体应用 21.5 热机效率 卡诺定理
统计物理学是从微观上来研究热学现象, 但很多问题都要涉及到分子的许多细节,如 分子的组成、分子的自由度等。有时并不能 完全知道这些。这时可从宏观上来研究,以 达相辅相成、互相补充的目的。
19/40
功
热量
2 过程 方程
内能
等压 过程
p
i dE v RT 2
V 恒量 T
E2 E1 vCV T2 T1
功
热量
A p(V2 V1 )
Q dE A, Qp vC p (T2 T1 )
20/40
3 过程 方程
功
等温 过程
T
pV 恒量
RT A pdV A pdV v dV V1 V1 V vRT ln(V2 / V1 ) vRT ln( p1 / p2 )
V2 V2
内能
热量
0
Q A, QT A
21/40
例. 一定量的理想气体在标准状态下体积为 1.010-2 m3 求:下列过程中气体吸收的热量: 1. 等温膨胀到体积为 2.010-2 m3 ; 2. 先等容冷却,再等压膨胀到(1)所到达的终态。 (1atm=1.013105 Pa ) p[pa] a 解: (1) 在 ab 等温过 p1 程中,ET=0.
零 二、热力学第零定律 A , B, C 三个热力学系统 定 在与外界隔离的条件下,如果A,B两个热力 律 学系统每一个都和系统C处于热平衡,则A和B两
系统必定处于热平衡。实验定律,非逻辑推理。 10/40
三、理想气体温标
1、玻意耳定律 一定质量的气体,温度不变时 pV = 常量 2、几个概念
1)、温标:温度的数值表示法 2)、建立温标的三要素 测温物质,测温属性,固定标准点 3)、理想气体模型(宏观) 在各种压强下都严格遵守玻 意耳定律的气体
( 1)
3、摩尔热容
C绝 0
等温膨胀时是从外界吸 热,对外作功,内能不减 少。绝热膨胀则是靠内能 的减少,系统温度要下降, 故斜率大。 26/40
所谓从宏观上来研究,主要指从能量的角 度来研究。主要内容有: 1)内能、功和热量; 2)热力学第一定律及其对理想气体的应用 3)热力学第二定律。
2/40
一、热力学系统
热力学系统(简称系统):由大量微观粒子组成 21.1
的有限的宏观物质系统。
外界(环境):系统以外的物质
基 孤立系统:与外界无物质和能量交换的系统 本 封闭系统:与外界无物质,但有能量交换的系统 概 开放系统:与外界有物质和能量交换的系统 念 二、热力学物理量
pV p V 将绝热方程 1 1 代入 A pdV 得
p1V1 A dV V1 V p1V1 1 1 1 1 1 V1 V2
V2
1 V1 p1V1 1 1 V2 1 p1V1 p2V2 1
单原子分子
刚性双原子分子 刚性多原子分子
i=3
i=5 i=6
1.671.40 1.333R Nhomakorabea4R
18/40
四、热力学第一定律在理想气体中的应用
1 过程 方程 内能
等容 过程
V
p 恒量 T i dE v RT 2 E2 E1 vCV T2 T1
0 dE = dQ ; QV = E2 - E1
25/40
2、等温线与绝热线比较
绝热线比等温线更陡。
p
绝热线
① 等温线:
pV C , pdV Vdp 0
A点斜率为
② 绝热线
pA
A 等温线
pA dp dV VA
1
pV C
o p V dV V dp 0
v
VA
p dV Vdp 0 pA dp A点斜率为 dV VA
P-V (P-T,V-T)图中“点”表示平衡态 理想气体状态方程 M pV RT
p
.Ⅰ(p V T )
1 1 1
Ⅱ(p2V2T2)
M:理想气体的质量 μ:理想气体的摩尔质量 R:8.31J/Mol/K普适常数
i
.
0
V
混合理想气体状态方程 pV piV
i
Mi
i
RT
4/40
2、过程 一个系统的状态发生变化时,我们说系统经历 了一个过程。 准静态过程 过程中的每一中间状态都可看成是平衡态。 非准静态过程: 驰豫时间为:即从非平衡到平衡所需的时间。若 过程所用的时间t >>,系统有充分时间达到平衡,可视 此过程为准静态过程。
QT 7.02 10 J
2
(吸热)
22/40
(2) 在ac等容降温和cb等压膨胀过程中,因 a、b温度 相同,故E=0。 p[pa] a p1 Qacb Aacb b c p2 V[m3] o Acb P2 V2 V1 V1 V2
PV P2 1 1 0.5 atm V2 Qacb 0.5 1.013 10 2 1 10
1、状态参量 描述处于平衡态的系统的性质的物理量,p, V, T。 p:气体对器壁单位面积上垂直作用力。帕
1 atm=760 mmHg=1.013 10 Pa
5
3/40
V:气体分子可以到达的空间。单位:立方米
1 m =1000 L
T:物体的冷热程度,分子热运动的剧烈程度。开
3
T (热力学温度) t (摄氏温度) 273.15
u 系统T1
外界对气体做功。 约为1ms , 压缩一次1s。准静态过程。
T1+△T T1+2△T T1+3△T
T2
系统从外界吸收升温的准静态过程
5/40
3、功 做功是使系统状态变化的一种方式,功是能量传递 dx 和转化的量度和重要表现形式。
系统对外做功(体积功)
A Fdx pSdx pdV
QT AT P dV
V1
V2
QT
V2
V1
PV V2 1 1 dV PV 1 1 ln V V1
p2 o
c
b
V[m3] V2
V1
5 2 3 2 3 P 1.013 10 pa, V 1.0 10 m , V 2.0 10 m 1 1 2
代入上式,得
V2
热力学第一定律的另一种表达方式 第一类永动机是不可能实现的
第一类永动机:系统从初态出发,不断地经历状态变 化回到原初态,过程中不需外界提供能量,而能对外 不断做功的永动机。
理想气体的热力学第一定律:
i Q v RT pdV 2 V1
15/40
V2
二、热容
物质的热容 系统温度升高dT,所吸收的热量为δQ Q C 与过程有关 可以 >0,= 0,<0 比热 摩尔热容
C p CV R 2i R 2
E CV T
pV RT
V R ( ) p T p
17/40
-----迈耶公式
3、热容比 γ
CV R i 2 CV CV i Cp
分子种类 自由度 Cv
3 R 2 5 R 2
Cp
5 R 2 7 R 2
热量与功的异同: 1) 过程量:与过程有关; 2) 等效性:改变系统状态的作用相同;
1卡=4.18焦, 1焦=0.24卡 3)功与热量的物理本质不同.
8/40
5、理想气体内能
分子无规则运动的动能、分子间相互作用的势能、 分子、原子内的能量、核内的能量等的总和,为气体 的内能。 理想气体的内能:分子的动能之和。
6、热力学第三定律
