2014年六合一模
2014年南京市六合区中考一模思想品德(政治)试卷及答案

2014年南京市六合区中考第一次模拟试卷九年级思想品德(友情提醒:本次考试思想品德、历史合场,考试时间100分钟。
请同学们合理分配时间!)一、单项选择题(在下列各题的四个选项中,只有一项是最符合题意的。
每小题2分,共30分)1.2013年11月9日至12日,中共第十八届中央委员会举行第三次全体会议,审议通过《中共中央关于___________若干重大问题的决定》。
A.严厉打击网络谣言 B.放开“单独二胎”C.群众路线教育实践活动 D.全面深化改革2.2014年2月27日,十二届全国人大常委会第七次会议经表决通过了关于设立南京大屠杀死难者国家公祭日的决定。
国家公祭日的时间是A.4月5日 B.9月3日 C.9月18日 D.12月13日3.设立南京大屠杀死难者国家公祭日的一个重要目的是A.警示人们要坚持“和平统一”方针 B.警示人们要坚持“一个中国”原则C.教育人们牢记历史,维护国家安全 D.教育人们牢记历史,不忘国仇家恨4.由全国人大常委会来决定设立南京大屠杀死难者国家公祭日,这A.符合人民代表大会这一根本政治制度B.是实行人民代表大会制度的具体表现C.反映了全国人民代表大会依法享有立法权D.表明全国人大常委会是最高国家权力机关5.“我们一定能够做出彩中国人,实现精彩中国梦!”这体现了A.自豪 B.自信 C.自立 D.自负6.建设中国特色社会主义的总依据是A.社会主义初级阶段 B.中国共产党的基本路线C.我国的根本大法——宪法 D.我国人口、资源、环境问题现状7.中华民族精神和时代精神的核心分别是A.爱国主义改革创新 B.自强不息开拓创新C.爱好和平自力更生 D.勤劳勇敢无私奉献8.公有制为主体,多种所有制经济共同发展,是我国的A.基本分配制度 B.基本经济制度C.一项基本国策 D.一项发展战略9.2014年3月14日,备受关注的南京江宁“男童被泼硫酸案”宣判,法院一审以故意伤害罪判处被告人蔡士林无期徒刑,剥夺政治权利终身,并给予经济赔偿。
南京市六合区2014年中考一模

南京市六合区2014年中考一模语文试卷(分值120分时间120分钟)一(28分)1.用诗文原句填空。
(10分)(1)窈窕淑女,▲。
(《诗经?关雎》)(2)学而不思则罔,▲ 。
(《论语?为政》)(3)▲,江春入旧年。
(王湾《次北固山下》)(4)▲,甲光向日金鳞开。
(李贺《雁门太守行》)(5)▲,春来江水绿如蓝。
(白居易《忆江南》)(6)大漠孤烟直,▲。
(王维《使至塞上》(7)人生自古谁无死,▲。
(文天祥《过零丁洋》)(8)越明年,▲,百废具兴。
(范仲淹《岳阳楼记》)(9)第二届青奥会即将在古都南京拉开帷幕,我国年轻的体育健儿将胸怀“▲,▲”(用杜甫《望岳》中的诗句填写)的气概,努力拼搏,傲视群雄。
2.给加点字注音,根据拼音写汉字。
(4分)(1)干涸▲ (2)气冲斗牛▲ (3)端xián ▲ (4)叱zhà▲风云3.下列句中加点成语使用正确的一项是(▲ )(2分)A. 金牛山上鸟语花香,各种树木鳞次栉比;金牛湖波光粼粼,大小游船来来往往。
B.阳春三月,我们站在桃花岛高处眺望,绿树如烟,水光山色,令人心旷神怡。
C.今年春节联欢晚会一曲《时间去哪儿了》让观众听后,不由得触目伤怀。
D.同学们相约来到龙池湖畔,或玩滑板,或放风筝,在大自然中尽情享受天伦之乐。
4.下列句子没有语病的一项是(▲ )(3分)A.即将在南京举办的江苏省大学生机器人大赛注重培养大学生科学探究和创新实践。
B.为了避免交通道路不拥挤,各地纷纷出台交通管理新措施。
C. 一个人能否成为真正的读者,关键在于他在青少年时期养成良好的读书习惯。
D. 近年来,学生书写水平逐渐下降的问题,引起了全社会的广泛关注。
综合性实践活动欣赏下面书法作品,回答相关问题。
(乙)(甲)5.把上面(甲)幅书法作品的三、四句用工整的简体楷书抄写在下面的方格中。
(3分)6.欣赏上面书法作品,下面选项中哪一个说法是正确的。
()(2分)A.(甲)是行书,精巧纤细,飘逸灵动。
2014年江苏省南京市联合体中考一模数学试题及答案-推荐下载

50 40 30 20 10
0 10 11 12 13 14 吨 吨 吨 吨 吨 吨 吨 吨
21.(8 分)小伟和小欣玩一种抽卡片游戏:将背面完全相同,正面分别写有 1,2,3,4 的四张卡片背面
向上冼匀后,小伟和小欣各自随 机抽取一张(不放回).将小伟的数字作为十位数字, 小欣的数字作为个位数字,组成一个两位数.如果所组成的两位数为偶数,则小伟胜;否 则小欣胜.
C
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关,1系电过,力管根保线据护敷生高设产中技工资术艺料0不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层,机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试2下卷2,高总而中体且资配可料置保试时障卷,各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并22工且22作尽22下可22都能22可地护以缩1关正小于常故管工障路作高高;中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整,处核或理对者高定对中值某资,些料审异试核常卷与高弯校中扁对资度图料固纸试定,卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置,跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等,料,编试要5写、卷求重电保技要气护术设设装交备备置底4高调、动。中试电作管资高气,线料中课并敷3试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术,技含以来术线及避槽系免、统不管启必架动要等方高多案中项;资方对料式整试,套卷为启突解动然决过停高程机中中。语高因文中此电资,气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技,进术合行,理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对:于于在调差分试动线过保盒程护处中装,高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时,术,作是应为指采调发用试电金人机属员一隔,变板需压进要器行在组隔事在开前发处掌生理握内;图部同纸故一资障线料时槽、,内设需,备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切,验除线报从缆告而敷与采设相用完关高毕技中,术资要资料进料试行,卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
江苏省南京市鼓楼区2014年中考一模数学试卷

南京市鼓楼区2014年中考一模数学试卷注意事项:1.本试卷共8页.全卷满分120分.考试时间为120分钟.考生答题全部答在答题卡上,答在本试卷上无效.2.请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合,再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上.3.答选择题必须用2B 铅笔将答题卡上对应的答案标号涂黑.如需改动,请用橡皮擦干净后,再选涂其他答案.答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置,在其他位置答题一律无效.4.作图必须用2B 铅笔作答,并请加黑加粗,描写清楚.一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有 一项是符合题目要求的,请将正确选项前的字母代号填在答题..卡.相应位置....上) 1.下列方程组中,解是⎩⎨⎧x =-5,y =1的是A .⎩⎨⎧x +y =6,x -y =4.B .⎩⎨⎧x +y =6,x -y =-6.C .⎩⎨⎧x +y =-4,x -y =-6.D .⎩⎨⎧x +y =-4,x -y =-4.2.计算2×(-9)-18×(16-12)的结果是A .-24B .-12C .-9D .63.利用表格中的数据,可求出 3.24+(4.123)2-190 的近似值是(结果保留整数).4.把边长相等的正五边形ABGHI 和正六边形ABCDEF 的 AB 边重合,按照如图的方式叠合在一起,连接EB ,交HI 于点K ,则∠BKI 的大小为5.反比例函数y =kx 和正比例函数y =mx 的部分图象如图所示.由此可以得到方程kx =mx 的实数根为A .x =1B .x =2A .3B .4C .5D .6A .90°B .84°C .72°D .88°A BCD E F G HI K (第4题)C .x 1=1,x 2=-1D .x 1=1,x 2=-26.如图, QQ 软件里的“礼盒”图标是一个表面印有黑色实线,顶端有图示箭头的正方体. 下列图形中,是该几何体的表面展开图的是二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题..卡.相应位置....上) 7.-3的绝对值等于 ▲ . 8. (12+8 )× 2 = ▲ . 9.使1x +2有意义的x 的取值范围是 ▲ .10. (2×103)2×(3×10-3) = ▲ .(结果用科学计数法表示)11.已知⊙O 1,⊙O 2没有公共点.若⊙O 1的半径为4,两圆圆心距为5,则⊙O 2的半径可以是 ▲ .(写出一个符合条件的值即可) 12.如图,在梯形ABCD 中,AB ∥CD ,∠B =90°,连接AC ,∠DAC =∠BAC .若BC =4cm ,AD =5cm ,则梯形ABCD 的周长为 ▲ cm .13.如图,在□ABCD 中,∠A =70° ,将□ABCD 绕顶点B 顺时针旋转到□A 1BC 1D 1,当C 1D 1首次经过顶点C 时,旋转角 ∠ABA 1= ▲ °.A .B .C .D .AD CB(第12题)ACDC 1D 1A 1 (第13题)(第6题)14.某科研机构对我区400户有两个孩子的家庭进行了调查,得到了 表格中的数据,其中(男,女)代表第一个孩子是男孩,第二个孩子 是女孩,其余类推.由数据,请估计我区两个孩子家庭中男孩与女 孩的人数比为 ▲ :▲ .15.如图,⊙O 的半径是5,△ABC 是⊙O 的内接三角形,过圆心O 分别作AB 、BC 、AC 的垂线,垂足为E 、F 、G ,连接EF . 若OG =2,则EF 为 ▲ .16. 将一张长方形纸片按照图示的方式进行折叠: ①翻折纸片,使A 与DC 边的中点M 重合,折痕为EF ;②翻折纸片,使C 落在ME 上,点C 的对应点为H ,折痕为MG ; ③翻折纸片,使B 落在ME 上,点B 的对应点恰与H 重合,折痕为GE .根据上述过程,长方形纸片的长宽之比ABBC= ▲ .三、解答题(本大题共11小题,共88分.请在答题..卡.指定区域....内作答,解答时应写出文字说明、证明过程或演算步骤) 17.(6分)计算:2x 2-4-12x -4.18.(6分)解不等式组⎩⎪⎨⎪⎧5+3x >18,x 3≤4-x -22. 并写出不等式组的整数解.19.(8分)已知:如图,在正方形ABCD 中,点E 、F 在对角线BD 上,且BF =DE . (1)求证:四边形AECF 是菱形.(2)若AB =2,BF =1,求四边形AECF 的面积.(第15题)ABC DFE(第19题)ABCD(第16题)20.(8分)甲、乙、丙三位歌手进入“我是歌手”的冠、亚、季军的决赛,他们通过抽签来决定演唱顺序.(1)求甲第一位出场的概率;(2)求甲比乙先出场的概率.22.(8分)(1)如图①,若BC =6,AC =4,∠C =60°,求△ABC 的面积S △ABC ; (2)如图②,若BC =a ,AC =b ,∠C =α,求△ABC 的面积S △ABC ;(3)如图③,四边形ABCD ,若AC =m ,BD =n ,对角线AC 、BD 交于O 点,它们所成 的锐角为β.求四边形ABCD 的面积S 四边形ABCD .23.(8分)如图,把长为40cm ,宽为30cm 的长方形硬纸板,剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),将剩余部分折成一个有盖..的长方体盒子,设剪掉的小正 方形边长为x cm .(纸板的厚度忽略不计)(1)长方体盒子的长、宽、高分别为 ▲ (单位:cm ); (2)若折成的一个长方体盒子的表面积为950cm 2,求此时长方体盒子的体积.30cm40cm (第23题)OB CAB C A 60° A B C D β (图①) (图②) (图③) (第22题)α24.(8分)2014年2月,纯电动出租车在南京正式上路运行,下表是普通燃油出租车和纯电动出租车的运价.12元.(1)直接写出y 1、y 2关于x 的函数关系式,并注明对应的x 的取值范围; (2)在如下的同一个平面直角坐标系中,画出y 1、y 2关于x 的函数图象;(3)结合图象,求出当乘客打车的路程在什么范围内时,乘坐纯电动出租车更合算.25.(8分)如图,在□ABCD 中,过A 、B 、D 三点的⊙O 交BC 于点E,连接DE,∠CDE =∠DAE .(1)判断四边形ABED 的形状,并说明理由; (2)判断直线DC 与⊙O 的位置关系,并说明理由;(3)若AB =3,AE =6,求CE 的长.y (元)(第24题)(第25题)26.(11分) 问题提出平面内不在同一条直线上的三点确定一个圆.那么平面内的四点(任意三点均不在同一直线上),能否在同一个圆呢? 初步思考设不在同一条直线上的三点A 、B 、C 确定的圆为⊙O . ⑴当C 、D 在线段AB 的同侧时,如图①,若点D 在⊙O 上,此时有∠ACB =∠ADB ,理由是 ▲ ;如图②,若点D 在⊙O 内,此时有∠ACB ▲ ∠ADB ;如图③,若点D 在⊙O 外,此时有∠ACB ▲ ∠ADB .(填“=”、“>”或“<”);由上面的探究,请直接写出A 、B 、C 、D 四点在同一个圆上的条件: ▲ . 类比学习(2)仿照上面的探究思路,请探究:当C 、D 在线段AB 的异侧时的情形.此时有 ▲ , 此时有 ▲ , 此时有 ▲ .由上面的探究,请用文字语言直接写出A 、B 、C 、D 四点在同一个圆上的条件: ▲ . 拓展延伸(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线? 已知:如图,AB 是⊙O 的直径,点C 在⊙O 上. 求作:CN ⊥AB .作法:①连接CA ,CB ;②在 ⌒CB上任取异于B 、C 的一点D ,连接DA ,DB ;图①图②图③③DA 与CB 相交于E 点,延长AC 、BD ,交于F 点; ④连接F 、E 并延长,交直径AB 于M ;⑤连接D 、M 并延长,交⊙O 于N .连接CN . 则CN ⊥AB .请按上述作法在图④中作图,并说明CN ⊥AB 的理由.(提示:可以利用(2)中的结论) 27.(9分)【课本节选】反比例函数y =kx (k 为常数,k ≠0)的图象是双曲线.当k >0时,双曲线两个分支分别在一、三象限,在每一个象限内,y 随x 的增大而减小(简称增减性);反比例函数的图象关于原点对称(简称对称性).这些我们熟悉的性质,可以通过说理得到吗? 【尝试说理】我们首先对反比例函数y =kx (k >0)的增减性来进行说理.如图,当x >0时.在函数图象上任意取两点A 、B ,设A (x 1,k x 1),B (x 2,kx 2),且0<x 1< x 2.下面只需要比较k x 1和kx 2的大小.k x 2—k x 1=k (x 1-x 2) x 1 x 2. ∵0<x 1< x 2,∴x 1-x 2<0,x 1 x 2>0,且 k >0. ∴k (x 1-x 2) x 1 x 2<0.即k x 2<k x 1.这说明:x 1< x 2时,k x 1>kx 2.也就是:自变量值增大了,对应的函数值反而变小了.即:当x >0时,y 随x 的增大而减小. 同理,当x <0时,y 随x 的增大而减小.(1)试说明:反比例函数y = kx (k >0)的图象关于原点对称.【运用推广】(2)分别写出二次函数y =ax 2 (a >0,a 为常数)的对称性和增减性,并进行说理. 说理:(第27题)(3)对于二次函数y =ax 2+bx +c (a >0,a ,b ,c 为常数),请你从增减性的角度.......,简要解释为何当x =—b2a 时函数取得最小值.鼓楼区2013-2014学年度第二学期调研测试卷九年级数学(一)参考答案与评分标准说明:本评分标准每题给出了一种解法供参考,如果考生的解法与本解答不同,参照本评分标准的精神给分.一、选择题(本大题共6小题,每小题2分,共12分.)二、填空题(本大题共10小题,每小题2分,共20分.)7.3 8.5 9.x ≠-2 10.1.2×104 11.答案不唯一,如0.5(满足0<r <1或r >9即可)12.22 13. 40 14. 417︰383 15. 21 16.2 三、解答题(本大题共11小题,共88分.)17.(6分)解:原式=2(x +2)(x -2)-12(x -2)········································· 2分=2-x2(x +2)(x -2) ······················································· 4分=-12x +4. ··························································· 6分18.(6分)解:解不等式①,得x >133; ······································································ 2分解不等式②,得x ≤6. ······································································· 4分 所以原不等式组的解集为133<x ≤6. ······················································ 5分它的整数解为5,6. ·········································································· 6分 19.(8分)(1)连接AC ,AC 交BD 于点O . 在正方形ABCD 中,OB =OD ,OA =OC ,AC ⊥BD .∵BF =DE ,∴OB -BF =OD -DE ,即OF =OE . ∴四边形AECF 是平行四边形. 又∵AC ⊥EF ,∴□AECF 是菱形. ············································································ 4分 (2)∵AB =2,∴AC =BD =AB 2+AD 2=22. ∴OA =OB =BD2=2. ∵BF =1,∴OF =OB -BF =2-1.∴S 四边形AECF =12AC ·EF =12×22×2(2-1)=4-22. ······························ 8分20.(8分)解:所有可能出现的结果如下:······································································································ 5分以上共有6种等可能的结果.其中甲第一位出场的结果有2种,甲比乙先出场的结果有3种. 所以P (甲第一位出场)=26=13. ························································· 7分P (甲比乙先出场)=36=12. ·························································· 8分(注:用树状图列举所有结果参照以上相应步骤给分.) 21.(8分)解:(1)不合理.因为如果1000人全部在金融行业抽取,那么全市城镇非私营单位员工被抽到的机会不相等,样本不具有代表性和广泛性. ···························· 2分 (2)人数市城镇非私营单位1 000人月收入统计图·················································································· 6分(3)本题答案不惟一,下列解法供参考.用平均数反映月收入情况不合理.由数据可以看出1000名被调查者中有670人的月收入不超过4000元,月收入的平均数受高收入者和低收入者收入变化的影响较大,月收入的中位数几乎不受高低两端收入变化的影响,因此,用月收入的中位数反映月收入水平更合理. ·················································································· 8分 (注:对于(1)(3)两问,学生回答只要合理,应酌情给分.) 22.(8分)(1)如图①,过点A 作AH ⊥BC ,垂足为H . 在Rt △AHC 中,AHAC=sin60°,∴AH =AC ·sin60°=4×32=23. ∴S △ABC =12×BC ×AH =12×6×23=63.…………………………………………3分(2)如图②,过点A 作AH ⊥BC ,垂足为H . 在Rt △AHC 中,AHAC =sin α,∴AH =AC ·sin α=b sin α.∴S △ABC =12×BC ×AH =12ab sin α.……………………………………………………5分(3)如图③,分别过点A ,C 作AH ⊥BD ,CG ⊥BD ,垂足为H ,G . 在Rt △AHO 与Rt △CGO 中,AH =OA sin β,CG =OC sin β; 于是,S △ABD =12×BD ×AH =12n ×OA sin β;S △BCD =12×BD ×CG =12n ×OC sin β;∴S 四边形ABCD = S △ABD +S △BCD =12n ×OA sin β+12n ×OC sin β=12n ×(OA +OC )sin β=12m n sin β.……………………………………………………………………8分23.(8分)(图①)(图②)(图③)解:(1)30-2x 、20-x 、x ; ························································· 3分 (2)根据图示,可得2(x 2+20x )=30×40-950 解得x 1=5,x 2=-25(不合题意,舍去)长方体盒子的体积V =(30-2×5)×5×(20-5)=20×5×15=1500(cm 3). 答:此时长方体盒子的体积为1500 cm 3.···································· 8分 24.(8分)(1)y 1=⎩⎪⎨⎪⎧11,(x ≤3)2.4x +3.8,(x >3)y 2=⎩⎪⎨⎪⎧9,(x ≤2.5)2.9x +1.75,(x >2.5) ····························································· 4分(2)画图正确. ··············································································· 6分(3)由2.4x +3.8=2.9x +1.75,解得,x =4.1.∴ 结合图象可知,当乘客打车的路程不超过 4.1公里时,乘坐纯电动出租车合算. ······································································································ 8分 25.(8分)(1)四边形ABED 是等腰梯形.理由如下:在□ABCD 中,AD ∥BC , ∴∠DAE =∠AEB . ∴ ⌒DE= ⌒AB ,DE =AB . ∵AB ∥CD ,∴AB 与DE 不平行. ∴四边形ABDE 是等腰梯形. ······················································· 2分(2)直线DC 与⊙O 相切. 如图,作直径DF ,连接AF . 于是,∠EAF =∠EDF . ∵∠DAE =∠CDE ,∴∠EAF +∠DAE =∠EDF +∠CDE ,即∠DAF =∠CDF . ∵DF 是⊙O 的直径,点A 在⊙O 上,∴∠DAF =90°,∴∠CDF =90°.∴OD ⊥CD .y (元)直线DC 经过⊙O 半径OD 外端D ,且与半径垂直,直线DC 与⊙O 相切. ·································································· 5分 (3)由(1),∠EDA =∠DAB . 在□ABCD 中,∠DAB =∠DCB ,∴∠EDA =∠DCB .又∵∠DAE =∠CDE ,∴△ADE ∽△DCE .∴AE DE =DE CE ,∵AB =3,由(1)得,AB =DE =DC =3.即 63=3DE.解得,CE =32.…………………………………………………………………………8分26.(11分)(1)同弧所对的圆周角相等. ∠ACB <∠ADB ,∠ACB >∠ADB .答案不惟一,如:∠ACB =∠ADB . ·················································· 4分 (2)如图:此时∠ACB +∠ADB =180°, 此时∠ACB +∠ADB >180°, 此时∠ACB +∠ADB <180 若四点组成的四边形对角互补,则这四点在同一个圆上.······································································································ 8分 (3)作图正确. ··············································································· 9分 ∵AB 是⊙O 的直径,C 、D 在⊙O 上, ∴∠ACB =90°,∠ADB =90°. ∴点E 是△ABF 三条高的交点. ∴FM ⊥AB . ∴∠EMB =90°. ∠EMB +∠EDB =180°, ∴点E ,M ,B ,D 在同一个圆上. ∴∠EMD =∠DBE .又∵点N ,C ,B ,D 在⊙O 上, ∴∠DBE =∠CND ,∠EMD =∠CND . ∴FM ∥CN .∴∠CPB =∠EMB =90°.(注:其他正确的说理方法参照给分.) 27.(9分)(1)在反比例函数y =kx (k >0)的图象上任取一点P (m ,n ),于是:mn =k .那么点P 关于原点的对称点为P 1(-m ,-n ).而(-m )(-n )=mn =k ,这说明点P 1也必在这个反比例函数y =kx的图象上.所以反比例函数y = kx (k >0)的图象关于原点对称.…………………………2分(2)对称性:二次函数y =ax 2 (a >0,a 为常数)的图象关于y 轴成轴对称. 增减性:当x >0时,y 随x 增大而增大;当x <0时,y 随x 增大而减小. 理由如下:①在二次函数y =ax 2 (a >0,a 为常数) 的图象上任取一点Q (m ,n ),于是n =am 2. 那么点Q 关于y 轴的对称点Q 1(-m ,n ).而n =a (-m )2,即n =am 2. 这说明点Q 1也必在在二次函数y =ax 2 (a >0,a 为常数) 的图象上. ∴二次函数y =ax 2 (a >0,a 为常数)的图象关于y 轴成轴对称,②在二次函数y =ax 2 (a >0,a 为常数)的图象上任取两点A 、B,设A (m ,am 2), B (n ,an 2) ,且0<m <n . 则an 2-am 2=a (n +m )(n -m ) ∵n >m >0,∴n +m >0,n -m >0; ∵a >0,∴an 2-am 2=a (n +m )(n -m )>0.即an 2>am 2. 而当m <n <0时, n +m <0,n -m >0; ∵a >0,∴an 2-am 2=a (n +m )(n -m )<0.即an 2<am 2.这说明,当x >0时,y 随x 增大而增大;当x <0时,y 随x 增大而减小. ······························································································· 7分 (3)二次函数y =ax 2+bx +c (a >0,a ,b ,c 为常数) 的图象可以由y =ax 2的图象通过平 移得到,关于直线x =—b 2a 对称,当x =—b2a 时,y =4ac -b 24a.由(2),当x ≥—b 2a 时,y 随x 增大而增大;也就是说,只要自变量x ≥—b2a ,其对应的函数值y ≥4ac -b 24a ;而当x ≤—b2a 时,y 随x 增大而减小,也就是说,只要自变量x≤—b2a ,其对应的函数值y ≥4ac -b 24a.综上,对于二次函数y =ax 2+bx +c (a >0,a ,b ,c 为常数),当x =—b 2a时取得最小值4ac -b 24a.。
六合中考模拟试卷(2014.三校)

2014年中考第一次模拟测试试题英语(满分90分,考试时间90分钟)选择题(共40分)(将答案按序号填在答卷纸上............)一、单项填空(共15小题;每小题1分,满分15分)从A、B、C、D四个选项中,选出可以填入空白处的最佳选项。
1. Air pollution has become a very serious in China nowadays.A. accidentB. behaviourC. problemD. question2. — Hi! Mr Li. May I know my score of this math test?— Sure. You can come with me and check it on my computer for .A. youB. yourC. yourselfD. yours3. — Where is the best location in a cinema when watching a 3-D film?— Oh, it‟s wise to sit it. We may feel better from a distance.A. from behindB. at the back ofC. in front ofD. in the front of4. Qingfeng Baozi has become more and more after President Xi bought it.A. deliciousB. famousC. expensiveD. healthy5. — Look! That teacher is explaining something to her students again and again. —teacher she is!A. How patientB. What patientC. How a patientD. What a patient6. — Excuse me, sir. You use your mobile phone at the gas station. It‟s verydangerous.— Sorry, I didn‟t notice it.A. mustn‟tB. can‟tC. shouldn‟tD. may not7. — Sorry, I‟m late. Has the meeting begun?— It doesn‟t matter. The meeting for several minutes.A. has just begunB. has just been overC. has just been onD. has just ended8. — The old lady is very great!— Yes. She has supported three children‟s schooling she is not very rich.A. as ifB. even thoughC. so thatD. what if9. — Have you heard of the activity called “Clear Your Plate”?— Sure. It suggests food by eating up the food on our plates.A. saveB. savedC. to saveD. savingto students to learn from each other in class.A. offerB. are offeredC. have offeredD. are offering11. From the girl‟s business card, we can know .A. how old is sheB. where she worksC. how old she isD. where does she work12. — Excuse me, which bus should I take to the Cultural Centre, Bus No.1 or No.3?—of them is OK, but you‟d better take Bus No.1. It‟s faster.A. EitherB. NeitherC. BothD. None13. — Daniel, the speech competition will begin soon. Please the microphoneto make everyone hear more clearly.— No problem!A. turn outB. turn upC. turn offD. turn down14. — I didn‟t know this is a one-way street, sir.—. Please show your driving license.A. I hope soB. It‟s none of my businessC. It‟s all rightD. Sorry, but that is not an excuse15. — Jenny, I have two tickets for today‟s dolphin show, do you want to go with me?—, but I‟ve already planned to see my doctor.A. You‟re welcomeB. I‟m afraid notC. I‟d love toD. That‟s all right二、完形填空(共10小题;每小题1分,满分10分)阅读下面短文,从短文后所给各题的四个选项(A、B、C、D)中,选出可以填入空白处的最佳选项。
2014年南京市中考一模试卷分类·非连续性文本阅读
2014年南京市中考一模试卷分类:非连续性文本阅读【玄武区】(三)阅读下面文本,完成13~16题。
(13分)南京:一座越来越宜居的古都【名城遗韵】南京,素有“江南佳丽地,金陵帝王都”的美誉,与北京、西安、洛阳并称“中国四大古都”。
山水城林融为一体,自然风貌久负盛名;历史在此又遗存下灿烂的文化,文化底蕴极厚。
但随着城市的发展,许多地面文物已经荡然无存,唱经楼、安乐寺、杏花村、子午路、凤凰台、仁孝里、赤石矶等老地名已经遗憾消失,让人追惜不已。
【花园城市】南京,春秋短,冬夏长,四时各有特色,自古就有“春游牛首烟岚”“夏赏钟阜晴云”“秋登栖霞胜境”“冬观石城霁雪”之说,是一座美丽的花园。
四月的南京,正是花的海洋,春花烂漫,诗意扑面。
下表内容即为(摘自龙虎网)【人文调查】调查一:据《南京市2012年度人口发展报告》显示,2012年南京市大学文化程度人口比例为28.5%左右,在全国副省级城市中列第一位,每万人大学生数量全国第一,研究生数量全国第二。
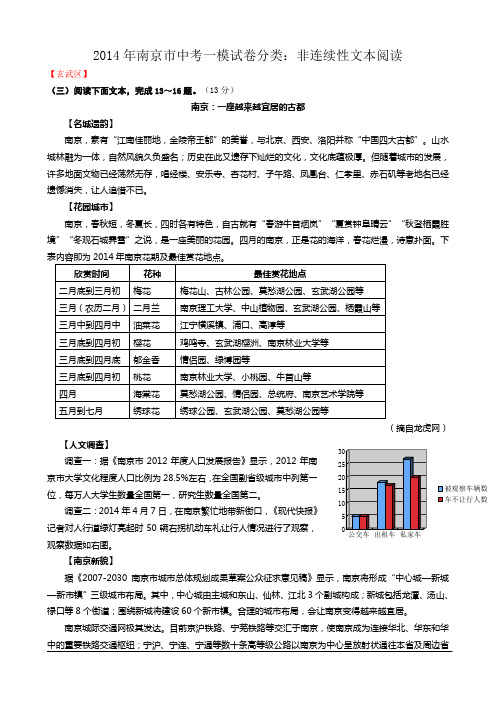
调查二:2014年4月7日,在南京繁忙地带新街口,《现代快报》记者对人行道绿灯亮起时50辆右拐机动车礼让行人情况进行了观察,观察数据如右图。
【南京新貌】据《2007-2030南京市城市总体规划成果草案公众征求意见稿》显示,南京将形成“中心城—新城—新市镇”三级城市布局。
其中,中心城由主城和东山、仙林、江北3个副城构成;新城包括龙潭、汤山、禄口等8个街道;围绕新城将建设60个新市镇。
合理的城市布局,会让南京变得越来越宜居。
南京城际交通网极其发达。
目前京沪铁路、宁芜铁路等交汇于南京,使南京成为连接华北、华东和华中的重要铁路交通枢纽;宁沪、宁连、宁通等数十条高等级公路以南京为中心呈放射状通往本省及周边省被观察车辆数车不让行人数市;禄口国际机场目前可满足年旅客吞吐量1200万人次、年货邮吞吐量40万吨。
南京城区内已开通2条地铁线路,正在建设3条地铁线路,有望能缓解城市(城区与副城、城区与郊区)目前极大的交通压力。
2014年六合区数学一模

六合区2014年中考模拟测试(一)数学注意事项:1.本试卷共6页.全卷满分120分.考试时间为120分钟.考生答题全部答在答题卡上,答在本试卷上无效.2.请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合,再将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上.3.答选择题必须用2B铅笔将答题卡上对应的答案标号涂黑.如需改动,请用橡皮擦干净后,再选涂其他答案.答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置,在其他位置答题一律无效.4.作图必须用2B铅笔作答,并请加黑加粗,描写清楚.一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡...相应位置....上)1.||-2的倒数是(▲ )A.2B.-2C.12D.-122.计算(a3b)2÷(ab)2的结果是(▲ )A.a3 B.a4 C.a3b D.a4b3.a满足以下说法:①a是无理数;2②<a<3;③a2是整数.那么a可能是(▲ )A.6B.10C.2.5D.20 74.下列图形中,既是轴对称图形,又是中心对称图形的为(▲ )A. B. C. D.5.点O1、O2在直线l上,⊙O1的半径为2cm,⊙O2的半径为3cm,4cm<O1O2<8cm.⊙O1与⊙O2不可能...出现的位置关系是(▲ )A.外离B.外切C.相交D.内切6.若方程kx x+1的解x0满足1<x0<2,则k可能是(▲ )A.1B.2C.3 D.6二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把答案直接填写在答题..卡相应位置.....上) 7.⎝⎛⎠⎞-12-2-(3.14-π)0= ▲ .8.钓鱼诸岛是中国的固有领土,位于中国东海,面积约6344000平方米,数据6344000用科学记数法表示为 ▲ .9.一个多边形的每个内角均为108°,则这个多边形是 ▲ 边形. 10.因式分解:-4a 2b +4a 3+ab 2= ▲ . 11.a 3=12,则a = ▲ .12.如图, 直线AB ∥CD ,∠E =90°,∠A =25°,则∠C = ▲ .13.如图,正方形ABCD 中,扇形BAC 与扇形CBD 的弧交于点E , AB =2cm .则图中阴影部分面积为 ▲ .14.在函数y =-1x 的图象上有三个点为(x 1,y 1)、(x 2,y 2)、(x 3,y 3),若y 1<0<y 2<y 3,则x 1,x 2,x 3的大小关系是 ▲ .15.甲、乙两名射击运动员在某场测试中各射击20次,测试成绩如下表:则 ▲ (选填甲、乙)运动员测试成绩更稳定. 16.如图,从原点A 开始,以AB =1为直径画半圆,记为第1个半圆;以BC =2为直径画半圆,记为第2个半 圆;以CD =4为直径画半圆,记为第3个半圆;以 DE =8为直径画半圆,记为第4个半圆;…,按此规 律,继续画半圆,则第6个半圆的面积为 ▲ (结 果保留π).乙的成绩环数 7 8 9 10 频数6 4 4 6甲的成绩环数 7 8 910频数4 6 6 4C A(第12题)B DE F (第13题)(第16题)三、解答题(本大题共11小题,共88分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明 过程或演算步骤)17.(6分)解不等式组 ⎩⎪⎨⎪⎧x -2≥1,1-3(x -1)<8-x .18.(6分)先化简,再求值:[(a -2)2-(a +2)(a -2)](a -1),其中a =-2.19.(6分)如图,四边形ABCD 为矩形,四边形AEDF 为菱形.(1)求证:△ABE ≌△DCE ;(2)试探究:当矩形ABCD 边长满足什么关系时,菱形AEDF 为正方形?请说明理由.20.(8分)下列为某校初三参加的“迎青奥”知识能力竞赛的25位同学的成绩:78,86,98,90,95, 88,94,80,89,77, 87,73,65,84,87, 96,84,74,98,86, 83,67,88,68,85. (1)完成下表:(2)补全频数分布直方图;组别 个位数字统计 频数59.5~69.5 5,7,8 369.5~79.5 ① ▲ ② ▲79.5~89.5 6,8,0,9,7,4,7,4,6,3,8,5 1289.5~99.5 8,0,5,4,6,8 6(第19题) B AD F C(3)若超过均分的将获奖,请计算本次竞赛获奖的比例.21.(8分)南京市为了构建立体的道路网络,大力发展江北经济,决定修建一条六合到主城的轻轨铁路.为了使工程提前3个月完成,需将原定的工作效率提高10%.原计划完成这项工程需要多少个月?22.(8分)桌面上有5张背面相同的卡片,正面分别写着数字“1”、“2”、“3”、“4”、 “5”.将卡片背面朝上洗匀.(1)小军从中任意抽取一张,抽到偶数的概率是 ;(2)小红从中同时抽取两张.规定:抽到的两张卡片上的数字之和为奇数,则小军胜,否则小红胜.你认为这个游戏公平吗?请用树状图或表格说明你的理由. 23.(8分)已知二次函数y =x 2+2ax -2.(1)求证:经过点(0,a )且与x 轴平行的直线与该函数的图象总有两个公共点; (2)该函数和y =-14x 2+(a -3)x+12的图象都经过x 轴上两个不同的点A 、B ,求a 的值.24.(8分)如图,以O 为圆心的弧BD⌒度数为60 o ,∠BOE =45o ,DA ⊥OB ,EB ⊥OB . (1)求BEDA 的值;(2)若OE 与BD ⌒交于点M ,OC 平分∠BOE ,连接CM .说明CM 为⊙O 的切线;(3)在(2)的条件下,若BC =1,求∠tan BCO 的值.25.(8分)已知一次函数y=x+b的图象与x轴,y轴交于点A、B.(1)若将此函数图象沿x轴向右平移2个单位后经过原点,则b=;(2)若函数y1=x+b图象与一次函数y2=kx+4的图象关于y轴对称,求k、b的值;(3)当b>0时,函数y1=x+b图象绕点B逆时针旋转n°(0°<n°<180°)后,对应的函数关系式为y=-3x+b,求n的值.26.(10分)如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-2,0)、B(4,0)、C(0,2).(1)请用尺规作出△ABC的外接圆⊙P(保留作图痕迹,不写作法);(2) 求出(1)中外接圆圆心P的坐标;(3)⊙P上是否存在一点Q,使得△QBC与△AOC相似?如果存在,请直接写出点Q坐标;如果不存在,请说明理由.(第26题)27.(12分)课本回顾如图,用半径R=3cm,r=2cm的钢球测量口小内大的内孔的直径D.测得钢球顶点与孔口平面的距离分别为a=4cm,b=2cm,则内孔直径D的大小为▲.问题拓展如图,在矩形ABCD内,已知⊙O与⊙O2互相外切,且⊙O1与边AD、DC相切,⊙O2与边AB、BC相切.若AB=4,BC=3,⊙O1与⊙O2的半径分别为r,R.求O1O2的值.灵活运用如图,某市民广场是半径为60米,圆心角为90°的扇形AOB,广场中两个活动场所是圆心在OA、OB上,且与扇形OAB内切的半圆☉O1、☉O2,其余为花圃.若这两个半圆相外切,试计算当两半圆半径之和为50米时活动场地的面积.六合区2014年中考模拟测试(一)数学试题参考答案及评分标准说明:本评分标准每题给出了一种或几种解法供参考,如果考生的解法与本解答不同,参照本评分标准的精神给分.一、选择题(本大题共6小题,每小题2分,共12分)二、填空题(本大题共10小题,每小题2分,共20分)7.3 8. 6.344×1069.五10.a (2a -b )2 11.612.115o13.π314.x 2<x 3<x 1(或x 2<x 3<0<x 1) 15.甲 16.128π三、解答题(本大题共11小题,共88分) 17.(本题6分)解不等式x –23≥1,得 x ≥5.……………………………………………… 2分 解不等式1–3(x –1)<8–x ,得 x >–2.…………………………………… 4分 ∴原不等式组解集为x ≥5.……………………………………………… 6分 18.(本题6分)原式=[a 2-4a +4-(a 2-4)](a -1) …………………………… 2分=(a 2-4a +4- a 2+4) (a -1)=(8-4a )(a -1)=8a -8-4a 2+4a =-4a 2+12a -8.…………………………… 4分 当a =-2时,原式=-4×(-2)2+12×(-2)-8=-16-24-8=-48. …………………………………6分19.(本题6分)(1)证明:∵四边形ABCD 为矩形,∴∠B =∠C =90o ,AB =DC .………… 1分∵四边形AEDF 为菱形,∴AE =DE . …………………………………………………2分在Rt △ABE 和Rt △DCE 中, ⎩⎨⎧AB =DCAE =DE, ∴Rt △ABE ≌Rt △DCE .…………………………………………………3分(2)当BC =2AB 时,菱形AEDF 为正方形.………………………………4分理由:∵Rt △ABE ≌Rt △DCE ,∴BE =CE ,∠AEB =∠DEC .又∵BC =2AB ,∴AB =BE .∴∠BAE =∠AEB =45o ,∴∠DEC =45o . ∵∠AEB +∠AED +∠DEC =180o ,∴∠AED =180o -∠AEB –∠DEC =90o . ∴菱形AEDF 是正方形.………………………………………………6分20.(本题8分)(1)①8,7,3,4;②4.……………………………………………………2分题号 1 2 3 4 5 6 答案C B A BD C(2)……………………5分(3)计算平均分=84(分), ………………………………………………………7分 ∵超过平均分的有14人,∴本次竞赛获奖的比例为1425.………………………………………………………8分 21.(本题8分)设原计划完成这项工程需要x 个月,根据题意,得(1+10%)·1x = 1x -3.…………………………………………4分解这个方程,得 x =33. ………………………………………………………6分 经经验 x =33是原方程的解.…………………………………………………7分 答:原计划完成这项工程需要33个月.………………………………………8分 (注:也可设原工作效率为x ,列方程:1x -1(1+10%)x =3去解.) 22.(本题8分)(1)2/5;………………………………………………………………………………2分 (2)这个游戏不公平.理由如下:任意抽取两个数,共有20种不同的抽法,它们是等可 能的,其中和为奇数的抽法共有12种. ∴P (和为奇数)=12/20=3/5, P (和为偶数)=2/5.(注:正确写出表格2分,还可以应用树状图分析)………8分23.(本题8分)(1)当y =a 时,x 2+2ax -2=a , x 2+2ax -2-a =0.∵b 2-4ac =4(a +12)2+7>0, …………………………………………2分 ∴方程x 2+2ax -2-a =0有两个不相等的实数根.即二次函数y =x 2+2ax -2的图象与经过点(0,a )且与x 轴平行的直线总有两个公共点. ……………………………………………………………………………4分(2)∵两个函数图象都经过x 轴上的两个不同的点A 、B ,∴两个函数图象的对称轴相同. ……………………………6分 即:-2a= -a -32×(-14), ∴a =2. ……………………………8分24.(本题8分)(1)∵EB ⊥OB ,∠BAC =45o ,∴∠E =45o .∴∠E =∠BOE .∴OB =BE . ……………1分 在Rt △OAD 中,sin ∠AOD =AD OD =32,∵OD =OB =BE ,∴BE DA =23=23.…………………2分(2)∵OC 平分∠BOC ,∴∠BOC =∠MOC .在△BOC 和△MOC 中, ⎩⎪⎨⎪⎧OB =OM∠BOC =∠MOC OC =OC∴△BOC ≌△MOC (SAS).………………………………………3分 ∴∠CMO =∠OBC =90o . 又∵CM 过半径OM 的外端,∴CM 为⊙O的切线.……………………………………………………5分(3) 由(1)(2)证明知∠E =45o ,OB =BE ,△BOC ≌△MOC ,CM ⊥ME .∵CM ⊥OE ,∠E =45o .∴∠MCE =∠E =45o ,∴CM =ME . 又∵△BOC ≌△MOC ,∴MC =BC .∴BC =MC =ME =1.……………………………………………………6分 ∵MC =ME =1,∴在Rt △MCE 中,根据勾股定理,得CE =2.∴OB =BE =2+1. …………………………………………………7分 ∵ tan ∠BCO =OBBC ,OB =2+1,BC =1,∴ tan ∠BCO =2+1.…………………………………………………8分 25.(本题8分)(1)2; ……………………………………………………………………………2分 (2)∵当x =0时,y =4,∴y 2=kx +4图象与y 轴交于点(0,4).∵(0,4)关于y 轴对称点就是本身,∴(0,4)在函数y =x +b 图象上. ∴b =4. …………………………………………………………………………4分 ∴一次函数y 1=x +4,它与x 轴的交点坐标为(-4,0). …………………5分 ∵y 2=kx -4的图象与y 1=x +4的图像关于y 轴对称, ∴y 2=kx -4的图象经过点(4,0),则0=4k +4,∴k =-1.…………………………………………………………………………6分 (3)∵当x =0时,y 1=b ,∴y 1=x +b 图象与y 轴交于点B (0, b ). ∵当y 1=0时,x =-b ,∴y 1=x +b 图象与x 轴交于点A (-b , 0).如图,∵AO =BO =b (b >0),∴∠ABC =45°.错误!未指定书签。
2014南京模拟卷

图2绝密★启用前2014年南京市普通高中学业水平测试(必修科目)模拟试卷地 理一、单项选择题:在下列各题的四个选项中,只有一个选项是最符合题目要求的。
请在答题卡上相应的方框内填涂(本大题共30题,每题2分,共60分)。
佩戴着五星红旗的“玉兔号”月球车于北京时间2013年12月15日4时35分成功着陆月球,其足迹清晰可见(如图1)。
读图完成1~2题。
1. “玉兔号”成功着陆月球时 A.北京该日昼长达一年中最小值B.南京该日正午太阳高度达一年中最小值C.地球公转速度在一年中较慢D.纽约(西五区)区时为14日15时35分2. “玉兔号”在月面上工作时可能遇到的最大困难是 A.黑暗环境 B.缺乏氧气C.无能量补给D.昼夜温差大图2为“三圈环流局部示意图”。
读图完成第3~4题。
3.图中④表示的风是A .东北风B .东南风C .西北风D .西南风4.图中与热带雨林气候形成密切相关的是 A .① B .② C .③ D .④注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷包含单项选择题(第1题~第30题,共30题60分)、判断题(第31题~第40题,共10题10分)、综合题(第41题~第44题,共4题30分)共三部分。
考生答题全部答在答题卡上,答在本试卷上无效。
本次考试时间为75分钟。
考试结束后,请将本试卷和答题卡一并放在桌面,等待监考员收回。
2.答题前,请务必将自己的姓名、准考证号用书写黑色字迹的0.5毫米签字笔填写在本试卷及答题卡上。
3.请认真核对监考员在答题卡右上角所粘贴奈形码上的姓名、准考证号是否与本人的相符合。
4.答单项选择题和判断题必须用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,请用橡皮擦干净后,再选涂其它答案。
答材料解析题和问答题必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置,在其他位置答题一律无效。
图1图3 图3为“热力环流中某区域高空气压中心及风向变化示意图”,图中X 、Y 、Z 为气压值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.钓鱼诸岛是中国的固有领土,位于中国东海,面积约 6344000 平方米,数据 6344000 用科 学记数法表示为 ▲ . ▲ 边形. 9.多边形的每一个内角是 108o,则这个多边形是 10.因式分解:-4a2b+4a3+ab2= 11. a = 3 1 ,则 a= 2 ▲ . ▲ . ▲ .
二、填空题(本大题共 10 小题,每小题 2 分,共 20 分) 7.3 12.115o 8. 6.344106 π 13. 3 14.x2<x3<x1 9.五 15.甲 10.a(2a-b)2 16.128π 11. 6 2
三、解答题(本大题共 11 小题,共 88 分) 17. (本题 6 分) x–2 解:解不等式 ≥1,得 x≥5. ………………………………………………2 分 3 解不等式 1–3(x–1)<8–x,得 x>–2. ……………………………………4 分 ∴原不等式组解集为 x≥5. ……………………………………………………… 6 分 18. (本题 6 分) 解:原式=[a2-4a+4-(a2-4)](a-1) =(a2-4a+4-a2+4) (a-1) =(8-4a)(a-1) =8a-8-4a2+4a =-4a2+12a-8. ………………………………………………… 4 分 当 a=-2 时, 原式=-4(-2)2+12(-2)-8 =-16-24-8 =-48……………………………………………………………6 分 19. (本题 6 分) 证明: (1)∵四边形 ABCD 为矩形, ∴∠B=∠C=90o,AB=DC. ∵四边形 AEDF 为菱形, ∴AE=DE. 在 Rt△ ABE 和 Rt△ DCE 中,
26. (10 分)如图,在平面直角坐标系中,△ ABC 的顶点坐标分别为 A(-2,0) 、B(4,0) 、 C(0,2) . (1)请用尺规作出△ ABC 的外接圆⊙P(保留作图痕迹,不写作法) ; (2)求出(1)中外接圆圆心 P 的坐标; (3)⊙P 上是否存在一点 Q,使得△ QBC 与△ AOC 相似? y 如果存在,请直接写出点 Q 坐标;如果不存在,请说明理由.
BE (1)求 的值; AD
⌒ (2)若 OE 与BD 交于点 M,OC 平分∠BOE,连接 CM.说明
E D M
CM 为⊙O 的切线; (3)在(2)的条件下,若 BC=1,求 tan∠BCO 的值.
C
O
A (第 24 题)
B
错误!未指定书签。 25. (8 分)已知一次函数 y1=x+b 的图象与 x 轴,y 轴交于点 A、B. (1)若将此函数图象沿 x 轴向右平移 2 个单位后经过原点,则 b= ▲ ; (2)若函数 y1=x+b 图象与一次函数 y2=kx+4 的图象关于 y 轴对称,求 k、b 的值; (3)当 b>0 时,函数 y1=x+b 图象绕点 B 逆时针旋转 no(0o<no<180o)后,对应的函 数关系式为 y3=- 3x+b,求 n 的值.
AB=DC 错误!未指定书签。 AE=DE
∴Rt△ ABE≌Rt△ DCE. ………………………………………………3 分
第 7 页 共 12 页
(2)当 BC=2AB 时,菱形 AEDF 为正方形. 理由:∵Rt△ ABE≌Rt△ DCE , ∴BE=CE,∠AEB=∠DEC. 又∵BC=2AB, ∴AB=BE. ∴∠BAE=∠AEB=45o, ∴∠DEC=45o. ∵∠AEB+∠AED+∠DEC=180o, ∴∠AED=180o-∠AEB–∠DEC=90o. ∴菱形 AEDF 是正方形.……………………………………………………6 分 20. (本题 8 分) (1)表格分别填写 8,7,3,4 和 4.……………………………………………………2 分 (2)
第 3 页 共 12 页
(2)根据频数分布表补全频数分布直方图;
某校初三参加“迎青奥”知识竞赛成绩频数分布直方图 频数 18 15 12 9 6 3 0 59.5 69.5 79.5 89.5 99.5 分数
(3)超过均分的都有奖,请计算本次竞赛获奖的比例.
21. (8 分)南京市为了构建立体的道路网络,大力发展江北经济,决定修建一条六合到主城 的轻轨铁路.为了使工程提前 3 个月完成,需将原定的工作效率提高 10%.原计划完成 这项工程需要多少个月?
A D
B
E (第 19 题)
C
20. (8 分)下列为某校初三参加的“迎青奥”知识能力竞赛的 25 位同学的成绩: 78,86,98,90,95, 88,94,80,89,77, 87,73,65,84,87, 96,84,74,98,86, 83,67,88,68,85. (1)完成下表: 组别 59.5~69.5 69.5~79.5 79.5~89.5 89.5~99.5 个位数字统计 5,7,8 ① ▲ 6,8,0,9,7,4,7,4,6,3,8,5 8,0,5,4,6,8 频数 3 ② ▲ 12 6
(第 16 题) E -5 CA B D -2 0 1 2 4
第 2 页 共 12 页
三、解答题(本大题共 11 小题,共 88 分.请在答题卡指定区域 内作答,解答时应写出文字说 ....... 明、证明过程或演算步骤)
x-2≥1, 17. (6 分)解不等式组 3 1-3(x-1)<8-x.
六合区 2014 年中考模式测试(一)
数
注意事项:
学
1.本试卷共 6 页.全卷满分 120 分.考试时间为 120 分钟.考生答题全部答在答题卡上,答 在本试卷上无效. 2.请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合,再将 自己的姓名、准考证号用 0.5 毫米黑色墨水签字笔填写在答题卡及本试卷上. 3.答选择题必须用 2B 铅笔将答题卡上对应的答案标号涂黑.如需改动,请用橡皮擦干净后, 再选涂其他答案.答非选择题必须用 0.5 毫米黑色墨水签字笔写在答题卡上的指定位置, 在其他位置答题一律无效. 4.作图必须用 2B 铅笔作答,并请加黑加粗,描写清楚. 一、选择题(本大题共 6 小题,每小题 2 分,共 12 分.在每小题所给出的四个选项中,恰有 一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡 相应位置 上) ... .... 1.|-2|的倒数是 A.2 B.-2 1 C. 2 C.a3b 1 D.- 2 D.a4b
O1
O
O2
B
(第 27 题③)
第 6 页 共 12 页
六合区 2014 年中考模式测试(一)
数学试题参考答案及评分标准
说明:本评分标准每题给出了一种或几种解法供参考,如果考生的解法与本解答不同,参照 本评分标准的精神给分. 一、选择题(本大题共 6 小题,每小题 2 分,共 12 分) 题号 答案 1 C 2 B 3 A 4 B 5 D 6 C
k 6.若方程 =x+1 的解 x0 满足 1<x0<2,则 k 可能是 x A.1 B.2 C .3 D.6
第 1 页 共 12 页
二、填空题(本大题共 10 小题,每小题 2 分,共 20 分.不需写出解答过程,请把答案直接 填写在答题卡相应位置 上) ....... 1 - 7.- 2-(3.14-π)0= 2 ▲ .
15.甲、乙两名射击运动员在某场测试中各射击 20 次,测试成绩如下表: 甲的成绩 环数 频数 7 4 8 6 9 6 10 4 环数 频数 乙的成绩 7 6 8 4 9 4 10 6
则
▲
(选填甲、乙)运动员测试成绩更稳定.
16.如图,从原点 A 开始,以 AB=1 为直径画半圆,记为第 1 个 半圆;以 BC=2 为直径画半圆,记为第 2 个半圆;以 CD=4 为直径画半圆,记为第 3 个半圆;以 DE=8 为直径画半圆, 记为第 4 个半圆;…,按此规律,继续画半圆,则第 6 个半圆 的面积为 ▲ (结果保留 π).
频数 15 12 9 6 3 0 59.5 69.5 79.5 89.5 99.5 分数 某校初三参加“迎青奥”竞赛成绩频数分布直方图
………………………………………………………………………………………………6 分 (3)计算平均分=84(分) , ∵超过平均分的有 14 人, 14 ∴本次竞赛获奖的比例为: .………………………………………………………8 分 25 21. (本题 8 分) 解:设原计划完成这项工程需要 x 个月, 根据题意,得 1 1 (1+10%)· = .…………………………………………………………………4 分 x x-3 解这个方程,得 x=33.…………………………………………………………………6 分 经经验 x=33 是原方程的解.…………………………………………………………7分 答:原计划完成这项工程需要 33 个月.………………………………………………8分 3 (注:方程可以列成: =10%去解;也可设工作效率为 x,列方程: x-3 1 1 - =3 去解. ) x (1+10%)x 22. (本题 8 分)
12.如图, 直线 AB∥CD,∠E=90o,∠A=25o,则∠C= cm2.
A E A F C (第 12 题) B D B
13.如图,正方形 ABCD 中,扇形 BAC 与扇形 CBD 的弧交于点 E, AB=2cm.则图中阴影 部分面积为 ▲
D
E
C (第 13 题)
1 14.在函数 y=- 的图象上有三个点的坐标分别为(x1,y1) 、 (x2,y2) 、 (x3,y3) ,若 y1<0 x <y2<y3,则 x1,x2,x3 的大小关系是 ▲ .
18. (6 分)先化简,再求值:[(a-2)2-(a+2)(a-2)](a-1),其中 a=-2.
19. (6 分)如图,四边形 ABCD 为矩形,点 E 在边 BC 上,四边形 AEDF 为菱形. F (1)求证:△ ABE≌△DCE; (2)试探究:当矩形 ABCD 长宽满足什么关系时,菱形 AEDF 为正方形?请说明理由.
