四川大学理论力学第10章第三课时
合集下载
四川大学理论力学第10章第三课时

B
O
aC
C
aA
A
B
运动学关系:
aA = rB = aC rD = aC
m2g
FT2
FA FAN
解: (1) 以重物A为研究对象, 受力如图。
aA
A
m2aA= m2 g sin-FT2-FA FAN-m2 g cos = 0 FA= FAN f
FT1 O F'T2
(2) 以 B 为研究对象。由刚 体定轴转动微分方程可得
z'
C y'
y
m=∑mi
LO = rC×mvC + LCr
dLO drC dvC dLCr mvC rC m dt dt dt dt
=0
=∑Fie
=∑ri×Fie =∑(rC+ r'i)×Fie
dLCr r'i Fi e MC (Fi e ) dt
即质点系相对于质心的动量矩对时间的导数等于 作用于质点系的外力系对质心的主矩。上述结论 称为质点系相对于质心的动量矩定理。
LA=MA(mvC) +JC ω
圆轮既滚且滑,设基点为O,故
vO
• vO C •O
r
A
ω
vCO
vC= vO+ vCO
•
vCO = rω/2
vC = vO+(rω/2)
MA(mvC)=(3mrvO /2)+(3mr2ω/4)
又
JC= JO – mr2/4 LA =(JO+mr2/2)ω+3mrvO /2
解: 圆轮纯滚,瞬心为A,故有
vC •C vO •O ω r
A
理论力学第十章PPT

(i )
) =0
∑ Fi dt = 0
d(mi vi ) = Fi (e) dt + Fi (i) dt
质点系: ∑d(mi vi ) = ∑ Fi (e) dt + ∑ Fi (i) dt
得 dp = ∑ F dt = ∑dI i
(e)
(e) i
或
dp (e) = ∑ Fi dt
称为质点系动量定理的微分形式 即质点系动量的增量等于作用于质点系的外力 元冲量的矢量和; 或质点系动量对时间的导数等于作用于质点系 的外力的矢量和。
在 t1 t2 内,动量由 p1~ p2 ,有 ~
p2 − p1 = ∑ Ii(e)
i=1
n
称为质点系动量定理的积分形式,即在某一时间 间隔内,质点系动量的改变量等于在这段时间内 作用于质点系外力冲量的矢量和。 动量定理微分形式的投影式
dpx = ∑ Fx(e) dt
dpy dt
= ∑F
(e) y
dpz = ∑ Fz(e) dt
动量定理积分形式的投影式
( p2x − p1x = ∑ I xe)
( p2y − p1y = ∑I ye)
p2z − p1z = ∑ I z(e)
3.质点系动量守恒定律 .
若 ∑F
(e)
≡ 0 , 则 p = 恒矢量
若 ∑ Fx
(e)
≡ 0, 则 px = 恒量
解决动量定理习题步骤
第十章 动 量 定 理
§10-1 动量与冲量
1.动量 . 质点的动量 质点系的动量
mv
n i=1
单位: kg⋅ m/ s
p = ∑mivi
dri d p = ∑mivi = ∑mi = ∑mi ri dt dt ∑mi ri 质心 rc = , m = ∑mi m
) =0
∑ Fi dt = 0
d(mi vi ) = Fi (e) dt + Fi (i) dt
质点系: ∑d(mi vi ) = ∑ Fi (e) dt + ∑ Fi (i) dt
得 dp = ∑ F dt = ∑dI i
(e)
(e) i
或
dp (e) = ∑ Fi dt
称为质点系动量定理的微分形式 即质点系动量的增量等于作用于质点系的外力 元冲量的矢量和; 或质点系动量对时间的导数等于作用于质点系 的外力的矢量和。
在 t1 t2 内,动量由 p1~ p2 ,有 ~
p2 − p1 = ∑ Ii(e)
i=1
n
称为质点系动量定理的积分形式,即在某一时间 间隔内,质点系动量的改变量等于在这段时间内 作用于质点系外力冲量的矢量和。 动量定理微分形式的投影式
dpx = ∑ Fx(e) dt
dpy dt
= ∑F
(e) y
dpz = ∑ Fz(e) dt
动量定理积分形式的投影式
( p2x − p1x = ∑ I xe)
( p2y − p1y = ∑I ye)
p2z − p1z = ∑ I z(e)
3.质点系动量守恒定律 .
若 ∑F
(e)
≡ 0 , 则 p = 恒矢量
若 ∑ Fx
(e)
≡ 0, 则 px = 恒量
解决动量定理习题步骤
第十章 动 量 定 理
§10-1 动量与冲量
1.动量 . 质点的动量 质点系的动量
mv
n i=1
单位: kg⋅ m/ s
p = ∑mivi
dri d p = ∑mivi = ∑mi = ∑mi ri dt dt ∑mi ri 质心 rc = , m = ∑mi m
10《理论力学》课件

n
r I (e)
i
i 1
--质点系动量定理微分形式的投影式 --质点系动量定理的积分形式
即在某一时间间隔内,质点系动量的改变量等于在这段时
间内作用于质点系外力冲量的矢量和.
p2 x
p1x
I
(e) x
p2 y
p1y
I (e) y
p2 z
p1z
I
(e) z
--质点系动量定理积分形式的投影式
3.质点系动量守恒定律
r dIi(e)
Fi(i)dtr dp
或
dt
r F (e)
i
--质点系动量定理的微分形式
即质点系动量的增量等于作用于质点系的外力元冲量的矢 量和;或质点系动量对时间的导数等于作用于质点系的外力的 矢量和.
dpx dt
F (e) x
dpy dt
F (e) y
dpz dt
F (e) z
pr 2
pr1
力在此段时间内的冲量.
2.质点系的动量定理
外力: 内力性质:
r Fi ( e,)
r
r
内力:
F (i) i
r
r
F (i) i
0
MO (Fi(i) ) 0
r Fi(i)dt
0
质 点: 质点系:
dpr
d(mivri )
r d(mivi
)
r
Fi(e)dt
r
r
Fi
(e)dt
r
Fi(i)dt
r
Fi(e)dt
问题:内力是否影响质心的运动? 质心运动定理与动力学基本方程有何不同?
在直角坐标轴上的投影式为:
ma
Cx
理论力学10 罗特军 川大

acceleration)和法向加速度(normal acceleration)。
小随时间的变化率。
at沿M点处轨迹的切线方向,反映了速度大 an的方向永远指向曲率中心,反映了速度方
向随时间的变化率,恒为正值。
例1. 图示曲柄连杆机构,已知r、l、h, = t, 求滑块B的运动方程、速度和加速度。
z
M
v
M'
r(t)
O
x
r r(t+t)
r dr • v lim r Δt→0 t dt
y
v的方向沿轨迹在该点的切线方向,其大小等于
ds dr ds dr v dt ds dt dt
3. 点的加速度
时刻t动点的加速度(acceleration)定义为
v dv • •• a lim vr Δt→0 t dt
动点(point)
刚体(rigid body)
3. 参考系
参考体(reference body)
参考系(reference system) 所谓相对于参考系的运动,即是在参考系上的观 察者所观察到的运动,或者说是将参考系当作“静 止的”,来研究物体的运动。
由于同一物体相对不同的参考系的运动是不同 的, 故不明确指出参考系, 论及物体的运动是毫无 意义的。 工程上通常以大地为参考系。
1 ds k d
曲率圆(circle of curvature)、 曲率半径及曲率中心(center of curvature)的几何意义 O
M'
M M''
■ 自然轴系
轨迹曲线在M点 处的曲率园所在的 平面称为曲线在该 点的曲率平面或密 切面(osculating plane)。
小随时间的变化率。
at沿M点处轨迹的切线方向,反映了速度大 an的方向永远指向曲率中心,反映了速度方
向随时间的变化率,恒为正值。
例1. 图示曲柄连杆机构,已知r、l、h, = t, 求滑块B的运动方程、速度和加速度。
z
M
v
M'
r(t)
O
x
r r(t+t)
r dr • v lim r Δt→0 t dt
y
v的方向沿轨迹在该点的切线方向,其大小等于
ds dr ds dr v dt ds dt dt
3. 点的加速度
时刻t动点的加速度(acceleration)定义为
v dv • •• a lim vr Δt→0 t dt
动点(point)
刚体(rigid body)
3. 参考系
参考体(reference body)
参考系(reference system) 所谓相对于参考系的运动,即是在参考系上的观 察者所观察到的运动,或者说是将参考系当作“静 止的”,来研究物体的运动。
由于同一物体相对不同的参考系的运动是不同 的, 故不明确指出参考系, 论及物体的运动是毫无 意义的。 工程上通常以大地为参考系。
1 ds k d
曲率圆(circle of curvature)、 曲率半径及曲率中心(center of curvature)的几何意义 O
M'
M M''
■ 自然轴系
轨迹曲线在M点 处的曲率园所在的 平面称为曲线在该 点的曲率平面或密 切面(osculating plane)。
理论力学第十章
理论力学
中南大学土木工程学院
3
§10-1
质点系的质心 内力与外力
z C
一、质点系的质心
质点系的质量中心称为质心,是表示 质点系质量分布情况的一个重要概念。 质心C点的位置:rC
rC xC i yC j zC k
mi ri mi ri mi m (m mi )
W3 W2
Fx(e) 0 px const
设沙箱滑动结束后车速为v,则有
v0
x
W1 W2 W3 W1 W2 v0 v g g
代入已知数据,解得 v =3 m/s 再以小车为研究对象,由动量定理有
W1
FN2 FN
F
FN1
px p0 x Ft
W1 W v 1 v0 Ft g行深入的研究。通常情况下,用这些定理来解答质点特别是
质点系的动力学问题非常方便简捷 。
本章研究质点和质点系的动量定理,建立了动量的改变
与力的冲量之间的关系,并研究质点系动量定理的另一重要 形式——质心运动定理。
理论力学 中南大学土木工程学院 2
C2 B
vC2
wr=w
系统质心的速度 p 5 vC lw v A 2m 4
理论力学
中南大学土木工程学院
9
二、冲量 力与其作用时间的乘积称为力的冲量,冲量表示力在 其作用时间内对物体作用的累积效应(过程量)。 1、力F是常矢量
I F (t2 t1 )
冲 量 I F dt
t2 t1
t 积分形式: mv 2 mv1 t12 F d t I
(在某一时间间隔内,动量的增量等于力在该时间内的冲量)
理论力学
[法律资料]理论力学 第10章 动静法
![[法律资料]理论力学 第10章 动静法](https://img.taocdn.com/s3/m/c863420e1eb91a37f1115c86.png)
m1 πR12l m2 π R22l
Jz
1 2
π l(R14
R24 )
1 2
π l(R12
R22 )(R12
R22 )
由 π l(R12 ,R22得) m
Jz
1 2
m(
R12
R22 )
h
21
5.实验法 思考:如图所示复摆如何确定对转轴的转动惯量?
1.平移
ai aC
rC
miri M
F g,F 1 g, 2,F g nF R g
,
F R gF g im ia i M a C
M g o m 0 ( F g ) i r i m i a i (m i r i ) a C
M r C a C r C ( M a C ) r C F Rg
力系平衡条件
Fi(e) Fi(i) Fgi 0 mo (Fi(e) ) mo (Fi(i) ) mo (Fgi ) 0
注意内力力系自相平衡
Fi(i) 0 mo (Fi(i) ) 0
推得
Fi(e) Fgi 0 mo (Fi(e) ) mo (Fgi ) 0
h
12
解:1. 研究重物H
Fy 0
Fg1m1a12m1a
P1TFg10
2. 研究三角板BCK
Fy 0
Tsi4 n5P 2Fg20
3. 运动学补充方程
vBco2s vH 0
aB t co2sv4B 2 lsin2aH0
h
13
2.定轴转动(平面)
F g1,F g2, ,F gn 向转轴O简化
质点系统动力学方程
F x ( e ) F gx 0
F y ( ) F gy 0
理论力学(第10章)
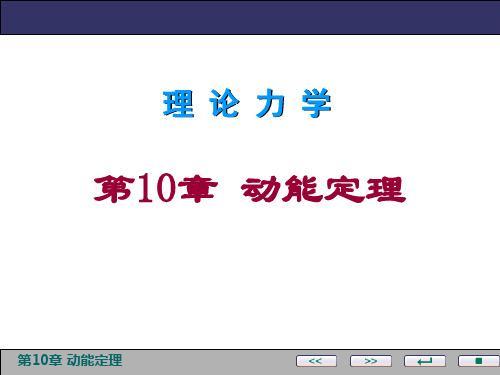
因为质心 C 的速度大小 vC = rC 。
由上式得
P C vC
rc
1 2 1 T m vC J C 2 2 2
即,平面运动刚体的动能 ,等于它以质心速度作平动时的动能 与相对于质心轴转动时的动能之和。
第10章 动能定理
10.2 动能及其计算
例10-1 求例9-6所示系统的动能,系统如图所示。 解 : 1.运动分析
约束力的功恒等于零。
FA
dr
FA dr dr FA (c)
(a)
(b)
第10章 动能定理
10.1 力 的 功
7.功率的概念 表示力做功的快慢是功率。通常用力在单位时间内所做的功
定义为力的功率,记为P。
δW P F v dt 当作用于转动刚体上的力矩为Mz,则其功率为
P Mz d M z dt
1 T J P 2 2
根据转动惯量的平行轴定理有
P
C
J P J C mrC
2
rc
vC
式中JC是对平行于瞬轴的质心轴的转 动惯量。
第10章 动能定理
10.2 动能及其计算
3. 平面运动刚体的动能
J P J C mrC
2
1 2 T ( J C mrC ) 2 2
mv2 mv2 d( ) d ( ) dT 2 2
故上式可写成
d T δW (e) δW (i)
即,质点系动能的微分等于作用于质点系所有外力元功和内 力元功的代数和—质点系动能定理的微分形式。
第10章 动能定理
10.3 动能定理
10.3.2 质点系动能定理
2.积分形式 由微分形式
代入运动学关系
由上式得
P C vC
rc
1 2 1 T m vC J C 2 2 2
即,平面运动刚体的动能 ,等于它以质心速度作平动时的动能 与相对于质心轴转动时的动能之和。
第10章 动能定理
10.2 动能及其计算
例10-1 求例9-6所示系统的动能,系统如图所示。 解 : 1.运动分析
约束力的功恒等于零。
FA
dr
FA dr dr FA (c)
(a)
(b)
第10章 动能定理
10.1 力 的 功
7.功率的概念 表示力做功的快慢是功率。通常用力在单位时间内所做的功
定义为力的功率,记为P。
δW P F v dt 当作用于转动刚体上的力矩为Mz,则其功率为
P Mz d M z dt
1 T J P 2 2
根据转动惯量的平行轴定理有
P
C
J P J C mrC
2
rc
vC
式中JC是对平行于瞬轴的质心轴的转 动惯量。
第10章 动能定理
10.2 动能及其计算
3. 平面运动刚体的动能
J P J C mrC
2
1 2 T ( J C mrC ) 2 2
mv2 mv2 d( ) d ( ) dT 2 2
故上式可写成
d T δW (e) δW (i)
即,质点系动能的微分等于作用于质点系所有外力元功和内 力元功的代数和—质点系动能定理的微分形式。
第10章 动能定理
10.3 动能定理
10.3.2 质点系动能定理
2.积分形式 由微分形式
代入运动学关系
理论力学第十章

简化方法就是采用静力学中的力系简化的理论。将虚拟的
惯性力系视作力系向任一点O简化而得到一个惯性力 R Q 和一个
惯性力偶 M QO 。
RQ Q m a M aC M
QO
与简化中心无关 与简化中心有关
m O (Q )
无论刚体作什么运动,惯性力系主矢都等于刚体质量与质
心加速度的乘积,方向与质心加速度方向相反。
Fi N i Q i 0 m O ( Fi ) m O ( N i ) m O (Q i ) 0
注意到 F i 0 , m O ( F i ) 0 划分, 则
Fi
(e)
(i)
(i)
, 将质点系受力按内力、外力
Qi 0
(e)
12
一、刚体作平动 向质心C简化:
RQ M aC
刚体平动时惯性力系合成为一过质心的合惯性力。
RQ M ac
13
二、定轴转动刚体 先讨论具有垂直于转轴的质量对称平面 的简单情况。 直线 i : 平动, 过Mi点, Q i m i a i 空间惯性力系—>平面惯性力系(质量对称面) O为转轴z与质量对称平面的交点,向O点简化: 主矢: 主矩:
d 2 dt
2
mC (F
(e)
)
20
§10-4 达朗伯原理的应用
应用动静法求动力学问题的步骤及要点: ①选取研究对象。原则与静力学相同。 ②受力分析。画出全部主动力和外约束反力。
③运动分析。主要是刚体质心加速度,刚体角加速度,标出
方向。 ④虚加惯性力。在受力图上画上惯性力和惯性力偶,一定要 在 正确进行运动分析的基础上。熟记刚体惯 性力系的简化结果。
惯性力系视作力系向任一点O简化而得到一个惯性力 R Q 和一个
惯性力偶 M QO 。
RQ Q m a M aC M
QO
与简化中心无关 与简化中心有关
m O (Q )
无论刚体作什么运动,惯性力系主矢都等于刚体质量与质
心加速度的乘积,方向与质心加速度方向相反。
Fi N i Q i 0 m O ( Fi ) m O ( N i ) m O (Q i ) 0
注意到 F i 0 , m O ( F i ) 0 划分, 则
Fi
(e)
(i)
(i)
, 将质点系受力按内力、外力
Qi 0
(e)
12
一、刚体作平动 向质心C简化:
RQ M aC
刚体平动时惯性力系合成为一过质心的合惯性力。
RQ M ac
13
二、定轴转动刚体 先讨论具有垂直于转轴的质量对称平面 的简单情况。 直线 i : 平动, 过Mi点, Q i m i a i 空间惯性力系—>平面惯性力系(质量对称面) O为转轴z与质量对称平面的交点,向O点简化: 主矢: 主矩:
d 2 dt
2
mC (F
(e)
)
20
§10-4 达朗伯原理的应用
应用动静法求动力学问题的步骤及要点: ①选取研究对象。原则与静力学相同。 ②受力分析。画出全部主动力和外约束反力。
③运动分析。主要是刚体质心加速度,刚体角加速度,标出
方向。 ④虚加惯性力。在受力图上画上惯性力和惯性力偶,一定要 在 正确进行运动分析的基础上。熟记刚体惯 性力系的简化结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
JOB = F'T2r -FT1r JO = m1r2/2
B
m1g
(3) 以圆柱D为研究对象,受 力如图。由刚体平面运动微 分方程有
m1aC = F'T1-FD JCD = FD r 式中 JC = m1r2/2
注意到运动学关系:
F'T1
D
aC
FDN C m1g
D
FD
aA = rB = aC rD = aC
z'
C y'
y
m=∑mi
LO = rC×mvC + LCr
dLO drC dvC dLCr mvC rC m dt dt dt dt
=0
=∑Fie
=∑ri×Fie =∑(rC+ r'i)×Fie
dLCr r'i Fi e MC (Fi e ) dt
即质点系相对于质心的动量矩对时间的导数等于 作用于质点系的外力系对质心的主矩。上述结论 称为质点系相对于质心的动量矩定理。
O C
系统动能
O R h
A
1 1 2 1 2 T J O mv J C 2 2 2 2 5 2 mv 8
由动能定理
B C R v
5 2 mv mgh 8 4 a g 5
v vB RC 2R v 2R
8 v gh 5
FT
取C, 由质心运动定理
dLCr M C ( Fi e ) dt
maC =∑Fi
(1) 式中LCr是质点系在质心平动坐标系中对质心 的动量矩,对于非质心平动系无类似结果。 (2) 质点系相对于质心的动量矩定理表明,内力不 能改变质点系相对于质心的动量矩。
(3) 当∑MC(Fie )≡ 0时,质点系对质心的动量矩守恒。
例3. 如图示,已知均质圆柱的半径为r,质量为m1, 重物的质量为m2,与水平桌面间的动摩擦系数为f, 试求圆柱质心C的加速度和绳的张力。
aB
B
运动学关系:
C
aC
r
a C = a B + r
解: (1) 以重物B为研究对象, 受力如图。
aB
FT 2
FN
m2g
B
m2 aB = FT 2-F F = m2 g f a C = a B + r
2. 质点系相对于质心的动量矩定理
因为
ri = rC + r'i
LO = ∑ri×mivi
LO = ∑(rC + r'i)×mivi
= rC×∑mivi +∑r'i×mivi
z mi ri rC O x x' r'i
LO = rC×mvC + LCr
即质点系对任一点O的动量 矩等于集中于系统质心的动 量对于点O的动量矩加上此 系统对于质心的动量矩。
C
x'
x
maC =∑Fi dLC / dt =∑MC (Fi)
将前一式投影于x轴和y轴,后一式投影于Cz' 轴得 此即刚体平面运动微分方程。
y mC Fx mC Fy J M z (F ) x
e
例1. 如图示,质量为m的圆轮 的质心为C,对O的转动惯量 为JO。若轮只滚不滑,已知r、 vO、OC=r/2,求它的动量和对 接触点A的动量矩。
由以上方程即可解出
m2 (sin f cos ) aC g 2m1 m2 m1m2 (sin f cos ) FD g 2(2m1 m2 )
点评:
求解系统的动力学问题时,一种比较直观的办 法就是将系统拆开成单个刚体, 分别列出相应的 动力学微分方程 , 然后联立求解。但是由于内力 的出现,导致未知量的数目增加,这种方法有时会 比较繁琐。
例2. 如图示,质量为m的圆轮的 质心为C,对O的转动惯量为JO。 若轮既滚且滑,已知r、vO、 ω、 OC=r/2,求它的动量和对接触 点A的动量矩。
ω
vO
•C •O
A
r
LO = rC×mvC + LCr
P=m(vO+rω/2)
•
LA =(JO+mr2/2)ω+3mrvO /2
LO = rC×mvC + LCr
C R mg
ma mg FT
1 FT mg 5
B
B
O
aC
C
aA
A
B
运动学关系:
aA = rB = aC rD = aC
m2g
FT2
FA FAN
解: (1) 以重物A为研究对象, 受力如图。
aA
A
m2aA= m2 g sin-FT2-FA FAN-m2 g cos = 0 FA= FAN f
FT1 O F'T2
(2) 以 B 为研究对象。由刚 体定轴转动微分方程可得
LC = ∑r'i×(mivC + mivir)
= (∑mi r'i)×vC +∑r'i×mivir
z ri rC O x x'
LC = LCr
即质点系在绝对运动中 对质心的动量矩与它在 相对质心平动坐标系的 相对运动中对质心的动 量矩是相等的。
mi r'i
z'
C y'
y
LCr =∑r'i×mivir
(4) 任意刚体的一般运动可分解为随质心的平动 和绕质心的转动,由质心运动定理和相对于质心的 动量矩定理共可得6个标量方程, 从而完全确定自 由刚体的6个坐标。
3. 刚体平面运动微分方程
设平面图形S在Oxy平面 内运动。取质心C为基点, 质心平动系为Cx'y'z',由质 心运动定理和相对于质心 的动量矩定理可得 y S z' O z y'
习题: 10-14, 10-15, 10-19, 10-21,
解:设圆盘A、B的角加速度分别为O、C,
则
O R h A
J O O FT R J C C FT R
因 所以
J O J C且FT FT
O C
B
C R
由于均从静止开始运动, 所以
P333 11.31
LA=MA(mvC) +JC ω
圆轮既滚且滑,设基点为O,故
vO
• vO C •O
r
A
ω
vCO
vC= vO+ vCO
•
vCO = rω/2
vC = vO+(rω/2)
MA(mvC)=(3mrvO /2)+(3mr2ω/4)
又
JC= JO – mr2/4 LA =(JO+mr2/2)ω+3mrvO /2
LO =∑ri×mivi
质点系在定系中相对质 心C的动量矩:
z ri rC O x
mi r'i
z' C y y'
LC =∑r'i×mivi
质点系在质心平动系中 相对质心C的动量矩:
x'
LCr =∑r'i×mivir
vi = ve + vir = vC + vir
因为
vi = vC + vir
LC =∑r'i×mivi
理论力学
欢 迎 光 临
dLO e M O ( Fi ) dt
dLx M x ( Fi e ) dt dLy e M y ( Fi ) dt dLz e M z ( Fi ) dt
12.4 质点系相对于质心的 动量矩定理
1. 质点系相对于质心的动量矩
质点系相对固定点O的动量矩:
m1 m2 ( 2 f ) aC g m1 3m2
m1m2 (1 f ) FT 1 g m1 3m2
例4. 如图示, 半径为r, 质量为m1的B和D均可视 为均质圆柱,且D沿水平面作纯滚动;重物的质量 为m2, 与倾角为的斜面间的动摩擦系数为f, 试 求圆柱D的质心C的加速度和水平面对它的摩擦 力。 D D
解: 圆轮纯滚,瞬心为A,故有
vC •C vO •O ω r
A
vO / r
vC 3vO / 2
p 3mvO / 2
•
LO = rC×mvC + LCr
又 J O J C mr / 4
2
LA M A (mvC ) J C
J C J O mr2 / 4
LA ( J O 2mr 2 )vO / r
F
FT 1
(2) 以圆柱为研究对象。由 刚体平面运动微分方程有
m1g
C
aC
r
m1aC = m1g-FT1 JC = FT1r 而 JC = m1r2/2 FT1=FT 2
aC = aB + r m2 aB = FT 2-F F = m2 g f m1aC = m1g-FT1 JC = FT1r JC = m1r2/2 FT1=FT 2
