四川大学理论力学第十二章
理论力学 第12章
P
δW dt
Mz
d
dt
M z
2.功率方程
dT
dt
n δWi i1 dt
n
Pi
i 1
—— 功率方程
即质点系动能对时间的一阶导数,等于作用于 质点系的所有力的功率的代数和.
功率方程常用来研究机器在工作时能量的变 化和转化的问题。
dT P输入 P有用 P无用 dt
或
dT dt P输入 P有用 P无用
mi
即： T
1 2
mvC2
（2）定轴转动刚体的动能
T
1 2mi
vi
2
12mi 2ri2
12
2
Jmz iri2
即：
T
1 2
J z 2
（3）平面运动刚体的动能
速度瞬心为P
T
质心为C
1 2
J pω2
Jp JC md2
T
1 2
mvC2
1 2
JC 2
平面运动刚体的动能等于随质心平移的动能与 绕质心转动的动能之和.
则杆的动能：
§12-3 动能定理
1.质点的动能定理
将 m dvr 两 端Fr 点乘 ，得dr：
dt
m
d
v
dr
F
d
r
dt
由于 dr v，d于t 是有：
mvr
dvr
r F
drr
由于 mvr
dvr
d(1
mv2 ),
r F
drr
δW
2
质点动能的增量 等于作用在质点 上力的元功
d(1 mv2 ) δW —— 质点动能定理的微分形式 2
3.机械效率
四川大学理论力学时PPT课件
面内落下。点C的初始高度为h。开始时杆系静
止，求铰链C与地面相碰时的速度v。
A
解：取杆AC，当铰链 C 与地面相碰时，速度 瞬心 D 与 A 重合。根据对称性，由动能定理得
2TAC
0
2mg
h 2
2
1
1
ml2
vC
2
mgh
2 3 l
1 k
m2 g2 2kmgh
由于弹簧的变形量是正值，因此取正号，即
δmax
mg k
1 k
m2 g2 2kmgh
第33页/共52页
例2、链条长l，质量m，展开放在光滑的桌面 上，如图所示。开始时链条静止，并有长度为a的 一段下垂。求链条离开桌面时的速度。
解：将链条分为两段考虑，下垂段重力作功为
桌面段重力作功为 由动能定理得
W12 (mzC1 mzC2 )g mg(zC1 zC2 )
即质点系重力的功等于质点系的总重量与其重心 高度差之乘积,重心降低为正,重心升高为负。
重力的功与路径无关,仅取决于重心的始末位置。
第6页/共52页
（2）弹性力的功
设弹簧刚性系数为k，弹簧变形为,则弹力为
弹性力的功为
F k
W
动惯量为2mr2/5 )。
C
JO
1 3
ml2
2 5
mr2
m(l
r)2
m 20l 2 21r2 30lr 15
T
1 2
J
O
2
m 30
20l 2 21r 2 30lr
2
第24页/共52页
例4. 己知长l的杆和半径为r的均质圆盘质量均为m, 均质圆盘沿水平面纯滚,质心速度为u，试求图示位 置时系统的动能。
理论力学习题册答案
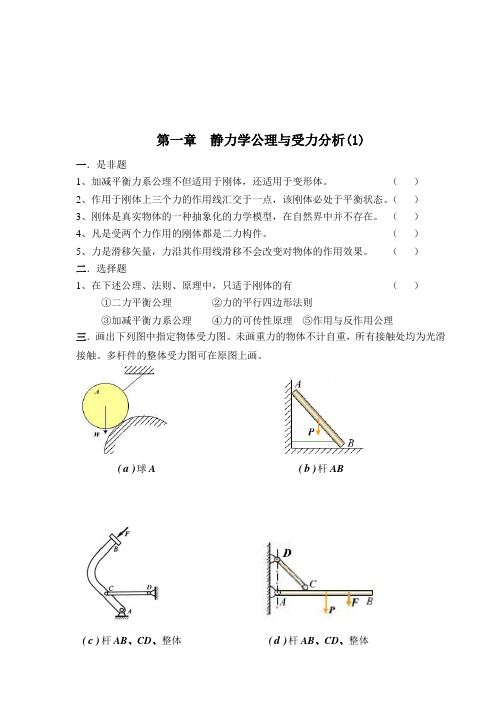
第一章静力学公理与受力分析(1)一．是非题1、加减平衡力系公理不但适用于刚体，还适用于变形体。
（）2、作用于刚体上三个力的作用线汇交于一点，该刚体必处于平衡状态。
（）3、刚体是真实物体的一种抽象化的力学模型，在自然界中并不存在。
（）4、凡是受两个力作用的刚体都是二力构件。
（）5、力是滑移矢量，力沿其作用线滑移不会改变对物体的作用效果。
（）二．选择题1、在下述公理、法则、原理中，只适于刚体的有（）①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三．画出下列图中指定物体受力图。
未画重力的物体不计自重，所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A )b(杆ABd(杆AB、CD、整体)c(杆AB、CD、整体)-2 -)e (杆AC 、CB 、整体)f (杆AC 、CD 、整体四．画出下列图中指定物体受力图。
未画重力的物体不计自重，所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a (球A 、球B 、整体)b (杆BC 、杆AC 、整体班级姓名学号- 3 -第一章静力学公理与受力分析（2）一．画出下列图中指定物体受力图。
未画重力的物体不计自重，所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WA DBCEOriginal FigureADBCEWWF AxF Ay F BFBD of the entire frame )a(杆AB、BC、整体)b(杆AB、BC、轮E、整体)c(杆AB、CD、整体)d(杆BC带铰、杆AC、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体- 4 -班级姓名学号- 5 -第二章平面汇交和力偶系一．是非题1、因为构成力偶的两个力满足F= - F’，所以力偶的合力等于零。
（）2、用解析法求平面汇交力系的合力时，若选用不同的直角坐标系，则所求得的合力不同。
梁坤京理论力学第十二章动量矩定理课后答案
动量矩定理12-1 质量为m 的点在平面Oxy 内运动，其运动方程为: x a cos t y bsin2 t 式中a 、b 和 为常量。
求质点对原点 O 的动量矩。
解：由运动方程对时间的一阶导数得原点的速度V xdxsin t dt aV y dy 2b cos2 t 质点对点 O 的动量矩为L O M o (mV x ) M 0(mV y )mv x y mv y x m ( a sin t) bsin2 t m 2b cos2 t acos t 2mab cos 3 t 12-3 如图所示，质量为m 的偏心轮在水平面上作平面运动。
轮子轴心为A,质心为C, AC = e ；轮子半径为 R,对轴心A 的转动惯量为J A ； C 、A 、B 三点在同一铅直线上。
（1 ）当轮子只 滚不滑时，若 V A 已知，求轮子的动量和对地面上 B 点的动量矩。
（2）当轮子又滚又滑时， 若V A 、 已知，求轮子的动量和对地面上 B 点的动量矩。
解：（1）当轮子只滚不滑时 B 点为速度瞬心。
轮子角速度V A R质心C 的速度V CBCR e轮子的动量p mv Cmv A (方向水平向右)R对B 点动量矩L B J B2 2 2由于 J B J C m (R e) J A me m (R e) 故 L B J A me 2 m （R e ）2食 （2）当轮子又滚又滑时由基点法求得 C 点速度。
V C V A V CA V A e 轮子动量 p mv C m(v A e) （方向向右） 对B 点动量矩L B mv C BC J Cm(v A 2e) (R e) (J A me) mv A (R e) (J A mRe) 12-13 如图所示，有一轮子，轴的直径为 50 mm 无初速地沿倾角 20的轨道滚下，设 只滚不滑，5秒内轮心滚动的距离为 s =3m 。
试求轮子对轮心的惯性半径。
解：取轮子为研究对象，轮子受力如图（ a ）所示，根据刚体平面运动微分方程有 ma C mgsi n F （ 1） J C = Fr （ 2）因轮子只滚不滑，所以有 a c = r （ 3） ® 12将式（3）代入式（1）、（2）消去F 得到mr sinm?g上式对时间两次积分，并注意到 t = 0时 0, 0,则 mgrt 2 sin mgrt 2s in 2(J C mr 2) 2(m 2 mr 2) 把 r = 0.025 m 及 t = 5 s 时，s 'grt 2sin f gt 2sin-r r「s r 1grt 2sin 2( 2 r 2) r 3 m 代入上式得0.0259.8 52si n202 30.09 m 90 mm12-17 图示均质杆 AB 长为I ，放在铅直平面内，杆的一端 A 靠在光滑铅直墙上，另一端 B 放在光滑的水平地板上，并与水平面成 °角。
理论力学第12章
i 1
n
n n (e) (i ) d (mi vi ) Fi dt Fi dt i 1 i 1
×
i 1
n
n n (e) (i ) d (mi vi ) Fi dt Fi dt i 1 i 1
质点系质点相互作用的内 力总是大小相等、方向相 反地成对出现，相互抵消
静反力：电机不转时，基础只有向上的反力；
y
动反力：电机转动时的基础反力；
附加的动反力：动反力与静反力的差值
m1 g
O1
p
Fx 0
Fy (m1 m2 ) g
e
m2 g
Fx m2 e sin t
2
Fy
Mo
Fx
Fy m2 2 e cost
n p mi vi i 1
n为质点数；mi为第i个质点的质量，vi 为质点的速度。 矢量和又称为主矢: 质点系的动量等于质点系动量的主矢。
×
例：三个物块用绳相连，它们都可视为质点，其质量分别为 m1 2 m 2 4 m 3 。绳质量和变形忽略不计，且 45 。求这三个 质点组成的质点系的动量 p.
第十二章 动量定理
沈阳建筑大学 侯祥林
第十二章 动量定理
第十二章引言
§12-1 动量与冲量
§ 12-2 动量定理
动量定理例题
§12-3
质心运动定理
质心运动定理例题
第十二章 动量定理
用质点动力学微分方程分析质点系动力学问题，可以逐个 质点列出动力学基本方程，联立求解困难。
用动力学普遍定理，即： 动量定理 动量矩定理 动能定理 从不同侧面提出质点和质点系的运动变化与其受力之间的 关系，尤其求解质点系动力学问题，很方便。
同济理论力学 第十二章 动量矩定理
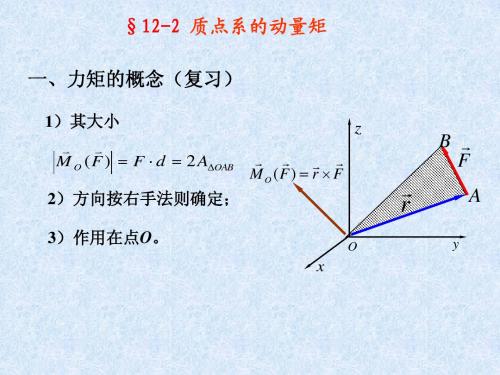
' ri rQ ri
Q为任一动点
dmvi
z
Mi
ri
rQ
O
ri
Q
y
' ' ' dri ( rQ vi )dm ( ri vQ )dm ( ri )dm dt
质点系动量矩守恒
L x 常量
有心力
mv
M
M O (mv ) r mv 常矢量
M O (mv ) 的大小始终不变，为两倍的 2、
A
r
h F O
1、行星运行轨道必为一平面轨迹
Δ OMA面积
M o (mv ) r mv mv h
dω P 2 dω 1 R1 FR1 解: 左轮: J1 dt 2 g dt d P2 2 d J R2 FR2 右轮: 2 dt 2 g dt
1 < 2,
1 < 2,
例12-7: 旋转调速器在外伸刚性臂上悬挂两个重量P的小球,初始 转动时角速度0,求当悬挂小球与垂直线夹角为时的角速度. 解:
P 初始转动时: L1 2 (a0 )a g
P 夹角为时: L2 2 (a l sin ) (a l sin ) g
vQ 0 2、当Q为固定点 ： LQ LO rQ p
rQC vQ 0
r // v Q 时 ： 3、当 QC
LO rQ p LQ
四、刚体的动量矩
１、平动刚体对任一固定点O的动量矩 LO ri mi vi mrc v rc p ２、定轴转动刚体对转轴的动量矩：
《理论力学Ⅰ》第八版课后习题解析
理论力学Ⅰ第 8 版课后习题答案目录：
第一章静力学公理和物体的受力分析
第二章平面力系
第三章空间力系
第四章摩擦
第五章点的运动学
第六章刚体的简单运动
第七章点的合成运动第
八章刚体的平面运动
第九章质点动力学的基本方程
第十章动量定理
第十一章动量矩定理
第十二章动能定理
第十三章达朗贝尔定理
第十四章虚位移定理
第一章
后面章节的课后答案请关注.微-.信.公众号：学糕
后面章节的课后答案请关注.微-.信.公众号：学糕
第二章
后面章节的课后答案请关注.微-.信.公众号：学糕
后面章节的课后答案请关注.微-.信.公众号：学糕
后面章节的课后答案请关注.微-.信.公众号：学糕
后面章节的课后答案请关注.微-.信.公众号：学糕
后面章节的课后答案请关注.微-.信.公众号：学糕
后面章节的课后答案请关注.微-.信.公众号：学糕
后面章节的课后答案请关注.微-.信.公众号：学糕。
理论力学(哈工大第八版)-教学课件-第12章
求:系统的运动微分方程。
解: s R
T
1
m
ds
2
2 dt
1 J d 2
2 dt
1 2
m
J R2
ds dt
2
ds
ds
P重力 mg dt , P弹性力 ks dt
dT dt P重力 P弹性力
2.势能
在势力场中,质点从点M运动到任意位置M0,有势力所 作的功为质点在点M相对于M0的势能.
V
M0 F dr
M
M0 M
Fxdx Fydy Fzdz
M 0称势能零点
（1）重力场中的势能
V
Z0 Z
mgdz
mg
z
z0
（2）弹性力场的势能
V
m2 ，纯滚动, 初始静止 ;θ ,M 为常力偶。
求:轮心C 走过路程S时的速度和加速度
解: 轮C与轮O共同作为一个质点系
W12 M m2gSsin
T1 0
T2
1 2
(m1R12 )12
1 2
m222
1 2
(1 2
m2
R2
2
)
2 2
1
C
R1
,2
C
R2
W12 T2 T1
第十二章 动 能 定 理
§12-1 力的功
一、常力在直线运动中的功
W
F
cos
s
F
理论力学精品课程第十二章 动量定理
第十二章 动量定理
3. 质点系动量守恒定律
dp dt
Fie
若作用于质点系的外力的主矢恒等于零， 质点系的动量保持不变。
pp0 恒矢量
dpx dt
Fx(e)
若作用于质点系的外力的主矢在某一轴上 的投影恒等于零，质点系的动量在该轴上的 投影保持不变。
px p0x 恒量
第十二章 动量定理
光滑台面
§12-1 动量与冲量
1动量
质点的动量 —— 质点的质量与质点速度的乘积
pmv
质点的动量是矢量，而且是定位矢量，它的方向与质点速 度的方向一致。其单位为 kg·m/s 或 N·s
质点系的动量 ——质点系中各质点动量的矢量和，称为质点 系的动量，又称为质点系 动量的主矢。
n
p mivi i 1
求： 转轴 O 处的约束力。
解：取杆为研究对象
aC t l; aC nl2
aC xaC t sinaC nco sl(sin2co )s aC yaC t co saC nsinl(co s2sin)
Fx(e) FOxmaCx Fy(e) FOymgmaCy
e 2
cost
yC
m2 m1 m2
e 2
s in t
由质心运动定理得:
Fx(e) Fx mx Fy(e) Fym1gm2gmy
Fx m2e2cost Fy (m1m2)gm2e2si nt
第十二章 动量定理
解法二：分析系统中各刚 体的运动
W。
求：风扇不致滑落的风扇底座与 台面之间的最小摩擦因数。
解：分析质量流的受力
考察刚要进入和刚刚排出的一段空气流，在Oxy坐标系中，空 气流所受叶片的约束力为FNx;这一段空气流都处于大气的包围之 中，两侧截面所受大气的总压力都近似为0。
理论力学目录
第一章静力学基础理论力学绪论§1-1 力和刚体§1-2 静力学公理§1-3 约束、约束类型§1-4 主动力，主动力分类§1-5 物体的受力分析，受力图§1-6 静力学计算机计算代码规定物体受力例题第二章力系的简化与合成§2-1 力对点的矩和力对轴的矩§2-2 基本力系----汇交力系和力偶系§2-3 力线平移定理§2-4 空间力系向一点简化，主矢和主矩§2-5 空间力系向一点简化结果分析第三章任意力系的平衡第四章静力学专题讨论第五章力系平衡条件下的计算机计算原理第六章点的运动学运动学引言§6-1 矢量法§6-2 直角坐标法§6-3 自然法§6-4 实例第七章刚体的简单运动§7-1 刚体的平行移动§7-2 刚体绕定轴的转动§7-3 转动刚体内各点的速度和加速度§7-4 轮系的传动比§7-5 矢量表示角速度和角加速度刚体简单运动例题第八章点的合成运动§8-1 相对运动.牵连运动.绝对运动§8-2 点的速度合成定理点的速度合成分析计算步骤：1. 选动点, 动坐标系2. 分析三种运动（绝对运动，相对运动，牵连运动），速度分析。
3. 速度合成定理: 建立动点速度的关系4. 计算速度§8-3 牵连动运动是平动时点的加速度合成定理加速度求解步骤1. 取动点，动系2.分析三种运动3. 速度分析4.加速度分析§8-4 牵连运动是转动时点的加速度合成定理. 科氏加速度第九章刚体的平面运动§9-1 刚体平面运动的概述和运动分解§9-2 求平面图形内各点速度的基点法§9-3 求平面图形内各点速度的瞬心法§9-4 用基点法求平面图形内各点的加速度§9-5 运动学综合应用举例§9-6 刚体绕平行轴转动的合成第十章运动构件系统分析和计算机计算§10-1 刚体一般运动概述§10-2 构件系统运动分析§10-3 构件系统运动计算机计算第十一章质点动力学基本方程§11-1 动力学的基本定律§11-2 质点的运动微分方程§11-3 质点动力学的两类基本问题质点动力学第一类基本问题例题质点动力学第二类基本问题例题§11-4 质点相对运动动力学的基本方程质点相对运动动力学问题例题第十二章动量定理§12-1 动量与冲量§12-2 动量定理§12-3 质心运动定理第十三章动量矩定量§13– 1 质点和质点系的动量矩§13– 2 动量矩定理§13– 3 刚体绕定轴的转动微分方程§13–4 刚体对轴的转动惯量§13–5 质点系相对于质心的动量矩定理§13-6 刚体的平面运动微分方程第十四章动能定理§14-1 力的功§14-2 质点和质点系的动能§14-3 动能定理§14-4 功率.功率方程.机械效率§14-5 势力场.势能.机械能守恒定律§14-6 普遍定理的综合应用举例第十五章碰撞(动力学专题)§15-1 碰撞现象碰撞力§15-2 普遍定理在碰撞过程的应用§15-3 恢复系数§15-4 碰撞问题举例§15-5 碰撞冲量对绕定轴转动刚体的作用撞击中心第十六章达朗贝尔原理§16-1 惯性力.质点的达朗贝尔原理§16-2 质点系的达朗贝尔原理§16-3 刚体惯性力系的简化§16-4 绕定轴转动刚体的轴承动反力第十七章虚位移原理§17-1 约束虚位移虚功§17-2 虚位移原理§17-3 自由度和广义坐标§17-4 以广义坐标表示的质点系平衡条件第十八章分析力学基础§18-1 自由度和广义坐标§18-2 以广义坐标表示的质点系平衡条件§18-3 动力学普遍方程§18-4拉格朗日方程第十九章机械振动基础§19-1 单自由度系统的自由振动§19-2 计算固有频率的能量法§19-3 单自由度系统的有阻尼自由振动§19-4 单自由度系统的无阻尼受迫振动§19-5 单自由度系统的有阻尼受迫振动§19-6 转子的临界转速§19-7 隔振。
理论力学 第六版部分习题答案 第12章
T=
m 2 2 2 ω l sin θ 6
12-5 自动弹射器如图 13-5a 放置，弹簧在未受力时的长度为 200 mm，恰好等于筒长。 欲使弹簧改变 10 mm，需力 2 N。如弹簧被压缩到 100 mm，然后让质量为 30 g 的小球自弹 射器中射出。求小球离开弹射器筒口时的速度。
Fk 30°
12-9 2 个质量均为 m2 的物体用绳连接，此绳跨过滑轮 O，如图 13-10 所示。在左方 物体上放有 1 带孔的薄圆板，而在右方物体上放有 2 个相同的圆板，圆板的质量均为 m1。 此质点系由静止开始运动，当右方物体和圆板落下距离 x1 时，重物通过 1 固定圆环板，而 其上质量为 2m1 的薄板则被搁住。摩擦和滑轮质量不计。如该重物继续下降了距离 x2 时速 度为零，求 x2 与 x1 的比。 解 第 1 阶段：系统由静止运动 x1 距离。由动能定理
12-6 平面机构由 2 匀质杆 AB，BO 组成，2 杆的质量均为 m，长度均为 l，在铅垂平 面内运动。在杆 AB 上作用 1 不变的力偶矩 M，从图 13-7a 所示位置由静止开始运动。不计 摩擦，求当杆端 A 即将碰到铰支座 O 时杆端 A 的速度。
P
P
θ
B vB
ω AB
vB vC vA
(c)
即
1 (2m1 g + m2 g ) x1 − (m1 g + m2 g ) x1 = (3m1 + 2m2 )v 2 2 1 （1） m1 gx1 = (3m1 + 2m2 )v 2 2 m2 gx2 − (m1 g + m2 g ) x2 = 0 − 1 (m1 + 2m2 )v 2 2
（2）
图 13-10
理论力学(盛冬发)课后习题答案ch12
理论力学(盛冬发)课后习题答案ch12|第12章动能定理.143.第12章动能定理1，真或假问题(括号内正确打勾，错误打勾“*”)1。
当一个圆形车轮纯滚动时，与地面接触点的法向约束力和滑动摩擦力不起作用。
(√) 2。
理想约束的约束反力所做的功之和等于零(√) 3。
因为粒子系统中的内力成对出现，所以内力功的代数和等于零(×) 4。
弹簧压缩了10厘米，从原来的长度延长了10厘米，弹簧力也同样起作用。
(√) 5。
粒子系统动能的变化与作用在粒子系统上的外力有关，而与内力无关。
(×) 6。
如果相同质量的三个粒子以相同的初始速度从相同的高度向上、水平和向下抛向地面，这三个粒子将以相同的速度落到地面。
(√)7。
动能定理的方程是向量(×) 8。
弹簧从其自然位置拉长10厘米，再拉长10厘米。
在这两个过程中，弹力的作用是相等的。
(x) 2。
填写问题1。
当一个粒子刚刚在一个垂直平面上转动一次，它的重力做功是02.在理想约束条件下，约束反力所做功的代数和为零3。
如图12.19所示，质量为m1的均质杆OA的一端铰接在质量为m2的均质圆形车轮的车轮中心，另一端位于水平面上。
圆形的轮子在地上滚动。
如果车轮中心的速度是vo，系统的动能t？1322m1v0？M2v0244..圆轮的一端连接一个刚度系数为K的弹簧，另一端连接一个重量为P的重物，如图12.201所示最初，春天自然很长。
当重量降到h时，系统的总功w？博士？kh22 o VO a k p h图12.19图12.205。
如图12.21所示，滑块a和滑块BC之间的摩擦力是系统的内力。
假设已知的摩擦力是f，等于一个常数，曲柄每转一周的摩擦力功是？4Fr6。
平行四边形机构如图12.22，O1A？O2B？R，O1A//O2B，以角速度转动O1A？5次旋转如果所有的棒都是同质的，质量是m，那么动能T =mr2？26. 143 .. 144 .理论力学7。
理论力学第十二章 动量矩定理 教学PPT解析
平面内力对点的矩：
z
B
Mz(F) = xFy yFx
MO (mv)
mv
和平面内力对点的矩相似，可
以得到质点动量mv在Oxy平面内 的投影(mv)xy对点O（z轴）的矩
rA
y
O
B
Mz(mv) = (xmvy ymvx) x
(mv)xy A
Mz(mv) = m (xvy yvx)
质点的动量矩
对点的动量矩与对轴的动量矩之间的关系
质点对点O的动量矩矢在z轴上的投影，等于质点 对z轴的动量矩，即：
[Mo (mv)]z M z (mv)
Mo F z Mz F
质点对轴的动量矩是代数量。
质点对点O的动量矩与对z轴的动量矩二者的关系， 同力对点的矩与力对轴的矩的关系相似。
在国际单位制中,动量矩的常用单位是 N • m • s
质点系的动量矩
z
Iz M
回转半径：设想将刚体的质量集中在与 转轴距离为z 处，则此集中质量对转轴 的转动惯量与刚体对转轴的转动惯量相 同。
转动惯量
转动惯量的平行轴定理
刚体对任一轴的转动惯量等于刚体对过质心且与该轴 平行的轴的转动惯量加上刚体质量与两轴之间距离平方 的乘积 记为
说明
J z J Z M d2
由转动惯量的平行轴定理和转动惯量叠加定理，可以 快捷的的求出由几个简单图形组合而成的刚体对任意轴的 转动惯量。有空心刚体=无空心整体-空心部分 (转动惯量）
绕定轴转动刚体的动量矩
Mz(mv) = mrz rz = mrz2
从而整个刚体对轴 z 的动量矩
Lz = ∑mz(mv) = ∑m量矩,等于这刚体对该轴的转动惯 量与角速度的乘积。
例题
理论力学 第十二章
2 ρz = R 5
3 3 2 2 (4r +l ) 80
ρx = ρy
=
π 2 rl 3
圆环
3 2 ρz = R2 + r2 2π2r2R Jz = m(R2 + r ) 4 4
3
椭圆形 薄板
m 2 2 (a +b ) 1 ρz = a2 +b2 4 2 m a Jy = a2 ρx = 4 2 b m 2 ρy = Jy = b 2 4 Jz =
回转半径（惯性半径） 2. 回转半径（惯性半径）
Jz ρz = m
或
Jz = m z ρ2
3．平行轴定理
Jz = JzC +m d 轴平行的轴， 式中 zC轴为过质心且与 z轴平行的轴，d 为 z
2
与 zC 轴之间的距离。 轴之间的距离。 即：刚体对于任一轴的转动惯量，等于刚体对于通过 刚体对于任一轴的转动惯量， 质心并与该轴平行的轴的转动惯量， 质心并与该轴平行的轴的转动惯量，加上刚体的质量 与两轴间距离平方的乘积. 与两轴间距离平方的乘积.
m ,初始角速度 ω0 。
θ 角时的
ω.
解：
θ = 0 时, Lz1 = 2maω0a = 2ma2ω0
θ ≠0
时,
Lz2 = 2m(a +l sin θ)2ω
a2ω0 ω= 2 (a +l sin θ)
Lz1 = Lz2
§12-3 刚体绕定轴的转动微分方程 12主动力: 主动力:
F, F ,⋯ , F ⋯ n 1 2
v dv 由 ω= = a ,得 R dt
M − mgR2 sin θ R a= J + mR2
例12-2：已知 12求:（1） α
C·A上传 【理论力学】第十二章 达朗伯原理
质点的达朗伯原理
r r r r FI m = F +F a N M r r r r FN r 改写上式 F + F + (m ) = 0 a N r F ma r r 令 质点的惯性力 假想地) 引进 FI = ma —— 质点的惯性力 (假想地)
方向: 惯性力的大小: 惯性力的大小: F = ma 方向: 与加速度相反 I 惯性力不是真实的力,没有作用在质点 质点上 惯性力不是真实的力,没有作用在质点上. 设质量为m的质点 在主动力 和约束反力F 的作用下运动. 设质量为 的质点M在主动力 和约束反力 N的作用下运动. 的质点 在主动力F和约束反力
方法三: 方法三:
应用动能定理 和质心运动定理
L 1 2 FI = mα , M IA = mL α 2 3 L L ∑M2 = 0 M IA mg 2 = 0 A
∑ ∑ Fx = 0
y
Fx = 0 Fy mg + FI = 0
L J Aα = mg 2 maCx = Fx
1 d( J Aω2 ) = mg vCdt 2 maCx = Fx
v v FI) = mac
y
惯性力主矩: 质心C简化: 惯性力主矩: 向质心C简化: v v v v M C ( FI ) = ∑M C ( FIi )
z
d v v v v v = ∑ ( ρ i × mi v i ) + ∑ (v i v c ) × mi v i dt v v v v v ∑ρi × mi vi = LC Q∑vi ×mivi = 0 v v v v vv v v v 惯性力主矢与简化 dLC vC FI) = mac× ∑mi vi = vC × mvC = 0 MC (FI ) = 中心的选择无关 dt
理论力学 12-h
3. 平行移轴定理 同一个刚体对不同轴的转动惯量一般是不相同的。
J z J zC md
2
刚体对某轴的转动惯量，等于刚体对于通过质心且与该轴平 行的轴的转动惯量，加上刚体的质量与两轴间距离的平方的乘积。
刚体对通过质心轴的转动惯量具有最小值。 [例:] z zC
O x
J ZC
l/2
l
l 2 J Z m( ) 2 1 ml 2 9 12
mivi
O
LO J O
17
[例 ]
O
l
1 2 LO J O ml 3
18
[例 ]
已知：均质杆的质量为m，均质圆盘的质量为2m， 求物体对于O轴的转动惯量和动量矩。 解： J O J O杆 J O盘 [ 1 ml 2 m( R l ) 2 ] 1 2mR 2 12 2 2
24
2．质点系的动量矩定理
设质点系有n个质点，作用于每个质点的力分为 内力 Fi ( i )
和外力 Fi ( e ) ，由质点动量矩定理：
d M O (mi vi ) M O ( Fi (i ) ) M O ( Fi (e) ) dt
共有n个方程，相加后得： 0 d (i ) (e) M ( m v ) M ( F ) M ( F dt O i i O i O i )
质点系相对于质心的动量矩定理
刚体的平面运动微分方程
习题课
3
§12-4 刚体对轴的转动惯量
z 一．定义：
J z mi ri
2
JZ 称为刚体对z 轴的转动惯量 若刚体的质量是连续分布，则 ri mi vi
J z m r 2dm
理论力学12-2-d9c
n n
i 1
i 1
i 1
i 1
i 1
n
mi rCi 0
(9-43)
质心运动守恒的系 统，各刚体质心的 位移之间的关系
9
若外力系的主矢在固连于惯性参考空间的固定坐标 轴如x轴上的投影为零，即e 0 ,且初始时系统质 FRx 心速度在该轴上的投影等于零，则
动量定理的投影式 向固连于惯性参考空间的固定坐标轴如x轴上投影， 得到相应的投影式：
e d p x d px FRx d t
(9-34)
(9-35)
2
p2 x p1x I x
e
4.质点系的动量守恒定律
若质点系的外力系的主矢 由此得到 则质点系的动量守恒：
e d p FR d t 0
2
x
Fy m1 g m2 g m2e cos t
2
(2) 若电动机不固定，求电动机的运动： 若电动机没有螺栓固定，因系统所受外力在水平方向投影为零， 且初始静止，故系统质心在水平方向运动守恒。 设转子转过 角时，定子向左移动 s ，则
m1s m2 ( s e sin ) 0 n ( ) aC2 aC1 aC2C1 aC1 s
n
n
n
i 1
n
mi xCi 0 (9-46)
在x方向上质心运动守恒的 系统，各刚体质心在x方向 上的位移满足的关系
10
以上结论均称为质心运动的守恒定律。
例 题 9-5
§9
动量原理
已知AB=l ,质量为m ；平板DE的质量为2m ，水平面 光滑， 初始系统静止 。求AB倒至 60 角时DE的 位移x和速度v 。 B
理论力学(盛冬发)课后习题答案ch12
·143·第12章 动能定理一、是非题(正确的在括号内打“√”、错误的打“×”)1．圆轮纯滚动时，与地面接触点的法向约束力和滑动摩擦力均不做功。
( √ ) 2．理想约束的约束反力做功之和恒等于零。
( √ ) 3．由于质点系中的内力成对出现，所以内力的功的代数和恒等于零。
( × ) 4．弹簧从原长压缩10cm 和拉长10cm ，弹簧力做功相等。
( √ ) 5．质点系动能的变化与作用在质点系上的外力有关，与内力无关。
( × ) 6．三个质量相同的质点，从距地相同的高度上，以相同的初速度，一个向上抛出，一个水平抛出，一个向下抛出，则三质点落地时的速度相等。
( √ )7．动能定理的方程是矢量式。
( × ) 8．弹簧由其自然位置拉长10cm ，再拉长10cm ，在这两个过程中弹力做功相等。
( × ) 二、填空题1．当质点在铅垂平面内恰好转过一周时，其重力所做的功为 0 。
2．在理想约束的条件下，约束反力所做的功的代数和为零。
3．如图12.19所示，质量为1m 的均质杆OA ，一端铰接在质量为2m 的均质圆轮的轮心，另一端放在水平面上，圆轮在地面上做纯滚动，若轮心的速度为o v ，则系统的动能=T222014321v m v m +。
4．圆轮的一端连接弹簧，其刚度系数为k ，另一端连接一重量为P 的重物，如图12.20所示。
初始时弹簧为自然长，当重物下降为h 时，系统的总功=W 21kh Ph -。
图12.19 图12.205．如图12.21所示的曲柄连杆机构，滑块A 与滑道BC 之间的摩擦力是系统的内力，设已知摩擦力为F 且等于常数，则曲柄转一周摩擦力的功为Fr 4-。
6．平行四边形机构如图12.22所示，r B O A O ==21，B O A O 21//，曲柄A O 1以角速度ω转动。
设各杆都是均质杆，质量均为m ，则系统的动能T =2265ωmr 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
MIC=∑MC(FIi) =∑ri×ቤተ መጻሕፍቲ ባይዱ– mi a) = – (∑ mi ri)×a = – mrC×a = 0
■ 定轴转动
仅考虑工程中常见的具有垂直于转轴z的质量对 称平面S的简单情况。首先将惯性力系简化为对称 平面S内的平面力系,然后再向z轴与S的交点O简化。 因为
∑Mz(FIin) = 0
mi
上式表明, 无论刚体作什么运动,惯性力系的主矢 都等于刚体质量与质心加速度的乘积, 方向与质 心加速度方向相反。
二、 惯性力系的主矩
一般说来,刚体惯性力系的主矩既与刚体的运 动形式有关,又与简化中心的位置有关。下面仅 就最常见的三种刚体运动形式进行讨论。
■ 平动
向质心简化。设刚体的平动加速度为a , 质元 mi 相对于质心的矢径为ri , 于是可得
14.2 质点系的动静法
考虑由n个质点组成的质点系,对其中每个质点 应用达朗贝尔原理得
Fi +FNi +FIi = 0
式中
i=1,2, …,n
FIi =－miai
将这样n个形式上的平衡力系加在一起仍然是一 个平衡力系,根据平衡条件可得
∑(Fi +FNi +FIi) = 0 ∑MO(Fi) +∑MO(FNi) +∑MO(FIi) = 0
理论力学
欢 迎 光 临
第12章
动静法
动静法提供了一个研究非自由质点系动力学 问题的普遍方法,在工程力学中有极其广泛的应 用。
该方法的特点是在引入虚加惯性力之后 , 用 静力学中研究平衡问题的方法来处理动力学中 不平衡的问题，故称动静法。
12.1 质点的动静法
由牛顿第二定律有 F +FN = ma FI = ma 令 ——惯性力 则上式可写成 F +FN +FI = 0 上式表明，如果在质点上除作用有主动力及约束力 外,再假想地加上惯性力,则这些力在形式上构成平 衡力系。这就是质点的达朗贝尔原理。 这种在加速运动的质点上虚加一个惯性力,而把动 力学问题在形式上转化为静力学问题的方法称为动 静法。
×
×
×
×
×
2. 直角形刚性杆OAB中均质杆AB的质量为m, OA的 质量不计, AB=2R, OA=R。图示瞬时绕O轴转动的角 速度与角加速度分别为ω与, 试求AB的惯性力系向 O点简化的结果。
FIR maC
n n
MIO
F IR
F IR
M IO
t
a Cn
n
2mR
t
2
a Ct
FIR maC
FI M F a
FR
FN
动静法的优点在单个质点的动力学问题中是难于 体现的,它主要表现在非自由质点系特别是刚体的动 力学问题中。 F = -ma
■ 关于惯性力的慨念
F' = -F = -ma
F F' a FI
I
关于惯性力的慨念
如果就研究对象本身而言,惯性力显得是虚加的, 但确有方向与a相反，大小等于ma的力存在，它作 用在使质点运动状态（速度v）发生改变的物体上。
ai = aC + aiCn + aiCt
对应的惯性力可表示为
t
FIi =
显然
FIiC
+
FIin
+ FIi
C
F Ii F Ii
C t
aC
aiCn
mi
F Ii
n
S
aC
∑MC(FIin) = 0
aiCt
而
∑MC(FIiC ) = ∑ri×(– mi aC) = – (∑ miri )×aC = – mrC×aC = 0 MIC =∑MC(FIit) = –∑ri (miaiCt ) = = – (∑mi ri2) = – JC
a O
B
C
FIB k
FIA = m2a FIB = m1a
FIA a
A α
M IC 1 2 m1r
2
a r
1 2
m1ra
8. 图示飞轮由于安装的误差,其质心不在转动轴 上。若飞轮质量为m,偏心距为e,飞轮以匀转速ω 转动,试求轴承A处的附加动反力。
l
l
解: 飞轮静止时,由静载荷引起的轴承的反力称为 静反力,即
14.3 刚体惯性力系的简化
将质点系的动静法用于刚体时 , 由于惯性力是 体积力 , 在每个质点上虚加惯性力实际上是不可 行的。为此 , 需要研究刚体惯性力系的简化。用 惯性力系的主矢和向某一点简化的主矩来代替与 之等效的惯性力系。
一、 惯性力系的主矢 FIR=∑FIi =－∑miai ∑miai = maC FIR=－maC
静平衡的刚体在转动时,是否还可能产生附 加动反力呢?
FI2
FNA FNB FI1
为了消除附加动反力,除了要求静平衡之外, 还要求惯性力系在通过转轴的平面内的惯性力 系的主矩(惯性力偶矩)也等于零,即惯性力系自 成平衡力系。这种现象称为动平衡。
怎样才能使旋转的物体达到动平衡呢？
研究表明，当旋转轴为刚体（或质点系）质 量的对称轴，轴承的动反力为零；这样的轴被 称为中心惯性主轴。所以动反力为零的充分与 必要条件是：刚体的转轴是中心惯性主轴。 动平衡的刚体一定是静平衡的，静平衡的刚 体不一定是动平衡的。 工程中为消除高速旋转刚体的附加动反力， 必须先使其静平衡，即把质心调整到转轴上， 然后再通过增加或减少某些部位的质量使其动 平衡，动平衡一般在动平衡机上进行。
习题: P.349 12-2, 12- 4, 12- 5
F'NA = F'NB = mg / 2
当飞轮匀速转动时,虚加惯性力如图示,其大小为
FIR = maC = meω2
由惯性力所引起的 轴承附加反力称为 动反力:
FIR aC FNA
l
F''NA=F''NB = meω2/2
mg
l
FNB
在高速转动的情况下,那怕是极小的偏心距, 也可能产生相当大的附加动反力,造成各种严重 的后果。 为了消除轴承的附加动反力, 首先应当消除 转动刚体的偏心现象,使刚体的质心位于转轴的 轴线上。这样,因为惯性力系的主矢等于零,由它 所引起的附加动反力也将等于零。没有偏心距 的刚体,若仅受重力作用,则不论刚体转到什么位 置,它都能保持静止。这种情况称为静平衡。
由此可见, 当一非自由质点系运动时, 作用于质 点系的主动力系、约束力系和质点系的惯性力系, 每一瞬时在形式上构成一个平衡力系。上述结论 称为质点系的达朗贝尔原理。在使用中应注意以 下几点: 1. 主动力系和约束力系中的内力不要计入; 2. 这里所谓的平衡仅仅是形式上的, 实质上动静法中 的平衡方程仍然表示质点系的运动和受力之间的 关系; 3. 实际应用中, 矢量方程可投影于直角坐标系或自然 轴系,类似于静力学中平衡方程的应用。
FIR
刚体定轴转动的几种特殊情况：
（1）点O与点C重合， 0 因 aC 0 所以
F IR Ma M
Iz
质量对称平面
aC C MIz
C
0
J C
（2）点O与点C不重合，
n
0
2
O
FIR
F IR M a C M a C mr C n
故有
C
F Ii F Ii
C t
aC aC
aiCn
mi
F Ii
n
S
式中JC是刚体对于通过质心C 且⊥质量对称平面S的轴的转 动惯量。
aiCt
三、 刚体惯性力系的简化结果
■ 平动
FIR=－maC
■ 定轴转动 FIR=－maC
作用线通过转轴O。
作用于质心C
质量对称平面
aC C
O
MIz=－JZ
MIz
O
MIz =∑Mz (FIit) = –∑ri (miait ) (∑mi ri2) = – Jz
F Ii
t
ain
n
S
=–
F Ii
ait
负号表示主矩MIz与角加速度的转向相反。
■ 平面运动
只考虑平面图形S为质量对称平面的情况。首 先将惯性力系简化为对称平面S内的平面力系,然 后再向质心C简化。取C为基点,则质元mi的加速 度可表示为
t
2mR
7 1 2 2 2 J O m(2 R) m( 2 R) mR 3 12
3. 如图示, 半径为r, 质量为m1的均质圆盘B沿水 平面纯滚;重物A质量为m2, 加速度为a, 滑轮质量 不计。试求A和B的惯性力系简化结果,并在图中 画出。
MIC
M
Iz
0
（3）点O与点C重合， 0
F IR M a C 0
M
Iz
0
■ 平面运动
FIR=－maC
作用线通过质心C。
质量对称平面
MIC
C
MIC =－JC
FIR
aC
S
1. 均质杆OA绕O轴在 铅垂平面内作定轴转动其 角速度为ω,角加速度为, 如图所示。在下面所画的 刚体惯性力系简化图中, 哪一个是正确的?