全等三角形知识树
(完整版)全等三角形知识点梳理,推荐文档

(完整版)全等三角形知识点梳理,推荐文档第十二章全等三角形2018.9 杨1.全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边.对应边相等。
2.全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角.对应角相等。
证明三角形全等基本思路:三角形全等的判定(1)三边分别相等的两个三角形全等,简写成边边边或SSS .1.如图,AB =AD ,CB =CD ,求证:(1)△ABC≌△ADC;(2)∠B =∠D.证明:(1)中,2.已知在四边形ABCD 中,AB=CD,AD=BC,,求证AD//BC做辅助线,连接AC ,利用SSS 证明全等,得到∠DAC=∠ACB ,从而证明平行三角形全等的判定(2)两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).两边和其中一边的对角对应相等的两个三角形不一定全等.1.如图,将两个一大、一小的等腰直角三角尺拼接(A ,B ,D 三点共线,AB =CB ,EB =DB ,∠ABC=∠EBD=90°),连接AE ,CD ,试确定AE 与CD 的关系,并证明你的结论.解:结论:AE =CD ,AE⊥CD.证明:延长AE 交CD 于F ,在△ABE 与△CBD 中,{AB =CB ,∠ABE =∠CBD ,BE =BD ,)∴△ABE≌△CBD(SAS ),∴AE=CD ,∠EAB=∠DCB,∵∠DCB+∠CDB=90°,∴∠EAB+∠CDB=90°,∴∠AFD=90°,∴AE⊥CD.2.在△ABC 和△CDE 中,CA=CB,CD=CE,∠ACB=∠DCE=90°,AE 与BD 交与点F (1)求证:△ACE≌△BCD(2)求证:AE⊥BD1,利用SAS 证明全等,AC=BC DC=EC ∠BCD=∠ACE2,全等得到角相等∠CAE=∠DCB∠CAB+∠EAB+∠ABC=90°∠DCB∠EAB+∠ABC=90°三角形全等的判定(3)两角和它们的夹边分别对应相等的两个三角形全等,简称角边角或ASA .两个角和其中一个角的对边分别相等的两个三角形全等,简称角角边或AAS .求证:三角形一边的两端点到这边的中线或中线延长线的距离相等.如图,AD 为△ABC 的中线,且CF⊥AD 于点F ,BE⊥AD,交AD 的延长线于点E ,求证:BE =CF.证法1:∵AD 为△ABC 的中线,∴BD=CD.∵BE⊥AD,CF⊥AD,∴∠BED=∠CFD=90°.在△BED 与△CFD 中{∠BED =∠CFD ,∠BDE =∠CDF ,BD =CD ,)F∴△BED≌△CFD(AAS ),∴BE=CF.证法2:∵S △ABD =AD·BE ,S △ACD =AD·C F ,1212且S △ABD =S △ACD (等底同高的两个三角形面积相等),∴AD·BE =AD·CF ,∴BE=CF.1212三角形全等的判定(4)斜边和一条直角边分别对应相等的两个直角三角形全等,简称“斜边、直角边”或“HL ”.如图,E ,F 分别为线段AC 上的两点,且DE⊥AC 于点E ,BF⊥AC 于点F ,若AB =CD ,AE =CF ,BD 交AC 于点M. 求证:BM =DM ,ME =MF.证明:∵AE=CF ,∴AE+EF =CF +EF∴AF=CE.在Rt △ABF与Rt △CDE 中{AB =CD ,AF =CE ,)∴Rt △ABF≌Rt △CDE(HL ),∴BF=DE.∵DE⊥AC,BF⊥AC,∴∠DEM=∠BFM=90°.在△BFM 与△DEM 中{∠BFM =∠DEM ,∠BMF =∠DME ,BF =DE ,)∴△BFM≌△DEM(AAS ),∴BM=DM ,ME =MF.角的平分线的性质角平分线的性质:角的平分线上的点到角的两边的距离相等.文字命题的证明方法:a .明确命题中的已知和求证;b .根据题意,画出图形,并用数学符号表示已知和求证;c .经过分析,找出由已知推出要证的结论的途径,写出证明过程.方法总结:(1)角平分线的性质是证明线段相等的另一途径.(2)在已知角平分线的条件下,也可想到翻折构造全等的方法.角平分线的性质是证线段相等的常用方法之一,角平分线的性质与判定通常是交叉使用,作角的平分线或过角的平分线上一点作角两边的垂线段是常用的辅助线.1.在△ABC 中,AD 是△ABC 的角平分线,E ,F 分别是AB ,AC 上一点,并且有∠EDF+∠EAF=180°.试判断DE 和DF的大小关系并说明理由.建议收藏下载本文,以便随时学习!解:结论:DE =DF.证明:过点D 作DG⊥AB 于点G ,作DH⊥AC 于点C ,∵AD 是△ABC 的角平分线,∴DG=DH.∵∠DGA=∠DHA=90°,∴∠GDH+∠BAC=180°,∵∠EDF+∠EAF=180°,∴∠GDH=∠EDF,∴∠GDH-∠EDH=∠EDF-∠EDH,∴∠GDE=∠FDH.在△DGE 与△DHF 中,{∠DGE =∠DHF =90°,DG =DH ,∠GDE =∠HDF ,)∴△DGE≌△DHF(ASA ),∴DE=DF 2.如图,在△ABC 中,D 是BC 边上一点,连接AD ,过点B 作BE ⊥AD 于点E ,过点C 作CF ⊥AD 交AD 的延长线于点F ,且BE =CF.求证:AD 是△ABC 的中线.利用AAS 证明全等∠BDE=∠F∠BDE=∠CDFBE=CF利用全等证明垂直此类题目中必有垂直,利用垂直角度和是90°,再根据全等转换一个角,达到另外的两个角度和是90°,得到第三个角是90°,进一步证明线的垂直关系。
全等三角形知识树PPT25页

31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
全等三角形知识树
1、纪律是管理关系的形式。——阿法 纳西耶 夫 2、改革如果不讲纪律,就难以成功。
3、道德行为训练,不是通过语言影响 ,而是 让儿童 练习良 好道德 行为, 克服懒 惰、轻 率、ቤተ መጻሕፍቲ ባይዱ 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸 美纽斯
5、教导儿童服从真理、服从集体,养 成儿童 自觉的 纪律性 ,这是 儿童道 德教育 最重要 的部分 。—— 陈鹤琴
全等三角形知识点

全等三角形知识点摘要:全等三角形是初中数学中的一个重要概念,它指的是两个三角形在形状和大小完全相同的情况下,它们的对应边和对应角完全相等。
本文将详细介绍全等三角形的定义、性质、判定条件以及在几何题中的应用。
关键词:全等三角形、对应边、对应角、判定条件、几何应用1. 全等三角形的定义全等三角形(Congruent Triangles)指的是两个三角形在几何形状和大小上完全相同,即它们的所有对应边和对应角都相等。
在数学符号中,我们通常用“≌”来表示全等。
2. 全等三角形的性质全等三角形具有以下性质:- 对应边相等:两个全等三角形的对应边长度完全相同。
- 对应角相等:两个全等三角形的对应角度数完全相同。
- 对应边上的高相等:两个全等三角形对应边上的高(垂直于边的线段)长度也相等。
- 对应角的平分线相等:两个全等三角形对应角的角平分线长度相等。
- 对应边上的中线相等:两个全等三角形对应边上的中线(连接顶点和对边中点的线段)长度相等。
3. 全等三角形的判定条件要判定两个三角形是否全等,可以通过以下几种条件:- SSS(边边边):如果两个三角形的三边分别相等,那么这两个三角形全等。
- SAS(边角边):如果两个三角形有两边及它们的夹角分别相等,那么这两个三角形全等。
- ASA(角边角):如果两个三角形有两角及它们之间的边分别相等,那么这两个三角形全等。
- AAS(角角边):如果两个三角形有两角及其中一角的对边分别相等,那么这两个三角形全等。
- HL(直角边-直角边):对于直角三角形,如果斜边和一条直角边分别相等,那么这两个三角形全等。
4. 全等三角形在几何题中的应用全等三角形的概念在解决几何问题时非常有用,尤其是在涉及角度和长度计算的问题中。
通过识别和证明三角形全等,我们可以得出隐藏的边长和角度关系,从而解决复杂的几何构造问题。
5. 结论全等三角形是几何学中的一个基础概念,它在解决几何问题中扮演着关键角色。
第12章全等三角形【教材知识点总结】
一、全等三角形
1.全等形
能够完全重合的两个图形叫做全等形. 2.全等三角形的相关概念及表示方法 (1)相关概念
①能够完全重合的两个三角形叫做全等三角形.
②把两个全等的三角形重合在一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角. (2)表示方法
全等符号:≅,读作:“全等于”.
ABC ∆与DEF ∆全等,记作:DEF ABC ∆≅∆,读作:
“三角形ABC 全等于三角形DEF ” 3.全等三角形的性质
全等三角形的对应边相等,全等三角形的对应角相等.
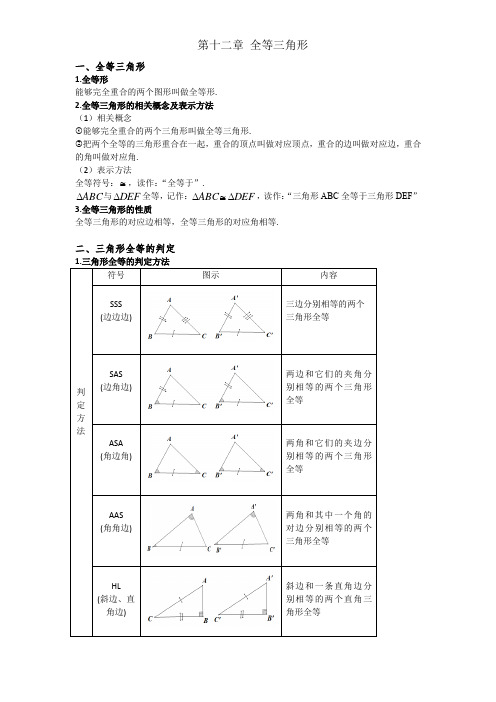
二、三角形全等的判定
第十二章 全等三角形
2.合理选择全等三角形的判定方法
已知两边⎪⎩
⎪
⎨⎧
已知一边一角⎪⎩
⎪
⎨⎧
三、角的平分线的性质 1.角的平分线的性质
角的平分线上的点到角的两边的距离相等. 2.角的平分线的判定
角的内部到角的两边的距离相等的点在角的平分线上.
找夹角→SAS 找第三边→SSS
找直角→HL 边为角的对边→找任一角→ASA 边为角的邻边→⎪⎩⎪⎨⎧ 找夹角的另一边→SAS 找夹角的另一角→ASA 找边的对角→AAS。
全等三角形知识点总结

全等三角形对应边相等,对应角相等全等形全等三角形解决问题边边边,边角边,角边角, 角角边,斜边、直角边二、 知识概念: 1.基本定义:(1)全等形:能够完全重合的两个图形叫做全等形.(2)全等三角形:能够完全重合的两个三角形叫做全等三角形. (注意对应的顶 点写在对应的位置上)(3)对应顶点:全等三角形中互相重合的顶点叫做对应顶点. (4)对应边:全等三角形中互相重合的边叫做对应边. (5)对应角:全等三角形中互相重合的角叫做对应角.夹边就是三角形中相邻两角的公共边,夹角就是三角形中有公共端点的两边所成的角。
两个三角形的形状、大小、都一样时,其中一个可以经过平移、旋转、对称等运动(或称变 换)使之与另一个重合, 一个三角形经过平移、翻折、旋转可以得到它的全等形。
2、 全等三角形的性质和表示性质:(1):全等三角形的对应边相等、对应角相等。
(2):全等三角形的周长相等、面积相等。
(3):全等三角形的对应边上的对应中线、角平分线、高线分别相等。
表示:全等用符号“≌”表示,读作“全等于”。
如△ABC ≌△DEF, 读作“三角形 ABC 全等于三角形 DEF”。
注:记两个全等三角形时,通常把表示对应顶点的字母写在对应的位置上。
3.全等三角形的判定定理:一、知识框架:等边三角形作图形的对称轴用坐标表示轴对称作轴对称图形轴对称变换生活中的对称等腰三角形轴对称(1)边边边 (SSS): 三边对应相等的两个三角形全等.(2)边角边 (SAS): 两边和它们的夹角对应相等的两个三角形全等.(3)角边角 (ASA): 两角和它们的夹边对应相等的两个三角形全等.(4)角角边 (AAS): 两角和其中一个角的对边对应相等的两个三角形全等.(5)斜边、直角边 (HL): 斜边和一条直角边对应相等的两个直角三角形全等.(只适用于两个直角三角形)4、学习全等三角形应注意以下几个问题:(1):要正确区分"对应边"与“对边”,"对应角”与“对角”的不同含义;(2):表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;(3):“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等;(4):时刻注意图形中的隐含条件,如“公共角”、“公共边”、“对顶角”5、全等变换只改变图形的位置,二不改变其形状大小的图形变换叫做全等变换。
全等三角形的知识点梳理

全等三角形的知识点梳理全等三角形一、结构梳理概念:全等:两个能够完全重合的图形称为全等图形,全等图形的形状和大小都相同。
全等三角形特征:形:能够完全重合的两个三角形叫全等三角形。
特例全等三角形。
全等三角形条件。
画三角形。
二、知识梳理一)概念梳理1.全等图形:两个能够完全重合的图形称为全等图形,全等图形的形状和大小都相同。
2.全等三角形:能够完全重合的两个三角形叫全等三角形。
符号“≌”表示图形大小和形状都相等。
二)性质与判定梳理1.全等图形性质:全等多边形的对应边、对应角分别相等。
全等三角形的对应边、对应角分别相等。
2.全等三角形的判定:判断两个三角形全等的方法有:1)三边对应相等的两个三角形全等,XXX为:SSS;2)两角和它们的夹边对应相等的两个三角形全等,XXX 为:ASA;3)两角和其中一角的对边对应相等的两个三角形全等,XXX为:AAS;4)两边和它们的夹角对应相等的两个三角形全等,XXX 为:SAS。
若是直角三角形,则还有斜边、直角边公理(HL)。
判断三角形全等的基本思路:要判定两个三角形全等,需要知道这两个三角形分别有三个元素(其中至少一个元素是边)对应相等,这样就可以利用题目中的已知边(角)去迅速准确地确定要补充的边(角),从而得到判定两个三角形全等的思路。
例如:已知两边,找另一边:SSS。
已知边为角的对边,找任一角:AAS。
已知两角,找任一边:ASA。
已知一边一角,找这条边上的对角:AAS。
边就是角的一条边,找该角的另一边:SAS。
找两角的夹边:ASA。
何格式错误,删除明显有问题的段落,改写如下。
学会辨认全等三角形的对应元素是很重要的。
方法是先找出全等三角形的对应顶点,再确定对应角和对应边。
例如,如果已知△ABC≌EFD,则A与E、B与F、C与D对应,因此三角形的边AB与EF、BC与FD、AC与ED对应。
对应边所夹的角就是对应角。
此外,还有如下规律:(1)全等三角形的公共边是对应边,公共角是对应角,对顶角是对应角;(2)全等三角形的两个对应角所夹的边是对应边,两条对应边所夹的角是对应角。
数学第七章三角形知识树
全等三角形
定义
两个三角形能够完全重合,则这两个三角形全等。
性质
全等三角形的对应边相等,对应角相等。
应用
利用全等三角形的性质解决实际问题,如几何证明、计算等。
证明方法
角边角(ASA)
两个角及一边分别相等,则两三角形全等。
边边边(SSS)
三边分别相等,则两三角形全等。
边角边(SAS)
两边及夹角分别相等,则两三角形全等。
面积公式
三角形面积公式
面积 = (底 × 高) ÷ 2
特殊三角形面积公式
直角三角形面积 = (底 × 高) ÷ 2,等边三角形面积 = (√3/4 × 底 ^2) ÷ 2
任意三角形面积公式
通过底和高计算,也可以通过底和对应的高计算。
面积的推导
1 2
通过相似三角形推导
利用相似三角形的性质,将任意三角形转化为等 腰三角形或直角三角形,再利用已知的面积公式 计算。
勾股定理
总结词
证明方法
勾股定理描述了直角三角形三边之间 的关系。
勾股定理有多种证明方法,其中最常 用的是利用相似三角形的性质进行证 明。
详细描述
勾股定理指出,在一个直角三角形中, 直角边的平方和等于斜边的平方。即, 如果直角边为a和b,斜边为c,则 a^2 + b^2 = c^2。
04
三角形的面积计算
通过底和高的关系推导
利用三角形的底和高之间的关系,推导出面积公 式。
3
通过割补法推导
通过将三角形割补成其他图形,利用其他图形的 面积公式推导出三角形的面积公式。
面积的应用
解决实际问题
01
利用三角形面积公式解决实际问题,如土地测量、建筑规划等。
八年级上册数学第十二章 全等三角形 知识点总结
第十二章全等三角形
一、知识框架:
二、知识概念:
1.基本定义:
⑴全等形:能够完全重合的两个图形叫做全等形.
⑵全等三角形:能够完全重合的两个三角形叫做全等三角形.
⑶对应顶点:全等三角形中互相重合的顶点叫做对应顶点.
⑷对应边:全等三角形中互相重合的边叫做对应边.
⑸对应角:全等三角形中互相重合的角叫做对应角.
2.基本性质:
⑴三角形的稳定性:三角形三边的长度确定了,这个三角形的形状、大小就全确定,这个性质叫做三角形的稳定性.
⑵全等三角形的性质:全等三角形的对应边相等,对应角相等.
3.全等三角形的判定定理:
⑴边边边(SSS ):三边对应相等的两个三角形全等.
⑵边角边(SAS ):两边和它们的夹角对应相等的两个三角形全等.
⑶角边角(ASA ):两角和它们的夹边对应相等的两个三角形全等.
⑷角角边(AAS ):两角和其中一个角的对边对应相等的两个三角形全等.
⑸斜边、直角边(HL ):斜边和一条直角边对应相等的两个直角三角形
全等.
4.角平分线:
⑴画法:
⑵性质定理:角平分线上的点到角的两边的距离相等.
⑶性质定理的逆定理:角的内部到角的两边距离相等的点在角的平分线上.
(三角形三条角平分线的交点到三边距离相等)
5.证明的基本方法:
⑴明确命题中的已知和求证.(包括隐含条件,如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系)
⑵根据题意,画出图形,并用数字符号表示已知和求证.
⑶经过分析,找出由已知推出求证的途径,写出证明过程.。
全等三角形知识点总结
全等三角形知识点总结一、全等三角形的定义1. 全等三角形的定义:如果两个三角形的三个对应角完全相等,那么这两个三角形就是全等的。
当且仅当两个三角形的对应边长都相等时,这两个三角形才是全等的。
2. 全等三角形的性质:a. 全等三角形的对应角相等,对应边相等。
b. 如果两个三角形是全等的,那么它们的内部三角形也全等。
二、全等三角形的判定定理1. SSS判定定理:如果两个三角形的三条边分别相等,那么这两个三角形是全等的。
2. SAS判定定理:如果两个三角形的两边及夹角分别相等,则这两个三角形是全等的。
3. ASA判定定理:如果两个三角形的两个角及夹边分别相等,则这两个三角形是全等的。
4. AAS判定定理:如果两个三角形有一对对应角相等,并且两个对应边分别相等,则这两个三角形是全等的。
5. RHS判定定理:如果两个直角三角形的两条直角边分别相等,则这两个直角三角形是全等的。
三、全等三角形的性质1. 全等三角形的对应边相等,对应角相等。
2. 全等三角形的内部三角形也是全等的。
3. 全等三角形的每个角的顶点到对边的距离也相等。
四、全等三角形的应用1. 在几何证明中,可以利用全等三角形的性质证明两个三角形相等。
2. 在计算中,可以利用全等三角形的性质求解未知边长和角度。
3. 在工程建设和日常生活中,可以利用全等三角形的性质进行测量和设计。
五、全等三角形的相关定理1. 全等三角形的相关定理包括:全等三角形的辅助线定理、全等三角形的平行线定理、全等三角形的垂直平分线定理等。
六、全等三角形的证明方法1. 证明两个三角形全等的一般步骤包括:1)找出两个三角形的对应角、对应边;2)通过对应边和对应角的关系来进行判定,通常使用SSS、SAS、ASA、AAS等定理。
七、全等三角形的应用举例1. 利用全等三角形的性质证明两个三角形全等。
2. 利用全等三角形的性质求解未知边长和角度。
3. 利用全等三角形的性质进行测量和设计。
总的来说,全等三角形是我们学习几何时必须掌握的重要知识点,它在证明、计算、测量和设计中都有广泛的应用。
初中数学 第十二章 全等三角形 知识点
第十二章全等三角形
一、知识框架:
二、知识概念:
1.基本定义:
⑴全等形:能够完全重合的两个图形叫做全等形.
⑵全等三角形:能够完全重合的两个三角形叫做全等三角形.
⑷对应边:全等三角形中互相重合的边叫做对应边.
⑸对应角:全等三角形中互相重合的角叫做对应角.
2.基本性质:
⑴三角形的稳定性:三角形三边的长度确定了,这个三角形的形状、大小就全确定,这个性质叫做三角形的稳定性.
⑵全等三角形的性质:全等三角形的对应边相等,对应角相等.
⑴边边边(SSS):三边对应相等的两个三角形全等.
⑵边角边(SAS):两边和它们的夹角对应相等的两个三角形全等.
⑷角角边(AAS):两角和其中一个角的对边对应相等的两个三角形全等.
⑸斜边、直角边(HL):斜边和一条直角边对应相等的两个直角三角形
全等.
4.角平分线:
1性质定理:角平分线上的点到角的两边的距离相等.
2性质定理的逆定理:角的内部到角的两边距离相等的点在角的平分线上.
5.证明的基本方法:
⑵根据题意,画出图形,并用数字符号表示已知和求证.
⑶经过分析,找出由已知推出求证的途径,写出证明过程.。
