湘教版八年级数学上册第一章分式小结复习(谷风讲课)
湘教版八年级数学上册第一章分式小结复习精选课件

三. 分式的运算
知能点1. 分式的乘除、乘方:
乘法法则:分式乘分式,用分子的积作 为积的分子,分母的积作为积的分母。
������ ������ ������ ·������ ������ ·������ = ������ ·������
谢谢聆听 门前小土坡在夜色下显得有些陌生而拘谨,似乎把我当成远方客人。得知我要回来,一进门就看到母亲正朝着门口快步走来,她打量着我一直笑,拉我进屋。 “快坐下,坐车很难受吧?”母亲像个得到心爱玩具后的孩子般兴奋,我便坐在沙发上。 “去洗洗手吧,一路上出汗多”,我刚要起身,母亲又赶忙示意我别动,对我说:“我给你端来,你别起来。”不等我回话,转身到院子里了。 母亲端来水,递给我毛巾,转身又小跑着到厨房去了。我知道母亲在给我做捞面。记得初中时候一天上午放学,由于母亲忙农活做饭晚了,我一生气准备不吃饭就上学去。母亲也是这样让我坐着,转身小跑到厨房为我做捞面。 吃了无数次母亲做的捞面,但从没认真看过她擀面条的样子。想到这里,我轻轻来到院子里,厨房门开着,我站在离厨房几米远的地方,正好可以看到母亲。 厨房里装的还是以前那种白织灯,夜色包围下加上腾空的水蒸气,白织灯散发的昏黄光线显得有点力不从心。母亲就在灯下,正用擀面杖擀面,擀面杖很粗大,她似乎要用很大的力气。面团在前后滚动的擀面杖下由崎岖粗糙变得慢慢平整,终于像一张纸一样平铺在案板上。就像从小到大我走过的路,多少荆棘坑洼,都被母亲用双手铺平。
“吃肉啊,那是我专门放面里的,快吃!” 我夹起一块肉吃在嘴里,她这才算满意,站在一边看我吃。我没有劝母亲去吃饭,因为我知道,我没吃完,她不肯去。 一碗面吃完,汗水顺着脸颊淌下,这捞面味道,一半在嘴里,香而纯,另一半在心里,有点酸楚。一小滴液体流进嘴里,涩涩的,咸咸的,不知道是汗,还是我眼角渗出的泪。,只因眷恋而去。很久都不曾写过文章了,上一篇文章还是四个月之前的。以此去命题,并非有什么轻生的念头,只是有感而发,勿念。其实我很想做个自私的人,因为这会让你吃尽苦头又吃足了甜头。而你却依然活的天真活的开心——序。
湘教版八年级初二上册单元小结与总结复习
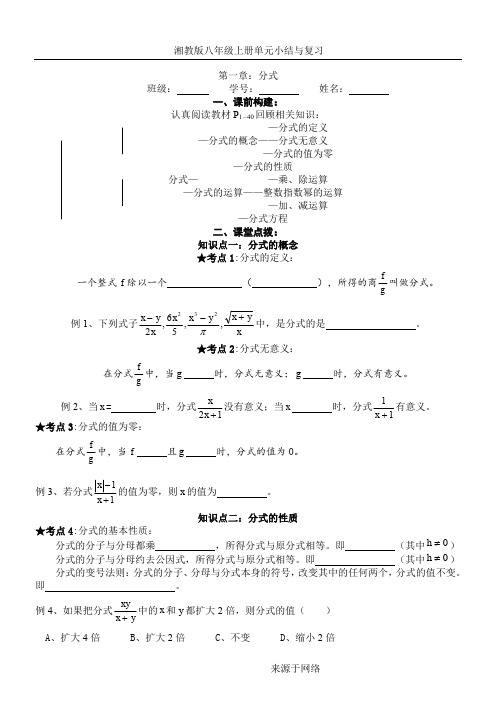
湘教版八年级上册单元小结与复习第一章:分式班级: 学号: 姓名:一、课前构建:认真阅读教材P 1-40回顾相关知识:—分式的定义—分式的概念——分式无意义—分式的值为零—分式的性质例 ★考点3例3知识点二:分式的性质★考点4:分式的基本性质:分式的分子与分母都乘 ,所得分式与原分式相等。
即 (其中0≠h ) 分式的分子与分母约去公因式,所得分式与原分式相等。
即 (其中0≠h ) 分式的变号法则:分式的分子、分母与分式本身的符号,改变其中的任何两个,分式的值不变。
即 。
例4、如果把分式yx xy +中的x 和y 都扩大2倍,则分式的值( ) A 、扩大4倍 B 、扩大2倍 C 、不变 D 、缩小2倍例5、根据分式的基本性质,分式ba a --可变形为( ) A 、b a a -- B 、b a a + C 、b a a -- D 、ba a +- ★考点5:最简分式(1)约分:把一个分式的分子与分母的公因式约去,称为分式的约分。
约分的方法:先把分子与分母因式分解,再约去公因式。
(2)最简分式:分子与分母没有 分式,叫做最简分式。
分式运算的最终结果若是分式,一定要化成最简分式。
例6、化简y x -222的结果是( )A 、y x - B 、y x + C 、y x - D 、y x -★考点6①②例8) A ★考点7例9例10、先化简211x x x +÷ ⎪-+⎝⎭,再取一个你认为合理的x 值,代入求原式的值。
知识点四:分式方程★考点8:分式方程的解法:⑴去分母法①去分母:在方程的两边都乘以最简公分母,约去分母,化成整式方程;②解方程:解上面所得的整式方程;③检验:把整式方程的根代入 ,看结果是不是零,使 的根是原方程的根,使 的根是增根。
⑵换元法 也就是把适当的分式换成新的未知数,求出新的未知数后求出原来的未知数。
例11、解下列方程:⑴x x x x -+-=+-3)2(4523 ⑵253113=-+-+-x x x x ★考点9:分式方程的应用:分析清楚题目中各个量,找出它们的等量关系。
新版湘教版秋八年级数学上册第一章分式小结与复习教学设计

新版湘教版秋八年级数学上册第一章分式小结与复习教学设计一. 教材分析湘教版秋八年级数学上册第一章分式小结与复习主要内容包括分式的概念、分式的运算、分式方程的解法等。
本章内容是初中的重要知识点,也是学生学习高中数学的基础。
通过本章的学习,使学生掌握分式的基本概念和运算方法,能够解决简单的实际问题,培养学生分析问题、解决问题的能力。
二. 学情分析八年级的学生已经学习了分式的基本概念和运算方法,但对分式方程的解法还不够熟练。
学生在学习过程中,对分式的理解存在一定的困难,特别是分式方程的解法,部分学生可能会感到迷茫。
因此,在教学过程中,需要教师引导学生加深对分式的理解,提高学生解决实际问题的能力。
三. 教学目标1.知识与技能:使学生掌握分式的基本概念和运算方法,能够解决简单的实际问题。
2.过程与方法:通过复习,引导学生自主探究,总结分式的性质和运算规律,提高学生的数学思维能力。
3.情感态度与价值观:培养学生热爱数学,勇于探究的精神,增强学生团队合作的意识。
四. 教学重难点1.重点:分式的基本概念和运算方法。
2.难点:分式方程的解法及其应用。
五. 教学方法1.采用问题驱动的教学方法,引导学生自主探究,总结分式的性质和运算规律。
2.运用小组合作学习,培养学生的团队合作精神和沟通能力。
3.利用多媒体辅助教学,提高学生的学习兴趣和效果。
六. 教学准备1.准备相关的教学课件和教学素材。
2.安排学生进行预习,了解分式的基本概念和运算方法。
3.设计好课堂练习和课后作业。
七. 教学过程1.导入(5分钟)教师通过复习分式的基本概念,引导学生回顾已学过的知识,为新课的学习做好铺垫。
2.呈现(15分钟)教师通过PPT展示分式的性质和运算规律,让学生自主探究,总结出分式的基本性质和运算方法。
3.操练(20分钟)教师设计一些分式运算的题目,让学生独立完成,检验学生对分式运算方法的掌握程度。
4.巩固(15分钟)教师给出一些实际问题,让学生运用所学的分式知识解决,巩固学生对分式的应用能力。
湘教版数学八年级上册知识点总结
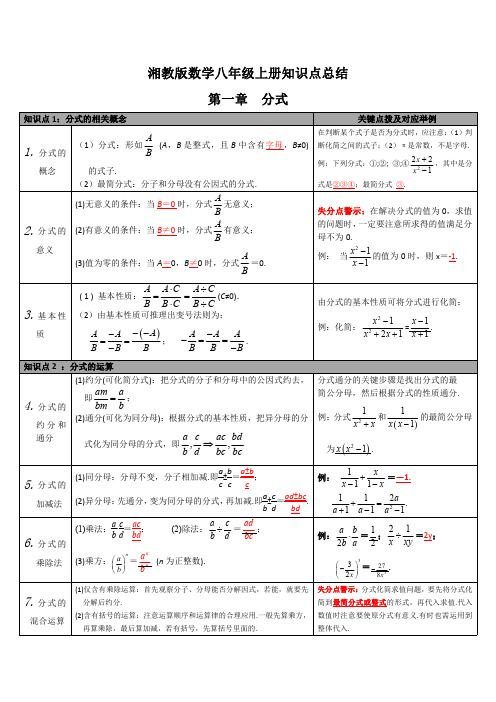
湘教版数学八年级上册知识点总结
第一章分式
第二章三角形
(1)斜边和一条直角边对应相等(HL)
(2)证明两个直角三角形等同样可以SAS,ASA和AAS.
)利用全等证明角、边相等或求线段长、求角度:将特征的边或角放到两个全等的三角形中,通过证明全等得到结论.在寻求全等的条件时,注意公共角、公共边、对顶角等银行条件.
)全等三角形中的辅助线的作法:
①直接连接法:如图①,连接公共边,构造全等.
SAS可得△ACD≌△例:
如图,在△ABC中,已知∠∠2,BE=CD,
AB=5,AE=2,
则CE=3.
等腰等边三角形知识清单梳理
1
AC=
2AB;
长度,若斜边不明确,应分类讨
论.
(3)在折叠问题中,求长度,往
往需要结合勾股定理来列方程解
决.
6.直角
三角
形的
判定
(1)有一个角是直角的三角形是直角三角形.即若∠C=90°,则
△ABC是Rt△;
(2)如果三角形一条边的中线等于这条边的一半,那么这个三角
形是直角三角形.即若AD=BD=CD,则△ABC是Rt△
(3)勾股定理的逆定理:若a2+b2=c2,则△ABC是Rt△.
第三章实数
第四章一元一次不等式(组)知识清单梳理
x≥a x>a x≤a x<a
:列不等式解决简单的实际问题
)一般步骤:审题;设未知数;找出不等式关系;列不等式;解不等式;验检是否有意义.
)应用不等式解决问题的情况:
第五章二次根式。
新湘教版八年级数学上册第一章分式小结与复习

混合运算
03
CHAPTER
分式方程
根据实际问题或数学问题,通过数学模型将问题转化为分式方程。
方程的建立
利用分式方程的解法,如去分母、换元法等,求解分式方程。
方程的求解
方程的建立与求解
利用分式方程解决与速度、时间和距离相关的实际问题,如追及问题、相遇问题等。
通过建立分式方程,解决与工作效率相关的实际问题,如工程问题、工作分配问题等。
分式与其他知识点的联系
整式和分式都是代数的基本形式,整式是由数字和字母通过有限次加、减、乘运算得到的代数式,而分式是整式的一种特殊形式,其分母中含有字母。
分式可以看作是整式的除法运算,即一个分式除以另一个分式等于被除数乘以除数的倒数。
分式的约分和通分也是基于整数的约分和通分原理,通过因式分解或找最大公约数来实现。
在几何学中,我们经常需要计算图形的面积或体积。当知道图形的边长或其他尺寸时,我们可以通过分式来表示和计算面积或体积。例如,计算矩形的面积时,我们可以用分式来表示长度和宽度的关系。
详细描述
面积、体积问题
分式在解决其他实际问题中也有广泛应用,如溶液的稀释、金融投资等。
总结词
除了速度、时间、距离和面积、体积问题外,分式在现实生活中还有许多应用。例如,在化学实验中,我们经常需要稀释溶液,这时可以用分式来表示稀释的比例。在金融领域,分式可以用来表示投资回报率或利率等经济指标。
Hale Waihona Puke 与整式的联系分式方程可以转化为整式方程,通过去分母或消去分母的方法,将分式方程转化为整式方程进行求解。
解分式方程时,需要注意验根,因为分母不能为零。
分式经常出现在方程中,尤其是高次方程和分式方程。
与方程的联系
湘教版八年级数学上册第一章分式小结复习 PPT

(C≠ 0)
知能点2. 分式的约分:
把一个分式的分 子与分母的公因 式约去,叫做分 式的约分。
确定最大公因式的方法: ①最大公因式的系数取 分子、分母系数的最大 公约数; ②取分子、分母相同的 字母因式的最低次幂.
知能点3. 最简公分母、通分: 分式的分子与分母没有公因式的分式叫最简单分式
知能点3. 分式值为0:
(1)分母不等于0 (2)分子等于0
知能点4. 分式值为正负数:
(1)分子分母同号 (2)分子分母异号
二. 分式的性质
知能点1. 分式的性质:
分式的分子与分母乘(或除以)同一个不等于0的整 式,分式的值不变。
用字母表示:
A B
=
A·C B·C
A B
=
A÷C B÷C
分式的变号法则: a a a a
小数点往后至第一个不为零的数字
上,所有零的个数,包括小数点前 面的那个零。
三. 分式方程
知能点1. 分式方程的意义和解法:
分母中含有未知数的方程叫分式方程。
解分式方程的一般步骤
(1)去分母 (2)解整式方程 (3)检 验
把几个异分母的分式分别化成与原来的分式相等的 同分母的分式,叫做分式的通分
三. 分式的运算
知能点1. 分式的乘除、乘方:
乘法法则:分式乘分式,用分子的积作 为积的分子,分母的积作为积的分母。
������ ������ ������ ·������ ������ ·������ = ������ ·������
{ 分
同分母
a b a±b
式 的
{加
字母表示: c ± c = c
法 则 : 先通分,变为同分母的分式,再加减
湘教版八年级数学上册第1章分式复习知识点及复习题解析

即 分式的分子、分母都乘 它们的公因式 , 所得分式与原分式相等。
f f f . g g g
分式及其分子、分母三处法符号,任意改 变两处的符号,即把负号移到另一处,分式的 值不变。
f mk m . g nk n
即 分式的分子、分母都约去 公因式 , 所得分式与原分式相等。
1. 分式乘分式把分子相乘的积作分子,把分母相 乘的积作分母。最后结果约分成 最简分式 .
概念和性质
乘、除运算
分
式
运算
整数指数幂的运算
加、减运算
可化为一元一次方程的分式方程
1. 整式f除以 非零 整式g(g中含有 字母 )所得 的商 f ,叫做分式。
g
2. 当分母 等于0 时,分式的值不存在(无意义); 当分子等于 等于0 但分母 不等于0 时,分式
的值等于0.
f f h h 0.
(ab)n=anbn
a b
n
an bn
am an
amn
1.同分母分式相加减,分母 不变 ,把分子 相加减 .
2.各分式的分母的 所有因式 的最高次幂的积,叫做 这些分式的最简公分母.
3.根据分式的基本性质,把异分母分式化成同分母 分式的过程叫做 通分 .通分的方法:先确定各分 母的 最简公分母 ,再将各分式的分子、分母都 乘最简公分母约去各分式的分母所得的整式。
【答案】x=±2.
2.先约分,再求值:
2x 6 x2 4x
4
x2 x2 3x
,其 中x
3.
【答案】原式=
2
xx
2
2 3
.
3.计算:
16a3b 3b;
2 24x5 y3 36x4 y4;
【优选整合】湘教版数学八年级上册第1章分式-小结与复习 教案

1第1章小结与复习教学目标1.系统了解本章的知识体系及知识内容.2.进一步知道分式的概念和分式的基本性质,能进行分式的约分、通分以及分式的加减、乘除、乘方混合运算.3.会用科学记数法表示绝对值小于1的数,能进行有关负整数次幂的有关运算. 4.会列分式方程解决简单的实际问题,会解分式方程.5.通过构建知识结构图,提高归纳、整理的能力,体会知识之间的内在联系和价值.教学重点分式的基本性质及运算,分式方程的解法及应用.教学难点分式的有关运算及分式方程的应用.教学流程:一、知识回顾要点一、分式的有关概念及性质 1.分式一般地,如果A 、B 表示两个整式,并且B 中含有字母,那么式子AB叫做分式.其中A 叫做分子,B 叫做分母.要点诠释:分式中的分母表示除数,由于除数不能为0,所以分式的分母不能为0,即当B ≠0时,分式AB才有意义.22.分式的基本性质(M 为不等于0的整式).3.最简分式分子与分母没有公因式的分式叫做最简分式.如果分子分母有公因式,要进行约分化简. 要点二、分式的运算 1.约分利用分式的基本性质,把一个分式的分子和分母的公因式约去,不改变分式的值,这样的分式变形叫做分式的约分. 2.通分利用分式的基本性质,使分子和分母同乘适当的整式,不改变分式的值,把异分母的分式化为同分母的分式,这样的分式变形叫做分式的通分. 3.基本运算法则分式的运算法则与分数的运算法则类似,具体运算法则如下: (1)加减运算a b a b c c c±±= ;同分母的分式相加减,分母不变,把分子相加减. ;异分母的分式相加减,先通分,变为同分母的分式,再加减.(2)乘法运算a c acb d bd⋅=,其中a b c d 、、、是整式,0bd ≠. 两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母. (3)除法运算a c a d adb d bc bc÷=⋅=,其中a b c d 、、、是整式,0bcd ≠. 两个分式相除,把除式的分子和分母颠倒位置后,与被除式相乘.(4)乘方运算3分式的乘方,把分子、分母分别乘方. 4.零指数.5.负整数指数6.分式的混合运算顺序先算乘方,再算乘除,最后加减,有括号先算括号里面的. 7.科学记数法(1)把一个绝对值大于10的数表示成10na ⨯的形式,其中n 是正整数,1||10a ≤<(2)利用10的负整数次幂表示一些绝对值较小的数,即10na -⨯的形式,其中n 是正整数,1||10a ≤<.用以上两种形式表示数的方法,叫做科学记数法. 要点三、分式方程 1.分式方程的概念分母中含有未知数的方程叫做分式方程. 2.分式方程的解法解分式方程的关键是去分母,即方程两边都乘以最简公分母将分式方程转化为整式方程. 3.分式方程的增根问题增根的产生:分式方程本身隐含着分母不为0的条件,当把分式方程转化为整式方程后,方程中未知数允许取值的范围扩大了,如果转化后的整式方程的根恰好使原方程中分母的值为0,那么就会出现不适合原方程的根---增根.要点诠释:因为解分式方程可能出现增根,所以解分式方程必须验根.验根的方法是将所得的根带入到最简公分母中,看它是否为0,如果为0,即为增根,不为0,就是原方程的解. 要点四、分式方程的应用列分式方程解应用题与列一元一次方程解应用题类似,但要稍复杂一些.解题时应抓住“找等量关系、恰当设未知数、确定主要等量关系、用含未知数的分式或整式表示未知量”等关键环节,从而正确列出方程,并进行求解.4二、探究活动1类型一、分式及其基本性质1、在中,分式的个数是( ) A.2 B.3 C.4 D.5【答案】C ;【解析】()21131x x a x x x y m+++,,,是分式.【总结升华】判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.2、当x 为何值时,分式293x x -+的值为0?【思路点拨】先求出使分子为0的字母的值,再检验这个值是否使分母的值等于0,当它使分母的值不等于0时,这个值就是要求的字母的值. 【答案与解析】解: 要使分式的值为0,必须满足分子等于0且分母不等于0.由题意,得290,30.x x ⎧-=⎨+≠⎩解得3x =.∴ 当3x =时,分式293x x -+的值为0.【总结升华】分式的值为0的条件是:分子为0,且分母不为0,即只有在分式有意义的前提下,才能考虑分式值的情况.【变式】(1)若分式的值等于零,则x =_______;ma y x xy x x x x 1,3,3,)1(,21,12+++π5(2)当x ________时,分式没有意义.【答案】(1)由24x -=0,得2x =±. 当x =2时x -2=0,所以x =-2; (2)当10x -=,即x =1时,分式没有意义.类型二、分式运算3、计算:2222132(1)441x x x x x x x -++÷-⋅++-.【答案与解析】解:222222132(1)(1)1(2)(1)(1)441(2)(1)1x x x x x x x x x x x x x x -+++-++÷-⋅=⋅⋅++-+-- 22(1)(2)(1)x x x +=-+-. 【总结升华】本题有两处易错:一是不按运算顺序运算,把2(1)x -和2321x x x ++-先约分;二是将(1)x -和(1)x -约分后的结果错认为是1.因此正确掌握运算顺序与符号法则是解题的关键.【变式】计算:(1)332212b b a a ab ⎛⎫⎛⎫⎛⎫-÷-÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;(2)2224222a a a a a a ⎛⎫- ⎪+--⎝⎭g ; (3)6333aa a a a a⎛⎫-÷⎪-+-⎝⎭. 【答案】解:(1)3322326331122b b b b a a ab a a a b ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-÷-÷=-÷-÷ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭6268233322b a a b a b a b ⎛⎫⎛⎫=--=⎪⎪⎝⎭⎝⎭g ; (2)2222244(2)(2)222(2)222a a a a a a a a aa a a a a a a ⎛⎫-+--== ⎪+--+-+-⎝⎭g g g (2)2aa a a =+=+g ; (3)6333a a a a a a⎛⎫-÷⎪-+-⎝⎭ (3)(3)3(3)(3)6a a a a aa a a +---=+-g63(3)(3)6a a a a a -=+-g 13a =-+. 4、计算:(1)5231010-⨯⨯; (2)134139m npmn p ----÷;(3)22223a a b b ⎛⎫-⎛⎫÷⎪ ⎪⎝⎭⎝⎭;(4)1322233(3)(2)(3)mn m n m n ----÷g . 【思路点拨】(1)题和(2)题只有乘除运算,按幂的乘法和除法法则进行计算;(3)题中出现了分式,可先将每一个分式转化为整数指数幂,然后再用法则计算;(4)题中出现了整数幂的乘法、除法、乘方计算;先算乘方,再算乘除. 【答案与解析】 解:(1)原式5233133103103101000-+-=⨯=⨯=⨯=; (2)原式5111(4)3(1)252221(39)33n mnpm n p m p ---------=÷==g g g ;7(3)原式242222244994a a a b b b b a=÷=g242222999444a b a a--+-===g ; (4)原式333244333(2)(3)m nm n m n ---=-÷g32434334(3)4443236363m m n m n n+-------⨯==-=-g . 【总结升华】(1)整数指数幂的运算结果一般要用正整数指数幂来表示.如:(4)题中的结果得到4436m n--后,还要化为4436m n-.(2)进行混合运算时特别要注意运算顺序. 5、用科学记数法表示下列各数:(1)0.00001;(2)0.000000203;(3)-0.000135;(4)0.00067 【答案与解析】 解:(1)0.00001=510-;(2)0.000000203=72.0310-⨯;(3)-0.000135=41.3510--⨯;(4)0.00067=46.710-⨯.【总结升华】注意在10na -⨯中n 的取值是这个数从左边起第一个不是零的数前面零的个数(包括小数点前边的零).类型三、分式方程的解法86、解方程23222x x x -=+- 【答案与解析】 解:23222x x x -=+- 方程两边同乘以()()22x x -+,得 ()()()()2232222x x x x x --+=+- 72x =27x =检验: 当27x =时,最简公分母()()22x x -+≠0, ∴27x =是原方程的解. 【总结升华】分式方程一定要记得检验. 举一反三:【变式】()1231244x x x -=---, 【答案】解: 方程两边同乘以()24x -,得()()12422332x x x =---=-∴检验:当32x =-时,最简公分母()240x -≠,9∴32x =-是原方程的解. 类型四、分式方程的应用7、某质检部门分别抽取甲、乙两厂相同数量的产品进行质量检查,测得甲厂有合格的产品48件,乙厂有合格的产品45件,甲厂的合格率比乙厂的合格率高5%,问甲厂的合格率是多少?【思路点拨】本题可间接设出甲、乙两厂分别抽取的产品件数,利用“甲厂的合格率比乙厂的合格率高5%列出等式. 【答案与解析】解:设质检部门抽取了x 件进行检测,则:48455%x x-=. 解方程,得x =60.∴ 甲厂的合格率是:48100%80%60⨯=. 答:甲厂的合格率是80%.【总结升华】本题若直接设未知数,解题过程非常繁琐,间接设未知数较方便. 举一反三:【变式】小明家、王老师家、学校在同一条路上,并且小明上学要路过老师家,小明到王老师家的路程为3 km ,王老师家到学校的路程为0.5 km ,由于小明的父母战斗在抗震救灾第一线,为了使他能按时到校、王老师每天骑自行车接小明上学.已知王老师骑自行车的速度是他步行速度的3倍,每天比平时步行上班多用了20 min ,王老师步行的速度和骑自行车的速度各是多少? 【答案】解:设王老师步行的速度为x km/h ,则他骑自行车的速度为3x km/h.根据题意,得230.50.520360x x ⨯+=+.解这个方程,得5x =.10经检验5x =是原方程的根且符合题意. 当5x =时,315x =.答:王老师步行的速度为5km/h ,他骑自行车的速度为15km/h . 三、知识小结谈一谈本节课你有什么收获? 四、当堂达标 第一章小结与复习。
