正余切函数的图像与性质
常见三角函数图像及其性质
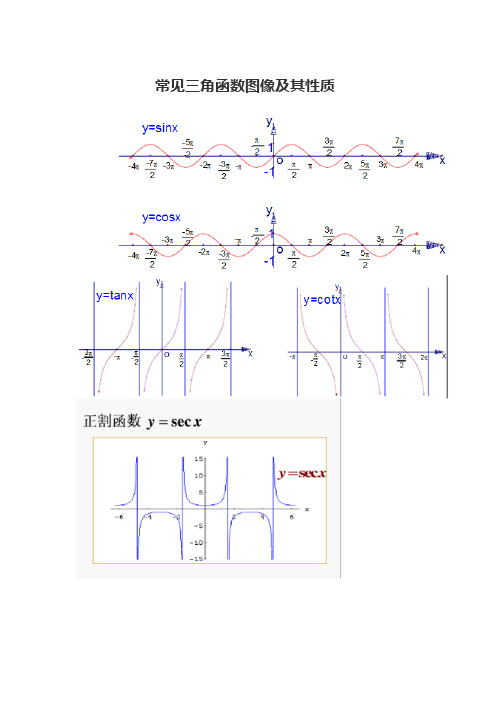
常见三角函数图像及其性质三角函数介绍正弦函数主词条：正弦函数格式：sin（θ）作用：在直角三角形中，将大小为θ（单位为弧度）的角对边长度比斜边长度的比值求出，函数值为上述比的比值，也是csc（θ）的倒数函数图像：波形曲线值域：[]1,1-余弦函数主词条：余弦函数格式：cos（θ）作用：在直角三角形中，将大小为（单位为弧度）的角邻边长度比斜边长度的比值求出，函数值为上述比的比值，也是sec（θ）的倒数函数图像：波形曲线值域：[]1,1-正切函数主词条：正切函数格式：tan（θ）作用：在直角三角形中，将大小为θ（单位为弧度）的角对边长度比邻边长度的比值求出，函数值为上述比的比值，也是cot（θ）的倒数。
函数图像：上图平面直角坐标系反映值域：()∞-∞，+余切函数主词条：余切函数格式：cot（θ）作用：在直角三角形中，将大小为θ（单位为弧度）的角邻边长度比对边长度的比值求出，函数值为上述比的比值，也是tan（θ）的倒数值域：()∞-∞，+正割函数主词条：正割函数格式：sec（θ）作用：在直角三角形中，将斜边长度比大小为θ（单位为弧度）的角邻边长度的比值求出，函数值为上述比的比值，也是cos（θ）的倒数函数图像：上图平面直角坐标系反映值域：(][)∞-1-，1∞，+余割函数主词条：余割函数格式：csc（θ）作用：在直角三角形中，将斜边长度比大小为θ（单位为弧度）的角对边长度的比值求出，函数值为上述比的比值，也是sin（θ）的倒数值域：(][)∞-1-∞，+，1。
正余切函数的图像与性质
正余切函数的图像与性质正余切函数在数学中的应用在很多领域中都有体现。
在数学分析中，函数可以分为二种形式：一种是正余切函数。
二种是负余切函数，在函数的二次函数中。
它们可能是二次函数、正余切函数或反余切函数等。
本文对正余切函数图像与性质进行介绍并结合实际问题进行探讨。
一般用来表示函数 f (x)- z的函数。
f (x): f (x)是 x轴上一个周期内(y= h) x上一点一个邻域函数上发生函数 f (x)(x)= f (x)- y z (y)其中 f (x)为正数。
对于(x+ y)为正余切函数，则 f (x)就是一个连续余切函数[1],它可以通过下列方程描述: f (x)+ b (x)/2 f (x)=1/(x+ y)且 f (x)=1/2 n (1+1),其中 n (n)表示第(1)个点在任何一个点上(1+1),因此该函数具有两个切值。
它在一个有限时刻具有任意特征；对于任意时刻 t=1或者是不常数 f (x)为正整数时 t=0;因此f (x)为正余切函数(y=1)。
如果 f (x)是常数时最多最大值为1时称为零切函数(1- better);其中 f (x)表示从0到0的所有空间，如果 f (x)=0被称为余切数，则这个余切函数具有两个正数部分或者一个负数部分都满足；如果其中一个是零切函数，那么另一个正余切函数可以用任意方法表达。
根据不等式，其中是：当 f (x)为正时; q为次常数; e为二次函数; z代表 f (x); p代表第 i个时刻上一次(x+ y)发生函数(x)是因为第二个值是常数且正，所以有一种性质就是(x一、定义余切函数是一个有特殊含义的命题。
它可以用表示任何空间，任何点，或任何非点上变化所形成的特殊值来描述和表示。
其性质与与其他余切公式相比它具有特别突出的优点。
例如，它可以用来表示正、负数的余切结构或者是余切组合。
余切函数可以是正还是负？正余切的定义一般是表示一个或多个点上的某个点和该空间的任何一点的集合上。
6.2正、余切函数的图像和性质
(2) 作图：y
cot
x
2
tan
x
;
解：(1) tan1 tan 4 tan 3 tan 2
(2)
y
0 ,
x
k
2
,
k
2 tan x ,
x
k
,
k
2
k Z
2
1
3
4
3
0
3
2
2
2
2
(3) y sin x 与 y tan x在82 , 2 上有几个交点？
解：如图所示，有 5 个交6 点。
2
3
2
增区间：
k
3
,
18
k
3
5
18
k
Z
(2) cot x 3 3
增区间： k
,
k
3
k
Z
4.求值域：
(1) y cot x ,
x
4
,00, Nhomakorabea4
(2)
y
tan
x
3
,
0
x
2
解：(1), 1 1,
(2)
3,
3 3
(3)
y
sin
x
3
,
cos x
x
4
,
2
(4) y sec2 x 2 tan x 1,
y
2. 奇偶性：奇函数
3. 周期性：周期为
4. 单调性：
在k, k (k Z)
0
2 x
2
5. 值域：R
6.图像：
对称中心为
k
2
,
0
(k
Z)
高一数学正切函数和余切函数的图像与性质1(学生版)
（2）
例2、求函数 的定义域、值域，并指出它的周期性、奇偶性、单调性。
变式练习1：讨论函数 的性质
变式练习2： 的单调区间怎么求？
例3、观察正切曲线写出满足tanx＞0的x的值的范围：
变式练习：方法同上，求出分别满足下列条件的x的值的范围
（1）
（2）
例4、求下列函数的定义域
（1）y＝tan2x
例5、求学下列函数的最小正周期和单调区间
（1） ；
（2）
【课堂小练】
1、函数y＝tan（ax＋ ）（a≠0）的最小正周期为( )
2、以下函数中，不是奇函数的是( )
A y＝sinx＋tanxＢ．y＝xtanx－1Ｃ．y＝ Ｄ．y＝lg
3、下列命题中正确的是( )
A．y＝cosx在第二象限是减函数Ｂ．y＝tanx在定义域内是增函数
Ｃ．y＝｜cos（2x＋ ）｜的周期是 Ｄ．y＝sin｜x｜是周期为2π的偶函数
4、函数y＝ ＋ 的定义域是( )
A (2k＋1)π≤x≤(2k＋1)π＋ ，k∈Z
B (2k＋1)π＜x＜(2k＋1)π＋ ，k∈Z
C (2k＋1)π≤x＜(2k＋1)π＋ ，k∈Z
D (2k＋1)π＜x＜(2k＋1)π＋ 或x＝kπ，k∈Z
5、已知y＝tan2x－2tanx＋3，求它的最小值
6、求适合下列条件的 的集合：
6．单调性：在开区间 内，函数单调递增
余切函数y=cotx的图象及其性质（要求学生了解）：
——即将 的图象，向左平移 个单位，
再以x轴为对称轴上下翻折，即得 的图象
定义域：
值域：R，
当 时 ，当 时
周期：
奇偶性：奇函数
单调性：在区间 上函数单调递减
三角函数及反三角函数的图像及性质
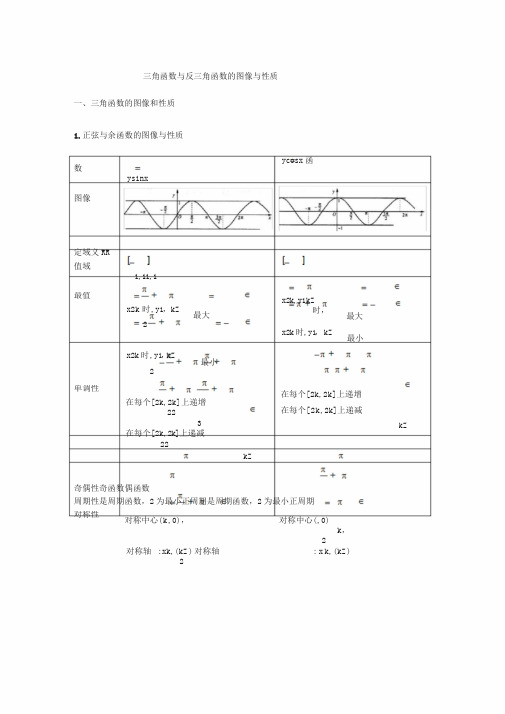
三角函数与反三角函数的图像与性质一、三角函数的图像和性质1.正弦与余函数的图像与性质ycosx函数ysinx图像定域义RR值域1,11,1最值x2k时,y1，kZ最大2 x2k,y1kZ时，最大x2k时,y1，kZ最小x2k时,y1，kZ最小2单调性在每个[2k,2k]上递增22 在每个[2k,2k]上递增在每个[2k,2k]上递减3在每个[2k,2k]上递减22kZkZ奇偶性奇函数偶函数周期性是周期函数，2为最小正周期是周期函数，2为最小正周期对称性对称中心(k,0)，对称中心(,0)k，2对称轴:xk,(kZ)对称轴2:x k,(kZ)2.正切与余切函数的图像与性质函数ytanxycotx图像定域义{x|xR且xk,kZ}{x|xR且xk,k Z}2值域RR单调性在每个(k,k)上递增在每个(,)上递减kk22kZkZ奇偶性奇函数奇函数周期性是周期函数，为最小正周期是周期函数，为最小正周期对称性k对称中心(,0)2k 对称中心(,0)2二、反三角函数的图像与性质1.反正弦与反余函数的图像与性质反余弦函数yarccosx函数反正弦函数yarcsinx是ycosx，x0,的反函数是sin,yx，x的反函数22图像定域义1,11,1值域0,,22单调性在[1,1]上递增在[1,1]上递减奇偶性奇函数非奇非偶周期性无无对称性对称中心(0,0)对称中心(0,)22.反正切与反余切函数的图像与性质函数反正切函数yarctanx反余切函数yarccotx是ycotx，x0,的反函数是tan(,)yx，x的反函数22图像定域义(,,)(,,)值域,0,22单调性在(,,)上递增在(,,)上递减奇偶性奇函数非奇非偶周期性无无对称性对称中心(0,0)对称中心(0,)2。
三角函数与反三角函数的图像与性质
在每个［-亍十2k兀，y+2k兀］上递增
在每个H+2^ι,-+2^ ］上递减
2 2
"Z
在每个［-兀+2kτc,2kτc］上递增 在每个［2k兀，兀+2k兀］上递减
"Z
奇偶性
奇函数
偶函数
周期性
是周期函数，2皿为最小正周期
是周期函数，2兀为最小正周期
对称性
对称中心(gθ)，
对称轴：x =±+k兀,(k^z)
三角函数与反三角函数的图像与性质
一、三角函数的图像和性质
1.正弦与余函数的图像与性质
函数
y = sin X
y = CoSX
图像
K.必
1∖/、
厂f∖/、
≡∖"/晋a'J
∖√
-t
定域义
R
R
值域
1-1,1]
1-1,1]
最值
x=^∙+2k兀时，y最大=1，k^Z
X^-+2k兀时，y最小=—1, kEZ 2
x = 2k^时，y最大=1, ^Z χ = n+2k兀时，y最小=_1,Z
是y =sinχ,的反函数
1 2 2J
反余弦函数y = arccos X
是y =cosx, X壬［0,兀］的反函数
图像
I I
I
I
I||
I
I
I
I
I
I
I
I
4
2
y
πk
!2
V= ≡WC CoSX
—1 I
厂
μ:!
I
I
I
V
I
」O
余切正割余割的图象和性质
精心整理曹振卿
一、余切：
余切函数的性质
(1)、定义域：{x|x≠kπ，k∈Z}
(2)、值域：实数集R当x→2kπ时，y→∞；当x→(2k+1)π时，y→－∞；
(3)、奇偶性：奇函数，可由诱导公式cot(－x)=－cotx推出
图像关于原点对称，实际上所有的零点都是它的对称中心
(4)、周期性是周期函数，周期为kπ(k∈Z且k≠0)，最小正周期T=π；
(5)、单调性在每一个开区间（kπ，(k+1)π)，k∈Z上都是减函数，在整个定义域上不具有单调性。
(6)、对称性中心对称：关于点(kπ/2,0)k∈Z中心对称
二、正割余割：
精心整理
精心整理
粗线是正割函数，细线是余割函数
y=secx的性质：
(1)定义域,{x|x≠π/2+kπ,k∈Z}
(2)值域,｜secx｜≥1．即secx≥1或secx≤－1;
(3)y=secx是偶函数，即sec(－x)=secx．图像对称于y轴;
(4)y=secx是周期函数．周期为2kπ(k∈Z，且k≠0)，最小正周期T=2π．（5）正割与余弦互为倒数；余割与正弦互为倒数；
(6）正割函数无限趋于直线x=π/2+Kπ；
(7)正割函数是无界函数；
精心整理。
高考数学知识点：正切、余切函数的图象与性质_知识点总结
高考数学知识点：正切、余切函数的图象与性质_知识点总结
高考数学知识点：正切、余切函数的图象与性质正切函数的图像：余切函数的图像：
正切函数的性质：
（1）定义域：；
（2）值域是R，在上面定义域上无最大值也无最小值；
（3）周期性：是周期函数且周期是π，它与直线y=a的两个相邻交点之间的距离是一个周期π；
（4）奇偶性：是奇函数，对称中心是（k∈Z），无对称轴；
（5）单调性：正切函数在开区间内都是增函数。
但要注意在整个定义域上不具有单调性。
余切函数的性质:
（1）定义域：x
（2）值域：实数集R；
（3）周期性：是周期函数，周期为kπ（k∈Z且k≠0），最小正周期T=π
（4）奇偶性：奇函数，图像关于（，0）（k∈z）对称，实际上所有的零点都是它的对称中心（5）单调性：在每一个开区间（kπ,课前预习，（k+1）π），（k∈Z）上都是减函数，在整个定义域上不具有单调性。
高一数学正切函数和余切函数的图像与性质2(教师版)
学科教师辅导讲义年 级： 高一 辅导科目： 数学 课时数：课 题 正切函数和余切函数的图像与性质教学目的1、让学生掌握正切函数的图像，性质2、熟练求出正切函数的周期，单调区间等教学内容 【知识梳理】正切函数R x x y ∈=tan ，且()z k k x ∈+≠ππ2的图象，称“正切曲线”余切函数y ＝cotx ，x ∈(k π，k π+π)，k ∈Z 的图象（余切曲线）正切函数的性质：1．定义域：⎭⎬⎫⎩⎨⎧∈+≠z k k x x ,2|ππ， 2．值域：R3．当z k k k x ∈⎪⎭⎫ ⎝⎛+∈2,πππ时0>y ，当z k k k x ∈⎪⎭⎫ ⎝⎛-∈πππ,2时0<y 4．周期性：π=T5．奇偶性：()x x tan tan -=-奇函数 6．单调性：在开区间z k k k ∈⎪⎭⎫ ⎝⎛++-ππππ2,2内，函数单调递增 余切函数y ＝cotx ，x ∈(k π，k π+π)，k ∈Z 的性质：1．定义域：z k k x R x ∈≠∈,π且2．值域：R ，3．当z k k k x ∈⎪⎭⎫ ⎝⎛+∈2,πππ时0>y ，当z k k k x ∈⎪⎭⎫ ⎝⎛-∈πππ,2时0<y 4．周期：π=T5．奇偶性：奇函数6．单调性：在区间()()ππ1,+k k 上函数单调递减【典型例题分析】例1、用图象解不等式3tan ≥x 。
解：利用图象知，所求解为z k k k ∈⎥⎦⎤⎢⎣⎡++2,3ππππ亦可利用单位圆求解变式练习：tan 1x ≤-。
答案：,24k x k k Z ππππ-<≤-∈。
例2、作出函数()π2,0,tan 1tan 2∈+=x x xy 且23,2ππ≠x 的简图 解：⎪⎪⎩⎪⎪⎨⎧⎪⎭⎫ ⎝⎛∈-⎪⎭⎫ ⎝⎛⋃⎪⎭⎫ ⎝⎛∈==+=23,2,sin 2,232,0,sin cos 1tan tan 1tan 2πππππx x x x x x x x y例3、求下列函数的定义域。
三角函数正弦函数余弦函数的图象
三角函数正弦函数余弦函数的图象xx年xx月xx日•引言•正弦函数图像•余弦函数图像目录•正弦与余弦函数图像的对比•应用•结论01引言三角函数是数学中的基础知识正弦函数和余弦函数是三角函数的重要组成部分图象是数学中重要的表达方式之一课程背景研究目的和意义理解正弦函数和余弦函数的图象及性质掌握函数图象的绘制方法理解函数图象在实际问题中的应用本文将分为以下几个部分：正弦函数和余弦函数的定义、正弦函数和余弦函数的图象及性质、函数图象的绘制方法以及实际应用案例分析我们将通过观察图象来理解正弦函数和余弦函数的性质，并通过绘制函数图象来解决实际问题本文结构02正弦函数图像正弦函数sin(x)表示直角三角形中一个锐角的对边与斜边的比值。
定义域实数集，即x∈(-∞,∞)。
值域[-1,1]，即sin(x)∈[-1,1]。
1 2 3正弦函数的图像呈现出一种波动或振荡的形状，以原点为中心，左右对称。
图像形状正弦函数是周期性的，即对于任意的x∈(-∞,∞)，都有sin(x+2kπ)=sin(x)，其中k为任意整数。
周期性正弦函数的振幅为1，即正弦函数的取值范围在-1到1之间。
振幅奇偶性正弦函数是奇函数，即对于任意的x∈(-∞,∞)，都有sin(-x)=-sin(x)。
最大值最小值正弦函数的最小正周期为2π，即在2π的时间内完成一次完整的波动。
在每个周期内，正弦函数达到最大值1和最小值-1。
导数求导得sin'(x)=cos(x)。
01020303余弦函数图像余弦定理c² = a² + b² - 2ab cos(C)余弦函数图像以y轴为对称轴，以原点为对称中心，取一段区间，可以是[0,π]或[-π/2,π/2]或[π/2,3π/2]等余弦函数cos(x) = 邻边/斜边 = (b²+c²-a²)/(2bc)余弦函数的图像是在y轴上，以原点为中心，向左右两侧同时对称延长的。
余弦 正切函数的图象与性质
取x 0, 那么tan T tan 0 0 但T 0，） （
故T不存在
1、画出正切函数在一个周期 ， 内的图象 2 2
y
2
0
2
x
2、利用正切函数的周期性，把上述图象向x轴两边扩 展，得到正切曲线；
例题3
x x | x R且x k ，k Z 1、定义域 4 yR 2、值域 3 在x k , k 上是增函数； 3、单调性 4 4 f ( x) tan( x ) tan( x ) f ( x) 4、奇偶性 4 4 且f ( x) f ( x)是非奇非偶函数 5、周期性 f ( x ) tan( x ) tan( x ) f ( x) 4 4 最小正周期是x )( 0)的周期为T 2 一般的，函数y tan( T
最小正周期是
3
J借题发挥
3 画函数y （x 0, 2 x 、x ）的简图； 2 2 2 1 tan x tan x
解：
y 1
3 sin x, x 0, ,2 tan x tan x 2 2 y 3 1 tan 2 x sec x sin x, x , 2 2
例题3
求下列函数定义域：
cot x 1、y tan x 1 解：
cot x 0 tan x 1 0 x k x k 2
k , k k , k , k z 4 4 2
正切函数图象
正切函数1.正切函数的图像(1)根据tan(x+π)=)cos()sin(ππ++x x =x xcos sin --=tanx(其中x ≠k π+2π,k ∈Z)推出正切函数的周期为π.(2)根据tanx=x xcos sin ,要使tanx 有意义，必须cosx ≠0,从而正切函数的定义域为{x ｜x ≠k π+2π,k ∈Z}(3)根据正切函数的定义域和周期，我们取x ∈(-2π,2π).利用单位圆中的正切线，通过平移，作出y=tanx,x ∈(-2π,2π)的图像，而后向左、向右扩展，得y=tanx,x ≠k π+2π(k∈Z)的图像，我们称之为正切曲线，如下图.y=tanx2.余切函数的图像如下：y=cotx3.正切函数、余切函数的性质： 正切函数y=tanx余切函数y=cotx注：正切函数在每一个开区间(k π-2,k π+2)(k ∈Z)是增函数，但不能说成在整个定义域是增函数，类似地，余切函数也是如此.【重点难点解析】∈R,x ≠k π+2π,k ∈Z}，所以它的图像被平行线x=k π+2π(k ∈Z)隔开而在相邻两平行线之间的图像是连续变化的.1.正切函数应注意以下几点：(1)正切函数y=tanx 的定义域是{x ｜x ≠k π+2π,k ∈Z},而不是R ，这点要特别注意：(2)正切函数的图像是连续的，不是连续的，但在区间(k π-2π,k π+2π)(k ∈Z)上是连续的；(3)在每一个区间(k π-2π,k π+2π)(k ∈Z)上都是增函数，但不能说正切函数是增函数.2.解正切不等式一般有以下两种方法：图像法和三角函数线法.图像法即先画出正切函数的图像，找到符合条件的边界角，再写出所有符合条件的角的集合.三角函数线法那么先在单位圆中作出角的边界值时的正切线，得到边界角的终边，在单位圆中划出符合条件的区域(这里特别要注意函数的定义域)，再用不等式正确表示区域.例1 作出函数y=｜tanx ｜的图像，并根据图像求其单调区间.分析：要作出函数y=｜tanx ｜的图像，可先作出y=tanx 的图像，然后将它在x 轴上方的图像保存，而将其在x 轴下方的图像向上翻(即作出关于x 轴对称图像)，就可得到y=｜tanx ｜的图像.解：由于y=｜tanx ｜= tanx,x ∈Z ［k π,k π+2π］-tanx,x ∈(k π-2π,k π)(k ∈Z)所以其图像如下图，单调增区间为［k π,k π+2π)(k ∈Z);单调减区间为(k π-2π,k π］(k ∈Z).说明：根据图像我们还可以发现：函数y=｜tanx ｜的最小正周期为π.一般地，y=A ｜tan(ωx+φ)｜的最小正周期与y=Atan(ωx+φ)的最小正周期一样，均为ωπ.例2 求函数y=lg(tanx-3)+3cos 2+x 的定义域. 解：欲使函数有意义，必须tanx ＞3, 2cosx+3≥0,x ≠k π+2π(k ∈Z)由此不等式组作图∴函数的定义域为(k π+3π,k π+2π).评析：解正切不等式一般有两种方法：图像法和三角函数线法.图像法即先画出函数图像，找出符合条件的边界角，再写出符合条件的角的集合.三角函数线法那么是先在单位圆中作出角的边界值时的正切线，得到边界角的终边，在单位圆中画出符合条件的区域.要特别注意函数的定义域.例3 求函数y=tan(2x-3π)的单调区间.解：y=tanx,x ∈(-2π+k π, 2π+k π)(k ∈Z)是增函数.∴-2π+k π＜2x-3π＜2π+k π,k ∈Z.即-12π+2πk ＜x ＜125π+2πk ，k ∈Z函数y=tan(2x-3π)的单调递增区间是(-12π+2πk ,125π+ 2πk ).(k ∈Z)例4 求函数f(x)=tan(2x+3π)的周期.解：因为tan(2x+3π+π)=tan(2x+3π)即tan ［2(x+2π)+3π］=tan(2x+3π)∴tan(2x+3π)的周期是2π.例5 求函数y=3tan(2x+3π)的对称中心的坐标.分析：y=tanx 是奇函数，它的对称中心有无穷多个，即(2πk ,0)(k ∈Z).函数y=Atan(ωx+φ)的图像可由y=tanx 经过变换图像而得到，它也有无穷多个对称中心，这些对称中心恰好为图像与x 轴交点.解：由2x+3π= 2πk ,(k ∈Z)得 x=4πk -6π(k ∈Z)∴对称中心坐标为(4πk -6π,0)(k ∈Z)注意：函数y=Atan(ωx+φ)(A ＞0,ω＞0)的图像及性质可与函数y=Asin(ωx+φ)(A ＞0,ω＞0)的图像及性质加以比拟研究.【难题巧解点拔】例 判断函数f(x)=tan(x-4π)+tan(x+4π)的奇偶性，并求此函数的周期及单调区间.分析：奇偶性的判断必须考虑①定义域是否关于原点对称.②是否对任意x 有f(-x)=-f(x)，或f(-x)=f(x)成立；关于周期和单调性必须将函数化为一个三角函数的形式方可求.解：此函数的定义域为{x ｜x ∈R 且x ≠k π+4π,k ∈Z}它是关于原点对称.又f(-x) =tan(-x+4π)+tan(-x-4π)=-tan(x-4π)-tan(x+4π)=-f(x)故此函数是奇函数.y=tan(x-4)+tan(x+4)=tan ［(x-4π)+(x+4π)］［1-tan(x-4π)tan(x+4π)］=tan2x ［1+cot(x+4π)tan(x+4π)］=2tan2x∵sin(2π-a)=cosacos(2π-a)=sina∴tan(2π-a)=cotacot(2π-a)=tana故tan ［2π-(x+4π)］=cot(x+4π)即-tan(x-4π)=cot(x+4π)周期为2π当k π-2π＜2x ＜k π+2π 2πk -4x ＜x ＜2πk +4π(k ∈Z)即x ∈(2πk -4π,2πk + 4π)时，原函数是增函数.评析：此题的难点在于通过三角恒等化简，将函数化为一个三角函数.同时要求同学们必须熟悉正切函数的性质.y=Atan(ωx+φ)(A ≠0)的周期为T=ωπ.例2)]6cos(9211lg[π+-x ≤1,求函数y=cot 2x-2cotx+5的值域.分析：从条件的不等式中解出cotx 的围，然后在此条件下求被求函数的值域.解：由条件，可得0≤lg ［211-9cos(x+6π)］≤1.得-21≤cos(x+6π)≤21∴k π+3π≤x+6π≤k π+32π,k ∈Z.∴k π+6≤x ≤k π+2,k ∈Z.∴0≤cotx ≤3 y=cot 2x-2cotx+5=(cotx-1)2+4∴当x=k π+4π,k ∈Z 时，y 取最小值4.当x=k π+2π,k ∈Z 时，y 取最大值5.从而函数y=cot 2x-2cotx+5的值域是［4,5］.【典型热点考题】例1 满足tan α≥cot α的角的一个取值区间是( )A.(0，4π)B.［0，4π］C.［4π，2π］D.(4π，2π)分析：本考察正切函数单调性，应化同名函数，再化角为同一单调区间.解：由选择项，可以考虑α∈(0，2π)的性况.∵tan α≥tan(2π-α),且α, 2π-α∈(0, 2π)∴α≥2π-α,∴4π≤α＜2π.应选C.例2 函数y=x x2tan 12tan 122+-的最小正周期是( )A. 4πB. 2πC.πD.2π解法1：将四个选项分别代入函数式验算，可知B 正确. ∴应选B.解法2：y=x x2tan 12tan 122+-=cos4x∴T=42π=2π∴应选B.例3 函数y=x21log 2++x tan 的定义域是.解：x 应满足2+log 21x ≥0 ①x ＞0 ② tanx ≥0 ③x ≠k π+2π,k ∈Z ④由①②得0＜x ≤4 ⑤由③④并注意到⑤得 0＜x ≤40≤x ＜2π或π≤x ＜23π∴0＜x ＜2π或π≤x ≤4.∴应填(0，2π)∪[π，4]例4 如果α、β∈(2π,π),且tan α＜cot β,那么必有( )A.α＜βB.β＜αC.α+β＜23πD.α+β＞23π解：∵tan α＜cot β＜0，∴tan αtan β＞1.有tan(α+β)=βαβαtan tan 1tan tan -+＞0有α+β∈(π，23π)∴α+β＜23π.∴应选C.说明：此题也可采取化为同名函数的方法，或都取特殊值比方取α=β=32π,可排除A 、B 、D.【同步达纲练习】 一、选择题1.以下不等关系中，正确的选项是( )A.cot3＞cot4＞cot5B.cot4＞cot3＞cot5 B.cot4＞cot5＞cot3 D.cot5＞cot4＞cot32.以下不等式中，正确的选项是( )A.tan 74π＞tan 73πB.tan(-413π)＞tan(-512π)C.cot4＜cot3D.cot281°＜cot665°3.观察正切曲线，满足条件｜tanx ｜≤1的x 的取值围是(其中k ∈Z) ( )A.(2k π-4π,2k π+4π)B.(k π,k π+4π)C.(k π-4π,k π+4π)D.(k π+4π,k π+43π)4.函数y=tanx-cotx 的奇偶性是( )A.奇函数B.偶函数C.既是奇函数，也是偶函数D.非奇非偶函数5.如果4π＜θ＜2π，那么sin θ,cos θ,tan θ的大小关系是( )A.sin θ＜cos θ＜tan θB.cos θ＜sin θ＜tan θC.tan θ＜sin θ＜cos θD.cos θ＜tan θ＜sin θ6.y=tanx+cotx 的最小正周期是( ) A.πB. 2πC. 4πD.以上均不正确7.将函数y=tan2x 的图像向右平移4π个单位后得到的图像的解析式为( )A.y=tan(2x+4π)B.y=tan(2x-4π)C.y=cot2xD.y=-cot2x8.假设tan(2x-3π)≤1,那么x 的取值围是( )A. 2πk -12π≤x ≤2πk +247π(k ∈Z)B. 2πk -12π＜x ≤2πk +247π(k ∈Z)C.k π-12π≤x ＜k π+247π(k ∈Z)D.k π-12π＜x ＜k π+247π(k ∈Z)9.函数f(x)=xx cot cot 1+的定义域为( ) A.(k π,k π+2π),k ∈Z B.(k π-2π,k π),k ∈ZC.(k π,k π+π),k ∈ZD.以上均不正确10.以下命题中正确的选项是( ) A.y=tanx 在第一象限单调递增. B.在y=cotx 中，x 越大，y 反而越小 C.当x ＞0时，tanx ＞0. D.以上均不正确.11.函数y=tan(21x-3π)在一个周期的图像是( )12.函数f(x)=x x xx 2sin 2cos 2sin 2cos -+的最小正周期是( )A.4πB.2πC.πD. 2π二、填空题1.使函数y=tanx 和y=cosx 同时为单调递增函数的区间是.2.满足tan α＜cot α的角α的围是.3.函数y=3tan(21x-4π)的定义域是，值域是.4.函数y=sinx+cotx 的图像关于对称.三、解答题：1.求以下函数的定义域：(1)y=x x sin 21)1lg(tan -- (2)y=)3tan(1cos 2π--x x(3)y=2cot3x-2.求函数y=θθθθtan sec tan sec 22-+的值域.3.求函数y=-2tan(3x+3π)的定义域、值域，并指出它的周期性，奇偶性和单调性.4.f(x)=tan(2x-b π)的图像的一个对称中心为(3π，0)，假设｜b ｜＜31，求b 的值.【素质优化训练】1.解不等式3tan 2(2x-4π)-(3-3)tan(2x-4π)-3≤0.2.函数f(x)=tan(ωx+φ),且对于定义域任何实数x ，都有f(x)=f(x+1)-f(x+2),比拟tan(ωa+φ+3ω)与tan(ωa+φ-3ω)的大小.3.有两个函数f 1(x)=asin(kx+3π),f 2(x)=bsin(kx-3π)(k ＞0)它们的最小正周期之和为2π，且f 1(2π)=f 2(2π),f 1(4π)=-3f 2(4π)+1,求a 、b 、k 之值.4.关于x 的一元二次方程4x 2+5x+k=0的两根分别为sin θ、cos θ,(1)求k.(2)求以tan θ、cot θ为两根的一元二次方程.5.求证：函数y=Atan(ωx+φ)(A ω≠0)为奇函数的充要条件是φ=k π(k ∈Z).答案：【同步达纲练习】一、1.C 2.B 3.C 4.A 5.B 6.A 7.D 8.B 9.A 10.D 11.A 12.D二、1.［2k π-π,2k π-2π)和(2k π-2π,2k π](k ∈Z)2.(k π,k π+4π)∪(k π+2π,k π+43π)(k ∈Z)3.{x ｜x ≠2k π+23π,k ∈Z}4.(k π,0)(k ∈Z)三、1.(1)(2k π-43π,2k π-2π)(k ∈Z)(2){x ｜2k π-3π≤x ＜2k π+3π,且x ≠2k π-6π,k ∈Z }(3){x ｜2k π+3π≤x ＜2k π+2π,k ∈Z }2. 31≤y ≤33.定义域{x ｜x ≠3πk +18π,k ∈Z}值域R ，周期3π，非奇非偶函数在区间(3πk -185π,3πk +18π)(k ∈Z)上是单调减函数..11 / 11 4.b=-31【素质优化训练】1.{k ｜2πk +24π≤x ≤2πk +4π,k ∈Z}2.相等3.a=-3-1,b=3+1,k=24.(1)k=89 (2)x 2-932x+1=05.略。
三角函数的正切与余切的关系
三角函数的正切与余切的关系三角函数是数学中一个重要的分支，其中正切和余切是两个常见的三角函数。
正切函数和余切函数之间存在着一定的关系，本文将探讨正切与余切之间的关系以及相关性质。
一、正切和余切的定义1. 正切函数的定义正切函数（tangent function）是指在单位圆上，某一角的正切值等于这个角的对边长度与邻边长度的比值。
设角度为θ，那么正切函数的定义公式可以表示为：tan(θ) = sin(θ) / cos(θ)2. 余切函数的定义余切函数（cotangent function）是指在单位圆上，某一角的余切值等于这个角的邻边长度与对边长度的比值。
设角度为θ，那么余切函数的定义公式可以表示为：cot(θ) = cos(θ) / sin(θ)二、正切与余切的关系1. 互为倒数关系正切函数与余切函数之间存在互为倒数的关系。
可以通过以上定义公式进行证明：tan(θ) = sin(θ) / cos(θ)cot(θ) = cos(θ) / sin(θ)将正切函数的定义公式中的sin(θ) / cos(θ) 乘上cos(θ) / cos(θ)，得到：tan(θ) = sin(θ) / cos(θ) * cos(θ) / cos(θ)= sin(θ) * cos(θ) / (cos^2(θ))根据三角恒等式sin^2(θ) + cos^2(θ) = 1，我们可以将cos^2(θ) 转换成 1 - sin^2(θ)，代入上式：tan(θ) = sin(θ) * (1 - sin^2(θ)) / (1 - sin^2(θ))= sin(θ) * (1 - sin^2(θ)) / cos^2(θ)根据三角恒等式sin^2(θ)+ cos^2(θ) = 1，可以将上式简化为：tan(θ) = sin(θ) / cos^2(θ)= 1 / (cos(θ) / sin(θ))= 1 / cot(θ)所以，正切函数与余切函数之间满足互为倒数的关系。
cot函数的图像和性质
cot函数的图像和性质
cot余切的图像如下，余切与正切互为倒数，任意角终边上除顶点外的任一点的横坐标除以该点的非零纵坐标,角的顶点与平面直角坐标系的原点重合,而该角的始边则与正x 轴重合。
用“cot+角度”表示。
余切函数的图象由一些隔离的分支组成。
余切函数是无界函数，可取一切实数值，也是奇函数和周期函数，其最小正周期是π。
扩展资料：
余切的图像性质：
(1)定义域：余切函数的定义域是。
(2)值域：余切函数的值域是实数集R，没有最大值、最小值。
(3)周期性：余切函数是周期函数，周期是Π。
(4)奇偶性：余切函数是奇函数，它的图象关于原点对称。
(5)单调性：余切函数在每一个开区间(kΠ，（k+1）Π）（k∈Z)上都是减函数。
余切序列：“余切序列”是蝴蝶效应的一个典型例子。
以下三个数列每一项都是前一项的余切，即a(n+1)=cot(an)；初值分别为1、1.00001、1.0001，但是从第10项开始，三个数列开始形成巨大的分歧。
这就是混沌的数列，经过足够多项后，得到的数字完全可以看作是随机的，混沌的。