正切函数和余切函数的图像和性质
正切函数和余切函数的图像和性质
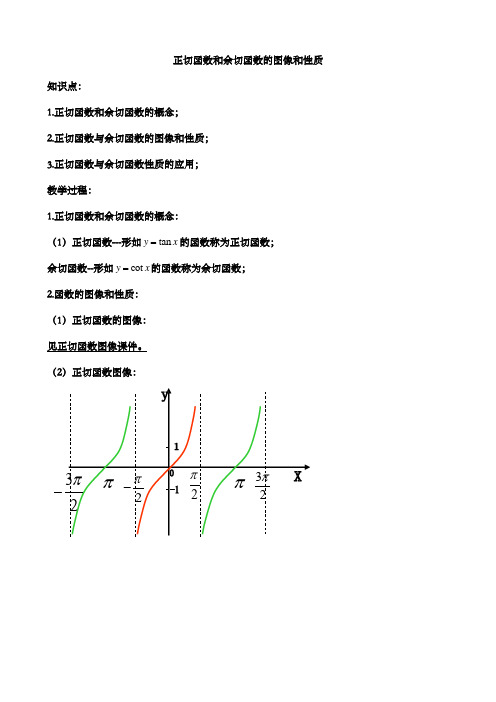
正切函数和余切函数的图像和性质知识点:1.正切函数和余切函数的概念;2.正切函数与余切函数的图像和性质;3.正切函数与余切函数性质的应用;教学过程:1.正切函数和余切函数的概念:(1)正切函数---形如tan=的函数称为正切函数;y x余切函数--形如cot=的函数称为余切函数;y x2.函数的图像和性质:(1)正切函数的图像:见正切函数图像课件。
(2)正切函数图像:-(3)与切函数的图像:归纳填表格:例1.求下列函数的周期: (1)tan(3)3y x π=-+;(2)221tgxy tg x=+;(3)cot tan y x x =-;(4)22tan21tan 2xy x=-; (5)sin 1tan tan 2x y x x ⎛⎫=+ ⎪⎝⎭例2.求下列函数的单调区间: (1)tan(2)24y x π=++;(2)tan()123x y π=-+-;(3)12log cot y x ⎛= ⎝⎭ 例3.求下列函数的定义域:(1)tan 4y x π⎛⎫=- ⎪⎝⎭;(2)y =(3)y = 例4.(1)求函数21)tan tan ]y x x =-的定义域; (2)解不等式:23tan (2)(3tan(2)044x x ππ+-+≤例5.已知2tan tan y x a x =-,当1[0,],[0,]34x a π∈∈时,函数max y =a 的值;例6.已知函数tan ,(0,)2y x x π=∈,若1212,(0,),2x x x x π∈≠。
求证:1212()()()22f x f x x xf ++>。
三角函数图像及性质的总结
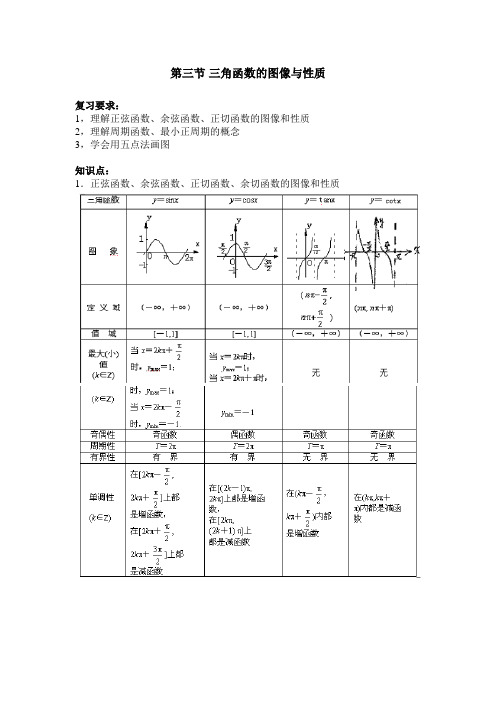
第三节三角函数的图像与性质复习要求:1,理解正弦函数、余弦函数、正切函数的图像和性质2,理解周期函数、最小正周期的概念3,学会用五点法画图知识点:1.正弦函数、余弦函数、正切函数、余切函数的图像和性质3.函数B x A y ++=)sin(ϕω),(其中00>>ωA最大值是B A +,最小值是A B -,周期是ωπ2=T ,频率是πω2=f ,相位是ϕω+x ,初相是ϕ;其图象的对称轴是直线)(2Z k k x ∈+=+ππϕω,凡是该图象与直线B y =的交点都是该图象的对称中心。
4.由y =sin x 的图象变换出y =sin(ωx +ϕ)的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换。
利用图象的变换作图象时,提倡先平移后伸缩,但先伸缩后平移也经常出现无论哪种变形,请切记每一个变换总是对字母x 而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少。
途径一:先平移变换再周期变换(伸缩变换)先将y =sin x 的图象向左(ϕ>0)或向右(ϕ<0=平移|ϕ|个单位,再将图象上各点的横坐标变为原来的ω1倍(ω>0),便得y =sin(ωx +ϕ)的图象。
途径二:先周期变换(伸缩变换)再平移变换。
先将y =sin x 的图象上各点的横坐标变为原来的ω1倍(ω>0),再沿x 轴向左(ϕ>0)或向右(ϕ<0=平移ωϕ||个单位,便得y =sin(ωx +ϕ)的图象。
5.由y =A sin(ωx +ϕ)的图象求其函数式:给出图象确定解析式y =A sin (ωx +ϕ)的题型,有时从寻找“五点”中的第一零点(-ωϕ,0)作为突破口,要从图象的升降情况找准..第一个零点的位置。
6.对称轴与对称中心: sin y x =的对称轴为2x k ππ=+,对称中心为(,0) k k Z π∈; cos y x =的对称轴为x k π=,对称中心为2(,0)k ππ+; 对于sin()y A x ωφ=+和cos()y A x ωφ=+来说,对称中心与零点相联系,对称轴与最值点联系。
常见三角函数图像及其性质
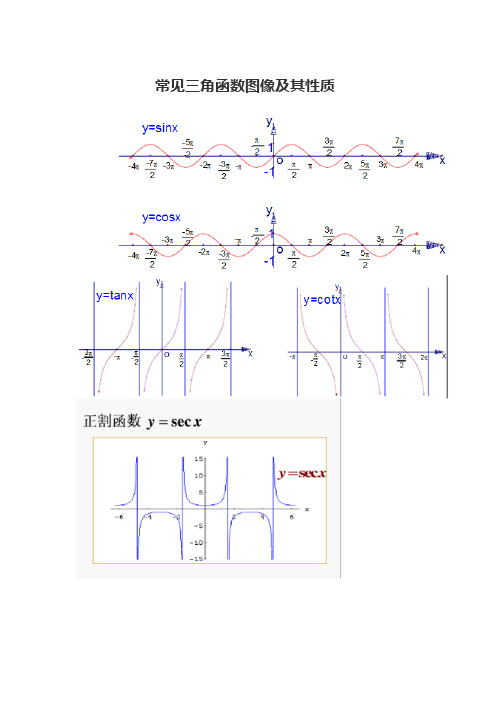
常见三角函数图像及其性质三角函数介绍正弦函数主词条:正弦函数格式:sin(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角对边长度比斜边长度的比值求出,函数值为上述比的比值,也是csc(θ)的倒数函数图像:波形曲线值域:[]1,1-余弦函数主词条:余弦函数格式:cos(θ)作用:在直角三角形中,将大小为(单位为弧度)的角邻边长度比斜边长度的比值求出,函数值为上述比的比值,也是sec(θ)的倒数函数图像:波形曲线值域:[]1,1-正切函数主词条:正切函数格式:tan(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角对边长度比邻边长度的比值求出,函数值为上述比的比值,也是cot(θ)的倒数。
函数图像:上图平面直角坐标系反映值域:()∞-∞,+余切函数主词条:余切函数格式:cot(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角邻边长度比对边长度的比值求出,函数值为上述比的比值,也是tan(θ)的倒数值域:()∞-∞,+正割函数主词条:正割函数格式:sec(θ)作用:在直角三角形中,将斜边长度比大小为θ(单位为弧度)的角邻边长度的比值求出,函数值为上述比的比值,也是cos(θ)的倒数函数图像:上图平面直角坐标系反映值域:(][)∞-1-,1∞,+余割函数主词条:余割函数格式:csc(θ)作用:在直角三角形中,将斜边长度比大小为θ(单位为弧度)的角对边长度的比值求出,函数值为上述比的比值,也是sin(θ)的倒数值域:(][)∞-1-∞,+,1。
初中数学知识归纳三角函数的基本变换与性质

初中数学知识归纳三角函数的基本变换与性质三角函数是数学中的重要概念之一,它在初中数学学科中也占有重要地位。
了解三角函数的基本变换与性质对于学生打下坚实的数学基础非常重要。
本文将对初中数学中三角函数的基本变换与性质进行归纳总结。
一、正弦函数与余弦函数的基本变换与性质1. 基本变换正弦函数和余弦函数都是周期函数,它们的图像在平面直角坐标系中表现出一定的规律。
- 平移变换:对于正弦函数和余弦函数的图像,当自变量增加或减少一个周期时,图像会向左或向右平移。
这是因为正弦函数和余弦函数的周期是固定的。
- 垂直方向的伸缩:正弦函数和余弦函数的图像在垂直方向上也会有伸缩变换。
通过改变函数的振幅值(即函数的最大值和最小值的差异),可以实现对图像的垂直伸缩变换。
2. 基本性质- 周期性:正弦函数和余弦函数的周期都是360度或2π。
换句话说,当自变量增加或减少360度或2π时,函数的值会重复。
- 范围:正弦函数和余弦函数的值在闭区间[-1, 1]内变动。
也就是说,对于任何一个角度,正弦函数的值和余弦函数的值都不会超过-1和1。
二、正切函数与余切函数的基本变换与性质1. 基本变换正切函数和余切函数也是周期函数,它们的图像在平面直角坐标系中表现出一定的规律。
- 平移变换:正切函数和余切函数的图像在自变量增加或减少π时,会向左或向右平移。
这是因为正切函数和余切函数的周期是π。
- 垂直方向的伸缩:正切函数和余切函数的图像在垂直方向上也会有伸缩变换。
通过改变函数的振幅值,可以实现对图像的垂直伸缩变换。
2. 基本性质- 周期性:正切函数和余切函数的周期都是π。
也就是说,当自变量增加或减少π时,函数的值会重复。
- 水平渐近线:正切函数和余切函数都有水平渐近线,即当自变量趋于某些特定值时,函数值趋于无穷大或无穷小。
三、基本变换与性质的应用举例1. 应用举例:在三角函数的学习中,我们经常需要根据给定的变换规律绘制函数图像,或者根据函数图像求解相关问题。
三角函数图像与性质知识点

三角函数图像与性质知识点三角函数是数学中的重要概念,它们的图像与性质对于理解和解决各种数学问题具有重要的作用。
本文将介绍三角函数的图像与性质的知识点,希望能帮助读者更好地掌握这一概念。
一、正弦函数的图像与性质正弦函数是最基本的三角函数之一,它的图像可以用来描述周期性变化的现象。
它的定义域为实数集,值域为[-1,1]。
正弦函数的图像为连续的波浪线,称为正弦曲线。
正弦函数的图像具有以下性质:1. 周期性:正弦函数的最小正周期为2π,在一个周期内,正弦函数的图像重复出现。
2. 奇偶性:正弦函数是奇函数,即满足f(-x)=-f(x)。
3. 对称性:正弦函数的图像关于y轴对称。
二、余弦函数的图像与性质余弦函数是与正弦函数相似的三角函数,它也可以用来描述周期性变化的现象。
它的定义域为实数集,值域为[-1,1]。
余弦函数的图像为连续的波浪线,称为余弦曲线。
余弦函数的图像具有以下性质:1. 周期性:余弦函数的最小正周期为2π,在一个周期内,余弦函数的图像重复出现。
2. 奇偶性:余弦函数是偶函数,即满足f(-x)=f(x)。
3. 对称性:余弦函数的图像关于y轴对称。
三、正切函数的图像与性质正切函数是另一个重要的三角函数,它描述的是角度的比值。
它的定义域为实数集,值域为全体实数。
正切函数的图像为由正无穷连续延伸到负无穷的曲线,称为正切曲线。
正切函数的图像具有以下性质:1. 周期性:正切函数的最小正周期为π,在一个周期内,正切函数的图像重复出现。
2. 奇偶性:正切函数是奇函数,即满足f(-x)=-f(x)。
3. 垂直渐近线:正切函数的图像有两条垂直渐近线,分别为x=π/2+kπ(k为整数)和x=-π/2+kπ(k为整数)。
四、割函数与余割函数的图像与性质割函数和余割函数是与正切函数和余弦函数相对应的两个三角函数。
割函数的定义域为实数集减去所有使得余切函数为0的点,即R\{kπ}(k为整数),值域为全体实数。
余割函数的定义域为实数集减去所有使得正弦函数为0的点,即R\{kπ}(k为整数),值域为全体实数。
高一数学正切函数和余切函数的图像与性质1(学生版)

(2)
例2、求函数 的定义域、值域,并指出它的周期性、奇偶性、单调性。
变式练习1:讨论函数 的性质
变式练习2: 的单调区间怎么求?
例3、观察正切曲线写出满足tanx>0的x的值的范围:
变式练习:方法同上,求出分别满足下列条件的x的值的范围
(1)
(2)
例4、求下列函数的定义域
(1)y=tan2x
例5、求学下列函数的最小正周期和单调区间
(1) ;
(2)
【课堂小练】
1、函数y=tan(ax+ )(a≠0)的最小正周期为( )
2、以下函数中,不是奇函数的是( )
A y=sinx+tanxB.y=xtanx-1C.y= D.y=lg
3、下列命题中正确的是( )
A.y=cosx在第二象限是减函数B.y=tanx在定义域内是增函数
C.y=|cos(2x+ )|的周期是 D.y=sin|x|是周期为2π的偶函数
4、函数y= + 的定义域是( )
A (2k+1)π≤x≤(2k+1)π+ ,k∈Z
B (2k+1)π<x<(2k+1)π+ ,k∈Z
C (2k+1)π≤x<(2k+1)π+ ,k∈Z
D (2k+1)π<x<(2k+1)π+ 或x=kπ,k∈Z
5、已知y=tan2x-2tanx+3,求它的最小值
6、求适合下列条件的 的集合:
6.单调性:在开区间 内,函数单调递增
余切函数y=cotx的图象及其性质(要求学生了解):
——即将 的图象,向左平移 个单位,
再以x轴为对称轴上下翻折,即得 的图象
定义域:
值域:R,
当 时 ,当 时
周期:
奇偶性:奇函数
单调性:在区间 上函数单调递减
三角函数及反三角函数的图像及性质
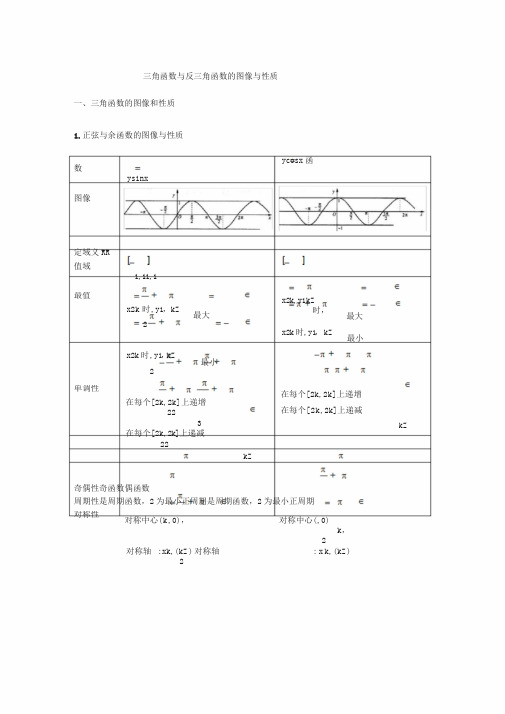
三角函数与反三角函数的图像与性质一、三角函数的图像和性质1.正弦与余函数的图像与性质ycosx函数ysinx图像定域义RR值域1,11,1最值x2k时,y1,kZ最大2 x2k,y1kZ时,最大x2k时,y1,kZ最小x2k时,y1,kZ最小2单调性在每个[2k,2k]上递增22 在每个[2k,2k]上递增在每个[2k,2k]上递减3在每个[2k,2k]上递减22kZkZ奇偶性奇函数偶函数周期性是周期函数,2为最小正周期是周期函数,2为最小正周期对称性对称中心(k,0),对称中心(,0)k,2对称轴:xk,(kZ)对称轴2:x k,(kZ)2.正切与余切函数的图像与性质函数ytanxycotx图像定域义{x|xR且xk,kZ}{x|xR且xk,k Z}2值域RR单调性在每个(k,k)上递增在每个(,)上递减kk22kZkZ奇偶性奇函数奇函数周期性是周期函数,为最小正周期是周期函数,为最小正周期对称性k对称中心(,0)2k 对称中心(,0)2二、反三角函数的图像与性质1.反正弦与反余函数的图像与性质反余弦函数yarccosx函数反正弦函数yarcsinx是ycosx,x0,的反函数是sin,yx,x的反函数22图像定域义1,11,1值域0,,22单调性在[1,1]上递增在[1,1]上递减奇偶性奇函数非奇非偶周期性无无对称性对称中心(0,0)对称中心(0,)22.反正切与反余切函数的图像与性质函数反正切函数yarctanx反余切函数yarccotx是ycotx,x0,的反函数是tan(,)yx,x的反函数22图像定域义(,,)(,,)值域,0,22单调性在(,,)上递增在(,,)上递减奇偶性奇函数非奇非偶周期性无无对称性对称中心(0,0)对称中心(0,)2。
余切函数的定义和性质

余切函数的定义和性质余切函数,又称作切割函数,是一种用于描述角度的数学函数。
它的定义域为全体实数,值域为全体实数。
在三角函数和解析几何中,余切函数的作用至关重要。
在这篇文章中,我们将讨论余切函数的定义和性质,帮助读者更好地理解和应用此函数。
一、余切函数的定义余切函数定义为正切函数的倒数,即:$$cotx=\frac{1}{tanx}$$其中,$x$ 为弧度制下的角度。
例如,当$x=\frac{\pi}{4}$ 时,$cotx$ 的值为 $1$。
二、余切函数的图像余切函数的图像可以通过正切函数的图像推导得到。
正切函数的周期为 $\pi$,在 $[0,\pi]$ 区间内是单调上升的。
正切函数在$x=0$ 处不存在定义,且在 $x=\frac{\pi}{2}$ 时不存在极限。
因此,在 $[0,\pi]$ 区间内,$cotx$ 的图像将存在一个垂直于 $x$ 轴的渐近线,且图像在 $0$ 和 $\pi$ 处存在一个奇点。
余切函数的图像如下所示:图像中黄色部分是余切函数的图像,蓝色的 $y=-\frac{\pi}{2}$ 和 $y=\frac{\pi}{2}$ 分别是余切函数的渐近线,绿点和紫点分别是余切函数的奇点。
三、余切函数的性质(1) 周期性余切函数的周期为 $\pi$,即 $cot(x+n\pi)=cotx$,其中 $n$ 为任意整数。
(2) 偶函数余切函数是偶函数,即 $cot(-x)=cotx$。
(3) 奇点余切函数在 $x=0$ 和 $x=\pi$ 处存在奇点。
当 $x$ 趋近于$0$ 或 $\pi$ 时,$cotx$ 的绝对值将趋近于无穷大。
(4) 符号变化余切函数的符号随角度的变化而变化。
当 $x$ 在$(0,\frac{\pi}{2})$ 范围内时,$cotx$ 为正数;当 $x$ 在$(\frac{\pi}{2},\pi)$ 范围内时,$cotx$ 为负数;当 $x$ 等于 $0$ 或$\pi$ 时,$cotx$ 不存在符号。
