2019-2020学年湘教版八年级数学上册期末检测卷(有答案)AlPlHH-最新推荐
湘教版2019-2020学年八年级上学期数学期末考试试卷(I)卷

湘教版2019-2020学年八年级上学期数学期末考试试卷(I)卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)下列图形中,是轴对称图形又是中心对称图形的是()A .B .C .D .2. (2分)计算结果正确的是()A .B .C .D .3. (2分)将2.05×10﹣3用小数表示为()A . 0.000205B . 0.00205C . 0.0205D . ﹣0.002054. (2分)如图,点B,E,C,F在同一条直线上,AB∥DE,AB=DE,要用SAS证明△ABC≌△DEF,可以添加的条件是()A . ∠A=∠DB . AC∥DFC . BE=CFD . AC=DF、5. (2分)下列分式中,最简分式是()A .B .C .D .6. (2分)如图,在△ABC中,AD是∠BAC的平分线,为AD上一点,且EF⊥BC于点F.若∠C=35°,∠DEF=15°,则∠B的度数为()A . 65°B . 70°C . 75°D . 85°7. (2分)如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一矩形如图,通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是()A . (a﹣b)(a+2b)=a2﹣2b2+abB . (a+b)2=a2+2ab+b2C . (a﹣b)2=a2﹣2ab+b2D . (a﹣b)(a+b)=a2﹣b28. (2分)若a=3﹣,则代数式a2﹣6a﹣2的值是()A . 0B . 1C . ﹣1D .9. (2分)如图,用直尺和圆规作一个角的平分线,是运用了“全等三角形的对应角相等”这一性质,由作图所得条件,判定三角形全等运用的方法是()A . SSSB . ASAC . AASD . SAS10. (2分)如图,在△ABC中,∠A=36°,AC=AB=2,将△ABC绕点B逆时针方向旋转得到△DBE,使点E在边AC上,DE交AB于点F,则△AFE与△DBF的面积之比等于()A .B .C .D .二、填空题 (共8题;共8分)11. (1分)一个点的纵坐标不变,把横坐标乘以-1,得到的点与原来的点的关系是________.12. (1分)如图,点E , F分别是四边形AB , AD上的点,已知△ EBC≌△ DFC,且∠A = 80°,则∠BCF的度数是 ________.13. (1分)在函数中,自变量x的取值范围是________.14. (1分)某校组织1080名学生去外地参观,现有A、B两种不同型号的客车可供选择.每辆B型客车的载客量比每辆A型客车多坐15人,若只选择B型客车比只选择A型客车少租12辆(每辆客车均坐满).设B型客车每辆坐x人,则列方程为________.15. (1分)如图所示,AB//CD,O为∠A、∠C的平分线的交点O,OE⊥AC于E,且OE=2,则AB与CD之间的距离等于________.16. (1分)如图,在矩形ABCD中,AB=2,对角线AC , BD相交于点O , AE垂直平分OB于点E ,则AD的长为________.17. (1分)若规定运算符号“★”具有性质:a★b=a2﹣ab.例如(﹣1)★2=(﹣1)2﹣(﹣1)×2=3,则1★(﹣2)=________.18. (1分)某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD 对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F,G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m,根据设计要求,若∠EOF=45°,则此窗户的透光率(透光区域与矩形窗面的面积的比值)为________.三、解答题 (共6题;共50分)19. (10分)计算:(1)﹣22×(π﹣3.14)0﹣|﹣5|×(﹣1)2019(2)3x2y2﹣4x3y2÷(﹣2x)+(﹣3xy)220. (10分)因式分解:(1)(2) .21. (5分)已知关于x的方程的解是,求代数式的值.22. (5分)佳佳文具店购进A,B两种款式的笔袋,其中A种笔袋的单价比B种袋的单价低10%.已知店主购进A种笔袋用了810元,购进B种笔袋用了600元,且所购进的A 种笔袋的数量比B种笔袋多20个.请问:文具店购进A,B两种款式的笔袋各多少个?23. (5分)如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=900 .小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?24. (15分)如图,在平行四边形ABCD中,点E,F分别是BC,AD的中点.(1)求证:△ABE≌△CDF;(2)若AE=CE,BC=2AB,BC=6,求四边形AECF的面积.参考答案一、单选题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共8题;共8分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、18-1、三、解答题 (共6题;共50分) 19-1、19-2、20-1、20-2、21-1、22-1、23-1、24-1、24-2、第11 页共11 页。
2019-2020年新湘教版八年级上册数学期末模拟试题及答案解析

第一学期期末八年级数学试卷一、选择题(共12个小题,每小题3分,共36分)1.若分式211x x --的值为0,则x 的值为( )A. 0B. 1C. -1D.1±2.化简22a b ab b a--结果正确的是( )A.ab B. ab - C. 22a b - D. 22b a -3.若代数式23x x -- 有意义,则x 的取值范围是( ) A .23x x >≠且 B .2x ≥ C .3x ≠ D .3x x ≠≥2且 4.在实数722,5-, 2π,38,3.14中,无理数有( ) A.1个 B.2个 C.3个 D.4个5. 下列图形中,不是..轴对称图形的是( )A .B .C .D .6.如图,两个较大正方形的面积分别为225,289,则字母A 所代表的正方形的面积为( )A .4B .8C .16D .647.已知一个三角形的三个内角的比是1∶2∶1,则这三个内角对应的三条边的比是( )A .1∶1∶ 2B .1∶1∶2C .1∶2∶1D .1∶4∶18. 将一副直角三角板,按如图所示叠放在一起,则图中∠α的度数是( ) A. 45o B. 60o C.75o D.90o9 . 下列运算错误的是( )A.2(3)3-= B.326⨯=C.632÷=D.325+=10. 已知:0132=+-a a ,则21-+aa 的值为( ) A . 15- B . 1 C . -1D . -511. 如图,AD 是△ABC 中∠BAC 的角平分线,DE ⊥AB 于点E ,S △ABC =7,DE=2,AB=4, 则AC 长是( )A.6B. 5C. 4D. 3第11题 第12题12. 如图,在Rt △ABC 中,∠ACB=90°,AC=6,BC=8,AD 是∠BAC 的平分线.若P ,Q 分别是AD 和AC 上的动点,则PC+PQ 的最小值是( ) A.2.4 B. 4 C. 4.8 D. 5二、填空题 (共8个小题,每小题3分,共24分) 13.16的平方根是 .14.计算:(53)(53)+-= .15.若实数x y ,满足23(2)0x y ++-=,则代数式2xy 的值是 .16.若2 016-(x -2 016)2=x ,则x 的取值范围是________.17.一个等腰三角形的两边长分别为5和6,则这个等腰三角形的周长是 .18.如图,等腰△ABC 中,AB=AC ,∠DBC=15°,AB 的垂直平分线MN 交AC 于点D ,则∠A 的度数是 _________ .DCBA第18题 第19题 19.如图,AB AC AD ==,80BAD ∠=︒ ,则BCD ∠的大小是 .20. 有一个计算程序,每次运算都是把一个数先乘以2,再除以它与1的和,多次重复进行这种运算的过程如下:则第n 次运算的结果n y = (用含字母x 和n 的代数式表示). 三、解答题 (共10个小题,每小题6分,共60分)21.计算:11(412489)43+-÷18 22、化简:2121a a a a a -+⎛⎫-÷⎪⎝⎭23. 已知:1x y -= , 3(2)343x y += ,求代数式32x y +的值.24. 如图,在△ABC 中,点D ,E ,F 分别是AB ,BC ,CA 的中点,AH 是边BC 上的高.(1)求证:四边形ADEF 是平行四边形;(2)求证:∠DHF=∠DEF.25. 解关于x 的方程:2131x x x =++-.26. 先化简,再求值:⎪⎭⎫ ⎝⎛--+÷--2526332a a a a a ,其中0132=-+a a .27. 为了进一步落实“节能减排”措施,冬季供暖来临前,某单位决定对9000平方米的“外墙保温”工程进行招标,现有甲、乙两个工程队参与投标,比较这两个工程队的标书发现:乙队每天完成的工程量是甲队的1.5倍,这样乙队单独干比甲队单独干能提前15天完成任务.问甲队每天完成多少平方米?28. 如图,四边形ABCD 中,90B ∠=︒,4AB =,3BC =,13CD =,12AD =,求四边形ABCD 的面积.29. 已知:如图,在ABC ∆中,点D 是BC 的中点,过点D 作直线交AB ,CA 的延长线于点E ,F . 当BE CF =时,求证:AE AF =.FEDCBA30. 如图,在ABC ∆中,90C ∠=︒,60BAC ∠=︒,1AC =,点D 在BC 上,点E 在AB 上,使得ADE ∆是等腰直角三角形,90ADE ∠=︒,求BE 的长. (提示: 可以运用“直角三角形中,30︒角所对的直角边等于斜边的一半”.31、已知:如图,ABC ∆中,点D 是BC 边上的一点,60ADE ABC ∠=∠=︒,DE 交ABC ∠的外角平分线于点E . 求证:ADE ∆是等边三角形.FEDCBAED CB A32.感知:如图①,点E在正方形ABCD的BC边上,BF⊥AE于点F,DG⊥AE于点G.可知△ADG≌△BAF.(不要求证明)拓展:如图②,点B、C在∠MAN的边AM、AN上,点E, F在∠MAN内部的射线AD 上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:△ABE≌△CAF.应用:如图③,在等腰三角形ABC中,AB=AC,AB>BC.点D在边B上.CD=2BD.点E, F在线段AD上.∠1=∠2=∠BAC.若△ABC的面积为9,则△ABE与△CDF的面积之和为_________.数学试题答案及评分参考一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 CBDBADDCDBDC二、填空题 题号 1314 151617 181920答案4±26-4717或1650︒ 140︒2(21)1n nxx -+三、解答题21. 解:原式=(83333)+-÷32 ………………………………………4分=63÷32 ……………………………………………5分6 ………………………………………………………… 6分22. 解:∵1x y -= , 3(2)343x y += ,∴ 127x y x y -=⎧⎨+=⎩ ……………………………………………………… 3分解得32x y =⎧⎨=⎩ ……………………………………………………5分∴32332213x y +=⨯+⨯= ……………………………………………6分23. 解:原式=221(1)a a a a--÷ ……………………………………………3分 =2(1)(1)(1)a a aa a +-⨯- ……………………………………………5分 11a a +=-. ………………………………………………6分24.证明:∵AD EB =,∴AD BD EB BD -=-.即AB ED =. ……………………………………………………………… 1分∵AC ∥EF ,∴A E ∠=∠. ……………………………………………………………… 2分 在△ABC 和△EDF 中,,,,AB ED A E AC EF =⎧⎪∠=∠⎨⎪=⎩∴ △ABC ≌△EDF . ……………………………………………………… 5分 ∴ BC=DF . ……………………………………………………………… 6分25. 解:方程两边同乘以(3)(1)x x +-,得(1)(3)(1)2(3)x x x x x -=+-++. ……………………………………………2分解这个整式方程,得35x =-. …………………………………………… 4分 检验:当35x =-时,(3)(1)0x x +-≠.…………………………………………5分 35x ∴=-是原方程的解. ……………………………………………6分26. 解:⎪⎭⎫ ⎝⎛--+÷--2526332a a a a a =()()()⎥⎦⎤⎢⎣⎡----+÷--25222233a a a a a a a …………………………………………… 2分 =()292332--÷--a a a a a …………………………………………… 3分 =()()()332233-+-•--a a a a a a …………………………………………… 4分=()()aa a a 3313312+=+ …………………………………………… 5分 ∵ 0132=-+a a ,∴ 132=+a a∴ 原式=31…………………………………………… 6分27. 解:设甲队每天完成x 平方米,则乙队每天完成1.5x 平方米………………… 1分根据题意列方程,得90009000151.5x x-= …………………………………………… 3分 解这个方程,得200x = ……………………………………………5分 经检验,200x =,是所列方程的解. ………………………………………6分答:甲队每天完成200平方米.28.解:连结AC .在△ABC 中,∵90B ∠=︒,AB=4,BC=3,∴5AC ==,………… 1分 1143622ABCSAB BC ==⨯⨯=. ………… 2分 在△ACD 中,∵AD=12,AC=5,CD=13,∴222AD AC CD +=. ………………………… 3分∴△ACD 是直角三角形.……………………………………………………… 4分 ∴115123022ACD SAC AD ==⨯⨯=. …………………………………… 5分 ∴四边形ABCD 的面积=63036ABCACDSS+=+=. (6)分29.证明:过点B 作BG ∥FC ,延长FD 交BG 于点G .∴G F ∠=∠.………………………… 1分 ∵点D 是BC 的中点,∴BD=CD . …………………………… 2分 在△BDG 和△CDF 中,,,,G F BDG CDF BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩ABCDGABCDEF∴△BDG≌△CDF.∴BG=CF.……………………………3分∵BE=CF,∴BE=BG.∴G BEG∠=∠.…………………………………………………………4分∵BEG AEF∠=∠,∴G AEF∠=∠.∴F AEF∠=∠.…………………………………………………………5分∴AE=AF.…………………………………………………………………6分30. 证明:在线段BA上截取BM,使BM=BD.…………………………1分∵∠ABC=60°,∴△BDM为等边三角形,∠ABF=120°,∴DM=DB,∠BDM=∠BMD=60°,∠AMD=120°,……………………2分又∵BE平分∠ABF,∴∠DBE=120°,∴∠AMD=∠DBE,…………………………………3分∵∠ADE =∠BDM =60°,∴∠1=∠2 …………………………………………4分∴△ADM≌△EDB(ASA).………………………5分∴AD=ED.∴△ADE为等边三角形.…………………………6分12MABC DE选做题 (5分)解:过点E 作EF ⊥BC 于F ,∵90ADE ∠=︒, ∴∠1+∠3=90°, ∵∠2+∠3=90°, ∴∠1=∠2,又∵∠DFE =∠ACD =90°,DE =AD ,∴△ACD ≌△DFE (AAS ).………………………… 2分 ∴AC=DF=1,∵在ABC ∆中,90C ∠=︒,60BAC ∠=︒,1AC =, ∴AB=2,DC =FE ,在Rt △ADE 中,设EF 为x ,则DC 为x , BE 为2x ,BF,∴1+x +=解得2x =-∴4BE =-…………………………………… 5分312FABCD E。
湘教版2019-2020八年级数学第一学期期末模拟测试题3(附答案)

23.已知a,b互为相反数,c,d互为倒数,x是3的平方根,求 的值.
24.先化简,再求值:( ,其中
25.如图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.
(1)求证:△ABE≌△BCF;
(2)若∠CBF=65°,求∠AGC的度数.
26.在△ABC中,O为内心,点E、F都在大边BC上.已知BF=BA,CE=CA.求证:∠EOF=∠ABC+∠ACB.
27.观察下面的式子: , , ,….
(1)类比上述式子,再写出几个同类型的式子(至少写3个);
(2)请你将发现的规律用含自然数 的等式表示出来,并给出证明.
故选:D.
点睛:本题考查了函数中自变量的取值范围、分式有意义的条件;由分式有意义得出不等式是解决问题的关键.
10.D
【解析】
【分析】
根据同底数幂的运算法则、幂的乘方、合并同类项的法则进行计算即可.
【详解】
解:A、应为a2•a3=a5,故本选项错误;
B、应为y3÷y3=1,故本选项错误;
C、3m与3n不是同类项,不能合并,故本选项错误;
【详解】
= .
故选A.
【点睛】
本题考查了负整数指数科学记数法,对于一个绝对值小于1的非0小数,用科学记数法写成 的形式,其中 ,n是正整数,n等于原数中第一个非0数字前面所有0的个数(包括小数点前面的0).
3.B.
【解析】
试题分析:根据平方根和立方根的定义逐一进行计算得出结论.A. ,故A错误;B. ,故B正确;C. ,故C错误;D. ,故D错误,只有B是正确的.
最新2019-2020年度湘教版八年级数学上学期期末模拟测试卷及答案解析-精编试题

湘教版最新八年级数学上学期期末测试一、选择题(每题3分)1、下列四个图案中,是轴对称图形的是 ( )2、如果把分式xyy x +中的x 和y 都扩大10倍,则分式的值( ) A 、扩大10倍 B 、缩小10倍 C 、不变 D 、扩大100倍3、已知一个等腰三角形两边长分别为5,6,则它的周长为( )A .16B .17C .16或17D .10或124、下列各式由左边到右边的变形中,是分解因式的为( ).A .ay ax y x a +=+)(B .4)4(442+-=+-x x x xC .)12(55102-=-x x x xD .x x x x x 3)4)(4(3162++-=+-5、△ABC 中,∠A :∠B :∠C=1:2:3,最小边BC=3cm,最长边AB 的长为( )A.9cmB. 8 cmC. 7 cmD.6 cm6、如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是( ) A 180° B 220° C 240° D . 300°7、下列运算正确的是 ( )A.4222x x x =+B.532.x x x =C.64216)2(x x =-D.(x+3y)(x-3y)=223y x -8、如图,将两根钢条AA'、BB'的中点O 连在一起,使AA'、BB'可以绕着点O 自由转动,就做成了一个测量工件,则A'B'的长等于内槽宽AB ,那么判定△OAB ≌△OA ′B ′的理由是( )A 、SASB 、ASAC 、SSSD 、AAS9、如图,在△ABC 中,AB =AC ,D 是AB 的中点,且DE ⊥AB 于点D ,AB=10,BC=4,则△BEC 的周长( )A 、14;B 、6;C 、9;D 、1210、如图:在△ABC 中,∠ACB=900,CD 是高,∠A=︒30,BD=4cm,则AD=( )cmA 、14;B 、6;C 、9;D 、12二、填空题(每题3分)11、16的算术平方根是。
湘教版2019--2020学年度第一学期期末考试八年级数学试卷
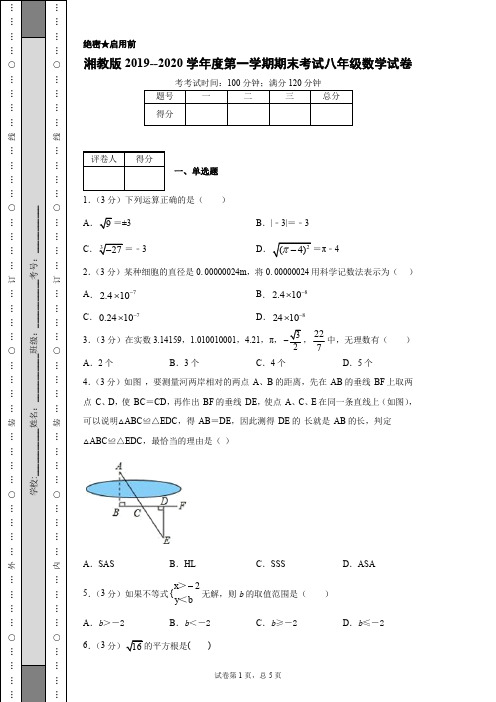
试卷第1页,总5页 绝密★启用前 湘教版2019--2020学年度第一学期期末考试八年级数学试卷 考考试时间:100分钟;满分120分钟 一、单选题1.(3分)下列运算正确的是( ) A ±3 B .|﹣3|=﹣3 C =﹣3 D π﹣4 2.(3分)某种细胞的直径是0. 00000024m ,将0. 00000024用科学记数法表示为( ) A .72.410-⨯ B .82.410-⨯ C .70.2410-⨯ D .82410-⨯ 3.(3分)在实数3.14159,1.010010001,4.21,π,,227中,无理数有( ) A .2个 B .3个 C .4个 D .5个 4.(3分)如图 ,要测量河两岸相对的两点 A 、B 的距离,先在 AB 的垂线 BF 上取两点 C 、D ,使 BC =CD ,再作出 BF 的垂线 DE ,使点 A 、C 、E 在同一条直线上(如图),可以说明△ABC ≌△EDC ,得 AB =DE ,因此测得 DE 的 长就是 AB 的长,判定△ABC ≌△EDC ,最恰当的理由是( ) A .SAS B .HL C .SSS D .ASA 5.(3分)如果不等式2{x y b -><无解,则b 的取值范围是( ) A .b >-2 B .b <-2 C .b ≥-2 D .b ≤-2 6.(3( )试卷第2页,总5页 A .﹣4 B .±2 C .±4 D .4 7.(3分)若分式方程13224a x x +=--有增根,则a 的值是( ) A .1 B .2 C .-1 D .-2 8.(3分)若x y >,且(3)(3)a x a y -<-,则a 的值可能是( ) A .0 B .3 C .4 D .5 9.(3分)已知:a ,b , 则a 与b 的关系是( ) A .1ab = B .0a b += C .0a b -= D .22a b = 10.(3分)十一期间,几名同学共同包租一辆中巴车去红海滩游玩,中巴车的租价为480元,出发时又有4名学生参加进来,结果每位同学比原来少分摊4元车费.设原来游玩的同学有x 名,则可得方程( )A .48048044x x -=+ B .48048044x x -=-C .48048044x x -=- D .48048044x x -=+二、填空题11.(4分)若代数式33x -有意义,则x 的取值范围是__.12.(4__________.13.(4分)小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带第_____块。
湘教版2019-2020学年上学期八年级数学期末模拟测试卷新版

湘教版2019-2020学年上学期八年级数学期末模拟测试卷新版一、单选题 (共10题;共30分)1. (3分)如图,AC=DF,∠1=∠2,如果根据“AAS”判定△ABC≌△DEF,那么需要补充的条件是()A . ∠A=∠DB . AB=DEC . BF=CED . ∠B=∠E2. (3分)若a,b,C是△ABC的三条边,且满足a2﹣2ab+b2=0,(a+b)2=2ab+c2 ,则△ABC的形状为()A . 直角三角形B . 等腰三角形C . 等边三角形D . 等腰直角三角形3. (3分)下列各组数中是勾股数的是()A . 4,5,6B . 0.3,0.4,0.5C . 1,2,3D . 5,12,134. (3分)下列命题中,正确的命题有几个()①对顶角相等②相等的角是对顶角③不是对顶角的两个角就不相等④不相等的角不是对顶角A . 1个B . 2个C . 3个D . 0个5. (3分)如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F,则下列结论正确的是()A . 点F在BC边的垂直平分线上B . 点F在∠BAC的平分线上C . △BCF是等腰三角形D . △BCF是直角三角形6. (3分)下列运算正确的是()A .B .C .D .7. (3分)下列各式中能用平方差公式的是()A . (2a﹣3)(﹣2a+3)B . (a+b)(﹣a﹣b)C . (3a+b)(b﹣3a)D . (a+1)(a﹣2)8. (3分)下列三个命题中,是真命题的有()①对角线相等的四边形是矩形;②三个角是直角的四边形是矩形;③有一个角是直角的平行四边形是矩形.A . 3个B . 2个C . 1个D . 0个9. (3分)(2017•广元)如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为F,连结DF,下列四个结论:①△AEF∽△CAB;②tan∠CAD= ;③DF=DC;④CF=2AF,正确的是()A . ①②③B . ②③④C . ①③④D . ①②④10. (3分)等腰△ABC中,AB=AC,∠A=36°,D是AC上的一点,AD=BD,则以下结论中正确的有()①△BCD是等腰三角形;②点D是线段AC的黄金分割点;③△BCD∽△ABC;④BD平分∠ABC.A . 1个B . 2个C . 3个D . 4个二、填空题 (共10题;共36分)11. (3分) =________.12. (3分)(2015•广东)分解因式:m2﹣4=________.13. (3分)(2017•重庆)计算:|﹣3|+(﹣4)0=________.14. (3分)(a2)3=________.15. (3分)如图,△ABC中,AB=AC,点D,E在BC边上,若要以“SAS”为依据说明△ABD≌△ACE,还要添加的条件为________.16. (9分)下列各数:、、π、﹣、、0.101001…中是无理数的有________17. (3分)如图,D为Rt△ABC中斜边BC的中点,过D作BC的垂线,交AC于E,且AE=DE,若BC=12cm,则AB的长为________cm.18. (3分)如图,AB∥CF,E为DF中点,AB=20,CF=15,则BD=________.19. (3分)如图,在矩形ABCD中,AD=6,AB=4,点E,G,H,F分别在AB,BC,CD,AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE,PF,PG,PH,则△PEF和△PG H的面积和等于________.20. (3分)如图,将△ABC绕点B按逆时针方向旋转得到△EBD,点E、点D分别与点A、点C对应,且点D在边AC上,边DE交边AB于点F,△BDC∽△ABC.已知BC= ,AC=5,那么△DBF的面积等于________.三、计算题 (共3题;共25分)21. (8分)计算:(1)(2)22. (9分)计算:(1);(2)(-a2b)2•2ab;(3)(4)(5x-2y)(5x+2y)23. (8分)因式分解(1)(2)(3)四、解答题 (共4题;共31分)24. (6分)如图,在方格纸中,线段AB的两个端点都在小方格的格点上,AB=5,请找到一个格点P,连结PA,PB,使得△PAB为等腰三角形(请画出两种,若所画三角形全等,则视为一种).25. (7分)如图,△ABC中,AD为∠BAC的平分线,且DF⊥AC于F,∠B=90°,DE=DC.求证:BE=CF.26. (8分)为培养学生的创造性思维,学校举行科技小制作比赛.对公开征集到的科技小制作作品的数量进行了分析统计,并制作了如下统计图.(1)学校共征集到作品多少件?(2)经过评选后,有2名男生和2名女生获得一等奖.现要从这4位同学中抽两人去参加表彰座谈会,请用树状图或列表法求出恰好抽中一男一女的概率.27. (10分)如图,在△ABC中,AB=AC,AD=DE=EB,BD=EC,试求∠A的度数.五、综合题 (共3题;共34分)28. (10分)如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,BC=DE.(1)求证:∠ACD=∠B;(2)若∠A=40°,求∠BCD的度数.29. (12分)如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.(1)求抛物线的解析式;(2)猜想并探究:对于任意一点P,PD与PF的差是否为固定值?如果是,请求出此定值;如果不是,请说明理由;(3)求:①当△PDE的周长最小时的点P坐标;②使△PDE的面积为整数的点P的个数.30. (12分)如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.(1)点M、N运动几秒后,M、N两点重合?(2)点M、N运动几秒后,可得到等边三角形△AMN?(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.参考答案一、单选题 (共10题;共30分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共10题;共36分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、18-1、19-1、20-1、三、计算题 (共3题;共25分) 21-1、21-2、22-1、22-2、22-3、22-4、23-1、23-2、23-3、四、解答题 (共4题;共31分) 24-1、25-1、26-1、27-1、五、综合题 (共3题;共34分)28-1、28-2、29-1、29-2、29-3、30-1、30-2、30-3、。
湘教版2019-2020学年八年级数学上学期期末原创卷(一)含解析版答案

湘教版2019-2020学年上学期期末原创卷(一)八年级数学(考试时间:120分钟试卷满分:120分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
5.考试范围:湘教版八上全册。
第Ⅰ卷一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.数π、227、、3.1416、0.3∙中,无理数的个数是A.1个B.2个C.3个D.4个2.若x y<,则下列不等式成立的是A.22x y-+<-+B.44x y>C.22x y-<-D.33x y-<-3.在-1,0,2四个数中,最大的数是A.-1 B.0C.2 D4.下列二次根式中属于最简二次根式的是A BC D5是同类二次根式的是A BC D6.下列运算中,正确的A=B2=C a=D.2=a+b7.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=A.40°B.50°C.60°D.75°8.把不等式组25322xx-≤⎧⎪⎨+<⎪⎩的解集在数轴上表示出来,正确的是A.B.C.D.9.计算224338()()42x x yx yy⋅-÷-的结果是A.3x-B.3xC.12x-D.12x10.若关于x的方程212x mx+=-+的解是负数,则m的取值范围是A.2m<-B.2m>-C.2m<-且4m≠D.2m>-且4m≠11.某次知识竞赛试卷有20道题,评分办法是答对一道记5分,不答记0分,答错一道扣2分,小明有3道题没答,但成绩超过60分,则小明至少答对了几道题A.13 B.14C .15D .1612.如图,ABC △、CDE △都是等腰三角形,且CA CB =,CD CE =,ACBDCE α∠=∠=,AD 、BE 相交于点O ,点M 、N 分别是线段AD 、BE 的中点.以下4个结论:①AD BE =;②180DOB α∠=︒-;③CMN △是等边三角形;④连OC ,则OC 平分AOE ∠.正确的是A .①②③B .①②④C .①③④D .①②③④第Ⅱ卷二、填空题(本大题共6小题,每小题3分,共18分) 13.|2|-=__________.14.101()(π2019)2---=___________. 15=__________.16.已知三角形其中两边a =3,b =5,则第三边c 的取值范围__________.17x =__________.18.不等式组4131x x+>⎧⎨-≥-⎩的最小整数解是__________.三、解答题(本大题共8小题,共66分.解答应写出文字说明、证明过程或演算步骤)19.(本小题满分6分)先化简2221(1)369x xx x -+÷--+,再从不等式组24324x x x -<⎧⎨<+⎩的整数解中选一个合适的x 的值代入求值.20.(本小题满分6分)计算:(1+2 (3)2-.21.(本小题满分8分)(1)计算:31(1)242a a a -÷---; (2)解方程:212112x x x=---.22.(本小题满分8分)已知2a -1是9的平方根,3a +b -1的算术平方根是4.(1)求a 与b ;(2)当ab >0时,求2a -b 2的立方根.23.(本小题满分9分)观察下列各式及其化简过程:=+1;.(1=__________;(2(3(a b >)中m 、n 与a b 、之间的关系. 24.(本小题满分9分)如图,在ABC △中,DM 、EN 分别垂直平分AC 和BC ,交AB 于M ,N 两点,DM 与EN 相交于点F .(1)若CMN △的周长为15cm ,求AB 的长; (2)若80MFN ∠=︒,求MCN ∠的度数.25.(本小题满分10分)某市为了提升菜篮子工程质量,计划用大、中型车辆共30辆调拨不超过190吨蔬菜和162吨肉制品补充当地市场.已知一辆大型车可运蔬菜8吨和肉制品5吨;一辆中型车可运蔬菜3吨和肉制品6吨.(1)符合题意的运输方案有几种?请你帮助设计出来;(2)若一辆大型车的运费是900元,一辆中型车的运费为600元,试说明(1)中哪种运输方案费用最低?最低费用是多少元?26.(本小题满分10分)某商店用1000元人民币购进水果销售,过了一段时间又用2800元购进这种水果,所购数量是第一次购进数量的2倍,但每千克的价格比第一次购进的贵了2元. (1)求该商店第一次购进水果多少千克?(2)该商店两次购进的水果按照相同的标价销售一段时间后,将最后剩下的50千克按照标价半价出售.售完全部水果后,利润不低于3100元,则最初每千克水果的标价是多少?2019-2020学年上学期期末原创卷八年级数学·全解全析1.【答案】B=2,是有理数,故这一组数中,无理数有π,2个.故选B . 2.【答案】C【解析】A 、x y <,则x y ->-,所以22x y -+>-+,故A 错误;B 、x y <,则44x y <,故B 错误; C 、x y <,22x y -<-,故C 正确;D 、x y <,则33x y ->-,故D 错误,故选C .3.【答案】C【解析】根据实数比较大小的方法,可得,∴在-1,0,2四个数中,最大的数是2.故选C . 4.【答案】A【解析】A被开方数中不含能开得尽方的因数,故A 正确; B=48的一个因数是16,开的尽,故B 不正确;C C 不正确;D 4,故D 不正确.故选A . 5.【答案】C【解析】A 的被开方数不同,故不是同类二次根式;B 的被开方数不同,故不是同类二次根式;C =的被开方数相同,故是同类二次根式;D 的被开方数不同,故不是同类二次根式.故选C .6.【答案】D【解析】A =A 错误;B 2|2==B 错误;C ||a ,故C 错误;D 项,2=a+b ,故D 项正确.故选D . 7.【答案】B【解析】∵∠B =∠D =90°,在Rt△ABC 和R t△ADC 中,BC CDAC AC =⎧⎨=⎩,∴Rt△ABC ≌Rt△ADC (HL ),∴∠2=∠ACB =90°–∠1=50°.故选B . 8.【答案】C【解析】25322x x -≤⎧⎪⎨+<⎪⎩①②,解不等式①得:x ≥-3,解不等式②得:x <1,故不等式组的解集为:-3≤x <1,在数轴上表示为:,故选C .9.【答案】D【解析】224338()()42x x y x y y ⋅-÷-=3432242()4x y y x y-⋅-=12x ,故选D . 10.【答案】D【解析】212x mx +=-+,去分母得22x m x +=--,移项得22x x m +=--, 合并同类项得32x m =--,系数化为1得23mx --=, ∵方程的解为负数,∴203m--<,解得2m >-,又∵当2x =-时,分式方程无解,将2x =-代入22x x m +=--,解得4m =,∴4m ≠, 故2m >-且4m ≠,故选D . 11.【答案】B【解析】设小明答对x 道题,则答错20-3-x =17-x 道题.根据题意得:5x -2(17-x )>60,即7x >94,∵x 为整数,∴x >13,∴13<x ≤17.成绩超过60分,则小明至少答对了14道题.故选B . 12.【答案】B【解析】①正确,理由如下:∵ACB DCE α∠=∠=,∴∠ACB +∠BCD =∠DCE +∠BCD ,即∠ACD =∠BCE ,又∵CA =CB ,CD =CE ,∴ACD BCE △≌△,∴AD =BE ,故①正确;②正确,理由如下:由①知,ACD BCE △≌△,∴∠CAD =∠CBE ,∵∠DOB 为ABO △的外角, ∴∠DOB =∠OBA +∠BAO =∠EBC +∠CBA +∠BAO =∠DAC +∠BAO +∠CBA =∠CBA +∠BAC ,∵∠CBA +∠BAC +∠ACB =180°,∠ACB =α,∴∠CBA +∠BAC =180°–α,即∠DOB =180°–α,故②正确; ③错误,理由如下:∵点M 、N 分别是线段AD 、BE 的中点,∴AM =12AD ,BN =12BE , 又∵由①知,AD =BE,∴AM =BN ,又∵∠CAD =∠CBE ,CA =CB ,∴CAM CBN △≌△, ∴CM =CN ,∠ACM =∠BCN ,∴∠MCN =∠MCB +∠BCN =∠MCB +∠ACM =∠ACB =α, ∴MCN △为等腰三角形且∠MCN =α,∴MCN △不是等边三角形,故③错误; ④正确,理由如下:如图所示,在AD 上取一点P 使得DP =EO ,连接CP ,OC ,由①知,ACD BCE △≌△,∴∠CEO =∠CDP ,又∵CE =CD ,EO =DP ,∴CEO CDP △≌△, ∴∠COE =∠CPD ,CP =CO ,∴∠CPO =∠COP ,∴∠COP =∠COE ,即OC 平分∠AOE ,故④正确, 故选B . 13.【答案】–1【解析】|2|-=23-=–1,故答案为:–1. 14.【答案】1【解析】原式=2–1=1.故答案为:1. 15.【答案】40【解析】原式40. 16.【答案】2<c <8【解析】根据三角形的三边关系有:5–3<c <5+3,∴2<c <8.故答案为:2<c <8. 17.【答案】4【解析】由题意得6x –5=7+3x ,∴x =4.故答案为:4. 18.【答案】-2【解析】4131x x +>⎧⎨-≥-⎩①②,由①得x >-3,由②得x ≤4,故不等式组的解集为-3<x ≤4,故原不等式组的最小整数解为-2.故答案为:-2.19.【解析】原式232(3)3(1)(1)x x x x x -+-=⨯-+-31x x -=+,(2分)解不等式组24324x x x-<⎧⎨<+⎩,得24x -<<,(4分)∴其整数解为-1,0,1,2,3,∵要使原分式有意义,∴x 可取0,2.∴当0x =时,原式3=-,(或当2x =时,原式13=-).(6分)20.【解析】(1=+32.(2分) (2-==4分)(3)2--2222]2]--⨯- (243)(272)=---8=.(6分)21.【解析】(1)原式332(2)2a a a a --=÷--322(2)3a a a a --=⋅--(2分)12=-.(4分)(2)去分母,得:212x x =-+, 解这个方程,得:1x =-.(6分)检验:当1x =-时210x -≠,1x =-是原方程的解.(8分) 22.【解析】(1)∵2a -1是9的平方根,3a +b -1的算术平方根是4,∴2a -1=3或2a -1=-3;3a +b-1=16,(2分)解得:a =2,b =11;a =-1,b =20.(4分) (2)由ab >0,a =2,b =11, 则2a -b 2=4-121=-117,(6分) -117的立方根是8分) 23.【解析】(1–1.(3分)–1–1.(2=.(6分) (3)通过以上规律不难发现:m =a +b ,n =ab .(9分) 24.【解析】(1)∵DM 、EN 分别垂直平分AC 和BC ,∴AM =CM ,BN =CN ,∴△CMN 的周长=CM +MN +CN =AM +MN +BN =AB ,(2分) ∵△CMN 的周长为15 cm , ∴AB =15 cm .(4分)(2)∵∠MFN =80°,∴∠MNF +∠NMF =180°−80°=100°, ∵∠AMD =∠NMF ,∠BNE =∠MNF , ∴∠AMD +∠BNE =∠MNF +∠NMF =100°,∴∠A +∠B =90°−∠AMD +90°−∠BNE =180°−100°=80°,(6分) ∵AM =CM ,BN =CN , ∴∠A =∠ACM ,∠B =∠BCN ,∴∠MCN =180°−2(∠A +∠B )=180°−2×80°=20°.(9分) 25.【解析】(1)设安排x 辆大型车,则安排(30)x -辆中型车,依题意,得:83(30)19056(30)162x x x x +-≤⎧⎨+-≤⎩,(2分)解得:1820x ≤≤.∵x 为整数,∴181920x =,,. ∴符合题意的运输方案有3种,方案1:安排18辆大型车,12辆中型车;方案2:安排19辆大型车,11辆中型车;方案3:安排20辆大型车,10辆中型车.(5分) (2)方案1所需费用为:900186001223400⨯+⨯=(元), 方案2所需费用为:900196001123700⨯+⨯=(元), 方案3所需费用为:900206001024000⨯+⨯=(元).(8分) ∵234002370024000<<,∴方案1安排18辆大型车,12辆中型车所需费用最低,最低费用是23400元.答:(1)符合题意的运输方案有3种,方案1:安排18辆大型车,12辆中型车;方案2:安排19辆大型车,11辆中型车;方案3:安排20辆大型车,10辆中型车;(2)方案1安排18辆大型车,12辆中型车所需费用最低,最低费用是23400元.(10分) 26.【解析】(1)设第一次购进水果x 千克,依题意可列方程,1000280022x x+=,(2分) 解得200x =,经检验:200x =是原方程的解. 答:第一次购进水果200千克.(5分)(2)设最初水果标价为y 元,依题意可列不等式,155050380031002y y +⋅-≥,(7分) 解得12y ≥, 答:最初每千克水果标价12元.(10分)。
2019年湘教版八年级数学上册期末检测卷(有答案)

期末检测卷一、选择题(每小题3分,共30分) 1.下列实数中,无理数是( ) A .-1 B.12 C .5 D. 32.计算(-2)-3的结果为( ) A .-5 B .6 C .-8 D .-183.已知下列命题,假命题是( ) A .绝对值最小的实数是0 B .若a ≥b ,则ac 2≥bc 2C .如果一个数的立方根等于这个数本身,那么这个数是0或±1D .有两边和其中一边的对角分别相等的两个三角形全等 4.不等式2≥-1的解集在数轴上表示正确的是( ) A. B. C.D.5.一元一次不等式组⎩⎪⎨⎪⎧2x +1>0,x -5≤0的解集中,整数解的个数是( )A .4个B .5个C .6个D .7个6.一个等腰三角形的两边长分别为1,5,则这个三角形的周长为( ) A .2+ 5 B .25+1C .2+5或25+1D .以上都不对 7.化简13-2-12的结果是( )A.3+ 2B.3- 2C.2- 3 D .33+ 28.如图,△ABC 和△DEF 中,AB =DE ,∠B =∠DEF ,添加下列哪一个条件仍无法证明△ABC ≌△DEF ( ) A .AC ∥DF B .∠A =∠D C .AC =DF D .∠ACB =∠F第8题图 第10题图9.某工程需要在规定日期内完成,如果甲工程队单独做,恰好如期完成,如果乙工程队单独做,则超过规定日期3天,现在甲、乙两队合做2天,剩下的由乙队独做,恰好在规定日期完成,求规定日期.如果设规定日期为天,下面所列方程中错误的是( )A.2x +x x +3=1B.2x =3x +3C.⎝ ⎛⎭⎪⎫1x +1x +3×2+x -2x +3=1 D.1x +x x +3=1 10.如图,AD 是△ABC 的角平分线,DE ⊥AC ,垂足为E ,BF ∥AC 交ED 的延长线于点F ,若BC 恰好平分∠ABF ,AE =2BF .给出下列四个结论:①DE =DF ;②DB =DC ;③AD ⊥BC ;④AC =3BF .其中正确的结论共有( )A .4个B .3个C .2个D .1个 二、填空题(每小题3分,共24分)11.用科学记数法表示的数-3.6×10-4写成小数是________. 12.16的平方根为________.13.不等式组⎩⎪⎨⎪⎧3x -5<2x ,x -12≤2x +1的解集是__________.14.如图,△ABC 中,BC 的垂直平分线交AB ,BC 于E ,D ,CD =5,△BCE 的周长为22,则BE =________.第14题图第16题图15.已知m=6,n=3,则2m -n的值为________.16.如图,已知△ABC ≌△AFE ,若∠ACB =65°,则∠EAC =________. 17.若y =x -4+4-x2-2,则(+y )y=________.18.已知关于的分式方程mx -1+31-x=1的解是非负数,则m 的取值范围为______________. 三、解答题(共66分)19.(12分)计算或化简:(1)⎝ ⎛⎭⎪⎫12-1-(3-2)0+|3-1|;(2)2x -4x 2-1÷x -2x 2+2x +1-2x x -1;(3)(π-3)0+⎝ ⎛⎭⎪⎫14-1-||32-6+(-1)2017-18.20.(6分)解不等式组⎩⎪⎨⎪⎧2(x +2)>3x ,3x -12≥-2,并将它的解集在数轴上表示出.21.(6分)如图,在△BCD 中,BC =4,BD =5.(1)求CD 的取值范围;(2)若AE ∥BD ,∠A =55°,∠BDE =125°,求∠C 的度数.22.(7分)如图,在Rt △ABC 中,∠B =90°.分别以A ,C 为圆心,大于12AC 长为半径画弧,两弧相交于点M ,N ,连接MN ,与AC ,BC 分别交于点D ,E ,连接AE .则:(1)∠ADE =________°;(2)AE ________EC (填“=”“>”或“<”); (3)若AB =3,BC =4,求△ABE 的周长.23.(7分)先化简,再求值:⎝ ⎛⎭⎪⎫a 2-b 2a 2-2ab +b 2+a b -a ÷b 2a 2-ab,其中a ,b 满足a +1+|b -3|=0.24.(8分)如图所示,AB =AC ,BD =CD ,DE ⊥AB 于点E ,DF ⊥AC 于点F ,求证:DE =DF .25.(10分)为支援灾区,某学校爱心活动小组准备用筹集的资金购买A 、B 两种型号的学习用品共1000件.已知B 型学习用品的单价比A 型学习用品的单价多10元,用180元购买B 型学习用品与用120元购买A 型学习用品的件数相同.(1)求A ,B 两种学习用品的单价各是多少元;(2)若购买这批学习用品的费用不超过28000元,则最多购买B 型学习用品多少件?26.(10分)如图,△ABC 中,∠ABC =45°,CD ⊥AB 于D ,BE 平分∠ABC ,且BE ⊥AC 于E ,与CD 相交于点F .(1)求证:BF =AC ; (2)求证:CE =12BF .参考答案与解析1.D 2.D 3.D 4.A 5.C 6.B 7.C 8.C 9.D10.A 解析:∵BF ∥AC ,∴∠C =∠CBF .∵BC 平分∠ABF ,∴∠ABC =∠CBF ,∴∠C =∠ABC ,∴AB =AC .∵AD 是△ABC 的角平分线,∴BD =CD ,AD ⊥BC ,故②③正确;在△CDE 与△BDF 中,⎩⎪⎨⎪⎧∠C =∠DBF ,CD =BD ,∠EDC =∠FDB ,∴△CDE ≌△BDF (ASA),∴DE =DF ,CE =BF ,故①正确;∵AE =2BF ,∴AC =3BF ,故④正确.故选A.11.-0.00036 12.±2 13.-1≤<5 14.6 15.12 16.50° 17.14 18.m ≥2且m ≠319.解:(1)原式= 3.(4分)(2)原式=2(x -2)(x +1)(x -1)·(x +1)2x -2-2x x -1=2x -1.(8分)(3)原式=1+4-|42-6|-1-32=5-(6-42)-1-32=5-6+42-1-32=2-2.(12分)20.解:⎩⎪⎨⎪⎧2(x +2)>3x ①,3x -12≥-2②.解不等式①,得<4.解不等式②,得≥-1.∴-1≤<4.(3分)∴原不等式组的解集在数轴上表示如下.(5分)∴不等式组的解集为-1≤<4.(6分)21.解:(1)∵在△BCD 中,BC =4,BD =5,∴1<CD <9.(3分)(2)∵AE ∥BD ,∠BDE =125°,∴∠AEC =180°-∠BDE =55°.又∵∠A =55°,∴∠C =180°-∠A -∠AEC =70°.(6分)22.解:(1)90(2分) (2)=(4分)(3)∵MN 是AC 的垂直平分线,∴AE =EC .∴C △ABE =AB +AE +BE =AB +EC +BE =AB +BC =7.(7分)23.解:原式=a 2-b 2+a (b -a )(a -b )2·a (a -b )b 2=b (a -b )(a -b )2·a (a -b )b 2=ab.(3分)∵a +1+|b -3|=0,∴a =-1,b =3,(5分)∴原式=-33.(7分) 24.证明:连接AD .(1分)在△ABD 和△ACD 中,⎩⎪⎨⎪⎧AB =AC ,BD =CD ,AD =AD ,∴△ABD ≌△ACD (SSS),(3分)∴∠DBA =∠DCA ,∴∠DBE =∠DCF .∵DE ⊥AE ,DF ⊥AF ,∴∠E =∠F =90°.(5分)在△DEB 和△DFC 中,⎩⎪⎨⎪⎧∠DBE =∠DCF ,∠E =∠F ,DB =DC ,∴△DEB ≌△DFC (AAS),(7分)∴DE =DF .(8分)25.解:(1)设A 型学习用品的单价为元,则B 型学习用品的单价为(+10)元,由题意得180x +10=120x,(2分)解得=20,经检验=20是原分式方程的根,且符合实际,则+10=30.(4分)答:A 型学习用品的单价为20元,B 型学习用品的单价为30元.(5分)(2)设购买B 型学习用品y 件,则购买A 型学习用品(1000-y )件,(6分)由题意得20(1000-y )+30y ≤28000,解得y ≤800.(9分)答:最多购买B 型学习用品800件.(10分)26.证明:(1)∵CD ⊥AB ,∠ABC =45°,∴△BCD 是等腰直角三角形,∴BD =CD .∵CD ⊥AB ,BE ⊥AC ,∴∠BDF =∠CDA =∠FEC =90°,∴∠DBF =90°-∠BFD ,∠DCA =90°-∠EFC ,且∠BFD =∠EFC ,∴∠DBF =∠DCA .(3分)在△DFB 和△DAC 中,⎩⎪⎨⎪⎧∠DBF =∠DCA ,BD =CD ,∠BDF =∠CDA ,∴△DFB ≌△DAC (ASA),∴BF =AC .(5分)(2)∵BE 平分∠ABC ,∴∠ABE =∠CBE .∵BE ⊥AC ,∴∠BEA =∠BEC =90°.在△BEA 和△BEC 中, ⎩⎪⎨⎪⎧∠ABE =∠CBE ,BE =BE ,∠BEA =∠BEC ,∴△BEA ≌△BEC (ASA).(8分)∴CE =AE =12AC .又由(1)知BF =AC ,∴CE =12AC =12BF .(10分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
期末检测卷一、选择题(每小题3分,共30分)1.下列实数中,无理数是( )A .-1 B.12 C .5 D. 32.计算(-2)-3的结果为( )A .-5B .6C .-8D .-183.已知下列命题,假命题是( ) A .绝对值最小的实数是0B .若a ≥b ,则ac 2≥bc 2C .如果一个数的立方根等于这个数本身,那么这个数是0或±1D .有两边和其中一边的对角分别相等的两个三角形全等 4.不等式2x ≥x -1的解集在数轴上表示正确的是( ) A. B.C.D. 5.一元一次不等式组⎩⎪⎨⎪⎧2x +1>0,x -5≤0的解集中,整数解的个数是( )A .4个B .5个C .6个D .7个6.一个等腰三角形的两边长分别为1,5,则这个三角形的周长为( ) A .2+ 5 B .25+1C .2+5或25+1D .以上都不对7.化简13-2-12的结果是( )A.3+ 2B.3- 2C.2- 3 D .33+ 28.如图,△ABC 和△DEF 中,AB =DE ,∠B =∠DEF ,添加下列哪一个条件仍无法证明△ABC ≌△DEF ( )A .AC ∥DFB .∠A =∠DC .AC =DFD .∠ACB =∠F第8题图 第10题图9.某工程需要在规定日期内完成,如果甲工程队单独做,恰好如期完成,如果乙工程队单独做,则超过规定日期3天,现在甲、乙两队合做2天,剩下的由乙队独做,恰好在规定日期完成,求规定日期.如果设规定日期为x 天,下面所列方程中错误的是( )A.2x +x x +3=1B.2x =3x +3C.⎝ ⎛⎭⎪⎫1x +1x +3×2+x -2x +3=1 D.1x +x x +3=1 10.如图,AD 是△ABC 的角平分线,DE ⊥AC ,垂足为E ,BF ∥AC 交ED 的延长线于点F ,若BC 恰好平分∠ABF ,AE =2BF .给出下列四个结论:①DE =DF ;②DB =DC ;③AD ⊥BC ;④AC =3BF .其中正确的结论共有( )A .4个B .3个C .2个D .1个二、填空题(每小题3分,共24分)11.用科学记数法表示的数-3.6×10-4写成小数是________. 12.16的平方根为________.13.不等式组⎩⎪⎨⎪⎧3x -5<2x ,x -12≤2x +1的解集是__________.14.如图,△ABC 中,BC 的垂直平分线交AB ,BC 于E ,D ,CD =5,△BCE 的周长为22,则BE =________.第14题图 第16题图15.已知x m =6,x n =3,则x 2m -n的值为________.16.如图,已知△ABC ≌△AFE ,若∠ACB =65°,则∠EAC =________. 17.若y =x -4+4-x2-2,则(x +y )y=________.18.已知关于x 的分式方程mx -1+31-x=1的解是非负数,则m 的取值范围为______________. 三、解答题(共66分)19.(12分)计算或化简:(1)⎝ ⎛⎭⎪⎫12-1-(3-2)0+|3-1|;(2)2x -4x 2-1÷x -2x 2+2x +1-2x x -1;(3)(π-3)0+⎝ ⎛⎭⎪⎫14-1-||32-6+(-1)2017-18.20.(6分)解不等式组⎩⎪⎨⎪⎧2(x +2)>3x ,3x -12≥-2,并将它的解集在数轴上表示出来.21.(6分)如图,在△BCD 中,BC =4,BD =5.(1)求CD 的取值范围;(2)若AE ∥BD ,∠A =55°,∠BDE =125°,求∠C 的度数.22.(7分)如图,在Rt △ABC 中,∠B =90°.分别以A ,C 为圆心,大于12AC 长为半径画弧,两弧相交于点M ,N ,连接MN ,与AC ,BC 分别交于点D ,E ,连接AE .则:(1)∠ADE =________°; (2)AE ________EC (填“=”“>”或“<”); (3)若AB =3,BC =4,求△ABE 的周长.23.(7分)先化简,再求值:⎝ ⎛⎭⎪⎫a 2-b 2a 2-2ab +b 2+a b -a ÷b 2a 2-ab,其中a ,b 满足a +1+|b -3|=0.24.(8分)如图所示,AB =AC ,BD =CD ,DE ⊥AB 于点E ,DF ⊥AC 于点F ,求证:DE =DF .25.(10分)为支援灾区,某学校爱心活动小组准备用筹集的资金购买A 、B 两种型号的学习用品共1000件.已知B 型学习用品的单价比A 型学习用品的单价多10元,用180元购买B 型学习用品与用120元购买A 型学习用品的件数相同.(1)求A ,B 两种学习用品的单价各是多少元;(2)若购买这批学习用品的费用不超过28000元,则最多购买B 型学习用品多少件?26.(10分)如图,△ABC 中,∠ABC =45°,CD ⊥AB 于D ,BE 平分∠ABC ,且BE ⊥AC 于E ,与CD 相交于点F .(1)求证:BF =AC ;(2)求证:CE =12BF .参考答案与解析1.D 2.D 3.D 4.A 5.C 6.B 7.C 8.C 9.D10.A 解析:∵BF ∥AC ,∴∠C =∠CBF .∵BC 平分∠ABF ,∴∠ABC =∠CBF ,∴∠C =∠ABC ,∴AB =AC .∵AD 是△ABC 的角平分线,∴BD =CD ,AD ⊥BC ,故②③正确;在△CDE 与△BDF 中,⎩⎪⎨⎪⎧∠C =∠DBF ,CD =BD ,∠EDC =∠FDB ,∴△CDE ≌△BDF (ASA),∴DE =DF ,CE =BF ,故①正确;∵AE =2BF ,∴AC =3BF ,故④正确.故选A.11.-0.00036 12.±2 13.-1≤x <5 14.615.12 16.50° 17.1418.m ≥2且m ≠319.解:(1)原式= 3.(4分)(2)原式=2(x -2)(x +1)(x -1)·(x +1)2x -2-2x x -1=2x -1.(8分)(3)原式=1+4-|42-6|-1-32=5-(6-42)-1-32=5-6+42-1-32=2-2.(12分)20.解:⎩⎪⎨⎪⎧2(x +2)>3x ①,3x -12≥-2②.解不等式①,得x <4.解不等式②,得x ≥-1.∴-1≤x <4.(3分)∴原不等式组的解集在数轴上表示如下.(5分)∴不等式组的解集为-1≤x <4.(6分)21.解:(1)∵在△BCD 中,BC =4,BD =5,∴1<CD <9.(3分)(2)∵AE ∥BD ,∠BDE =125°,∴∠AEC =180°-∠BDE =55°.又∵∠A =55°,∴∠C =180°-∠A -∠AEC =70°.(6分)22.解:(1)90(2分) (2)=(4分)(3)∵MN 是AC 的垂直平分线,∴AE =EC .∴C △ABE =AB +AE +BE =AB +EC +BE =AB +BC =7.(7分)23.解:原式=a 2-b 2+a (b -a )(a -b )2·a (a -b )b 2=b (a -b )(a -b )2·a (a -b )b 2=ab .(3分)∵a +1+|b -3|=0,∴a =-1,b =3,(5分)∴原式=-33.(7分) 24.证明:连接AD .(1分)在△ABD 和△ACD 中,⎩⎪⎨⎪⎧AB =AC ,BD =CD ,AD =AD ,∴△ABD ≌△ACD (SSS),(3分)∴∠DBA =∠DCA ,∴∠DBE =∠DCF .∵DE ⊥AE ,DF ⊥AF ,∴∠E =∠F =90°.(5分)在△DEB 和△DFC 中,⎩⎪⎨⎪⎧∠DBE =∠DCF ,∠E =∠F ,DB =DC ,∴△DEB ≌△DFC (AAS),(7分)∴DE =DF .(8分)25.解:(1)设A 型学习用品的单价为x 元,则B 型学习用品的单价为(x +10)元,由题意得180x +10=120x,(2分)解得x =20,经检验x =20是原分式方程的根,且符合实际,则x +10=30.(4分)答:A 型学习用品的单价为20元,B 型学习用品的单价为30元.(5分)(2)设购买B 型学习用品y 件,则购买A 型学习用品(1000-y )件,(6分)由题意得20(1000-y )+30y ≤28000,解得y ≤800.(9分)答:最多购买B 型学习用品800件.(10分)26.证明:(1)∵CD ⊥AB ,∠ABC =45°,∴△BCD 是等腰直角三角形,∴BD =CD .∵CD ⊥AB ,BE ⊥AC ,∴∠BDF =∠CDA =∠FEC =90°,∴∠DBF =90°-∠BFD ,∠DCA =90°-∠EFC ,且∠BFD =∠EFC ,∴∠DBF =∠DCA .(3分)在△DFB 和△DAC 中,⎩⎪⎨⎪⎧∠DBF =∠DCA ,BD =CD ,∠BDF =∠CDA ,∴△DFB ≌△DAC (ASA),∴BF =AC .(5分)(2)∵BE 平分∠ABC ,∴∠ABE =∠CBE .∵BE ⊥AC ,∴∠BEA =∠BEC =90°.在△BEA 和△BEC 中, ⎩⎪⎨⎪⎧∠ABE =∠CBE ,BE =BE ,∠BEA =∠BEC ,∴△BEA ≌△BEC (ASA).(8分)∴CE =AE =12AC .又由(1)知BF =AC ,∴CE =12AC =12BF .(10分)。
