《微积分(第四版)》第一章 函数
《微积分》讲义
《微积分》讲义第一章极限一、函数极限的概念：f＝A要点：⑴x 为变量；⑵A 为一常量。
二、函数极限存在的充分必要条件：f＝A f＝A，f＝A 例：判定是否存在？三、极限的四则运算法则⑴＝f±g⑵＝f·g⑶＝……g≠0⑷k·f＝k·f四、例：⑴⑵⑶⑷五、两个重要极限⑴＝1 ＝1⑵＝e ＝e ………型理论依据：⑴两边夹法则：若f≤g≤h，且limf＝limh＝A，则：limg＝A⑵单调有界数列必有极限。
例题：⑴＝⑵＝⑶＝⑷＝⑸＝六、无穷小量及其比较1、无穷小量定义：在某个变化过程中趋向于零的变量。
2、无穷大量定义：在某个变化过程中绝对值无限增大的变量。
3、高阶无穷小，低阶无穷小，同阶无穷小，等价无穷小。
4、定理：f＝A f＝A＋a （a＝0）七、函数的连续性1、定义：函数y＝f在点处连续……在点处给自变量x一改变量x：⑴x0时，y0。
即：y＝0⑵f＝f⑶左连续：f＝f右连续：f＝f2、函数y＝f在区间上连续。
3、连续函数的性质：⑴若函数f和g都有在点处连续，则：f±g、f·g、（g()≠0）在点处连续。
⑵若函数u＝j在点处连续，而函数y＝f在点＝j()处连续，则复合函数f(j(x)) 在点处连续。
例：＝＝＝4、函数的间断点：⑴可去间断点：f＝A，但f不存在。
⑵跳跃间断点：f＝A ，f＝B，但A≠B。
⑶无穷间断点：函数在此区间上没有定义。
5、闭区间上连续函数的性质：若函数f在闭区间上连续，则：⑴f在闭区间上必有最大值和最小值。
⑵若f与f异号，则方程f＝0 在内至少有一根。
例：证明方程式－4＋1＝0在区间内至少有一个根。
第二章一元函数微分学一、导数1、函数y＝f在点处导数的定义：x y＝f－f＝A f'＝A ……y'，，。
2、函数y＝f在区间上可导的定义：f'，y'，，。
3、基本初等函数的导数公式：⑴＝0⑵＝n·⑶＝，＝⑷＝·lnɑ，＝⑸＝cosx，＝－sinx＝x，＝－＝secx·tanx，＝－cscx·cotx⑹＝－＝－4、导数的运算：⑴、四则运算法则：＝±＝·g(x)＋f(x)·＝例：求下列函数的导数y＝2－5＋3x－7f(x)＝＋4cosx－siny＝⑵、复合函数的求导法则：y u，u v，v w，w x y x'＝''''例：y＝lntanxy＝lny＝arcsin⑶、隐函数的求导法则：把y看成是x的复合函数，即遇到含有y 的式子，先对y求导，然后y再对x求导。
《微积分》(上下册) 教学课件 01.第1章 函数、极限、连续 高等数学第一章第9-10节
定义 2 设函数 f ( x)在U(x0, )内有定义,如果
y
lim f (x) f (x )，
x x0
0
y f (x)
称函数 f ( x)在点 x 连续. 0
如 f ( x) x2，
0
x0
x
lim f ( x) lim x2 4 f (2)，
x2
x2
f ( x) x2在x 2点连续.
说明 y f (x)在x x0点连续 下列三条同时成立 (1) f (x0)有定义；
(2) lim f (x)存在； xx0
（3）lim x x0
f
(x)
f (x0 ).
13
例1
试证函数
f
ห้องสมุดไป่ตู้
(
x)
x
sin1 x
,
0,
处连续.
证 lim x sin 1 0,
x0
x
又 f (0) 0, lim f ( x) f (0), x0
3、反函数函数的连续性
严格单调的连续函数必有严格单调的连续反函数. 例如, y sin x在[ , ]上单调增加且连续,
22 故 y arcsinx 在[1,1]上也是单调增加且连续.
同理 y arccosx 在[1,1]上单调减少且连续;
y arctanx, y arccot x 在(,)上单调且连续.
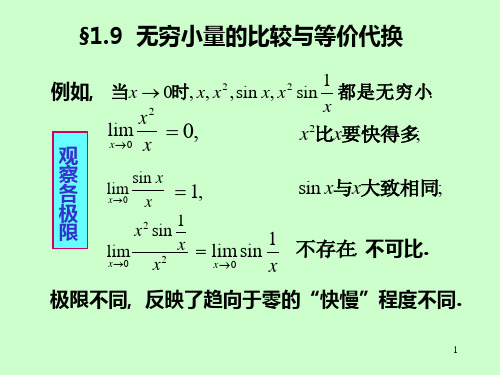
§1.9 无穷小量的比较与等价代换
例如, 当x 0时, x, x2,sin x, x2 sin 1 都是无穷小.
x2
lim 0,
观
x0 x
x x2比x要快得多;
察 各 极 限
lim sin x x0 x
大学微积分第一章 函数
X
f
Y f (X )
①满射 若 f ( X ) Y ,则称 f 为满射;
②单射
若
有
X
Y
则称f 为单射; ③双射 若f 既是满射又是单射, 则称 f 为双射 或一一映射.
2.【逆映射与复合映射】
⑴【逆映射】 设
f :X Y
是单射
记作
1
定义
称映射
g
g : f (X ) X
为映射
f
的逆映射
周期为
【注】 周期函数不一定存在最小正周期 . 【例如】 常量函数 f ( x ) C
狄里克雷函数
1, 0,
x 为有理数 x 为无理数
五、复合函数
1【定义】 设有函数链
y f ( u), u D1
且 g( D ) D 1
① ②
则 称为由①, ②确定的复合函数, u 称为中间变量. 【说明】通常 f 称为外层函数，g 称为内层函数.
y 与之对应则称这个对应 D 上的一个一元函数，简
因变量
y f ( x ) , x D, 函数值
定义域
函数
自变量
x 0 处的
当 x 0 D 时 , 称 f ( x 0 )为函数在点
函数值 值域
函数值全体组成的数集 R f { y y f ( x ), x D } 称为函数的
2.【函数的两要素】定义域与对应法则.
第一章
函数
一. 区间和邻域 二. 映射 三. 函数概念 四. 函数的特性 五. 复合函数 六. 基本初等函数
七. 初等函数
八. 经济学中常用的函数
预备知识
一.区间和邻域
⑴【区间】 是指介于某两个实数之间的全体实数. 这两个实数叫做区间的端点.
微积分第一章
y log a x
(1,0)
(a 1)
y log 1 x
a
29
5. 三角函数
正弦函数
y sin x
y sin x
余弦函数
y cos x
y cos x
30
正切函数
y tan x
y tan x
余切函数
y cot x
y cot x
31
正割函数
y sec x
3
1-1 函数的概念及其基本特性 一、集合及其运算
概念（集合与元素）、分类、表示法. 特殊集合表示法: N----自然数集 Q----有理数集 Z----整数集 R----实数集
4
二、区间与邻域
区间是指介于某两个实数之间的全体实数，这两
个实数叫做区间的端点.
a, b R, a b.
{ x a x b} 称为开区间, 记作 (a, b)
素的情况下，这些经济变量都只与产品的产量或
销量x有关，可以看成是x的函数。
38
1. 成本函数TC(x)
生产既定产量的总成本 (TC)由固定成
本( FC )和可变成本 (VC )两部分构成 .即
TC ( x ) FC VC ( x )
其中x表示产量 . 相应地 ,有
平均成本 ( AC )、平均固定成本 ( AFC )和 平均可变成本 ( AVC )
9
四、复合函数和反函数
1. 复合函数
设 y u, u 1 x 2 ,
y 1 x2
定义: 设函数 y f (u) 的定义域 D f , 而函数
称函数 y f ( x ) 为 x 的复合函数 .
微积分第一章
高等数学教案、第一章 函数、极限与与连续本章将在分别研究数列的极限与函数的极限的基础上，讨论极限的一些重要性质以及运算法则,函数的连续性，闭区间上连续函数的性质。
具体的要求如下：1． 理解极限的概念（理解极限的描述性定义,对极限的N -ε、δε-定义可在学习过程中逐步加深理解,对于给出ε求N 或δ不作过高要求）。
2． 掌握极限四则运算法则。
3． 了解极限存在准则（夹逼准则和单调有界准则），会用两个重要极限求极限。
4． 了解无穷小、无穷大及无穷小的阶的概念.能够正确运用等价无穷小求极限。
5。
理解函数在一点连续的概念,理解区间内（上）连续函数的概念。
6. 了解间断点的概念，会求函数的间断点并判别间断点的类型。
7. 了解初等函数的连续性和闭区间上连续函数的性质（最大、最小值定理、零点定理、介值定理）。
第一章共12学时,课时安排如下绪论 §1.1、函数 §1.2初等函数 2课时 §1。
4数列极限及其运算法则 2课时 §1.4函数极限及其运算法则 2课时 §1。
4两个重要极限 无穷小与无穷大 2课时 §1.4函数的连续性 2课时 第一章 习题课 2课时绪论数学:数学是研究空间形式和数量关系的一门学科，数学是研究抽象结构及其规律、特性的学科.数学具有高度的抽象性、严密的逻辑性和应用的广泛性。
关于数学应用和关于微积分的评价：恩格斯：在一切理论成就中,未必再有像17世纪下叶微积分的微积分的发现那样被看作人类精神的最高胜利了。
如果在某个地方我们看到人类精神的纯粹的和唯一的功绩，那就正是这里.华罗庚：宇宙之大,粒子之微，火箭之速，化工之巧,地球之变，生物之迷,日用之繁,无处不用数学。
张顺燕:微积分是人类的伟大结晶，它给出了一整套科学方法，开创了科学的新纪元，并因此加强和加深了数学的作用。
……有了微积分，人类才有能力把握运动和过程;有了微积分，就有了工业革命，有了大工业生产,也就有了现代的社会。
经济数学基础微积分第一篇第一章--函数
(2)自变量可以取一， 个还 数可 值以取 一个表达式。
例 31： . 给定 fx 函 x2数 x2,试计 f0,f(x2),f1x.
解： f(0)02022
f(x 2 ) (x 2 )2 (x 2 ) 2 x 4 x 2 2
给定 r2, 就有 S4;
给定 r3, 就有 S9;
例 y 如 fx x 2 ： x 1
给定 x1, 就y有 f11;
给定 x1, 就y 有 f1 3 ;
【注y 意 f】 x
二. 求定义域
函数的定义域：是使函数有意义的 自变量x取值的全体。 也就是自变 量x允 许取值的范围。
确定函数定义域的三条基本要求： (1) 分式的分母不能为零。即若 y 1
【公 ln x式 kkln 】 x， lo ： ax g kkloax g
【解】 1 fx lx n 2 2 lx n(x 0 ) g x 2 ln x(x 0 )
表达式不同，定义域不同 所以它们是不同的函数。
2 fx lx n 3 3 lx n ( x 0 )
g x 3 ln x(x 0 )
－3 －2
2
x
【练习1】
求函 f(x数 )lo2g (x1)
1 的定.义 x21
【解】 要使f(x) 有意义，必须有
x 1 0
x
2
1
0
xx11x10
xx
1 1
或
x
1
即： x1
公共部分
写成区间 (1, ： )
【练习2】
求函f(x数 ) 1 3x的定.义 lnx(3)
【解】 要使f(x) 有意义，必须有
高等数学微积分第一章函数及其图形(共44张PPT)
如果A，B互相包含，即A B且B A，则称A与B相等，记为A=B。
如果把 y看作自变量，x 看作因变量，按照函数的定义就得到一个新的函数，这个新函数称为函数y=f(x)的反函数，记作 x=j(y)。
解: 要使函数有意义，必须x 0，且x2-4³0。
如果A，B互相包含，即A B且B A，则称A与B相等，记为A=B。
1
O
x
3．对数函数
指数函数y=ax的反函数叫做对数函数，记为
y=logax(a>0，a 1)． 对数函数的定义域是区间(0，+ )．
单调性：
若a>1，则logax单调增加； 若0<a<1，则logax单调减少．
性质见书P34
y y=ax
1
O
y=logxax
a>1
4．三角函数
U(a)。 设>0，则称区间(a-, a+)为点a 的邻域，记作U(a, )，
即 U(a, ) ={x|a-<x<a+} ={x| |x-a|<}。
其中点 a 称为邻域的中心, 称为邻域的半径。
O a-
a+ x
去心邻域:
U
(a,)
={x
|0<|
x-a
|<}。
O a- a a+ x
左（右）邻域、M领域的概念见书中第七页。
bx
[a, b]={x|axb}称为闭区间。
[a， b]
Oa
bx
[a, b)={x|ax<b}及 (a, b]={x|a<xb}称为
半开区间。 [a， b)
Oa
bx
(a， b]
Oa
bx
微积分第一章PDF
3 2
2
3
y [ x]
3 2
1
1 O 1 1
2 3
x
取整函数 [ x ] 的一个重要性质 :
对任何实数 x , 存在绝对不等式 [ x ] x [ x ] 1.
例如, [0.99] 0.99 [0.99] 1 为 0 0.99 1.
e x e x 解方程 y ( x 0) : 2 (e x ) 2 2 y e x 1 0, ex y x ln( y y 2 1, y 2 1)
O
y ln( x x 2 1)
y
x
y arch x ln( x x 2 1)
x x y u , u cot v , v 2 复合成函数 y cot 2 ; 函数 y arcsin u, u 2 x 2 不能复合 , 前者的定义域与
后者的值域的交集是空的, 即 arcsin(2 x 2 ) 无意义．
8. 初等函数
由常数和基本初等函数经过有限次四则运算和有 限次复合所得到的有意义的函数, 称为 初等函数.
1
y
x
O
1
x
y 1 x
(2) 指数函数:
y a (a 0, a 1)
x
y
1 y ( a )x
a1
y ax
1
x
O
(3) 对数函数: y log a x (a 0, a 1)
y
a1
y log a x
x
O
1
y log a 1 x
(4) 三角函数
微积分第四版课后习题答案
微积分第四版课后习题答案微积分是数学中的一门重要学科，它研究的是变化和积分的关系。
对于学习微积分的同学来说，课后习题是巩固知识和提高能力的重要途径。
然而，有时候我们会遇到一些难题，没有答案或者不知道如何解答。
为了帮助大家更好地学习微积分，本文将为大家提供微积分第四版课后习题的一些答案和解析。
在微积分的学习中，函数是一个非常重要的概念。
函数是一种映射关系，它将一个自变量的值映射到一个因变量的值。
在微积分中，我们经常需要求解函数的导数和积分。
导数表示函数在某一点的变化率，积分则表示函数在一段区间上的累积效应。
对于求解导数的问题，我们可以使用导数的定义或者一些常用的求导法则。
例如，对于函数 f(x) = x^2，我们可以使用导数的定义来求解它的导数。
根据导数的定义，我们有：f'(x) = lim(h→0) [f(x+h) - f(x)] / h将函数 f(x) = x^2 代入上述公式，我们可以得到：f'(x) = lim(h→0) [(x+h)^2 - x^2] / h化简上述表达式，我们可以得到：f'(x) = lim(h→0) [2xh + h^2] / h继续化简，我们可以得到：f'(x) = lim(h→0) 2x + h由于 h 在趋于 0 的过程中，2x 是一个常数，所以我们可以得到：f'(x) = 2x因此，函数 f(x) = x^2 的导数为 f'(x) = 2x。
对于求解积分的问题，我们可以使用积分的定义或者一些常用的积分法则。
例如，对于函数 f(x) = 2x，我们可以使用积分的定义来求解它的积分。
根据积分的定义，我们有：∫f(x)dx = lim(n→∞) Σ[f(xi)Δx]将函数 f(x) = 2x 代入上述公式，我们可以得到：∫2xdx = lim(n→∞) Σ[2xiΔx]化简上述表达式，我们可以得到：∫2xdx = lim(n→∞) 2Σ[xiΔx]继续化简，我们可以得到：∫2xdx = 2lim(n→∞) Σ[xiΔx]由于 n 在趋于无穷大的过程中，Σ[xiΔx] 是一个常数，所以我们可以得到：∫2xdx = 2Σ[xiΔx]因此，函数 f(x) = 2x 的积分为∫2xdx = x^2 + C，其中 C 为常数。
微积分第四版曹定华李建平课后习题答案
习题 1.1
微积分第四版曹定华 李建平课后习题答案
获取更多课后习题答案请关注微信公众号学糕
获取更多课后习题答案请关注微信公众号学糕
获取更多课后习题答案请关注微信公众号学糕
获取更多课后习题答案请关注微信公众号学糕
获取更多课后习题答案请关注微信公众号学糕
获取更多课后习题答案请关注微信公众号学糕
习题 1.2
获取更多课后习题答案请关注微信公众号学糕
获取更多课后习题答案请关注微信公众号学糕
获取更多课后习题答案请关注微信公众号学糕
习题 1.3
获取更多课后习题答案请关注微信公众号学糕
获取更多课后习题答案请关注微信公众号学糕
赵树嫄-《微积分(第四版)》第一章 函数
(六) 集合运算律
交换律： A B B A AB B A
结合律： ( A B) C A (B C) (A B) C A(B C)
分配律： A (B C) ( A B) ( A C) A(B C) (A B) (AC)
2232??????xx????????????????????22322322xxxx?????????????????0304322xxxx?????????????????3041xxx或01??????x或43????xx01??43即即4301?????x
1
在一切理论成就中，未必有什么 像17世纪下半叶微积分的发明那 样被看作人类精神的卓越胜利了 （恩格斯）
U
A B
U A
B
例如， R - Q 表示全体无理数组成的集合。
基本性质： A B A B
15
4、补集 A { x | x U 且 x A} , 其中 U为全集。
U A
例如，U {0, 1, 2, 3, } , A {0, 2, 4, 6, } ,
则 A {1, 3, 5, 7, }
解 由容斥原理，至少熟悉一种语言的人有
47 35 23 59 ,
两种语言都不熟悉的人有
47 23 35
100 59 41 .
41
25
| A B|| A|| AB|
E
B
A
特别，若 B A ，则| A B | | A | | B | 。
E BA
26
例2 在12000的整数中，有多少整数 (1) 能被6或8整除； (2) 既不能被6也不能被8整除； (3) 能被6整除而不能被8整除.
《微积分》各章习题及详细答案
第一章 函数极限与连续一、填空题1、已知x x f cos 1)2(sin +=,则=)(cos x f 。
2、=-+→∞)1()34(lim22x x x x 。
3、0→x 时,x x sin tan -就是x 的 阶无穷小。
4、01sin lim 0=→xx kx 成立的k 为 。
5、=-∞→x e xx arctan lim 。
6、⎩⎨⎧≤+>+=0,0,1)(x b x x e x f x 在0=x 处连续,则=b 。
7、=+→xx x 6)13ln(lim 0 。
8、设)(x f 的定义域就是]1,0[,则)(ln x f 的定义域就是__________。
9、函数)2ln(1++=x y 的反函数为_________。
10、设a 就是非零常数,则________)(lim =-+∞→xx ax a x 。
11、已知当0→x 时,1)1(312-+ax 与1cos -x 就是等价无穷小,则常数________=a 。
12、函数xxx f +=13arcsin )(的定义域就是__________。
13、lim ____________x →+∞=。
14、设8)2(lim =-+∞→xx ax a x ,则=a ________。
15、)2)(1(lim n n n n n -++++∞→=____________。
二、选择题1、设)(),(x g x f 就是],[l l -上的偶函数,)(x h 就是],[l l -上的奇函数,则 中所给的函数必为奇函数。
(Ａ))()(x g x f +;(Ｂ))()(x h x f +;(C))]()()[(x h x g x f +;(D))()()(x h x g x f 。
2、xxx +-=11)(α,31)(x x -=β,则当1→x 时有 。
(Ａ)α就是比β高阶的无穷小; (Ｂ)α就是比β低阶的无穷小; (C)α与β就是同阶无穷小; (D)βα~。
高等数学(第四版) 上、下册(同济大学 天津大学等编)1_1 函数-PPT精选文档
全体实数集 R 可记作, ．
[a,b]
(a,b)
a (a) b x
O a (b) b x
i 只日光灯． （2）描述法 用一个命题（或一句话）来描述集
合中所有元素的属性，以表示集合的方法为描述法．
例如：上例 A 可表示为 A x x是小于10的正奇数；
C 是方程 x2 4x 3 0的解集：
列举法：C 1,3；描述法：C x x2 4x 3 0 .
如果 a 是集合 A 的元素，记为a A； 如果 b 不是集合 A 的元素，记b A为 (或b A)．
2． 集合的表示法 （1）列举法 将集合中的元素列举出来的表示法． 例 如 ： 小 于 10 的 正 奇 数 所 组 成 的 集 合
A 1,3,5,7,9；如果一个教室里有五只日光灯所组成的 集合 B b1,b2,b3,b4,b5．其中bi i 1, 2,3, 4,5分别表示第
数集字母的右上角标上“+”时，表示该数集内排除 0 与负数的集合，全体实数集合 R, R为排除数 0 的实数集， R 表示全体正实数集．全体整数集为 Z ，全体有理数的 集合为Q ．
（4）空集 不含任何元素的集合称为空集，记作 ．
例如： x x R且x2 2 0 是空集．
（二）区间与邻域
的元素，称A是B的子集．记为AB或BA
（2）相等子集 若集合A与集合B含有相同的元素，
称A与B相等，记为AB或B A
（3）真子集 若AB且AB，称A是B的真子集， 记为AÖ B
高等数学(微积分学)教学课件
三、两个重要极限
重要极限Ⅰ lim sin x 1 x0 x
它可以拓展为 lim sin[ f (x)] 1 f (x)0 f (x)
sin 2x
例：lim x 2x
1
1 cos x
lim
x0
x2
lim
x0
2 sin 2 x 2
4 x2 4
lim
1
sin
x 2
x0 2 x
2
2
1 2
判断：lim sin x 1
叫做因变量.
数集 D 称为这个函数的定义域.
全体函数值的集合称为函数的值域.
2. 函数的表示法
解析法（公式法）：用解析表达式（或公式）表示函数关系.
y x 1
表格法：用列表的方法来表示函数关系.
x123456789 y 1 4 9 16 25 36 49 64 81
图示法：用平面直角坐标系 xoy 上的曲线来表示函数关系.
x
x
1 0
x
x
1
1
1 lim( x0 1
x
)
1 x
x
lim
x0
(1 (1
x) x
1
x) x
lim x0
(1 x) x
1 (1)
[1 (x)] x
e e1
e2
一类特殊极限
若f
(x)
a0 xm a1xm1 a2 xm2 b0 xn b1xn1 b2 xn2
am1x am bn1x bn
x 果对于定义区间的任意点 , 恒有 f (x) f (x) , 则称f (x)
为 D 内的偶函数；如果恒有 f (x) f (x) , 则称 f (x)为D
赵树嫄微积分第四版微分方程与差分方程简介
两边积分, g(y)d yf(x)d x
设 函 数 G (y )和 F (x )是 依 次 为 g (y )和 f(x )
的 某 个 原 函 数 ,
则 G (y ) F (x ) C 为微分方程的通解。
可分离的微分方程的解法 (1)分离变量 g(y)dyf(x)dx (2)两边同时积分
定义 含有自变量，自变量的未知函数以及未知函数 的若干阶导数或微分的函数方程称为微分方程.
定义 出现在微分方程中的未知函数的最高阶导数或 微分的阶数，称为微分方程的阶.
未知函数是一元函数的微分方程称为常微分方程，未 知函数是多元函数的微分方程称为偏微分方程.在本书 中只讨论常微分方程，如下例：
yxy, 一阶 dyxd yx
22
2
s d x x i n cx s d x c l|n cx s c cx o | C t
例 求 方 程 y x 1 ( 1 y y x 2 2 )满 足 y ( 1 ) 2 的 特 解 .
解
y
1
分离变量， 1y2dyx(1x2)dx
两边积分
1l
n1(
y2)
1
2
2
x2(11x2)dx2
dx x y2 , dy y
此 即 一 阶 线 性 方 程 , 解 得 通 解 为
将y和y代入原方程 u(x 得 )eP(x)dxQ (x),
积分得 u (x )Q (x )e P (x )d x d x C ,
所以原方程的通解为:
y e P (x ) d x [Q (x )e P (x ) d x d x C ]
y e P (x ) d x [Q (x )e P (x ) d x d x C ]
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
分配律： A ( B C ) ( A B ) ( A C ) A ( B C ) ( A B ) ( A C )
对偶律： ABA B
A BAB
.
17
例1 证明对偶律 ABA B.
证明 设xAB，则xAB，
即 x A 且 x B ， 于 是 x A 且 x B ，
因 此xA B，所 以 A B A B；
xA B
所 以 A BA B。
.
19
例2 证明 ABA B.
U
证明 对 任 意 的 x A B
A
x A 且 x B B
x A 且 x B
xA B
所 以 A BA B 。
.
20
例3 证明吸收律 A (AB )A.
证明 A(A B) (A U ) (A B ) A(UB) A U
A.
反 之 ， 若 x A B， 即 xA且 xB， 也 即 x A 且 x B ， 于 是 x A B，
从 而xAB，所 以 A B A B。
综 上 所 述 ， A B A B 。
.
18
例1 证明对偶律 ABA B.
或证 对 任 意 的 xAB
xAB x A 且 x B
x A 且 x B
1、并集 A B {x |x A 或 x B }
U
A
B
例如，A{1,2,3}, B{3,4,5}, 则 A B {1 ,2 ,3 ,4 ,5 }
基本性质： A A B ,B A B
A A ,A U U ,A A A
.
13
2、交集 A B {x |x A 且 x B }
.
4
第一章 函 数
.
5
第一节 集合
(一) 集合的概念
把一些确定的、彼此不同的事物作为一个整体来看待
时，这个整体便称为是一个集合。
组成集合的那些个体称为集合的元素。 例如 全体中国人可组成一个集合，每一个中国人均 是这个集合的元素。
通常用大写字母 A、B、C 等表示集合，用小写字母 a、 b、c 等表示集合的元素。
吸收律 A(AB)A证明留作练习。
.
21
例4 证明 A (A B )A B
证明 A(AB)
ABA B
Hale Waihona Puke A (A B)A (AB)(AA)(AB)
(AB)A B.
.
22
例5 证明 A B A A B
证明 "" 设ABA,A BA,
A B (A B) BA (B B)
A .
"" 设AB ,
实数集 R{全体实}数
例如：2 N，2.5 N，-3 N，2.5 Q，-3 Z 。 由有限个元素构成的集合称为有限集，由无限多个 元素构成的集合称为无限集。
.
7
(二) 集合的表示法
通常集合的表示有两种方法： (1) 列举法：按任意顺序逐一列举集合中的元素于花 括号内，元素之间用逗号隔开。
例如：A = { 2, a, b, 9 }, B = { 4, 5, 6, 7, 8 } (2) 描述法：给定一个条件 P(x)，当且仅当元素 a 使 P(a) 成立时，a A。其一般形式为 A = {a | P(a) }。
.
1
在一切理论成就中，未必有什么 像17世纪下半叶微积分的发明那 样被看作人类精神的卓越胜利了 （恩格斯）
.
2
教材：
《微积分》
主编 赵树嫄 （第四版）
中国人民大学出版社
.
3
微积分(Calculus)是一门以变
量为研究对象、以极限方法作为研 究工具的数学学科，应用极限方法 研究各类变化率问题和几何学中曲 线的切线问题，就产生了微分学； 应用极限方法研究诸如曲边梯形的 面积等涉及到微小量无穷积累的问 题，就产生了积分学。英国数学家 牛顿和德国数学家莱布尼兹 同时发 明了微积分，微积分研究的主要对 象就是函数。
如果 A 是 B 的子集，且 B 中至少有一个元素不属于
A ，则称 A 是 B 的真子集，记作 A B 或 B A .
B A
如果集合 A 和 B 互相包含，即A B 且 B A，则称
A 和 B 的相等 ，记作 A = B 。
.
11
对任一集合 A ，有 AU. 常用数集： NZQR
.
12
(五) 集合的运算
如果a是集合A的元素，则记作 aA，读作a属于A；
如果a不是集合A的元素，则记作 aA ，读作a不属于A。
.
6
常见数集的记号：
自然数集 N {0 ,1 ,2 ,3 , ,n , }
整数集 Z {0 , 1 , 2 ,3 , , n , }
正整数集 Z{1,2,3,,n,}
有理数集 Q{p|pN,qZ,且p,q互}素 q
基本性质： A B A B
.
15
4、补集 A {x|x U 且 x A },其中 U为全集。
U A
例如， U{0,1,2,3,},A{0,2,4,6,},
则 A{1,3,5,7,}
基本性质： AAU, AA
.
(六) 集合运算律
交换律： ABBA A BB A
结合律： (A B ) C A (B C ) (A B )C A (B C )
例如 上述集合 B = { a | a N 且 4 a 8 }
又如 C{2i |iN} 即 C{20， 21， 22， 23， }
D {2 x |x N 且 x 5},0 即 D {0 ， 2 ， 4 ， ， 9,1 8} 0
.
8
集合以及集合间的关系可以用如下的图形表示，称 为文氏图，即用一个平面区域表示一个集合。
ABA B(A B)
(AB)(AB)A (BB)
A E A .
.
23
集合元素的计数问题：
定义 集合 A 中所含元素的个数称为集合 A 的基数， 记作 | A |。
AB
U
A
B
.
9
(三) 全集与空集
在研究某一问题时，如果所讨论的集合都是某一集 合的子集，则称此集合为全集，记作 U . 不含任何元素的集合称为空集，记为 Ø。
.
10
(四) 子集
如果集合 A 的元素也是集合 B 的元素，则称 B 包含
A ，或称 A 是 B 的子集，记作： A B 或 B A .
U
A
B
例如， A{x|x1}, B {x|0x2},则 A B {x |0 x 1 }.
基本性质： A B A ,A B B
A ,A U A ,A A A
.
14
3、差集 A B {x |x A 但 x B }
U
A B
U A
B
例如， R - Q 表示全体无理数组成的集合。