高等数学11-1第二次单元测验试卷答案201212
河北衡水中学2011～2012学年度下学期一调考试高三数学试题 全解析(理科 )
河北衡水中学2011～2012学年度下学期一调考试高三数学试题 全解析（理科 ）本试卷分第I 卷（选择题60分）和第Ⅱ卷（非选择题90分）两部分。
一共6页。
共24题。
本试卷共150分，考试时间120分钟.祝各位考生考试顺利！第I 卷（选择题60分）一、选择题（每小题5分，共60分。
下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上）1.集合{}Z x x x A ∈≤+=,21,{}11,3≤≤-==x x y y B ，则=B A ( D ) A ．(]1,∞-B.[]1,1-C.φD.{}1,0,1-2.若z 是复数，且()13=+i z (i 为虚数单位)，则z 的值为 ( B )A ．i +-3 B.i --3 C.i +3 D.i -33．已知甲、乙两名篮球运动员某十场比赛得分的茎叶图如图所示， 则甲、乙两人在这十场比赛中得分的平均数与方差的大小关系为( D ) A ． 乙甲x x < 22x x S S <<乙甲，乙甲 B. 乙甲x x < 22x x S S <>乙甲，乙甲 C. 乙甲x x >22x x S S >>乙甲，乙甲D. 乙甲x x > 22x x S S><乙甲，乙甲4. 一个几何体的三视图如图所示，则该几何体的体积为（ C ）A ．2B ．1C ．23 D ．135．设x ，y 满足36020,3x y x y x y --≤⎧⎪-+≥⎨⎪+≥⎩若目标函数z=ax+y （a>0）的最大值为14，则a=（ B ） A ．1 B ．2C ．23D ．5396.等差数列{n a }前n 项和为n s ，满足4020s s =，则下列结论中正确的是（ D ） A 、30s 是n s 中的最大值 B 、30s 是n s 中的最小值 C 、30s =0 D 、60s =0 7．阅读右面程序框图，任意输入一次(01)x x ≤≤与(01)y y ≤≤，则能输出数对(,)x y 的概率为（ A ）A ．13B ．23C ．14 D ．34乙 甲 8 6 4 3 1 58 6 3 2 4 58 3 4 9 45 01 3 1 6 798.若函数sin()y A x ωϕ=+（0A >，0ω>，||2πϕ<）在一个周期内的图象如图所示，,M N 分别是这段图象的最高点和最低点，且ON OM ⋅=0，（O 为坐标原点）则A ω⋅=（ C ） A 、6πB 、712π C 、76π D 、73π 9.已知双曲线221916x y -=，其右焦点为F ，P 其上一点，点M 满足MF =1，0=⋅MP MF ，则MP 的最小值为（ B ）A 3B 3C 2D 210.设D 是正123PP P ∆及其内部的点构成的集合，点0P 是123PP P ∆的中心，若集合0{|,||||,1,2,3}i S P P D PP PP i =∈≤=，则集合S 表示的平面区域是( D )A ． 三角形区域B ．四边形区域C ． 五边形区域D ．六边形区域11．如图，已知平面α⊥平面β，A 、B 是平面α与平面β的 交线上的两个定点，,DA CB ββ⊂⊂，且DA α⊥，CB α⊥，4AD =，8BC =，6AB =，在平面α上有一个动点P ，使得APD BPC ∠=∠，则PAB ∆的面积的最大值是（ C ）A239 B 536 C 12 D 2412．已知函数()||,()xx af x e a R e=+∈在区间[0,1]上单调递增，则实数a 的取值范围是（ C ）A ． [0,1]a ∈B ． ]0,1[-∈a C. [1,1]a ∈- D. ),[],(22+∞⋃--∞∈e e a 第Ⅱ卷（ 90分）二、填空题（本大题共4小题,每小题5分,共20分）13. 为了测量一古塔的高度，某人在塔的正西方向的A 地测得塔尖的仰角为45°，沿着A 向北偏东30°前进100米到达B 地（假设A 和B 在海拔相同的地面上），在B 地测得塔尖的仰角为，则塔高为_____ 米5014.已知函数()f x 满足：1(1)4f =，4()()()(),(,)f x f y f x y f x y x y R =++-∈，则(2010)f =____________．12βαA CBP D解：令1y =则4()(1)(1)(1),(,)f x f f x f x x y R =++-∈()(1)(1)f x f x f x ∴=++-∴(1)(2)()f x f x f x +=++ ∴()(2)f x f x =+ ∴(2010)(0)f f =令1y =则1(0)2f =∴1(2010)2f =15.在平面直角坐标系中，定义点),(),,(2211y x Q y x P 之间的“直角距离”为||||),(2121y y x x Q P d -+-=。
福建师大附中11-12学年度下学期高一数学期末模块测试新人教A版
某某师大附中2011—2012学年度下学期末模块测试高一数学试题本试卷共4页．满分150分，考试时间120分钟．注意事项：将答案填写在答卷纸上，考试结束后只交答案卷.一、选择题：本大题有12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项符合题目要求. 1．sin 300tan 240oo+的值是 A ．23-B ．23C ．321+-D ．321+ 2．函数2cos 2y x =+是A ．最小正周期为π的偶函数B ．最小正周期为π的奇函数C ．最小正周期为2π的偶函数D ．最小正周期为2π的奇函数 3．已知(2,3)A ，(3,0)B ，且2AC CB =-，则点C 的坐标为 A ．(3,4)-B ．(4,3)-C ．8(,1)3D ．8(1,3-4．已知a b a ,2||,1||==与b 的夹角为600，若ka b +与b 垂直，则k 的值为A ．4-B ．4C ．43-．435．若把函数cos y x =的图象上所有点的横坐标缩小到原来的一半（纵坐标不变），然后再把图象向左平移6π个单位，则所得图象对应的函数解析式为 A ．1cos(26y x π=+B ．1cos()212y x π=+C ．cos(2)6y x π=+D ．cos(2)3y x π=+6．已知扇形的周长是6cm ，面积是22cm ,则扇形的中心角的弧度数是 A ．1 B ．4 C ．1 或4D ．2 或47．若,αβ为锐角，且满足45cos ,cos(),513ααβ=+= 则sin β的值是 A ．1665B ．3365C ．5665D ．63658．已知函数sin()y A x B ωϕ=++的一部分图象如图所示，如果2||,0,0πϕω<>>A ，则第14题图A ．4=AB ．1=ωC ．6πϕ=D ．4=B9．已知以原点O 为圆心的单位圆上有一质点P ，它从初始位置013()2P 开始，按逆时针方向以角速度1/rad s 做圆 周运动.则点P 的纵坐标y 关于时间t 的函数关系为 A ．sin(),03y t t π=+≥B ．sin(),06y t t π=+≥ C ．cos(),03y t t π=+≥D ．cos(),06y t t π=+≥ 10．若(010,)4k k k Z πθ=≤≤∈，则sin cos 1θθ+≥的概率为 A ．15B ．25C ．211D ．61111．设()2sin()f x x m ωϕ=+-，恒有()()2f x f x π+=-成立，且(14f π=-，则实数m的值为A ．1±B ．3±C ．－3或1D ．－1或312．若两个函数的图象仅经过若干次平移后能够重合，则称这两个函数为“同形”函数．给出下列三个函数：1()22f x x =，2()sin cos f x x x=+，3()2)16f x x π=++，则A ．123(),(),()f x f x f x 两两为“同形”函数B ．12(),()f x f x 为“同形”函数，且它们与3()f x 不为“同形”函数C ．23(),()f x f x 为“同形”函数，且它们与1()f x 不为“同形”函数D ．123(),(),()f x f x f x 两两不为“同形”函数二、填空题：本大题有5小题，每小题4分，共20分，把答案填在答卷的相应位置. 13．已知5sin()6x π+=，则2cos()3x π+的值为 *** ； 14．如图,在平行四边形ABCD 中,,,3AB a AD b AN NC ===,则BN = *** (用,a b 表示) ；15．设a ＝)sin ,23(α，b ＝31,(cos α，且a ∥b ，则锐角α的大小为 *** ；16．定义在R 上的函数()f x 既是偶函数又是周期函数，若()f x 的最小正周期是2π，且当[0,]4x π∈ 时，()cos f x x =，则()3f π= *** ；17．定义平面向量之间的一种运算“⊗”如下：对任意的向量(,),(,)a m n b p q ==，令a b mq np ⊗=-，给出下面四个判断：①若a 与b 共线，则0a b ⊗=； ② 若a 与b 垂直，则0a b ⊗=；③a b b a ⊗=⊗； ④2222()()||||a b a b a b ⊗+⋅=.其中正确的有 *** （写出所有正确的序号）.三、解答题：本大题有6题，共70分，解答应写出文字说明、证明过程或演算步骤. 18．（本小题满分10分）已知||2,||1,(23)(2)9a b a b a b ==⋅+=－. （Ⅰ）求a b 与的夹角θ； （Ⅱ）求向量a 在()a b +上的投影.19．（本小题满分12分）如图，在平面直角坐标系xOy 中，以Ox 轴为始边作两个锐角α、β，它们的终边分别与单位圆相交于A 、B 两点.已知A 、B 的横坐标分别为102，552.（Ⅰ）求)tan(βα+的值；（Ⅱ）求22sin sin 26cos cos 2αααα++的值.20．（本小题满分12分）已知向量(cos 2,4),(1,cos )a x b x λ=-=，其中,[0,]2R x πλ∈∈.设函数()f x a b =⋅.（Ⅰ）求)(x f 的解析式； （Ⅱ）若()f x 的最小值是23-，求λ的值．21．(本小题满分12分) （Ⅰ）已知：3sin cos 5αβ+=,4cos sin 5αβ-=,求sin()αβ-的值; （Ⅱ）类比（Ⅰ）的过程与方法，将（Ⅰ）中已知条件中两个等式的左边进行适当改变，写出改变后的式子，并求cos()αβ-的值.22．(本小题满分12分)如图，在半径为1，圆心角为6π的扇形OAB 的弧上任取一点C ，作CD OA ，交OB 于点D ，求OCD ∆的最大面积.23．（本小题满分12分）已知函数()cos 2(),(0,0,0)222A A f x x A πωϕωϕ=-+>><<的图象过点(1,2)，相邻两条对称轴间的距离为2，且()f x 的最大值为2. （Ⅰ）求()f x 的单调递增区间； （Ⅱ）计算(1)(2)(2012)f f f +++；（Ⅲ）设函数()()1g x f x m =--，试讨论函数()g x 在区间[1，4]上的零点情况.参考答案一、选择题：1－12：BABADCBCADDC 二、填空题： 13．5-．1344a b -+ 15.4π16.2 17. ①④ 三、解答题：18．解: （Ⅰ）22(23)(2)4439a b a b a a b b +=-⋅-=－, 即16439a b -⋅-=∴1a b ⋅=∴1cos 2||||a b a b θ⋅==∵[0,]θπ∈∴3πθ=（Ⅱ）222||27a b a a b b +=+⋅+= ∴||7a b +=，设a 与()a b +的夹角为α∴向量a 在()a b+上的投影为2()()5||cos ||7||||||||7a ab a a b a a b a a a a b a b a b α⋅+⋅++⋅=====+++ 19．解:由条件得102cos =α，552cos =β，∵α，β为锐角， ∴1027cos 1sin 2=-=αα，55cos 1sin 2=-=ββ， 因此7cos sin tan ==ααα，21cos sin tan ==βββ. （1）32171217tan tan 1tan tan )tan(-=⨯-+=-+=+βαβαβα. （2）2222222sin sin 2sin 2sin cos tan 2tan 491436cos cos 27cos sin 7tan 7492αααααααααααα++++====-+--- 20．解：（Ⅰ）,cos 42cos )(x x x f λ-=]2,0[π∈x（Ⅱ）∵()cos 24cos f x x x λ=-222(cos )12.x λλ=---]2,0[π∈x∵]2,0[π∈x ， ∴.1cos 0≤≤x设cos ,0 1.t x t =≤≤则222()12,0 1.y t t λλ=---≤≤01<'λ当、时，当且仅当min 0,1t y ==-时，这与已知矛盾． 101≤≤''λ当、时，当且仅当2min ,12t y λλ==--时.由已知得23212-=--λ，解得.21=λ 11>'''λ当、时，当且仅当min 1,14t y λ==-时.由已知得2341-=-λ，解得85=λ，这与1>λ相矛盾．综上所述，21=λ为所求． 21．解：（Ⅰ）∵53cos sin =+βα①54sin cos =-βα②①的平方+②的平方，得22(sin cos cos sin )1αβαβ+-=21)sin(-=-∴βα（Ⅱ）可将（Ⅰ）（1）中已知条件改为，3sin sin 5αβ+=，54cos cos =+βα，将两式平方后求和得1)cos cos sin (sin 22=++βαβα21)cos(-=-∴βα22．解：作DE OA ⊥于点E ，CF OA ⊥于点F ，设AOC α∠=,则0π在Rt OCF∆中，sin CFα=，cos OF α= 在Rt ODE ∆中，∴OE α===∴cos EF OFOE αα=-= ∴21111sin (cos )sin cos 2222OCD S CD CF EF CF αααααα∆=⋅=⋅=⋅=1cos 2)1sin 2sin 2cos 244444αααα-=-=+-1sin(2)234πα=+-，06πα<<. ∵06πα<<，所以22333πππα<+<∴当232ππα+=，即12πα=时，OCD S ∆有最大值且为124- 23．解：（Ⅰ）22,4,02224T T T πππωωω==>∴==∴=， 由于()f x 的最大值为2且A>0， ∴ 所以222A A+=即A=2∴()1cos 2()4f x x πϕ=-+，又函数()f x 的图象过点(1,2)则cos 2()1sin 21422,,24024k k k Zπϕϕππϕπϕππϕπϕ+=-∴=∴=+=+∈<<∴=∴()1cos 2()1sin 442f x x x πππ=-+=+ 由22(),222k x k k Z πππππ-≤≤+∈得1414(),2k x k k Z π-+≤≤+∈∴)(x f 的单调增区间是[14,14]().k k k Z -++∈ （Ⅱ）由（Ⅰ）知()1sin2f x x π=+，∴()f x 的周期为4，而2012=4×503 且(1)2,(2)1,(3)0,(4)1f f f f ==== ∴原式45032012=⨯=（Ⅲ）()()1cos()sin 222g x f x m x m x m πππ=--=-+-=-函数()g x 的零点个数即为函数sin2y x π=的图象与直线y m =的交点个数.在同一直角坐标系内作出这两个函数的图象(如下图所示)，由图象可知:x1） 当1m >或1m <-时，函数sin 2y x π=的图象与直线y m =无公共点，即函数()g x 无零点；2） 当01m <≤或1m =-时，函数sin2y x π=的图象与直线y m =有一个公共点，即函数()g x 有一个零点； 3） 当10m -<≤时，函数sin2y x π=的图象与直线y m =有两个公共点，即函数()g x 有两个零点.。
河北省衡水中学11-12学年高一下学期二调考试(数学文)
2011—2012学年度第二学期第二次调研考试高一年级数学（文科）试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分，共150分。
考试时间120分钟。
第Ⅰ卷（选择题 共60分）注意事项：1.答卷Ⅰ前，考生将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.答卷Ⅰ时，每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。
一、 选择题（每小题5分，共60分。
下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上）1. 下列两个变量之间的关系是相关关系的是 ( )A.正方体的棱长和体积B.单位圆中角的度数和所对弧长C.单产为常数时，土地面积和总产量D.日照时间与水稻的亩产量2.在下列各数中，最小的数是 （ ）A 、)9(85B 、)6(210C 、)4(1000D 、)2(111113.阅读右侧程序：如果输入x ＝2，则输出结果y 为 ( )A ．π－5B ．－π－5C ．3＋πD ．3－π4.与01303终边相同的角是 （ ）A ．0763B ．0493C ．0371-D ．047-5. 已知点A (1,2，－1)，点C 与点A 关于xOy 面对称，点B 与点A 关于x 轴对称，则|BC |的值为 ( ) A. 2 5 B. 4 C. 2 2 D. 276.图1是某地参加2011年高考的学生身高统计图，从左到右的各长方形表示的学生人数依次记为1021,A A A ，，（如2A 表示身高（单位：cm ）在[)150,155内的学生人数）．图2是统计图1中身高在一定范围内学生人数的一个算法流程图．现要统计身高在160～185cm （含160cm ，不含185cm ）的学生人数，那么在流程图中的判断框内应填写的条件是 （ ） Ａ．9i < Ｂ．8i < Ｃ．7i < Ｄ．6i <第3题7.有四个游戏盘面积相等，将它们水平放稳后，在上面扔一颗玻璃小球，若小球落在阴影部分，则可中奖，小明要想增加中奖机会，应选择的游戏盘是 （ ）8.某产品的广告费用x 与销售额y 的统计数据如下表根据上表可得回归方程ˆˆybx a =+中的ˆb 为9．4，据此模型预报广告费用为6万元时销售额为（ ） A ．63．6万元 B ．65．5万元 C ．67．7万元 D ．72．0万元9. 执行如图所示的程序框图，若输出的n ＝6，则输入整数p 的最大值是（ ）A.32B.31C.15D.1610.已知圆的方程为08622=--+y x y x 设该圆中过点（3，5）的最长 弦和最短弦分别为AC 和BD ，则四边形ABCD 的面积是 （ ）A ．610B ．620C ．630D ．640第9题图S=S+2 n-111.某初级中学有学生270人，其中一年级108人，二、三年级各81人，现要利用抽样方法抽取10人参加某项调查，考虑选用简单随机抽样、分层抽样和系统抽样三种方案．使用简单随机抽样和分层抽样时，将学生按一、二、三年级依次统一编号为1,2，…，270；使用系统抽样时，将学生统一随机编号为1,2，…，270，并将整个编号依次分为10段．如果抽得号码有下列四种情况：①7,34,61,88,115,142,169,196,223,250；②5,9,100,107,111,121,180,195,200,265；③11,38,65,92,119,146,173,200,227,254；④30,57,84,111,138,165,192,219,246,270.关于上述样本的下列结论中，正确的是 ( )A ．②、③都不能为系统抽样B ．②、④都不能为分层抽样C ．①、④都可能为系统抽样D ．①、③都可能为分层抽样12. 对任意实数,a b ，定义运算“*”如下：x x f b a b b a a b a 221log )23(log )().(),(*-=⎩⎨⎧>≤=*则函数 x x x f b a b b a a b a 221log )23(log )().(),(*-=⎩⎨⎧>≤=*则函数的值域为 （ ） A ．[)+∞,0 B ．(]0,∞- C ．)0,32(log 2 D ．),32(log 2+∞ 第Ⅱ卷（非选择题 共90分）二、 填空题（每题5分，共20分。
2011-2012学年第一学期期末高二数学(理科)试题及答案
肇庆市中小学教学质量评估 2011—2012学年第一学期统一检测题高二数学（理科）一、选择题：本大题共8小题，每小题5分，满分40分. 在每小题给出的四个选项中，只有一项是符合题目要求的. 1．在空间中，下列命题正确的是A ．垂直于同一平面的两条直线平行B ．垂直于同一平面的两个平面平行C ．平行于同一直线的两个平面平行D ．平行直线的平行投影重合 2．下列是全称命题且是真命题的是A ．0,2>∈∀x R xB ．0,,22>+∈∀y x R y xC ．Q x Q x ∈∈∀2,D ．1,20>∈∃x Z x 3．双曲线142522=-y x 的渐近线方程是 A ．x y 52±= B ．x y 25±= C ．x y 254±= D ．x y 425±=4．命题“若a >-3，则a >-6”以及它的逆命题、否命题、逆否命题中，真命题的个数为A ．1B ．2C ．3D ．45．已知向量)0,1,1(=a ，)2,0,1(-=b ，且b a k +与b a -2互相垂直，则k 的值是A ．1B ．51C ．53D ．576．若焦点在x 轴上的椭圆1222=+k y x 的离心率为21，则实数k 等于 A ．3 B ．32 C ．38 D ．23 7．若圆02)1(222=-+-++m my x m y x 关于直线01=+-y x 对称，则实数m 的值为A ．-1或3B ．-1C ．3D ．不存在8．如图，某几何体的正视图、侧视图和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体体积为A ．34B ．32C ．4D ．2二、填空题：本大题共6小题，每小题5分，满分30分.9．用一个平面截半径为25的球，截面面积是225π，则球心到截面的距离为 ▲ .10．若A （-2，3）、B （3，-2）、C （21，m ）三点共线，则m 值为 ▲ .11．双曲线14222=-y x 的离心率等于 ▲ . 12．若动点P 在122+=x y 上，则点P 与点Q （0，-1）连线中点的轨迹方程是 ▲ . 13．不等式0)1)((<++x x a 成立的一个充分而不必要条件是12-<<-x ，则a 的取值范围是 ▲ .14．如图，在梯形ABCD 中，AB //CD ，AB =4，CD =2. E 、F 分别为AD 、BC 上点，且EF =3， EF //AB ，则梯形ABFE 与梯形EFCD 的面积 比为 ▲ .三、解答题：本大题共6小题，满分80分. 解答须写出文字说明、证明过程和演算步骤. 15．（本小题满分12分）求满足下列条件的直线的方程：（1）经过点A （3，2），且与直线4x +y -2=0平行；俯视图正视图侧视图A BCDEF（2）经过点B （2，-3），且平行于过点M （1，2）和N （-1，-5）的直线； （3）经过点C （3，0），且与直线2x +y -5=0垂直.16．（本小题满分12分）如图，一个高为H 的三棱柱形容器中盛有水. 若侧面AA 1B 1B 水平放置时，液面恰好过AC 、BC 、A 1C 1、B 1C 1的中点E 、F 、E 1、F 1. 当底面ABC 水平放置时，液面高为多少？17．（本小题满分14分）求与x 轴相切，圆心在直线3x -y =0上，且被直线x -y =0截得的弦长为72的圆的方程.18．（本小题满分14分）如图，棱长为a 的正方体1111D C B A ABCD -中，M 、N 、E 、F 分别是A 1B 1、A 1D 1、B 1C 1、C 1D 1的中点.（1）求证：B 、D 、E 、F 四点共面； （2）求证：平面AMN //平面BEFD ； （3）求点A 1到平面AMN 的距离．19．（本小题满分14分）如图，在长方体ABCD —A 1B 1C 1D 1中，E 、F 分别是棱BC 、CC 1上的点，CF =AB =2CE ，AB :AD :AA 1=1:2:4.（1）求异面直线EF 与A 1D 所成角的余弦值； （2）证明：AF ⊥平面A 1ED ；（3）求二面角A 1—ED —F 的大小的正弦值．111A 1B 120．（本小题满分14分）已知F 1、F 2分别为椭圆C 1：)0(12222>>=+b a bx a y 的上、下焦点，其中F 1也是抛物线C 2：y x 42=的焦点，点M 是C 1与C 2在第二象限的交点，且35||1=MF . （1）求椭圆C 1的方程；（2）已知A （b ，0），B （0，a ），直线 y =kx （k >0）与椭圆C 1相交于E 、F 两点. 求四边形AEBF 面积的最大值.2011—2012学年第一学期统一检测题 高二数学（理科）参考答案及评分标准一、选择题二、填空题9．20 10．2111．3 12．24x y =13．（2，+∞） 14．7:5 三、解答题15．（本小题满分12分）解：（1）由直线4x +y -2=0得直线的斜率为-4， （2分） 所以经过点A （3，2），且与直线4x +y -2=0平行的直线方程为y -2=-4(x -3)，即4x +y -14=0. （4分） （2）由已知，经过两点M （1，2）和N （-1，-5）的直线的斜率271125=----=k ， （6分） 所以，经过点B （2，-3），且平行于MN 的直线方程为)2(273-=+x y ，即7x -2y -20=0. （8分） （3）由直线2x +y -5=0得直线的斜率为-2， （9分） 所以与直线2x +y -5=0垂直的直线的斜率为21. （10分） 所以，经过点C （3，0），且与直线2x +y -5=0垂直的直线方程为)3(21-=x y ，即x -2y -3=0. （12分）16．（本小题满分12分）解：当侧面AA 1B 1B 水平放置时，水的体积V 等于 四棱柱ABFE —A 1B 1F 1E 1的体积，H S V V ABFE •==梯形四棱柱. （3分）当底面ABC 水平放置时，设水面高为h ，则水的体积h S V ABC •=∆. （6分） 因为E 、F 为AC 、BC 的中点，所以ABC CEF S S ∆∆=41， 所以ABC ABFE S S ∆=43梯形. （8分） 由h S H S ABC ABFE •=•∆梯形，即h S H S ABC ABC •=•∆∆43，得H h 43=. （11分）故当底面ABC 水平放置时，液面高为H 43. （12分）17．（本小题满分14分）解：设所求的圆的方程是)0()()(222>=-+-r r b y a x ， （2分） 则圆心到直线x -y =0的距离为2||b a -， （4分）所以222)7()2||(+-=b a r ，即14)(222+-=b a r ① （6分）111因为所求的圆与x 轴相切，所以22b r = ② （8分） 又因为所求圆心在直线3x -y =0上，所以3a -b =0 ③ （10分）联立①②③，解得⎪⎩⎪⎨⎧===,3,3,1r b a 或⎪⎩⎪⎨⎧=-=-=.3,3,1r b a （12分）故所求圆的方程为9)3()1(22=-+-y x 或9)3()1(22=+++y x . （14分）18．（本小题满分14分） （1）证明：如图，连接B 1D 1. 因为E 、F 为B 1C 1、C 1D 1的中点， 所以EF //B 1D 1. （2分） 又因为BD //B 1D 1，所以EF //BD . （3分） 故B 、D 、E 、F 四点共面. （4分） （2）证明：连接EN .因为M 、N 为A 1B 1、A 1D 1的中点，所以MN //B 1D 1.又EF //B 1D 1，所以MN / / EF . （5分） 因为EF ⊂平面BEFD ，所以MN //平面BEFD . （6分） 因为E 、N 为B 1C 1、A 1D 1的中点，所以EN //A 1B 1，且EN =A 1B 1. 又AB //A 1B 1，且AB =A 1B 1，所以NE / / AB ，且NE =AB .所以四边形ABEN 为平行四边行，故AN //BE . （7分） 因为BE ⊂平面BEFD ，所以AN //平面BEFD . （8分） 因为MN ⊂平面AMN ，AN ⊂平面AMN ，且MN ∩AN =N ，所以平面AMN //平面BEFD . （9分） （3）证明：设A 1到平面AMN 的距离为d . 在∆AMN 中，a a a AN AM 254122=+==，a a a MN 22414122=+=， 所以22283162452221a a a a S AMN =-⨯⨯=∆. （11分）A 1因为MN A A AMN A V V 11--=三棱锥三棱锥， （12分）即a a d a ⨯⨯=⨯⨯2281318331， （13分） 解得3a d =,故A 1到平面AMN 的距离为3a. （14分）19．（本小题满分14分）解：以A 为原点，建立如图所示的空间直角坐标系． 设AB =1，依题意得A （0，0，0），A 1（0，0，4）， D （0，2，0），E （1，23，0），F （1，2，1）. （2分） （1）易得)1,21,0(=EF ，)4,2,0(1-=D A ． （3分）所以535225410||||,cos 111-=⨯-+=•>=<D A EF D A EF D A EF ， （5分）故异面直线EF 与A 1D 所成角的余弦值为53． （6分）（2）易得)1,2,1(=AF ，)4,23,1(1-=E A ，)4,2,0(1-=D A . （7分）因为04311=-+=•E A AF ，04401=-+=•D A AF ， （8分） 所以E A AF 1⊥，D A AF 1⊥. （9分） 又A 1E ⊂平面A 1ED ，A 1D ⊂平面A 1ED ，A 1E ∩A 1D = A 1，所以AF ⊥平面A 1ED ． （10分） （3）设平面EFD 的法向量为),,(z y x m =．由)1,21,0(=EF ，)0,21,1(-=ED ，⎪⎩⎪⎨⎧=•=•,0,0m ED m EF得⎪⎪⎩⎪⎪⎨⎧=+-=+,021,021y x z y 解得⎩⎨⎧-=-=.2,z y z x不妨令1-=z , 得)1,2,1(-=m ． （11分）由（2）可知，)1,2,1(=AF 为平面A 1ED 的一个法向量. （12分） 于是3266141||||,cos =⨯-+=•>=<AF m AF m AF m ， （13分） 从而35,sin >=<AF m . 所以二面角A 1—ED —F 的大小的正弦值为35. （14分）20．（本小题满分14分）解：（1）设)0)(,(000<x y x M .由C 2：y x 42=，得F 1（0，1）. （1分） 因为M 在抛物线C 2上，故024y x =. ① （2分） 又35||1=MF ，则3510=+y . ② （3分） 解①②得⎪⎪⎩⎪⎪⎨⎧=-=.32,36200y x （4分） 因为点M 在椭圆上，故1)362()32(2222=-+b a ，即1389422=+ba ③ （5分） 又c =1，则122+=b a ④ （6分）解③④得⎪⎩⎪⎨⎧==.3,422b a 故椭圆C 1的方程为13422=+x y . （7分） （2）不妨设),(11y x E ，),(22y x F ，且21x x <.将kx y =代入13422=+x y 中，可得431222+=k x ， （8分） 即4332212+=-=k x x ，所以4332212+=-=k k y y . （9分）由（1）可得2||,3||==OB OA . （10分） 故四边形AEBF 的面积为22223232212221y x y x S S S AEF BEF +=⨯⨯+⨯⨯=+=∆∆. （11分） 所以43341324364334222++•=+++=k kk k k S （12分）因为k k 34432≥+，所以143342≤+k k. （13分）所以62≤S ，当且仅当332=k 时，等号成立. 故四边形AEBF 面积的最大值为62. （14分）。
11-12-1高数(一)期终考试试题答案及评分标准(A)
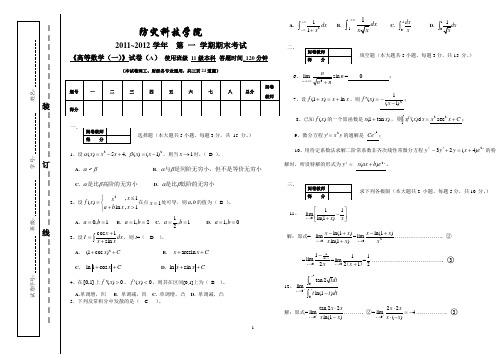
| | | | | | | |装| | | | |订|| | | | |线| | | | | | | | |防灾科技学院2011~2012学年 第 一 学期期末考试《高等数学（一）》试卷（A ） 使用班级 11级本科 答题时间_120分钟（本试卷理工、财经各专业通用，共三页24道题）一、选择题（本大题共5小题，每题3分，共 15 分。
）1、设22()54,()(1)x x x x x αβ=-+=-，则当1x →时，（ D ）。
A. ~αβ B. αβ与是同阶无穷小，但不是等价无穷小C.αβ是比高阶的无穷小 D. 低阶的无穷小是比βα2、设2,1(),1ln x xf x x a b x ≤⎧=⎨>+⎩在点1=x 处可导，则,a b 的值为（ B ）。
A. 0,1a b == B. 1,2a b == C. 1,12a b == D. 1,0a b == 3、设⎰++=dx x x x I sin 1cos ，则I =（ D ）。
A. 2(1cos )x C ++ B. a r c s i n x x C ++C. l n 1c o s x C ++D. ln sin x x C ++4、在[0,1]上''()0f x >，0)('<x f ，则其在区间[0,1]上为（ B ）。
A.单调增，凹 B. 单调减，凹 C. 单调增，凸 D. 单调减，凸5．下列反常积分中发散的是（ C ）。
A. 211dx x +∞-∞+⎰ B. 1+∞⎰C.1dxx⎰D. 1⎰二、 填空题（本大题共5小题，每题3分，共15 分。
）6、n nn n n sin lim3++∞→= 0 ；7、设x x x f ln )1(+=+，则()''=f x 2)1(1--x ；8、已知)(x f 的一个原函数是)tan 1(x x +，⎰='x x f x d )(则C x x +22sec ；9、微分方程y x y 2'=的通解是 3x Ce ；10、用待定系数法求解二阶常系数非齐次线性常微分方程xe x y y y 2//)4(23+=+'-的特解时，所设特解的形式为=*y x e b ax x 2)(+。
河北省衡水中学11-12学年高一数学下学期一调考试 理
2011—2012学年度第二学期第一次调研考试高一年级数学（理科）试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分，共150分。
考试时间120分钟。
第Ⅰ卷（选择题共60分）注意事项：1.答卷Ⅰ前，考生将自己的某某、某某号、考试科目涂写在答题卡上。
2.答卷Ⅰ时，每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。
一、选择题（每小题5分，共60分。
下列每小题所给选项只有一项符合题意，请将正确答案的序号填涂在答题卡上）1.已知}104|{+∈=N x x x A 的公倍数，与是，},20|{+∈==N m m x x B ，则 （ ） A ．B A ⊆且B A ≠B ．A B ⊆且B A ≠C ． B A =D ．B A ∈2.已知函数⎩⎨⎧>≤=)0(log )0(3)(2x x x x f x ，那么1[()]8f f 的值为( ) A ．27 B ．127C ．27-D ．127- 3.某四棱锥的三视图如图所示，该四棱锥的表面积是 （ ） A.32 B.16+162C.48 D.16322+4.若直线y x b =-与曲线1)2(22=+-y x 有两个不同的公共点，则实数b 的取值X 围为 （ ） A.(22,1)- B.[22,22]-+ C.(,22)(22,)-∞-++∞D.(22,22)-+5.已知直二面角l αβ--,点A α∈，AC l ⊥,C 为垂足,B β∈，BD l ⊥,D 为垂足,若2,1AB AC BD ===，则CD =（ ）D.16.设)(x f 为定义在R 上的奇函数，当0≥x 时，b x x f x++=22)((b 为常数)，则)1(-f =（ ）A .3 B.1 C.－1 D.－37.设(0,0),(1,1),(4,2)A B C ，若线段AD 是△ABC 外接圆的直径，则点D 的坐标是（）． A ．(-8,6) B ．(8，-6) C ．(4，-6) D ．(4，-3) 8.如图，M 是正方体1111ABCD A B C D -的棱1DD 的中点，给出命题①过M 点有且只有一条直线与直线AB 、11B C 都相交； ②过M 点有且只有一条直线与直线AB 、11B C 都垂直； ③过M 点有且只有一个平面与直线AB 、11B C 都相交； ④过M 点有且只有一个平面与直线AB 、11B C 都平行. 其中真命题是( )A ．②③④ B．①③④ C．①②④ D．①②③ 9.定义新运算“&”与“*”：1&y x y x -=，(1)log x x y y -*=，则函数(&3)1()32xx f x +=*是（ ）A 、奇函数B 、偶函数C 、非奇非偶函数D 、既是奇函数又是偶函数 10.若点A （2，-3）是直线0111=++y b x a 和0122=++y b x a 的公共点，则相异两点),(11b a 和),(22b a 所确定的直线方程为 （ ） A.0132=--y x B.0123=+-y x C.0132=+-y x D. 0123=--y x 11.在边长为1的菱形ABCD 中，∠ABC=60O，将菱形沿对角线AC 折起，使折起后BD=1，则三棱锥B-ACD 的体积为为（ ） A.122 B.121 C.62 D.42B 11M12.已知直线01243:=-+y x l ，若圆上恰好存在两个点P 、Q ，他们到直线l 的距离为1，则称该圆为“完美型”圆。
高等数学统考卷11-12届附答案
高等数学统考卷 1112届附答案一、选择题（每题1分，共5分）1. 下列函数中，哪个函数是奇函数？A. y = x^3B. y = x^2C. y = x^4D. y = |x|A. 积分的上下限互换，积分值不变B. 被积函数乘以常数，积分值也乘以该常数C. 积分区间可加性D. 积分中值定理3. 下列极限中，哪个是正确的？A. lim(x→0) (sin x) / x = 0B. lim(x→0) (1 cos x) / x^2 = 1C. lim(x→∞) (1 / x) = 0D. lim(x→∞) (x^2 1) / x = 1A. ∫∫(x^2 + y^2) dxdyB. ∫∫xy dxdyC. ∫∫x dxdyD. ∫∫y dxdy5. 下列级数中，哪个是收敛的？A. 1 + 1/2 + 1/3 + 1/4 + …B. 1 1/2 + 1/3 1/4 + …C. 1 + 2/3 + 4/9 + 8/27 + …D. 1 + 1/2 + 1/4 + 1/8 + …二、判断题（每题1分，共5分）1. 高斯公式可以用来计算曲面积分。
（）2. 泰勒公式可以用来近似计算函数值。
（）3. 无穷小量相乘仍为无穷小量。
（）4. 拉格朗日中值定理是罗尔定理的推广。
（）5. 偏导数连续必可微。
（）三、填空题（每题1分，共5分）1. 函数f(x) = e^x 在x = 0处的导数值为______。
2. 曲线y = x^3 在点(1, 1)处的切线方程为______。
3. 若f(x, y) = x^2 + y^2，则f_x(1, 2) =______。
4. 设A为矩阵，若|A| = 0，则A为______矩阵。
5. 空间曲线r(t) = (cos t, sin t, t) 在t = π/2处的切线方向向量为______。
四、简答题（每题2分，共10分）1. 简述罗尔定理的内容。
2. 解释复合函数求导法则。
3. 举例说明什么是隐函数。
11-12-2高等数学下(通信、电子本科)A卷及标准答案
2011 - 2012学年第二学期期末考试《高等数学(下)》试卷(A)答卷说明：1、本试卷共6页，四个大题，满分 100分，120分钟完卷。
2、闭卷考试。
3、适用班级：11级通信系、电子系本科各班题号-一--二二三四总分分数评阅人： ____________ 总分人： __________________________、单项选择题(共 10小题，每小题3分，共30分)。
【A 】设有直线L ： 口 =丄二二2及平面二:2x y =1,则直线L1 -2 1(A)平行于二 (B) 在二内 (C)垂直于二 (D) 与二斜交【D 】2.锥面z立体在xoy 面的投影为[A l 4.函数z = f (x, y)在点(x 0, y 0)处可微分，则函数在该点1 1【C 】5.将二次积分pdx. f(x,y)dy 转化成先对x ,后对y 的二次积分为(A)必连续 (C)必有极值(D)(B)偏导数必存在且连续偏导数不一定存在(A) (x -1)2 y 2=1 (B) (x-1)2 y 2 乞 1(C)z= 0,(x -1)2y 2 -1(D)z =0,(x_1)2y 2 _1【C 3.设函数z 二z(x, y)由方程e z = e + xyz 确定，则一z的值为(1,0,1)(A) d(B)e (C)(D)11 1 x( A )°dy y f(x, y)dx(B)°dy 0f(x,y)dx( C )1 y0dy 0f(x,y)dx(D) 1 10dy 0f(x,y)dx【D] 6.设L为圆周x22y =1(逆时针方向),则口L(x y)dx (3y -2x)dy( A 3 二(B) 2 二(C) 4 二(D) -3'：【D】7.下列级数中，收敛的级数是001(A) ----------- (B)n4 . 2n 1f (3n4 2n(C)1 nn4 1 * n2(D)nm n ■ 1°°(x _1)n 【B] 8.幕级数a(x n丿■的收敛域为心n3n(A) ( -2, 4) (B)[-2,4)(C)[-2,4](D)(-2, 4]【C】9.微分方程y - y = 0满足初始条件y l x出=2的特解为(A) y =e x1( B)xy = e 2x x(C) y = 2e (D) y = e【B] 10.具有特解y1.x .x二e , y2 二xe的二阶常系数齐次线性微分方程是(A) y -2y y = 0(B)y 2y y = 0(C) y y - 2y = 0(D)y - y 2y = 0得分|二、填空题(共5小题，每小题3分,共15分)1. 设两点A(1,2,1)及B (2,1,3),则| AB | = | AB | = •、6 _；向量AB与z轴的夹角为，r则方向余弦COS ；* = ____ . COS f = ----32. 设z = y x,则dz=_dz = y x In yd^xy x^dy.3. 函数f(x, y) =x2y — y2在点P(1,1)处方向导数的最大值为_T5 _____________ .4. 设L是连接(1,0)及(0,1)两点的直线段，则[(x + y)ds=_J2 _______________ .15.函数 展开成X 的幕级数为3 x1.已知曲面Z =x 2 ・y 2-2上一点M (2,1,3)，⑴ 求曲面在M 点处的一个法向量；(2) 求曲面在M 点处的切平面及法线方程•2.求函数 f (x, y) = 2(x 「y)「x 2「y 2 的极值.2 2 2 23.平面薄片的面密度为」(x,y)=x y 1,所占的闭区域 D 为圆周x y =1及坐标轴所围成的第一象限部分，求该平面薄片的质量.4.利用高斯公式计算曲面积分(3z 2x)dydz - (y 3 -2xz)dxdz - (3x 2z)dxdy ,其中Z为上半球面z = a 2 -x 2 - y 2及平面z = 0所围立体的整个边界曲面的外侧5.设曲线通过原点，且曲线上任一点 M (x, y)处的切线斜率等于 x - y ,求该曲线的方程.6. 求微分方程y -3y ，2y =e x 的通解.3n7. 判断级数v (-1)n °半是否收敛？如果收敛，是绝对收敛还是条件收敛?心 4四、综合应用题(共2小题，共13分，其中第1题6分，第2题7分).1. (6分)要用钢板造一个体积为4( m 3)长方体无盖容器，应如何选择容器的尺寸，使n 1n z03nx , -3 ：：三、计算题(共7小题，每小题6分,共42分)得用料最省？》 2 * 》2. (7分)设在xoy平面有一变力F(x, y) =(x • y2) i (2x^8) j构成力场,(1)证明质点在此力场中移动时,场力所作的功与路径无关 ；(2)计算质点从点 A(1,0)移动到点《高等数学(下)》试卷(A) 第5页 共6页B(2,1)时场力所作的功(1)|ABH<6; COS 63x(2) dz = y Inydx xy x_l dy、2「¥x n ,—3»3n £3三.计算题(每小题6分,共42分).1.(6 分)(1)由 z = x 2y 2 -2 得，Z x =2x,Z y =2y ,曲面在点M (2,1,3)处的一个法n=(-4, -2,1))2分)⑵ 在点M (2,1,3)的切平面方程为4(x-2)，2(y-1)-(z-3) =04x 2y-z -7 -0选择题每小题3分共30分)..填空题(每小题3分,共15分).... (2 分) 法x y 42分)线z -3 -1A 二 f xx （1,—1） = —2,B 二 f xy （1,—1） = °,C 二 f yy （1, — 1） = -2,则2AC - B=4 ° , A ：： ° , .................................................................................. （2 分）所 以 （-1 为 极 大 值 点 ， 极 大 值f （1,—1） =2 ............................................................. （2 分） 3.（6分）平 面 薄 片的 质M 二 J（x, y ）dxdy 二（x 2 y 2 1）dxdy .......................... （ 2 分）DD1 o2dr C 1）Z ° - °v/【丄加丄詩彳二3二 ................................ （2分）2 4 2 84.（6 分）所围空间区域 门={（ x, y, z ） |0 _ z _ a 2-X 2 - y 2} 由高斯公式，有原式r "耳◎迅）dv0 ex oy cz!!! （3z 2 3y 2 3x 2）dv ............................. （ 2 分）Q2 a=3茁 2sin 「d 「r 2 r 2dr ................................. （ 2 分）0 - 0 02.（6 分）f x =2_2x, f y =-2—2yf x 二 0,占八（2 分）y=°,（2 分）（-1 xy丑1 6=3 2二[-cos J： [ r5]0 a5......................... ( 2 分)5 55.(6分)设所求曲线为y = y(x),由题意得，y = x- y , y(0) = 0,该方程为一阶线性微分方程y・y=x, 其中P( x) 1 Q, x ........................... x .......................... ( 2 分)_p(x)dx |P(x)dx _|dx f dx故通解为y = e [ e Q(x)dx C] =e [ xe dx C] [xe x dx C]二e ▲ (xe x _ e x C)二Ce」x -1(2 分)2分)从而Q(x)二-x,特解y - -xe x, (2 分)y(0)=0 从而所求曲线为6.(6 分)对应的齐次方程y”-3y、2y=0的特征方程为r2-3r•2=0，得特征根则对应的齐次方程的y =C1e x C2e2x2分)对于非齐次方程y ” -3y： 2y二e x, ' =1为r2-3r *2=0的单根，P(x) =1,设其* y特解为y -Q(x)e x,其中Q(x)=ax, a为待定系数，Q(x)满足Q (x) (2' p)Q(x)二P(x)0 (2 1 _3)(a) =17.(6分)由于》(一1)n 4 3n4ny 二C^x C2e2x_xe x.而|im 加=lim匸匕=丄 , 贝U (—2卑1 )收y u n F 4n 4 心4n 敛，................................... （ 3 分）3n从而'•（_ ni i3n ）也收敛，且为绝对收心4n敛. ....................................... （3分）四、综合应用题（共2小题,共13分,其中第1题6分,第2题7分）.41.（6分）设该容器的长，宽，高为x, y,z,由题意知xyz=4,则z ,容器的表面积xy4 8 8A = xy 2yz 2xz = xy 2(x y) xy , x 0, y 0xy x y分）( 2 分)因实际问题存在最小值，且驻点唯一，所以当x二y = 2（ m）, z = 1（ m）时，容器的表面积最小，从而用料最省. .....................................................................（1分）2.（7 分）证明：（1）P（x, y）=x y2, Q（x, y） = 2xy-8,由于在xoy面内，—=2y Q恒成立，且P连续，® ex cy ex2分)故质点在该力场中移动时场力所作的功与路径无关. ................................... （4分）⑵质点从点A（1,0）移动到点B（2,1）时场力所作的功（与路径无关），路径L可取折线段A > C,C > B,其中点C(2,0),从而(2,1) * (2,1)W F dr Pdx Qdy%,。
河北衡水中学2011～2012学年度下学期一调考试高三数学试题全解析(理科)
x2 y 2 解： 解 :（ 1）因为椭圆 E: a2 b2 1 （ a,b>0）过 M （ 2， 2 ） ， N( 6 ,1)两点 ,
42
11
所以 a2 6
b2 1
1
解得
a2
1
8 所以 a2
8
椭圆 E 的方程为
x2
1
b2 4
8
y2 1
4
a2 b2 1
b2 4
（ 2）假设存在圆心在原点的圆， 使得该圆的任意一条切线与椭圆 E 恒有两个交点 A,B,
0.6 ，高考分数
达到该大学录取分数线的概率是 0.3 ．
（I ）求这名同学参加考试次数
的分布列及数学期望；
（II ）求这名同学被该大学录取的概率．
解：（ I ）记“获省高中数学竞赛优胜奖”为事件
A; 记“获国家高中数学联赛一等奖”为事
件 B；记“通过自主招生考试” 为事件 C；记 “高考分数达到一本分数线”为事件 D; 记“高
P( ABCD )
随机变量 的分布列为：
2
4
0.55
0.45
P( )
E( ) 2 0.55 4 0.45 2.90
（II ）记“这名同学被该大学录取”为事件 M 则 M AB AE ABCD ABCE
P( M ) P(AB AE ABCD ABCE)
P( M ) P( AB) P( AE) P( ABCD) P( ABCE )
C
12
D 24
2
5
P
A
B
D C
12．已知函数 （C ）
f ( x) | ex
a ex
|,(
a
R) 在区间 [0,1] 上单调递增，则实数
11-12(2)高等代数与解析几何试卷(A)参考答案及评分标准
中国计量学院2011 ~ 2012学年第 2 学期《高等代数》(2)课程试卷（A ）参考答案及评分标准一、单项选择题(每小题3分，共15分)1.D2.B3.D4.C5.A二、填空题(每小题3分，共15分)1.1111⎛⎫ ⎪-⎝⎭；2. __1，-3__；3.100010011⎛⎫⎪ ⎪⎪⎝⎭； 4. 20x y +-= 5.222x y pz +=．三、计算题1．(12分)设A 是3P 中的线性变换，且A 在基)1,1,1(1-=η,)1,0,1(2-=η,)1,1,0(3=η下的矩阵为101110121A ⎛⎫ ⎪= ⎪ ⎪-⎝⎭求A 在基123(1,0,0),(0,1,0),(0,0,1)εεε===下的矩阵.解 因为(1η,2η,3η)=(1ε,2ε，3ε)⎪⎪⎪⎭⎫⎝⎛--111101011， 所以 (1ε,2ε，3ε)=(1η,2η,3η)⎪⎪⎪⎭⎫ ⎝⎛---101110111=(1η,2η,3η)X ，-------------4分故A 在基1ε,2ε，3ε下的矩阵为B =X 1-AX=⎪⎪⎪⎭⎫ ⎝⎛--111101011⎪⎪⎪⎭⎫ ⎝⎛-121011101⎪⎪⎪⎭⎫ ⎝⎛---101110111=⎪⎪⎪⎭⎫⎝⎛--203022211 -------------12分2．(12分)求λ矩阵222211λλλλλλλλλλ()A ⎛⎫-⎪=- ⎪ ⎪+-⎝⎭的标准形、不变因子、行列式因子、初等因子．解 对-λ矩阵作初等变换,有A =)(λ ⎪⎪⎪⎭⎫⎝⎛-+--222211λλλλλλλλλ→ ⎪⎪⎪⎭⎫⎝⎛--222101λλλλλλ→ ⎪⎪⎪⎭⎫⎝⎛+--)1(00001λλλλ → )()1(0000001λλλλD =⎪⎪⎪⎭⎫⎝⎛+ 标准形为: ⎪⎪⎪⎭⎫⎝⎛+=)1(000001)(λλλλD ；----------------------6分 不变因子为：)1()(,)(,1)(321+===λλλλλλd d d ；----------------------8分 行列式因子为：)1()(,)(,1)(2321+===λλλλλλD D D ；----------------------10分 初等因子为：1,,2+λλλ.----------------------12分3．(12分) 设二次型()222123123121323,,22448f x x x x x x x x x x x x =---++ ，求一正交变换 x Ty =，将二次型化为标准形. 解 二次型对应的矩阵为⎪⎪⎪⎭⎫ ⎝⎛---=242422221A ，----------------------2分且A 的特征多项式为 2)2)(7(-+=-λλλA E ，特征值为2,7321==-=λλλ．---------------------4分 相应的特征向量为 ()()()1,0,2,0,1,2,2,2,1321=-=-=ααα，---------------------6分正交化,可得()()⎪⎭⎫ ⎝⎛=-=-=1,54,52,0,1,2,2,2,1321βββ， 再单位化,有⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛-=535,534,532,0,51,52,32,32,31321ηηη， ----------------------8分令X=TY ，其中⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=53503253451325325231T ，----------------------10分 则 232221'227y y y AX X ++-=．----------------------12分4.(12分) 求顶点在原点，准线为01,0122=+-=+-z y z x 的锥面方程. 解 设为锥面上任一点),,(z y x M ，过M 与O 的直线为：z Zy Y x X ==----------------------3分 设其与准线交于),,(000Z Y X ，即存在t ，使zt Z yt Y xt X ===000,,， -----------6分 将它们代入准线方程，并消去参数t ，得：0)()(222=-+--y z y z z x即：0222=-+z y x此为所要求的锥面方程. ----------------------12分5. (12分)求过双曲抛物面z y x =-41622上的点（2,1,0）的直母线方程. 解：双曲抛物面z y x =-41622的两族直母线为：⎪⎪⎩⎪⎪⎨⎧=-=+z y x u uy x )24(24 及 ⎪⎪⎩⎪⎪⎨⎧=+=-z yx v v yx 24(24----------------------6分将点（2,1,0）分别代入上面两族直母线的方程，求得,1==v u----------------------10分因此，所求的直母线方程为：⎪⎪⎩⎪⎪⎨⎧=-=+z y x yx 24124 及 ⎪⎩⎪⎨⎧==-024z y x ----------------------12分四、证明题((每小题5分，共10分)1.在2R 中，定义变换(,)(2,2)x y x y x y σ=++． （1）证明：σ是2R 的线性变换.（2）取2R 的一组基：12(1,0),(0,1)εε==，求σ的值域2()σR 及2()σR 的一组基.证明(1)设1221x x A y y σξ⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭，σ是2R 到R 的映射，且2,,k αβ∀=∈∀∈R R ，有()()k l A k l kA lA σαβαβαβ+=+=+，所以σ是线性变换；-----------------3分(2) 对于2R 的基：12(1,0),(0,1)εε==，有12()(1,2),()(2,1)σεσε==，易知12(),()σεσε线性无关，于是它们构成2()σR 的一组基，且值域为 12()((),())((1,2),(2,1))L L σσεσε==3R .-----------------5分 2.欧氏空间V 中的线性变换A 称为反对称的，如果对任意α，β∈V ，有（A α，β）= —（α，A β）． 证明：如果V 1是反对称线性变换A —子空间，则V 1⊥也是A —子空间．证明 任取∈αV 1⊥，可证A ∈αV 1⊥，即A ∈αV 1，事实上，任取β∈V 1，由于V 1是A 子空间，因此A β1V ∈，而∈αV 1⊥，故（α，A β）=0．----------------------3分再由题设，A 是反对称的，知（A α，β）= —（α，A β）=0，----------------------4分由β的任意性，即证A ∈αV 1 ．从而V 1⊥也是A —子空间．----------------------5分。
11-12高等数学试题(A)解答
广州大学2011-2012学年第一学期考试卷高等数学Ⅰ1（90学时）参考解答与评分标准一．填空题（每空2分，本大题满分30分） 1．曲线1cos 1x y x x=+有水平渐近线y =1和铅直渐近线x =1-.2．设1()(12)xf x x =+，则0lim ()x f x →=2e ，lim ()xf x →+∞=1.3．设2y x x =-，当2x =，0.01x ∆=时，y ∆=0.0301，d y =0.03.4．设sin sin cos x ty t t t =⎧⎨=+⎩，则d d y t =cos t t，d d yx=t.5．若点(1,2)为曲线326y ax x b =-+的拐点，则常数a =2，b =6.6．设22,0()1sin ,0x e bx a x f x x x x ⎧++≤⎪=⎨>⎪⎩在点0x =处连续且可导，则常数a =1-，b =2-.7．设31()sin d xf x t t -=⎰，则(1)f =0，()f x '=3sin x ，(10)(0)f =9!6-.二．解答下列各题（每小题8分，本大题满分24分）1．求函数y=.解：y''=。
（2分）321(4)xx=-=。
（5分）y''=4=。
（8分）2．求曲线33(1)9y x y x+-+=在点1x=处的切线方程.解：将1x=代入曲线方程，得2y=，切点为(1,2). 。
（1分）曲线方程两边对x求导，得22d d3(1)30d dy yy y x xx x++-+=。
（5分）将1x=，2y=代入上式，得切线斜率1,2d5d12x yykx====-，。
（6分）切线方程为52(1)12y x-=--，即512290x y+-=. 。
（8分）3．求函数()cosxf x e x=的极大值和极小值.解：()cos sinx xf x e x e x'=-，。
高等数学11-1(09-10-1)答案[1]
![高等数学11-1(09-10-1)答案[1]](https://img.taocdn.com/s3/m/764e7866ddccda38376baf76.png)
高等数学Ⅱ-1试题答案（09-10-1）一、填空题（每小题2分，共10分）1．设2,1()5,1x x f x x x ⎧≤=⎨+>⎩，则(5)f x -= 2(5),6(5).,6x x f x x x ⎧-≤-=⎨>⎩ 2．2x →= 23．当0x →+x 的 阶无穷小。
144．设ln mx t y t=⎧⎨=⎩，则22d y dx = 2mm t 5．1cos 1cos xdx x -=+⎰ 解：221cos tan sec 2tan .1cos 222x x x xdx dx dx x c x -===-++⎰⎰⎰ 二、计算题（一）（每小题7分，共21分） 1．已知(sin )cos 12xf x =+，求(cos ).2x f解：(cos )(sin())(sin )cos()1cos 12222x x xf f f x x πππ-=-==-+=-+另：22(sin )12sin 122sin 222x x x f =-+=- 22()22(cos )22cos .22x xf t t f =-⇒=-2．求2220ln(sin )lim .ln()2x x x x e xx e x→+-+-解：222222200ln(sin )ln (sin 1)lim limln()2ln (1)2x x x x x x x x x e x e x e xx e x e x e x→→+-+-=+-+- 22222200ln(sin 1)sin lim lim 1ln(1)x xx x x x x e x e x e x e→→+===+ 另：222222200ln(sin )sin 222lim lim 12sin ln()2x x x xx x x x x e xx e x e x e x e x e x →→⎡⎤⎡⎤+-++=--⎢⎥⎢⎥+++-⎣⎦⎣⎦2222001sin 2sin 12cos 2sin 2lim lim 12sin 212x x x x x x e x x x xx e x x x→→+--=⋅==+--3．指出函数22()(1)x xf x x x -=-的间断点及其类型。
2011-2012学年合肥工业大学第二学期《高等数学》试卷和参考答案
2011----2012学年第二学期期末考题解答一.填空题(每小题3分, 满分15分)1. 过直线L:x-1y+2z-2==且垂直于平面3x+2y-z=5的平面方程是2-32_________．【解】应填：x-8y-13z+9=0．直线L的方向向量s={2,-3,2}．已知平面的法向量n1={3,2,-1}，设所求平面的法向量为n，由题意知n⊥s且n⊥n1，故可取ijk n=s⨯n1=2-32={-1,8,13}，32-由条件知，所求平面过点P0(1,-2,2)于是所求平面方程为，-(x-1)+8(y+2)+13(z-2)=0，即x-8y-13z+9=0．2. 设x2+2xy+y+zez=1，则dz【解】应填：-2dx-dy．由x+2xy+y+ze=1，两边求全微分，得 2z(0,1)=2xdx+2ydx+2xdy+dy+(1+z)ezdz=0，当x=0,y=1时，代入原方程得z=0，所以dz(0,1)=-2dx-dy．3. 椭圆抛物面∑：z=2x+y在点P0(1,-1,3)处的法线方程是___________.【解】应填：22x-1y+1z-3==. 4-2-1曲面∑在点P0(1,-1,3)处的法向量可取为n={4x,2y,-1}(1,-1,3)={4,-2,-1}，于是曲面∑在点P0(1,-1,3)处的法线方程为x-1y+1z-4=-2=3-1.4.曲面z=与z=x2+y2所围立体的体积为．【解】应填：6． V=⎰⎰⎰dv=2π0dθ1rπΩ⎰⎰0rdr⎰r2dz=6．5. 设L为上半圆周y=⎰(xL-xy+y2)ds=____________．【解】应填：π．由对称性，代入技巧及几何意义可得⎰2L(x-xy+y2)ds=⎰Lds+0=π二.选择题(每小题3分, 满分15分)1．方程y''-3y'+2y=1+2x-3ex的特解形式为（）． (A)(ax+b)ex (B) (ax+b)xex(C) ax+b+cex(D) ax+b+cxex【解】选（D）2.设unn=(-1)，则级数（）．（A）∑∞∞∞u2n与∑un都收敛（B）n=1n=1∑u2n与n=1∑un都发散n=1 （C）∑∞∞∞∞u2n收敛，而n发散（D）u2n发散，而n收敛n=1∑un=1∑n=1∑u【解】选（C）3．二元函数f(x,y)的两个偏导数fx¢(x,y)，fy¢(x,y)在点P0(x0,y0)处都连续是f(x,y)在点P0(x0,y0)处可微分的（）(A) 充分条件 (B) 必要条件(C) 充要条件 (D) 既非充分也非必要条件【解】若fx¢(x,y)，fy¢(x,y)在点P0(x0,y0)都连续，则f(x,y)在点P0(x0,y0)处可微分，选(A)4.⎰10dx⎰2x1=（）（A）121 （B）)131 （C)（D【解】原积分=⎰dy0101121==⎰231．选（B） )⎧x2-π≤x<05. 设f(x)=⎨，则周期为2π的函数f(x)的傅立叶级数在x=2π处⎩x-π0≤x<π收敛于．（A）-π2 （B）-π （C）0 （D）π 2【解】选(A)三. (10分) 设z=f(xy,xy)+g()，其中f有二阶连续偏导数，g有二阶导yx∂2z数，求．∂x∂y【解】根据复合函数求偏导公式得∂z1y=f1'⋅y+f2'⋅+g'⋅(-2), ∂xyx∂2z∂⎛∂z⎫∂⎛1y⎫= ⎪= f1'⋅y+f2'⋅+g'⋅(-2)⎪∂x∂y∂y⎝∂x⎭∂y⎝yx⎭x11xy1=f1'+y[f11''x+f12''⋅(-2)]-2f2'+[f21''x+f22''⋅(-2)]-g''⋅3-g'⋅2yyyyxx1xy1=f1'+xyf11''-2f2'-3f22''-3g''-2g'yyxxx2四. (10分) 求z=f(x,y)=x-y在闭区域D：+y2≤1上的最大值和最小值．22【解】在D的内部，⎧fx'=2x=0⇒(0,0)为驻点，且f(0,0)=0 ⎨'f=-2y=0⎩y在D的边界上，x2x25x22222+y=1⇒y=1-⇒z=x-y=-1由444(-2≤x≤2)dz5x==0⇒x=0，此时，y=±1,，则有f(0,±1)=-1,dx2比较上述函数值知，f(±2,0)=4函数z=f(x,y)=x-y在D上的最大值为4,最小值为-1．五. (10分) 求微分方程y''=22y'+xex的通解. x1p=xex， x【解】不显含y，故令y'=p,则y''=p'，代入原方程得p'-利用通解公式求得通解为p=x(ex+C1)，积分得原方程通解为1y=(x-1)ex+C1x2+C2．2六. (12分)（Ⅰ）试确定可导函数f(x)，使在右半平面内，y[2-f(x)]dx+xf(x)dy为某函数u(x,y)的全微分,其中f(1)=2；（Ⅱ）求u(x,y)；【解】（Ⅰ）P=y[2-f(x)]，Q=xf(x)．因为y[2-f(x)]dx+xf(x)dy是函数u(x,y)的全微分，所以有即∂Q∂P， =∂x∂yf(x)+xf'(x)=2-f(x)，故xf'(x)+2f(x)=2．上述微分方程的通解为f(x)=1+所以C.由f(1)=2得C=1, x21． x2f(x)=1+（Ⅱ）在右半平面内取(x0,y0)=(1,0)，则11u(x,y)=⎰P(x,0)dx+⎰Q(x,y)dy=⎰0(x+)dy=y(x+)．10xxxyy七. (12分) 求幂级数∞∑n(n+1)xn=1∞n的收敛域及和函数．【解】易求得其收敛域为(-1,1)，令S(x)=∑n(n+1)x=x∑n(n+1)xnn=1n=1∞n-1=x⋅S1(x)，其中S1(x)=∑n(n+1)xn-1，n=1∞∞两边积分⎰再积分xS1(x)dx=∑⎰n(n+1)xn=1∞xn-1dx=∑(n+1)xn，n=1⎰(⎰xxS1(x)dx)dx=∑⎰(n+1)xdx=∑xnn=1∞x∞n+1n=1x2． =1-x因此x22S1(x)=()''=，1-x(1-x)3故原级数的和S(x)=2x，x∈(-1,1)．(1-x)3八. (12分) 计算积分I=⎰⎰(y-z)dzdx+(x+2z)dxdy∑，其中∑是抛物面z=x2+y2(0≤z≤1)，取下侧．【解】补S0:z=1(x2+y2 1),取上侧,设∑与∑0围成空间区域Ω, Ω及∑0在xOy平面上的投影区域Dxy:x+y≤1.由Gauss公式，I=22∑+∑0 ⎰⎰(y-z)dzdx+(x+2z)dxdy-⎰⎰(y-z)dzdx+(x+2z)dxdy ∑0=⎰⎰⎰[Ω∂∂(y-z)+(x+2z)]dv-⎰⎰(y-z)dzdx+(x+2z)dxdy ∂y∂z∑0∑0=3⎰⎰⎰dv-⎰⎰(y-z)dzdx+(x+2z)dxdy. Ω因为∑0垂直于zOx平面，∑0在zOx平面上的投影区域面积为零，所以⎰⎰(y-z)dzdx=0.∑0I=3⎰⎰[⎰2Dxy1x+y2dz]dxdy-⎰⎰[x+2(x2+y2)]dxdy Dxy2π1=⎰⎰(3-5x2-5y2)dxdy=⎰dθ⎰(3-5r2)rdr=Dxy00π.2九. (4分) 设函数ϕ(y)具有连续导数，在围绕原点的任意分段光滑简单闭曲线L 上，曲线积分ϕ(y)dx+2xydy2x+y24L的值恒为同一常数．证明：对右半平面x>0内的任意分段光滑简单闭曲线C，有ϕ(y)dx+2xydy2x+y24C=0；【证明】将C分解为：C=l1+l2，另作一条曲线l3围绕原点且与C相接，则ϕ(y)dx+2xydy2x+y24C=ϕ(y)dx+2xydy2x+y24l1+l3-ϕ(y)dx+2xydy2x+y24l2+l3=0．。
(2021年整理)高等代数2011-2012第一学期期末试卷答案
（完整）高等代数2011-2012第一学期期末试卷答案（完整）高等代数2011-2012第一学期期末试卷答案编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）高等代数2011-2012第一学期期末试卷答案）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（完整）高等代数2011-2012第一学期期末试卷答案的全部内容。
（完整）高等代数2011-2012第一学期期末试卷答案高等代数2011—2012第一学期期末试卷答案课程名称:《高等代数》参考答案及评分标准（A 卷）考试(考查）：考试 时间：200 年 月 日 本试卷共7页，满分100 分； 考试时间:120 分钟答题前请将密封线内的项目填写清楚一．选择题（本大题共8个小题，每小题3分，共24分.请在每小题的四个备选答案中选出一个正确的答案,并将其号码填入题后的括号内)。
1．在[]F x 里一定能整除任意多项式的多项式是 【 B 】 A ．零多项式 B ．零次多项式 C ．本原多项式 D ．不可约多项式2．设()1g x x =+是6242()44f x x k x kx x =-++-的一个因式，则=k 【 C 】A ．4B ．3C ．2D ．13．A ,B 是n 阶方阵，则下列结论成立的是 【 C 】A .AB O A O ≠⇔≠且B O ≠ B 。
0A A O =⇔=C ．0AB A O =⇔=或B O =D . 1||=⇔=A I A4．设n 阶矩阵A 满足220A A I --=，则下列矩阵哪个不可逆 【 B 】A 。
2A I +B 。
A I +C ．A I -D .A5．设A 为3阶方阵，且1)(=A r ，则 【 A 】 A 。
2011年高考全国卷Ⅱ数学(理)考试试题(真题和答案)
2011年普通高等学校招生全国统一考试理科数学（必修+选修II ）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分。
第I 卷1至2页，第II 卷3至4页。
考试结束后，将本试卷和答题卡一并交回。
第I 卷注意事项：1.答题前，考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并贴好条形码。
请认真核准条形码上的准考证号、姓名和科目。
2.每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。
在试题上作答无效．．．．．．．．。
3.第I 卷共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。
（1）复数z ＝1+i ，z 为z 的共轭复数，则z z -z -1＝（A ）-2i （B ）-i （C ）i （D ）2i（2）函数y ＝x ≥0）的反函数为（A ）y ＝24x （x ∈R ） （B ）y ＝24x （x ≥0） （C ）y ＝24x （x ∈R ） （D ）y ＝24x （x ≥0）（3）下面四个条件中，使a >b 成立的充分而不必要的条件是（A ）a >b +1 （B ）a >b -1 （C ）2a >2b （D ）3a >3b（4）设n S 为等差数列{}n a 的前n 项和，若11a =，公差d = 2, 224k k S S +-=,则k =(A ) 8 (B) 7 (C) 6 (D) 5(5) 设函数()()cos 0f x x ωω=>，将()y f x =的图像向右平移3π个单位长度后，所得的图像与原图像重合，则ω的最小值等于（A ）13（B ）3 （C ）6 （D ）9 （6）已知直二面角α –ι- β, 点A ∈α ，AC ⊥ ι ,C 为垂足，B ∈β，BD ⊥ ι，D 为垂足，若AB=2，AC=BD=1，则D 到平面ABC 的距离等于（ ）（A ）3（B ）3 (C) 3 (D) 1 (7) 某中学有同样的画册2本，同样的集邮册3本，从中取出4本赠送给4位朋友，每位朋友1本，则不同的赠送方法共有（ ）（A ）4种 (B) 10种 (C) 18种 (D)20种（8）曲线21x y e -=+在点（0,2）处的切线与直线0y =和y x =围成的三角形的面积为（A ）13 （B ）12 （C ）23 （D ）1（9）设()f x 是周期为2的奇函数，当01x ≤≤时，()f x 2(1)x x =-，则5()2f -= （A ）12-（B ）14- （C ）14 （D ）12 （10）已知抛物线C:2y =4x 的焦点为F ，直线y=2x-4与C 交于A,B 两点，则cos<AFB=( ) (A) 54 (B)53 (C).—53 (D) —54（11）已知平面α截一球面得圆M,过圆心M 且与 成60 二面角的平面β截该球面得N 。
工科类本科《高等数学》第11,12章自测题参考答案
工科类本科《高等数学》第11,12章自测题参考答案1. 若L 是抛物线 x y =2上从点A )1,1(-到点B )1,1(的一段弧，则()Lx y dx +=⎰43；(3)Lx y dy -=⎰ 2 . 解：L 的方程为2,x y y =从-1变到1，而2dx ydy =，于是()1111232211104()222043Lx y dx yy ydy y dy y dy y dy ---+=+⋅=+=+=⎰⎰⎰⎰⎰.()1111222111(3)33602Lx y dy y y dy y dy ydy y dy ----=-=-=-=⎰⎰⎰⎰⎰.注意：定积分的积分区间关于原点对称，考虑被积函数的奇偶性可以简化计算. 2.已知L 为圆周 122=+y x 沿逆时针方向，则曲线积分()(sin )xLey dx y x dy -++⎰=2π.解：计算封闭曲线积分，一般考虑用格林公式，这里(),sin ,112x Q P P e y Q y x x y ∂∂=-=+-=--=∂∂.于是()222211(sin )222xLx y x y ey dx y x dy dxdy dxdy π+≤+≤-++===⎰⎰⎰⎰⎰.注意：221x y dxdy +≤⎰⎰等于圆域221x y+≤的面积.3.若曲线积分()3222(cos )1sin 30Laxy y x dx ay x x y dy -+-+=⎰，则a =__2___.解：依题意，有Q P x y∂∂=∂∂，这里3222cos ,1sin 3,P axy y x Q ay x x y =-=-+2232cos ,cos 6.P Q axy y x ay x xy y x ∂∂=-=-+∂∂比较可得2a =. 4.若22xdy aydxx y-+在右半平面0x >内是某个函数的全微分，则a =__1__. 解：依题意，有Q P x y∂∂=∂∂，这里2222,,ay xP Q x y x y -==++ ()()()()()()2222222222222222222222,.a x y ay y x y x x P ax ay Q x y y x x y x y x y x y -++⋅+-⋅∂-+∂-+====∂∂++++ 比较可得1a =. 5.将()1x f x x +＝展开为x 的幂级数1xx=+()1231, 1.n n x x x x x --+-+-+<或1xx=+()111,1n n n x x ∞-=-<∑.解：当1x <时，()()11x x f x x x =+--＝为首项是x 公比为x -的等比级数，所以()()1123111, 1.1n n nn n xx x x x x x x∞--==-+-+-+=-<+∑6. 幂级数∑∞=1n 3n n x n的收敛半径R= 13，收敛域是11-33⎡⎫⎪⎢⎣⎭，.解：n n 113311,lim lim 33n n n n n n a n a R n a n +→∞→∞++===⋅=收敛半径，收敛区间是11-33⎛⎫⎪⎝⎭，，而当13x =-时，级数n 1131(1)n n n n x n n ∞∞===-∑∑是条件收敛的交错级数；当13x =时，级数n 1131n n n x n n∞∞===∑∑是发散的调和级数.故收敛域是11-33⎡⎫⎪⎢⎣⎭，.7.下列级数发散的是（ A ）.A.11ln 1n n ∞=⎛⎫+ ⎪⎝⎭∑; B. 211n n∞=∑； C. 115n n ∞=∑； D. 111(1)2n nn ∞-=-∑. 解：A.1ln 1n u n ⎛⎫=+ ⎪⎝⎭，取1n v n =，由lim 1n n nu v →∞=，而调和级数11n n ∞=∑发散，故11ln 1n n ∞=⎛⎫+ ⎪⎝⎭∑发散.B 选项是p 级数，21p =>，故211n n∞=∑收敛.C 选项是公比为15q =的等比级数，由115q =<知115n n ∞=∑收敛.D选项是交错级数，而正项级数11111(1)22n n n n n ∞∞-==-=∑∑115q ⎛⎫=< ⎪⎝⎭是收敛的等比级数，故111(1)2n n n ∞-=-∑绝对收敛.8.下列级数收敛的是（ C ）. A.11sin n n ∞=∑; B. 1n ∞= C. 115n n ∞=∑；D. n ∞=解：A 选项1sin n u n =，取1n v n =，由lim 1n n nu v →∞=，而调和级数11n n ∞=∑发散，故11sin n n ∞=∑发散.B选项15nn u -==，由0lim 510n n u →∞==≠知级数n ∞=. C 选项是公比为15q =的等比级数，由115q =<知115n n ∞=∑收敛. D选项1151n n n∞∞===∑是p 级数，115p =<，故n ∞=. 9.计算曲线积分22(3)(3),Lx y dx y x dy +++⎰其中L 是从O(0, 0)沿上半圆224(0)x y x y +=≥到A(4,0)的曲线段.解：已知22(,)3,(,)3P x y x y Q x y y x =+=+，则3,3P Qy x∂∂==∂∂.因为P Qy x∂∂=∂∂，所以曲线积分与路径无关.选取x 轴上直线段OA 路径，此时0,y x =从0 到4，0dy =，于是44222300164(3)(3)33Lx y dx y x dy x dx x +++===⎰⎰. 10.计算曲线积分3(2)(2)Ly x dy x y dx +-+⎰其中L 是从A(2, 0)沿上半圆222(0)x y x y +=≥到O(0,0)的曲线段.解： 已知3(,)(2),(,)2P x y x y Q x y y x =-+=+，则2,2,4P Q Q P y x x y∂∂∂∂=-=-=∂∂∂∂. 为了使用格林公式，添加辅助直线段OA ,记它与L 所围成的区域为D,D 是上半圆域222,0x y x y +≤≥，且边界封闭曲线方向是规定的正向. 而直线段OA 方程为：0,y x =从0到2，此时0dy =.则 3(2)(2)Ly x dy x y dx +-+⎰33(2)(2)(2)(2)L OAOAy x dy x y dx y x dy x y dx +=+-+-+-+⎰⎰()2342001444D Ddxdy x dx dxdy x =--=+⎰⎰⎰⎰⎰1442 4.2ππ=⋅+=+（注Ddxdy ⎰⎰等于上半圆域D 的面积）11.设dy y xy x dx y xy x du )32()23(2222+--+-=，求原函数),(y x u . 解法一：已知2222(,)32,(,)(23)P x y x xy y Q x y x xy y =-+=--+， 而22,22P Q x y x y y x ∂∂=-+=-+∂∂.因为P Qy x∂∂=∂∂，所以曲线积分L Pdx Qdy +⎰与路径无关.取折线路线0AB ：(0,0)(,0)(,)O A x B x y →→.其中直线段OA 方程为：0,y x =从0到x ，此时0dy =；直线段AB 方程为：,x x y =从0到y ，此时0dx =.则原函数 (,)OAB OAABu x y Pdx Qdy C Pdx Qdy Pdx Qdy C =++=++++⎰⎰⎰22203(23)xy x dx x xy y dy C =+--++⎰⎰3223x x y xy y C =-+-+解法二：已知2222(32),(23)u ux xy y x xy y x y∂∂=-+=--+∂∂，两式子分别对,x y 两边积分，有 22322(,)(32)()u x y x xy y dx x x y xy y ϕ=-+=-++⎰，22223(,)(23)()u x y x xy y dy x y xy y x ψ=--+=-+-+⎰.从而，有 322223()()x x y xy y x y xy y x ϕψ-++=-+-+， 比较上式两边，有 33(),()y y C x x C ϕψ=-+=+.故 3223(,)u x y x x y xy y C =-+-+. 解法三：依题意，知2232u x xy y x ∂=-+∂（1）， 22(23)ux xy y y∂=--+∂（2）.（1）式两边对x 积分，得 22322(,)(32)()u x y x xy y dx x x y xy y ϕ=-+=-++⎰（3）（3）式两边对y 求偏导，得22()ux xy y yϕ∂'=-++∂ （4）. 比较（2）、（4）式，得 2()3y y ϕ'=-，两边对y 积分，得 3()y y C ϕ=-+. 故 3223(,)u x y x x y xy y C =-+-+. 12.判别下列正项级数的敛散性：（1）12sin 3nn n π∞=∑；（2）2121n n n n ∞=+-∑；（3）13!n nn n n ∞=⋅∑；（4）121nn n n ∞=⎛⎫ ⎪+⎝⎭∑. 解：（1）()22sin2333nnn n nn u n πππ⎛⎫=⋅=→∞ ⎪⎝⎭，取23nn v ⎛⎫= ⎪⎝⎭.由23lim lim 23nn n n n nu v ππ→∞→∞⎛⎫ ⎪⎝⎭==⎛⎫ ⎪⎝⎭，又已知等比级数122133n n q ∞=⎛⎫⎛⎫=< ⎪ ⎪⎝⎭⎝⎭∑收敛. 因此根据正项级数的比较判别法知 级数2sin3n nπ∑收敛.（2）221n n u n n =+-，取1n v n =. 由22lim lim 121n n n nu n v n n →∞→∞==+-，又已知调和级数1n ∑发散.因此根据正项级数的比较判别法知 级数221nn n +-∑发散.（3）13!n nn n n∞=⋅∑ 解：3!n n n n u n ⋅=，因为 ()()11131!13lim lim 3lim 3lim 13!1111nn n n n n n n n n n nn u n n u n n e n n +++→∞→∞→∞→∞⋅+⎛⎫=⋅===> ⎪⋅+⎝⎭+⎛⎫+ ⎪⎝⎭， 所以根据正项级数的比值判别法知 级数3!n nn n ⋅∑发散.（4）21n n n ⎛⎫ ⎪+⎝⎭∑ 解：21nn n u n ⎛⎫= ⎪+⎝⎭，因为1lim 1212n n n n →∞==<+， 所以根据正项级数的根值判别法知 级数21nn n ⎛⎫⎪+⎝⎭∑收敛.13.求下列幂级数的和函数：（1）111n n x n -∞=+∑；（2）11n n nx ∞-=∑. 解：（1）此幂级数的收敛半径为1，收敛区间为(1,1)-.设幂级数的和函数为()s x ，则11()1n n x s x n -∞==+∑ （1x <）， 1(0)2s =对121()1n n x x s x n +∞==+∑逐项求导，得()1211()11n n n n x x x s x x n x +∞∞=='⎛⎫'=== ⎪+-⎝⎭∑∑ ()11x -<< 对上式从0到x 积分，得 ()[]2000111()1ln(1).111xx x t t x s x dt dt dt x x t t t --⎛⎫⎛⎫==-=--=-+- ⎪ ⎪---⎝⎭⎝⎭⎰⎰⎰ 于是当0x ≠时，有 2ln(1)()x x s x x +-=-.从而 和函数2ln(1),01;()1,0.2x x x xs x x +-⎧-<<⎪⎪=⎨⎪=⎪⎩.特殊的，当1x =-时，级数()()112111n nn n n n-∞∞==--=+∑∑收敛.所以2ln(1)()x x s x x +-=-在1x =-也成立.（2）此幂级数的收敛半径为1，收敛区间为(1,1)-.设和函数为()s x ，则11()n n s x nx∞-==∑ （1x <）.对上式从0到x 逐项积分，得111()1x xn n n n xs t dt nt dt x x∞∞-=====-∑∑⎰⎰ 对上式求导，得22(1)(1)1()1(1)(1)x x x s x x x x '--⋅-⎛⎫=== ⎪---⎝⎭，1x <.。
广西师范大学11级高等数学2试卷A答案
6 6 x 2 xyz 6 4 y 2 xyz 6 2 z 2 xyz 2y2 z2 6 0
…… 19 分
解之得所求点坐标为 (
6 , 1, 3
2 ) ,此时四面体有最小体积 V 3 3 .
………… 21 分
四、证明题（本大题 6 分） 证明 令 f ( x , y )dxdy A ，则有 f ( x, y ) xy A .
0 0 2 3
2] d
………………… 9 分
第 2 页 共 3 页
6. 解 1) 令 F ( x, y, z ) 3 x 2 2 y 2 z 2 6 则 Fx (1,1,1) 6 ， Fy (1,1,1) 4 ， Fz (1,1,1) 2 …………………… 3 分
0 e
4
1
e
2 sec
0
f ( ) d ；5．0； 6．[-2,2).
三、计算题（本大题 6 小题，共 64 分） 1.解 令 F ( x, y, z )
1 xz x z 1 ln ，则有 Fx ， Fy ， Fz 2 ，………… 4 分 z z y y z
P Q . 6 xy 2 2 y cos x y x
………………………………… 2 分
由格林公式知 所以有
L OB BA
Pdx Qdy (
D
Q P )dxdy 0 ，…………………… 5 分 x y
(2 xy
L L
3
y 2 cos x)dx (1 2 y sin x 3 x 2 y 2 )dy
OB BA
Pdx Qdy Pdx Qdy Pdx Qdy
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
重庆大学 高等数学Ⅱ-1-2 课程试卷juan2012 ~2013学年 第 1学期 开课学院： 数学 课程号： 10019565 考试日期： 20121215考试方式：考试时间： 120 分钟一、单项选择题（每小题3分，共15分）1.若lim ()x f x k →∞'=，则lim[()()]x f x a f a →∞+-为【A 】A ．kaB ．kC ．aD ．不存在2.若()xf x e -=，则(ln )f x dx x'=⎰【A 】 A ．1c x+ B ．1c x -+ C ．x c + D ．x c -+3.曲线221x xy x +=-渐近线的条数为【C 】A ．0B ．1C ．2D ．34.极限2lim ln()()x x x x a x b →+∞=-+【C 】 A ．0 B ．1 C ．a b -D ．b a -5.设曲线2x y e-=，则其拐点的个数为【B 】A ．1B ．2C ．3D ．4二、填空题（每小题3分，共15分） 1.设ln sin y x =，在5[,]66ππ上满足罗尔中值定理中的ξ=2π 2.= ln(x c ++3.若()f x 的一个原函数为tan x x ，则()xf x dx '=⎰ 22t a n s e c x x c x-+ 4.极限011lim ln(1)x x x →⎡⎤-=⎢⎥+⎣⎦ 12 5.曲线2()sin()f x x =，则(6)(0)f= 120-解法1：2()sin(),(0)0f x x f ==2()2cos(),(0)0f x x x f ''==22222()2cos 4sin 2cos 4(),(0)2f x x x x x x f x f ''''=-=-=222()4sin 8()4()12()4(),(0)0f x x x xf x x f x xf x x f x f ''''''''=---=--= (4)2()12()12()8()4()f x f x xf x xf x x f x ''''=----212()20()4()f x xf x x f x '''=---(5)2()12()20()20()8()4()f x f x f x xf x xf x x f x '''''''''=-----232()28()4()f x xf x x f x ''''''=---(6)2(4)()32()28()28()8()4()f x f x f x xf x xf x x f x ''''''''''=-----2(4)60()36()4()f x xf x x f x '''''=---.(6)(0)120f=-解法2：3511sin 3!5!x x x x =-++ 2261011()sin 3!5!f x x x x x ==-++(6)1(0)6!1203!f =-⋅=-三、计算题（一）（每小题8分，共24分）命题人：组题人：审题人：命题时间：教务处制学院 专业、班 年级 学号 姓名公平竞争、诚实守信、严肃考纪、拒绝作弊封线密1.求a ，使函数1()sin sin 33f x a x x =+在3x π=处取得极值，并问3x π=是()f x 的极大值还是极小值，再求其极值。
解：因()cos cos3f x a x x '=+，则1()1032f a π'=-=知2a =，故()2sin 3sin3f x x x ''=--()03f π''=<，从而()3f π=2.计算不定积分(sin cos )cos 2nI x x xdx =+⎰，其中n 为正整数。
解法1：()22(sin cos )cossin nI x x x x dx =+-⎰1(sin cos )(sin cos )n x x d x x +=++⎰ 21(sin cos )2n x x c n +=+++ 解法2：22211(1sin 2)sin 2(1sin 2)22n n I x d x x c n +=+=+++⎰ 解法3：22sin()sin 2()44nn I x x dx ππ⎡⎤=++⎢⎥⎣⎦⎰1122sin()sin()44n nx d x ππ++⎡⎤=++⎢⎥⎣⎦⎰222sin()24nn x c n π+⎡⎤=++⎢⎥+⎣⎦3.计算不定积分3.dx ⎰解法1：令2tan ,arctan ,22x x t x x ππ==-<<，则33238tan 2sec 8tan sec 2sec ttdt t tdt t =⋅=⎰⎰2388(sec 1)sec sec 8sec 3t d t t t c =-=-+⎰313c =- 解法2：32221122x t ==222341412(4)423ut u u udu u du u u c u =--⋅=-=-+⎰⎰313c =-四、计算题（二）（第1至2题每小题8分，第3题9分，共25分） 1.计算积分22(ln )x x dx ⎰。
解法1：2223322111(ln )(ln )(ln )2ln 333x x dx x dx x x x xdx ==-⋅⎰⎰⎰32312(ln )ln ()39x x xd x =-⎰ 3233122(ln )ln 3927x x x x x c =-++ 解法2：令ln ,ux u x e ==，则222223(ln )u u ux x dx e u e du u e du =⋅=⎰⎰⎰2.计算极限1lim.1ln xx x x x x→--+ 解：教材上的例子3.一商家销售某种商品的价格满足关系70.2p x =-（万元/吨），x 为销售量（单位：吨），商品的成本函数是31c x =+（万元）。
（1）若每销售一吨商品，政府要征税t 万元，求该商家获最大利润时的销售量；（2）t 为何值时，政府税收总额最大。
解：（1）总税额T tx =，商品销售总收入为2(70.2)70.2R px x x x x ==-=-利润函数为2()0.2(4)1L x R C T x t x =--=-+--令()0.440L x x t '=-+-=，得10 2.5x t =-，且0.40L ''=-<， 故10 2.5x t =-为利润最大时的销售量。
（2）将10 2.5x t =-代入T tx =，得210 2.5T t t =-令1050dTt dt=-=，得2t =，且2250d T dt =-<故当2t =时，T 最大。
此时，政府税收总额最大。
五、证明题（每小题7分，共21分）1.证明：0x >时，11(1)x e x ++>。
证：令1()(1)ln(1)1f x x x=++-11()ln(1)0f x x x'=+-<所以当0x >时，()f x 单减，从而()()lim ()0x f x f f x →+∞>+∞==。
故11(1)x e x++>。
2.设函数()y f x =在某0x x r -<内有四阶连续的导数，(4)0000()()()0,()0f x f x f x f x ''''''===≠ 。
证明0()f x 为极值。
证法1：由已知(4)0()0fx ≠，不妨设(4)0()0f x >，因()f x 有四阶连续的导数，故由极限的保号性知，存在0δ>，当0(,)x U x δ∈时，有(4)()0f x >。
0(,)x U x δ∈，由泰勒公式：2000001()()()()()()2!f x f x f x x x f x x x '''=+-+- 3(4)400011()()()()3!4!f x x x f x x ξ'''+-+-，其中0(,)U x ξδ∈ (4)40001()()()()4!f x f x x f x ξ=+->所以0()f x 为极小值。
同理可证，(4)0()0f x <时，0()f x 为极大值。
证法2：课堂上所讲方法。
课堂上的证明方法是没有已知()f x 有四阶连续的导数的证明方法，只已知了四阶导数(4)0()0fx ≠。
3.设函数()f x 在[)0+∞，上可导，对(0,)x ∀∈+∞，()0f x k '≥>（k 为一常数）。
证明：存在0M >及0Z >，x Z ∀>有().f x Mx ≥证明：因()f x 在[)0+∞，上可导，故0x ∀> ()(0)()()f x f f x kx x ξ'-=>→+∞→+∞从而()f x →+∞，当x →+∞时，故存在0,Z x Z >∀>，有()0f x >。
x Z ∀>，(2)()()(2)()f x f x f x kx f x kx f x kx ξ'-=≥⇒≥+≥取,22k x M Z =∀>，有()2xf x k Mx ≥⋅=。