第二章 土壤水分运动基本方程2
2章-1水的势能

例题1:坐标轴向上,基准面1 例题2:坐标轴向上,基准面2 例题3:坐标轴向下,基准面1 目的: 比较基准面对单点重力势的影响; 比较基准面对两点重力势差的影响; 比较坐标轴方向对单点重力势的影响; 比较坐标轴方向对两点重力势差的影响
13/37
1.1 水的势能与水头(重力势)
1.1.1 重力势jg
7/37
标准参考面
1.1 水的势能与水头(概念1)
土水势的单位(量纲)
土水势的表示 方法
符号 名称
量纲
SI单位
以重力势为例
能量/质量 能量/容积 能量/重量
μ
T
化学势 土壤水势 土壤水头
L2/T2 M/LT2 L
J/kg N/m2 m
gh ρ gh h
ΨT hT
最后一种表示方法,即水头表示法最常用
例1:如右图, z 轴向上为正
z A=15cm; jg A= + zA =15cm
1
z
z A=15cm
z B= – 10cm; jg B= + zB = – 10cm
A、B两点间的重力势差:
jg = jg A – jg B
=15 – ( – 10)=25cm
z B=-10cm
第二章 地下水的运动
计算条件
土壤水分运动

gradient)
饱和导水的特点: 1.水力梯度(水头梯度 hydraulic gradient):为两端间的压力势之差和重力势之 差的和 △H=(Hp+Hg)i-(Hp+Hg)out 2.导水率(Ks hydraulic conductivity) (1)对于同一种土壤它是一个常数,它的大小随着土壤质地和结构有所不同。 也就是说它仅是土壤基模特性的函数,与土壤通气孔度有直接关系,与土壤总孔 度没有密切的相关关系,与土壤水分含量和水分的传导过程也无关。 (2)它在土壤不同空间方向上有一定差异,即它是各向异性的。在应用时要 注意。 3.达西定律表示的是稳态流,也就是说通量沿流动系统保持不变,每一点水力梯 度保持不变。
f =
η 为粘滞度(泊:达因 ⋅ 秒 / 平方厘米) ρ 为流体密度(克 / 立方厘米)
g 为重力加速度(厘米 / 秒 2 )
ρg η
L −1T −1
(2)(内)透水率(k): 取决于土壤孔隙几何特性 Kη k= ( L2 ) ρg 关于温度对导水率影响包含在对粘滞系数影响范围了。 如果不是水,而是其 它液体时,达西定律形式为: ρg q = −k ∇H η
一、饱和土壤中水分运动 Flow of water in saturated soils
(三)导水率、透水率和流动性(hydraulic conductivity ,permeability,and Fluidity) 1.导水率(hydraulic conductivity) 导水率是通量q与水头梯度(△H / △X)的比率,或者是通量对梯度关系的 斜率。
一、饱和土壤中水分运动 Flow of water in saturated soils
(二)通量、流速和弯曲度(Flux,Flow velocity,and Tortuosity) 1.通量(q)(flux)和流速( flow velocity ): 达西定律中q叫它通量或通量密度(flux density):它是指单位时间通过单位 横截面积的水量(flux density is the volume of water passing through a unit crosssection area (perpendicular to the flow direction) per unit time. 它的量纲(the dimensions of the flux are)q=Q/At=L3/L2T=L/T(LT-1) 由此可见,q具有速度单位,人们就把通量密度也称为流速(flow velocity)。 其实应用“通量”要比“流速”好。因为土壤孔隙的复杂性(形状、宽度和方向) 都是变化的,土壤中真实流速也是极不稳定的。如果要用流速的话,最好用“平 均流速”略微接近实际。 2.弯曲度(Tortuosity):水分通过一段土壤标本的孔隙所经过的实际距离与土 壤标本的表观长度之比。(讨论的是L问题) Toutuosity can be defined as the average ratio of the actual roundabout path to the apparent, or straight, flow path。 弯曲度是一个比值,无量纲。它取决于土壤孔隙的几何 特性,永远大于1,也可能大于2。它反映了土壤孔隙的连 续性。
第二章非饱和土壤水运动基本方程9...

摘要随着近代数学、物理学以及电子计算机的广泛应用,各学科的研究进展极为迅速,因此,如何将高、精、尖的现代化科学技术手段合理运用到土壤物理学的实验研究当中已经成为该学科寻求快速发展的主要途径。
本论文在参阅国内外文献资料的基础上,通过大量的室内实验与数据分析,对利用实验数据自动采集系统测定非饱和土壤水运动参数的方法进行了实验研究和理论探讨,并对自动测定系统和传统实验所得的实测结果进行了对比分析。
论文的主要内容分为以下几个方面:首先,比较系统的分析和总结了国内外关于非饱和土壤水运动参数测定方法的文献资料,在此基础上提出了本论文的研究内容。
其次,在研究并总结了国内外确定土壤水分特征曲线的各种方法的基础上,选用15bar压力膜仪对实验土样进行了土壤水分特征曲线的测定。
本论文重点介绍了土壤水力传导度和扩散度的实验装置和实验方法,并通过室内实验和计算机自动采集、处理数据的联合应用,分析了实验自动处理系统和传统手工实验所得结果的差别并提出了该系统在实验过程中存在的问题。
最后,对分析结果进行了总结,并提出了需要进一步改进和提高的问题。
关键词:非饱和土壤水运动参数;实验室测定;实验数据自动采集系统;传统实验方法IAbstractWith the wide application of modern mathematics, physics and computer, all the academic disciplines have being developed quickly, so how to make use of these modern science and technology in the soil physics experimental study has become the main way to develop this subject.Based on referring internal and external literatures, by many laboratory test and data analysis, the paper represented the cause of making use of the automatic data acquisition system to measure the soil hydrodynamic parameter and making a comparison with the traditional test results. The main contests are:First, generalize and analyze the internal and external literatures which are related to the measurement of the soil hydrodynamic parameter, in a systematical way. Based on the generalization and analysis, the study contests are advanced. The second, generalize the determine methods of the characteristic curve of soil water, and use 15 bar pressure-membrane apparatus to test. Introduce the experimental facility and experimental method of the conductivity and diffuseness of the soil hydraulic power; by laboratory experiments and computer automatic data acquisition and manipulation, analyze the difference and problems between automatic processing system and traditional manual experiments.Finally generalize the whole fruiting; propose the problems which need improving in future.Keywords: dynamic parameters of unsaturated soil water; laboratory test; automatic experimental data acquisition system; traditional experimental methodsIV第一章绪论第一章绪论1.1研究目的和意义随着社会的快速发展、人民对生活质量的要求不断提高,水资源短缺和水土环境恶化已成为制约我国农业乃至整个国民经济可持续发展的重要因素。
第4讲 土壤水份运动基本方程

What is hydraulic conductivity?
K is a property of both media and fluid. Experiments show: K is the intrinsic permeability (L2), a property of media only. ρ is the mass density (M/L3) μ is the dynamic viscosity (M/LT) and measures the resistance of fluid to shearing that is necessary for flow.
导水率K
综合反映了多孔介质对流体流动的阻碍作用
多孔介质的基质特征:质地、结构… 流体物理性质:粘滞性、密度…
实验室测定 现场测定
双环入渗试验 Guelph渗透仪 抽水试验
Darcy定律的微分形式:
微分形式与差分 形式有区别吗?
dH q = −K s dL
Return to fluid potential equation, Neglect velocity (kinetic) term, and substitute for p
m
)
θ方程(扩散型方程):
引入扩散率D:
D (θ ) = K (θ ) = K (θ C (θ )
)
dθ dψ m
∂ψ m dψ m ∂θ ∂θ = K (θ ) = D(θ ) K (θ ) ∂x dθ ∂x ∂x
∂θ ∂ ⎡ ∂θ ⎤ ∂ ⎡ ∂θ ⎤ ∂ ⎡ ∂θ ⎤ ∂K (θ ) = D(θ ) ⎥ + ⎢ D(θ ) ⎥ + ⎢ D(θ ) ⎥ ± ∂t ∂x ⎢ ∂x ⎦ ∂y ⎣ ∂y ⎦ ∂z ⎣ ∂z ⎦ ∂z ⎣
土壤水水分移动和循环PPT讲稿

K(m)为非饱和导水率,d/dx
为总水势梯度
(water potential gradient)
非饱和导水率是土壤基质 势的函数。
现在您浏览的位置是第八页,共四十页。
非饱和条件下土壤水流的数学表达式 与饱和条件下的类似,二者的区别在 于:
饱和条件下的总水势梯度可用差分形 式,而非饱和条件下则用微分形式:
“冻后聚墒”的多少,主要决定于该土壤的含水量和 冻结的强度。含水量高冻结强度大,“冻后聚墒”
就比较明显。一般对土壤上层增水作用为2-4%左 右。
现在您浏览的位置是第十九页,共四十页。
第三节 土壤水循环、平衡及有效性
一、农田土壤水分循环及平衡
田间土壤水分平衡示意图,据此可列出其土壤水分平衡的数学表达式 :
现在您浏览的位置是第三十页,共四十页。
二、分子扩散与溶质弥散 (一)分子扩散
扩散是指由于分子的不规则热运动即布朗运动引 起的运动, 是一个不可逆过程。 扩散作用常用费克第一定律来表示:
dC J s D0 dx
式中Js为溶质的扩散通量,mol·m-2s-1或kg·m-2s-1;D0为溶质的有效扩散系 数m2·s-1;dC/dx为浓度梯度。
现在您浏览的位置是第三十四页,共四十页。
第六节、土壤水的调控
一、水分高效利用的途径:
合理开采、分配和管理;
减少输水损失; 提高灌溉效率。
现在您浏览的位置是第三十五页,共四十页。
二、土壤水的调控措施 主要包括土壤水的保蓄和调节。 1、耕作措施 秋耕 中耕 镇压等
2、地面覆盖 薄膜覆盖 秸秆覆盖
3、灌溉措施 喷灌、滴灌、渗灌 4、生物节水
W=P+I+U-ET-R-In-D
田间蒸腾和蒸发很难截然分开, 常合在一起,统称蒸散ET。 (evapotranspiration)-一定时间内一 定面积上土壤蒸发和植物蒸腾的总和 。
3土力学与基础工程第二章-土中水的运动规律

渗透理论
图2-2 (a) 水在土孔隙中的运动
• 考虑到实际工程中并不需要了解具体孔隙中的渗流情况, 可以对渗流作出如下二方面的简化: • 一是不考虑渗流路径的迂回曲折,只分析它的主要流向; • 二是不考虑土体中颗粒的影响,认为孔隙和土粒所占的空 间之总和均为渗流所充满。 • 作了这种简化后的渗流其实只 是一种假想的土体渗流,称之 为渗流模型,如图2-2(b)所示。
k 为渗透系数,其值等于梯度为1时水的渗透速度,cm/s。 上式所表示的关系称为达西定律,它是渗透的基本定律。
• 达西实验的装置
①:直立圆筒。横截面积为A , 上端开口。在圆筒侧壁装有 两支相距为L的侧压管。 ②:滤板。滤板上填放颗粒均 匀的砂土。 ③:溢水管。水由上端注入圆 筒,多余的水从此溢出,使 筒内水位维持一恒定值。 ④:短水管。渗透过滤板的水 从此流入⑤。 ⑤:量杯。计算渗流量q。
1
3
2
4
• 同时读取
断面1—1和断面2—2处的侧压 管水头值h1、h2,得到两断 面之间的水头损失△h= (L+h )-h
5
图2-3 达西渗透实验装置图
2. 达西定律的适用范围 • 达西定律是由砂质土体(中砂、细砂、粉砂等)实验得到的,后 来经过修正后推广应用于其他土体如粘土和具有细裂隙的岩石 等。进一步的研究表明,在某些条件下,渗透并不一定符合达 西定律,因此在实际工作中还要注意达西定律的适用范围。大 量试验表明: (1) 当渗透速度较小时,渗透的沿程水头损失与流速的一次方 成正比。在一般情况下,砂土、粘土中的渗透速度很小, 其渗流可以看作是一种水流流线互相平行的流动—层流, 渗流运动规律符合达西定律,渗透速度v与水力梯度i的关 系可在v-i坐标系中表示成一条直线,如图(a)所示。 (2) 粗颗粒土(如砾、卵石等)的试验结果如图(b)所示。
10.第2节土壤水分解析

稳定入渗速率:stable infiltration rate
几种不同质地土壤的最后稳定入渗速率(毫米/小时)
土壤
砂质和
砂
粉质土 壤土
壤
最后入
渗速率 >20
10-20
5-10
粘质 土壤
碱化粘 质土壤
1-5
<1
2、土壤水分再分布 (soil water redistribution)
概念:土壤水分入 渗过程结束后,水 在重力和吸力梯度 影响下在土壤中向 下移动重新分布的 过程。
决定,可近似为水面蒸发强度E0。此阶段含水率的 下限,一般认为该值相当于毛管水断裂时的含水率
或田间持水量的50%—70% 。
2、表土蒸发强度随含水率变化的阶段(土壤导 水率控制阶段)
蒸发速率急剧降低,有利于土壤墒情的保持
3、水汽扩散阶段
土壤输水能力极弱,不能补充表土蒸发损失的 水分,土壤表面形成干土层。在此阶段,蒸发 面不是在地表,而是在土壤内部,蒸发强度的 大小主要由干土层内水汽扩散的能力控制,并 取决于干土层厚度,一般来说,其变化速率十 分缓慢而且稳定。
土壤含水量%
机理:墨水瓶效应、闭塞空气 的作用和接触角效应 沙土比粘土明显
三、 土壤水分运动
土壤水流动 水分蒸发 水分入渗 水分再分配
(一)土壤液态水运动 1、饱和流 (Saturated Soil Water Flow)
饱和流的推动力:主要是重力势梯度和压力势梯度
基本上服从饱和状态下多孔介质的达西定律(Darcy’s law) ***:
第
土
二
壤
节
水
土壤水的重要性:
•土壤水是土壤形成发育的催化剂 •土壤水是土壤的最重要组成部分之一 •土壤水是作物吸水的最主要来源 •土壤水关系到生物圈和人类生存的生态环境
降雨和灌水入渗条件下土壤水分运动2
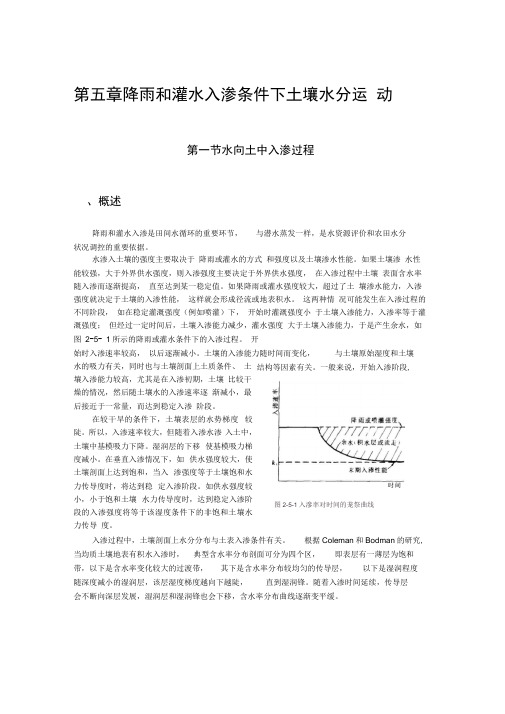
第五章降雨和灌水入渗条件下土壤水分运 动第一节水向土中入渗过程、概述降雨和灌水入渗是田间水循环的重要环节, 与潜水蒸发一样,是水资源评价和农田水分状况调控的重要依据。
水渗入土壤的强度主要取决于 降雨或灌水的方式 和强度以及土壤渗水性能。
如果土壤渗 水性能较强,大于外界供水强度,则入渗强度主要决定于外界供水强度, 在入渗过程中土壤 表面含水率随入渗而逐渐提高, 直至达到某一稳定值。
如果降雨或灌水强度较大,超过了土 壤渗水能力,入渗强度就决定于土壤的入渗性能, 这样就会形成径流或地表积水。
这两种情 况可能发生在入渗过程的不同阶段, 如在稳定灌溉强度(例如喷灌)下, 开始时灌溉强度小 于土壤入渗能力,入渗率等于灌溉强度; 但经过一定时间后,土壤入渗能力减少,灌水强度 大于土壤入渗能力,于是产生余水,如图 2-5- 1所示的降雨或灌水条件下的入渗过程。
开始时入渗速率较高, 以后逐渐减小。
土壤的入渗能力随时间而变化,与土壤原始湿度和土壤水的吸力有关,同时也与土壤剖面上土质条件、 土壤入渗能力较高,尤其是在入渗初期,土壤 比较干燥的情况,然后随土壤水的入渗速率逐 渐减小,最后接近于一常量,而达到稳定入渗 阶段。
在较干旱的条件下,土壤表层的水势梯度 较陡。
所以,入渗速率较大,但随着入渗水渗 入土中,土壤中基模吸力下降。
湿润层的下移 使基模吸力梯度减小。
在垂直入渗情况下,如 供水强度较大,使土壤剖面上达到饱和,当入 渗强度等于土壤饱和水力传导度时,将达到稳 定入渗阶段。
如供水强度较小,小于饱和土壤 水力传导度时,达到稳定入渗阶段的入渗强度将等于该湿度条件下的非饱和土壤水力传导 度。
入渗过程中,土壤剖面上水分分布与土表入渗条件有关。
根据Coleman 和Bodman 的研究,当均质土壤地表有积水入渗时, 典型含水率分布剖面可分为四个区, 即表层有一薄层为饱和带,以下是含水率变化较大的过渡带,其下是含水率分布较均匀的传导层,以下是湿润程度随深度减小的湿润层,该层湿度梯度越向下越陡, 直到湿润锋。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 土壤水分运动基本方程如前所述,达西定律是由达西(Darcy ,Henry 1856)通过饱和砂柱渗透试验得出,后由Richards (1931)将其扩伸至非饱和水流中,并规定导水率为土壤负压h 的函数,即()H h k q ∇= (2-2-1)式中:H ∇——为水势梯度;k (h )——为导水率,是土壤负压h 的函数; q ——为水流通量或流速。
Richards 方程垂向一维方程为)1)(( )(±∂∂-=∂∂-=zhk zH k q z θθ注意:H=h ±z ,垂直坐标向上为“+”;向下时为“–”。
由于k (h )受滞后影响较大,上式仅适用于单纯的吸湿或脱湿过程。
若将导水率作为容积含水率函数,即以k (θ)代替人k (h ),则可避免滞后作用的影响。
一般说来达西定律对饱和与非饱和水流均可适用,即水流通量与势能梯度成正比。
但在饱和土壤中,压力为正值,其总水头包括了由该点在地下水面以下深度来确定的静水压力(正值)和相对于基准面高度来确定的位置水头,总水头为压力水头和位置水头之和,水由总水头高处向低处流动。
在非饱和土壤中,基质势为负值,土水势在不考虑溶质势、温度势及气压势时,只包括重力势和基质势。
因此,总水头常以负压水头和位置水头之和来表示。
一维Richards 方程的几种形式:根据()()θθθD hk =∂∂(K=C ×D )得: x h k q x ∂∂-=)(θ x D q x ∂∂-=θθ)( y h k q y ∂∂-=)(θ yD q y ∂∂-=θθ)( )1)((±∂∂-=z h k q z θ )]()([θθθk zD q z ±∂∂-=第一节 直角坐标系中土壤水分运动基本方程一、基本方程的推导土壤水分运动一般遵循达西定律,且符合质量守恒的连续性原理。
土壤水分运动基本方程可通过达西定律和连续方程进行推导。
如图2-2-1所示,从土壤中取出微分单元体abcdefgh ,其体积为z y x ∆∆∆,由于该立方体很小,在各个面上的每一点流速可以看成是相等的,设其流速为z y x v v v 、、,在t ~t+Δt 时段内,流入立方体的质量为(3个面流入):t y x v t z x v t z y v m z y x ∆∆∆+∆∆∆+∆∆∆=ρρρ入 (2-2-2)流出立方体的质量为(3个面流出):t z y x x v v m x x ∆∆∆⎪⎭⎫⎝⎛∆∂∂+=ρ出t y x z z v v t z x y y v v z zy y ∆∆∆⎪⎭⎫ ⎝⎛∆∂∂++∆∆∆⎪⎪⎭⎫ ⎝⎛∆∂∂++ρρ (2-2-3) 式中:ρ––––水的密度;z y x ∆∆∆,,––––分别表示微分体x 、y 、z 方向长度;x x v x ∆∂∂,y y v y ∆∂∂,z zvz ∆∂∂––––分别表示水流经微分体后,其流速在x 、y 、z 方向的变化值。
由式(2一2-2)、式(2-2-3)之差可求得流入和流出立方体的质量差:出入m m m -=∆ ⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂-=z v y v xv z y x ρt z y x ∆∆∆∆⨯ (2—2—4) 设θ为立方体内土壤含水率,则在Δt 时间内立方体内质量变化又可写为t z y x tm ∆∆∆∆∂∂=∆θρ(2—2—5) 根据质量平衡原理(流入量-流出量=储存量变化量),式(3-2-4)、式(3—2—5)应相等,即⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=∂∂z v y v xv t z y x θ(2-2-6) 根据达西定律得:()x H k v x ∂∂-=θ,()y H k v y ∂∂-=θ,()zHk v z ∂∂-=θ (2-2-7)式中k (θ)––––土壤水力传导度,为含水率的函数;H ––––总土水势,为基质势与重力势之和(H =h +z )。
因此,式(2-2—6)可以写作以下形式:()()()zz H k y y H k x x H k t ∂⎥⎦⎤⎢⎣⎡∂∂∂+∂⎥⎦⎤⎢⎣⎡∂∂∂+∂⎥⎦⎤⎢⎣⎡∂∂∂=∂∂θθθθ (2-2-8)上式可以简写为()[]H k t∇∇=∂∂θθ(2-2-9) 式(2-2-8)或式(2-2-9)为土壤水分运动基本方程。
在饱和土壤中,含水量和基质势均为常量。
水力传导度也为常量,常称渗透系数,则方程(2-2-8)可写为0222222=∂∂+∂∂+∂∂zHy H x H (2-2-10) 或写作02=∇H (2-2-10‘)2222222zy x ∂∂+∂∂+∂∂=∇ (2-2-11)式中:▽2––––拉普拉斯算子。
式(2-2-10)或式(2-2-10‘)为饱和土壤水流的拉普拉斯方程。
二、基本方程的不同形式为运用基本方程分析各种实际问题的方便,可将基本方程改写为多种表达形式。
为简便起见,以下均以一维垂向土壤水分运动为例,给出基本方程的不同表达形式。
(一)以含水率θ为变量的基本方程由式(2-2-8)可得一维垂向土壤水分运动的基本方程为()⎥⎦⎤⎢⎣⎡∂∂∂∂=∂∂z H k z t θθ (2-2-12) 式中:H ––––总土水势;z ––––为水流方向坐标,取z 向上为正。
因为H=h 十z ,所以上式可写作()()zk z h k z t ∂∂+⎥⎦⎤⎢⎣⎡∂∂∂∂=∂∂θθθ (2-2-13) 式(2-2-13)为以θ为变量的基本方程,将zh z h ∂∂∂∂=∂∂θθ代入式(2-2-13)得: ()()z k z h k z t ∂∂+⎥⎦⎤⎢⎣⎡∂∂∂∂∂∂=∂∂θθθθθ 令()()θθθD hk =∂∂,则式(2—2—13)可以写成(一维垂向土壤水分运动方程): ()()zk z D z t ∂∂+⎥⎦⎤⎢⎣⎡∂∂∂∂=∂∂θθθθ (2-2-14) 在水平运动的情况下,重力项等于0,所以()xD v x ∂∂-=θθ,其形式与Fick 扩散定律相同。
式(2-2-14)具有扩散方程的形式,故将D (θ)称为扩散度。
()⎥⎦⎤⎢⎣⎡∂∂∂∂=∂∂x D x t θθθ (2-2-14‘) Fick 定律:自由水中溶质的分子扩散通量符合Fick 定律:xc DJ ∂∂-= 式中:J 为溶质的扩散通量; D 为溶质的扩散系数;xc∂∂为溶质的浓度梯度。
(二)以基质势h 为变量的基本方程 由于()th h c t h h t ∂∂=∂∂∂∂=∂∂θθ ,则式(2-2-14)可以写成: ()()()zh k z h h k z t h h c ∂∂+⎥⎦⎤⎢⎣⎡∂∂∂∂=∂∂ (2-2-15)式中:c (h )––––比水容量(也称容水度),c (h )=h∂∂θ,表示单位基质势变化时含水率变化。
(三)以参数v 为因变量的基本方程采用Kirchhoff 变换,令()()()⎰⎰⎰-∞==ccch hh hh d k Vd k d k v ττττττ1则()h k Vh v 1=∂∂ ()⎰∞=ch d k V ττ由式(2-2-15)得:()()zh k z z h h k t h h ∂∂+∂⎥⎦⎤⎢⎣⎡∂∂∂=∂∂∂∂θ()()zv v h h h k z z v v h h k t v v h h ∂∂∂∂∂∂+∂⎥⎦⎤⎢⎣⎡∂∂∂∂∂=∂∂∂∂∂∂θ()()()()()zv h k V h h k z z v h k V h k t v h k V h ∂∂∂∂-∂⎥⎦⎤⎢⎣⎡∂∂∂=∂∂∂∂θ()()zvv X z v t v v Y ∂∂+∂∂=∂∂22 (2-2-16) 式中h c ––––土壤的进气值,即土壤含水率开始小于饱和含水率时的负压值。
另外,()()()()()h k h c h D h h k v Y ==∂∂=11θ;()()()hh k h k v X ∂∂=1在非饱和区:()01<=⎰hh cd k Vv ττ在饱和区:()01>=⎰hh cd k Vv ττ且因为 ()0=∂∂=h h c θ,()0=∂∂hh k 所以 ()0=v Y ;()0=v X则方程式(2-2-16)为:022=∂∂zv(四)以位置坐标z 为变量的土壤水运动方程以z 为变量,则z 为θ、t 的函数,z (θ,t )为未知函数。
已知θ=θ(z ,t ),当0≠∂∂zθ处,可以解出z= z (θ,t ),即[14]()()0,,≡-t t z z z θ对z ,t 分别求导数:01=∂∂∂∂-z z θθ,0=∂∂-∂∂∂∂-tzt z θθ于是 θθ∂∂=∂∂z z 1及θθ∂∂∂∂-=∂∂z t zt 将以上式子代入方程(2-2-14)得:()()z k z D z t ∂∂+⎥⎦⎤⎢⎣⎡∂∂∂∂=∂∂θθθθ ()z k z z D z t z∂∂∂∂+∂∂⎪⎭⎫ ⎝⎛∂∂∂∂=∂∂∂∂-θθθθθθθ()zk z z D z t z ∂∂∂∂+∂∂⎪⎭⎫ ⎝⎛∂∂∂∂=∂∂∂∂-θθθθθθθ ()θθθθθ∂∂+∂∂⎪⎭⎫ ⎝⎛∂∂∂∂=∂∂-kz z D t z (2-2-17)(五)以参数u 为因变量的土壤水运动方程 定义()()()⎰⎰⎰==θθθθθθθθθθθθisiid D Ud D d D u 1式中:i θ––––初始含水率;()⎰=θθθθid D U ;s θ—饱和含水率。
由式(2-2-14)得:()()zk z k z t ∂∂+⎥⎦⎤⎢⎣⎡∂∂∂∂=∂∂θθθθ()t uu k z u u D z t u u ∂∂∂∂∂∂+⎥⎦⎤⎢⎣⎡∂∂∂∂∂∂=∂∂∂∂θθθθθ将()θθD Uu 1=∂∂代入上式得:()()()()z uD U k z u D U D z t u D U ∂∂∂∂+⎥⎦⎤⎢⎣⎡∂∂∂∂=∂∂θθθθθ 所以 ()z uk zu D t u ∂∂∂∂+∂∂=∂∂θθ22 (2-2-18) 以上各式中式(2-2-14)、式(2-2-15)是二种经常采用的形式,形式的选定取决于要解决问题的边界条件和初始条件。
以含水率θ为因变量的基本方程常用于求解均质土层或全剖面为非饱和流动问题,这种方程形式对于层状土壤或求解饱和—非饱和流问题不适用;以负压水头h 为因变量的基本方程是应用较多的一种形式,可适用于饱和—非饱和水流求解及层状土壤的水分运动分析计算,但由于非饱和土壤水的导水率k (h )及容水度c(h),受滞后影响较大,计算中参数选取不当会造成较大误差;以v ,u 为因变量基本方程实际上分别相当于以负压水头h 和含水率θ为因变量的基本方程,在某些情况下由于经代换后方程较为简单,易于求解;以坐标为因变量的基本方程根据定解条件需要求解较简单的土壤水分运动问题。
