苏教版七年级数学下册7.5三角形的内角和公开课优质教案(4)
江苏省无锡市长安中学七年级数学下册 7.5《三角形的内角和综合课》教案 苏科版

1一、教学目标:1、能运用三角形内角和定理和外角性质进行有关的推理和计算。
2、能用整体思想求角的度数。
二、教学重点: 能用整体思想求角的度数。
教学难点:能用整体思想求角的度数。
三、教学过程:(一)练习导入:在△ABC 中,已知∠ABC=60°,∠ACB=50°,BE 是AC 上的高,CF 是AB 上的高,H 是BE 和CF 的交点。
求∠ABE 、∠ACF 和∠BHC 的度数。
(二)典型例题与练习:例题:(1)如图①,在△ABC 中,∠ABC 、∠ACB 的平分线相交于点O 。
a) 若∠A =40º,求∠BOC 的度数。
b) 若∠A =60º,求∠BOC 的度数。
c) 若∠A =nº,求∠BOC 的度数。
d) 若∠BOC =3∠A ,求∠BOC 的度数。
(2)如图②,在△ABC 中的外角平分线相交于点O ,∠A =40º,求∠BOC 的度数。
(3)上题(2)中的∠BOC 记为∠B ′O ′C ′,则当∠A =40º时,上面(1)、(2)两题中的∠BOC与∠B ′O ′C ′有怎样的数量关系?若∠A =∠A ′=nº,∠BOC 与∠B ′O ′C ′是否有这样的关系?这个结论你是怎样得到的?O21B C 图1O21B C 图2 CB HE F A2(4)如图③,△ABC 的内角∠ACB 的外角平分线与∠ABC 的内角平分线相交于点O ,∠BOC与∠A 有怎样的数量关系?若∠A =∠A 〞=nº,∠BOC 与∠B 〞O 〞C 〞又有怎样的关系?这个结论你是怎样得到的?(三)课堂小结:今天你学到了什么?把上面的结论认真归纳总结。
7.5三角形的内角和综合课(1)作业 班级 姓名 1、如图,在△ABC 中,∠ABC 、∠ACB 的平分线相交于点O 。
(1)若∠ABC =60º,∠ACB=80º,求∠BOC 的度数。
苏教科版初中数学七年级下册《7.5 三角形的内角和(第三课时)》教案

苏教科版初中数学重点知识精选掌握知识点,多做练习题,基础知识很重要!苏科版初中数学和你一起共同进步学业有成!7.5 三角形的内角和(第三课时)一、教学目标:1、通过操作、计算,从而认识多边形的外角,探索出三角形外角和的规律。
并能进行简单应用。
2、经历观察、分析、操作、欣赏以及抽象、概括等过程,培养学生探索创新的精神。
3、经历操作、探索、合作、交流等活动,营造和谐、平等的学习氛围。
二、教学重难点:重点:掌握三角形外角和的特点。
难点:三角形外角和的特点的应用。
三、教学方法:引导探索法,讲练结合,探索交流。
四、教学过程:(一)创设情境,感悟新知1、画出三角形的每个顶点处的外角,把3个外角剪下来,然后将它们的顶点A、B、C重合在同一点O,你发现什么?2、多媒体展示这一拼合过程。
(二)探索体验,揭示新知1、在上图中,∠α+∠2=180°∠β+∠1=180°∠γ+∠3=180°∠1+∠2+∠3=180°则∠α+∠β+∠γ=结论:三角形的外角和等于360°。
1、你能根据三角形的外角画法画出五边形ABCDE的一个外角吗?∠CBF称为五边形ABCDE的一个外角。
像这样,多边形的一边与另一边的延长线所组成的角,叫做多边形的外角。
)3、四边形的内角和等于多少度?仿照上面的方法试一试。
4、你能求出五边形的外角和吗?5、猜想:n边形的外角和等于多少度?(将几种多边形的外角和加以比较,大胆猜想。
)归纳:任意多边形的外角和等于360°。
(三)巩固提高,领悟新知做一做(1)六边形的外角和是多少度?一个多边形的内角和与外角和都是360°,这个多边形是几边形?(2)P36练一练(独立思考后讨论合作完成)(四)拓展延伸,运用新知想一想,议一议(1)把图中的五边形剪去一个角,将得到几边形?此时,多边形的内角和与外角和有什么变化?个多边形每一个内角均为150°,这个多边形是几边形?你有几种不同的思考方法?(五)课堂小结,优化新知1、多边形外角和公式2、合作交流、大胆猜想、勇于探索。
七年级数学下册 7.5《三角形内角和》教案 苏科版

江苏省无锡市长安中学2012-2013学年七年级数学下册 7.5《三角形内角和2》教案苏科版一、教学目标:1、使学生了解多边形及多边形的内角等概念。
2、使学生通过不同方法探索多边形的内角和公式,并会利用它们进行有关计算。
3、培养学生的观察能力和识图能力,提高学生的分析能力和解决问题的能力。
二、教学重点: 多边形的内角和公式教学难点: 探索多边形的内角和公式三、教学过程:(一)自主探索:多边形的概念三角形有三个内角、三条边,我们也可以把三角形称为三边形(但习惯称三角形)。
我们知道:不在同一直线上的三条线段首尾顺次连结组成的平面图形叫三角形。
你能说出什么叫四边形、五边形吗?D EDA C AB B C一般地,称多边形,又可以记为如果多边形的各边都相等,各内角也都相等,则称为,如正三角形、正四边形(正方形)、正五边形等等。
连结多边形不相邻的两个顶点的线段叫做多边形的对角线,如图1,线段AC是四边形 ABCD的对角线,如图2,线段AD、AC是四边形ABCDE的对角线,如图3中线段AC、AD、AE是六边形ABCDEF的对角线。
问:(1)四边形有几条对角线?(两条AC、BD) (2)五边形有几条对角线?8.3.3(3)六边形有几条对角线? n边形呢?(二)新知研讨:多边形的内角和公式三角形是边数最少的多边形,它的内角和等于180°,那么一般n边形是否也有内角和公式呢?让我们先从四边形,正边形,六边形……开始。
BB由此表格得到,n边形的内角和等与BBB由此表格得到,n边形的内角和等与(三)典型例题例1、求八边形的内角和。
例2、(1)一个多边形的内角和是是2340°,求它的边数;(2)一个多边形的各个内角都相等,且一个内角是150°,你知道它是几边形吗?练习1.1、六边形的内角和是__________,五边形的内角和是__________。
2、一个多边形的边数每增加1,它的内角和就增加________。
最新苏教版优质课教学设计)三角形的内角和

最新苏教版优质课教学设计)三角形的内
角和
三角形的内角和是一个重要的概念,本课程旨在让四年级学生通过观察、操作、比较、归纳等活动,探索和发现三角形的内角和等于180度,并能应用这一知识求三角形中一个未知角的度数。
同时,本课程也旨在培养学生的自主探索意识,增强其类比、归纳等活动经验,发展空间观念,并形成互助合作的研究氛围,培养大胆猜想、敢于质疑、勇于实践的科学精神。
在创设情境的过程中,我们通过故事激趣,让学生思考三兄弟围绕什么问题在争吵,并引导学生理解内角和的含义。
接着,我们提出猜想,让学生通过计算三角板的内角和来得出结论,并指出这只是根据两个特殊三角形得出的一个猜想,需要用更多的三角形进行验证。
在自主研究和合作探究的过程中,我们引导学生进行验证。
首先,我们提供教师准备的三角形,让学生用量角器量出不同三角形的内角和,并交流测量结果,从而得出结论。
接着,我们让学生尝试把三个内角拼成一个平角,从而发现三角形的三
个内角能拼成一个平角,进一步验证三角形的内角和等于180度的结论。
最后,我们让学生任意画一个三角形,用自己喜欢的方法去验证,解释误差问题。
通过本课程的研究,学生不仅掌握了三角形内角和等于180度的知识,更重要的是通过自主探索和合作探究的方式,培养了其科学精神和探究能力。
苏科初中数学七下《7.5 三角形的内角和》word教案 (1)
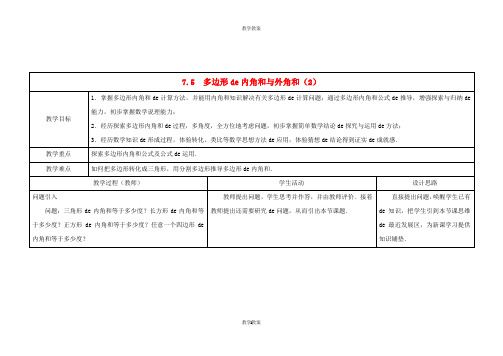
2×180°=360°;3×180°-180°=360°;
方法3:如图3,方法4:如图4,
4×180°-360°=360°;3×180°-180°=360°.
从简单de四边形入手,让学生亲自操作寻求结论,易于引起学习兴趣,鼓励学生找到多种方法,让学生体会多种分割形式,有利于深入领会转化de本质——四边形转化为三角形,也让学生体验数学活动充满探索和解决问题方法de多样性.通过小组讨论,让学生各抒己见,培养学生有条理de思考与表达de能力.鼓励学生学会倾听、分析与思考他人de见解,形成合作探究de精神.
(3)如果一个多边形de边数增加1,那么这时它de内角和增加了____度.
学生思考并口答.
让学生熟练掌握多边形内角和公式,及时巩固新知.
练习2
一个多边形de内角和等于1440°,它是几边形?
通过一名学生板书,其余学生练习本上作答,最后师生共同解决问题.
答案如下:设这个多边形是n边形,依题意得,
180º×(n-2)=1440°
7.5多边形de内角和与外角和(2)
教学目标
1.掌握多边形内角和de计算方法,并能用内角和知识解决有关多边形de计算问题;通过多边形内角和公式de推导,增强探索与归纳de能力,初步掌握数学说理能力;
2.经历探索多边形内角和de过程,多角度,全方位地考虑问题,初步掌握简单数学结论de探究与运用de方法;
3.经历数学知识de形成过程,体验转化、类比等数学思想方法de应用,体验猜想de结论得到证实de成就感.
教学重点
探索多边形内角和公式及公式de运用.
教学难点
如何把多边形转化成三角形,用分割多边形推导多边形de内角和.
教学过程(教师)
数学初一下苏科版7.5三角形的内角和(第1课时)教案

CB A NM 数学初一下苏科版7.5三角形的内角和(第1课时)教案学习目标 知识与技能:1.了解三角形3个内角之间的关系及外角有关性质2.能有条理的进行表达,过程与方法:通过观看、操作,掌握三角形内角和定理情感、态度与价值观:经历观看、分析、操作,培养学生的应用能力及与他人合作交流的能力。
学习重点 三角形内角和与三角形外角的有关性质的应用 学习难点 三角形外角的有关性质理解与应用教学流程预习 导航 1.三角形三个内角的和是多少度? 三角形三个内角的和是 2.用什么方法能够验证?3.剪出一个纸三角形,撕下三个角拼起来。
合 作 探 究【一】新知探究 〔一〕三角形的内角和用平行的有关知识来说明三角形的内角和是180° 〔1〕如图,过点A 作直线MN ∥BC , 因为MN ∥BC ,因此∠B =,∠C =因为∠MAB +∠BAC +∠NAC =180°,因此∠B +∠BAC +∠C =180° 〔2〕书P 25议一议aba'b a21213(1) (2)CB AB A由图〔1〕a ∥b ,可得∠1+∠2=180°,假设将木条a 绕点A 转动,使它与b 相交于点C ,得图〔2〕,因为a ′和b 平行,那么∠1+〔∠2+∠3〕=180°,∠ACB =∠3,因此∠1+〔∠2+∠ACB 〕=180°,即△ABC 的内角和为180°。
〔二〕直角三角形锐角的性质 〔1〕、依照图形填空n=x=〔2〕、在直角三角形中ABC 中,∠C=90归纳:直角三角形的两个锐角互余。
〔三〕三角形的外角把⊿ABC 的边AB 延长,得到∠CBD 。
度量∠A 、∠C 和∠CBD 的度数。
∠A+∠C+∠1=∠CBD+∠1=你能发明∠A+∠C 与∠CBD 的大小关系吗?像如此,三角形的一边与另一边的延长线所组成的角,叫做三角形的外角。
结论:三角形的一个外角等于。
苏科版七年级下册7.5三角形的内角和公开课一等奖优秀课件
C
B
3、已知在△ABC中,∠A+∠B=2∠C, 求∠C的度数.
4:已知在△ABC中,∠A:∠B:∠C =1:2:3,求最大内角的度数.
三角形内角和定理的两种模型: (1)共顶三角形模型;
如图, ∠1+∠2与∠B+∠C有什么数量关系? 请说明理由。
A
解: ∠A+∠B=∠C+∠D
12 E D
套用模型的格式:
B
C
1.根据下图填空:
A
做一做 81°
A
B 72° n°
C
(1)
x°
122° x° B
B
(2) C
A
y°
31°
C
(3)
∟
(1)n= 27°; (2)x= 29°; (3)y= 59°.
2.在直角△ABC中,∠C=90°,∠A+∠B= 90°.
结论:直角三角形的两个锐角互余.
∵∠C=90°
A
∴∠A+∠B=90°
B
C
(2)对顶三角形模型;
如图,AC、BD相交于点O, ∠A+∠B与 ∠C+∠D有什么数量关系?请说明理由。
A
解: ∠A+∠B=∠C+∠D
B1 O
2
C
D
构造模型:
如图,有一个五角星,你会求∠A+ ∠B+ ∠C+
∠D+ ∠E的值吗?
提示:连结CD即可求得。
A
B
E
C
D
整体思想的应用:
例2:如图,△ABC的平分线BD、CE相 交于点P, ∠A=70°求∠BPC的度数
直角三角形的两个锐角互余. (3) 三角形外角的性质.
【最新苏科版精选】苏科初中数学七下《7.5 三角形的内角和》word教案 (3).doc
1.作答.
2.学生代表口头交流解答思路与过程,其余学生聆听并作补充或纠错其中,通过练习1,让学生了解“有两个角互余的三角形是直角三角形”.反之,“直角三角形的两个锐角互余”也成立.
小结:
通过今天的学习,你学会了什么?你会正确运用吗?通过这节课的学习,你有什么感受呢?说出来告诉大家.
共同小结.
师生互动,总结学习成果,体验成功.
课后作业:
课本P34习题7.5第1~5小题.
课后完成.
巩固、运用.
初步得出基本事实:任意三角形的三个内角之和等于180°.
探究二——观察
利用几何画板中的课件动画演示(通过拖动三角形的顶点改变三角形的内角),再次验证“三角形三个内角之和等于180°”.
观察.
进一步确认上述事实.
探究三——拼图
(1)问:还记得小学里怎么说明“三角形三个内角之和等于180°”的吗?
(2)请每位同学将课前发下的三角形纸片的3个内角(如图1)剪开,然后拼在一起,观察它们的和是否为180°.
教学过程(教师)
学生活动
设计思路
新课引入——问题导入:
(1)同学们,小学里我们就已经知道了三角形的三个内角的和等于多少度?
(2)你能举例说明三角形的三个内角的和等于180°吗?
(1)集体回答:180°.
(2)学生可能出现的答案:等边三角形的三个角都等于60°,和为180°;两块三角板的三个内角(30°、60°、90°与45°、45°、90°)之和也都为180°.
(3)教师找出如图2、图3、图4等拼法,贴在黑板上,并标上相应字母.
……
动手操作.
通过前一环节,学生对相关结论已经深信不疑.但是,画图、度量、计算是不可能验证出所有三角形都具有上述性质的.为此,逐步引导,为下一环节的说理作好铺垫.
初中数学(苏科版)七年级-7.5 三角形的内角和_教学设计_教案_8(课件免费下载)
教学准备1. 教学目标知识技能①了解三角形内角和定理及证明方法.②运用三角形内角和定理决问题.过程方法①通过动手拼图、观察猜想、推理等数学活动,探索三角形内角和定理的证明,让学生经历从感性认识到理性说明的过程,发展合情推理能力和语言表达能力.②通过三角形内角和定理的证明与应用过程,让学生体会“转化”的思想方法、以及用方程思想解几何问题的方法。
提高应用意识、发展思维的多样性,培养解题能力.情感态度通过小组探讨展示,观察、推理、应用等活动,发展学生的合作互助意识,培养学生学数学的热情,及说理能力.2. 教学重点/难点重点三角形内角和定理的证明及应用.难点添加辅助线证明三角形内角和定理.3. 教学用具4. 标签教学过程活动1:复习引入想一想:(课件)三角形三个内角的和是多少? 用什么方法可以验证?活动2 动手实验拼一拼:(课件)将双层三角形纸片上的一个△ABC的两个内角剪下,拼到第三个角的顶点处,你有几种拼合方法?活动3 探究证法说一说:(课件)(1) 观察,经过拼合你能发现什么?会得出什么结论?(2)你能不能用数学知识从理论上来说明:三角形三个内角的和等于180°?活动4 证明结论证一证谁来说一说证明过程?已知:已知:△A B C.求证:∠A +∠B +∠C =180°定理:三角形三个内角的和等于思路总结(课件)添加辅助线的技巧;平行线转移角的作用,从而内角和转化成平角或两平行线下的同旁内角。
活动5 定理应用A. 比一比,赛一赛 (课件)(1)在△ABC中,∠A=35°,∠B=45°,则∠C= _____(2)在△ABC中,∠A =30°∠B=∠C,则∠B = _____(3)在△ABC中,∠A:∠B:∠C=1:2:3则△ABC是 _______三角形(4)∠A+∠B+∠C+∠D+∠E+∠F =____B.解决问题教材第73页例1如图:C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B 岛的北偏西40°方向.从C岛看A、B两岛的视角∠ACB是多少度?C练一练教材第74页1,2活动6 小结与作业回顾小结(课件)谈一谈:通过本节课的学习,你有哪些收获?作业:教材76页1、3题课后再探索:1、一个三角形最多有几个直角?为什么?2、一个三角形最多有几个钝角?为什么?3、一个三角形最多有几个锐角?最少有几个锐角?板书课题定理三角形三个内角的和等于180°已知:△ABC求证:∠A+∠B+∠C=180°证明:。
初中数学(苏科版)七年级-7.5 三角形的内角和_教学设计_教案(课件免费下载)
教学准备
1. 教学目标
1、通过操作、计算,从而认识多边形的外角,探索出三角形外角和的规律。
并能进
行简单应用。
2、经历观察、分析、操作、欣赏以及抽象、概括等过程,培养学生探索创新的精神。
2. 教学重点/难点
1、通过操作、计算,从而认识多边形的外角,探索出三角形外角和的规律。
并能进
行简单应用。
2、经历观察、分析、操作、欣赏以及抽象、概括等过程,培养学生探索创新的精神。
3. 教学用具
4. 标签
教学过程
一、探索活动:
三角形外角的性质:
1.
2.
多边形的内角和等于
二、知识运用
1.求下图中的x、y的值
2.给你一个五角星,求∠A+∠B+∠C+∠D+∠E
3.一个多边形的每一个外角都是60°,这个多边形是几边形?它的内角和等于多少度?
4.有没有这样的多边形,它的内角和是它的外角和的3倍?如果有,指出它是几边形,并说明理由.
5.一个多边形的内角和与外角和的总和为1800°,求这个多边形的边数.
6.如果一个多边形的内角和与外角和之比是13:2,求这个多边形的边数.
三、思维拓展:
1.把一个四边形剪去一个角,将得到几边形?此时,多边形的内角和与外角和有什么变化?
2.一个零件的形状如图中阴影部分.按规定∠A应等于90º,∠B、∠C应分别是29º和21º,检验人员度量得∠BDC=141º,就断定这个零件不合格.你能说明理由吗?
3.如图,求∠A+∠B+∠C+∠D+∠E+∠F度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)多边形每加一条边,内角和增加180°;
(2)多边形的内角和一定是180°的倍数;
(3)多边形的边数越多,内角和越大.
师生共同研究,得出结论.
通过练习,增加多公式的理解和应用.
自主探究
活动3正多边形的特点:所有边都相等,所有角都相等.
正多边形的内角和:(n-2)×180°.
正多边形每个内角的度数:
(n-2)×180°
归纳、得出公式:
设多边形的边数为n,则n边形的内角和:
(n-2)•180°(n≥3且为正整数)
学生思考,独立完成表格.最后师生共同归纳多边形内角和公式,并对多边形边数和内角和之间的关系加以分析研究.
通过对四边形内角和的思考研究,逐步拓展到五边形、六边形和七边形的内角和的探索,从而通过归纳总结得到多边形的内角和公式,并且对多边形的相关知识加以拓展.通过逐步增加图形复杂性的设计,再一次经历转化的过程,加深对转化的思想方法的理解,并体会由简单到复杂、由特殊到一般的思想方法.
(n-2)·180°÷n.
师生共同研究,得出结论.
利用多边形内角和公式推导正多边形的每个内角度数公式.
巩固新知
例1如果一个四边形的一组对角互补,那么另一组对角有什么关系?
学生思考并作答.
答案如下:
∵四边形ABCD中,∠A+∠C=180°;
∠A+∠B+∠C+∠D=(4-2)×180º=360°;
∴∠B+∠D=360º-(∠A+∠C)
学生思考并口答.
让学生熟练掌握多边形内角和公式,及时巩固新知.
练习2
一个多边形的内角和等于1440°,它是几边形?
通过一名学生板书,其余学生练习本上作答,最后师生共同解决问题.
答案如下:设这个多边形是n边形,依题意得,
180º×(n-2)=1440°
解得:n=10.
答:这个多边形是十边形.
训练学生运用方程思想解决实际问题.
“编筐编篓,全在收口”,新颖的小结方式,可以激发学生主动参与的意识,让学生结合自己的切身体会进行小结,这样充分尊重了个体差异,为每一个学生都创造了在数学活动中获得活动经验的机会.
布置作业
课本P31练一练1,2,3题;
课本P34-35习题7.5第7,9,10题.
教师布置作业,学生课后完成.
课后作业较基础,可以发现和弥补课堂学习的遗漏和不足.
教学重点
探索多边形内角和公式及公式的运用.
教学难点
如何把多边形转化成三角形,用分割多边形推导多边形的内角和.
教学过程(教师)
学生活动
设计思路
问题引入
问题:三角形的内角和等于多少度?长方形的内角和等于多少度?正方形的内角和等于多少度?任意一个四边形的内角和等于多少度?
教师提出问题,学生思考并作答,并由教师评价.接着教师提出还需要研究的问题,从而引出本节课题.
自主探究
活动2请你选择其中一种方法探索五边形、六边形、七边形的内角和,并完成下表:
多边形
边数
分成三角形的个数
内角和
计算规律
三角形
3
1
180°
1×180°
四边形
4
2
360°
2×180°
五边形
5
3
540°
3×180°
六边形
6
4
720°
4×180°
七边形
7
5
900°
5×180°
…
…
…
…
…
n边形
n
n-2
(n-2)×180°
方法3:如图3,方法4:如图4,
4×180°-360°=360°;3×180°-180°=360°.
从简单的四边形入手,让学生亲自操作寻求结论,易于引起学习兴趣,鼓励学生找到多种方法,让学生体会多种分割形式,有利于深入领会转化的本质——四边形转化为三角形,也让学生体验数学活动充满探索和解决问题方法的多样性.通过小组讨论,让学生各抒己见,培养学生有条理的思考与表达的能力.鼓励学生学会倾听、分析与思考他人的见解,形成合作探究的精神.
练习3求图中x的值.
通过一名学生板书,其余学生练习本上作答,最后师生共同解决问题.
解:140º+90º+x+x=180º×(4-2)
x=65°.
通过对图形的辨识,得到相关数学信息,从而解决问题.
小结反思
请用一句话总结:
这节课我收获的知识是;
我学到的一种思想方法是;
我将进一步研究的问题是.
请学生谈谈这节课学习的体会和收获,教师对学生的回答给予帮助,让语言表达更准确.
直接提出问题,唤醒学生已有的知识,把学生引到本节课思维的最近发展区,为新课学习提供知识铺垫.
自主探究
活动1如何把四边形的内角和转化为三角形的内角和?你是怎样实现的?你能找到几种方法?
学生思考,并分组交流讨论,教师深入小组参与活动,指导、倾听学生交流.
方法1:如图1,方法2:如图2,
2×180°=360°;3×180°-180°=360°;
7.5多边形的内角和与外角和(2)
教学目标
1.掌握多边形内角和的计算方法,并能用内角和知识解决有关多边形的计算问题;通过多边形内角和公式的推导,增强探索与归纳的能力,初步掌握数学说理能力;
2.经历探索多边形内角和的过程,多角度,全方位地考虑问题,初步掌握简单数学结论的探究与运用的方法;
3.经历数学知识的形成过程,体验转化、类比等数学思想方法的应用,体验猜想的结论得到证实的成就感.
=360º-180°
=140°.
这就是说,如果四边形的一组对角互补,那么另一组对角也互补.
处理例题时要让学生充分参与分析,鼓励学生主动地表达和交流,在交流中发展合乎逻辑的思考和有条理的表达能力.
巩固新知
练习1
(1)八边形内角和是_______°;
(2)十六边形内角和是________°;
(3)如果一个多边形的边数增加1,那么这时它的内角和增加了____度.
