杨浦区第二学期八年级期中考试数学试卷
杨浦区第二学期八年级期中考试数学试卷

杨浦区2021学年度第二学期初二数学期中考试卷〔考试时间:90分钟总分值100分〕2021、4一、填空题:〔本大题共12题,每题2分,总分值24分〕1.假设函数y(k1)x1是一次函数,那么k的取值范围为.2.一次函数ykxb的图像经过点A(0,2),并与直线y4x平行,那么这个一次函数解析式是_ .3.如果一次函数 y kx 1中y随x的增大而减小,那么这个一次函数一定不经过第___ 象限.4.在图中,将直线OA向上平移3个单位,所得直线的函数解析式为.5.方程2x1x的解是__.第4题图A6.方程组x y2的解为.xy37.十二边形的内角和为_______度.OB C第10题图8.用换元法解方程x233x313.如果设y23,那么原方程可化为y的整x22x式方程是.9.一个多边形的每个外角都为72,那么这个多边形是边形.10.如图,□ABCD的周长是28cm,AC和BD交于O,△OAB的周长比△OBC的周长小2cm,那么AB=,BC=.11.解方程组x2y22时,可先化为和两个方x25xy6y20程组.12.如果直y2x k与两坐所成的三角形面是9,k的.二、〔本大共6,每2分,分12分〕13.函数y x 3,假设当x a,y5;当x b,y3,a和b的大小关系是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯〔〕〔A〕a>b;〔B〕a=b;〔C〕a<b;〔D〕不能确定.14.以下方程中,是二方程的⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯〔〕〔A〕21;〔〕2x0;〔〕8;〔〕.B xCx Dx015.以下方程中, 有数解的是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯〔〕〔A〕x610;〔B〕x2;〔C〕x230;〔D〕2xx.x2x216.某灾区恢复生,划在一定内种60蔬菜,播种每天比原划多种3,因此提前一天完成任,种了几天?种了x 天,可列方程⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯〔〕〔A63;〔B〕60603;〔C〕60601;〔D〕60601〕600.xx1x1x xx3x3x 17.平行四形的一条14,以下各数中,能分作它的两条角的是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯〔〕〔A〕10与16;〔B〕12与16;〔C〕20与22;〔D〕10与18.18.一个面积为2的平行四边形被直线分成面积为x,y的两局部,那么y与x之间的函数关系只可能是〔〕三、简答题〔本大题共5题,每题6分,总分值30分〕19.解关于x的方程:b(x2)4.20.解方程:2x3x.解:解:7,①4y2 21.解方程组:x y22.解方程组:x 22xy291.②x y解:解:23.:如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF.求证:∠MAE=∠NCF.四、解答题〔本大题共3题,每题8分,总分值24分〕24.如图,A〔4,a〕,B〔-2,-4〕是一次函数y=kx+b的图象和反比例函数y=m的图象的交点.x1〕求反比例函数和一次函数的解祈式;2〕求△A0B的面积.解:25.某区需修建一条2400米长的封闭式污水处理管道.为了尽量减少施工对市民生活等的影响,实际施工比原方案每天多修10米,结果提前20天完成了任务.试问实际每天修多少米?解:26.如图,:在平行四边形ABCD中,∠C=60°,E、F分别是AB、CD的中点,且AB=2AD.求证:DE∶BD=3∶3.五、〔本大题总分值10分,第〔1〕小题2分,第〔2〕①②小题各4分〕27.如图一次函数y=-x+7与正比例函数y=4x的图象交于点A,且与x轴3交于点B.1〕求点A和点B的坐标;2〕过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O﹣C﹣A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒(t0).①当t为何值时,以A、P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是QA=QP的等腰三角形?假设存在,求的值;假设不存在,请说明理由.解:。
上海市杨浦区2018-2019学年八年级下学期期中考试数学试卷(解析版)

2018学年第二学期期中初二年级质量调研卷一、填空题(本大题15题,每题2分,满分30分)1.一次函数与x轴的交点是____________2.要使直线不经过第四象限,则该直线至少向上平移__________个单位3.直线与平行,且经过点(2,1),则k=______b=_______4.已知,一次函数的图像经过点A(2,1)(如下图所示),当时,x的取值范围是______5.已知点,是直线上的两点,且当<时,>,则该直线经过______________象限.6.关于x的方程的解是一切实数,那么实数a=_________7.已知方程若设,则原方程可化为关于y的整式方程__8.方程的解是_______________9.将方程组:转化成两个二元二次方程组分别________和____________10.若方程有增根,则a的值为______________11.关于x的方程:是二项方程,k=_____________12.如图,平行四边形ABCD中,对角线AC⊥BD,AC=10,BD=24 ,则AD=____________13.平行四边形ABCD中,∠A:∠B=2:7,则∠C=_________º14.如果从某个多边形的一个顶点出发的对角线共有2 条,那么该多边形的内角和是____度.15.如果一个平行四边形的一个内角的平分线分它的一边为1:2两部分,那么称这样的平行四边形为“协调平行四边形”,称该边为“协调边”,当协调边为6时,它的周长为______二、选择题(本大题共4题,每题3分,满分12分)16.下列方程组中,属于二元二次方程组的是()A. B. C. D.17.有实数根的方程是()A. B. C. D.18.一个多边形,边数每增加1,内角和是()A. 不变B. 增加1 ºC. 增加180 ºD. 增加360 º19.一次函数,若y 随着x的增大而减小,则该函数的图像经过()A一、二、三 B. 一、二、四 C. 二、三、四 D. 一、三、四三、简答题(本大题共5题,每题6分,满分30分)20.解方程:21.解方程:22.解方程组:23.声音在空气中传播速度y(米/秒)是气温x (摄氏度)的一次函数,下表列出了一组不同气温时的音速。
最新杨浦区学年度第二学期期中考试初二数学学科试卷2014.4

杨浦区2013学年度第二学期期中考试初二数学学科试卷2014.490分钟 100分(基础部分)+50分(拓展部分)基础部分一、填空题(本大题共12题,每题3分,满分36分)1.方程04224=-x x 的解是 。
2.直线12-+=b x y 在y 轴上的截距是2,则b= 。
3.如果一次函数y=kx+b 图像与直线y=2x 平行,且过(-3,5),则这个一次函数的解析式是 。
4.请写出一个二项方程,使其有一解为-2,这个二项方程是: 。
5.直线13+--=m x y 上有两点A (a ,-2)、B (b ,-3),则a b 。
(填“>”、“<”或“=”)6.直角梯形的一腰长6cm ,这条腰与一条底边所成的角为60°,则另一腰长为 。
7.一个多边形的内角和与外角和的度数之比为9:2,则这个多边形的边数是 。
8.矩形的一条对角线长6cm ,它把一个内角分成1:2两部分,则矩形的面积为 平方厘米。
9.如图,菱形ABCD 的对角线AC 、BD 相交于点O ,且AC=8,BD=6,过点O 作OH ⊥AB ,垂足为H ,则点O 到边AB 的距离OH= 。
第9题 第10题10.如图,已知一次函数b x k y +=11的图像与反比例函数xk y 22=的图像交于A (-2,1)和)34,23(-B 两点,当21y y >时,x 的取值范围是 。
11.菱形ABCD 的一条对角线长为6,边AB 的长是方程01272=+-x x 的一个根,则菱形ABCD 的周长为 。
12.如图,在梯形ABCD 中,AD ∥BC ,E 是BC 的中点,AD=5,BC=12,点P 是BC 边上一动点,当PB= 时,以点P 、A 、D 、E 为顶点的四边形为平行四边形。
二、选择题(本大题共4题,每题3分,满分12分)13.右图反映了一辆汽车从甲地开往乙地的过程中,汽车离开甲地的距离s (千米)与所用时间t (分)之间的函数关系。
2018-2019上海市杨浦区八年级(下)期中数学试卷资料

51. 如图,在平面直角坐标系 xOy 中,O 为坐标原点,已知直线 l1 经过点 A (-6,0),它与 y 轴交于点 B,点 B 在 y 轴正半轴上,且 OA=2OB.
52. (1)求直线 l1 的函数解析式; 53. (2)若直线 l2 也经过点 A(-6,0),且与 y 轴交于点 C,如果△ABC
பைடு நூலகம்
5. 一次函数 y=-2x-7 与 x 轴的交点是______.
6. 要使直线 y=3x-2 不经过第四象限,则该直线至少向上平移______个单
位.
7. 直线 y=kx+b 与 y=-5x+1 平行,且过(2,1),则 k=______,
b=______.
8. 已知,一次函数 y=kx+b 的图象经过点 A(2,1)
2018-2019 学年上海 市杨浦区八年级(下)
期中数学试卷
2018-2019 学年上海市杨浦区八年级(下)期中数学试卷
副标题
题号 得分
一
二
三
四
总分
一、选择题(本大题共 4 小题,共 12.0 分)
1. 下列方程组中,属于二元二次方程组的是( )
A.
B.
C.
D.
2. 有实数根的方程是( )
A.
B.
C.
D.
3. 若一个多边形的边数增加 1,它的内角和( )
A. 不变
B. 增加 1°
C. 增加 180° D. 增加 360°
4. 一次函数 y=kx-k,若 y 随着 x 的增大而减小,则该函数的图象经过
()
A. 一、二、三 B. 一、二、四 C. 二、三、四 D. 一、三、四
二、填空题(本大题共 15 小题,共 30.0 分)
杨浦区2013学年第二学期初二数学期终考试试卷最后两题
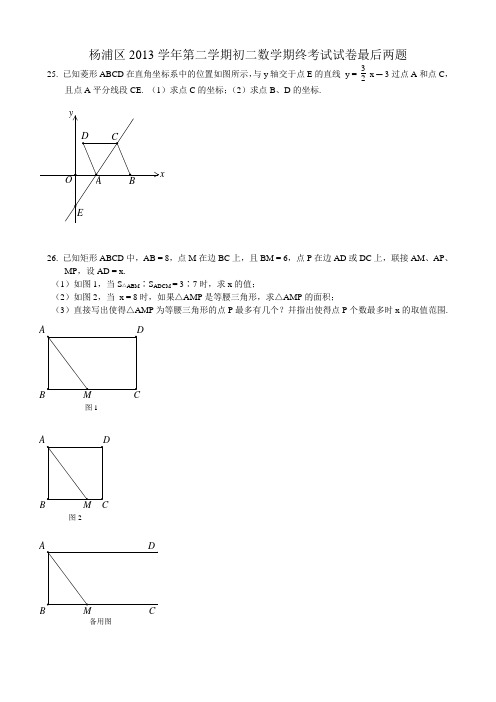
杨浦区2013学年第二学期初二数学期终考试试卷最后两题25. 已知菱形ABCD 在直角坐标系中的位置如图所示,与y 轴交于点E 的直线 y = 32x ─ 3过点A 和点C ,且点A 平分线段CE. (1)求点C 的坐标;(2)求点B 、D 的坐标.26. 已知矩形ABCD 中,AB = 8,点M 在边BC上,且BM = 6,点P 在边AD 或DC 上,联接AM 、AP 、 MP ,设AD = x.(1)如图1,当S △ABM ∶S ADCM = 3∶7时,求x 的值;(2)如图2,当 x = 8时,如果△AMP 是等腰三角形,求△AMP 的面积;(3)直接写出使得△AMP 为等腰三角形的点P 最多有几个?幷指出使得点P 个数最多时x 的取值范围.图1 图2 备用图初二:±⊥─∠°·∥2∣∣×÷.∵∴∶·•≌ a ≠0 <>≤≥△π 2 2 5 3 6 ①②③④⑤⑥⑦⑧⑨⑩αβγθ>22332553343415″′λ6(-8)218612 ─ 112 ─31a 2+1b 2(─8)23─3 18186mna3a 327 x1 , x 2 (1)23213─234314343554152535456516″′ y = k x ( k≠0 ) y =kx( k≠0 )x 41x ab m n→f ( x )△a b m n→f ( x )△一、选择题(本大题共4小题,每题3分,满分12分)二、简答题(本大题共4小题,每题6分,满分24分)三、解答题(本大题共3小题,每题8分,满分24分)四、综合题(本题满分12分)AD。
2020-2021学年上海市杨浦区初二数学第二学期期中数学试卷及解析

2020-2021学年上海市杨浦区初二数学第二学期期中数学试卷一、填空题(每题2分,共30分)1.(2分)一次函数23y x =--的截距是 . 2.(2分)已知一次函数(1)2y m x m =-+-,当m 时,y 随x 的增大而增大.3.(2分)将一次函数23y x =-的图象向上平移 个单位后,图象过原点.4.(2分)当m 取 时,关于x 的方程2mx m x +=无解.5.(2分)已知一次函数32y x k =+-的图象不经过第二象限,则k 的取值范围是 .6.(2分)已知一次函数(0)y kx b k =+≠的图象如图所示,那么关于x 的不等式0kx b +>的解集是 .7.(2分)分式方程2101x x -=-的解是 . 8.(2分)二项方程41802x -=的实数根是 . 9.(2分)如果关于x 的方程220x k -=无实数解,那么k 的取值范围是 .10.(2分)无理方程(4)30x x ++=的解是 .11.(2分)用换元法解分式方程221231x x x x -+=-,若设21x y x-=,则原方程可以化成关于y 的整式方程是 .12.(2分)某服装厂准备加工400套运动装,在加工完160套后,采用了新技术,使得工作效率比原计划提高了20%,结果共用了18天完成任务,问计划每天加工服装多少套?在这个问题中,设计划每天加工x 套,则根据题意可得方程为 .13.(2分)如果一个正多边形的每个外角都是30︒,那么这个多边形的内角和为 .14.(2分)在平行四边形ABCD 中,AE 平分BAD ∠交直线BC 于点E ,:2:1BE EC =,且6AB =,那么这个四边形的周长是 .15.(2分)在ABCD 中,5AB =,7BC =,对角线AC 和BD 相交于点O ,如果将点A 绕着点O 顺时针旋转90︒后,点A 恰好落在平行四边形ABCD 的边AD 上,那么AC 的长是 .二、选择题(每题3分,共12分)16.(3分)以下函数中,属于一次函数的是( )A .2x y =-B .(y kx b k =+、b 为常数)C .(y c c =为常数)D .2y x = 17.(3分)下列方程中,在实数范围内有解的是( ) A .210x x -+= B .2120x -+= C .1455x x x -=-- D .220x x -+-=18.(3分)已知一次函数y kx k =-,若函数值y 随着自变量x 值的增大而增大,则该函数的图象经过( )A .第一、二、三象限B .第一、二、四象限C .第二、三、四象限D .第一、三、四象限 19.(3分)如图,已知直线:2MN y kx =+交x 轴负半轴于点A ,交y 轴于点B ,30BAO ∠=︒,点C 是x 轴上的一点,且2OC =,则MBC ∠的度数为( )A .75︒B .165︒C .75︒或45︒D .75︒或165︒三、简答题(每题6分,共30分)20.(6分)解方程:2231211x x x x-=--- 21.(63631x x ++.22.(6分)解方程组:2269423x xy y x y ⎧-+=⎨-=⎩①② 23.(6分)某地区为了进一步缓解交通拥堵问题,决定修建一条长8千米的公路.如果平均每天的修建费y (万元)与修建天数x (天)之间在50100x 时具有一次函数关系,如表所示:x (天) 6080 100 y (万元)45 40 35 (1)直接写出y 关于x 的函数解析式是 ;(2)后来在修建的过程中计划发生改变,政府决定多修3千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了21天,求原计划每天的修建费?24.(6分)如图,平行四边形ABCD中,2AD AB=,E为AD的中点,CE的延长线交BA的延长线于点F.(1)求证:FB AD=.(2)若70DAF∠=︒,求EBC∠的度数.四、解答题(每题8分,满分16分)25.(8分)现有一段20千米长,可供长跑爱好者跑步的笔直跑道MN,已知甲、乙两人都从M点出发,甲跑到途中的P点后原地休息了20分钟,之后继续跑到N点,共用时间2小时;乙虽然比甲晚出发半小时,但和甲同时到达N点.假设两人跑步时均为匀速,在甲出发后的2小时内两人离开M点的距离y(千米)与时间x(小时)的函数关系如图所示.请回答下列问题:(1)图中B点的坐标为(2)甲从点P跑到点N的速度为千米/时;(3)求图中线段CD的表达式.并写出定义域.26.(8分)如图,在平面直角坐标系中,直线2y x=与反比例函数kyx=在第一象限内的图象交于点(,2)A m,将直线2y x=向下平移后与反比例函数kyx=在第一象限内的图象交于点P,且POA∆的面积为2.(1)求k的值.(2)求平移后的直线的函数解析式.五、综合题(满分12分)27.(12分)如图,已知一次函数7y x=-+与正比例函数43y x=的图象交于点A,且与x轴交于点B.(1)求点A和点B的坐标;(2)过点A作AC y⊥轴于点C,过点B作直线//l y轴,动点P从点O出发,以每秒1个单位长的速度,沿O C A--的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒(0)t>.①当t为何值时,以A、P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是AP AQ=的等腰三角形?若存在,求t的值;若不存在,请说明理由.参考答案与试题解析一、填空题(每题2分,共30分)1.【解答】解:在一次函数23y x =--中, 3b =-,∴一次函数23y x =--在y 轴上的截距3b =-. 故答案是:3-.2.【解答】解:当10m ->时,y 随x 的增大而增大, 所以1m <.故答案为:1<.3.【解答】解:因为一次函数23y x =-的图象向上平移3个单位后2332y x x =-+=,图象过原点, 故答案为:3.4.【解答】解:移项得:2mx x m -=-,合并同类项得:(2)m x m -=-.关于x 的方程2mx m x +=无解,20m ∴-=.解得:2m =.故答案为:2.5.【解答】解:一次函数32y x k =+-的图象不经过第二象限, 则可能是经过一三象限或一三四象限,经过一三象限时,320k -=,解得23k =, 经过一三四象限时,320k -<.解得23k <故23k . 故答案为23k. 6.【解答】解:当不等式0kx b +>时,一次函数y kx b =+的图象在x 轴上方,故2x >. 故答案为:2x >.7.【解答】解:2101x x -=- 方程两边同乘以1x -得,210x -=则(1)(1)0x x +-=10x ∴+=或10x -=得,1x =-或1x =.检验:1x =-时,10x -≠;1x =时,10x -=,故1x =舍去. 故分式方程的根为:1x =-.故答案为:1x =-.8.【解答】解:41802x -=. ∴221()82x =. 24x ∴=(负值舍去). 2x ∴=±.故答案为:2x =±.9.【解答】解:20x k --=,即2k +无实根, 20k ∴+<,2k ∴<-.故答案为:2k <-.10.【解答】解:(4)0x +40x ∴+=或30x +=,解得4x =-,3x =-,当4x =-时,被开方数无意义;故方程的解为3x =-,故答案为:3x =-.11.【解答】解:21x y x -=, ∴2221x x y =-, 代入原方程得:23y y+=, 方程两边同乘以y 整理得:2320y y -+=. 故答案为:2320y y -+=.12.【解答】解:采用新技术前所用时间为:160x,采用新技术后所用时间为:400160(120%)x-+,∴所列方程为:16040016018(120%)x x-+=+.13.【解答】解:一个多边形的每个外角都是30︒,3603012n∴=︒÷︒=,则内角和为:(122)1801800-︒=︒.故答案为:1800︒.14.【解答】解:四边形ABCD是平行四边形,//AD BC∴,AEB DAE∴∠=∠,AE平分BAD∠,BAE DE∴∠=∠,BAE AEB∴∠=∠,6BE AB∴==,如图1,:2:1BE EC=,3EC∴=,9AD BC∴==,6AB CD==,∴这个四边形的周长是:969630+++=;如图2,:2:1BE EC=,3EC∴=,3AD BC∴==,6AB CD==,∴这个四边形的周长是:363618+++=;∴这个四边形的周长是:30或18.故答案为:30或18.15.【解答】解:如图,过O点作OE AD⊥于E,过C点作CF AD⊥于F,将点A绕着点O顺时针旋转90︒后,点A恰好落在平行四边形ABCD的边AD上,AOA∴∆'是等腰直角三角形,∴△AAC '是等腰直角三角形,设AA x '=,则CF x =,7DF x =-,在Rt CDF ∆中,222(7)5x x +-=,解得14x =,23x =,在Rt CFA ∆中,42AC =或32.故答案为:42或32.二、选择题(每题3分,共12分)16.【解答】解:A 、是一次函数,故A 正确; B 、0k =时,不是一次函数,故B 错误; C 、不含一次项,不是一次函数,故C 错误; D 、未知数x 的次数为1-,不是一次函数,故D 错误. 故选:A .17.【解答】解:A 、1a =,1b =-,1c =,△241430b ac =-=-=-<,方程无实数根,故A 不符合题意;B 、非负数与正数的和是正数,得2122x -,故B 错误;C 、方程两边都乘以(5)x -,得 41x -=,解得5x =,经检验:5x =不是分式方程的根,原分式方程的解,故C 不符合题意; D 220x x --=,得20x -且20x -,解得2x =,故D 符合题意,故选:D .18.【解答】解:一次函数y kx k =-,若函数值y 随着自变量x 值的增大而增大,k∴>,k∴-<,∴此函数的图象经过一、三、四象限.故选:D.19.【解答】解:由已知可得120MBO∠=︒.如图,分两种情况考虑:①当点C在x轴正半轴上时,145C BO∠=︒,11204575MBC∠=︒-︒=︒;②当点C在x轴负半轴上时,212045165MBC∠=︒+︒=︒.故选:D.三、简答题(每题6分,共30分)20.【解答】解:方程两边都乘以(1)(1)x x+-得:232(1)(1)(1)x x x x x-=+-++,23210x x--=,解得:11 3x=-,21x=,经检验:11 3x=-是原方程的解,21x=不是原方程的解,所以原方程的解为13x=-.21.【解答】解:36030xx+⎧⎨+⎩.2x∴-.3631x x++3631x x++.将方程两边平方可得:363123x x x+=++++31x x+=+.再两边平方可得:2321x x x +=++. 整理得:220x x +-=.解得:2x =-或1x =.经检验:当2x =-,左边为1-,右边为1,则左边≠右边, 2x ∴=-不是无理方程的解,当1x =时,左边=右边1=,1x ∴=是无理方程的解.22.【解答】解:由①,得2(3)4x y -=, 32x y ∴-=±,∴原方程组可转化为:3223x y x y -=⎧⎨-=⎩或3223x y x y -=-⎧⎨-=⎩解得1151x y =⎧⎨=⎩或22135x y =⎧⎨=⎩ 所以原方程组的解为:1151x y =⎧⎨=⎩或22135x y =⎧⎨=⎩ 23.【解答】解:(1)设y 关于x 的函数解析式为(0)y kx b k =+≠, 图象过点(60,45),(80,40),∴60458040k b k b +=⎧⎨+=⎩, 解得1460k b ⎧=-⎪⎨⎪=⎩,y ∴关于x 的函数解析式为1604y x =-+. 故答案为:1604y x =-+; (2)设原计划修完这条路需要m 天, 根据题意得81121m m =+, 解得56m =,经检验56m =是原方程的根,50100m ,15660464y ∴=-⨯+=(万元), 答:原计划每天的修建费是46万元.24.【解答】(1)证明E 为AD 的中点,DE AE ∴=,四边形ABCD 是平行四边形,//AB CD ∴,AB DC =,EDC EAF ∴∠=∠,在DEC ∆和AEF ∆中,DEC AEF DE AE EDC EAF ∠=∠⎧⎪=⎨⎪∠=∠⎩,()DEC AEF ASA ∴∆≅∆,DC FA ∴=,2AD AB =,AB DE EA FA ∴===,FB AD ∴=;(2)解:四边形ABCD 是平行四边形,//DA CB ∴,70CBF DAF ∴∠=∠=︒,AEB EBC ∠=∠,又AE AB =,AEB ABE ∴∠=∠,35EBC ABE ∴∠=∠=︒.四、解答题(每题8分,满分16分)25.【解答】解:(1)由题意可得,点B 的横坐标为:2041603+=,纵坐标为:15, ∴点B 的坐标为4(3,15), 故答案为:4(3,15); (2)甲从点P 跑到点N 的速度为:20157.5423-=-千米/时, 故答案为:7.5;(3)由题意可得,点D 的坐标为(0.5,0),点C 的坐标为(2,20), 设线段CD 的函数函数表达式为y kx b =+,0.50220k b k b +=⎧⎨+=⎩,得403203k b ⎧=⎪⎪⎨⎪=-⎪⎩, 即线段CD 的表达式是4020(0.52)33y x x =-. 26.【解答】解:(1)点(,2)A m 在直线2y x =, 22m ∴=,1m ∴=,∴点(1,2)A ,点(1,2)A 在反比例函数k y x=上, 2k ∴=, (2)方法一、如图,设平移后的直线与y 轴相交于B ,过点P 作PM OA ⊥,BN OA ⊥,AC y ⊥轴 由(1)知,(1,2)A ,5OA ∴5sin sin AC BON AOC OA ∠=∠= 115222POA S OA PM PM ∆=⨯==, 45PM ∴= PM OA ⊥,BN OA ⊥,//PM BN ∴,//PB OA ,∴四边形BPMN 是平行四边形,45BN PM ∴==5sin BN BON OB OB ∠==, 4OB ∴=,//PB AO ,(0,4)B ∴-,∴平移后的直线PB 的函数解析式24y x =-, 方法二、如图1,过点P 作PC y ⊥轴交OA 于C ,设点P 的坐标为(n ,2)(1)n n>, 1(C n ∴,2)n, 1PC n n∴=-, POA ∆的面积为2.(1,2)APOA PCO PCA S S S ∆∆∆∴=+112112()()(2)22n n n n n n=-⨯+-- 11()22n n=-⨯ 1n n=- 2=,1n ∴=)或1n =+(1P ∴+2),//PB AO ∴,∴设直线PB 的解析式为2y x b =+,点P 在直线PB 上,22(1b ∴=++,4b ∴=-,∴平移后的直线PB 的函数解析式24y x =-,方法三,过点A 作AM x ⊥轴于M ,过点P 作PN x ⊥轴于N , 点A ,P 是反比例函数2y x=图象上, AOM PON S S ∆∆∴=, 2AOP AMNP S S ∆∴==梯形,(1,2)A ,2AM ∴=,1OM =, 设点2(,)P m m,(1)m > ON m ∴=,2PN m=, 1MN m ∴=-,()()11221222AMNP S PN AM MN m m ⎛⎫∴=+⨯=+⨯-= ⎪⎝⎭梯形, 12m ∴=(舍)或12m =,(12P ∴+222),//PB AO ∴,∴设直线PB 的解析式为2y x b =+,点P 在直线PB 上,2222(12)b ∴=++,4b ∴=-,∴平移后的直线PB 的函数解析式24y x =-,五、综合题(满分12分)27.【解答】解:(1)已知一次函数7y x =-+与正比例函数43y x =的图象交于点A ,且与x 轴交于点B ,(7,0)B ∴,(3,4)A , (2)①当04t <<时,PO t =,4PC t =-,BR T =,7OR t =-, 过A 作AM x ⊥轴于点M ,以A 、P 、R 为顶点的三角形的面积为8,8ACP POR ARB ACOB S S S S ∆∆∆∴---=梯形, ∴1111(37)43(4)(7)482222t t t t +⨯-⨯⨯--⨯⨯--⨯=, 28120t t ∴-+=,解得12t =,26t =(舍),当47t 时,12(7)82S APR AP OC t ∴∆=⨯⨯=-=, 3t ∴=(舍),∴当2t =时,以A 、P 、R 为顶点的三角形的面积为8. ②存在,当04t <时,直线l 与AB 相交于Q ,直线AB 与y 轴交于点N , NO OB =,45OBN ONB ∴∠=∠=︒,直线//l y 轴,RQ RB t ∴==,4AM BM ==,2QB t ∴=,422AQ t =,RB OP QR t ===,//PQ OR ∴,7PQ OR t ==-,AP AQ =,723t ∴-=⨯,1t ∴=,当47t 时,若AP AQ =, 575(7)3t t ∴-=--, 418t ∴=. 1t ∴=或418t =,以A 、P 、Q 为顶点的三角形是AP AQ =的等腰三角形.。
上海杨浦区复旦大学第二附属学校2020-2021学年八年级下学期期中考试数学试题(解析版)

多边形的内角和是: .
故选:B.
【点睛】本题考查了多边形的内角和与外角和公式,熟练掌握公式是解题的关键.
4.下列关于x的方程一定有实数解的是( )
A. B.
C. D.
【4题答案】
【答案】A
【解析】
【分析】根据一元二次方程根的判别式、二次根式有意义的条件、分式方程的增根逐一判断即可得.
2.下列说法正确的是().
A. 是分式方程B. 是无理方程
C. 是二元二次方程组D. 是二项方程
【2题答案】
【答案】C
【解析】
【分析】根据分式方程、无理方程、二元二次方程组、二项方程的定义,即可一一判定.
【详解】解:A选项: 是一元一次方程,故错误;
B选项: 是分式方程,故错误;
C选项: 是二元二次方程组,故正确;
2020~2021学年上海杨浦区复旦大学第二附属学校
一、选择题
1.下列函数中, 是 的一次函数的有().
① ;② ;③ ;④ ;⑤ .
A.1个B.2个C.3个D.4个
【1题答案】
【答案】B
【解析】
【分析】根据一次函数 定义逐一判断即可求解.
【详解】解:① 的次数是1, 是 的一次函数,所以本选项符合题意,故①正确;
【10题答案】
【答案】
【解析】
【分析】根据一元二次方程的解法即可求出答案.
【详解】解:∵
∴ 或 (舍去)
∴
故答案为: .
【点睛】本题考查高次方程的解法,解题的关键是熟练运用一元二次方程的解法,本题属于基础题型.
11.如果 是方程 的一个解,那么 ______.
【11题答案】
【答案】
2020-2021下海杨浦初级中学八年级数学下期中模拟试卷(含答案)
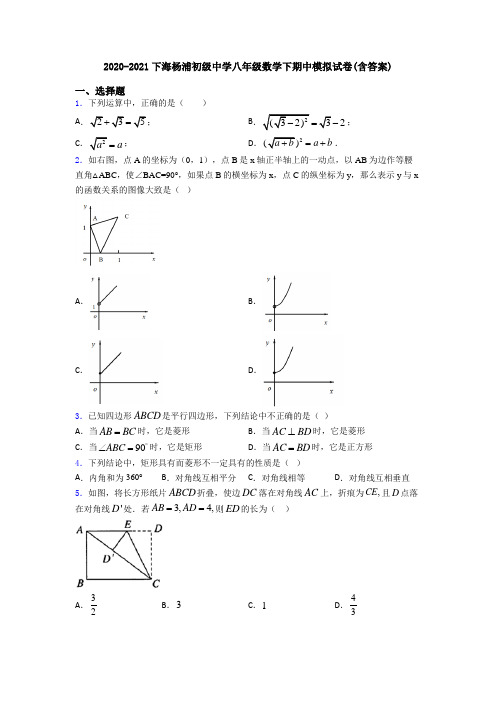
2020-2021下海杨浦初级中学八年级数学下期中模拟试卷(含答案)一、选择题1.下列运算中,正确的是( )A .235+=;B .2(32)32-=-;C .2a a =;D .2()a b a b +=+.2.如右图,点A 的坐标为(0,1),点B 是x 轴正半轴上的一动点,以AB 为边作等腰直角△ABC ,使∠BAC=90°,如果点B 的横坐标为x ,点C 的纵坐标为y ,那么表示y 与x 的函数关系的图像大致是( )A .B .C .D .3.已知四边形ABCD 是平行四边形,下列结论中不正确的是( )A .当AB BC =时,它是菱形B .当AC BD ⊥时,它是菱形 C .当90ABC ︒∠=时,它是矩形D .当AC BD =时,它是正方形 4.下列结论中,矩形具有而菱形不一定具有的性质是( )A .内角和为360°B .对角线互相平分C .对角线相等D .对角线互相垂直 5.如图,将长方形纸片ABCD 折叠,使边DC 落在对角线AC 上,折痕为,CE 且D 点落在对角线'D 处.若3,4,AB AD ==则ED 的长为( )A .32B .3C .1D .436.函数y =11x x +-中,自变量x 的取值范围是( ) A .x >-1B .x >-1且x ≠1C .x ≥一1D .x ≥-1且x ≠1 7.若一次函数y =(k -3)x -k 的图象经过第二、三、四象限,则k 的取值范围是( )A .k <3B .k <0C .k >3D .0<k <3 8.如图,函数y=2x 和y=ax+4的图象相交于A(m ,3),则不等式2x ax+4<的解集为( )A .3x 2>B .x 3>C .3x 2<D .x 3<9.如图,矩形纸片ABCD ,3AB =,点E 在BC 上,且AE EC =.若将纸片沿AE 折叠,点B 恰好落在AC 上,则矩形ABCD 的面积是( )A .12B .63C .93D .1510.《九章算术》勾股章有一问题,其意思是:现有一竖立着的木柱,在木柱上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵着绳索退行,在离木柱根部8尺处时绳索用尽,请问绳索有多长?若设绳索长度为x 尺,根据题意,可列方程为 ( )A .82﹢x 2 = (x ﹣3)2B .82﹢(x +3)2= x 2C .82﹢(x ﹣3)2= x 2D .x 2﹢(x ﹣3)2= 8211.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y (米)与甲出发的时间t (分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了32分钟;③乙用16分钟追上甲;④乙到达终点时,甲离终点还有300米其中正确的结论有( )A .1个B .2个C .3个D .4个12.如图,点E F G H 、、、分别是四边形ABCD 边AB 、BC 、CD 、DA 的中点.则下列说法:①若AC BD =,则四边形EFGH 为矩形;②若AC BD ⊥,则四边形EFGH 为菱形;③若四边形EFGH 是平行四边形,则AC 与BD 互相平分;④若四边形EFGH 是正方形,则AC 与BD 互相垂直且相等.其中正确的个数是( )A .1B .2C .3D .4二、填空题13.若由你选择一个喜欢的数值m ,使一次函数()2y m x m =-+的图象经过第一、二、四象限,则m 的值可以是___________.14.如图所示的网格是正方形网格,则BAC DAE ∠-∠=__________︒(点A ,B ,C ,D ,E 是网格线交点).15.如图,在矩形ABCD 中,AD=9cm ,AB=3cm ,将其折叠,使点D 与点B 重合,则重叠部分(△BEF)的面积为_________cm 2.16.将函数31y x =+的图象平移,使它经过点()1,1,则平移后的函数表达式是____.17.甲、乙两人分别从A ,B 两地相向而行,匀速行进甲先出发且先到达B 地,他们之间的距离s(km)与甲出发的时间t(h)的关系如图所示,则乙由B 地到A 地用了______h .18.化简()213-=_____________;19.如图,ABC V 是以AB 为斜边的直角三角形,4AC =,3BC =,P 为AB 上一动点,且PE AC ⊥于E ,PF BC ⊥于F ,则线段EF 长度的最小值是________.20.如图,已知函数y ax b =+和y kx =的图象交于点P, 则根据图象可得,关于y ax b y kx =+⎧⎨=⎩的二元一次方程组的解是_____________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
杨浦区第二学期八年级期中考试数学试卷
Document number:WTWYT-WYWY-BTGTT-YTTYU-2018GT
O A D B 杨浦区2011学年度第二学期初二数学期中考试卷
(考试时间:90分钟 满分100分) 2012、4
一、填空题:(本大题共12题,每题2分, 满分24分)
1.若函数(1)1y k x =-+是一次函数,则k 的取值范围为 .
2.已知一次函数b kx y +=的图像经过点)2,0(-A ,并与直线x y 4-=平行,那么这个
一次函数解析式是 _.
这个
3.如果一次函数1-=kx y 中y 随x 的增大而减小,那么
一次函数一定不经过第___ 象限.
4.在图中,将直线OA 向上平移3个单位,所得直线的函数解析式为 .
5.方程x x =-12的解是 _ _. 6.方程组⎩⎨⎧-==+3
2xy y x 的解为 . 7.十二边形的内角和为_______度. 8.用换元法解方程2
1333322=-+-x x x x .如果设x x y 32-=,则原方程可化为y 的整式方程是 .
9.已知一个多边形的每个外角都为︒72,那么这个多边形是 边形.
10.如图,□ABCD 的周长是28cm ,AC 和BD 交于O ,△OAB 的周长比△OBC 的
周长小2cm ,则AB = ,BC = .
11.解方程组⎪⎩⎪⎨⎧=+-=+0
65202222y xy x y x 时,可先化为 和 两个方程组. 12.如果直线k x y +-=2与两坐标轴所围成的三角形面积是9,则k 的值为 .
二、选择题(本大题共6题,每题2分, 满分12分)
第4题图 第10题图
13.已知函数3-=x y ,若当a x =时,5=y ;当b x =时,3=y ,a 和b 的大小关系
是……………………………………………………………………………… ( )
(A )a>b ; (B )a=b ; (C )a<b ; (D )不能确定.
14.下列方程中,是二项方程的为………………………………………………( )
(A )122=+x x ; (B )02=+x x ; (C )083=-x ; (D )0=x .
15.下列方程中, 有实数解的是…………………………………………………( )
(A )016=+x ; (B )2
22-=-x x x ; (C )032=+-x ; (D )x x =-2. 16. 某灾区恢复生产,计划在一定时间内种60亩蔬菜,实际播种时每天比原
计划多种3亩,因此提前一天完成任务,问实际种了几天现设实际种了x 天,则可列方程…………………………………………………………………………………( )
(A )316060=+-x x ; (B )360160=--x x ; (C )13
6060=+-x x ; (D )160360=--x
x . 17.已知平行四边形的一条边长为14,下列各组数中,能分别作它的两条对角线长的
是…………………………………………………………………………………( )
(A )10与16; (B )12与16; (C )20与22; (D )10与18.
18.一个面积为2的平行四边形被直线分成面积为x ,y 的两部分,则y 与x 之间的函
数关系只可能是………………………………………………………………( )
三、简答题(本大题共5题,每题6分, 满分30分)
19.解关于x 的方程: 4)2(=+x b . 20.解方程:
3x =.
解: 解:
21.解方程组: 517,
311.x y x y x y x y ⎧+=⎪+-⎪⎨⎪-=⎪+-⎩①
②22.解方程组: ⎪⎩⎪⎨⎧=+-=-92 042222y xy x y x
解: 解:
23.已知:如图,O 为平行四边形ABCD 的对角线AC 的中点,过点O 作一条直线分
别与AB 、CD 交于点M 、N ,点E 、F 在直线MN
上,且OE
=OF .
求证:∠MAE =∠NCF .
四、解答题(本大题共3题,每题8分, 满分24分)
24.如图,已知A (4,a ),B (-2,-4)是一次函数y =kx +b 的图象和反比例函数y
=x m 的图象的交点. (1)求反比例函数和一次函数的解祈式;
(2)求△A0B 的面积.
解:
25.某区需修建一条2400米长的封闭式污水处理管道.为了尽量减少施工对市民生
活等的影响,实际施工比原计划每天多修10米,结果提前20天完成了任务.试问实际每天修多少米
解:
26.如图,已知:在平行四边形ABCD 中,∠C =60°,E 、F 分别是AB 、CD 的中
点,且AB =2AD .
求证:DE ∶BD =3∶3.
五、(本大题满分10分,第(1)小题2分,第(2)
①②小题各4分)
27.如图已知一次函数y =-x +7与正比例函数y =
x 3
4的图象交于点A ,且与x 轴交于点B .
(1)求点A和点B的坐标;
(2)过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O﹣C﹣A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒)0
t.
(
①当t为何值时,以A、P、R为顶点的三角形的面积为8
②是否存在以A、P、Q为顶点的三角形是QA=QP的等腰三角形若存在,求t的
值;若不存在,请说明理由.
解:。
