湖北省七市(州)2014届高三联合考试 数学文试题B卷 Word版含答案
2014年湖北省高考数学文科试卷(含解析)

2014年湖北省高考数学文科试卷(含解析)绝密★启用前2014年湖北省高考数学文科试卷(含解析)本试题卷共5页,22题。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1.答卷前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用统一提供的2B铅笔将答题卡上试卷类型A后的方框涂黑。
2.选择题的作答:每小题选出答案后,用统一提供的2B铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.填空题和解答题的作答:用统一提供的签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.2014•湖北卷]已知全集U={1,2,3,4,5,6,7},集合A={1,3,5,6},则∁UA=()A.{1,3,5,6}B.{2,3,7}C.{2,4,7}D.{2,5,7}1.C解析]由A={1,3,5,6},U={1,2,3,4,5,6,7},得∁UA={2,4,7}.故选C.2.2014•湖北卷]i为虚数单位,1-i1+i2=()A.1B.-1C.iD.-i2.B解析]1-i1+i2=(1-i)2(1+i)2=-2i2i=-1.故选B. 3.2014•湖北卷]命题“∀x∈R,x2≠x”的否定是()A.∀x∈/R,x2≠xB.∀x∈R,x2=xC.∃x0∈/R,x20≠x0D.∃x0∈R,x20=x03.D解析]特称命题的否定方法是先改变量词,然后否定结论,故命题“∀x∈R,x2≠x”的否定是“∃x0∈R,x20=x0”.故选D.4.2014•湖北卷]若变量x,y满足约束条件x+y≤4,x-y≤2,x≥0,y≥0,则2x+y的最大值是()A.2B.4C.7D.84.C解析]作出约束条件x+y≤4,x-y≤2,x≥0,y≥0表示的可行域如下图阴影部分所示.设z=2x+y,平移直线2x+y=0,易知在直线x+y=4与直线x-y=2的交点A(3,1)处,z=2x+y取得最大值7.故选C.5.2014•湖北卷]随机掷两枚质地均匀的骰子,它们向上的点数之和不超过5的概率记为p1,点数之和大于5的概率记为p2,点数之和为偶数的概率记为p3,则()A.p1<p2<p3B.p2<p1<p3C.p1<p3<p2D.p3<p1<p25.C解析]掷出两枚骰子,它们向上的点数的所有可能情况如下表:123456123456723456783456789456789105678910116789101112则p1=1036,p2=2636,p3=1836.故p16.2014•湖北卷]根据如下样本数据x345678y4.02.5-0.50.5-2.0-3.0得到的回归方程为y^=bx+a,则()A.a>0,b<0B.a>0,b>0C.a<0,b<0D.a<0,b>06.A解析]作出散点图如下:由图像不难得出,回归直线y^=bx+a的斜率b0,所以a>0,b图1-1 7.2014•湖北卷]在如图1-1所示的空间直角坐标系O-xyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2).给出编号为①、②、③、④的四个图,则该四面体的正视图和俯视图分别为()图1-2A.①和②B.③和①C.④和③D.④和②7.D解析]由三视图可知,该几何体的正视图显然是一个直角三角形(三个顶点坐标分别是(0,0,2),(0,2,0),(0,2,2))且内有一虚线(一锐角顶点与一直角边中点的连线),故正视图是④;俯视图是一个斜三角形,三个顶点坐标分别是(0,0,0),(2,2,0),(1,2,0),故俯视图是②.故选D.8.、2014•湖北卷]设a,b是关于t的方程t2cosθ+tsinθ=0的两个不等实根,则过A(a,a2),B(b,b2)两点的直线与双曲线x2cos2θ-y2sin2θ=1的公共点的个数为()A.0B.1C.2D.38.A解析]由方程t2cosθ+tsinθ=0,解得t1=0,t2=-tanθ,不妨设点A(0,0),B(-tanθ,tan2θ),则过这两点的直线方程为y=-xtanθ,该直线恰是双曲线x2cos2θ-y2sin2θ=1的一条渐近线,所以该直线与双曲线无公共点.故选A.9.、2014•湖北卷]已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-3x,则函数g(x)=f(x)-x+3的零点的集合为()A.{1,3}B.{-3,-1,1,3}C.{2-7,1,3}D.{-2-7,1,3}9.D解析]设x0,所以f(x)=-f(-x)=-(-x)2-3(-x)]=-x2-3x.求函数g(x)=f(x)-x+3的零点等价于求方程f(x)=-3+x的解.当x≥0时,x2-3x=-3+x,解得x1=3,x2=1;当x10.2014•湖北卷]《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术“置如其周,令相乘也.又以高乘之,三十六成一.”该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式V≈136L2h.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V≈275L2h相当于将圆锥体积公式中的π近似取为()A.227B.258C.15750D.35511310.B解析]设圆锥的底面圆半径为r,底面积为S,则L=2πr.由题意得136L2h≈13Sh,代入S=πr2化简得π≈3.类比推理,若V≈275L2h时,π≈258.故选B.11.2014•湖北卷]甲、乙两套设备生产的同类型产品共4800件,采用分层抽样的方法从中抽取一个容量为80的样本进行质量检测.若样本中有50件产品由甲设备生产,则乙设备生产的产品总数为________件.11.1800解析]设乙设备生产的产品总数为n,则80-50n=804800,解得n=1800.12.、2014•湖北卷]若向量OA→=(1,-3),|OA→|=|OB→|,OA→•OB→=0,则|AB→|=________.12.25解析]由题意知,OB→=(3,1)或OB=(-3,-1),所以AB=OB-OA=(2,4)或AB=(-4,2),所以|AB|=22+42=25. 13.2014•湖北卷]在△ABC中,角A,B,C所对的边分别为a,b,c.已知A=π6,a=1,b=3,则B=________.13.π3或2π3解析]由正弦定理得asinA=bsinB,即1sinπ6=3sinB,解得sinB=32.又因为b>a,所以B=π3或2π3.14.2014•湖北卷]阅读如图1-3所示的程序框图,运行相应的程序,若输入n的值为9,则输出S的值为________.图1-314.1067解析]第一次运行时,S=0+21+1,k=1+1;第二次运行时,S=(21+1)+(22+2),k=2+1;……所以框图运算的是S=(21+1)+(22+2)+…+(29+9)=1067. 15.2014•湖北卷]如图1-4所示,函数y=f(x)的图像由两条射线和三条线段组成.若∀x∈R,f(x)>f(x-1),则正实数a的取值范围为________.图1-415.0,16解析]“∀x∈R,f(x)>f(x-1)”等价于“函数y=f(x)的图像恒在函数y=f(x-1)的图像的上方”,函数y=f(x-1)的图像是由函数y=f(x)的图像向右平移一个单位得到的,如图所示.因为a>0,由图知6a16.2014•湖北卷]某项研究表明:在考虑行车安全的情况下,某路段车流量F(单位时间内经过测量点的车辆数,单位:辆/小时)与车流速度v(假设车辆以相同速度v行驶,单位:米/秒)、平均车长l(单位:米)的值有关,其公式为F=76000vv2+18v+20l.(1)如果不限定车型,l=6.05,则最大车流量为________辆/小时;(2)如果限定车型,l=5,则最大车流量比(1)中的最大车流量增加________辆/小时.16.(1)1900(2)100解析](1)依题意知,l>0,v>0,所以当l=6.05时,F=76000vv2+18v+121=76000v+121v+18≤760002v•121v+18=1900,当且仅当v=11时,取等号.(2)当l=5时,F=76000vv2+18v+100=76000v+100v+18≤2000,当且仅当v=10时,取等号,此时比(1)中的最大车流量增加100辆/小时.17.2014•湖北卷]已知圆O:x2+y2=1和点A(-2,0),若定点B(b,0)(b≠-2)和常数λ满足:对圆O上任意一点M,都有|MB|=λ|MA|,则(1)b=________;(2)λ=________.17.(1)-12(2)12解析]设点M(cosθ,sinθ),则由|MB|=λ|MA|得(cosθ-b)2+sin2θ=λ2(cosθ+2)2+sin2θ,即-2bcosθ+b2+1=4λ2cosθ+5λ2对任意的θ都成立,所以-2b=4λ2,b2+1=5λ2.又由|MB|=λ|MA|,得λ>0,且b≠-2,解得b=-12,λ=12.18.、、、2014•湖北卷]某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系:f(t)=10-3cosπ12t-sinπ12t,t∈0,24).(1)求实验室这一天上午8时的温度;(2)求实验室这一天的最大温差.18.解:(1)f(8)=10-3cosπ12×8-sinπ12×8=10-3cos2π3-sin2π3=10-3×-12-32=10.故实验室上午8时的温度为10℃.(2)因为f(t)=10-232cosπ12t+12sinπ12t=10-2sinπ12t+π3,又0≤t所以π3≤π12t+π3当t=2时,sinπ12t+π3=1;当t=14时,sinπ12t+π3=-1.于是f(t)在0,24)上取得最大值12,最小值8.故实验室这一天最高温度为12℃,最低温度为8℃,最大温差为4℃. 19.、、2014•湖北卷]已知等差数列{an}满足:a1=2,且a1,a2,a5成等比数列.(1)求数列{an}的通项公式.(2)记Sn为数列{an}的前n项和,是否存在正整数n,使得Sn>60n+800?若存在,求n的最小值;若不存在,说明理由.19.解:(1)设数列{an}的公差为d,依题意知,2,2+d,2+4d成等比数列,故有(2+d)2=2(2+4d),化简得d2-4d=0,解得d=0或d=4,当d=0时,an=2;当d=4时,an=2+(n-1)•4=4n-2,从而得数列{an}的通项公式为an=2或an=4n-2.(2)当an=2时,Sn=2n,显然2n此时不存在正整数n,使得Sn>60n +800成立.当an=4n-2时,Sn=n2+(4n-2)]2=2n2.令2n2>60n+800,即n2-30n-400>0,解得n>40或n此时存在正整数n,使得Sn>60n+800成立,n的最小值为41.综上,当an=2时,不存在满足题意的正整数n;当an=4n-2时,存在满足题意的正整数n,其最小值为41.20.、2014•湖北卷]如图1-5,在正方体ABCD-A1B1C1D1中,E,F,P,Q,M,N分别是棱AB,AD,DD1,BB1,A1B1,A1D1的中点.求证:(1)直线BC1∥平面EFPQ;(2)直线AC1⊥平面PQMN.图1-520.证明:(1)连接AD1,由ABCD-A1B1C1D1是正方体,知AD1∥BC1.因为F,P分别是AD,DD1的中点,所以FP∥AD1.从而BC1∥FP.而FP⊂平面EFPQ,且BC1⊄平面EFPQ,故直线BC1∥平面EFPQ.(2)如图,连接AC,BD,A1C1,则AC⊥BD.由CC1⊥平面ABCD,BD⊂平面ABCD,可得CC1⊥BD.又AC∩CC1=C,所以BD⊥平面ACC1A1.而AC1⊂平面ACC1A1,所以BD⊥AC1.因为M,N分别是A1B1,A1D1的中点,所以MN∥BD,从而MN⊥AC1. 同理可证PN⊥AC1.又PN∩MN=N,所以直线AC1⊥平面PQMN.21.2014•湖北卷]π为圆周率,e=2.71828…为自然对数的底数.(1)求函数f(x)=lnxx的单调区间;(2)求e3,3e,eπ,πe,3π,π3这6个数中的最大数与最小数.21.解:(1)函数f(x)的定义域为(0,+∞).因为f(x)=lnxx,所以f′(x)=1-lnxx2.当f′(x)>0,即0当f′(x)e时,函数f(x)单调递减.故函数f(x)的单调递增区间为(0,e),单调递减区间为(e,+∞).(2)因为e即ln3e于是根据函数y=lnx,y=ex,y=πx在定义域上单调递增可得,3e故这6个数中的最大数在π3与3π之中,最小数在3e与e3之中.由e即lnππ由lnπππ3.由ln33综上,6个数中的最大数是3π,最小数是3e.22.2014•湖北卷]在平面直角坐标系xOy中,点M到点F(1,0)的距离比它到y轴的距离多1.记点M的轨迹为C.(1)求轨迹C的方程;(2)设斜率为k的直线l过定点P(-2,1),求直线l与轨迹C恰好有一个公共点、两个公共点、三个公共点时k的相应取值范围.22.解:(1)设点M(x,y),依题意得|MF|=|x|+1,即(x-1)2+y2=|x|+1,化简整理得y2=2(|x|+x).故点M的轨迹C的方程为y2=4x,x≥0,0,x(2)在点M的轨迹C中,记C1:y2=4x(x≥0),C2:y=0(x依题意,可设直线l的方程为y-1=k(x+2).由方程组y-1=k(x+2),y2=4x,可得ky2-4y+4(2k+1)=0.①当k=0时,y=1.把y=1代入轨迹C的方程,得x=14.故此时直线l:y=1与轨迹C恰好有一个公共点14,1.当k≠0时,方程①的判别式Δ=-16(2k2+k-1).②设直线l与x轴的交点为(x0,0),则由y-1=k(x+2),令y=0,得x0=-2k+1k.③(i)若Δ12.即当k∈(-∞,-1)∪12,+∞时,直线l与C1没有公共点,与C2有一个公共点,故此时直线l与轨迹C恰好有一个公共点.(ii)若Δ=0,x00,x0≥0,由②③解得k∈-112或-12≤k即当k∈-1,12时,直线l与C1只有一个公共点,与C2有一个公共点.当k∈-12,0时,直线l与C1有两个公共点,与C2没有公共点.故当k∈-12,0∪-1,12时,直线l与轨迹C恰好有两个公共点.(iii)若Δ>0,x0即当k∈-1,-12∪0,12时,直线l与C1有一个公共点,与C2有一个公共点,故此时直线l与轨迹C恰好有三个公共点.综上所述,当k∈(-∞,-1)∪12,+∞∪{0}时,直线l与轨迹C恰好有一个公共点;当k∈-12,0∪-1,12时,直线l与轨迹C恰好有两个公共点;当k∈-1,-12∪0,12时,直线l与轨迹C恰好有三个公共点.。
湖北省部分重点中学2014届高三第二次联考数学(文)试题 含答案

湖北省部分重点中学2014届高三第二次联考高三数学试卷(文史类)(含答案)考试时间:2014年元月20日下午14:00—16:00 试卷满分:150分一、选择题:(本大题共10小题,每小题5分,共50分;在每小题给出的四个选项中,只有一个选项是符合题目要求的.) 1、已知全集U= {}1,2,3,4,5,集合A= {}3,4,B= {}1,2,3,则()U C A B I 等于( ) A .{}3 B .{}1,3 C .{}1,2 D .{}1,2,3 2、已知a 是实数,iia -+1是纯虚数,则a 等于( )A .1-B .1C .2D .3、已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积是( )A .13cmB .23cmC .33cmD .63cm4、已知{}n a 是各项为正数的等比数列,12341,4,a a a a +=+=则5678a a a a +++=( )A .80B .20C .32D .25535、若a= 3(,sin )2α,b= 1(cos ,)3α,且a // b ,则锐角α=( )A .015B .030C .045D .0606、已知 1.224log log ,0.7x y z π-===,则( )A .x y z <<B .z y x <<C .y z x <<D . y x z << 7、设函数()sin()(0,)2f x x πωϕωϕ=+><的图象关于直线23x π=对称,且它的最小正周期为π,则 ( )A. ()f x 在区间53,124ππ⎡⎤⎢⎥⎣⎦上是减函数 B. ()f x 的图象经过点0,2⎛ ⎝⎭C.()f x 的图象沿着x 轴向右平移6π个单位后所得图象关于y 轴对称 D. ()f x 在30,4π⎡⎤⎢⎥⎣⎦上的最小值为1-8、已知直二面角l αβ--,点A ∈α,B ∈β,A 、B 到棱l 的距离相等,直线AB与平面β所成的角为030,则AB 与棱l 所成的角的余弦是( )A B C .12 D9、已知点(,0)(0)F c c >是双曲线12222=-by a x 的右焦点,F 关于直线3y x =的对称点A 恰在该双曲线的右支上,则该双曲线的离心率是( )A 1B 1 D .251+ 10、已知()ln 2f x x x =+-,()ln 2g x x x x =+-在()1,+∞上都有且只有一个零点,()f x 的零点为1x ,()g x 的零点为2x ,则( )A .2112x x <<<B .1212x x <<<C .1212x x <<<D .212x x << 二、填空题:(本大题共7小题,每小题5分,共35分) 11.若4cos()5πα+=,则sin(2)2πα-=__________.12.不等式lg(1)0x +≤的解集是__________. 13.已知a 、b 为实数,0a >,则ba b b a++的最小值为__________. 14.ABC ∆中,过点A 作AH BC ⊥,垂足为H ,3,2BH HC ==,则()32AB AC BC +uu u r uuu ruu ur g =__________. 15.由直线2y x =+上的点向圆22(4)(2)1x y -++=引切线,则切线长的最小值为__________.16.某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按40个工时计算)生产空调器、彩电、冰箱共120台、且冰箱至少生产20台。
湖北省七市州2014年4月高三数学联考(Word解析版)
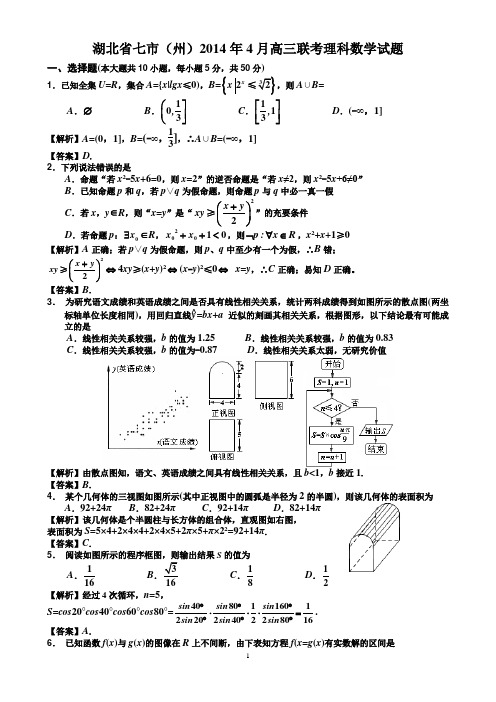
Hale Waihona Puke -1 x 0 1 2 3 f(x) -0.677 3.011 5.432 5.980 7.651
g(x) -0.530 3.451 4.890 5.241 6.892 A.(-1,0) B.(0,1) C.(1,2) D.(2,3) 【解析】设 h(x)=f(x)-g(x),则 h(-1)=-0.147,h(0)=-0.44,h(1)=0.542, ∴h(0)· h(1)<0,h(x)的零点在(0,1)内,即 f(x=g(x)的解属于(0,1). 【答案】B.
湖北省七市(州)2014 年 4 月高三联考理科数学试题
一、选择题(本大题共 10 小题,每小题 5 分,共 50 分)
1.已知全集 U=R,集合 A={x|lgx≤0),B= x 2 x ≤ 3 2 ,则 A∪B=
1 1 B. 0 , C . , 1 3 3 1 【解析】A=(0,1],B=(-∞, ],∴A∪B=(-∞,1] 3 【答案】D.
2
2
【解析】由散点图知,语文、英语成绩之间具有线性相关关系,且 b<1,b 接近 1. 【答案】B. 4. 某个几何体的三视图如图所示(其中正视图中的圆弧是半径为 2 的半圆),则该几何体的表面积为 A.92+24π B.82+24π C.92+14π D.82+14π 【解析】该几何体是个半圆柱与长方体的组合体,直观图如右图, 表面积为 S=5× 4+2× 4× 4+2× 4× 5+2π× 5+π× 22=92+14π. 【答案】C. 5. 阅读如图所示的程序框图,则输出结果 S 的值为
2
1 , 8
A.
湖北省七市(州)2014届高三4月联合考试 数学理-含答案

2014年湖北省七市(州)高三年级联合考试数学试题(理工类)第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U=R,集合A={x|lgx≤0),B=,则A∪B=A.ø2.下列说法错误的是A.命题“若x2-5x+6=0,则x=2”的逆否命题是“若x≠2,则x2-5x+6≠0”B.已知命题p和q,若p∨q为假命题,则命题p与q中必一真一假C.若x,y∈R,则“x=y”是的充要条件D.若命题p:∈R,则3.为研究语文成绩和英语成绩之间是否具有线性相关关系,统计两科成绩得到如图所示的散点图(两坐标轴单位长度相同),用回归直线近似的刻画其相关关系,根据图形,以下结论最有可能成立的是A.线性相关关系较强,b的值为1.25B.线性相关关系较强,b的值为O.83C.线性相关关系较强,b的值为-0.87D.线性相关关系太弱,无研究价值4.某个几何体的三视图如图所示(其中正视图中的圆弧是半径为2的半圆),则该几何体的表面积为A.92+24B.82+24C.92+14D.82+145.阅读如图所示的程序框图,则输出结果s的值为6.已知函数f(x)与g(x)x)=g(x)有实数解的区间是A.(-1,0) B.(0,1) C7.已知O为坐标原点,A,B两点的坐标均满足不等式组,设与的夹角为θ,则tanθ的最大值为8.设两条直线的方程分别为x+y+a=0,x+y+b=0,已知a,b是方程x2+x+c=0的两个实根,且0≤c≤,则这两条直线之间的距离的最大值和最小值分别是9.如果对定义在R上的函数f(x),对任意x1≠x2,都有x1f(x1)+x2f(x2)>x1f(x2)+x2f(x1)则称函数f(x)为“H函数”.给出下列函数:①y=-x3+x+1;②y=3x-2(sinx-cosx);.其中函数式“H函数”的个数是:A.4 B.3 C.2 D.110.已知双曲线的两个焦点为F1、F2,其中一条渐近线方程为P 为双曲线上一点,且满足|OP|<5(其中O为坐标原点),若|PF1|、|F1F2|、|PF2|成等比数列,则双曲线C的方程为第Ⅱ卷(非选择题,共100分)二、填空题:本大题共6小题,每小题5分,考生共需作答5题,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,横棱两可均不得分.(一)必考题:(11-14题)11.若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数的共轭复数是.12.设,则a4= .13.物体A以速度v=3t2+1(t的单位:s,v的单位:m/s)在一直线上运动,在此直线上与物体A出发的同时,物体B在物体A的正前方5m处以v=10t(t的单位:s,v的单位:m/s)的速度与A同向运动,则两物体相遇时物体A运动的距离为m.14.将长度为l,(l≥4,l∈N*)的线段分成n(n≥3)段,每段长度均为正整数,并要求这n段中的任意三段都不能构成三角形.例如,当l=4时,只可以分为长度分别为1,1,2的三段,此时n的最大值为3;当l=7时,可以分为长度分别为1,2,4的三段或长度分别为1,1,1,3的四段,此时n 的最大值为4.则:(1)当l=12时,n的最大值为;(2)当l=100时,n的最大值为.(二)选考题:请考生在第15、16两题中任选一题作答,请先在答题卡指定位置将你所选的题目序号的方框用2B铅笔涂黑.如果全选,则按第15题作答结果计分.15.(几何证明选讲)如图,已知PA是⊙O的切线,A是切点,直线PO交⊙O于B,C两点,D是OC的中点,连接AD并延长交⊙O于点E,若PA=2;∠APB=30°,则AE= .16.(坐标系与参数方程)在直角坐标平面内,以坐标原点O为极点、x轴的非负半轴为极轴建立极坐标系,已知点M的极坐标为,曲线C的参数方程为(α为参数),则点M到曲线C上的点的距离的最小值为.三、解答题:本大题共6小题,共75分.解答应写出必要的文字说明、证明过程或演算步骤.17.(本小题满分12分)已知向量,设函数(1)求函数f(x)的单调递增区间:(2)在△ABC中,角A、B、C的对边分别为a、b、c,且满足求f(C)的值.18.(本小题满分12分)已知数列{an}是等差数列,{bn}是等比数列,其中a1=b1=1,a2≠b2,且b2为a1、a2的等差中项,a2为b2、b3的等差中项.(1)求数列{an}与{bn}的通项公式;(2)记,求数列{cn}的前n项和Sn.三、解答题:本大题共5小题,共65分.解答应写出文字说明,证明过程或演算步骤.18.(本小题满分12分)己知向量设函数(Ⅰ)求函数f(x)的单调递增区间;(Ⅱ)在△ABC中,角A、B、C的对边分别为a、b、c,且满足求f(C)的值.19.(本小题满分12分)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠ABC=90°,AD∥BC,且PA=AD=2,AB=BC=1,E为PD的中点.(Ⅰ)设PD与平面PAC所成的角为α,二面角P-CD-A的大小为β,求证:tanα=cosβ.(Ⅱ)在线段AB上是否存在一点F(与A,B两点不重合),使得AE∥平面PCF?若存在,求AF的长;若不存在,请说明理由.20.(本小题满分12分)小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.(Ⅰ)根据图中的数据信息,求出众数x0;(Ⅱ)小明的父亲上班离家的时间y在上午7:00至7:30之间,而送报人每天在x0时刻前后半小时内把报纸送达(每个时间点送达的可能性相等)①求小明的父亲在上班离家前能收到报纸(称为事件A)的概率;②求小明的父亲周一至周五在上班离家前能收到报纸的天数X的数学期望.21.(本小题满分13分)已知椭圆的离心率为,以原点为圆心、椭圆的短半轴长为半径的圆与直线相切.(Ⅰ)求椭圆C的方程;(Ⅱ)设A(-4,0),过点R(3,0)作与X轴不重合的直线l交椭圆于P、Q两点,连结AP、AQ分别交直线于M、N两点,试问直线MR、NR的斜率之积是否为定值,若为定值,请求出;若不为定值,请说明理由.22.(本小题满分14分)已知函数(Ⅰ)设F(x)=f(x)+g(x),求函数F(x)的图像在x=1处的切线方程:(Ⅱ)求证:对任意的x∈(0,+∞)恒成立;(Ⅲ)若a,b,c∈R+,且求证:参考答案说明1.本解答列出试题的一种或几种解法,如果考生的解法与所列解法不同,可参照解答中评分标准的精神进行评分。
2014年湖北七市(州)高三年级联合考试文综试题及答案 20140419

绝密★启用前2014年湖北七市(州)高三年级联合考试文科综合能力测试注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2. 回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号框涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号框。
写在本试卷上无效。
3. 回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷和草稿纸上无效。
4. 考试结束,将本试卷和答题卡一并交回。
5. 本试卷共16页,如遇缺页、漏页、字迹不清等情况,考生须及时报告监考老师。
第Ⅰ卷本卷共35小题。
每小题4分,共140分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
2013年12月27日,我国南极科考船“雪龙号”因救援俄罗斯客船途中遭遇暴风雪而被困于(66°39′S、144°25′E)南极浮冰区。
2014年2月8日,我国第四个南极科考站泰山站正式建成并开站。
根据图文材料完成1~3题。
图1 图21.导致“雪龙号”遭遇暴风雪天气的直接原因是A.西风带内的气旋活动所造成B.极地东风带的强风所致C.极地高压强烈下沉气流造成D.东南信风势力强劲所致2.泰山站雄伟壮观,外形设计采用圆环形外表、碟形结构和高架设计,主要是因为①视野开阔②减少风阻③防潮④避免飞雪掩埋⑤保温A.①②③B.②④⑤C.②③⑤D.①②④3.下列对我国四个南极科考站的叙述正确的是A.中山站常年吹东北风B.昆仑站气压最高C.泰山站年日照时数最长D.长城站降雪量最大读我国某地生态工业园区的循环经济模式图,回答4~5题。
图34.该工业园区主导产业的工业导向类型属于A.原料导向型B.市场导向型C.劳动力导向型D.技术导向型5.该生态工业园区A.最可能位于湖北B.属于高科技产业园C.具有高效的资源利用及和谐的生态功能D.生产过程中所有工业产品都能循环利用图4所示区域陆地地势平坦,图5中为图4中河流甲、乙两处的年径流量曲线。
[VIP专享]湖北省七市(州)2014届高三联合考试语文试题B卷 版含答案
![[VIP专享]湖北省七市(州)2014届高三联合考试语文试题B卷 版含答案](https://img.taocdn.com/s3/m/9acfacb1910ef12d2af9e798.png)
机密★启用前2014年湖北七市(州)高三年级联合考试语 文本试卷共8页,六大题23小题,全卷满分150分,考试用时150分钟。
★祝考试顺利★注意事项:1.答题前,请考生认真阅读答题卡上的注意事项。
非网评考生务必将自己的学校、班级、姓名、考号填写在答题卡密封线内,将考号最后两位填在登分栏的座位号内。
网评考生务必将自己的姓名、考号填写在答题卡上指定位置,贴好条形码或将考号对应数字涂黑。
用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用2B铅笔把对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试题卷、草稿纸上无效。
3.非选择题用0.5毫米黑色墨水签字笔直接答在答题卡上每题对应的答题区域内,答在试题卷、草稿纸上无效。
4.考生必须保持答题卡的清洁。
考试结束后,监考人员将答题卡和机读卡一并收回,按小号在上、大号在下的顺序分别封装。
一、语文基础知识(共15分,共5小题,每小题3分)1. 下列各组词语中加点的字,每对的读音全都相同的一组是A.废黜/沸反盈天锻炼/放诞无礼潦倒/百无聊赖B.谗言/缠绵悱恻鉴赏/间或一轮伺候/垂手侍立C.呜咽/弃甲曳兵怯弱/锲而不舍嘱咐/人烟阜盛D.溺爱/华冠丽服替身/扪参历井采撷/度长絜大2.下列各组词语中,没有错别字的一组是A.光阴推衍稍纵即逝躁动不安B.贤惠昧心义气用事卑鄙无赖C.吝啬辩别礼尚往来冠冕堂皇D.禁受悲戚古陌荒阡前合后揠3B.耳熟能详约定俗成蹿红无非C.口授心传习以为常传扬大概D.通俗易懂司空见惯蹿升也许4.下列各项中,没有语病的一项是A.许多帮助过别人的人,总是在他人需要时伸出援手,当时什么也没想,事后也没觉得自己很高尚,不过帮人之后心里总感觉热乎乎的。
B.在就业难和研究生自费的双重夹击下,湖北省2014年的考研人数和录取率首次减少,今年全省的考研报名人数为111820人,比2013年减少1394人,降幅为1.24%。
湖北省七市(州)2014届高三4月联合考试数学(文)试题 扫描版含答案

2014年湖北省七市(州)高三年级联合考试数学试题(文史类)参考答案说明1.本解答列出试题的一种或几种解法,如果考生的解法与所列解法不同,可参照解答中评分标准的精神进行评分。
2.评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅。
当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解未改变这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数的一半,如果有较严重的概念性错误,就不给分。
3.解答题中右端所标注的分数,表示考生正确做到这一步应得的该题分数。
A 卷:1~5:CDDBA 6~10:ACBACB 卷:1~5:DCDBD 6~10:CABAB11、1i -+ 12、4 13、4 14、9214π+ 15、()223292x y ⎛⎫-++= ⎪⎝⎭ 16、10 17、(1)5n =;(2)9n =(注:第一问2分,第二问3分)18.解:(1)211()cos cos 1cos 22222x x x f x x x =-+=-+ 1sin 62x π⎛⎫=-+ ⎪⎝⎭ 4分 令222,22()26233k x k k x k k Z πππππππππ-≤-≤+-≤≤+∈ 6分所以所求增区间为2[2,2]()33k k k Z ππππ-+∈ 7分 (2)由226cos a b ab C +=,2sin 2sin sin C A B =,22c ab = 8分2226cos 2cos 3cos 122a b c ab C ab C C ab ab +--===-,即1cos 2C = 10分又∵0C π<<,3C π=11分()()13f C f π∴== 12分19.(1)证明: 1PA AB ==,F 为PB 中点, ∴AF PB ⊥ 1分 又 PA ⊥平面ABCD ,∴PA BC ⊥ 2分 又 ABCD 是矩形,∴AB BC ⊥ 3分 ∴BC PAB ⊥平面,而AF PAB ⊂平面 4分 ∴AF BC ⊥,∴AF PBC ⊥平面 5分 而PC PBC ⊂平面,∴AF PC ⊥ 6分(2) 解:由(1)知:PB BC ⊥且AB BC ⊥ 7分 ∴PAB ∠为二面角P BC A --的一个平面角,则PAB ∠=60° 8分∴0tan 60PA AB =⨯9分 ∴11111 3226F ACE V EC -=⨯⨯⨯⨯,解得EC = 11分即CE =时,三棱锥F ACE -的体积为16 12分20.(1)解: 17:00x =2分由频率分布直方图可知26:507:10x <<即2410430x <<3分∴20×0.0033 + 20×0.0117 + (x 2-410)×0.0233=20×0.0100 + 20×0.0017 + (430-x 2) ×0.0233 4分 解得2419x =分即26:59x = 6分(2)解:设报纸送达时间为x 7分 则小明父亲上班前能取到报纸等价于 6.57.577.5x y x y≤≤⎧⎪≤≤⎨⎪≤⎩, 10分 如图可知,所求概率为1381142P =-= 13分21.(1)由题意:b ==2分222221164a b e a a -==⇒=4分故椭圆C 的方程为2211612y x +=5分(2)设1122(,),(,)P x y Q x y ,若直线PQ 与纵轴垂直,则,M N 中有一点与A 重合,与题意不符,故可设直线:3PQ x my =+. 6分将其与椭圆方程联立,消去x 得:22(34)18210m y my ++-= 7分1212221821,3434m y y y y m m --+==++ 8分由,,A P M 三点共线可知,1116443M y y x =++,112834M yy x =⋅+, 9分 同理可得222834N y y x =⋅+10分1212916161649(4)(4)3333N M N M MR NR y y y y y y k k x x ⋅⋅=⋅==++--11分而212121212(4)(4)(7)(7)7()49x x my my m y y m y y ++=++=+++ 12分 所以2222211616(21)1234211844977493434MR NR m k k m m m m m -⨯⨯-+⋅===---⨯⋅+⋅+++故直线MR 、NR 的斜率为定值127-.14分22.解:(1)'()1(x 0)aa xf x x x -=-=>,1分当0a ≤时,'()0f x <,()f x 减区间为(0,)+∞ 2分当0a >时,由()0f x '>得0x a <<,由()0f x '<得x a > 3分∴()f x 递增区间为()0,a ,递减区间为(),a +∞4分(2)由(1)知:当0a ≤时,()f x 在(0,)+∞上为减区间,而(1)0f = ∴()0f x ≤在区间(0,)x ∈+∞上不可能恒成立 5分当0a >时,()f x 在()0,a 上递增,在(),a +∞上递减, max ()()ln 1f x f a a a a ==-+,令()ln 1g a a a a =-+,6分依题意有()0g a ≤,而()ln g a a '=,且0a >∴()g a 在()0,1上递减,在()1,+∞上递增,∴min ()(1)0g a g ==,故1a =9分(3)由(2)知:1a =时,()ln 1f x x x =-+且()0f x ≤恒成立即ln1x x≤-恒成立则()()lnln1ln1()()1nn n m mf n f m mn m n m n m-+--+-==----1111nmn m m-≤-≤--11分又由ln1x x≤-知ln1x x-≥-在()0,+∞上恒成立∴ln ln1()()11111n m mf n f m m n nn m n m n m n m n---=-=-≥-=-----13分综上所述:对任意的0m n<<,证明:()()1111f n f mn n m m--<<--14分。
2014年湖北七市(州)高三年级联合考试_5

2014年湖北七市(州)高三年级联合考试理科综合能力测试参考答案及评分标准物 理(A 卷)14.D 15.C 16.B 17.A 18.A 19.BD 20.CD 21.ACD (B 卷)14.A 15.B 16.A 17.C 18.D 19.AD 20.CD 21.ACD22. (1)0.3289~0.3291 (3分,说明:在此范围内均给3分,若超出此范围不给分) (2)12tt dtt d -(3分) 23. (1)电路如图所示(3分,说明:见错不给分)(2)所作图线如右图所示(2分,说明:必须描点,不描点,不用直线连线不能得分) (3)1.50(1.48~1.52,说明:在此范围内均给1分,若超出此范围不给分)(1分) 15.0(14.0~16.0,)(1分)(4)0.100(0.098~0.102,说明:在此范围内均给2分,若超出此范围不给分)(2分)24.(13分) 解析:质点的加速度大小为:a = F/m =2m/s 2……………1分第一个2秒末质点的速度为V 1 =a t = 4m/s 方向沿X 正方向……………1分第一个2秒末质点的位移为X 1 =at 2/2 =4m 方向沿X 正方向 ……………1分 第二个2秒质点做类平抛运动,V 2X =V 1 = 4m/sV 2Y =a t = 4m/s ……………1分X 2 =V 2X t =8m Y 2= at 2/2 =4m ……………1分 所以:⒈ 前4秒内质点位移的大小为410 m ……………1分 ⒉ 第4秒末质点的速度为42m/s 方向东偏南450…………………2分⒊ 第3个2秒内质点还是做类平抛运动 ………………1分 沿V 2方向运动S 3=42×2=82m …………………1分 沿垂直V 2方向运动S 4=at 2/2 =4m …………………1分 故第6秒末质点的位置坐标为:2X= 4+8+S 3×sin450+S 4×sin450= (20+22)m ………………1分Y= 4+S 3×sin450-S 4×sin450= (12-22)m ………………1分(评分说明:各评分点只涉及表述式,不对中间过程物理量的计算结果作要求,只要表达式正确,可以给分)25. (19分)解:(1)粒子在磁场中做圆周运动,如图为粒子运动轨迹描绘,洛仑兹力提供向心力:Rv m Bqv 2= ……………2分得圆轨道半径BqmvR =第一段圆弧轨迹OA 为半圆,A 点横坐标为2R 粒子再次由点B(2R ,R 332)进入磁场,进入磁场时与边界OP 夹角θ2=60º………1分 粒子再次出磁场即第三次经过磁场边界在位置C ,由几何关系BC=2R sin θ2=R 3 ……………………………1分 由此易得C 点坐标(R 61,R 63),即(Bq mv 6,Bqmv 63) ……………………2分 (2)粒子在磁场中运动周期周期Bqmv R T ππ22==…………2分 粒子第一段圆弧OA 圆心角180º,第二段圆弧BC 圆心角为360º-2θ2=240º…………1分由几何关系,粒子第三次进入磁场时,速度与边界O x 夹角θ3=30º,这也是粒子第三次出磁场时速度与边界O x 的夹角,因为∠Po x =α=30º,所以第三次出磁场后粒子速度与OP 平行,不再能进入磁场。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1题图NMy2014年湖北省七市(州)高三年级联合考试数学试题(文史类)全卷满分150分,考试时间120分钟.★ 祝考试顺利 ★第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合M = {x | x 2-2x -3 < 0}和N = {x | x > 1}的关系如图所示,则阴影部分所表示的 集合为 A .{x | x > 1} B .{x | x < 3} C .{x |-1 < x < 1}D . {x | 1 < x < 3}2.已知命题p :∃x ∈R ,cos x =54;命题q :∀x ∈R ,x 2-x +1>0.则下列结论正确的是A .命题p q ∨是假命题B .命题p q ∧是真命题C .命题()()p q ⌝∨⌝是真命题D .命题()()p q ⌝∧⌝是真命题3.从装有2个红球和2个黑球的口袋内任取2个球,那么互斥而不对立的两个事件是 A .“至少有一个黑球”与“都是黑球” B .“至少有一个黑球”与“都是红球” C .“至少有一个黑球”与“至少有一个红球” D .“恰有一个黑球”与“恰有两个黑球” 4.为研究语文成绩和英语成绩之间是否具有线性相关关系, 统计两科成绩得到如图所示的散点图(两坐标轴单位长度相 同),用回归直线y bx a =+近似的刻画其相关关系,根据图形,以下结论最有可能成立的是A .线性相关关系较强,b 的值为1.25B .线性相关关系较强,b 的值为0.83C .线性相关关系较强,b 的值为-0.87D .线性相关关系太弱,无研究价值 5.《莱因德纸草书》是世界上最古老的数学著作之一,书中有这样的一道题目:把100个面包分给5个人,使每人所得成等差数列,且使较大的三份之和的17是较小的两份之和,则最小的1份为A .116 B . 56 C .103D . 536.将函数()3sin(2)6g x x π=+图像上所有点向左平移6π个单位,再将各点横坐标缩短为原来的12倍,得到函数f (x ),则A .f (x ) 在(0)4π,单调递增B .f (x ) 在3()44ππ,单调递增C .f (x )在(0)4π,单调递减D .f (x )在3()44ππ,单调递减7.角α顶点在坐标原点O ,始边与x 轴的非负半轴重合,tan 2α=-,点P 在α的终边 上,点(3,4)Q --,则OP 与OQ 夹角余弦值为AB .C. D8.已知函数()f x 与()g x 的图像在R 上不间断,由下表知方程f (x )=g (x )有实数解的区间是A.(-1,0)9.已知双曲线)0,0(12222>>=-b a b y a x 的右焦点为F ,若过点F 且倾斜角为45°的直线与双曲线的左支没有公共点,则此双曲线离心率的取值范围是 A .(B .(C .)+∞D .)+∞10.德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数1,()0,R x Qf x x Q∈⎧=⎨∈⎩ð被称为狄利克雷函数,其中R 为实数集,Q 为有理数集,则关于函数()f x 有如下四个命题:①()()0ff x =; ②函数()f x 是偶函数;③任取一个不为零的有理数T ,()()f x T f x +=对任意的x ∈R 恒成立;④存在三个点()()()112233,(),,(),,()A x f x B x f x C x f x ,使得ABC ∆为等边三角形. 其中真命题的个数是A .4B .3C .2D .1二、填空题:本大题共7小题,7每小题5分,共35分. 请将答案填在答题卡对应题号.......的位置上. 答错位置,书写不清,模棱两可均不得分.11. 设复数z 满足(1)2i z i -=,其中i 为虚数单位,则=z .12.若x ,y 满足约束条件1020x y x y ≤⎧⎪≥⎨⎪-+≥⎩•,则z x y =+的最大值为 .13. 某程序框图如图所示,判断框内为“k n ≥?”,n 为正整数,若输出的26S =,则判断框内的n =________;第13题图 第14题图14.某个几何体的三视图如图所示,(其中正视图中的圆弧是半径为2的半圆),则该几何体的表面积为 . 15.圆心在曲线3(0)y x x=->上,且与直线3430x y -+=相切的面积最小的圆的方程是 .16. 一环保部门对某处的环境状况进行了实地测量,据测定,该处的污染指数等于附近污染源的污染强度与该处到污染源的距离之比.已知相距30km 的A ,B 两家化工厂(污染源) 的污染强度分别为1和4,它们连线上任意一点处的污染指数等于两化工厂对该处的污 染指数之和.现拟在它们之间的连线上建一个公园,为使两化工厂对其污染指数最小, 则该公园应建在距A 化工厂 公里处. 17. 将长度为(4,)l l l N *≥∈的线段分成(3)n n ≥段,每段长度均为正整数,并要求这n 段 中的任意三段都不能构成三角形.例如,当4l =时,只可以分为长度分别为1,1,2的三 段,此时n 的最大值为3;当7l =时,可以分为长度分别为1,2,4的三段或长度分别为 1,1,2,3的四段,此时n 的最大值为4.则:(1) 当12l =时,n 的最大值为________; (2) 当100l =时,n 的最大值为________.三、解答题:本大题共5小题,共65分.解答应写出文字说明,证明过程或演算步骤. 18.(本小题满分12分)已知向量2(cos,1),(3sin ,cos )222x x xm n =-=,设函数 ()1f x m n =⋅+.(Ⅰ)求函数()f x 的单调递增区间;(Ⅱ)在ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c , 且满足226cos a b ab C +=,2sin 2sin sin C A B =,求()f C 的值. 19.(本小题满分12分)如图所示,PA ⊥平面ABCD ,ABCD 是矩形, AB = 1,AD F 是PB 的中点,点E 在边BC 上移动. (Ⅰ)若1PA =,求证:AF PC ⊥;(Ⅱ)若二面角P BC A --的大小为060,则CE 为何PABCDEF值时,三棱锥F ACE -的体积为16.20.(本小题满分13分) 小明家订了一份报 纸,寒假期间他收集了每天报纸送达时间的 数据,并绘制成频率分布直方图,如图所示.(Ⅰ)根据图中的数据信息,求出众数1x 和中位数2x (精确到整数分钟);(Ⅱ)小明的父亲上班离家的时间y 在 上午7:007:30至之间,而送报人每天在1x 时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件A )的概率.21.(本小题满分14分) 已知椭圆2222:1(0)x y C a b a b+=>>的离心率为12, 以原点为圆心、椭圆的短半轴长为半径的圆与直线0x y -+=相切.(Ⅰ)求椭圆C 的方程;(Ⅱ)设(4,0)A -,过点(3,0)R 作直线l (不与x 轴重合)交椭圆于P 、Q 两点,连结AP 、AQ 分别交直线163x =于M 、N 两点,试探究直线MR 、NR 的斜率之积是否为定值,若为定值,请求出;若不为定值,请说明理由. 22.(本小题满分14分)已知函数R a x x a x f ∈+-=,1ln )(.(Ⅰ)求)(x f 的单调区间;(Ⅱ)若()0≤x f 在()+∞∈,0x 上恒成立,求所有实数a 的值; (Ⅲ)对任意的n m <<0,证明:()11)(11-<--<-mm n m f n f n第19题图2014年湖北省七市(州)高三年级联合考试数学试题(文史类)参考答案命题:陈子俊、郭仁俊、杨 田朱中文、李治国审题:向立政、方延伟、程世平何 亮、周继业A 卷:1~5:CDDBA 6~10:ACBACB 卷:1~5:DCDBD 6~10:CABAB11、1i -+ 12、4 13、4 14、9214π+ 15、()223292x y ⎛⎫-++= ⎪⎝⎭16、10 17、(1)5n =;(2)9n =(注:第一问2分,第二问3分)18、解:(1)211()cos cos 1cos 222222x x x f x x x =-+=-+ 1sin 62x π⎛⎫=-+ ⎪⎝⎭ 4分令222,22()26233k x k k x k k Z πππππππππ-≤-≤+-≤≤+∈ 6分 所以所求增区间为2[2,2]()33k k k Z ππππ-+∈ 7分 (2)由226cos a b ab C +=,2sin 2sin sin C A B =,22c ab = 8分2226c o s 2c o s3c o s 122a b c ab C ab C C ab ab+--===-,即1cos 2C = 10分 又∵0C π<<,3C π= 11分 ()()13f C f π∴== 12分19. (1)证明:1PA AB ==,F 为PB 中点,∴AF PB ⊥ 1分 又PA ⊥平面ABCD ,∴PA BC ⊥ 2分 又ABCD 是矩形,∴AB BC ⊥ 3分∴BC PAB ⊥平面,而AF PAB ⊂平面 4分 ∴AF BC ⊥,∴AF PBC ⊥平面 5分而PC PBC ⊂平面,∴AF PC ⊥ 6分(2) 由(1)知:PB BC ⊥且AB BC ⊥ 7分∴PAB∠为二面角P BC A --的一个平面角,则PAB ∠=60° 8分∴0tan60PA AB =⨯= 9分 ∴11111 3226F ACE V EC -=⨯⨯⨯⨯,解得EC =11分 即CE =F ACE -的体积为16 12分20. 解:(1)17:00x = 2分 由频率分布直方图可知26:507:10x <<即2410430x <<, 3分 ∴()2200.0033200.01174100.0233x ⨯+⨯+-⨯()2200.0100200.00174300.x =⨯+⨯+-⨯解得2419x =分即26:59x = 6分 1. 设报纸送达时间为x 7分 则小明父亲上班前能取到报纸等价于6.57.577.5x y x y ≤≤⎧⎪≤≤⎨⎪≤⎩, 10分如图可知,所求概率为1381142P =-= 13分21.解(1)b ==222221,164a b e a a -===,故22:11612x y C += 5分(2)设1122(,),(,)P x y Q x y ,若直线PQ 与纵轴垂直,则,M N 中有一点与A 重合,与题意不符, 故可设直线:3PQ x my =+. 6分将其与椭圆方程联立,消去x 得:22(34)18210m y my ++-= 7分1212221821,3434m y y y y m m --+==++ 8分 由,,A P M 三点共线可知,1116443M y yx =++,112834M y y x =⋅+, 9分同理可得222834N y y x =⋅+ 10分 1212916161649(4)(4)3333N M N M MR NR y y y y y y k k x x ⋅⋅=⋅==++-- 11分 而212121212(4)(4)(7)(7)7()49x x my my m y y m y y ++=++=+++ 12分所以2222211616(21)1234211844977493434MR NR m k k m m m m m -⨯⨯-+⋅===---⨯⋅+⋅+++故直线MR 、NR 的斜率为定值127-. 14分22. 解:(1)'()1(x 0)a a xf x x x-=-=>, 1分 当0a ≤时,'()0f x <,()f x 减区间为(0,)+∞ 2分 当0a >时,由()0f x '>得0x a <<,由()0f x '<得x a > 3分 ∴()f x 递增区间为()0,a ,递减区间为(),a +∞ 4分 (2)由(1)知:当0a ≤时,()f x 在(0,)+∞上为减区间,而(1)0f =∴()0f x ≤在区间(0,)x ∈+∞上不可能恒成立 5分 当0a >时,()f x 在()0,a 上递增,在(),a +∞上递减,max ()()ln 1f x f a a a a ==-+,令()ln 1g a a a a =-+, 6分依题意有()0g a ≤,而()ln g a a '=,且0a >∴()g a 在()0,1上递减,在()1,+∞上递增,∴min ()(1)0g a g ==,故1a = 9分(3)由(2)知:1a =时,()ln 1f x x x =-+且()0f x ≤恒成立即ln 1x x ≤-恒成立则()()lnln 1ln 1()()1nn n m m f n f m m n m n m n m-+--+-==---- 1111n m n m m-≤-≤-- 11分又由ln 1x x ≤-知ln 1x x -≥-在()0,+∞上恒成立,∴lnln 1()()11111n m mf n f m m n n n m n m n m n m n---=-=-≥-=----- 13分 综上所述:对任意的n m <<0,证明:()11)(11-<--<-mm n m f n f n 14分。
