【推荐】江西省2019年中考数学总复习第七单元视图投影与变换第25课时视图与投影高效集训本课件.ppt

九年级数学中考知识点归纳复习第24讲平移、对称、旋转与位似视图和投影

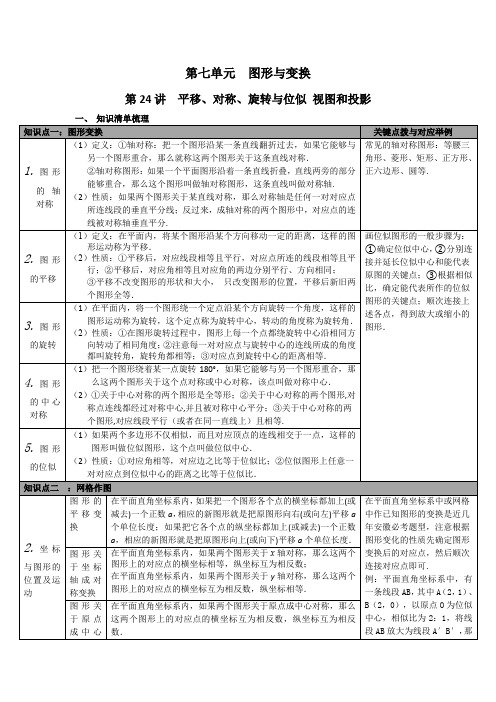
图形关于原点成位似变换
在平面直角坐标系内，如果两个图形的位似中心为原点，相似比为k，那么这两个位似图形对应点的坐标的比等于k或－k．
视图与投影
二、知识清单梳理
知识点一：三视图内容
关键点拨
1.三视图
主视图：从正面看到的图形.
俯视图：从上面看到的图形.
左视图：从左面看到的图形.
例：长方体的主视图与俯视图如图所示，则这个长方体的体积是36 .
4.图形的中心对称
（1）把一个图形绕着某一点旋转180°，如果它能够与另一个图形重合，那么这两个图形关于这个点对称或中心对称，该点叫做对称中心．
（2）①关于中心对称的两个图形是全等形；②关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分；③关于中心对称的两个图形,对应线段平行（或者在同一直线上）且相等.
2.三视图的对应关系
(1)长对正：主视图与俯视图的长相等，且相互对正；
(2)高平齐：主视图与左视图的高相等，且相互平齐；
(3)宽相等：俯视图与左视图的宽相等，且相互平行．
3.常见几何体的三视图常见几何体的三视图
正方体：正方体的三视图都是正方形.
圆柱：圆柱的三视图有两个是矩形，另一个是圆.
圆锥：圆锥的三视图中有两个是三角形，另一个是圆.
第七单元图形与变换
第24讲平移、对称、旋转与位似视图和投影
一、知识清单梳理
知ห้องสมุดไป่ตู้点一：图形变换
关键点拨与对应举例
1.图形的轴对称
（1）定义：①轴对称：把一个图形沿某一条直线翻折过去，如果它能够与另一个图形重合，那么就称这两个图形关于这条直线对称．
②轴对称图形：如果一个平面图形沿着一条直线折叠，直线两旁的部分能够重合，那么这个图形叫做轴对称图形，这条直线叫做对称轴.

中考数学第一轮考点系统复习第七章图形与变换第25讲尺规作图及投影与视图讲本

错误的是( D ) A.AD＝CD
B.∠ABP＝∠CBP
C.∠BPC＝115°
D.∠PBC＝∠A
3.(2020·武威)如图，在△ABC中，D是边BC上一点，且BD＝BA. (1)尺规作图(保留作图痕迹，不写作法)：
①作∠ABC的平分线，交AD于点E；
②作线段DC的垂直平分线，交DC于点F；解：(1)①如图，BE即为所求. ②如图，线段DC的垂直平分线交DC于点F.
③最后由主视图的竖列得到构成几何体的小正方体从左至右的列数；由主视图中的横行得到构成几何体的小正方体所摆的层数. 注意：该方法也适用于由三视图判定小正方体的个数. 3.由几何体的三视图及其所标尺寸计算几何体的表面积或体积问题，关键是先由以上方法还原几何体，再将三视图的尺寸对应标注在几何体上，最后利用几何体的相关计算公式求解.
A.5
B.6
C.7
D.8
考点3 立体图形的展开与折叠考点精讲 5.(2020·泰州)把如图所示的纸片沿着虚线折叠，可以得到的几何体是( A )
A.三棱柱 B.四棱柱 C.三棱锥 D.四棱锥
6.(2021·广东)下列图形是正方体的展开图的有( C )
A.1个
B.2个
C.3个
D.4个
正方体表面展开图的记忆口诀：中间四个面，上下各一面；中间三个面，一二隔河见；中间二个面，楼梯天天见；中间没有面，三三连一线.(结合知识点4中的正方体展开图的常见类型及相对面进行理解)
第七章图形与变换
第25讲尺规作图及投影与视图
知识点1 尺规作图及其基本步骤 1.定义：只用直尺和圆规来完成画图，称为尺规作图.
2.基本步骤： (1)已知：写出已知的线段和角，画出图形. (2)求作：求作什么图形，使它符合什么条件. (3)作法：运用五种基本尺规作图，保留作图痕迹. (4)证明：验证所作图形的正确性. (5)结论：对所作的图形下结论.

第1部分第25讲视图与投影-2021年中考数学一轮复习课件(江西专版)

A
B
C
D
第2题图
方法指导
1．常见几何体三视图的判断可根据“主视图与俯视图长对正，主视图与左视图高平齐，左视图与俯视图宽相等”的性质进行判断，或者通过牢记正方体、圆柱、圆锥、球、长方体几种常见几何体三视图的特点进行判断．
方法指导
2．常见几何体组合体的三视图判断首先要明确所判断视图的观察方向，再根据组合体中两个常见几何体的摆放位置，通过判断各自的视图，再根据看得见的部分是实线，看不见的部分是虚线进行判断．另外，在判断有一个面为圆的组合体的三视图时，要注意观察与圆接触的面的长(宽)与圆直径的大小关系，这直接关系到三视图中图与此几何图形的关系是内含，相切或是隐藏(虚线)．
重难点2 常见几何体的展示与折叠(重点) (2020·衡阳)下列不是三棱柱展开图的是( B )
A
B
C
D
3．一个正方体的平面展开图如图所示，折叠后可折成的图形是( D )
A
B
C
D
第3题图
2021权威预测
1.如图是由一个圆锥和一个长方体组成的几何体，从上面看它得到的平面图形是( A )
A
B
C
展开图
图示(其中一种)
六个大小相等的正方形
两个等圆和一个矩形
常见几何体
展开图一个圆和一个扇形
图示(其中一种)
两个全等的三角形和三个矩形
常见几何体
展开图三组两两全等的矩形
图示(其中一种)
5．下面图形是一些立体图形的展开图，围成的立体图形是棱柱的是( B
)
A
B
C
D
6．如图是一个正方体的平面展开图，那么“3”的对立面是__6_．(填编号 )

中考数学一轮复习第七章图形变化第二节投影与视图课件

2021/12/8
第六页，共三十页。
知识点二视图
1．视图：用_____正__投__影的方法绘制的物体在投影面上的
图形(túxíng)，称为物体的视图．
2．三视图
(1)主视图：从_______得到的视图叫做主视图．
正面(zhèngmiàn) (2)左视图：从_______得到的视图叫做左视图．
(3)俯视图：从_左__面__(_z_uǒ得mià到n)的视图叫做俯视图．
2021/12/8
第二十六页，共三十页。
正方体展开图口诀(kǒujué)：正方体展有规律，十一种类看仔细；中间四个成一行，两边各一无规矩；二三紧连错一个，三一相连一随意；两两相连各错一，三个两排一对齐；一条线上不过四，田七和凹要放弃；相间之端是对面，间二拐角面相邻．
2021/12/8
第二十七页，共三十页。
上面
2021/12/8
第七页，共三十页。
在三种视图(shìtú)中，主视图(shìtú)反映物体的长和高，左视图 (shìtú)反映了物体的宽和高，俯视图(shìtú)反映了物体的长和宽．
2021/12/8
第八页，共三十页。
3．三视图的画法
长度(chángdù)相
(1)画三视图要注意三要素：主视图与俯视图 ___等______；
开图，则原正方体相对面上的数字之和最小的
是(
)
A．4
B．6
C．7
D．8
2021/12/8
第二十五页，共三十页。
【分析】根据正方体的表面展开(zhǎn kāi)图确定相对的面上的数
字，进而得出答案．
【自主解答】由图可知，“1”与“5”相对，和为6；“2”与“6”相对，和为8；“3”与“4”相对，和为7，所以原正方体相对两个面上的数字和最小是6.故选B.

江西专用2019中考数学总复习第一部分教材同步复习第七章图形与变换第25讲视图与投影课件201902141102

22
重难点2
例2
由三视图还原几何体
重点
C
（2018· 襄阳）一个几何体的三视图如图所示，则这个几何体是（
）
A
23
B
C
D
• 2．（2018·武汉）一个几何体由若干个相同的正方体组成，其主视图和俯视图如图所示，则这个几何体中正方体的个数最多是（ C ）
• A ．3 个 • C ．5 个
24
B ．4 个 D ．6 个
第一部分
教材同步复习
第七章图形与变换
第25讲视图与投影
知识要点 · 归纳
知识点一投影
• 1．平行投影平行光线形成的投影叫做平行投影．太阳光线可以看成是平行光线， • 由①________ 如物体在太阳光的照射下形成的影子（简称日影）就是平行投影．日影的方向可以反映当地时间． • 2．中心投影中心投影 • 由同一点（点光源）发出的光线形成的投影叫做②________ ，如物体在灯泡发出的光照射下形成的影子就是中心投影．
A
B
C
D
19
重难点 · 突破
重难点1 几何体三视图的判断
重点
B
例1 （2018· 菏泽）如图是两个等直径圆柱构成的“T”形管道，其左视图是（
）
A
20
B
C
D
• 1．（2018·安徽）一个由圆柱和圆锥组成的几何体如图水平放置，其主（正）视图为（ A ）
A
21
B
C
D
方法指导
• （1）判断简单几何体的三视图，首先是要确定主视方向，然后要遵循 “长对正，高平齐，宽相等”的规律，牢记几何体的长对主视图的长，高对左视图的高，宽对俯视图的宽，同时要注意在画三视图时看得见的部分的轮廓画实线，看不见的部分的轮廓画虚线． • （2）对常见几何体的组合体，在判断其三视图时，要注意分清每一部分的三视图形状，然后根据其摆放位置及各部分大小决定组合体的具体视图．

中考数学总复习第七单元视图、投影与变换第25课时视图、投影及尺规作图课件

2021/12/10
第二十一页，共二十三页。
强化训练
考点(kǎo diǎn)四：基本作图
解：Ⅰ、过直线外一点作这条直线的垂线；Ⅱ、作线段的垂直平分线；
Ⅲ、过直线上一点作这条直线的垂线；Ⅳ、作角的平分线．如图是按上述要求排乱顺序(shùnxù)的尺规作图：
则正确的配对是：①﹣Ⅳ，②﹣Ⅰ，③﹣Ⅱ，④﹣Ⅲ．故选：D．
2021/12/10
第十九页，共二十三页。
归纳(guīnà)拓展
解答(jiědá)本考点的有关题目，关键在于掌握各种几何体的展开图的形状.
注意以下要点：
要能够通过空间想象，将展开图折叠成几何体，需熟记各种简单几何体的展开图.
2021/Hale Waihona Puke 2/10第二十页，共二十三页。
强化训练
考点(kǎo diǎn)四：基本作图
第十八页，共二十三页。
强化训练
考点三：由视图确定(quèdìng)实物
例3（2018•白银）已知某几何体的三视图如图所示，其中(qízhōng)俯视图为正六边形，则
该几何体的侧面积为
．108
解：观察该几何体的三视图发现该几何体为正六棱柱，其底面边长为3，高为6，所以其侧面积(miàn jī)为3×6×6=108，故答案为：108．
②在主视图的正下方画出俯视图，注意与主视图长对正；
③在主视图的正右方画出左视图，注意与主视图高平齐，与俯视图宽相等.
2021/12/10
第二页，共二十三页。
温馨提示 (wēn xīn)
画物体的三视图的口诀：主、俯：长对正；主、左：高平齐；俯、左：宽相等. 注意：几何体看得见部分的轮廓线画成实线，被其他(qítā)部分遮挡而看不见的部分的轮廓线画成虚线. 由三视图确定几何体的方法（1）由三视图想象几何体的形状，首先应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状. （2）由物体的三视图想象几何体的形状是有一定难度的，可以从以下途径进行分析：

中考数学一轮复习：第25课时矩形课件

2
No
返回目录
第25课时矩形
③当DP＝DC时，如解图①，过点D作DQ⊥AC于点Q，则PQ＝CQ.
∵S△ADC＝
1 2
AD·DC＝
1 2
AC·DQ，
∴DQ＝ AD·DC＝24 ， AC 5
∴CQ＝ DC2－DQ2＝18 ， ∴PC＝2CQ＝ 36 ， 5
5 ∴AP＝AC－PC＝ 14，
第2题解图①
返回目录
【提分要点】判定四边形是矩形，可以先判定这个四边形是平行四边形，然后找角或者对角线的关系，若角度容易求，则可找其一角为90°，便可判定是矩形；若对角线容易求，则证明其对角线相等即可判定其为矩形．
No
第25课时矩形
回归教材 1. 证明：有三个角是直角的四边形是矩形．已知：如图，在四边形ABCD中，∠A＝∠B＝∠C＝90°. 求证：四边形ABCD是矩形．【自主作答】证明：∵∠A＝∠B＝∠C＝90°， ∴AD∥BC，AB∥CD， ∴四边形ABCD是平行四边形． ∵∠A＝90°， ∴四边形ABCD是矩形．
①若∠BCE＝4∠DCE，则∠COE＝___3_6_ﾟ___ ； ②过点B作CE的平行线BF，过点C作BE的平行线CF，两平行线相交于点F，则
四边形BFCE是_矩___形__，判定根据为__有__一__个__角__是__直__角__的__平__行__四__边__形__是__矩__形____ ；
例题图②
2 又∵OC2＋CE2＝
1
BD2＋
2 1
BD2＝
1
BD2，
4
4
2
∴OC2＋CE2＝OE2，
∴∠OCE＝90°.
∵OD＝OC，
∴∠OCD＝∠ODC＝60°，
∴∠DCE＝∠OCE－∠OCD＝30°.

【推荐】江西省2019年中考数学总复习第七单元视图投影与变换第25课时视图与投影高效集训本课件.ppt

九年级数学中考知识点归纳复习 第24讲 平移、对称、旋转与位似 视图和投影