函数的连续性
第六节 函数的连续性

如果函数 f ( x )在开区间 (a , b)内连续 , 且在 左端点x a处右连续 , 在右端点 x b处左连续 , 则称函数f ( x )在闭区间 [a, b]上连续 .
连续函数的图形是一条连续而不间断的曲线.
6
例3 证明函数y sinx在区间 (,)内连续 .
证 x (,),
x 0 x 0
f ( x ) lim f ( x ) f ( x ).
故 f ( x)在( , )上连续 .
12
例5 设f ( x )在( 0, )上连续,且满足x (0, ), f ( x ) f ( x ). 证明 f ( x )在 (0, ) 上为常数.
1 当 x 0 时, lim f ( x ) 2, l i m f ( x ) f (0). x 0 x 0 a 1 所以当 a 时 ,f ( x )在 ( , ) 内 是 连 续 的 ; 2 1 当a 时 ,f ( x )在 ( , 0) (0, ) 内 连 续 2 23 且x 0 是 第 一 类 跳 跃 型 间 断.点
y sin 1 x
1 解 因 为 f ( x )在x 0 处 没 定 义 , 且limsin 不 存 在 , x 0 x 所以 x 0 为第二类间断点 .
这种情形称为振荡型间断点.
19
第 一 类 间 断 点 第 二 类 间 断 点
y
y 可去型
y 跳跃型
o
x0
x
o y
x0
x
o
x0
x
o
x 振荡型
lim f [ ( x )] f [ lim ( x )] f [ ( x0 )] f ( u0 ).
函数的连续性

第九节 函数的连续性和间断点有了极限的概念,我们就可以来讨论函数的一种重要特性——连续性。
首先,我们应注意到连续性也是客观现实的反映,是从许多自然现象的观察中抽象出来的一种共同特性。
如气温T 随时间t 的变化而连续变化,铁棒长度l 随着温度u 的变化而连续变化等。
它们的共同特性是:一方面在变化,另一方面是在逐渐变化的。
可在很短一段时间内,T 的变化很小;同样当温度u 变化很小时,l 的变化也很小。
这些现象反映在数学上就是自变量有一个微小的变化时,函数的变化也是微小的。
下面我们就专门来讨论这种概念。
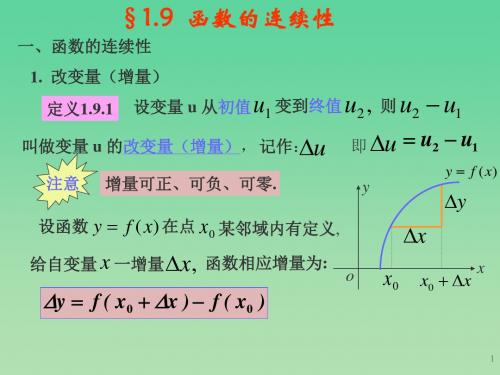
一、函数的连续性1. 预备知识改变量:设变量u 从它的一个初值1u 变到终值2u ,终值与初值的差21u u -,就叫u 的改变量,记作21u u u ∆=-。
改变量也叫增量。
注意:①1u ,2u 并不是u 可取值的起点和终点,而是u 变化过程中从1u 变到2u 。
②u ∆可正可负。
③u ∆是一个整体记号,不是某个量∆与变量u 的乘积。
2. 函数()y f x =在0x x =定义1 当自变量x 在点0x 的改变量x ∆为无穷小时,相应函数的改变量()()()()000y f x x f x f x f x ∆=+∆-=- 也是同一过程中的无穷小量,即0lim x y ∆→∆则称()f x 在0x 处连续,见图1-37.定理1 ()f x 在0x 处连续的充要条 件是()()00lim x x f x f x →=。
证明 由定义1,()()()()()000000lim 0lim lim lim 0lim .x x x x x x x x x y f x f x f x f x f x ∆→→→→→∆=⇔⎡⎣⇔-=⇔=由定理1,我们可将定义1改写为以下定义2.定义2 如果0ε∀>,0δ∃>,当0x x δ-<时,有()()0f x f x ε-<,则()f x 在0x 处连续。
函数的连续性与间断点

设函数 f (x) 在点 x0 的某去心邻域内有定义,如果 函数 f (x) 在点 x0 满足下列三种情况之一,则点 x0 为
f (x) 的间断点:
①、在 x0 处没有定义;
②、在 x0 处有定义,但 lim f (x) 不存在;
xx0
③、在 x0 处有定义,且 lim f (x) 存在,但
xx0
例3 证明函数 y sin x 在 (, ) 内连续 .
证 x (, )
y sin(x x) sin x
2sin
x 2
cos(x
x 2
)
y
2
sin
x 2
cos(x
x 2
)
2
x 2
1
x
0
(x 0)
即
lim y 0
x0
这说明 y sin x 在 (, ) 内连续 .
同样可证:函数 y cos x 在 (, ) 内连续 .
五、函数的间断点
定义5 如果函数 f (x) 在点 x0 不连续, 则称 f (x)
在点 x0 处间断, 并称点 x0为函数 f (x) 的间断点或
不连续点 .
1
o
x
1
解 因为 lim f (x) lim(x 1) 1 f (0 0)
x0
x0
lim f (x) lim (x 1) 1 f (0 0)
x0
x0
但
f (0 0) f (0 0)
所以是跳跃间断点 .
第二类间断点
如果函数 f (x) 在 x0 的左、 右极限至少有一个 不存在, 则称 x0 为 f (x) 的第二类间断点 .
函数的连续性

函数的连续性
函数的连续性是指函数在定义域上的变化情况,其主要内容是有限性、连续性和可导性。
有限性的概念是指函数的解析可以是有限的,它可以用有限的表示法来描述。
例如,函数y = x^2 + 2x - 4的解析表示式就是一个有限的表达式。
有限性是理解函数特征的基础,而连续性是更进一步理解函数特征的手段。
连续性定义为:存在任意位置x0处,它的函数值y0(即
y=f(x0)=y0)与其附近的函数值的差别不会超过一定的正定值,当此附近的自变量值在x0处的改变量趋近于零时,此函数值
的改变量也趋近于零,我们就称该函数在x0处是连续的,写
成数学形式就是:lim (x→x0) f(x) = y0
可导性是连续性的强化,也就是说它综合考虑了函数的变化和变化量之间的关系,它是指函数在定义域上任意一点x处,只要自变量x存在可导的微分,就说明函数y有可导的前提。
可导性的表述方式就是不等式:|f(x1)-f(x2)| ≤ M|x1-x2|,即自变
量x1和x2之间的变化量应小于某个正常数M,函数值在x1
和x2之间的变化量应小于M |x1-x2|。
函数的连续性是数学分析中的基本概念,它与微积分的应用紧密相连。
它的概念很容易理解,但在实际应用中却要求解答者拥有较强的抽象意识和概括能力,因此学习和研究它的概念是非常重要的。
《高等数学》第三节 函数的连续性

如果 x0 是函数 第一类间断点 可去间断点
f ( x) 的间断点,可将其分成两类:
f ( x) 在点 x0 处的左右极限存在;
其它
f ( x) 在点 x0 处的左右极限至少有
第二类间断点
一个不存在. 无穷间断点 振荡间断点 其它
例2 考察函数
2 x 0 x 1 f ( x) 1 x 1 在 x 1处的连续性. 1 x x 1
解 该函数在点x 1 处没有定义,所以函数在x 1 处间断;又因为
1 x 1 x 1 lim
,极限
x 1
不存在,趋于无穷,所以 是函数
f ( x)
1 x 1 的第二类间断点,
且为无穷间断点.
例4 考察函数
解 该函数在
1 f (x) sin 在 x 0 处的连续性. x
lim y lim f ( x0 x) f ( x0 ) 0 函数增量 y 也趋于零,即 x0 x0
,则称函数
y f ( x) 在点 x0
处连续,x0 称为函数 f ( x)
的连续点.
若记 x x0 x ,则 y f ( x) f ( x0 ) ,且当
x 0 处没有定义,
所以函数在 x 0 处间断,又因为当
x0
时,极限不存在,函数值在1与-1之间无
限次地振荡,所以 x 0 是
f ( x ) sin 1 x
的第二
类间断点,且为振荡间断点.
二、初等函数的连续性
g ( x) 均 定理1(连续函数的四则运算) 如果 f ( x)、
在点
f (b) ,
为介于 f (a) 与 f (b) 之间的任一实
高等数学:第一讲 函数的连续性

y f (x)
f (x0 )
0
x0
x
2.函数在一点的连续性同极限一样,都是函数的局部性质.
3. 判别函数y=f (x)在点x0连续的步骤:
(1) y = f (x)在点x0的某个邻域内有定义, y = f (x0) 存在;
(2) 极限
存在;
(3) 函数在 x0 处极限值等于函数值,即
例1 讨论函数 f (x)=x+1在x=2处的连续性.
且
lim
x x0
f (x)
f ( x0 ) , 称y = f (x) 在x0处左连续.
设函数y = f (x) 在[x0, x0+ ) 有定义,
且
lim
x x0
f (x)
f ( x0 ) , 称y = f (x) 在x0处右连续.
定理1
函数 y f ( x)在点 x0处连续的充要条件
是函数 y f ( x)在点 x0处既左连续又右连续,即
定义 2 设函数y=f (x)在点x0的某邻域内有定义,如
果x→x0时,相应的函数值f(x)→f(x0)
,即
lim
x x0
f (x)
f ( x0 ),
则称函数 y=f (x)在点x0连续,点x0为函数y=f (x)的连续点.
说明:
1. 函数 y=f (x)在点x0连续的几何意义:函数图形在x0不断开, 图像是连续不断的.
函数的连续性
函数的连续性
1、函数y=f (x) 在点 x0处的连续性
定义1 设y=f (x)在点x0的某邻域内有定义,如果当x在
x0处的增量x趋于零时,相应的函数增量y=f (x0+ x)- f(x0)也
函数的连续性
y y f x
a o
x b
17
例1.证明方程 x3 3x2 1 在(0,1)内至少有一个根. 证. 设 f (x) x3 3x2 1, f (x) C[0,1],
f (0) 1, f (1) 1, f (0) f (1) 0,
由零点定理知,在(0,1)内至少有一点 ,使得 f ( ) 0.
间断点的分类:
第一类间断点 ( 特点:左、右极限都存在 )
f f
( (
x0 x0
0) 0)
f ( x0 f ( x0
0 ), 0 ),
可去间断点; 跳跃间断点;
第二类间断点 (特点:左、右极限至少有一个不存在)
7
例4. 函数 f (x) 1 在x 0处无定义, 从而间断.
所以 f (x)在 x 0 处连续.
6
二、函数的间断点及其分类
f
(x) 在点x0
处连续.
12))..fli(mx0
) f
; (x)
;
3)
.
x x0
lim
x x0
f (x)
f ( x0 ).
以上三个条件只要有一条不满足,函数f (x) 在点 x0 处不连续. 即 f (x) 在点 x0 处间断, 并称 x0为函数f (x)的间断点.
10
定理1.9.2 (复合函数的连续性)
设函数 u g( x ) 在点 x x0 处连续, 函数 y f (u)在点u u0处连续, 则 函数 y f ( g( x )) 在点 x x0 处连续
g( x0 ) u0
lim f ( g( x )) f ( lim g( x ))
数学知识点:函数的连续性_知识点总结

数学知识点:函数的连续性_知识点总结
(1)如果函数y=f(x)在点x=x0处及其附近有定义,并且满足,则称函数y=f(x)在点x=x0处连续;否则称y=f(x)在点x=x0处不连续,或间断点。
(2)如果函数f(x)在某一开区间(a,b)内每一点处都连续,就说函数f(x)在开区间(a,b)内连续,对于闭区间[a,b]上的函数f(x),高考语文,如果在开区间(a,b)内连续,在左端点x=a处有,在右端点x=b处有,就说函数f(x)在闭区间[a,b]上连续。
3、如果f(x)是闭区间[a,b]上的连续函数,那么在闭区间[a,b]上f(x)一定有最大值和最小值。
函数的连续性的特点:
(1)f(x)在x0处有定义;
(2)f(x)在x0处的极限存在;
(3)f(x)在点x0处的极限等于函数值。
三大特点,缺一不可。
常用结论:
如果f(x)是闭区间[a,b]上的连续函数,那么在闭区间[a,b]上f(x)一定有最大值和最小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九节 函数的连续性和间断点有了极限的概念,我们就可以来讨论函数的一种重要特性——连续性。
首先,我们应注意到连续性也是客观现实的反映,是从许多自然现象的观察中抽象出来的一种共同特性。
如气温T 随时间t 的变化而连续变化,铁棒长度l 随着温度u 的变化而连续变化等。
它们的共同特性是:一方面在变化,另一方面是在逐渐变化的。
可在很短一段时间内,T 的变化很小;同样当温度u 变化很小时,l 的变化也很小。
这些现象反映在数学上就是自变量有一个微小的变化时,函数的变化也是微小的。
下面我们就专门来讨论这种概念。
一、函数的连续性1. 预备知识改变量:设变量u 从它的一个初值1u 变到终值2u ,终值与初值的差21u u -,就叫u 的改变量,记作21u u u ∆=-。
改变量也叫增量。
注意:①1u ,2u 并不是u 可取值的起点和终点,而是u 变化过程中从1u 变到2u 。
②u ∆可正可负。
③u ∆是一个整体记号,不是某个量∆与变量u 的乘积。
2. 函数()y f x =在0x x =定义1 当自变量x 在点0x 的改变量x ∆为无穷小时,相应函数的改变量()()()()000y f x x f x f x f x ∆=+∆-=- 也是同一过程中的无穷小量,即0lim x y ∆→∆则称()f x 在0x 处连续,见图1-37.定理1 ()f x 在0x 处连续的充要条件是()()00lim x x f x f x →=。
证明 由定义1,()()()()()000000lim 0lim lim lim 0lim .x x x x x x x x x y f x f x f x f x f x ∆→→→→→∆=⇔⎡⎣⇔-=⇔=由定理1,我们可将定义1改写为以下定义2.定义2 如果0ε∀>,0δ∃>,当0x x δ-<时,有()()0f x f x ε-<,则()f x 在0x 处连续。
3. 函数()y f x =在点0x 连续的要求⑴()f x 在点0x 有意义,即有确定的函数值()0f x ; ⑵()0lim x x f x →存在;⑶极限值=函数值,即()()00lim x x f x f x →=。
这三要素缺一不可。
4. 连续与极限的区别当()f x 在0x 处有极限时,()f x 在0x 处可无定义,也可有()()00lim x x f x f x →≠。
而当()f x 在0x 处连续时,()f x 在0x 一定有意义并且()()00lim x x f x f x →=必成立。
所以,函数()y f x =在点0x 处连续,则函数()y f x =在0x 点处必有极限,反之不成立。
5. 左右连续定义3 如果()()()000lim 0x x f x f x f x +→=+=,则称()f x 在0x 处右连续;如果()()()000lim 0x x f x f x f x -→=-=,则称()f x 在0x 处左连续。
所以()f x 在0x 处连续亦可用以下定义描述。
定义4 若()()()00000f x f x f x +=-=,即函数()y f x =在点0x 处左极限等于右极限等于函数值,则函数()y f x =在点0x 处连续。
6. ()f x 在某区间连续⑴()f x 在(),a b 内连续是指()0,x a b ∀∈,()f x 在0x 处连续。
⑵()f x 在[],a b 上连续是指()f x 在(),a b 内连续,在x a =点右连续,在x b =点左连续。
注意:证明分断点处的连续性时一定要用定义4.若()f x 在(),a b 内连续,则称(),a b 为()f x 的连续区间。
7. 连续函数的几何意义连续函数()y f x =的图形是一条不断开的曲线。
例1 证明()31y f x x ==+在1x =处连续。
证明 注意()()()113113113y f x f x x ∆=+∆-=+∆+-⨯-=∆⎡⎤⎣⎦,所以lim lim 3x x y x ∆→∆→∆=∆从而y 在1x =处连续。
例2 讨论()1,01,01,0x x f x x x x ->⎧⎪==⎨⎪+<⎩在0x =处的 连续性。
解 因为()()()000lim lim 11x x f f x x ++→→+==-=, ()()()000lim lim 11x x f f x x --→→-==+=, ()01f =,所以()()()00000f f f +=-=。
由定义4,()f x 在0x =处连续,见图1-38.例3 证明多项式函数在(,)-∞+∞内连续。
证明 设()1011n n n n P x a x a x a x a --=++++。
由极限运算法则知0(,)x ∀∈-∞+∞,()()101110010100lim (lim )(lim )lim n n n nx x x x x x x x n n n n P x a x a x a x a a x a xa x a P x --→→→→--=++++=++++=由0x 的任意性知()P x 在(,)-∞+∞内连续。
例4 证明有理函数()()()P x F x Q x =(P 为m 次多项式,Q 为n 次多项式),在 ()0Q x ≠点处处连续。
证明 0(,)x ∀∈-∞+∞,且()00Q x ≠,有()()()()()()()()00000lim lim lim x x x x x x P x P x P x F x F x Q x Q x Q x →→→====,所以()F x 在其定义域内处处连续。
例5 求证sin y x =在(,)-∞+∞内连续。
证明 (,)x ∀∈-∞+∞,给x 一个增量()x x x x ∆=+∆-,则2sin()sin 2sin cos22x x xy x x x ∆+∆∆=+∆-=, 从而000lim lim 2sin cos lim 2cos 02222x x x x x x x y x x ∆→∆→∆→∆∆∆∆⎛⎫⎛⎫∆=+=+= ⎪ ⎪⎝⎭⎝⎭,所以sin y x =在x 点连续。
由x 的任意性知sin x 在(,)-∞+∞内连续。
例6 证明cos y x =在(,)-∞+∞内连续。
证明 (,)x ∀∈-∞+∞,()x x x x ∆=+∆-,有cos()cos 2sin sin 22x x y x x x x ∆∆⎛⎫∆=+∆-=-+ ⎪⎝⎭, 所以000lim 2lim sin sin 2lim sin 02222x x x x x x x y x x ∆→∆→∆→∆∆∆∆⎛⎫⎛⎫∆=-+=-+= ⎪ ⎪⎝⎭⎝⎭,所以cos x 在(,)-∞+∞内连续。
二、函数的间断点与函数的连续性相对的概念是函数的间断性。
1. 间断点的定义若()f x 在点0x 处不连续,则称0x 为()f x 的一个间断点。
函数间断的几何解释是()f x 的图形在0x x =处断开。
例7 讨论()2,00,02,0x x y f x x x x -<⎧⎪===⎨⎪+>⎩的间断点。
解 注意 ()()()()()()()000,00lim lim 22,00lim lim 2xx x x f f f x x f f x x +-→→→→=+==+=-==- 可见()()()00000f f f +≠-≠,所以()f x 在0x =处不连续,即0x =为()y f x =的间断点。
这种()()0000f x f x +≠-的间断点,我们称其为跳跃间断点,见图1-39. 2. 间断点的分类函数()f x 在0x ⑴()f x 在0x 点无意义,即()0f x 不存在; ⑵()f x 在0x 点极限不存在,即()0lim x x f x →不存在;⑶极限值≠函数值,即()()00lim x x f x f x →≠。
我们称左右极限都存在的间断点为第一类间断点;其余间断点统称为第二类间断点。
进而,设0x 为()f x 的第一类间断点,如果还有()()0000f x f x +=-,则称0x 为()f x 的可去间断点;如果有()()0000f x f x +≠-,则称0x 为()f x 的跳跃间断点。
下表给出了间断点的分类情况。
()()()()()()()()()00000000000lim 0000x x f x f x f x f x f x f x f x f x f x →⎧⎧⎧⎪⎪⎪+=-⎨⎪≠⎪⎪⎩⎪+-⎪⎪⎨⎨⎪⎪+≠-⎪⎪⎪⎩⎪⎪⎩无意义:可补充定义可去间断点第一类间断点:可修改定义和间断点均存在不可去间断点(跳跃间断点)第二类间断点:除去第一类均为第二类间断点3. 函数的连续区间讨论函数的连续区间,就是在其定义域内排除间断点,主要在分段点、端点来考虑是否为间断点。
例8 研究tan y x =在2x π=处的连续性。
解 因为tan y x =在2x π=处无意义,所以2x π=是间断点。
又因为2lim tan x x π→=∞,即极限不存在,所以2x π=属第二类间断点,通常称其为无穷间断点,见图1-40.例9 讨论1sin y x=在0x =点的连续性。
解 因为1sin y x =在0x =处无意义,且01limsin x x →不存在,所以0x =为y 的第二类间断点。
这时,1sin y x =在-1和1通常称其为振荡间断点,见图1-41. 例10讨论211x y x -=-在点1x =解 因为y 在1x =处无意义,故1x =为间断点。
但111(1)(1)lim lim lim(1)1x x x x x y x x →→→-+==+-(1)2y =函数21,112,1x x y x x ⎧-≠⎪=-⎨⎪=⎩在定义域内处处连续。
例11 讨论,11,12x x y x ≠⎧⎪=⎨=⎪⎩在点1x =处的连续性,见图1-42.解 注意1(1)2y =而11lim lim 1(1)x x y x y →→==≠所以1x =为第一类可去间断点,修改定义(1)y 1=后,则函数,11,1x x z x ≠⎧=⎨=⎩处处连续,称函数z 为函数,11,12x x y x ≠⎧⎪=⎨=⎪⎩的连续延拓函数。
习题1.91.设函数()2,012,12x x f x x x ⎧≤≤=⎨-<≤⎩,试讨论()f x 在1x =处的连续性。
2.指出下列函数的间断点,并指明是哪一类间断点。
(1)()22132x f x x x -=-+; (2)()211f x x =-;(3)()1x f x e =; (4)()1cos f x x =3.设()()11xf x x =+,问怎样补充定义()0f ,才能使()f x 在0x =处连续。
