华东理工大学概率论 卷积公式补充例子
华东理工大学 概率论课件 2C12概率定义与性质41ps
有重复排列:从含有n个元素的集合中随机 抽取k 次,每次取一个,记录其结果 后放回,将记录结果排成一列,
nnn
n
共有nk种排列方式.
无重复排列:从含有n个元素的集合中随机抽取k 次, 每次取一个,取后不放回,将所取元素排成一列,
n n-1 n-2
nk+1
共有Ank=n(n-1)…(n-k+1)种排列方式.
10 2
6
P(B) 3 10
9 7
即:取得能被 3 整除的数字的概率为 3/10。
例2. 三白二黑共 5 个球,从中任取两个,则两个都是 白球的概率。
解:设 A 表示两个都是白球,
样本空间中样本点的总数为C52 ,
事件A 所包含的样本点个数为C32 .
P( A)
C32 C52
3 5!
3
10
大于 / 6的概率。
y
A
6
0
23
解:
4
x
SA
3 0
4x x2
3 3
x
dx
3 4
3
则所求事件的概率为
3 4
P(A)
3
2
1.2.2、古典概型
返回 复习
1.定义:若样本空间 的元素只有有限个; 每个基本事件发生的可能性相同,则 这种试验称为等可能概型,即古典概 型。
2.计算公式:设样本空间 中样本点的总数为 N , 事件A 所包含的样本点个数为 M ,则 事件A 发生的概率为
此时数值 p 称为随机事件 A 发生的概率,记作
P(A) p 。
可用Excel进行抛掷均匀硬币的实验:
RANDBETWEEN(-1000,1000)产生随机数,按所得 数的正负,分别计算频率,观察频率的稳定性。
卷积公式
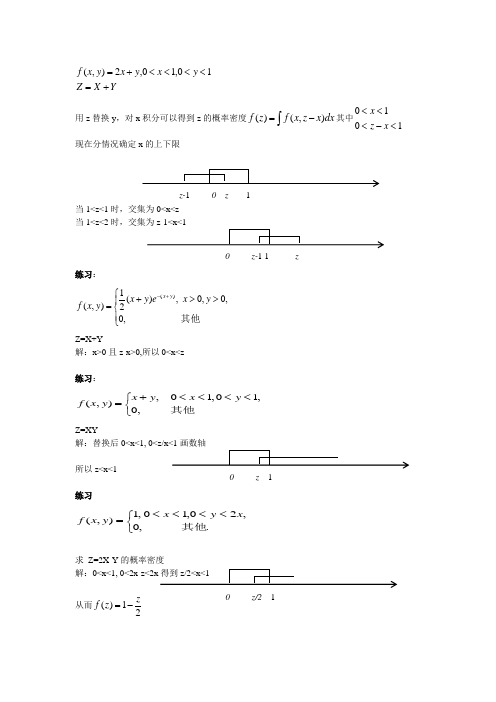
YX Z y x y x y x f +=<<<<+=10,10,2),( 用z 替换y ,对x 积分可以得到z 的概率密度()(,)f z f x z x dx =-⎰其中1010<-<<<x z x 现在分情况确定x 的上下限当1<z<1时,交集为0<x<z当1<z<2时,交集为z-1<x<1练习: ⎪⎩⎪⎨⎧>>+=+-其他 ,0,0,0 ,)(21),()(y x e y x y x f y xZ=X+Y解:x>0且z-x>0,所以0<x<z练习:, 01,01,(,)0, x y x y f x y +<<<<⎧=⎨⎩其他Z=XY解:替换后0<x<1, 0<z/x<1画数轴所以z<x<1练习 .,20,10,0,1),(其他x y x y x f <<<<⎩⎨⎧=求 Z=2X-Y 的概率密度解:0<x<1, 0<2x-z<2x 得到z/2<x<1从而21)(z z f -=z-1 0 z 1 0 z-1 1 z0 z 10 z/2 1教材例题:x>0, 0<y<20求Z=X+Y解:x>0, 0<z-x<20,如果z<20,交集0<x<z如果z>20,交集z-20<x<z教材练习:0<x<1,0<y<2Z=X+Y解:换掉y ,得到0<x<1, 0<z-x<2以下分类讨论0<z<2时,交集0<x<z如果1<z<2,交集0<x<1如果2<z<3,交集z-2<x<1确定了每种情况的上下限,使用卷积公式即可求出具体的概率密度函数参考资料:概率论第3章.百度文库.光昌国概率论与数理统计(14).百度文库.刘春华00概率论、数理统计与随机过程 第三章 张帼奋主编z-20 0 z 0 z-20 z z-2 0 z 1 z-2 0 1 z 0 z-2 1 z。
华东理工大学概率论与数理统计课件第四章资料

注 以上定理表明只要n比较大,就有近似结果:
n
X i ~ N( n ,n 2 )
i 1
返回
例1 用机器包装味精,每袋味精净重为随机变量,期 望值为100克,标准差为10克,一箱内装200袋味精,求 一箱味精净重大于20500克的概率?
解 设一箱净重为X,箱中第i袋味精净重为Xi,(i=1,2,…,200)
得对任意的ε>0,有
lim
P
n
n
Xi
i 1
n
an
1
则称{Xn}服从大数定律.
返回
大数定理
马尔可夫大数定理 切比雪夫大数定理 泊松大数定理 伯努利大数定理 辛钦大数定理
即最多可以装98箱.
返回
定理2 若随机变量μn~B(n,p)(n=1,2,…),则对任
意a<b有 lim P(a n np b) (b) (a)
n
np(1 p)
注:
(1) 定理称为棣莫佛-拉普拉斯定理.
(2)它表示当n很大时,二项分布可用正态分布近似逼近:
即 若X~B(n,p),当n很大时,有近似结果X~N[np,np(1-p)].
则 X1,X2,…,X200独立同分布, EXi=100, DXi=102=100,且
200
X X i 由中心极限定理得X近似服从正态分布, i 1
EX=200EXi=20000, DX=200DXi=20000,
所求为P(X>20500)= 1-P(X≤20500)
1(
20500 20000 20000
= 2.14 2.86=1 0.9838 1 0.9979
0.0141
返回
例7: 某车间有200台独立工作的车床,各台车床开 工的概率都是0.6,每台开工车床要耗电1千瓦, 问供电所至少要供给这个车间多少千瓦电力, 才能以99.9%的概率保证这个车间不会因供电 不足而影响生产。
卷积积分(Convolution)的定义(精)

一、卷积积分(Convolution)的定义 定义: 设 f1(t), f2(t) t < 0 均为零
f1 (t ) * f 2 (t ) f1 ( ) f 2 (t )d
0
t
二、卷积积分的性质 性质1
f1 ( t ) * f 2 ( t ) f 2 ( t ) * f 1 ( t )
2
1
0 0 1
t0
0 t 1
f (t ) 0
f (t ) 2e ( t )d 2 2e t
0 1 0 t
t t
t
t 1
1
f (t ) 2e ( t )d 2e ( t 1) 2e t
2
1 -1 0 0
e-
t0
0 t 1 t 1
e(k ) ph (t k )
e( t )
t k : 脉冲作用时刻 2 r( t ) k (k+1) t t 时刻观察到的响应 应为 0 ~ t 时间内所有 激励产生的响应的和
e(0)
o
t
t :观察响应时刻
0
2
N
k (k+1)
t
激励 e( t )
f (t ) 0
f (t ) 2e d 2 2e t
0 t t 1 t
t-1
t
1
t t
f (t ) 2e d 2e ( t 1) 2e t
积分变量(激励作用时刻)
例1. iS R iC C + uC
已知:R=500 k , C=10 F , uC(0)=0
iS 2e t (t ) mA
卷积公式的例子

卷积公式的例子
卷积公式的应用非常广泛,以下是5个具体的例子:
1. 丢骰子:有两枚骰子,求两枚骰子点数加起来为4的概率。
可以把它写成卷积的形式:(f∗g)(4)=∑m=13f(4−m)g(m)。
2. 做馒头:假设馒头的生产速度是f(t),腐败函数为g(t),那么一天后生产出来的馒头总量就是f(t)和g(t)的卷积,即馒头生产出来之后,会随时间不断腐败。
3. 信号处理:如果一个系统对输入信号的响应是g(t),那么在t=0时刻有一个输入,这个输入将随时间按g(t)的规律衰减,这也是卷积的应用。
4. 图像处理:在图像处理中,卷积常常用来进行滤波操作。
比如,有一个滤波器h,和一幅图像f,那么滤波后的图像g就是f和h的卷积。
5. 物理学:在物理学中,卷积被用来描述两个函数之间的关系。
例如,如果一个力在时间上作用于一个物体,那么该物体在时间上的位移就是该力和单位冲激响应的卷积。
卷积积分(Convolution)的定义(精)

e(t) r(t) r ( t ) e ( t ) * h( t )
即
线性网络 零状态
t
h(t)
r (t ) e( )h(t )d
0
物理解释: 将激励 e(t)看成一系列宽度为 ,高度为 e(k )矩形脉冲叠加的。
e( t )
e(0)
o
2
k (k+1)
性质4筛分性性质3时刻观察到的响应应为0时间内所有激励产生的响应的和冲激响应积分参变量观察响应时刻解
6.10 卷积积分
一、卷积积分(Convolution)的定义 定义: 设 f1(t), f2(t) t < 0 均为零
f1 (t ) * f 2 (t ) f1 ( ) f 2 (t )d
f1 (t ) f 2 ( )d f 2 ( t ) * f1 ( t )
性质2
f1 (t ) *[ f 2 (t ) f 3 (t )] f1 (t ) * f 2 (t ) f1 (t ) * f 3 (t )
性质3
[ f1 (t ) * f 2 (t )]* f 3 (t ) f1 (t ) *[ f 2 (t ) * f 3 (t )]
0
t
二、卷积积分的性质 性质1
f1 ( t ) * f 2 ( t ) f 2 ( t ) * f 1 ( t )
t
证明 f1 (t ) * f 2 (t ) 0 f1 ( ) f 2 (t )d
f1 ( t ) f 2 ( )(d )
t
t 0
0
令 = t :0 t : t 0
f (t ) 2e d 2e ( t 1) 2e t
华东理工大学 概率论课件 15C35向量函数的分布24ps
Z X Y 的取值范围
a
在[2a,2a] 。
z0
z 2a , FZ (z) 0
a o
ax
( Z z 是不可能事件)
a
z 2a
2a z 0
2a z 0
ay
za
zx 1
FZ ( z )
a
dx a
4a 2 dy
-a 0
ax
-a x+y=z
0 z 2a
( z a )22az
4a
1 z2 2
, 8 2a2 )
,
2a z 0 0 z 2a
1 ,
z 2a
pZ (z)
1
4a 2 1
4a 2
(z (z
2a) 2a
)
,
0,
2a z 0
, 0 z 2a 其它
具有以上密度函数的随机变量的分布称为辛普
森(Simpson)分布。
pZ (z)
1/2a
-2a
0
2a
z
例 4. X ~ N (1, 21) , Y ~ N (2 , 22) , X 与 Y 独立, 求 Z X Y 的分布。
解:
pX (x)
1
2
1
( x1 )2
e 2
2 1
,
pY
(
y)
1
( y2 )2
e 2
2 2
, 2 2
pZ (z)
1
( x1 )2
例 2.设 X ~ P(1) , Y ~ P(2 ) , X 与 Y 独立. 求 Z X Y 的分布。
解: Z 的一切可能取值为0,1,2,3,
k
P(Z k ) P( X i)P(Y k i)
东华理工大学概率论期末考试试卷总结版
东华理⼯⼤学概率论期末考试试卷总结版东华理⼯⼤学《概率论与数理统计》考试试卷(A1)(A ))(x F 取值为(0,)+∞ (B ))(x F 为单调递减(C )0 F(x)1≤≤ (D) F(x)1≤3、设~[2,4]X U ,当122<4x x <<时,=<<)(21x X x p () (A)122x - (B )224x - (C ) 244x - (D) 212x x - 4、设总体X 的数学期望为µ,⽅差为2σ,),(21X X 是X 的⼀个样本,则在下述的4个估计量中,最优的是()。
(A) 11241?55X X µ=+ (B) 2127188X X µ=+ (C) 31211?42X X µ=+ (D) 41211?32X X µ=+ 5、设(X,Y)为连续型随机向量,其联合密度为),(y x f ,两个边缘密度分别为()X f x 与()Y f y ,则下式中错误的是( ). (A) ()X EX xf x dx +∞-∞=(B) ?+∞∞-+∞∞-=dxdy y x xf EX ),((C) ()22()X Y EY y f x f y dy +∞+∞-∞-∞=(D) ()(,)E XY xyf x y dxdy +∞+∞6、已知~(2,1)X N -,~(3,1)Y N ,且,X Y 相互独⽴,记28,~Z X Y Z =-+则( ).(A))5,0(N (B))12,0(N (C))54,0(N (D))2,1(-N 7、在0H 为原假设,1H 为备择假设的假设检验中,则称()为犯第⼀类错误.0000(A)(B)H H H H 为真,接受不真,接受 0101(C)(D)H H H H 为真,接受不真,接受⼀.填空题:(本⼤题共7⼩题,每⼩题3分,共21分)1.设A 、B 为随机事件,P (A )=0.6,P (A-B )=0.3,则P (|B A )= 。
大学概率论与数理统计公式总结,期末考试不挂科的法宝
概率公式整理 A uQ = Q I.随机事件及其概率吸收律:AU0=A A 5人〃)=4 = A/In0 = 04n(4u/^) = 4A-B = AB = A-(AB)反演律:AuB = A B AB = A<j B P(A) = 1-P(A) P(B-A) = P(B)-P(AB) U A =A AA A =U Ar=l r=l f=l i=l 若 AuB => P[B -A) = P(B) - P(A) 2. 概率的定义及其计算: 对任意两个事件人B,有 加法公式:对任意两个事件有P(A uB) = P(A) + P(B) - P(AB) P(CjA)述P(AJ-工P(AC)+ E) + - + (-1)"'1P(A,A 2 • • • A n ) /«1 r=l lii<j<n l<i<j<kin 3. 条件概率 P(B | A)= 些凹 乘法公式 P(AB) = P(A)P(B\A)(P(A) > 0) P(4) P( A"…人)"(A )P (爲 ⑷…P(九I A A …A” J (P(A,2 …心)>0) 全概率公式 P(A) = £ P(AB,) = 2 P(BJ P(A I fi,) Bayes 公式 P(B k \ A)= “仲i=l P(4)P(AuB)<P(A) + P(B) =P (城)P(4| 以)r=l略hl 血-iz 甘4旷 ◎十"拓“饴 PS <X<b) = P(X< h)-P(X< a) 随机变山及其分布分布函数计畀— =F (b) — F (a) 离散型随机变量(1) 0 - I 分布P(X =k) = p A (l-p)' \ k = 0y l 二项分布 〃(〃,/?)若 P(4)=" P(X=k) = C"(l_p 严,"0,1,k k k 2 才 * Possion 定理 lim/zp,, =2>0 有 >!^CnPn(l ~Pn) =e 万 "0,12 …4. 5. ⑵ n — (3) Poisson 分布 P(久) P(X=R) =小一,k=o,12•… k\6.连续型随机变量(1) 均匀分布b-a (X ,ci<x<bF(g其他 x-a⑵指数分布 £(2) /(X)=0, x>0 具他 09 1 一严 x<() ,x>0 ⑶止态分布N(〃,cr2)] r"-")2 -oo<x<+oo F(x) = /—— f e 2a :d/ 2a 2 1 _ 匚 i x d (p(x) = -J=-e 3 -oo<x<-Foo 0(x) = -^=J l e 7dz -oo<x <+<x> 二维随机变显(X,Y)的分布函数 F(x,y)=「[' f(i h v)dvclu J_8 J 一8 边缘分布函数与边缘密度函数(x) = j' j^*5f(u y v)dvdu f x (x) = ^f\x,v)dv人(y)=L*7V(0J)—标准正态分布 7 •多维随机变昴及具分布 />(y)= P f f(u.v)dudvJ ・8 er —oo&连续型二维随机变量 (1)区域G 上的均匀分布,=U,V)eG0, 其他(2)二维正态分布.( — “J,一 2 P/(^y)= ------------- xer 」2勿0 2寸1 _ P ・ —OQ < X < -H» OO < y < +009.二维随机变竝的条件分布f (x, y) = f x (x)/r j x (y|x) X 的 R 阶中心矩 E((X-E(X))*) X 的 方差 E((X-E(X))2) = D(X)X,Y 的k + l 阶混合原点矩 E(X k Y l) X.Y 的k + l 阶混合中心矩 E((X-E(X)r(Y-£(Y))‘) X 9Y 的二阶混合原点矩 E(XY) X 9Y 的二阶混介中心矩 X"的协方差E((X-E(X))(y-E(r)))'(x-E(x))(y-E(y))、< J D (X )莎百 丿X 的方差 D(X) = E((X ・E(X))2) AXX) = £(X 2)-£C(X) 协方差 cov(x,y)=E ((X - E(x))(y 一E(r)))=E(XY)-E(X)E(Y) = ±^(D(X±Y)-D(X)-D(Y))相关系数C :组合数 中心n, n>h m>0, n. m^N.⑴排列数公式= yi(n-lXw- 2)---(n -m + 1)=出=?2! = ?2(«-1\^- 2)・・・2 1(2)组合数公式AW>0 =fy(y)f x \Y (x\y)A(y)>o+8fx (x) = L /(x, y)dy = L £|y (彳 y)齐(y)〃y A(y)= J m /(^ y)^ = L 环(妝)人(兀皿二 f(x,y) fx\Y(^fy(y) =AW 「E(X)= [ ^xf(x)dx J —8x 的k 阶绝对原点矩E (I x r)如④)=册-屉如凹10.随机变量的数字特征 数学期望E(X) =工5 “1随机变虽函数的数学期望X 的k 阶原点矩E(X k)A(y)Ard)fx(x) 4«oX#的相关系数cov(XV)4D (X)/D (Y)1.排列数(MI <M )V C:(3)组合数性质:一””(心)册亦等(5 c; +C;A +C;“ +・・・ + C;。
华东理工大学 概率论课件 1C11随机事件及运算33ps
事件 仅含一个样本点的随机事件称为基本事件.
含有多个样本点的随机事件称为复合事件.
事件常用大写字母A、B、C等表示。
事件 A发生——该子集 A 中至少有一个样本点出现。
特例—必然事件Certainty Events
必然事件 ——记作Ω
•样本空间Ω也是其自身的一个子集 •Ω也是一个“随机”事件 •每次试验中必定有Ω中的一个样本点出现 •必然发生
到了20世纪的30年代,人们开始研究随机过程, 而著名的马尔可夫过程的理论在1931年才被奠定其 地位。而苏联数学家柯尔莫哥洛夫在概率论发展史上 亦作出了重大贡献,
到了近代,出现了理论概率及应用概率的分支,及
将概率论应用到不同范畴,从而开展了不同学科。因 此,现代概率论已经成为一个非常庞大的数学分支。
?
目的:全面研究随机试验,揭示客观存在的 统计规律性。
1.两个例子
例 1.抛硬币,H 表示正面,T 表示反面,抛一次硬币,
得样本空间 {H ,T} 。
引入变量 X ,将随机试验的结果与 X 的取值对应起
来,
假设:X
1, 0,
H T
H T
X X ()
X ( ) 的所有可能取值为 Rx {0,1} ,Rx 即为X ( ) 的 值域。
随机试验
可在相同条件下重复进行。 每次试验的可能结果不止一个,并且事先明确试验的 所有可能结果。 试验前无法预知究竟哪个结果出现。
基本事件与样本空间
样本点 Sample Point 随机试验中的每一个可能出现的试验结果称为这
个试验的一个 样本点 ,记作i .
样本空间 Sample Space 全体样本点组成的集合称为这个试验的样本空间,
