常考专题讲座(二)
专题讲座---水和水的溶液(原卷版)
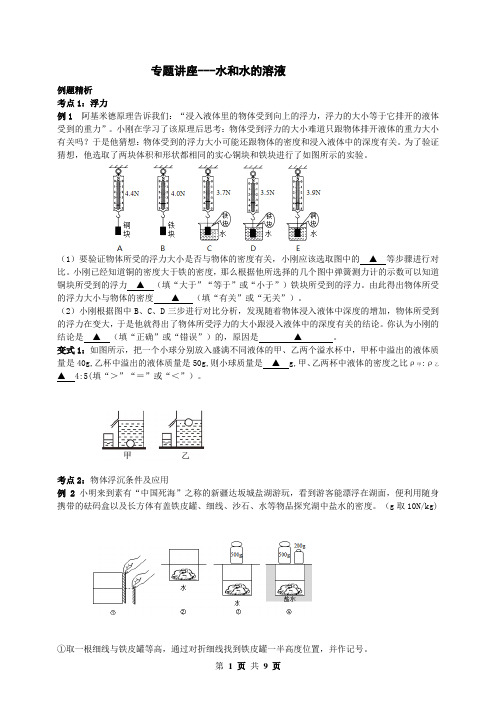
专题讲座---水和水的溶液例题精析考点1:浮力例1阿基米德原理告诉我们:“浸入液体里的物体受到向上的浮力,浮力的大小等于它排开的液体受到的重力”。
小刚在学习了该原理后思考:物体受到浮力的大小难道只跟物体排开液体的重力大小有关吗?于是他猜想:物体受到的浮力大小可能还跟物体的密度和浸入液体中的深度有关。
为了验证猜想,他选取了两块体积和形状都相同的实心铜块和铁块进行了如图所示的实验。
(1)要验证物体所受的浮力大小是否与物体的密度有关,小刚应该选取图中的▲等步骤进行对比。
小刚已经知道铜的密度大于铁的密度,那么根据他所选择的几个图中弹簧测力计的示数可以知道铜块所受到的浮力▲(填“大于”“等于”或“小于”)铁块所受到的浮力。
由此得出物体所受的浮力大小与物体的密度▲(填“有关”或“无关”)。
(2)小刚根据图中B、C、D三步进行对比分析,发现随着物体浸入液体中深度的增加,物体所受到的浮力在变大,于是他就得出了物体所受浮力的大小跟浸入液体中的深度有关的结论。
你认为小刚的结论是▲(填“正确”或“错误”)的,原因是▲。
变式1:如图所示,把一个小球分别放入盛满不同液体的甲、乙两个溢水杯中,甲杯中溢出的液体质量是40g,乙杯中溢出的液体质量是50g,则小球质量是▲ g,甲、乙两杯中液体的密度之比ρ甲:ρ乙▲ 4:5(填“>”“=”或“<”)。
考点2:物体浮沉条件及应用例2小明来到素有“中国死海”之称的新疆达坂城盐湖游玩,看到游客能漂浮在湖面,便利用随身携带的砝码盒以及长方体有盖铁皮罐、细线、沙石、水等物品探究湖中盐水的密度。
(g取10N/kg)①取一根细线与铁皮罐等高,通过对折细线找到铁皮罐一半高度位置,并作记号。
②在铁皮罐内加入适量沙石并加盖密封,使之漂浮时一半浸入水中。
③在铁皮罐上加砝码,直至铁皮罐恰好浸没在水中。
④将该铁皮罐放入盐水中,加砝码,直至铁皮罐恰好浸没在盐水中。
问:(1)铁皮罐的体积有多大?(2)铁皮罐和沙石的总重有多大?(3)盐水的密度有多大?变式2:我国某型号潜艇水舱未充水时总质量为9.27×105kg,它漂浮在海面上受到的浮力为▲ N,向潜艇的水舱中充入适量的海水后,潜艇在海水中由漂浮变为悬浮,在此过程中潜艇受到的浮力将▲(填“变大”“变小”或“不变”)。
高考数学专题讲座 第2讲 二次函数的综合应用问题

高考数学专题讲座 第二讲二次函数的综合应用问题一、考纲要求1.理解二次函数,一元二次不等式及一元二次方程三者之间的关系,掌握一元二次不等式的解法; 2.以二次函数为背景的不等式问题作为代数推理题在高考中频繁出现,二次函数和绝对值不等式相结合的题目也在高考中出现多次;3.二次函数是简单的非线性函数之一,有着丰富的内涵,成为高考的一个热点.二、基础过关1.若关于x 的不等式01)1()1(22<----x a x a 恒成立,则a 的取值X 围是( B ).A .53-<a 或1>a B .a <-53≤1C .53≤a ≤1或1-=a D .以上均不对 2.函数54)(2+-=mx x x f 在区间2[-,)∞+上是增函数,则)1(f 的取值X 围是( A ).A .)1(f ≥25B .25)1(=fC .)1(f ≤25D .25)1(>f3.若32)1()(2++-=mx x m x f 为偶函数,则)(x f 在3(-,)1上是( B ).A .单调递增B .单调递减C .先增后减D .先减后增4.已知a ,∈b N *,方程022=++b ax x 和方程022=++a bx x 都有实根,则b a +的最小值是( D ).A .3B .4C .5D .65.已知函数32)(2+-=x x x f 在区间0[,]a )0(>a 上的最大值为3,最小值为2,那么 实数a 的取值X 围是 1≤a ≤2 .6.已知函数a b b ax x x f (1)(22+-++-=,∈b R )对任意实数x 都有)1()1(x f x f -=+成 立,若当1[-∈x ,]1时,0)(>x f 恒成立,则b 的取值X 围是 b<-1或b>2 .三、典型例题例1 已知函数22)(2++=ax x x f ,5[-∈x ,]5.(1)当1-=a 时,求函数)(x f 的最大值与最小值;(2)某某数a 的取值X 围,使)(x f y =在区间5[-,]5上是单调函数. 解:(1)当a =-1时, f (x )=x 2-2x +2=(x -1)2+1, x ∈ [-5,5] ∴x =1时,f (x )的最小值为1,x =-5时,f (x )的最大值为37.(2)函数f (x )=(x +a )2+2-a 2图象的对称轴为x =-a ∵f (x )在区间[-5,5]上是单调函数 ∴-a ≤-5或-a ≥5 即a ≥5或a ≤-5 故a 的取值X 围为 a ≤-5或 a ≥5.例2 (1)将长度为1的铁丝分成两段,分别围成一个正方形和一个圆形,要使正方形与圆的面积之和最小,正方形的周长应为π+44. (2)已知函数∈+-=x b ax x x f (|2|)(2R ),给出下列命题:①()f x 必是偶函数;② 当)2()0(f f =时,)(x f 的图象必关于直线1=x 对称; ③ 若b a -2≤0,则)(x f 在区面a [,)∞+上是增函数; ④)(x f 有最大值||2b a -. 其中正确命题的序号是③.例3 已知函数∈++-=x m x m x x f ()1()(2R ).(1)设A 、B 是ABC ∆的两个锐角,且A tan ,B tan 是方程04)(=+x f 的两个实根, 求证:m ≥5;(2)当m ≥3时,函数)(sin αf 的最大值是8,求m 的值. 解:(1) 方程f (x )+4=0 即x 2-(m +1)x +m +4=0依题意,得⎪⎩⎪⎨⎧>+=⋅>+=+≥+-+=∆04tan tan 01tan tan 0)4(4)1(2m B A m B A m m 解之得 ⎪⎩⎪⎨⎧->->≥-≤4153m m m m 或∴m ≥5(2)f (sin α)=sin 2α-(m +1)sin α+m =(sin α2)21+-m +m 4)1(2+-m ∵m ≥3 ∴221≥+m ∴ 当sin α=-1时,f (sin α)取得最大值2m +2由题意得 2m +2=8 ∴m =3例4 已知函数x x x f (1)(2-=≥1)的图象为1C ,曲线2C 与1C 关于直线x y =对称. (1)求曲线2C 的方程)(x g y =;(2)设函数)(x g y =的定义域为M ,1x ,M x ∈2,且21x x ≠.求证:|||)()(|2121x x x g x g -<-;(3)设A 、B 为曲线2C 上任意两个不同点,证明直线AB 与直线x y =必相交. 解(1) ∵ C 1,C 2关于直线y =x 对称, ∴g (x )为f (x )的反函数. ∵y =x 2-1, 即 x 2=y +1, 又 x ≥1 ∴x =1+y∴ 曲线C 的方程为 g (x )=1+x (x ≥0)(2)设x 1,x 2∈M, 且x 1≠x 2, 则 x 1-x 2≠0 又 x 1≥0, x 2≥0∴|g (x 1)-g (x 2)|=|||2||11|||112121212121x x x x x x x x x x -<-≤+++-=+-+ (3)设A(x 1,y 1) 、B(x 2,y 2)为曲线C 2上任意两个不同的点, x 1,x 2∈M, 且 x 1≠x 2 由(2)知|k AB |1|||)()(|||21212121<--=--=x x x g x g x x y y∴直线AB 的斜率|k AB |≠1 又直线y =x 的斜率为1 ∴直线AB 与直线y =x 必相交.四、热身演练1.函数x x y (321--=≥)2的反函数是( B ).A .∈+-=x x x y (2212R )B .x x x y (2212+-=≤)0 C .∈-+=x x x y (2212 R ) D .x x x y (2212-+=≤)0 2.设函数()(2c bx ax x f ++=)0a <,满足)1()1(x f x f +=-,则)2(x f 与)3(x f 的大小关系是( C ).A .)2()3(x x f f >B .)2()3(x x f f <C .)3(x f ≥)2(x fD .)3(x f ≤)2(x f3.若a ,b ,c 成等差数列,则函数c bx ax x f ++=2)(的图象与x 轴的交点个数是( D ).A .0B .1C .2D .不确定4.已知二次函数12)2(24)(22+----=p p x p x x f ,若在区间1(-,)1内至少存在一个 实数c ,使0)(>c f ,则实数p 的取值X 围是( C ).A .21(-,)1 B .3(-,)21- C .3(-,0)23 D .21(-,)235.一辆中型客车的营运总利润y (单位:万元)与营运年数∈x x (N )的变化关系如下表所示,则客车的运输年数为( B )时,该客车的年平均利润最大.A .4B .5C .6D .76.已知函数422)(2++-=a ax x x f 的定义域为R ,值域为1[,)∞+,则a 的取值X 围 为 [-1,3] .7.如果函数)(x f 对于任意∈x R ,存在M 使不等式|)(|x f ≤||x M 恒成立(其中M 是与x 无关的正常数),则称函数)(x f 为有界泛函,给出下列函数: ①1)(1=x f ;②22)(x x f =;③)cos (sin )(3x x x x f +=;④1)(24++=x x xx f . 其中属于有界泛函的是③④(填上正确序号).8.若方程02=++b ax x 有不小于2的实根,则22b a +的最小值为516. 9.已知不等式032<+-t x x 的解集为m x x <<1|{,∈x R }.(1)求t ,m 的值;(2)若函数4)(2++-=ax x x f 在区面-∞(,]1上递增,求关于x 的不等式0)23(log 2<-++-t x mx a 的解集.解:(1)依题意 ⎩⎨⎧==+t m m 31∴⎩⎨⎧==22t m(2)∵f (x )=-(x -44)222a a ++在]1,(-∞上递增∴12≥a即 2≥a 又 )32(log )23(log 22x x t x mx a a +-=-++-<0∴13202<+-<x x 解之得 210<<x 或1<x <23 故 不等式的解集为 {x |0<x <21或1<x <23}.10.定义在R 上的函数)(x f 满足:如果对任意1x ,∈2x R ,都有)2(21x x f +≤)]()([2121x f x f +, 则称函数)(x f 是R 上的凹函数.已知二次函数∈+=a x ax x f ()(2 R ). (1)求证:当0>a 时,函数)(x f 是凹函数;(2)如果0[∈x ,]1时,|)(|x f ≤1,试某某数a 的取值X 围. 解:(1)对任意x 1,x 2∈R ,a >0,都有[f (x 1)+f (x 2)]-2f (221x x +)=a 21x +x 1+ax 22+x 2-2[a (2)221221x x x x +++] =ax 21+ax 22-21a (x 1+x 2+2x 1x 2) =21a (x 1-x 2)2≥0∴f ()]()([21)22121x f x f x x +≤+故函数f (x )是凹函数.(2)由|f (x )|≤1知: -1≤f (x )≤1 即 -1≤ax 2+x ≤1当 x =0时, a ∈R当x ∈(0,1)时, ⎩⎨⎧+-≤--≥1122x ax x ax 恒成立即 ⎪⎩⎪⎨⎧--=-≤++-=--≥41)211(1141)211(112222x x x a x x x a 恒成立 ∵x ∈(0,1) ∴11≥x当x 1=1 即x =1时, 41)211(2++-x 取最大值-2, 41)211(2--x 取最小值0 ∴ -2≤a ≤0, 而 a ≠0 ∴-2≤a <0 即 为所求. 11.已知二次函数c bx ax x f ++=2)(.(1)若a c b >>且0)1(=f ,是否存在实数m ,使得当a m f -=)(成立时,)3(+m f 为正数?若存在,则证明你的结论;若不存在,则说明理由.(2)若+∞<<<∞-21x x ,)()(21x f x f ≠且方程)]()([21)(21x f x f x f +=有两个不相等的实数根,求证:必有一实数根存1x 与2x 之间.证:(1)由f (1)=a +b +c 及a >b >c 得a >0,c <0,ac0< ∵ 1是0)(=x f 的一个根,记另一根为α,则ac=α0<又,,c a b c b a --=>>∴a >-a -c >c ∴-2a <c 即 -2<ac<0假设存在实数m ,使f (m )=-a 成立则由a c ,1是f (x )=0的两根知: f (x )=a (x -ac)(x -1) 从而 f (m )=0)1)((<-=--a m a c m a ∴1<<m ac进而33+<+m ac∴m +3>1 又f (x )在[1,)∞+上单调递增 ∴f (m +3)>f (1)=0 故满足条件的实数m 存在.(2)令g (x )=f (x )-)]()([2121x f x f +, 则g (x )为二次函数∴g (x 1)=f (x 1)-)]()([2121x f x f +∴g (x 2)=f (x 2)-)]()([2121x f x f +∴g (x 1)·g (x 2)=-0)]()([41221<-x f x f又x 1<x 2∴g (x )=0必有一根在x 1,x 2之间 故f (x )=)]()([2121x f x f +必有一根在x 1,x 2之间12.已知函数)0(12)(22<+++=b x cbx x x f 的值域为1[,]3. (1)某某数b ,c 的值;(2)判断函数)(lg )(x f x F =在1[-,]1上的单调性;(3)若∈t R ,求证:57lg≤|)61||61(|+--t t F ≤513lg .解:(1)由∆法得 b =-2 c =2(2) 由(1)f (x )=1221222222+-=++-x xx x x 用定义判断f (x )在[-1,1]上单调递减. ∴F(x )在[-1,1]上单调递减. (3)∵||t -61|-|t +61||≤|t -6161--t |=31∴31|61||61|31≤+--≤-t t∵F(x )在[-1,1]上为减函数∴)31(|)61||61(|)31(F t t F F ≤+--≤-即 513lg |)61||61(|57lg ≤+--≤t t F。
第二期健康教育讲座(老年人中医药保健)

第二期健康教育讲座(老年人中医药保健) 健康教育知识讲座资料第2期村卫生室2018年3月15日目录:1.记录表2.计划3.通知4.课件5.签到册6.总结7.照片资料内容:记录表活动时间:2018年3月15日活动形式:健康教育讲座活动主题:中医药健康知识讲座组织者:主讲人:接受健康教育人员类别:中老年人活动地点:村卫生室接受健康教育人数:30余人健康教育资料发放种类及数量:老年人中医保健30份活动内容:介绍老年人中医保健常识,引起疾病的一些惯和平常应注意的事项等。
活动总结评价:讲座后群众对所讲的中医药保健等知识不了解的地方进行了讨论和提问,我都一一的做了解答,得到了群众的一致好评,群众反响很激烈,要求多举办此类的讲座来增加群众对健康知识的认识和提高。
存档材料请附后填表人(签字):负责人(签字):填表时间:2018年3月15日健康教育讲座计划老年人中医药保健知识讲座为提高全乡人民的健康知晓率,健康行为形成率及疾病知识认知率的重要措施,开展健康教育讲座。
为提高健康文明素质、提高全乡人民生活质量,增加辖区居民的防病意识,特制订中医药健康知识讲座计划。
一、讲座主题:老年人中医药保健知识讲座主讲人:二、时间:2018年3月15日三、地点:村卫生室四、参加单位:村卫生室五、参加人员:村村民六、形式:现场讲座七、内容:介绍老年人中医保健常识,引起疾病的一些惯和平常应注意的事项等。
村卫生室2018年3月10日通知村民:为提高农村居民的健康意识,现举办中医药健康知识讲座,其目的是为了让农村居民进一步了解中医药的分类和使用的知识,树立健康的生活理念。
决定举办健康教育讲座活动,现通知如下:时间:2018年3月15日地点:村卫生室院内讲座内容:介绍老年人中医保健常识,引起疾病的一些惯和平常应注意的事项等。
村卫生室2018年3月14日通知村民:为提高农村居民的健康意识,现举办中医药健康知识讲座,其目的是为了让农村居民进一步了解中医药的分类和使用的知识,树立健康的生活理念。
小学五年级奥数专题讲座25行程问题(二)

第25讲行程问题(二)本讲重点讲相遇问题和追及问题。
在这两个问题中,路程、时间、速度的关系表现为:在实际问题中,总是已知路程、时间、速度中的两个,求另一个。
例1甲车每小时行40千米,乙车每小时行60千米。
两车分别从A ,B 两地同时出发,相向而行,相遇后3小时,甲车到达B 地。
求A ,B 两地的距离。
分析与解:先画示意图如下:图中C 点为相遇地点。
因为从C 点到B 点,甲车行3时,所以C ,B 两地的距离为40×40×3=1203=120(千米)。
这120千米乙车行了120÷120÷60=260=2(时),说明相遇时两车已各行驶了2时,所以A ,B 两地的距离是两地的距离是 (40+60)×2=200(千米)。
例2小明每天早晨按时从家出发上学,李大爷每天早晨也定时出门散步,两人相向而行,小明每分钟行60米,李大爷每分钟行40米,他们每天都在同一时刻相遇。
有一天小明提前出门,因此比平时早9分钟与李大爷相遇,这天小明比平时提前多少分钟出门?分析与解:因为提前9分钟相遇,说明李大爷出门时,小明已经比平时多走了两人9分钟合走的路,分钟合走的路,即多走了即多走了即多走了((60+40)×9=900(米),所以小明比平时早出门900÷900÷60=1560=15(分)。
例3小刚在铁路旁边沿铁路方向的公路上散步,他散步的速度是2米/秒,秒,这时迎面开来一列火车,从车头到车尾经过他这时迎面开来一列火车,从车头到车尾经过他身旁共用18秒。
已知火车全长342米,求火车的速度。
分析与解:在上图中,A 是小刚与火车相遇地点,B 是小刚与火车离开地点。
由题意知,18秒小刚从A 走到B ,火车头从A 走到C ,因为C 到B 正好是火车的长度,所以18秒小刚与火车共行了342米,推知小刚与火车的速度和是342÷342÷18=1918=19(米/秒), 从而求出火车的速度为19-2=17(米/秒)。
中考备考专题讲座

中考备考专题讲座中考,对于每一位初中生来说,都是人生中的一次重要挑战。
它不仅是对我们多年学习成果的检验,更是决定我们未来发展方向的关键一步。
为了帮助同学们更好地应对中考,今天我们来一起探讨一下中考备考的相关问题。
一、明确中考的重要性中考是我们人生中的第一个重要转折点。
它决定了我们能否进入理想的高中,而高中的学习环境和资源又在很大程度上影响着我们能否考上好大学,进而影响我们未来的职业选择和人生道路。
因此,我们必须要高度重视中考,以积极的态度和充分的准备去迎接它。
二、了解中考的考试内容和形式中考通常包括语文、数学、英语、物理、化学、历史、地理、生物等科目。
不同地区的考试科目和分值可能会有所不同,但总体来说,这些科目都是我们初中阶段学习的重点内容。
在考试形式上,一般分为笔试和实验操作、体育测试等部分。
笔试部分主要考查我们对知识的理解、掌握和运用能力;实验操作则考验我们的动手能力和实践操作技巧;体育测试则要求我们具备一定的身体素质和运动能力。
三、制定合理的备考计划1、合理安排时间首先,我们要根据中考的时间安排,制定一个详细的备考计划。
将复习时间合理分配到各个科目上,确保每个科目都有足够的复习时间。
同时,要注意留出一定的时间进行模拟考试和自我检测,以便及时发现问题并进行调整。
2、分阶段复习备考可以分为三个阶段:基础复习阶段、强化复习阶段和冲刺复习阶段。
基础复习阶段,要系统地回顾和梳理初中三年所学的知识,查漏补缺,夯实基础。
对于那些容易遗忘的知识点,可以通过制作笔记、绘制思维导图等方式进行强化记忆。
强化复习阶段,要针对中考的重点和难点进行专项突破。
多做一些历年中考真题和模拟试题,熟悉考试题型和命题规律,提高解题能力和应试技巧。
冲刺复习阶段,要进行最后的综合复习和模拟考试。
通过模拟考试,调整考试状态,适应考试节奏,提高答题速度和准确性。
四、掌握有效的学习方法1、做好课堂笔记课堂笔记是我们复习的重要资料。
在课堂上,要认真听讲,及时记录老师讲的重点、难点和易错点。
膜结构专题讲座1 (2)

膜结构的荷载态分析与结构设计武岳胥传喜(哈尔滨工业大学)(RIGHT TECH(S) PTE LTD)提要由于膜结构特殊的力学特点,其结构分析与设计过程明显不同于传统结构。
文章着重对膜结构荷载态分析中的一些主要问题进行了探讨,包括荷载取值、特别是风荷载的确定方法;荷载态分析的方法及需要注意的一些问题;常见的膜结构分析软件等等。
在此基础上,还介绍了如何根据计算结果来判定结构性能的优劣,以及设计膜、索及索具等构件。
关键词:膜结构风荷载褶皱构件设计Structural Analysis and Design of Membrane StructuresWu Yue Xu Chuanxi(Harbin Institute of Technology)(RIGHT TECH(S) PTE LTD)Abstract: Due to the unique mechanics characters, the analysis and design process of membrane structure is quite different from traditional structures. In this paper, some key problems of membrane structure analysis were discussed. The first question is how to determine the load case, especially for wind effects. Then, the structural analysis methods and some questions should be note were presented. It also introduced some design software of membrane structures. Moreover, it is recommended in this paper that the specified maximum displacement and stress of membrane structure, which can be used to assess the structural performance and select cable and membrane members.Key words: membrane structure, wind load, wrinkling, member design在通过找形得到结构的几何形状和相应的预应力分布后,接下来的工作就是对结构进行荷载态响应分析。
专题02 新定义阅读型问题-中考数学专题拓展提高讲练(教师版)九年级数学中考复习专题讲座

专题二:新定义阅读型问题(学生版)★考点一:规律题型中的新定义◆典例一:定义: a是不为1的有理数,我们把称为a的差倒数.如:2的差倒数是=-1,-1的差倒数是= .已知a1=-,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,a2009=.◆典例二:古希腊数学家把1,3,6,10,15,21,…叫做三角形数,其中1是第一个三角形数,3是第二个三角形数,6是第三个三角形数,…,依此类推,第100个三角形数是__5_050__.★考点二:运算题型中的新定义◆典例一:对于两个不相等的实数a、b ,定义一种新的运算如下,a*b= (a+b>0),如: 3*2==,那么6*(5*4)= 1◆典例二:对于任意实数m,n,定义一种运算m※n=mn-m-n+3,等式的右边是通常的加减和乘法运算.例如:3※5=3×5-3-5+3=10.请根据上述定义解决问题:若a<2※x<7,且解集中有两个整数解,则a的取值范围是__4≤a<5__.★考点三:探索题型中的新定义◆典例一:设a,b是任意两个实数,用max{a,b}表示a,b两数中较大者,例如:max{-1,-1}=-1,max{1,2}=2,max{4,3}=4,参照上面的材料,解答下列问题:(1)max{5,2}=__5__,max{0,3}=__3__;(2)若max{3x+1,-x+1}=-x+1,求x的取值范围;(3)求函数y=x2-2x-4与y=-x+2的图象的交点坐标,函数y=x2-2x-4的图象如图1-1-2所示,请你在图中作出函数y=-x+2的图象,并根据图象直接写出max{-x+2,x2-2x+4}的最小值.◆典例二:定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.如图①,等腰直角四边形ABCD ,AB =BC ,∠ABC =90°. ①若AB =CD =1,AB ∥CD ,求对角线BD 的长. ②若AC ⊥BD ,求证:AD =CD .针对训练1. 定义一种新的运算:x *y =x +2y x ,如:3*1=3+2×13=53,则(2*3)*2=____.2. 如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”,下列各组数据中,能作为一个智慧三角形三边长的一组是( ) A .1,2,3 B .1,1, 2 C .1,1, 3D .1,2, 33. 我们定义:当m ,n 是正实数,且满足m +n =mn 时,就称P ⎝⎛⎭⎫m ,mn 为“完美点”,已知点A (0,5)与点B 都在直线y =-x +b 上,且B 是“完美点”,若C 也是“完美点”且BC =2,则点C 的坐标可以是( )A .(1,2)B .(2,1)C .(3,4)D .(2,4)4. 如果关于x 的一元二次方程ax 2+bx +c =0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,正确的是____(写出所有正确说法的序号). ①方程x 2-x -2=0是倍根方程;②若(x -2)(mx +n )=0是倍根方程,则4m 2+5m n +n 2=0;③若点(p ,q )在反比例函数y =2x的图象上,则关于x 的方程px 2+3x +q =0是倍根方程;④若方程ax 2+bx +c =0是倍根方程,且相异两点M (1+t ,s ),N (4-t ,s )都在抛物线y =ax 2+bx +c 上,则方程ax 2+bx +c =0的一个根为54.5. 若抛物线L :y =ax 2+bx +c (a ,b ,c 是常数,abc ≠0)与直线l 都经过y 轴上的一点P ,且抛物线L 的顶点Q 在直线l 上,则称此直线l 与该抛物线L 具有“一带一路”关系.此时,直线l 叫做抛物线L 的“带线”,抛物线L 叫做直线l 的“路线”.(1)若直线y =mx +1与抛物线y =x 2-2x +n 具有“一带一路”关系,求m ,n 的值;(2)若某“路线”L 的顶点在反比例函数y =6x的图象上,它的“带线”l 的表达式为y =2x -4,求此“路线”L 的表达式;(3)当常数k 满足12≤k ≤2时,求抛物线L :y =ax 2+(3k 2-2k +1)x +k 的“带线”l 与x 轴,y 轴所围成的三角形的面积的取值范围.1.考点解析所谓“新定义”型问题,主要是指在问题中定义了中学数学中没有学过的一些概念、新运算、新符号,要求学生读懂题意并结合已有知识、能力进行理解,根据新定义进行运算、推理、迁移的一种题型.2.考点分类:考点分类见下表考点分类考点内容考点分析与常见题型常考热点三角形三角形的性质与定理一般考点二次函数结合高中二次函数的内容冷门考点圆圆,曲线的新定义【方法点拨】“新定义型专题”关键要把握两点:一是掌握问题原型的特点及其问题解决的思想方法;二是根据问题情景的变化,通过认真思考,合理进行思想方法的迁移.一、中考题型分析“新定义”型问题成为近年来中考数学压轴题的新亮点.在复习中应重视学生应用新的知识解决问题的能力。
【步步高】2014届高三化学一轮总复习 第三章 金属及其化合物 专题讲座二 无机化工流程题复习策略与

(2) 用 化 学 平 衡 移 动 原 理 解 释 Ca(OH)2 溶 液 能 溶 解 杂 卤 石 浸 出 K + 的 原 因 :
_加__入___C_a__(O__H__)_2_溶__液__,___M__g_2_+__与__O__H__-_结___合__生___成__M__g_(_O__H__)_2沉___淀__,___M__g_2_+_浓___ 度___减__小___,__平__衡___正__向___移__动__,___K__+_增___多__。 (3)“除杂”环节中,先加入K__2_C_O__3__溶液,经搅拌等操作后,过滤,再加入__H_2_S__O_4__
专题讲座二 无机化工流程题复习策略与解题 方法指导
一、解题策略
化工流程中常见的操作与名词
化工流程题目在流程上一般分为3个过程:
原料处理 ―→ 分离提纯 ―→ 获得产品
(1)原料处理阶段的常见考点与常见名词 ①加快反应速率 ②溶解:通常用酸溶。如用硫酸、盐酸、浓硫酸等 水浸:与水接触反应或溶解 浸出:固体加水(酸)溶解得到离子 浸出率:固体溶解后,离子在溶液中含量的多少(更多转化) 酸浸:在酸溶液中反应使可溶性金属离子进入溶液,不溶 物通过过滤除去的溶解过程
(4)其他常见考点 ①化学方程式 ②实验仪器 ③计算 ④信息
二、热点题型探究 热点1 碱金属及其矿物的开发利用
【例 1】 (2012·广东理综,32)难溶性杂卤石(K2SO4·MgSO4·2CaSO4·2H2O)属于“呆 矿”,在水中存在如下平衡: K2SO4·MgSO4·2CaSO4·2H2O(s) 2Ca2++2K++Mg2++4SO24-+2H2O 为能充分利用钾资源,用饱和 Ca(OH)2 溶液溶浸杂卤石制备硫酸钾,工艺流程如下:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1 下列说法不.正确的是(双选)( ) A.磷酸的摩尔质量与阿伏加德罗常数(NA)个磷酸分子的质量 在数值上相等 B.常温常压下,0.5NA 个 CO 分子所占体积是 11.2 L C.1 mol(碳正离子)中含有的电子数为 10NA D.12.4 g 白磷中含有的白磷分子数为 0.1NA
【解析】 审题时,首先要注意题目的要求是选择“不正确” 的选项;其次要留意 B 选项中的“常温常压”、C 选项中的 是 CH4 去掉氢阴离子后形成的碳正离子以及 D 选项中的白磷 的化学式是 P4 等。
3.掌握一些常见的解题方法 解选择题,不但要掌握常规思路,而且要能在短时间内产生超 常的思路。要能针对试题特征,寻找隐含信息,敢于从多角度 多层次寻求答案。要善于运用化学的学科思想抓住变化过程的 某个方面,分析清楚,就能形成解题思路,找到解法。守恒原 理(如氧化还原中的“电子得失守恒”、溶液中的“电荷守 恒”、变化过程中的“某元素守恒”、还有质量守恒、体积守 恒等等)、差量原理、平均值原理、整体思维、十字交叉法、 等效原理、极限思维等,往往是“巧思妙解”的基础。
常考专题讲座(二) 选择题常见解法指导
命题研究
在认真审题的基础上,利用自己掌握的概念、原理和热点、重 点知识,通过仔细的分析、比较,周密的思考和全面的判断, 使知识整合,滴水不漏,从而做出正确解答。选择题具有构思 新颖、灵活巧妙、知识容量大、覆盖面广,考试的客观性强, 评分容易、准确等优点;不但能考查考生基础知识的掌握程度, 还能考查学生的思维敏捷性,是化学高考中广泛采用的一种题 型。选择题命题的要求一般是了解、理解层次,虽然难度不大, 但涉及面广、分值高,约占总分的 50%,因此掌握选择题的 解法,快速、准确地解答好选择题是夺取化学高分的关键之一。
通入足量澄清石灰水中,得到 60 g 沉淀,则该氧化物是( )
A.FeO
B.Fe2O3
C.CuO
D.Cu2O
【解析】 思路一:设氧化物为 MOx,然后找关系式,讨论 得答案。 思路二:根据氧化物与二氧化碳的质量比来求解。 根据题意,可知,则 m(氧化物)∶m(二氧化碳)=32.0∶26.4= 1.212,则 M(氧化物)=53.3x,根据选项中的氧化物的摩尔质 量判断 x=1.5,B 项正确。 思路三:根据氧化物中氧的质量分数来求。 根据题意,可知 CO2 比 CO 多了 0.6 mol 的氧原子(9.6 g),是 CO 从氧化物里夺取的,所以氧化物中氧的质量分数为 0.3。 在四个选项中,只有 B。
【答案】 D
(2)排除筛选,步步为营 排除法又称筛选法或淘汰法。根据题干所给的条件和要求,将 选项中不合题意的答案逐个排除,加以淘汰,剩下来的就是正 确答案。 例3 水的状态除了气、液和固态外,还有玻璃态,它是由液 态水急速冷却到 165 K 时形成的,玻璃态的水无固定形状,不 存在晶体结构,且密度与普通液态水的密度相同,有关玻璃态 水的叙述正确的是( ) A.水由液态变为玻璃态,体积缩小 B.水由液态变为玻璃态,体积膨胀 C.玻璃态是水的一种特殊状态 D.玻璃态水是分子晶体
【答案】 B
(4)打破常规,快速作答
例5 在一密闭容器中有 CO、H2、O2 共 16.5 g,用电火花
点燃,使其完全燃烧,再将燃烧后的气体用 Na2O2 充分吸收,
Na2O2 增重 7.5 g,则原混合气体中 O2 的质量分数是( )
A.36%
B.54.5%
C.40%
D.33.3%
【解析】 本题如能求出 CO、H2 的质量,则 O2 的质量分数 便可得出。本题按照常规解题思路是:
热点分析
1.认真审题,把握要点 审题是“审”而不是“看”,审题目的过程中要注意分析题目 中概念的层次,要特别注意试题中一些关键性的字、词,要边 阅读边思索。一要细心审清题目过程的要求:如“不正确的 是”、“错误的是”、“由强到弱排列的是”、“最大的是”、 “一定”、“可能”等。二要准确审清题目的条件:如“所有 主族元素”、“标准状况下”、“温度不变”、“室温时”、 “无色”、“酸性溶液”等。三要留心题目的“陷阱”,对常 见的一些陷阱要千万警惕:如考查气体时经常是非标准状况如 常温常压下、25 ℃时等;考查气体摩尔体积时,常用在标准 状况下非气态的物质来迷惑考生,如 H2O、SO3、己烷、CHCl3 等;考查电解质溶液中微粒数目或浓度时常涉及弱电解质的电 离、盐类水解方面的陷阱。
(1)直接求解,准确无误 例2 已知自然界氧的同位素是168O、187O、188O,氢的同位素
是 H、D、T,从水分子的原子组成来看,自然界的水一共有
() A.6 种
B.9 种
C.12 种
D.18 种
【解析】 从水的分子组成(H2O)来看,3 种氧原子分别与 3 种氢原子可构成 9 种水分子,此外,3 种氢原子混合与 3 种氧 原子又可构成 9 种水分子,因此自然界中的水一共有 18 种。
【解析】 本题是一个信息给予题,读懂信息是解题的关键。 由题给信息知,玻璃态水的“密度与普通液态水的密度相 同”,表明水由液态变玻璃态其体积不变;此外,“玻璃态水 无固定形状,不存在晶体结构”,因而答案 A、B、D 错误。
【答案】 C
(3)广开思路,左右逢源
例4 用足量的 CO 还原 32.0 g 某种氧化物,将生成的气体
第一步写出有关反应的方程式: ①2CO+O2==点=燃==2CO2 ②2H2+O2==点=燃==2H2O ③2CO2+2Na2O2===2Na2CO3+O2 ④2H2O(g)+2Na2O2===4NaOH+O2 第二步设出 CO 和 H2 的质量,并由方程式①和②分别计算出 CO2 和 H2O 的质量。 第三步由 CO2 和 H2O 的质量,根据方程式③和④分别计算出
【答案】 BC
2.注重对高考热点、重点知识的理解 常见的热点、重点知识很多,如阿伏加德罗常数;原子结构、 元素周期表的应用;化学键、晶体类型及性质;氧化还原反应 的概念,氧化还原反应的规律,氧化还原反应方程式的配平; 判断离子方程式的正误,离子共存;溶液浓度、离子浓度的大 小比较及计算;电化学知识;计算化学反应速率,等效平衡, 化学平衡移动及平衡图像等。
