工程光学习题参考答案第一章几何光学基本定律
工程光学-第一章-习题及解答

l
B
200mm
●● ●
A’ A B
2. 一束平行细光束入射到一半径r=30mm、 折射率n=1.5的玻璃球上,求其会聚点的位 置。如果在凸面镀反射膜,其会聚点应在何 处?如果在凹面镀反射膜,则折射光束在玻 璃中的会聚点又在何处?反射光束经前表面 折射后,会聚点又在何处?说明各会聚点的 虚实。
1
r5 30mm
代入①式,得:l5' 75mm (虚像)
距 1 面右侧75mm处
1
2
.
C
3. 有平凸透镜r=100mm,r=∞,d=300mm, n=1.5,当物体在-∞时,求高斯像的位置l’。 在第二面上刻一十字丝,
问: 其通过球面的共轭像处? 当入射高度h=10mm时,实际光线的像方 截距为多少?与高斯像面的距离为多少?
l,l ' , r
dl r l r l'
d
l
l'
0
112
l' l r
Q
C
l
ON
M
h
Q’ N O
l' r
6. 两薄透镜的焦距为 f1' 5.0cm
和
f
' 2
10.0cm
,相距5.0cm。若
一高为2.50cm的物体位于第一透镜前15.0cm处,求最后所成像
4. 一球面镜半径r=-100mm,求β=0,-0.1, -0.2, -1,1,5,10,∞时的物距和像距。
解:
1 12
l
l l r
l
5. 试从费马原理出发,导出凹球面反射镜 近轴成像公式: 1 1 2 ,做出示意图。
工程光学第一章练习参考答案

l 2 ' 15 mm
第一章 16
(2)凸面镀反射膜 r1
l , r 30 , n 1 , n ' 1 n' l' l' n l n' n ' n n ' n r r 1 11 30 15 mm
第一章 16
(3)凹面镀反射膜 (a)在左球面折射
l 2 ' 10 mm
第一章 16
(4)凹面镀反射膜 (a)在左球面折射 (b)在右球面第二次反射
r1
r2
l 2 ' 10 mm
(c)再左球面第三次折射
l 50 mm , r 30 , n 1 . 5 , n ' 1 n' l' 1 l' n l 1 .5 50 n ' n r 1 1 .5 30
n1
I2’
n 1 sin I 1 n 1 sin I 2 ' I1 I 2'
第一章 8
I1’ I1 n 0 sin I 1 n 1 sin I 1 ' n 1 sin I 2 n 2 sin 90 n 2 I 1 ' 90 I 2 I2
n0 n2 n1
3 10 1 . 526
8
1 . 966 10 m / s
8 8
3 10 2 . 417
1 . 241 10 m / s
第一章 4
D=?
h=200mm
全反射问题. (1)
n sin I 1 sin 90 sin I 1 I 41 . 81 n
I
1
工程光学第一章习题及解答

解题技巧总结
建立清晰的解题思路
根据题目要求,建立清晰的解 题思路,明确解题方向和步骤。
提高计算能力
通过练习和总结,提高自己的 计算能力和准确性,避免因计 算失误导致错误。
仔细审题
在开始解题之前,务必仔细阅 读题目,明确题目要求和给定 条件。
准确应用公式和定理
在解题过程中,准确应用相关 的公式和定理,确保适用条件 和范围正确。
注意细节和隐含条件
在解题过程中,注意细节和隐 含条件,确保解题思路和结果 完整准确。
05 习题拓展
相关知识点拓展
01
光的干涉
光的干涉是光波动性的重要表现之一,它涉及到光的相干性、干涉条件、
干涉图样等知识点。可以进一步了解干涉现象在日常生活和科技领域中
的应用,如光学干涉仪、薄膜干涉等。
02
光的衍射
光的衍射描述了光在传播过程中遇到障碍物时发生的偏离直线传播的现
象。可以深入了解衍射与干涉的区别和联系,以及衍射在光学仪器设计、
光谱分析等领域的应用。
03
光学仪器
了解各种光学仪器的基本原理和应用,如显微镜、望远镜、照相机等。
探究这些仪器中光的干涉、衍射等现象的应用,以及如何提高光学仪器
的性能。
类似题目推荐
题目
什么是光的偏振现象?请举例说明。
答案
光的偏振现象是指光波的电矢量或磁矢量在某一特定方向 上振动。例如,自然光通过偏振片后,只能沿特定方向振 动的光波通过,形成线偏振光。
题目
简述光的色散现象。
答案
光的色散现象是指不同波长的光在传播速度上存在差异, 导致白光通过棱镜后分解成不同颜色的光谱。这是因为不 同波长的光在介质中的折射率不同。
取为无穷大。
工程光学习题解答

60 70
A
O
A
A
n0 sin I1 n1 sin I 2 6、解: I 2 900 I m n1 sin I m n2 sin 900 sin I m n2 n1
2 2 n2 n2 2 cos I m 1 2 n0 sin I1 n1 1 2 n12 n2 n1 n1
lr
lp
7-1
或:近视眼的远点距离为 lr 0.5m,其戴上眼睛能看清的远 点距离为物距 l,通过眼镜后成像在眼睛的远点距离 lr 上: 即:由 1 1 2D, 1 1 1 1D 得: l 1m 1000 mm
l lr f 1m l
(5)由于 A R P 8D lr l p 得: l 1 0.11m
H
F2 F1
lH
f
F
d
(lk ) lF
L
第二章 理想光学系统
9、已知一透镜 r1 200mm, r2 300mm, d 50mm, n 1.5 , 求其焦距、光焦度、基点位置。 nr1r2 解: f 1440mm 1.44m (n 1)[ n(r2 r1 ) (n 1)] 1 0.69 D f n 1 n 1 f lH d1 120mm, lH f d 2 80mm n n lH f 1560mm, lF l H f 1360mm lF
tan y / 250 y h P 250 h y 而:y D P 2 250 h 500 h 500 9 2y 10(mm ) 所以: P P 9 50
y
l 200 mm 250 mm
工程光学习题解答(第1章)

第一章1.举例说明符合光传播基本定律的生活现象及各定律的应用。
答:(1)光的直线传播定律影子的形成;日蚀;月蚀;均可证明此定律.应用:许多精密的测量,如大地测量(地形地貌测量),光学测量,天文测量.(2)光的独立传播定律定律:不同光源发出的光在空间某点相遇时,彼此互不影响,各光束独立传播。
说明:各光束在一点交会,光的强度是各光束强度的简单叠加,离开交会点后,各光束仍按各自原来的方向传播。
2.已知真空中的光速c≈3×108m/s,求光在水(n=1。
333)、冕牌玻璃(n=1。
51)、火石玻璃(n=1。
65)、加拿大树胶(n=1。
526)、金刚石(n=2.417)等介质中的光速。
解:v=c/n(1)光在水中的速度:v=3×108/1。
333=2.25×108 m/s(2)光在冕牌玻璃中的速度:v=3×108/1。
51=1。
99×108 m/s(3)光在火石玻璃中的速度:v=3×108/1。
65=1。
82×108 m/s(4)光在加拿大树胶中的速度:v=3×108/1。
526=1。
97×108 m/s(5)光在金刚石中的速度:v=3×108/2.417=1。
24×108m/s*背景资料:最初用于制造镜头的玻璃,就是普通窗户玻璃或酒瓶上的疙瘩,形状类似“冠”,皇冠玻璃或冕牌玻璃的名称由此而来。
那时候的玻璃极不均匀,多泡沫。
除了冕牌玻璃外还有另一种含铅量较多的燧石玻璃(也称火石玻璃).3.一物体经针孔相机在屏上成像的大小为60mm,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:⇒l=300mm4.一厚度为200mm的平行平板玻璃(设n=1。
5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:本题是关于全反射条件的问题。
工程光学习题答案

⼯程光学习题答案⼯程光学习题答案第⼀章习题及答案1、已知真空中的光速c=3*108m/s,求光在⽔(n=1.333)、冕牌玻璃(n=1.51)、⽕⽯玻璃(n=1.65)、加拿⼤树胶(n=1.526)、⾦刚⽯(n=2.417)等介质中的光速。
解:则当光在⽔中, n=1.333 时,v=2.25*108m/s,当光在冕牌玻璃中,n=1.51 时,v=1.99*108m/s,当光在⽕⽯玻璃中,n=1.65 时,v=1.82*108m/s,当光在加拿⼤树胶中,n=1.526 时,v=1.97*108m/s,当光在⾦刚⽯中,n=2.417 时,v=1.24*108m/s。
2、⼀物体经针孔相机在屏上成⼀60mm ⼤⼩的像,若将屏拉远50mm,则像的⼤⼩变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则⽅向不变,令屏到针孔的初始距离为x,则可以根据三⾓形相似得出:所以x=300mm 即屏到针孔的初始距离为300mm。
3、⼀厚度为200mm 的平⾏平板玻璃(设n=1.5),下⾯放⼀直径为1mm 的⾦属⽚。
若在玻璃板上盖⼀圆形纸⽚,要求在玻璃板上⽅任何⽅向上都看不到该⾦属⽚,问纸⽚最⼩直径应为多少?解:令纸⽚最⼩半径为x,则根据全反射原理,光束由玻璃射向空⽓中时满⾜⼊射⾓度⼤于或等于全反射临界⾓时均会发⽣全反射,⽽这⾥正是由于这个原因导致在玻璃板上⽅看不到⾦属⽚。
⽽全反射临界⾓求取⽅法为:(1)其中n2=1, n1=1.5,同时根据⼏何关系,利⽤平板厚度和纸⽚以及⾦属⽚的半径得到全反射临界⾓的计算⽅法为:(2)联⽴(1)式和(2)式可以求出纸⽚最⼩直径x=179.385mm,所以纸⽚最⼩直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1 为光在光纤内能以全反射⽅式传播时在⼊射端⾯的最⼤⼊射⾓)。
工程光学第3版第一章习题答案
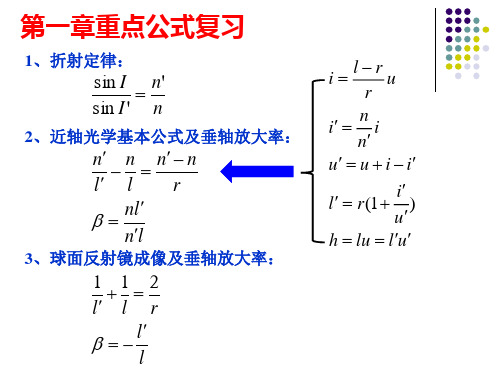
n sinቤተ መጻሕፍቲ ባይዱI3 sin I 4 , I 4 60
[习题15]一直径为20mm的玻璃球,其折射率 为 3 ,今有一光线以60入射角入射到该玻璃 球上,试分析光线经过玻璃球的传播情况。
同理,由B点发出的反射光线可以 到达C点处,并发生反射折射现象。 C点发出的反射光线再次到达A点, 并发生反射折射现象。 即在ABC三点的反射光线构成正三 角形的三条边,同时,在这三点 有折射光线以60°角进入空气中。
lr i u r n i i n u u i i i l r (1 ) u h lu l u
[习题20] 一球面镜半径r=-100mm,求=0、0.1×、-0.2×、-1×、1×、5×、10×、时的物距 和像距。
解:根据球面反射镜成像及垂轴放大率公式
[习题16解答]
(3)光束先经左侧球面折射形成 , 像 A1 ,再经右侧球面反射形成像 A2 。 最后经左侧球面折射形成像 A3 由(1)得,l2 30 代入公式: 1 1 2 l l r l2 10, 2 0 得, l2 l2
12 12 0
[习题16]一束平行细光束入射到一半径为 r=30mm、折射率n=1.5的玻璃球上,求其会聚 点的位置。如果在凸面镀上反射膜,其会聚点 应在何处?如果在凹面镀反射膜,则反射光束 在玻璃中的会聚点又在何处?反射光束经前表 面折射后,会聚点又在何处?说明各会聚点的 虚实。
[习题16解答]
(1)折射玻璃球 成像过程:光束先经左侧 球面折射形成像 A 1 ,再经 。 右侧球面折射形成像 A2 n n n n l l r nl1 求得: l1 90, 1 0 nl1
1 1 2 l l r l l
工程光学第一章习题及解答

n2
1.5
n' 2
1
r2
30mm
1
2
l2 90 60 30mm
.
带入①式可得:l2' 15mm(实像) C
距 2 面右侧15mm处
解: (2)满足②式 1/ l' 1/ l 2 / r
l3 r3 30mm
带入②式可得:l3' 15mm (虚像)
l3
l
' 2
10cm
n3 1.5
nl ' / n'l
n3' 1
r3 20cm y3 1 / 6cm
得:
l
' 3
8cm
3 1.2
y3 0.2cm
l'
r
l
解: L() Q M MQ ' h2 (2r )
L() (l )2 h2 (l' )2 h2
l2 2(r l) l'2 2(r l')
dl
rl
r l'
d l2 2(r l) l'2 2(r l')
1
r5 30mm
代入①式,得:l5' 75mm (虚像)
距 1 面右侧75mm处
1
2
.
C
3. 有平凸透镜r=100mm,r=∞,d=300mm, n=1.5,当物体在-∞时,求高斯像的位置l’。 在第二面上刻一十字丝,
问: 其通过球面的共轭像处? 当入射高度h=10mm时,实际光线的像方 截距为多少?与高斯像面的距离为多少?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 几何光学基本定律1.已知真空中的光速c =3810⨯m/s ,求光在水(n=)、冕牌玻璃(n=)、火石玻璃(n=)、加拿大树胶(n=)、金刚石(n=)等介质中的光速。
解:则当光在水中,n=时,v= m/s, 当光在冕牌玻璃中,n=时,v= m/s, 当光在火石玻璃中,n =时,v= m/s , 当光在加拿大树胶中,n=时,v= m/s , 当光在金刚石中,n=时,v= m/s 。
2. 一物体经针孔相机在 屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:,所以x=300mm即屏到针孔的初始距离为300mm 。
3. 一厚度为200mm 的平行平板玻璃(设n =),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形的纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片的最小直径应为多少1mmI 1=90︒ n 1 n 2200mmL I 2x2211sin sin I n I n =66666.01sin 22==n I745356.066666.01cos 22=-=I88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ,包层的折射率为2n ,光纤所在介质的折射率为0n ,求光纤的数值孔径(即10sin I n ,其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有: n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n 0 .5. 一束平行细光束入射到一半径r=30mm 、折射率n=的玻璃球上,求其会聚点的位置。
如果在凸面镀反射膜,其会聚点应在何处如果在凹面镀反射膜,则反射光束在玻璃中的会聚点又在何处反射光束经前表面折射后,会聚点又在何处说明各会聚点的虚实。
解:该题可以应用单个折射面的高斯公式来解决,设凸面为第一面,凹面为第二面。
(1)首先考虑光束射入玻璃球第一面时的状态,使用高斯公式:会聚点位于第二面后15mm处。
(2)将第一面镀膜,就相当于凸面镜像位于第一面的右侧,只是延长线的交点,因此是虚像。
还可以用β正负判断:(3)光线经过第一面折射:, 虚像第二面镀膜,则:得到:(4)在经过第一面折射物像相反为虚像。
6.一直径为400mm,折射率为的玻璃球中有两个小气泡,一个位于球心,另一个位于1/2半径处。
沿两气泡连线方向在球两边观察,问看到的气泡在何处如果在水中观察,看到的气泡又在何处解:设一个气泡在中心处,另一个在第二面和中心之间。
(1)从第一面向第二面看(2)从第二面向第一面看(3)在水中7.有一平凸透镜r1=100mm,r2,d=300mm,n=,当物体在时,求高斯像的位置'l。
在第二面上刻一十字丝,问其通过球面的共轭像在何处当入射高度h=10mm,实际光线的像方截距为多少与高斯像面的距离为多少解:8.一球面镜半径r=-100mm,求=0 ,⨯-1.0 ,⨯-2.0 ,-1⨯ ,⨯1 ,⨯5,⨯10,∝时的物距和象距。
解:(1)(2) 同理,(3)同理, (4)同理,(5)同理,(6)同理,(7)同理,(8)同理,9. 一物体位于半径为r 的凹面镜前什么位置时,可分别得到:放大4倍的实像,当大4倍的虚像、缩小4倍的实像和缩小4倍的虚像解:(1)放大4倍的实像(2)放大四倍虚像(3)缩小四倍实像(4)缩小四倍虚像10.一个直径为200mm的玻璃球,折射率为,球内有两个小气泡,从球外看其中一个恰好在球心。
从最近的方位去看另一个气泡,它位于球表面和球心的中间。
求两气泡的实际位置。
(解题思路)玻璃球内部的气泡作为实物经单球面折射成像。
由于人眼的瞳孔直径很小,约2—3毫米,且是从离气泡最近的方位观察,所以本题是单球面折射的近轴成像问题。
题中给出的是像距s’, 需要求的是物距是s。
解:(1)n= n’= r=-100mms’=-100mm 代入成像公式s=-100mm物为实物,且和像的位置重合,且位于球心。
(2)对另一个气泡,已知n=;n’=; r=-100mms’=-50mm . 代入成像公式s=-60.47mm气泡为实物,它的实际位置在离球心()=39.53mm的地方。
讨论:对于第一个气泡,也可以根据光的可逆性来确定。
因为第一个气泡和像是重合的,由可逆性将像视为物,经球面折射后仍成在相同的位置。
所以像和物只能位于球心。
11一直径为20mm 的玻璃球,其折射率为3,今有一光线一60。
入射角入射到该玻璃球上,试分析光线经玻璃球传播情况。
解:在入射点A 处。
同时发生折射和反射现象2211sin sin I n I n =Θ 5.0360sin sin 2==︒I302︒=I∴在A 点处光线以30︒的折射角进入玻璃球,同时又以60︒的反射角返回原介质。
根据球的对称性,知折射光线将到达图中B 点处,并发生折射反射现象。
3023︒==I I Θ 305︒=∴II I n 43sin sin = 23sin 4=I ︒=604I同理:由B 点发出的反射光线可以到达C 点处,并发生反射折射现象︒=307I 608︒=IB 点的反射光线可再次到达A 点,并发生折、反现象。
309︒=I 30210︒==I I60110︒='=I I由以上分析可知:当光线以60︒入射角射入折射率为3的玻璃球,后,可在如图A ,B ,C 三点连续产生折射反射现象。
ABC 构成了玻璃球的内解正三角形,在ABC 三点的反射光线构成了正三角形的三条边。
同时,在ABC 三点有折射光线一60︒角进入空气中事实上:光照射到透明介质光滑界面上时,大部分折射到另一介质中,也有小部分光反射回原来的介质中当光照射到透明介质界面上时,折射是最主要的,反射是次要的12有平凸透镜r 1=100mm ,r 2=∞,d=300mm ,n=,当物体在-∞时,求高斯像的位置l’。
在第二面上刻一十字丝,问其通过球面的共轭像处当入射高度h=10mm 时,实际光线的像方截距为多少与高斯像面的距离为多少解 1) 由r nn l l -'=-'11代入 ∞=1l , 5.11='n ,11=n ,1001=r 得: mm l 3001='mm d l l 030030012=-=-'=mm l 02='∴即:物体位于-∞时,其高斯像点在第二面的中心处。
2)由光路的可逆性可知 :第二面上的十字丝像在物方∞处。
3)当mm h 101=时1.010010sin 11===r h I 06667.01.0*5.11sin *sin =='='I n n I ︒=='822.306667.0arcsin I︒=-+='-+='9172.1822.3739.50I I u umm u I r L 374.299)0334547.006667.01(*100)sin sin 1(*/=+='+=' mm d L L 626.012-=-'=︒='=-9172.12u I05018.09172.1sin *5.1sin *1sin 22-=︒-=='I n I ︒-='87647.22I︒︒︒︒=+-='-+='87647.287647.29172.19172.12222I I u u由△关系可得:mm tg u tg L x 02095.09172.1*626.02-=-='=︒mm tg L 4169.087467.202095.02-=-='︒ 它与高斯像面的距离为-0.4169mm重点:1︒ 所有的折射面都有贡献。
2︒ 近轴光线和远轴光线的区别。
13一球面镜半径r =-100mm ,求β=0,-0.1x ,-0.2x ,-1x ,1x ,5x ,10x,∞时的物距和像距。
求β=0,-x , -x ,-1x ,1x ,5x ,10x ,∞时的l,l’解:r l l 211=+' ,ll '-=β1) 0=β时, ,50-=l -∞=l0='l , 50-='l (可用解)2) 1.0-=β时, ,550-=l mm l 55-='3) 2.0-=β时, mm l 300-=, mm l 60-='4) 1-=β时, ,100mm l -= mm l 100-='5) 1=β时, mm l 0=, mm l 0='6) 5=β时, mm l 40-=, mm l 200='7) 10=β时, mm l 45-=, mm l 450='8) ∞=β时, mm l 50-=, -∞='l14 思考题:为什么日出或日落时太阳看起来是扁的答:日出或日落时,太阳位于地平线附近。
对于地球的一点,来自太阳顶部、中部和底部的光线射向地球大气层的入射角依次增大。
同时,由于大气层的密度不均匀,引起折射率n 随接近地面而逐渐增大。
所以当光线穿过大气层射向地面时,折射率n 逐渐增大,其折射角逐渐减少,光线的传播路径发生弯曲。
我们沿着光线看去,看到的发光点位置比其实际位置抬高。
另一方面,折射光线的弯曲程度还与光线入射角有关。
入射角越大的光线,弯曲越厉害,视觉位置被抬的越高。
因此从太阳上部到太阳下部发出的光线,入射角逐渐增大,下部的视觉位置就依次比上部抬的更高。
所以,日出和日落时太阳看起来呈扁椭圆形。
