三角形单元复习精品课件
合集下载
全等三角形单元复习课 —初中数学课件PPT

( C)
A. 7 cm B. 5 cm C. 8 cm D. 无法确定
知识点2:全等三角形的判定方法 【例2】(2017宜宾)如图1-12-18-3,已知点B,E,C,F在 同一条直线上,AB=DE,∠A=∠D,AC∥DF. 求证:BE=CF.
证明:∵AC∥DF,∴∠ACB=∠F. 在△ABC和△DEF中,
解:(1)∵t=1 s, ∴BP=CQ=3×1=3(cm). ∵AB=10 cm,点D为AB的中点, ∴BD=5 (cm). 又∵BC=8 cm, ∴PC=BC-BP=8-3=5(cm). ∴PC=BD. 又∵∠B=∠C,∴△BPD≌△CQP (SAS). (2)∵vP≠vQ,∴BP≠CQ. 又∵△BPD与△CQP全等,∠B=∠C, 则BP=PC=4(cm),CQ=BD=5(cm). ∴点P,点Q运动的时间
∴△BOE≌△COF(SAS). ∴∠E=∠F. ∴EB∥CF.
拓展提升
8. 如图1-12-18-11,在△ABC中,AB=AC,BE⊥AC于点
E,CF⊥AB于点F,且BE,CF交于点D,则下列结论:①△ABE≌△ACF;②△B源自F≌△CDE;③D点在∠BAC的平分
线上.其中正确的是
(
)D
A. ① B. ①② C. ②③ D. ①②③
第一部分 新课内容
第十二章 全等三角形
全等三角形单元复习课
核心知识
1. 全等三角形的定义及性质. 2. 全等三角形的判定方法. 3. 角的平分线的性质及相关证明.
典型例题
知识点1:全等三角形的定义及性质
【例1】如图1-12-18-1,△ABC≌△CDA,AC=7 cm,AB=5
cm,BC=8 cm,则AD的长是
A. 15° B. 30° C. 45° D. 60°
《三角形复习》课件

(13 厘米)
( 7 厘米)
(20厘米)
(13 厘米)
( 7 厘米)
(20厘米)
有两条线段长度的和等于第三条线段的长度 不能围成三角形
想一想:这三根小棒能围成三角形吗?为什么? (9 厘米) (15厘米) (20厘米)
(15厘米)
(9 厘米) (20厘米) Nhomakorabea(15厘米)
(9 厘米) (20厘米)
平 面
图图 形形 的 分 类
立 体 图 形
由
线
平
段 围
面
成 的
图图 形形
图 形
的
由
分
曲 线
类
围 成
的
图
立
形
体
图
形
平 面 图
图形 形 的 分 类
立 体 图 形
由
线
三
段
角
围
形
成
的
图
四
形
边
形
由 曲 线 围 成 的 图 形
学习目标
1、学会整理知识点提纲,能熟练掌 握三角形的相关知识。
2、利用三角形的知识解决实际问题。
快速看书24页—31页内容,想一想,我们都学习 了哪些有关三角形的知识? 1、把三角形按角、按边进行分类。 2、梳理“三角形内角和”的知识。 3、梳理“三角形边的关系”的知识。 4、归纳关于三角形知识点提纲, 并作好记录。
先自学,再在小组内交流, 5分钟后,比一比谁的提纲整理得最完整。
三角形分类
2008北京奥运会主体育场—鸟巢。
埃及的金字塔每个侧面都是三 角形,距今有四五千年的历史, 依然屹立不倒。
这是世界著名建筑,法国的埃菲尔铁塔, 它的每个侧面都是由许多三角形组成的。
三角形全等判定复习ppt课件
N 明方法与前题基本相同,只
须证明⊿ABN≌⊿BCM
A
C
B
变式4:如图,⊿ABD,⊿ACE都是正三角形, 求证CD=BE
D
A
E
B
C
分析:此题实质上是把题目中的条件B,A,C三点改为 不共线,证明方法与前题基本相同.
变式6:如图,分别以⊿ABC的边AB,AC为一边 画正方形AEDB和正方形ACFG,连结CE,BG.
求证BG=CE
E
分析:此题是把两个三
角形改成两个正方形而
D
A
G 以,证法类同
FBBiblioteka C小结:1.证明两个三角形全等,要结合题目的条件 和结论,选择恰当的判定方法
2.全等三角形,是证明两条线段或两个角相 等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三 角形中。
②分析要证两个三角形全等,已有什么条件,还缺 什么条件。
AB=CB
A
AD=CD
BD=BD
_
=
P
∴ △ABD≌△CBD(SSS)
B
D
∴∠ABD=∠CBD
_
=
在△ABP和△CBP中
C
AB=BC
∠ABP=∠CBP
BP=BP
∴ △ABP ≌ △CBP(SAS)
∴PA=PC
例4。已知:如图AB=AE,∠B=∠E,BC=ED AF⊥CD 求证:点F是CD的中点
分析:要证CF=DF可以考虑CF 、 DF所在的两个三角形全等,为此可 添加辅助线构建三角形全等 ,如何 添加辅助线呢?
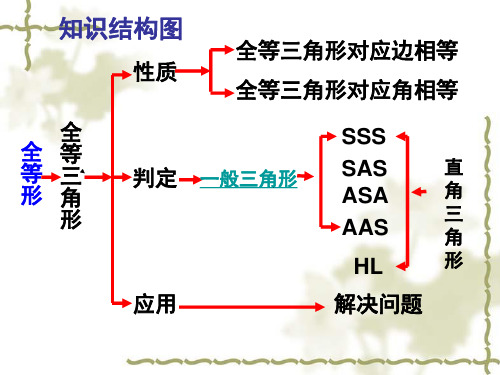
知识结构图
性质
全等三角形对应边相等 全等三角形对应角相等
全 全等 等三 形角
形
人教版八年级数学上册第12章 全等三角形 单元复习 课件

∵BF∥AC,DE⊥AC,∴BF⊥DF,
∵BC平分∠ABF,DH⊥AB,DF⊥BF,∴DH=DF,
∴DE=DF,
∴点D为EF的中点.
(2)∵BF∥AC,∴∠C=∠DBF,
∵BC平分∠ABF,∴∠ABD=∠DBF,∴∠C=∠ABD,
∵AD平分∠BAC,∴∠CAD=∠BAD,
又AD=AD,∴△DCA≌△DBA,∴∠CDA=∠BDA,
应角与对角的概念.一般地,对应边、对应角是对两个三
角形而言,而对边、对角是对同一个三角形的边和角而言,
对边是指角的对边,对角是指边的对角.
1.已知△ABC≌△A1B1C1,A和A1对应,B和B1对应,
∠A=70°,∠B1=50°,则∠C的度数为( D )
A.70°
B.50°
C.120°
D.60°
2.(全国视野)(2022南京模拟)如图,四边形ABCD的对角
证明:(1)在Rt△BOF和Rt△COE中,
∵OF=OE,OB=OC,
∴Rt△BOF≌Rt△COE(HL).
∴∠FBO=∠ECO,即∠ABO=∠ACO.
(2)连接AO.∵OF⊥AB,OE⊥AC,且OF=OE,
∴∠BAO=∠CAO.
∵∠ABO=∠ACO,AO=AO,
∴△BOA≌△COA(AAS),∴AB=AC.
则BD=
1 .
22.如图,过点B,D分别向线段AE作垂线段BQ和DF,
点Q和F是垂足,连接AB,DE,BD,BD交AE于点C,且
AB=DE,AF=EQ.
(1)求证:△ABQ≌△EDF;
(2)求证:点C是BD的中点.
证明:(1)∵AF=EQ,∴AQ=EF,在Rt△ABQ和Rt△EDF中,
=
完整版-全等三角形总复习PPT教学课件

AC=BC
∠BCE=∠DCA
DC=EC
∴ △ACD≌△BCE (SAS)
∴ BE=AD
2024/3/9
29
6. 如图A、B、C在一直线上,△ABD,△BCE都是等边 三角形,AE交BD于F,DC交BE于G,求证:BF=BG。
AB
=
DB
∠ABE = ∠ DBC
BE=BC ∴△ABE≌△DBC(SAS)
D
C
2
1
A
B
思路3: 已知一边一角(边与角相邻):
找夹这个角的另一边
AD=CB (SAS)
找夹这条边的另一角
∠ACD=∠CAB(ASA)
找边的对角
∠D=∠(B AAS)
15
如图,已知∠B= ∠E,要识别△ABC≌ △AED,需 要添加的一个条件是--------------
A
D
C
E
思路4:
找夹边
AB=AE (ASA)
∴ △ADC ≌ △EDB
D
C
∴ AC = EB
在△ABE中,AE < AB+BE=AB+AC
E
即 2AD < AB+AC
∴ AD 1 (AB AC) 2
2024/3/9
35
12.如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA, CD过点E,则AB与AC+BD相等吗?请说明理由。
C A
∵ QD⊥OA,QE⊥OB,QD=QE(已知). ∴点Q在∠AOB的平分线上.(到角的两边的距
离相等的点在角的平分线上)
2024/3/9
10
2.如图, △ABC的角平分线BM,CN相交于点P, 求证:点P到三边AB、BC、CA的距离相等
人教版八年级上册 三角形小结与复习课件 (共39张PPT)

广东省怀集县凤岗镇初级中学 黎方和
一、基础知识
练一练: 1、已知△ABC中,∠A=∠B+∠C,则∠A的度数为 ( B)
A.100° B.90° C.80° D.85°
2、三角形的每个外角都为120°,则这个三角 形是( C )
A、直角三角形 B、等腰三角形 C、等边三角形 D、钝角三角形
一、基础知识
A.11
B.12
C.13
D.14
4.如图,在△ABC 中,∠ACB=100°,∠A=20°,D 是 AB 上一点,
将△ABC 沿 CD 折叠,使 B 点落在 AC 边上的 B′处,则∠ADB′等于( D )
A.25°
B.30°
C.35°
D.40°
第4题
二、填空题 5.如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三 角形具有____稳定 _____性.
角形的第三边长m的取值范是 6〈m〈10
.
广东省怀集县凤岗镇初级中学 黎方和
一、基础知识
3、如图,在△ABC中,AD是BC上的中线,BE 是△ABD中AD边上的中线,若△ABC的面积是 24,则ABE的面积是( B )
A
A、3
B、6
E
C、9
D、12
C
B
D
广东省怀集县凤岗镇初级中学 黎方和
一、基础知识
F
B 广东省怀集县凤岗镇初级中学
G 黎方和
E C
二. 强化训练 8.如图,∠A=∠C=90°,BE,DF分别为 ∠ABC与∠ADC的平分线,能判断BE∥DF吗? 试说明理由.
广东省怀集县凤岗镇初级中学 黎方和
一、选择题 章末检测
1.如图,在△ABC 中,∠BAC=x°,∠B=2x°,∠C=3x°,则∠BAD 的度数( B )
一、基础知识
练一练: 1、已知△ABC中,∠A=∠B+∠C,则∠A的度数为 ( B)
A.100° B.90° C.80° D.85°
2、三角形的每个外角都为120°,则这个三角 形是( C )
A、直角三角形 B、等腰三角形 C、等边三角形 D、钝角三角形
一、基础知识
A.11
B.12
C.13
D.14
4.如图,在△ABC 中,∠ACB=100°,∠A=20°,D 是 AB 上一点,
将△ABC 沿 CD 折叠,使 B 点落在 AC 边上的 B′处,则∠ADB′等于( D )
A.25°
B.30°
C.35°
D.40°
第4题
二、填空题 5.如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三 角形具有____稳定 _____性.
角形的第三边长m的取值范是 6〈m〈10
.
广东省怀集县凤岗镇初级中学 黎方和
一、基础知识
3、如图,在△ABC中,AD是BC上的中线,BE 是△ABD中AD边上的中线,若△ABC的面积是 24,则ABE的面积是( B )
A
A、3
B、6
E
C、9
D、12
C
B
D
广东省怀集县凤岗镇初级中学 黎方和
一、基础知识
F
B 广东省怀集县凤岗镇初级中学
G 黎方和
E C
二. 强化训练 8.如图,∠A=∠C=90°,BE,DF分别为 ∠ABC与∠ADC的平分线,能判断BE∥DF吗? 试说明理由.
广东省怀集县凤岗镇初级中学 黎方和
一、选择题 章末检测
1.如图,在△ABC 中,∠BAC=x°,∠B=2x°,∠C=3x°,则∠BAD 的度数( B )
鲁教版(五四制)七上数学第一章三角形单元综合复习课件

所以△ NBM≌△NCM(SSS).所以∠NBM=∠NCM. 所以∠NBM+∠ABN=∠NCM+∠DCN. 所以∠ABC=∠DCB.
10.用尺规画直角的正确方法是( C ) A.用量角器 B.用三角板 C.平分平角 D.作两个锐角互余
【解析】用尺规作图时要使用没有刻度的直 尺和圆规作图.
11.已知四边形ABCD是平行四边形,如图,把△ABD 沿对角线BD翻折180°得到△A′BD.利用尺规作出 △A′BD.(要求保留作图痕迹,不写作法)
解:因为AD⊥BC,所以∠BDA=90°. 因为∠B=60°,所以∠BAD=180°-90°-60°=30°. 因为∠BAC=80°, 所以∠DAC=∠BAC-∠BAD=80°-30°=50°. 因为 AE 平分∠DAC,所以∠DAE=12∠DAC=25°.
3.下列图形中,是全等图形的有( C ) A.2组 B.3组 C.4组 D.5组
解:如图,连接AC,BD,交于点O,公共展厅应建 在O处.理由如下: 在平面上任取一点P,P与O不重合,连接 PA,PB,PC,PD,则PA+PC>AC,PB+PD>BD, 即PA+PC+PB+PD>AC+BD=AO+BO+CO+DO, 所以建在点O处,四个工艺品厂到公共展厅的距离之 和最短.
7.如图,在Rt△ABC中,∠ACB=90°,且AC= BC=4 cm.已知△BCD≌△ACE,求四边形 AECD的面积. 【解析】线段AC把四边形AECD分成 两部分,我们把△ACE移至△BCD的 位置,使之与△ACD恰好构成△ACB, 进而可求面积.
(2)以∠AEC为内角的三角形有哪些? 【解析】用字母表示一个三角形时,不要漏 写符号“△”.在复杂图形中数三角形个数 的方法:按组成三角形的图形个数去数;
10.用尺规画直角的正确方法是( C ) A.用量角器 B.用三角板 C.平分平角 D.作两个锐角互余
【解析】用尺规作图时要使用没有刻度的直 尺和圆规作图.
11.已知四边形ABCD是平行四边形,如图,把△ABD 沿对角线BD翻折180°得到△A′BD.利用尺规作出 △A′BD.(要求保留作图痕迹,不写作法)
解:因为AD⊥BC,所以∠BDA=90°. 因为∠B=60°,所以∠BAD=180°-90°-60°=30°. 因为∠BAC=80°, 所以∠DAC=∠BAC-∠BAD=80°-30°=50°. 因为 AE 平分∠DAC,所以∠DAE=12∠DAC=25°.
3.下列图形中,是全等图形的有( C ) A.2组 B.3组 C.4组 D.5组
解:如图,连接AC,BD,交于点O,公共展厅应建 在O处.理由如下: 在平面上任取一点P,P与O不重合,连接 PA,PB,PC,PD,则PA+PC>AC,PB+PD>BD, 即PA+PC+PB+PD>AC+BD=AO+BO+CO+DO, 所以建在点O处,四个工艺品厂到公共展厅的距离之 和最短.
7.如图,在Rt△ABC中,∠ACB=90°,且AC= BC=4 cm.已知△BCD≌△ACE,求四边形 AECD的面积. 【解析】线段AC把四边形AECD分成 两部分,我们把△ACE移至△BCD的 位置,使之与△ACD恰好构成△ACB, 进而可求面积.
(2)以∠AEC为内角的三角形有哪些? 【解析】用字母表示一个三角形时,不要漏 写符号“△”.在复杂图形中数三角形个数 的方法:按组成三角形的图形个数去数;
12章--全等三角形-复习课件

∠B=∠C
D
E
AB=AC
B
C
∠A=∠A
∴ △ACD≌△ABE
(ASA)
∴ AD=AE
第9页,共29页。
3、如图,OB⊥AB,OC⊥AC,垂足为B,C,OB=OC, AO平分∠BAC吗?为什么?
B
答: AO平分∠BAC
理由:∵ OB⊥AB,OC⊥AC
A
O
∴ ∠B=∠C=90°
在Rt△ABO和Rt△ACO中
证明:在△ABC和△ADC中
A
AC=AC
AB=AD
CB=CD
∴ △ABC≌△ADC (SSS)
∴ ∠BAC= ∠DAC
B
C
∴ AC平分∠BAD
D
第8页,共29页。
2、如图,D在AB上,E在AC上,
AB=AC ,∠B=∠C, 试问AD=AE吗?为什
么?
解: AD=AE
A
理由: 在△ACD和△ABE中
第26页,共29页。
5、如图5,已知:AB=CD,AD=CB,O为AC任 一点,过O作直线分别交AB、CD的延长线于F、E, 求证:∠E=∠F.
提示:由条件易证△ABC≌△CDA 从而得知∠BAC=
∠DCA ,即:AB∥CD.
第27页,共29页。
知识梳理:
1:什么是全等三角形?一个三角形经过哪些变化 可以得到它的全等形?
变式:以上条件不变,将
△ABC绕点C旋转一定角度(大
AC=BC
于零度而小于六十度),以上的 结论还成立吗?
∠BCE=∠DCA
DC=EC
∴ △ACD≌△BCE (SAS)
∴ BE=AD
第17页,共29页。
例题精析:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)按边的相等关系分类:
三边都不相等的三角形
三角形
等腰三角形
底边和腰不相等的等腰三角形 等边三角形
(3)三角形的主要线段: ①三角形的高:
∠BEC=90°, ∠ADB=90°, S△ABC=12BC·AD=12AC·BE.
②三角形的中线:
1 BD=CD=2BC,
1 S△ABD=S△ACD=2S△ABC.
③三角形的角平分线: 1
∠ABD=∠CBD=2∠ABC.
(4)三角形三边关系: 三角形的两边之和 大于 第三边, 三角形的两边之差 小于 第三边.
(5)三角形的稳定性.
三角形单元复习精品课件
对点训练
1.下列各组值代表线段的长度,其中能组成三角形的是( B )
A.1,2,3 B.20,15,8 C.5,15,8 D.4,5,9
(4)三角形的外角性质:
①三角形的外角和等于 360° ; ②三角形的一个外角 等于 和它不相邻的两个内角的和.
(5)直角三角形:
有一个角为 90° 的三角形,叫做直角三角形. 在直角三角形中,两个锐角 互余 .
三角形单元复习精品课件
三角形单元复习精品课件
4.在△ABC 中,如果∠A=60°,∠B=45°,那么∠C 等于( C )
A.115°
B.105°
C.75°
D.45°
三角形单元复习精品课件
三角形单元复习精品课件
5.如图,在△ABC 中,点 D 是 BC 上一点,∠ADB=130°,
∠CAD=54°,则∠C= 76°.
三角形单元复习精品课件
三角形单元复习精品课件
6.如图,则∠1= 85 °,∠2= 95 °,∠3= 45 °.
三角形单元复习精品课件
三角形单元复习精品课件
7.如图,在 Rt△ABC 中,∠ACB=90°,∠A=36°,△ABC 的外角∠CBD 的平分线 BE 交 AC 的延长线于点 E. (1)求∠CBE 的度数; (2)点 F 是 AE 延长线上一点,过点 F 作∠AFD=27°,交 AB 的延长线于点 D.求证:BE∥DF.
三角形单元复习精品课件
三角形单元复习精品课件
知识点三:多边形及其内角和
(1)在平面内,由一些线段首尾顺次相接组成的 封闭 图形叫
做多边形.
(2)多边形内角和定理: (n-2)×180°(n≥3 且 n 为整数).
此公式推导的基本方法是从 n 边形的一个顶点出发引出(n-3) 条对角线,将 n 边形分割为(n-2)个三角形,这(n-2)个三角 形的所有内角之和正好是 n 边形的内角和.将多边形转化为三 角形,这也是研究多边形问题常用的方法.
9.(2020 黑河模拟)已知一个多边形的每个外角都是 24°,此多
边形是 十五 边形.
三角形单元复习精品课件
三角形单元复习精品课件
10.求下列正多边形每个内角及其外角的度数: (1)正五边形; (2)正八边形; (3)正十二边形. 解:(1)108°,72°. (2)135°,45°. (3)150°,30°.
三角形单元复习精品课件
三角形单元复习精品课件
(1)解:∵在 Rt△ABC 中,∠ACB=90°,∠A=36°, ∴∠ABC=90°-∠A=54°,∴∠CBD=126°. ∵BE 是∠CBD 的平分线,∴∠CBE=21∠CBD=63°. (2)证明:∵∠ACB=90°,∠CBE=63°, ∴∠CEB=90°-63°=27°. 又∵∠F=27°,∴∠F=∠CEB=27°,∴BE∥DF.
三角形单元复习精品课件
三角形单元复习精品课件
2.如图,在△ABC 中,AD 是高,AE 是角平分线,AF 是中
线,则下列说法中错误的是( C )
A.BF=CF B.∠C+∠CAD=90° C.∠BAF=∠CAF D.S△ABC=2S△ABF
三角形单元复习精品课件
三角形单元复习精品课件
3.在△ABC 中,AB=9,BC=2,AC=x. (1)求 x 的取值范围; 解:由题意知 9-2<x<9+2,即 7<x<11.
三角形单元复习精品课件
第十一章 三角形
《三角形》单元复习
三角形单元复习精品课件
目录
01
知识要点
02
对点训练
03
精典范例
04
变式练习
知识要点
知识点一:与三角形有关的线段 (1)三角形的概念: 由不在同一条直线上的三条线段 首尾顺次相接 所组成的图 形叫做三角形. 组成三角形的线段叫做三角形的 边 . 相邻两边的公共端点叫做三角形的 顶点 . 相邻两边组成的角叫做三角形的 内角 .
三角形单元复习精品课件
精典范例
11.【例 1】下列长度的三条线段,不能围成三角形的是( A )
A.3,8,4
B.9,15,8
C.15,20,8
D.6,4,9
小结:三角形任意两边之和大于第三边,任意两边之差小于 第三边.
变式练习
17.一个三角形的两边长分别为 10cm 和 3cm,则此三角形第三
边长可能是( B )
A.13cm
B.8cm
C.7cm
D.5cm
12.【例 2】如图,盖房子时,在窗框未安装之前,木工师傅常 常先在窗框上斜钉一根木条,使其不变形,这种做法的根据是
(B )
A.两点之间,线段最短 B.三角形的稳定性 C.长方形的四个角都是直角 D.四边形的稳定性
三角形单元复习精品课件
知识点二:与三角形有关的角 (1)三角形的内角的概念:三角形的内角是三角形三边的夹角. (2)三角形的内角和定理:三角形的内角和等于 180° . (3)三角形外角的定义:三角形的一边与 另一边的延长线 组成的角,叫做三角形的外角.
三角形单元复习精品课件
三角形单元复习精品课件
三角形单元复习精品课件
三角形单元复习精品课件
(3)多边形的外角和等于 360° . (4)各个角都 相等 ,各条边都 相等 边形.
的多边形叫做正多
三角形单元复习精品课件
三角形单元复习精品课件
8.(2020 厦门模拟)下列角度不可能是多边形内角和的是( A )
A.270°
B.360°
C.540°
D.900°
三角形单元复习精品课件
三角形单元复习精品课件
(2)若△ABC 的周长为偶数,则△ABC 的周长为多少? 解:∵7<x<11,∴x 的值是 8 或 9 或 10, ∴△ABC 的周长为 9+2+8=19(舍去), 或 9+2+9=20 或 9+2+10=21(舍去), 即△ABC 的周长为 20.
三角形单元复习精品课件
