圆柱体常用量计算器

1小学数学科学教学仪器配备标准(教育部061001)

个
8~23
√
+12
演示用，500g,1g
台
2√
+2
200g,1g
台
8~23
√
+12
指针式，1kg
台
2√
+2
质量单位，2.5kg
个
2√
+2
0.1s
块
4~12
√
+12
演示用，60°、45°各1
套
12 √
-1 +12
演示用，附橡皮脚
套
4√
-4
演示用，0~180°
个
2√
-1
1m,m、dm、cm、mm四种单位
-1
编号名称
1 计算机 1001 计算机 1013 计算器
2 一般 2002 打孔器 2015 打气筒 2020 仪器车 2041 显微镜
2043 生物显微演示装置 2045 学生显微镜 2051 放大镜 2052 放大镜 2061 天文望远镜 2075 酒精喷灯 2077 电加热器
2086 电冰箱
√
12
个
12~23
√
12
套
12~23
√
12
套
12~23
√
12
套
12~23
√
12
套
12~23
√
12
个
23~45
√
45
台
1√
1
个
12~23
√
12
套
8~12
√
交流2V-12V,5A,每2V一档;直
流1.5V--12V,2A,分为1.5V、台

过盈连接压装力计算器

序号
名称
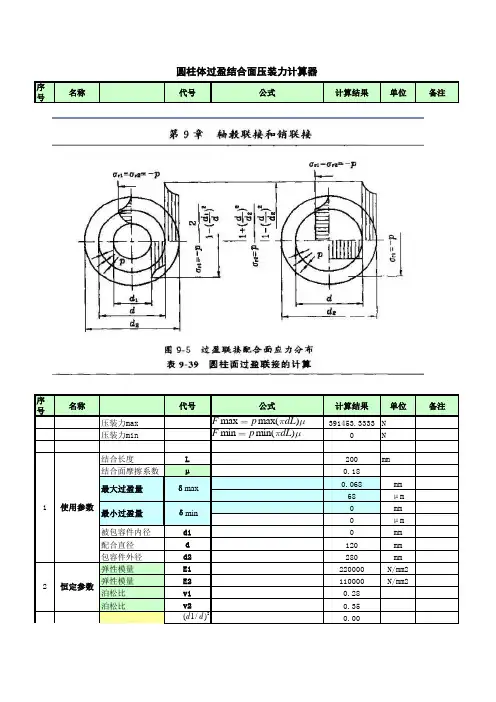
圆柱体过盈结合面压装力计算器
代号
公式
计算结果
单位
备注
序号
名称
压装力max
压装力min
代号
公式
F max p max( dL) F min p min( dL)
计算结果单位
391453.3333 N
0
N
结合长度结合面摩擦系数
最大过盈量
1 使用参数最小过盈量
被包容件内径配合直径包容件外径弹性模量 2 恒定参数弹性模量泊松比泊松比
C1 C2 E1 E2
0.00001964
最大压力【压强】
pmax
最小压力【压强】 4 计算结果
结合面正压力
pmin
p max
max d (C1 C2) 103 28.85802469
Mpa
E1 E2
p min
min d (C1 C2) 103
0
Mpa
E1 E2
p max( dL) 2174740.741 N
N/mm2 N/mm2
压装力max 压装力min
F1 F max pmax( dL)
F2
F min p min( dL)
391453.3333
39145.33333 0 0
轴向摩擦 N力 kg N kg
1MPa=10kg/c m2 =100N/100mm 2=1N/mm2
备注
3 计算参数
简化系数
简化系数 3 计算参数
中间参数
(d1/ d)2
C1
C1
1 (d1 / d )2 1 (d1 / d )2
v1
0.72
(d / d 2)2

常用圆柱弹簧计算器-压缩与拉伸弹簧Excel计算表

有效圈数, n = 5
总圈数, N = 7
输出
线圈节距, p = (L - 3*d) / n
= 0.75
mm
压并高度, H = d * (N + 1)
= 3.125
mm
端部开放 + 未平切
输入
展开长度, L = 4.000
mm
线径, d = 0.125
mm
有效圈数, n = 5
总圈数, N = 7
输出
线圈节距, p = (L - d) / n
= 0.775
mm
压并高度, H = d * (N + 1)
= 3.125
mm
端部开放 + 平切
输入
展开长度, L = 4.000
mm
线径, d = 0.125
mm
有效圈数, n = 5
总圈数, N = 7
输出
线圈节距, p = L / n
= 0.8
mm
压并高度, H = d * (N + 1)
常用圆柱弹簧计算器
圆柱弹簧 - 圆线
压缩与拉伸弹簧强度计算
输入
试验载荷, P = 24.00
N
线径, d = 0.188
mm
弹簧中径, D = 2.000
mm
有效圈数, n = 10
-
材料的切变模量, G = 10,000,000
Mpa
输出
弹簧刚度系数, R = G*d^4 / (8*n*D^3)
= 19.52
= 3.125
mm
圆柱弹簧 - 方线
压缩与拉伸弹簧计算
试验载荷, 线截面厚, 线截面高, 弹簧中径, 有效圈数, 材料的切变模量,

教学常规仪器分类统计表

份
适量
√
合
计
小学科学
编号
名称
0 通用
00 视听
00001 书写投影器
00005 视频展示台
00006 液晶投影机
00007 银幕
00008 彩色电视机
00009 录象机
00010 影碟机
00011 数码照相机
00013 摄像机
1 计算机
01001 计算机
01012 计算器
2 一般
02002 打孔器
规格型号功能
小学教学仪器
小学数学
编号
名称
0 通用 1 计算机 01012 计算器 1 测量 10 长度 10007 软尺 10008 卷尺 11 质量 11006 托盘天平 11007 简易天平 11018 台秤(弹簧度盘秤) 11023 弹簧秤 12 时间 12003 电子停表 2 专用仪器 20 数学 20001 三角板 20002 圆规 20004 量角器 20501 专用直尺 20505 标杆 20506 测绳
29018 热传导实验材料
256Hz
套 12~23 √ 套 12~23 √ 套 12~23 √ 套 12~23 √ 个 23~45 √ 台1 √ 个 12~23 √ 套 12~23 √ 套 12~23 √ 套 12~23 √ 套 12~23 √ 支 12~23 √ 个 12~23 √ 套 12~23 √
2√
30502 钟表模型
演示用，两针，非联动，12时表示
套
2
√
30503 钟表模型 30504 钟表模型 30505 钟表模型
演示用，三针，联动，24时表示学生用，两针,非联动学生用，三针联动
套2 √

小学数学教学仪器(9所学校)

1、小学数学教学仪器（9所学校）
注：所有仪器设备按照设备编号规定的标准进行生产，符合JY0001-2003<<教学仪器产品一般质量要求>>的有关规定；按照9所学校进行包装，送到相应学校。

2、初中数学教学仪器（2所学校）
注：所有仪器设备按照设备编号规定的标准进行生产，符合JY0001-2003<<教学仪器产品一般质量要求>>的有关规定；按照2所学校进行包装，送到相应学校。

3、小学科学教学仪器（9所学校）
注：所有仪器设备按照设备编号规定的标准进行生产，符合JY0001-2003<<教学仪器产品一般质量要求>>的有关规定；按照9所学校进行包装，送到相应学校。

4、初中地理教学仪器（2所学校）
注：所有仪器设备按照设备编号规定的标准进行生产，符合JY0001-2003<<教学仪器产品一般质量要求>>的有关规定；按照9所学校进行包装，送到相应学校。

5、小学卫生器材（8所学校）
注：所有仪器设备按照设备编号规定的标准进行生产，符合JY0001-2003<<教学仪器产品一般质量要求>>的有关规定；按照8所学校进行包装，送到相应学校。

6、初中卫生器材（2所学校）
注：所有仪器设备按照设备编号规定的标准进行生产，符合JY0001-2003<<教学仪器产品一般质量要求>>的有关规定；按照9所学校进行包装，送到相应学校。

7、小学美术器材（9所学校）。

怎样快捷准确地计算出零件的重量

件重量时，就只需打开该表格就可以了。
打开表格，按照“长方体重量计算”和“圆柱体重量计算”两种不同类型建立表头。如下图所示，为便于理解记忆，分别用 L1、L2、L3 表
0c04f2a 易博
示长方体零件的长、宽、高的尺寸，D、d、L 分别代表圆柱体零件的外圆直径、内圆直径和长度，M 表示零件的重量。
在工程设计当中，经常要计算各种零件的重量。其中，最常见的零件形状要算圆柱体和长方体了。例如，时常用到的钢板就是长方体，轴类零件是圆柱体的组合。如果用计算器一个一个地
计算的话，费时费力。下面我教大家巧用 Excel 软件快速计算零件的方法。
新建一个 Excel 电子表格文档，可以命名为 “质量计算”，这样方便记忆。以后”。
0c04f2a 易博
宽 500mm 的钢板，计算出的重量是 39.25kg。同理，设置圆柱体零件的计算范例。两种范例设计好后，以后计算这两类零件的
0c04f2a 易博
重量只需填入零件的长宽高或者直径与长度的值然后复制上一行的公式就得出结果了。注意事项
本文中长、宽、高、直径、长度的单位都是
特别要说明的是：如果圆柱体零件是实心
的，则只需将内圆直径 d 设为“0”就行了。
设置长方体零件重量的计算范例。先拟设长方体的长、宽、高的尺寸，如下图，分别设 L1、 L2 和 L3 为 20、500 和 500（当然，也可以设其
0c04f2a 易博
它任意数字），然后根据这三个数值根据公式计算出其重量（重量=体积×密度，单位直接换算成“kg”）。公式即图中红色线框中所示内容。得出重量 39.25kg。也就是说厚度 20mm，长 500mm，

小学数学科学教学仪器配备标准(教育部0610)

小学数学科学教学仪器配备标准（教育部0610）
小学数学科学教学仪器配备标准（教育部0610）
小学数学科学教学仪器配备标准（教育部0610）
小学数学科学教学仪器配备标准（教育部0610）
小学数学科学教学仪器配备标准（教育部0610）
小学数学科学教学仪器配备标准（教育部0610）
小学数学科学教学仪器配备标准（教育部0610）
小学数学科学教学仪器配备标准（教育部0610）
小学数学科学教学仪器配备标准（教育部0610）
小学数学科学教学仪器配备标准（教育部0610）
小学数学科学教学仪器配备标准（教育部0610）
小学数学科学教学仪器配备标准（教育部0610）
小学数学科学教学仪器配备标准（教育部0610）
小学数学科学教学仪器配备标准（教育部0610）
小学数学科学教学仪器配备标准（教育部0610）
小学数学科学教学仪器配备标准（教育部0610）。

圆柱纵截面体积计算

圆柱纵截面体积计算圆柱是一个常见的几何体，它的纵截面体积是一个有趣的数学问题。

我们可以通过计算来得到圆柱的纵截面体积，而无需使用复杂的数学公式。

我们需要了解圆柱的结构。

圆柱有一个圆形的底面和一个平行于底面的顶面，这两个面之间由直线连接而成。

底面和顶面的半径相等，我们用r表示。

圆柱的高度用h表示。

我们可以将圆柱分成无数个纵截面，每个纵截面都是一个圆形。

如果我们将圆柱沿着高度方向切割成许多薄片，每个薄片的厚度非常小，那么每个薄片的纵截面都可以看作是一个圆形。

现在，我们来计算一个纵截面的体积。

假设我们取一个距离底面h1的纵截面，它的半径是r1。

由于纵截面是圆形，我们可以使用圆的面积公式来计算纵截面的面积，即πr1^2。

由于纵截面的厚度非常小，我们可以将整个圆柱看作是无数个纵截面的叠加。

每个纵截面的面积都是πr1^2，而纵截面的数量就是圆柱的高度h。

因此，整个圆柱的体积可以表示为Σ(πr1^2 * h1)，其中Σ表示求和。

我们可以将Σ(πr1^2 * h1)简化为πΣ(r1^2 * h1)。

由于每个纵截面的半径和高度都可以不同，我们需要对每个纵截面进行求和。

通过将纵截面的半径和高度相乘，并将结果累加起来，我们可以得到整个圆柱的体积。

通过这种方法，我们可以计算任意形状的圆柱的纵截面体积，而无需使用复杂的数学公式。

这种计算方法简单直观，适用于各种实际问题，如容器的容积计算、建筑物的结构设计等。

当然，在实际计算中，我们可以使用计算器或计算机程序来快速得到结果。

通过这个简单的例子，我们可以看到数学在解决实际问题中的重要性。

数学不仅是一门学科，更是一种思维方式和工具，可以帮助我们理解和解决各种问题。

无论是计算圆柱的纵截面体积，还是解决更复杂的数学问题，数学的应用都离不开我们的思考和努力。

让我们一起探索数学的奥秘，感受数学的美妙吧！。

教学仪器编号

30002 组合几何体模型 5 50 500 挂图、软件及资料数学教学挂图(图片)
50001 中学数学数与代数教学挂图 50002 中学数学空间与图形教学挂图 50003 中学数学统计与概率教学挂图 50004 中学数学资料挂图 501 教学投影片、幻灯片
50101 中学数学数与代数教学投影片 50102 中学数学空间与图形教学投影片 50103 中学数学统计与概率教学投影片 50104 中学数学资料投影片 503 多媒体教学软件
数学数学
3 30 30001 几何形体模型
数学数学数学数学数学数学数学数学套套套套 2 2 2 2 √ √ √ √ 数学数学数学数学数学数学套套套套 2 2 2 2 √ √ √ √ 数学数学数学数学数学数学套套 1～8 1 √ √ 不同版本，不同功能特点的计算机数学教学软件数学数学
JY/T
XXXX-200X
初中理科教学仪器配备标准(教育部06.12)
配备要求编号 10 10001 演示直尺 10002 木直尺 10004 钢直尺 10005 钢卷尺 10009 布卷尺 10010 游标卡尺 10011 外径千分尺(螺旋测微器) 11 11001 物理天平 11002 学生天平 11004 托盘天平 11005 托盘天平 11010 电子天平 11015 单杠杆天平 11018 案秤 11020 弹簧度盘秤 11021 金属钩码 11022 金属槽码 12 12001 机械停表 12002 机械停钟 12003 电子停表 12004 电子停钟时间 0.1s 0.1s 0.1s 0.1s 块块块块 13～25 13～25 13～25 13～25 √ √ √ √ QB/T 1908 QB/T 1534 J01215 质量 500g 200g， 0.02g 200g， 0.2g 500g， 0.5g 100g，0.001g 100g，0.01g，链式 10kg，10g 8kg，8g 10g×1，20g×2，50g×2，200g ×2 10g×1，20g×2，50g×2，200g ×1，另附10g金属槽码盘台台台台台台台台套套 1 13～25 13～25 1 1 1 1 1 13～25 13～25 √ √ √ √ √ √ √ √ √ √ GB/T 4168 JY 104 QB/T 2087 QB/T 2087 JB/T 5374 GB/T 4168 GB/T 335 GB/T 11883 JY1 05 J00706 J00707 J00203 J00204 J00205 J00205 J00231 名称长度 1000mm 1000mm 200mm 2000mm 30m 125mm，0.05mm或0.02mm 25mm，0.01mm 只只只盒盒把只 1 13～25 13～25 1～25 1 1 1 √ √ √ √ √ √ √ JY 168 JY 168 GB/T 9056 QB/T 2443 QB/T 1519 GB/T 1214.2 GB/T 1216 J00001 J00002 J00002 J00010 J00010 J00005 J00007 规格型号功能单位数量基本选配现有数量执行标准代号备注分类与代码学科物理物理物理物理物理物理物理物理物理物理物理物理物理物理物理物理物理物理物理物理物理物理物理物理物理物理

圆柱体的体积计算

圆柱体的体积计算圆柱体是几何学中一个重要的二维形体，它具有两个平行且相等的圆底面，并由连接两底面的侧面组成。

在实际生活中，圆柱体的体积计算常常用于工程、建筑、制造等领域。

下面将介绍如何计算圆柱体的体积，以及相关的公式和实例。

一、圆柱体体积的公式圆柱体的体积（V）可以通过以下公式来计算：V = π * r^2 * h其中，π是一个常数，约等于3.14；r表示圆柱体底面的半径；h表示圆柱体的高度。

二、圆柱体体积计算的步骤下面以一个例子来演示如何计算圆柱体的体积。

例子：将半径为5cm，高度为12cm的圆柱体的体积计算出来。

1. 根据给定的数据，获得圆柱体的半径r和高度h。

半径r = 5cm高度h = 12cm2. 将半径r和高度h代入圆柱体体积的公式V = π * r^2 * h中。

V = 3.14 * 5^2 * 123. 进行计算，并得出结果。

V = 3.14 * 25 * 12≈ 942.48cm^3所以，半径为5cm，高度为12cm的圆柱体的体积约为942.48立方厘米。

三、圆柱体体积计算的注意事项在进行圆柱体体积计算时，需要注意以下几点：1. 确保半径和高度的单位一致。

如果半径使用的是厘米，那么高度也应使用厘米，以保证计算的准确性。

2. 在使用计算器计算过程中，应当注意保留足够的小数位数，以免影响最终结果的准确性。

最好将计算结果四舍五入至合适的位数。

3. 在实际应用中，如果需要进行大量的圆柱体体积计算，可以编写程序或使用电子表格软件来自动计算，提高工作效率和准确性。

四、其他常见形体的体积计算公式除了圆柱体，还有许多其他常见形体的体积计算公式，例如：1. 球的体积计算公式：V = (4/3) * π * r^3其中，r表示球的半径。

2. 正方体的体积计算公式：V = a^3其中，a表示正方体的边长。

3. 长方体的体积计算公式：V = l * w * h其中，l表示长方体的长度，w表示宽度，h表示高度。