光学 分子间作用力势能与真实气体物态方程
1.7分子间作用势能与真实气体物态方程讲解

当温度升高时,EK0 增加,横轴r’升高,d 将减小,说明 d 与气体温度
有关。温度越高,d 越小。
表示动能的横坐标
分子碰撞 有效直径 表示势能的横坐标
表示两 分子碰 撞时挤 压情况
关于分子的直径:
• 由于原子核外的电子呈电子云分布,因而原子或分子没有明确的边界, 也就谈不上有什么明确的直径。
分子力是一种电磁相互作用力,因此它是一 种保守力,具有势能,称为分子作用力势能。
二、分子间互作用势能曲线 1、分子间互作用势能曲线 • 分子力是一种保守力,具有势能,而保守力作功的负值 等于势能Ep的增量, • 故分子作用力势能的微小增量为
dE p (r ) F (r)dr
dr 若令分子间距离r 趋向无穷远时的势能为零,则
(2)另一种理解的分子直径是指:
分子碰撞有效直径 d —两分子相互作 对心碰撞时,两分子质心间最短距离。
图中r0 与 d 不相等,但通常情况下差异不大。 • 图中对分子间碰撞的分析限于两分子间对心碰撞(即两分子间的碰撞 均在分子联心轴线上发生)。
• 实际发生的分子间碰撞基本上都是非对心的,因而以后要引入分子碰 撞截面的概念。
只有两分子相互“接触”、“挤压”时才呈现出排斥力。
可简单认为排斥力作用半径就是两分子刚好“接触”时两质心间的距离, 对于同种分子,它就是分子的直径。
因为吸引力出现在两分子相互分离时,故排斥力作用半径 比吸引力半径小。
引力和斥力都随着分子间距离的增大而减小,随着分子间距 离的减小而增大,但是斥力变化更为剧烈。
f
斥
分
子
力
力
o
r
力
引
分子力曲线
2、分子力与分子热运动
1.7分子间作用势能与真实气体物态方程

2、利用分子势能曲线解释固体内分子的运动是振动
分子振动 的平衡位
置曲线
表示总能量 不变的曲线
3、利用分子势能曲线解释固体的热膨胀
r
r'
r" 2
r0
r 随着温度上升而增加,因而产生线膨胀。
四、范德瓦耳斯方程
• 1873年荷兰物理学家范德瓦耳斯针对理想气体的两条基本 假定:
• 忽略分子固有体积、 • 忽略除碰撞外分子间相互作用力 • 作出了两条重要修正,得出了能描述真实气体行为的范德
• 气体分子每与器壁碰撞往返一次所导致器壁的冲量减少了2△k的数值 (往返各减少△k )。
pi {单位时间内碰在单位面积上平均分子数} 2k
(1 / 6)nv 2k
△k与分子数密度n 成正比,设比例系数为K,1 nv 2Kn 6
( N A )2 v 2( K
排斥力 吸引力
用势能来表示相互作用要比直接用 力来表示相互作用方便有用,所以 分子互作用势能曲线常被用到。
势能极小值
平衡位置 平衡位置
三、碰撞有效直径、固体分子热振动、固体热膨胀 1、用分子势能曲线解释分子间对心碰撞
表示动能的横坐标
表示势能的横坐标
表示两分 子碰撞时 挤压情况
在图中a2向 a1靠近时,在相互距离为d 时,它们受到的挤压达到最大,然 后a2反向运动。所以
分子吸引力作用半径的存在:
只有当分子质心相互接近到某一距离内,分 子间相互吸引力才较显著,把这一距离称为 ---分子吸引力作用半径。
很多物质的分子引力作用半径约为分子直径的2-4倍左 右,超过这一距离,分子间相互作用力已很小,可予 忽略。
(2)排斥力 能说明排斥力的现象: ①固体、液体都很难压缩; ②气体分子经过碰撞而相互远离。 排斥力作用半径:
§1.7 分子间作用力势能与真实气体物态方程
与分子作用力曲线所对应的互作用势能曲线
r
E p ( r ) F ( r )dr ~ r
在平衡位置 r = r0处,分子 力F(r) = 0,势能有极小值 , 它是负的. 在r>r0处,F(r)<0, 势能曲线斜率是正的—吸引 力
图中的 d 是两分子对心碰撞时相互接近最短 质心间距离,故称 d = 分子碰撞有效直径 当温度升高时,EK0 也增加,因而横轴升高, d 将减小,说明 d 与气体温度有关。 温度越高,d 越小。
• 设分子在相互分离时的吸 引力为球对称分布, 吸引力作用半径为R0, • 每一分子均有以 R0 为半径 的吸引力作用球。 • 气体内部的分子在越过界面层向器壁运动, 以及在与器壁碰撞以后返回、穿过界面层过 程中,都受到一指向气体内侧的力。
分子吸引力修正
器壁实际受到压强要比气体内部的压强小, 使气体施于器壁的压强减少了一个量值pi , 这称为气体内压强修正量。若仪器所测出的气 体压强为p, 则 p = p内 - pi 因气体内部分子受到其它分子吸引力的合力相 消,故气体的内部压强 p内 与分子吸引力无关. 气体内部压强等于理想气体压强 p内 = p理
(三) 范德瓦尔斯方程 (Van der Waals equation of state)
将△pi = a/Vm2 代入 p +△pi = RT/ (Vm-b)
得到
a ( p 2 )(Vm b) RT Vm
m 2 a m m [p( ) ( 2 )][V ( )b] RT Mm V Mm Mm
§1.7.1分子间互作用势能曲线
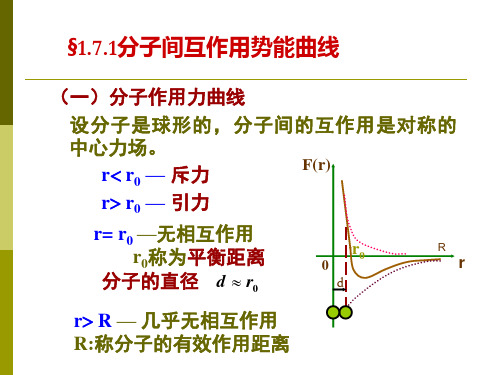
(一)分子作用力曲线 设分子是球形的,分子间的互作用是对称的 中心力场。 F(r) r r0 — 斥力 r r0 — 引力 r= r0 —无相互作用 r0称为平衡距离 分子的直径 d r0 r R — 几乎无相互作用 R:称分子的有效作用距离
高等工程热力学——第七章

第七章实际气体状态方程7—1气体分子之间的作用力实际气体的区分实际气体的状态不符合关系的主要原因是,由于理想气体的模型和状态方程,是在假定气体分子不占有容积,气体分子之间没有相互作用力的基础上建立的。
而实际气体分子却占有容积,并且分子间有相互作用力,这使得实际气体不能完全符合理想气体状态方程。
范德瓦尔斯引力:气体分子相距较远时相互吸引,相距很近时相互排斥。
分子间引力主要包括三个方面:即静电力、诱导力和色散力。
①静电力(葛生力)指分子的永久偶极矩间的相互作用。
1912年葛生提出,范德瓦尔斯引力就是极性分子的偶极矩间的引力,作用力的大小和性质与它们的相对方向相关。
当两个偶极矩方向相同时,相互作用势能为负,并达到最小值;当两个偶极矩的方向相反时,相互作用势能为正,并达到最大值。
如果、在各种相对方向出现的几率相同,则相互作用平均势能=0.然而,按照波尔兹曼分布定律,温度越低,和在低势能的相对方向出现的可能性越大,因此对各种方向加和后,平均静电相互作用势能0,而是式中r为两偶极矩的中心距离,k为波尔兹曼常数。
②诱导力(拜得力)是指被诱导的偶极矩与永久偶极矩间的相互作用。
拜得注意到,一个分子的电荷分布受到其他分子电场的影响,因为提出诱导力。
永久偶极矩与被其诱导的偶极矩之间的相互作用为诱导作用。
诱导作用不仅发生在极性分子与非极性分子之间,也发生在极性分子和极性分子之间。
不同分子间的诱导相互作用势能为③色散力(伦敦力)是指诱导偶极矩之间的相互作用。
在某一瞬间,电子环绕核可以是非对称分布的,原子具有瞬时偶极矩,它产生的电场将会使邻近分子极化。
两个诱导偶极矩之间的相互作用表现为相互吸引,这就是色散作用。
色散力产生的相互作用势能可近似为式中是1、2的电离能,是它们的极化率,r是分子中心距离。
范德瓦尔斯引力的特性有:①它是存在于分子或原子间的一种作用力。
②它是吸引力,作用势能的数量级为0.41868-4.1868J/mol.③范德瓦尔斯引力的作用范围约为3-5*m.④范德瓦尔斯引力最主要的色散力。
高等工程热力学——第七章

第七章实际气体状态方程7—1气体分子之间的作用力实际气体的区分实际气体的状态不符合关系的主要原因是,由于理想气体的模型和状态方程,是在假定气体分子不占有容积,气体分子之间没有相互作用力的基础上建立的。
而实际气体分子却占有容积,并且分子间有相互作用力,这使得实际气体不能完全符合理想气体状态方程。
范德瓦尔斯引力:气体分子相距较远时相互吸引,相距很近时相互排斥。
分子间引力主要包括三个方面:即静电力、诱导力和色散力。
①静电力(葛生力)指分子的永久偶极矩间的相互作用。
1912年葛生提出,范德瓦尔斯引力就是极性分子的偶极矩间的引力,作用力的大小和性质与它们的相对方向相关。
当两个偶极矩方向相同时,相互作用势能为负,并达到最小值;当两个偶极矩的方向相反时,相互作用势能为正,并达到最大值。
如果、在各种相对方向出现的几率相同,则相互作用平均势能=0.然而,按照波尔兹曼分布定律,温度越低,和在低势能的相对方向出现的可能性越大,因此对各种方向加和后,平均静电相互作用势能0,而是式中r为两偶极矩的中心距离,k为波尔兹曼常数。
②诱导力(拜得力)是指被诱导的偶极矩与永久偶极矩间的相互作用。
拜得注意到,一个分子的电荷分布受到其他分子电场的影响,因为提出诱导力。
永久偶极矩与被其诱导的偶极矩之间的相互作用为诱导作用。
诱导作用不仅发生在极性分子与非极性分子之间,也发生在极性分子和极性分子之间。
不同分子间的诱导相互作用势能为③色散力(伦敦力)是指诱导偶极矩之间的相互作用。
在某一瞬间,电子环绕核可以是非对称分布的,原子具有瞬时偶极矩,它产生的电场将会使邻近分子极化。
两个诱导偶极矩之间的相互作用表现为相互吸引,这就是色散作用。
色散力产生的相互作用势能可近似为式中是1、2的电离能,是它们的极化率,r是分子中心距离。
范德瓦尔斯引力的特性有:①它是存在于分子或原子间的一种作用力。
②它是吸引力,作用势能的数量级为0.41868-4.1868J/mol.③范德瓦尔斯引力的作用范围约为3-5*m.④范德瓦尔斯引力最主要的色散力。
重力场中真实气体内能与状态方程的关系

h
பைடு நூலகம்
kT
h
dh
1 Na
P
kT
气体的量为 1mol,(1.10)变为
气体的内能为:
Ep
1
P
RT
(1.11)
E
x RT 2
E p
(1.12)
对(1.12)对密度微分得到
E 1 P RT
E
E0
2b V
w2 P 1 P V 2 s M V
下面计算绝热下,P 和 V 的微分关系。由于绝热,
dQ dE PdV E dT E dV PdV 0 T V
(2.1) (2.2)
(2.3) (2.4)
E P dV dT V
uP
1 Na
Ep
(0.2)
外力作用下,气体密度不均匀,分子作用力在宏观表现为
f1
u p r
(0.3)
在外场作用下,气体的内部相互作用影响宏观分布,通过分析气体的宏观分布可以得 出气体的内能。本文主要研究重力场中气体。
这里讨论的气体密度 的单位是[mol/m3],后面要用到的一个密度 ' ,单位是[kg/m3]。
112对112对密度微分得到113考虑气体的量为1mol状态方程和声速之间的关系的推导状态方程可以改写为21由1105可以得到气体内能22音速的计算公式为23下面计算绝热下ppdvdvpdvdedq2425压强的微分式为dv2626代入26得到27将212718代入23得到28而密度比较小时有2929代入28得到210音速第二维里系数如下2113
2.2 气体的状态方程(EOS)

(1)维里方程
概述: 根据J.Mayer的集团理论,考虑气 体分子间作用力后,可用“维里系数” 来表示P-V-T关系。“维里”(Virial) 一词是从拉丁文字演变得来的,它的 原意为“力”。维里系数表征对气体 理想性质的差异。
由图2-3(第5页)所示气相区的T1 等温线,可知,V随P增大而减小,气体 压力与摩尔体积的乘积PV接近某一定值。 可预料,沿等温线变化的PV乘积能用一 个P的幂级数表示,即 : PV=a+bP+cP2+… 令 b=aB’,c=aC’,d=aD’,… 则 上 式 可 写为: PV=a(1+B’P+C’P2+D’P3+…)
2
Tc
2 2
34Tc来自将 P=RT/(V-b)- a/V2应用于 临界点,即代入 Vc、Pc、Tc, 并与b=Vc/3, a=9RTcVc/8联立, 得 :PcVc/RTc=3/8, 故可求出: b=RTc/8Pc,a=27(RTc)2/64Pc =3 PcVc2
缺点 :
Van der Waals 方程中的每一 相虽然可赋予一定的物理解释,但 这种改进式毕竟是过于简单,用它 来推算流体的P-V-T性质误差很大, 实用价值不大。
利用临界等温线在临界点上的 拐点的特殊条件,即 =0 =0 把 Van der Waals 方程代入上 2a 2a RTc ∂P 述条件,得 : ∂V = (Vc − b) + Vc 3 = 0 2RTc 6a ∂ P = - Vc =0 ∂V (Vc− b) 联立上述方程, b=Vc/3,a=9RTcVc/8.
Van der Waals(范德华)方程: Waals(范德华)方程:
1873年首次导出了能表达从 气态到液态的连续性状态方程: (P+
高中物理公式:分子动理论、能量守恒定律

高中物理公式:分子动理论、能量守恒定律r=r0,f引=f斥,F分子力=0,E分子势能=Emin(最小值)r>r0,f引>f斥,F分子力表现为引力r>10r0,f引=f斥≈0,F分子力≈0,E分子势能≈0热力学第一定律W+Q=ΔU{(做功和热传递,这两种改变物体内能的方式,在效果上是等效的),W:外界对物体做的正功(J),Q:物体吸收的热量(J),ΔU:增加的内能(J),涉及到第一类永动机不可造出〔见第二册P40〕}热力学第二定律克氏表述:不可能使热量由低温物体传递到高温物体,而不引起其它变化(热传导的方向性);开氏表述:不可能从单一热源吸收热量并把它全部用来做功,而不引起其它变化(机械能与内能转化的方向性){涉及到第二类永动机不可造出〔见第二册P44〕}注:布朗粒子不是分子,布朗颗粒越小,布朗运动越明显,温度越高越剧烈;温度是分子平均动能的标志;分子间的引力和斥力同时存在,随分子间距离的增大而减小,但斥力减小得比引力快;分子力做正功,分子势能减小,在r0处F引=F斥且分子势能最小;气体膨胀,外界对气体做负功W<0;温度升高,内能增大ΔU >0;吸收热量,Q>0物体的内能是指物体所有的分子动能和分子势能的总和,对于理想气体分子间作用力为零,分子势能为零;r0为分子处于平衡状态时,分子间的距离;其它相关内容:能的转化和定恒定律〔见第二册P41〕/能源的开发与利用、环保〔见第二册P47〕/物体的内能、分子的动能、分子势能〔见第二册P47〕。
加速度a=(Vt-V0)/t(以V0为正方向,a与V0同向(加速)a>0;a与V0反向(减速)则a<0)实验用推论Δs=aT2(Δs为连续相邻相等时间(T)内位移之差)主要物理量及单位:初速度(V0):m/s;加速度(a):m/s2;末速度(Vt):m/s;时间(t):秒(s);位移(s):米(m);路程:米;速度单位换算:1m/s=3.6km/h。
a=(Vt-V o)/t只是测量式,不是决定式;其它相关内容:质点、位移和路程、参考系、时间与时刻、s--t 图、v--t图/速度与速率、瞬时速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的范德瓦尔斯方程:
3.说明:*
p
a v2
v
b
RT
4.习题:
例1.根据公式 特定律.
P 23和nt
,t试 32从KT分子运动论推证玻意耳-马略
例2.在容积为V 6的0l容器内装有理想气体,当 T 3时00,K气
体的压强
P .问5.容0器10中3 P气a 体的分子数是多少?
例3.在容积为 5.0的l 容器内贮有 和O2 组N2成的混合气体,其中 有O2 3..已21知0混5 g 合气体的 , T.试 35求0K容P器中2.7P分a 子数.
一.用分子势能曲线解释分子间对心碰撞
1.分析(右图):*
2.分子碰撞有效直径:两分子对心碰撞时相互接近的最 短质心间距,用d表示.
3.说明:*
二.固体及液体中分子的振动*
三.利用分子势能曲线解释固体的热膨胀(阅读教材39页)
§1.7.3范德瓦斯方程*
一.非理想气体与理想气体的本质区别
我们推导范氏方程的思路是:从微观结构上找到非理想 气体与理想气体的本质区别,考虑到这些区别对气体压强 造成的影响,将理想气体压强进行修正,就得到了非理想气 体的范氏方程.
子引力可忽略.在平衡状态下,分子数密度均匀分布,球内分
子对 是对称分布 的.所以这些分子对 的引力作用相互抵
消,合力为零.
A’
B B’
(2).在距器壁AB为R0的距离处作一假想平面A’B’,平行于 AB. 分子在进入A’B’与AB之间的空间前,所受引力相互 抵消.假设 分子在A’B’处碰撞,给予器壁的压强不受引 力的影响.事实上, 分子在 AB处才碰撞.当 分子进入A’B’ 与AB的空间区域后,以 分子质心为心再作引力作用球, 此球中有一部分便落在了容器之外.于是球内分子对 分 布左右不对 称.所以作用在 分子上的其它分子的引力在 水平方向上不能抵消,产生一指向容器内垂直于器壁的 合力,且随着 靠近器壁,这个合力在增大.于是 分子在 向器壁运动过程中,在这个合力作用下垂直器壁的速度 分量在减小.这样 分子与器壁碰撞给予器壁的冲量比理 想气体分子不受引力作用给予器壁的冲量要小.于是大 量分子与器壁碰撞时,考虑到引力作用,对器壁的压强要 比没有引力时小一个分量,设为 .
N2
例4.一容器内贮有O2,,其 P 1.010Pa,,试T 求 3:00K
(1)分子数密度;(2)O2的密度;(3)氧分子的质量;(4)分子间 的平均距离;(5)分子的平均平动动能.
2.b的大小:*
P RT vb
A’
3.b与v的比较:*
三.考虑分子引力的修正:
1.修正结果:
B
B’
(1)在容器内取一分子,以 质 心为球心,以分子引力作用
力程R0为半径作球,叫分子引力球.若为理想气体,由于分 子质心间距比引力力程大,所以引力球内没有分子.对于非
理想气体,球内分布有分子,球内分子对 都有引力,球外分
非理想气体与理想气体在微观结构上的区别主要是非 理想气体分子数密度大,因此:
1.分子平均距离小,分子线度与平均距离比较不能忽略.所 以,分子不能当质点看待,即分子本身体积不能忽略(分子 斥力不能忽略).
2.分子间平均距离小,在引力力程之内分子引力不能忽略, 分子间除碰撞外还有引力作用,这个引力的存在对分子碰 撞器壁的冲量产生一定的影响.
说明:*
两分子在平衡位置附近的吸引
和排斥,和弹簧在平衡位置附近被
压缩和拉伸类似.
液体和固体中分子的振动就是
利用分子力这一特性来解释.
由于用势能来表示相互作用要
比直接用力来表示相互作用方便有
用,所以分子互作用势能曲线常被
用到.
§1.7.2分子碰撞有效直径 固体分子热振动 固体热膨胀
下面我们利用分子势能曲线解释分子间对心碰撞及固 体分子的振动及固体的热膨胀现象.
范氏考虑到这两点区别:
(1)把气体分子当作直径为d的刚球,即两分子只能靠近到 质心距离为d的程度.
(2)分子间有引力,在r>d时表现为引力.
从这两点出发对理想气体压强进行修正.
二.考虑到分子本身占据体积的修正
1.修正结果: 对1mol理想气体P=RT/v(v是1mol气体占据的容器体积).
理想气体分子当质点看待,每个分子运动时可达到容器各个 角落.因此,v是理想气体分子自由活动的空间范围(即容器容 积).对非理想气体,分子本身大小不能忽略,其它分子占据的 地方,分子运动时不能达到.因此非理想气体每个分子活动 的空间范围比v小.考虑到这一点,对非理想气体在压强表达 式中应从v中减去一个量.设为b,则有:
为便于分析,常设分子是球形的,分子间的互作用是对称 的中心力场.以r为横坐标,两分子间作用力F(r)为纵坐标, 画出两分子间互作用力曲线,如图:
(2)说明:*
二.分子势能
分子力是保守力(提问保守力的特点),其所作的功等于势 能增量的负值.故:
dEp (r) F(r)dr
这就决定了分子间相互作用能是分子势能,用Ep表示. 若令分子间距离r趋向无穷远时的势能为零,一般r大于
f rs rt
r为两分子质心距离; f 为两分子质心距离为r时的相互作用力;
, , s,t对同一种分子是常数,由实验确定.
其中s 9 : 15;t 4 : 7;
rs
----斥力,为正;
rt
----引力,为负.
(2)斥力取正,引力取负的原因:* 3.分子力曲线: (1)定义:既然两分子相互“接触”时排斥力占优势,相互分 离时分子间吸引力占优势,则两分子质心间应存在某一平 衡距离r0,在该距离分子间相互作用力将达平衡.
P
P RT P vb
即:
P Pv b RT
2.P的大小:
用 表K示由于分子引力作用,一个分子到达器壁时
在垂直于器壁方向上动量减少的数值.由于压强等于单
位时间与单位面积器壁发生碰撞的分子给予器壁的平均
冲量.
P 单位时间与单位面积器壁碰撞的分子数 2K 2K
因为分子数密度n越大,作用在分子上的引力就越大,则 越大K,所以 正比于K n.
分子力的力程(数量级大于10-9m)就可看作r为无穷.此时 分子力为零,分子力势能随r变化.
1.分子力势能Ep的表达式:
依F(r)=- dEp
dr
有: Ep
r
F (r)dr
r
r s
rt
dr
所以 :
Ep
r s1
r t1
,
式中=
s-1
,
t 1
2.势能曲线:
依Ep
r s1
r t 1
可在Ep
r坐标平面上作出分子势能曲线.如图:
又Q nv ,即: n 6
故 : P n2
而n N NA ,n2 1
Vv
v2
从而有 : P 1 ,即: P a
v2
v2
这里,a由气体性质决定,表示1mol气体当占有的体积v为
单位体积时,由于分子引力作用所引起的压强减小量.下面
将
代入P
a v2
P中 ,且P去v 掉b R的T 上角号,则得P到1mol气体
§1.7分子间作用力势能与真实气体物态方程*
pVm f ( p) RT
§1.7.1分子间互作用势能曲线*
一.分子力
1.分子力产生原因:*
2.分子力的公式(雷纳德-琼斯模型)
(1)模型:分子间相互作用比较复杂,很难用简单的数学公 式表达.在分子运动论中,一般是在实验基础上采用一些简 化模型来处理问题.一种常用的模型是假设分子间相互作 用是有球对称形式.故也叫做球对称模型.公式如下:
