实际气体节流过程
气体绝热节流

什么?
h
1 cp
T
v T
p
v
h hBiblioteka h0 0 0– 取决于节流前的气体状态
– 理想气体
dh
cpdT
T
v T
p
vdp
v v T T
pv RT
T不变 T降低 T增加
获得低温的方法--绝热节流
• 微分节流效应
– 三种情况的内在机理
dh du d pv 0
即du d ( pv)
– 只有低于上转化温度后,节流才降温
获得低温的方法--绝热节流
• 转化温度与转化 曲线
– 实践证明,当 p pmax 时出现一条转化温度 的曲线。
– 如节流前气体状态在 区间p 内pm,ax,则Tin"v节 T流后Tin' v产 生制冷效果。
获得低温的方法--绝热节流
思考题: • 微分节流效应、积分节流效应、等温节流
u u动 u势
– 节流后v 增加,du势 ,0但d(pv)不定
– 因此,du动 du势 也d不( p确v)定
获得低温的方法--绝热节流
• 积分节流效应:压力变化一定时,温度变化的量
T
p2 p1
hdp
h (
p2
p1)
hp
获得低温的方法--绝热节流
• 等温节流效应:
hT h1 h0
– 节流后等压升温到节 流前的温度所需的热 量
– 也即节流的制冷量, 但并非是节流装置制 冷
– 谁提供了制冷能力?
为何会制冷?
获得低温的方法--绝热节流
• 转化温度与转化曲线
– h 0 对应的温度为转化温度 Tinv
《物理化学第4版》第一章-8 节流过程ppt课件

W2= - p2(V2) 在压缩和膨胀时体系净功的变化应该是
两个功的代数和。 W=p1V1- p2 V2
W=W1+W2=p1V1-p2V2
即 U2 U1 p1V1 p2V2
移项 U2 p2V2 U1 p1V1
H2=H1
节流过程是等焓过程。 T变而H不变:实际气体的H 不只是T 的函数。
实际气体的焓不仅是温度的函数,还是 压力p的函数,即 H= f(T,p)。
实际气体分子间有相互作用力,使得分子间 的势能对热力学能有贡献,即U=f(T,V)。
等温过程,实际气体的dU、dH不等于零。
3.焦-汤系数
JT
def
dT dp
H
JT 称为焦-汤系数(Joule-
Thomson coefficient),它表示经节流
过程后,气体温度随压力的变化率。
因为节流过程的dp<0 , 所以:
若 J-T<0,则节流后 温度升高?降低?不变? J-T>0, 节流后 温度升高?降低?不变? J-T=0, 节流后 温度升高?降低?不变?
用于制冷设备的实际气体,其J-T>0,例如氨气。
低压低温气体
p ,则T
节流过程(管内有
填充物)
冰
箱
从
外
冰
侧
箱
向
内
环
吸
境
热
放
热
高压高温气体
电冰箱工作原理示意图
T1
Q T2
由环境付出电功
§1-8 实际气体的焓和热力学能
实际气体的热力学能 U=f (T, V)
实际气体的焓
H=f (T, p)
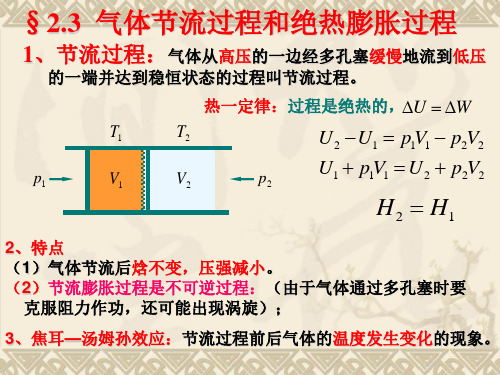
气体节流过程和绝热膨胀过程
T
1
T p
H
T p
H
T H
p
H p
T
1 Cp
T
V T
p
V
对理想气体, V nR,求得 0,即理想气体节流后温
度不变。 T p p
对实际气体(如范氏气体), 的正负取决T、p取值,用实际 气体进行节流过程可获得低温。
T p
H
V Cp
T
1
T 1 0 温度不变
pdV
dH dH=Vdp+TdS
dU TdS
dU=-pdV+TdS
V A,P,m,q电荷量 p ,E,0, 电动势 12
二、绝热去磁致冷效应
忽略磁介质体积变化, 则有 dG SdT 0md ,
三、 气体自由膨胀后的温度变化
W 0 Q 0 ΔU 0 气体自由膨胀后内能不变。
dU
CV dT
T
p T
V
pdV
T ?? V U
T V
U
1 CV
T
p T
V
p
p CV
T
1
理想气体 T 0 自由膨胀后温度不变。 V U
范氏气体
p
n2a V2
V
nb
nRT
2a RT b 0 T 0
温度降低 焦耳— 汤姆逊正效应 温度升高 焦耳— 汤姆逊负效应 温度不变 焦耳— 汤姆逊零效应
(3)在某个温度 Ti 时,实际气体的 0 ,它在节流过程中的
行为与理想气体一样。对不很稠密的范德瓦耳斯气体,
Ti 2a RT 时, 0 ,Ti称为转换温度,一般情况下,这
T V
U
n2a CVV 2
0
气体的节流过程和绝热膨胀过程.docx

示为 H=H(T,p)。节流过程所产生的效应可用焦
效应,若
,则温度升高,节流为负效应,
若
,则温度不发生变化,节流为零效应。对于理想气体而言,
这就是说理想气体在节流过程前中后温度不变,不能用节流膨胀的方法使 理想气体降温。而
对于实际气体,
■可能大于零也可能小于零,因此节流可
3
绵阳师范学院 2011 届本科毕业设计(论文)
引言
低温制冷技术在已经在各领域的到广泛应用;有研究表明,寿命与环
境温度的关系非常密切,如青蛙生活在
2C 的水中的寿命,比它在 2「C 的水
中高出 960 倍。生命在低温技术下可以长时间得以保存,如科学家在南极冰 岩 400 米深的
冰层里发现冷冻着的许多古代微生物,如果将其慢慢解冻,有 些小生命会从沉睡中苏醒过
来。因而如果能够把那些目前不治之症的病人 在低温下冻结,让其生命保存起来,待将来医
疗技术有了突破后再将其解 冻后进行治疗,在医学上有重要意义。低温技术为超导应用提供
了最基本 的运行条件,成为超导系统整体的一个重要而又不可分割的部分,其直接 关系到
超导设备的效率和安全可靠性。还有在高压补燃氢氧发动机的研制 过程中,如果解决一系列
1.1 节流过程 .............................................................. 1 1.1.1 节流过程的定义及特征 ............................................. 1 1.1.2 焦耳-汤姆逊效应 ................................................. 2
绵阳师范学院
本科生毕业论文(设计)
第9节实际气体的节流膨胀

nl 1.612 0.322 1.29 mol
第一步是理想气体等温压缩过程
U1=0, H1=0
W1=
nRT ln
p1 p2
1.6128.3145373 ln
5104 1105
3.465
kJ
Q1= -W1=-3.465 kJ
第二步是气体的相变过程,没有相变的不用计算
n p1V1 5104 100 103 1.612 mol RT 8.3145 373
V2
nRT p2
8.3145 373 1.612 110 5
50
dm3
ng,2
p2V3 RT
1105 10 103 8.3145 373
0.322
mol
Q2= ΔH2=-1.29×40.670=-52.464 kJ
W2=-p外×ΔV=-105×(-40×10-3)=4.00 kJ
U2=W2+Q2=-48.464 kJ Q=Q1+Q2= -55.929 kJ
W=W1+W2= 7.465 kJ U=-48.464 kJ H=-52.464 kJ
μJ-T >0 经节流膨胀后,气体温度降低。 μJ-T <0 经节流膨胀后,气体温度升高。 μJ-T =0 经节流膨胀后,气体温度不变。
习题36 将100℃ ,5×104Pa的水蒸气100 dm3 定温可逆压缩至标准压力(此时仍全为水蒸气), 并继续在标准压力下压缩到体积为10dm3时为 止(此时已有一部分水蒸气凝结成水)。试计算 此过程的Q、W、 U和 H。假设凝结成水的 体积可忽略不计;水蒸气可视为理想气体。
§1.9 节流膨胀
一、Joule-Thomson实验-节流过程(Throttling Process)
第9节 实际气体的节流膨胀

nl1.61 0 2 .321 2 .29 mol
.
第一步是理想气体等温压缩过程
U1=0, H1=0 W1= nR ln p p 1 2 T 1 .6 1 8 .3 21 34 7 l5 5 1 n 3 1 15 4 0 0 3 .46 k5 Q1= -W1=-3.465 kJ
第二步是气体的相变过程,没有相变的不用计算 Q2= ΔH2=-1.29×40.670=-52.464 kJ
np1 V 15140 10 103 01.61m 2ol RT 8.313 47 53
nR8 T .3 V 2p2
1 1 3 1 45 7 0 5 1.6 31 5 2d 03 m
ng, 2p R 2 V 3T 1 8 1 .350 1 1 3 4 0 17 5 3 0 3 0.32m 2ol
μHale Waihona Puke -T >0 经节流膨胀后,气体温度降低。 μJ-T <0 经节流膨胀后,气体温度升高。 μJ-T =0 经节流膨胀后,气体温度不变。
.
习题36 将100℃ ,5×104Pa的水蒸气100 dm3 定温可逆压缩至标准压力(此时仍全为水蒸气), 并继续在标准压力下压缩到体积为10dm3时为 止(此时已有一部分水蒸气凝结成水)。试计算 此过程的Q、W、 U和 H。假设凝结成水的 体积可忽略不计;水蒸气可视为理想气体。
§1.9 节流膨胀
一、Joule-Thomson实验-节流过程(Throttling Process)
在一个圆形绝热筒的中部有一个多孔塞和 小孔,使气体不能很快通过,并维持塞两边的压 差。
实验装置如图所示。图1是始态,左边有状 态为p1, V1, T1的气体。
图2是终态,左边气体压缩,通过小孔,向右 边膨胀,气体的终态为p2, V2, T2 。
实际气体的节流效应讲解学习
焦耳一汤姆逊效应气体在节流反应过程里产生的温度变化,被称之为焦耳一汤姆逊作用(简称焦一汤作用)。
产生上述现象的根部原因,是由于气体的烩值,并不是简单的温度函数,同时也受到压强、气体性能的影响。
大部分气体在室温条件下,完成节流反应的时候,都会产生冷却作用,也就是通过节流设备之后的温度快速减小,上述温度改变就是正焦耳一汤姆逊作用。
只有很少数的气体在室温条件下,完成节流反应之后温度上升,这类温度改变就被称之为负焦耳一汤姆逊作用。
在相同温度条件下,焦耳一汤姆逊作用的正负性可以发生转化,这类温度就被称之为反转温度。
所有气体都具有自身独特的反转温度。
例如,空气,氮气和氧气的反转温度都比室温高。
节流过程节流过程是一类不可逆反应过程,在反应过程里,流体处于非平衡状态。
分析节流反应过程,就是研究从节流反应之前一直到节流反应之后,流体依次处于不同平衡状态的时候,所有指数经过反应过程产生的改变。
在绝热节流反应过程中,保持能量守恒。
这是因为在反应过程里,流体和外界没有产生热量传递,也没有能量的转化,假如维持流体在节流反应之后的高度、流速恒定,也就是没有重力势能以及运动势能的改变(或者改变非常小,基本忽略不计),那么节流反应之后,流体的烩h2和节流反应之前的烩hl保持一致,也就是h2=hl与此同时,由于绝热节流是一种不可逆的反应过程,节流后流体的嫡绝对增加,有s2>s1在气态流体通过绝热节流之后,体积会随着压强的减小而不断变大,但是液态流体的体积在节流反应前后,并不会产生显著地改变。
节流的温度效应在绝热节流反应前后,流体温度的改变被称之为节流反应的温度效应。
节流反应之后流体的实际温度快速减小,被称之为节流反应冷效应;节流反应之后流体的实际温度快速升高,被称之为节流反应热效应;节流反应前后流体的实际温度保持一致,被称之为节流反应零效应。
节流反应的温度效应和液体的类别,温度、压强都具有密切的联系。
绝热节流反应的温度效应可以采用绝热节流反应指数来表达。
实际气体的节流膨胀
解:
T=373 K 等温压缩
T=373K
p1=0.05 MPa V1=100 dm3 水蒸气(ng,1)
Q1、W1、 U1和H1
p2=0.1 MPa V2=?
水蒸气(ng,1)
Q2、W2、 U2和H2
等温等压相变
T=373 K
p2=0.1 MPa V3=10 dm3 水(nl)和水蒸气(ng,2)?
§1.9 节流膨胀
L/O/G/O
一、Joule-Thomson实验-节流过程(Throttling Process)
在一个圆形绝热筒的中部有一个多孔塞和 小孔,使气体不能很快通过,并维持塞两边的压
差。 实验装置如图所示。图1是始态,左边有状
态为p1, V1, T1的气体。
图2是终态,左边气体压缩,通过小孔,向右 边膨胀,气体的终态为p2, V2, T2 。
第一步是理想气体等温压缩过程
U1=0, H1=0
W1= nRT ln
p1 p2
1.6128.3145373 ln
5104 1105
3.465
kJ
Q1= -W1=-3.465 kJ
第二步是气体的相变过程,没有相变的不用计算
Q2= ΔH2=-1.29×40.670=-52.464 kJ
W2=-p外×ΔV=-105×(-40×1 5104 100 103 1.612 mol RT 8.3145 373
V2
nRT p2
8.3145 373 1.612 110 5
50
dm3
ng,2
p2V3 RT
1105 10 103 8.3145 373
0.322
mol
ch.2-3 气体的节流过程和绝热膨胀过程
二、绝热膨胀过程
如果把绝热膨胀过程近似看作是准静态的,则过程 中气体的熵保持不变。因此,绝热膨胀过程也称为等熵过 程。 S S dS 由 dT dp 0
T p
p T
可得
T S p S p T
可改写为
或
U2-U1=p1V1-p2V2 U2+p2V2=U1+p1V1
H2 = H1
(2.3.1)
上式说明,气体在节流前后的两个状态的焓值相等。 要注意的是,尽管气体的流动足够缓慢,节流过程也不能 认为是无摩擦的准静态过程。由于气体经历的是一系列的 非平衡态,焓是没有定义的。所以,(2.3.1)式只表示节流 过程的初态和终态的焓值,并非指整个节流过程中焓值不 变。
● 程序(ex4433)
① 计算焦耳-汤姆逊系数的表达式(ex44331)
syms R T a b v p dp_dT dp_dv Cp ; p=R*T/(v-b)-a/v^2; dp_dT=diff(p,T); dp_dv=diff(p,v); mu=-1/Cp/dp_dv*(T*dp_dT+v*dp_dv); a=0.1350; b=0.03868e-3; %取N2气的修正系数值 R=8.31; Cp=5*R/2; mu=vpa(subs(mu),3) 运行结果: mu=-.481e-1/(-8.31*T/(v-.387e-4)^2+.270/v^3)*(8.31*T/(v-.387e-4)+v*(8.31*T/ (v-.387e-4)^2+.270/v^3))
R p 可求得 T V v b
RT a p 2 v b v
RT 2a p 3 2 v V T (v b)
实际气体绝热节流膨胀过程的△u
实际气体绝热节流膨胀过程的△u在热力学中,气体的绝热节流膨胀过程是指气体从高压区域通过狭窄的孔口进入低压区域,过程中没有热量交换的现象。
在这个过程中,气体的内能发生变化,我们将其表示为△u。
本文将从理论和实际两个方面来探讨实际气体绝热节流膨胀过程的△u。
理论方面,根据绝热过程的定义,气体在绝热节流膨胀过程中,没有热量交换发生。
因此,气体的内能变化完全取决于气体的外界功。
根据热力学第一定律,内能变化△u等于外界对气体所做的功。
在绝热节流膨胀过程中,气体通过狭窄的孔口进入低压区域,气体分子受到孔口的限制而加速运动,从而使气体的动能增加,内能也随之增加。
因此,实际气体绝热节流膨胀过程的△u是正值。
实际方面,绝热节流膨胀过程广泛应用于工业生产中,例如气体喷嘴、气体涡轮等。
在这些应用中,气体通过狭窄的孔口进入低压区域,从而产生高速气流,用于推动机械设备或实现特定的工艺过程。
在实际应用中,我们可以通过测量气体的入口和出口参数来计算实际气体绝热节流膨胀过程的△u。
我们需要测量气体的入口压力和温度,以及出口压力。
根据理论方面的分析,气体的内能变化△u等于外界对气体所做的功。
在绝热节流膨胀过程中,外界对气体所做的功可以通过压力差来计算。
根据热力学第一定律,功等于压力差乘以气体的体积变化。
因此,△u等于压力差乘以气体的体积变化。
我们需要计算气体的体积变化。
在绝热节流膨胀过程中,气体通过狭窄的孔口进入低压区域,气体的体积发生变化。
根据理想气体状态方程,PV=nRT,气体的体积与物质的量成正比。
因此,我们可以通过测量气体的入口和出口物质的量来计算气体的体积变化。
我们可以将测得的压力差和体积变化代入△u的计算公式,从而得到实际气体绝热节流膨胀过程的△u值。
需要注意的是,在计算过程中,我们需要考虑气体的物性参数,如气体的摩尔质量、绝热指数等,以保证计算结果的准确性。
实际气体绝热节流膨胀过程的△u是正值,表示气体在绝热节流膨胀过程中内能的增加。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
CH4 RT
E
p
273K下的pVm-p关系图
• 一般气体的pVm-p关系如图. • 低温下, 气体的pVm值先随p的 升高而下降, 在此区间,气体的 J-T系数才可能大于零, 气体 节流降温. • 温度升高时, 曲线斜率为负的 区间将会缩小, 当体系达到一 定温度时, pVm-p关系曲线不再 出现凹陷现象, 此时的温度记 为 TB.称为波义尔温度. 气体在 波义尔温度以上时, 无法用节 流膨胀的方法使之液化. • H2的波义尔温度是195K, 约 ﹣78℃, 故欲液化氢气, 首先需 把氢气的温度降至195K以下.
∵dp<0,
dU>0
• 实际气体的第一项总是正值.
第二项:
见pV-p关系图:
蓝线:理想气体, pV值为常 数. 绿线:CH4, 在E点之前斜率为负, [((pV)/p)T]CH4 < 0 CH4: 的第一项>0, 第二项>0, 故 (273K,CH4)>0,节流降温. 红线是H2的曲线, 曲线斜率一直 为正值, 即: [((pV)/p)T]H2 > 0
E CH4 RT pVm
H2
H2: 的第一项>0, 第二项<0, 且 第二项的绝对值大于第一项的绝 对值, 故有:
(273K,H2)<0, 节流升温.
p
273K下的pVm-p关系图
气体在曲线的斜 率为负值区间的 焦汤系数才会大 于零。 在此区间才可能 用节流膨胀的方 法液化。
节流降温
pVm
H2
• 理想气体: =0, 节流膨胀后温度不变.
• B. 实际气体: • =-1/Cp[((U/p)T] - 1/Cp[((pV)/p)T] • 第一项: 实际气体分子间存在范德华引力
• p 降低, V增加, 分子间距增大, 需吸收能量以克服分 子间的引力, 体系的势能升高,故有:
•
(U/p)T<0
• 由热力学第二定律,可得下式:
• (U/V)T=T (p/T)V-p =T([RT/(Vm-b) -a/Vm2]/T)V-p
=TR/(Vm-b) -[RT/(Vm-b) -a/Vm2]
• ∴ =a/Vm2 dU= CVdT+a/Vm2 dV
•
Um=∫[CV,mdT+a/Vm2 dV]
转化温度(inversion temperature)
• 气体在转化温度下进行节流膨胀, 气温不会发生变化.
• 对J-T系数的分析:
• J-T节流膨胀是一等焓过程, dH=0, 故:
•
•
•
dH=(H/T)pdT+ (H/p)Tdp=0 (H/T)pdT=- (H/p)Tdp (dH=0)
pVm
RT4
RT3
RT2
RT1
p
等焓线(isenthalpic curve)
作节流实验:左方 维持在p1T1, 右方为 p2T2,在T-p图中标 出点1与2。 左方继续维持在 p1T1,右方维持在 p3T3, 相应地在图 中标出点3, 重复 可得一系列的等 焓点。
T
4 5
6 7
3
2(p2T2) 1(p1T1)
p
将点连起来便得到等焓线,线上各体系点的焓相等。
T
4 5 6 7
3
2(p2T2) 1(p1T1)
p
等焓曲线上任意一点的斜率为(T/p)H=, 即为焦-汤系数,在极点(点3)处=0。 在点3的左边, >0, 节流降温; 在点3的右边, <0, 节流升温.
转化曲线 (inversion curve)
p
不同气体的转化曲线
三、
实际气体的U和H
• 实际气体的U和H不仅仅是温度的函数, 也与压力和体积相关. • 以范德华气体为例: • (p+a/Vm2)(Vm-b)=RT • p=RT/(Vm-b) -a/Vm2 • dU = (U/T)VdT+ (U/V)TdV = CVdT+ (U/V)TdV
• 积分可得范德华气体Um的计算式:
• Um=CV(T2﹣T1)+a(1/Vm,1-1/Vm,2)
•
Hm= U+ (pV)
• 可以证明恒温下:
•
Hm=RT(Vm,2/(Vm,2-b) -Vm,1/(Vm,1-b)) +2a(1/Vm,1-1/Vm,2)
焦汤节流装置
返回
T1
T2
gas
pppVV11 p1 1V1V 111 p2pp2 V2 V V2 22
• • • • • • • • • •
左边: 环境对体系做功 W1=p1V1 右边: 体系对环境做功 W2=-p2V2 因为可视为绝热过程 Q=0 由热力学第一定律: U=W=W1+W2=p1V1-p2V2 U2-U1= p1V1-p2V2 整理可得: U2+p2V2=U1+p1V1 ∴ H2=H1 上式说明:气体绝热节流过程是等焓过程。
实际气体 节流过程
第七节
实际气体、节流过程
• 一、物质的状态方程(state equation)
• 任何纯物质的状态均可用状态方程来表示,所谓状
态方程是联系体系p-V-T三者之间关系的方程式。 • 最常见的状态方程是理想气体状态方程:
•
pV=nRT
• 实际气体因分子之间的作用势能不能忽视,故不遵 守理想气体状态方程。对于实际气体人们从大量的 实验数据总结出几百种状态方程。
=(T/p)H= - (H/p)T/ (H/T)p =-1/Cp[((U+pV)/p]T ∵(H/T)p=Cp
• 整理:
•
•
= -1/Cp[(U/p)T+((pV)/p]T
• A. 理想气体: • • (U/p)T=0 ((pV)/p]T=0
= -1/Cp[(U/p)T+((pV)/p]T =0
由T1p1为起点, 由节流实 验可得一条等焓线。 另由T1’p1’为起点, 可得 第二条等焓线。重复此 操作, 绘出多条等焓线。 将各条等焓线的极点用 虚线连接起来,虚线左 边所包围的区域为致冷 区,>0;虚线外的区 间, <0, 节流时气体的 温度反而升高。
T
<0
>0
T1’’ p1’’ T 1 ’ p1 ’ T 1 p1
• 气体经J-T等焓节流后,温度会发生变化: • • : J-T系数 • • • <0 >0 =0
令: =(T/p)H
dp<0 dT>0 气体节流后温度升高;
dp<0 dT<0
气体节流后温度降低;
气体节流后温度不变.
• 大多数气体的在常温下大于零, 故节流后温度 降低.
• 利用J-T效应, 可以使液化.
• 常用的状态方程还有: • • • • • • • • • 维里方程: (与热容的维里方程式相似) pVm=A+B/Vm+C/Vm2+… 贝赛罗方程: p=RT/(Vm-b) -a/(TVm2) 贝蒂方程: V=(+)(1﹣) -A/RT 式中: =RT/p =B0(1﹣b/a) =c/aT3 A=A0(1﹣a/ )
• 氢气曾被认为是不可液化的气体, 因为在常温下, 氢 气经节流膨胀后, 温度不但不降低, 反而升高. 这是因 为氢气的J-T系数在常温下小于零的缘故.当将氢气温 度降至195K以下时, 氢气的才变为正值, 在此温度之 下,对氢气进行节流膨胀, 氢气才会液化. • 气体的J-T系数是温度的函数. 在某一特定温度值下, 气体的J-T系数等于零: =0,此时所对应的温度称为: •
二. 节流过程
• 1843年Joule曾进行过气体自由膨胀的实验, 并由此得出理想气体的U与体积V无关的结论. 但当时的实验是不精确的. • 1852年, Joule-Thomson设计了新的装置重新 测定气体的体积发生变化时, 其温度随之变化 的情况. 焦耳与汤姆逊设计了一种节流装置.
• 这个过程可视为绝热过程. 可设体系在左边是 体积为V1, 经节流膨胀后, 压力降为p2, 体积变 为V2.
• 最著名、最常用的非理想气体的状态方程式是范 氏方程,即van der Waals equation:
•
(p+a/Vm2)(Vm-b)=RT
• 式中的a,b均为取决于物质本身性质的常数.
• a/Vm2:表示分子间的作用力所产生的压力, 称为 内压力; • b: 是对体系体积的修正,理论上,统计热力学 可以证明, b的数值等于分子体积的4倍.
