数学八年级上北师大版第七章平行线的证明单元测试A
第七章 平行线的证明数学八年级上册-单元测试卷-北师大版(含答案)

第七章平行线的证明数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题,共计45分)1、如图,在△ABC中,点D在BC边上,DE垂直平分AC边,垂足为点E,若∠B=70°,且AB+BD=BC,则∠BAC的度数是( )A.65°B.70°C.75°D.80°2、如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=60°,则∠3的度数为()A.50°B.60°C.70°D.80°3、如图,在△ABC中,AB=AC,BE⊥AC,D是AB的中点,且DE=BE,则∠C的度数是()A.65°B.70°C.75°D.80°4、已知等腰三角形一腰上的高线等于另一腰长的一半,那么此等腰三角形的一个底角等于()A.15°或75°B.15°C.75°D.150°或30°5、若等腰三角形一腰上的高和另一腰的夹角为25°,则该三角形的一个底角为()A.32.5°B.57.5°C.65°或57.5°D.32.5°或57.5°6、已知等腰三角形其中一个内角为70°,那么这个等腰三角形的顶角度数为()A.70°B.70°或55°C.40°或55°D.70°或40°7、如图:在△ABC中,BC=BA,点D在AB上,AC=CD=DB,则∠B=()A.30°B.36°C.45°D.60°8、如图,在平行四边形中,对角线与相交于点,是边的中点,连接.若,,则的度数为()A. B. C. D.9、如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F,∠F的度数为()A.120°B.135°C.150°D.不能确定10、在等腰三角形ABC中,∠A与∠B度数之比为5∶2,则∠A的度数是()A.100°B.75°C.150°D.75°或100°11、如图,中,,,,则的度数是()A. B. C. D.12、如图所示,把一个三角形纸片ABC顶角向内折叠3次之后,3个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6的度数和是()A.180°B.270°C.360°D.无法确定13、由线段组成的三角形不是直角三角形的是()A. B. C.D.14、如图所示,D 为 BC 上一点,且 AB=AC=BD,则图中∠1 与∠2 的关系是()A.∠1=2∠2B.∠1+∠2=180°C.∠1+3∠2=180°D.3∠2﹣∠1=180°15、如图,在中,的垂直平分线交于点,交于点,若,则的度数为()A. B. C. D.二、填空题(共10题,共计30分)16、平行公理是:________.17、如图,在中,平分交于点,交于点,若,则________.18、已知命题“线段垂直平分线上的任意一点到这条线段两个端点的距离相等”,用“如果…,那么…”的形式写出它的逆命题,并判断其真假.逆命题:________.这个逆命题是________ 命题(填“真”或“假”).19、如图,FE∥ON,OE平分MON,FEO=28°,则∠MON=________20、如图,在长方形纸片ABCD中,点E、F分别在AD、BC上,将长方形纸片沿直线EF折叠后,点D、C分别落在点的位置,如果∠=40°,那么∠EFB的度数是________度.21、右图的网格纸中,AB∥________ ,AB⊥________ .22、如图,已知AB∥EF,∠C=90°,则α、β与γ的关系是________.23、如图,l1∥l2,的顶点B、C在直线l2上,已知∠A= ,∠1= ,则∠2的度数为________.24、如图,直线a、b被直线c所截,a∥b,∠1=70°,则∠2=________.25、如图,AB∥CD,CE平分∠BCD,∠B=36°,则∠DCE等于________.三、解答题(共5题,共计25分)26、观察下列各式,,…利用上述三个等式及其变化过程,计算的值.27、如图,在△ABC中,∠A=70°,外角平分线CE∥AB.求∠B和∠ACB的度数.28、如图,AD、AE分别是△ABC的角平分线和高,∠B=50°,∠C=70°,求∠ADE和∠DAE的度数.29、如图,▱ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.求证:四边形AECF是平行四边形.30、如图,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=70°,∠C=50°,求∠DAC和∠BOA的度数.参考答案一、单选题(共15题,共计45分)1、C2、C3、C4、A5、D6、D7、B8、A9、B10、D11、B12、C13、D14、D15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、27、28、29、30、。
第七章 平行线的证明 单元测试 2022-2023学年北师大版数学八年级上册
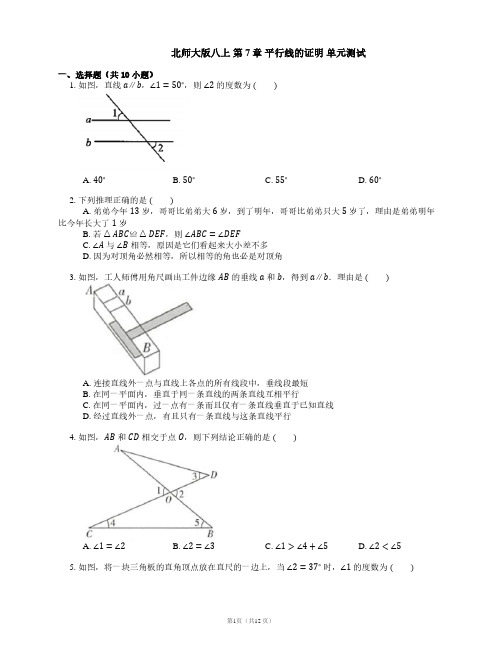
北师大版八上第7章平行线的证明单元测试一、选择题(共10小题)1. 如图,直线a∥b,∠1=50∘,则∠2的度数为( )A. 40∘B. 50∘C. 55∘D. 60∘2. 下列推理正确的是( )A. 弟弟今年13岁,哥哥比弟弟大6岁,到了明年,哥哥比弟弟只大5岁了,理由是弟弟明年比今年长大了1岁B. 若△ABC≌△DEF,则∠ABC=∠DEFC. ∠A与∠B相等,原因是它们看起来大小差不多D. 因为对顶角必然相等,所以相等的角也必是对顶角3. 如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b.理由是( )A. 连接直线外一点与直线上各点的所有线段中,垂线段最短B. 在同一平面内,垂直于同一条直线的两条直线互相平行C. 在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线D. 经过直线外一点,有且只有一条直线与这条直线平行4. 如图,AB和CD相交于点O,则下列结论正确的是( )A. ∠1=∠2B. ∠2=∠3C. ∠1>∠4+∠5D. ∠2<∠55. 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=37∘时,∠1的度数为( )A. 37∘B. 43∘C. 53∘D. 54∘6. 下列命题中,是真命题的是( )A. √9的算术平方根是3B. 数据−2,1,0,2,2,3的方差是83C. y=kx+b(k,b为常数)是一次函数D. 如果一个角的两边与另一个角的两边分别平行,那么这两个角相等7. 如图,在△ABC中,点D在AC上,延长BC至E,连接DE,则下列结论不成立的是( )A. ∠DCE>∠ADBB. ∠ADB>∠DBCC. ∠ADB>∠ACBD. ∠ADB>∠DEC8. 如图是汽车灯的剖面图,从位于O点的灯发出光照射到凹面镜上反射出的光线BA,CD都是水平线,若∠ABO=α,∠DCO=60∘,则∠BOC的度数为( )A. 180∘−αB. 120∘−αC. 60∘+αD. 60∘−α9. 如图,a∥b,M,N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3=( )A. 180∘B. 360∘C. 270∘D. 540∘10. 如图,△ABC中,将∠A沿DE翻折,点A落在Aʹ处,∠CEAʹ,∠BDAʹ,∠A三者之间的关系是( )A. ∠CEAʹ=∠BDAʹ+∠AB. ∠CEAʹ−3∠A=∠BDAʹC. ∠CEAʹ=2(∠BDAʹ+∠A)D. ∠CEAʹ−∠BDAʹ=2∠A二、填空题(共6小题)11. 命题“没有公共点的两条直线是平行的”的条件是,结论是,这个命题是命题.12. 如图,若AB∥CD,∠A=110∘,则∠1=∘.13. 如图,AB∥CD,EF分别与AB,CD交于点B,F.若∠E=30∘,∠EFC=130∘,则∠A=.14. 如图,将分别含有30∘,45∘角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65∘,则图中角α的度数为.15. 如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为.(任意添加一个符合题意的条件即可)16. 一个大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150∘,则∠ABC=∘.三、解答题(共5小题)17. 补全证明过程:(括号内填写理由)如图,一条直线分别与直线BE,直线CE,直线BF,直线CF相交于A,G,H,D,如果∠1=∠2,∠A=∠D,求证:∠B=∠C.证明:∵∠1=∠2,(已知)∠1=∠3,()∴∠2=∠3()∴CE∥BF,()∴∠C=∠4,()又∵∠A=∠D,()∴AB∥,()∴∠B=∠4,()∴∠B=∠C.(等量代换)18. 如图,把一张长方形纸片ABCD沿EF折叠后,点D,C分别落在Dʹ,Cʹ的位置上,EDʹ与BC的交点为G,若∠EFG=55∘,求∠1,∠2的度数.19. 如图①,在三角形ABC中,∠BAE=1∠BAC,∠C>∠B,且FD⊥BC于点D.2(1)试推出∠EFD,∠B,∠C之间的关系;(2)如图②,当点F在AE的延长线上时,其他条件不变,(1)中推导的结论还成立吗?请直接写出结论.20. 如图,AD是△ABC的角平分线,点E在BC的延长线上,求证:∠B+∠1=2∠2.21. 如图①,在平面直角坐标系中,A(0,1),B(4,1),C为x轴正半轴上一点,且AC平分∠OAB.(1)求证:∠OAC=∠OCA;(2)如图②,若分别作∠AOC的三等分线及∠OCA的邻补角的三等分线交于点P,即∠POC=1 3∠AOC,∠PCE=13∠ACE,求∠P的大小;(3)如图③,若∠POC=1n ∠AOC,∠PCE=1n∠ACE,猜想∠OPC的大小.(用含n的式子表示)答案1. B2. B【解析】由全等三角形的性质可知,B 正确.3. B 【解析】由题意得 a ⊥AB ,b ⊥AB ,∴a ∥b (在同一平面内,垂直于同一条直线的两条直线平行).4. A【解析】∵∠1 和 ∠2 是对顶角,∴∠1=∠2,故A 正确;∵∠2=∠A +∠3,∴∠2>∠3,故B 错误;∵∠1=∠4+∠5,故③错误;∵∠2=∠4+∠5,∴∠2>∠5,故D 错误.故选A .5. C【解析】如图,∵AB ∥CD ,∠2=37∘,∴∠2=∠3=37∘,∵∠1+∠3=90∘,∴∠1=53∘.6. B【解析】A .√9=3,3 的算术平方根是 √3,原命题是假命题,不符合题意;B .数据 −2,1,0,2,2,3 的平均数是 1,方差=16×[(−2−1)2+(1−1)2+(0−1)2+(2−1)2×2+(3−1)2]=83,原命题是真命题,符合题意;C .y =kx +b (k ,b 为常数,且 k ≠0)是一次函数,原命题是假命题,不符合题意;D .如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补,原命题是假命题,不符合题意.故选B .7. A【解析】A 选项无法判断;∵∠ADB 是 △BCD 的一个外角,∴∠ADB >∠DBC ,∠ADB >∠ACB ,故选项B ,C 均成立;∵∠ACB 是 △CDE 的一个外角,∴∠ACB >∠DEC ,∴∠ADB >∠DEC ,故选项D 成立.8. C【解析】连接 BC ,∵AB∥CD,∴∠ABO+∠CBO+∠BCO+∠OCD=180∘,又∠CBO+∠BCO+∠BOC=180∘,∴∠BOC=∠ABO+∠DCO=α+60∘.9. B 【解析】过点P作PA∥a,∵a∥b,PA∥a,∴a∥b∥PA,∴∠1+∠MPA=180∘,∠3+∠APN=180∘,∴∠1+∠MPA+∠3+∠APN=180∘+180∘=360∘,∴∠1+∠2+∠3=360∘.10. D【解析】如图,由折叠得∠A=∠Aʹ,∵∠CEAʹ=∠A+∠1,∠1=∠Aʹ+∠BDAʹ,∴∠CEAʹ=∠A+∠Aʹ+∠BDAʹ=2∠A+∠BDAʹ,∴∠CEAʹ−∠BDAʹ=2∠A.故选D.11. 两条直线没有公共点,这两条直线互相平行,假12. 70【解析】如图,∵AB∥CD,∴∠2=∠A=110∘.又∵∠1+∠2=180∘,∴∠1=180∘−∠2=180∘−110∘=70∘.13. 20∘【解析】∵AB∥CD,∴∠ABF+∠EFC=180∘,∵∠EFC=130∘,∴∠ABF=50∘,∵∠A+∠E=∠ABF=50∘,∠E=30∘,∴∠A=20∘.14. 140∘【解析】如图,∵∠ACB=90∘,∠DCB=65∘,∴∠ACD=∠ACB−∠BCD=90∘−65∘=25∘,∵∠A=60∘,∴∠DFB=∠AFC=180∘−∠ACD−∠A=180∘−25∘−60∘=95∘,∵∠D=45∘,∴∠α=∠D+∠DFB=45∘+95∘=140∘.15. ∠A+∠ABC=180∘或∠C+∠ADC=180∘或∠CBD=∠ADB或∠C=∠CDE(答案不唯一)【解析】若∠A+∠ABC=180∘,则BC∥AD;若∠C+∠ADC=180∘,则BC∥AD;若∠CBD=∠ADB,则BC∥AD;若∠C=∠CDE,则BC∥AD,故答案为∠A+∠ABC=180∘或∠C+∠ADC=180∘或∠CBD=∠ADB或∠C=∠CDE(答案不唯一).16. 120【解析】如图,过点B作BG∥CD.∵CD∥AE,CD∥BG,∴∠C+∠CBG=180∘,BG∥AE,∴∠BAE+∠ABG=180∘,又易知∠BAE=90∘,∴∠ABG=90∘,∵∠C=150∘,∴∠CBG=30∘,∴∠ABC=∠ABG+∠CBG=90∘+30∘=120∘.17. 对顶角相等;等量代换;同位角相等,两直线平行;两直线平行,同位角相等;已知;CD;内错角相等,两直线平行;两直线平行,内错角相等18. ∵AD∥BC,∠EFG=55∘,∴∠2=∠GED,∠DEF=∠EFG=55∘,由折叠知∠GEF=∠DEF=55∘,∴∠GED=110∘,∴∠1=180∘−∠GED=70∘,∠2=110∘.19. (1)∠EFD=90∘−∠FED=90∘−(∠B+∠BAE)=90∘−∠B−12∠BAC=90∘−∠B−12(180∘−∠B−∠C)=90∘−∠B−90∘+12∠B+12∠C=12(∠C−∠B).(2)(1)中推导的结论仍成立,∠EFD=12(∠C−∠B).20. ∵AD是△ABC的角平分线,∴∠BAC=2∠BAD,∵∠1=∠B+∠BAC,∠2=∠B+∠BAD,∴∠B+∠1=∠B+∠B+∠BAC=2∠B+2∠BAD=2∠2.21. (1)∵A,B的纵坐标相等,所以AB∥OC,∴∠BAC=∠OCA,又AC平分∠OAB,∴∠OAC=∠BAC,∴∠OAC=∠OCA.(2)由(1)得∠OAC=∠OCA,∴OA=OC,∴∠OAC=∠OCA=45∘,∴∠ACE=135∘,∵∠POC=13∠AOC,∠PCE=13∠ACE,∴∠P=∠PCE−∠POC=13∠ACE−13∠AOC=13×(∠ACE−∠AOC)=13×(135∘−90∘)=15∘.(3)∠OPC=45∘n .证明:∠OPC=∠PCE−∠POC(∠ACE−∠AOC)=1n(135∘−90∘)=1n=45∘.n第11页(共12 页)第12页(共12 页)。
北师大版八年级数学上册第7章《平行线的证明》单元测试(含答案)

第7章《平行线的证明》单元测试一、选择题(本题共10小题,每小题3分,共30分)1.下列语句中,是命题的为().A.延长线段AB到C B.垂线段最短C.过点O作直线a∥b D.锐角都相等吗2.下列命题中是真命题的为().A.两锐角之和为钝角B.两锐角之和为锐角C.钝角大于它的补角D.锐角大于它的余角3.“两条直线相交,有且只有一个交点”的题设是().A.两条直线B.交点C.两条直线相交D.只有一个交点4.如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是().A.相等B.互余或互补C.互补D.相等或互补5.若三角形的一个外角等于与它不相邻的一个内角的4倍,等于与它相邻的内角的2倍,则三角形各角的度数为().A.45°,45°,90°B.30°,60°,90°C.25°,25°,130°D.36°,72°,72°6.如图所示,AB⊥EF,CD⊥EF,∠1=∠F=30°,则与∠FCD相等的角有().A.1个B.2个C.3个D.4个7.下列四个命题中,真命题有().(1)两条直线被第三条直线所截,内错角相等.(2)如果∠1和∠2是对顶角,那么∠1=∠2.(3)一个角的余角一定小于这个角的补角.(4)如果∠1和∠3互余,∠2与∠3的余角互补,那么∠1和∠2互补.A.1个B.2个C.3个D.4个8.如图所示,∠B=∠C,则∠ADC与∠AEB的大小关系是().A.∠ADC>∠AEB B.∠ADC=∠AEBC.∠ADC<∠AEB D.大小关系不能确定9.如图所示,AD平分∠CAE,∠B=30°,∠CAD=65°,则∠ACD=().A.50°B.65°C.80°D.95°10.如图所示,已知AB∥CD,AD和BC相交于点O,若∠A=42°,∠C=58°,则∠AOB 的度数为().A.45°B.60°C.80°D.90°二、填空题(本大题共10小题,每小题4分,共40分)11.如图所示,∠1=∠2,∠3=80°,那么∠4=__________.12.如图所示,∠ABC=36°40′,DE∥BC,DF⊥AB于点F,则∠D=__________.13.如图所示,AB∥CD,∠1=115°,∠3=140°,则∠2=__________.14.如果一个三角形三个内角的比是1∶2∶3,那么这个三角形是__________三角形.15.一个三角形的三个外角的度数比为2∶3∶4,则与此对应的三个内角的比为__________.16.如图所示,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠A=65°,则∠BFC=__________.17.“同角的余角相等”的题设是__________,结论是__________.18.如图所示,AB∥EF∥CD,且∠B=∠1,∠D=∠2,则∠BED的度数为__________.19.如果一个等腰三角形底边上的高等于底边的一半,那么这个等腰三角形的顶角等于__________.20.过△ABC的顶点C作AB的垂线,如果该垂线将∠ACB分为40°和20°的两个角,那么∠A,∠B中较大的角的度数是__________.三、解答题(本大题共5小题,共30分)21.(5分)如图所示,已知∠1=∠2,AE∥BC,求证:△ABC是等腰三角形.22.(5分)如图所示,已知直线BF∥DE,∠1=∠2,求证:GF∥BC.23.(6分)如图所示,已知直线AB∥CD,FH平分∠EFD,FG⊥FH,∠AEF=62°,求∠GFC的度数.24.(6分)如图所示,已知直线AB∥CD,∠AEP=∠CFQ,求证:∠EPM=∠FQM.25.(8分)在△ABC中,BE平分∠ABC,AD为BC边上的高,且∠ABC=60°,∠BEC =75°,求∠DAC的度数.参考答案1答案:B2答案:C3答案:C4答案:D5答案:B6答案:B7答案:C8答案:B9答案:C10答案:C11答案:80°∴∠4=∠3=80°.12答案:53°20′13答案:75°14答案:直角15答案:5∶3∶116答案:122.5°17答案:两个角是同一个角的余角这两个角相等18答案:90°19答案:90°20答案:70°21证明:∵AE∥BC,(已知)∴∠2=∠C,(两直线平行,内错角相等)∠1=∠B.(两直线平行,同位角相等)∵∠1=∠2,(已知)∴∠B=∠C.(等量代换)∴AB=AC,△ABC是等腰三角形.(等角对等边)22证明:∵BF∥DE,(已知)∴∠2=∠FBC.(两直线平行,同位角相等)∵∠2=∠1,(已知)∴∠FBC=∠1.(等量代换)∴GF∥BC.(内错角相等,两直线平行)23解:∵AB∥CD,∴∠AEF=∠EFD=62°,∠CFE=180°-∠AEF=118°.又FH平分∠EFD,∴∠EFH=31°.又GF⊥FH,∴∠EFG=90°-31°=59°.∴∠GFC=∠CFE-∠EFG=59°24证明:∵AB∥CD,(已知)∴∠AEF=∠CFM.(两直线平行,同位角相等)又∵∠PEA=∠QFC,(已知)∴∠AEF+∠PEA=∠CFM+∠QFC,(等式性质)即∠PEF=∠QFM.∴PE∥QF.(同位角相等,两直线平行)∴∠EPM=∠FQM.(两直线平行,同位角相等)25解:∵BE平分∠ABC,且∠ABC=60°,∴∠ABE=∠EBC=30°.∴∠C=180°-∠EBC-∠BEC=180°-30°-75°=75°. 又∵∠C+∠DAC=90°,∴∠DAC=90°-∠C=90°-75°=15°.。
第七章 平行线的证明数学八年级上册-单元测试卷-北师大版(含答案)

第七章平行线的证明数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题,共计45分)1、如图,在四边形ABCD中,∠A=∠BDC=90°,∠C=∠ADB,点P是BC边上的一动点,连接DP,若AD=4,则DP的长不可能是()A.6B.5C.4D.32、如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,交AB于点M,则∠2等于()A.20°B.25°C.30°D.40°3、如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,若∠BFC=116°,则∠A=()A.51°B.52°C.53°D.58°4、等腰三角形的一个底角是,则它的顶角是()A. B. C. D.5、一个三角形三个内角的度数之比是2∶3∶5,则这个三角形一定是()A.直角三角形B.等腰三角形C.钝角三角形D.锐角三角形6、如图.在△ABC中.∠B=30°.∠C=70°.AD是△ABC的一条角平分线.则∠CAD的角数为( )A.40°B.45°C.50°D.55°7、在□ ABCD中, AD=2AB,点E为边AD的中点. 则∠ BEC的度数为()A.60°B.90°C.120°D.150°8、一个等腰三角形的底角为70°,则它的顶角为()A.100°B.140°C.50°D.40°9、如图,已知△ABC中,∠A=75°,则∠1+∠2=()A.335°B.255°C.155°D.150°10、如图所示,将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上,若∠1=38°,则∠2的度数()A.28°B.22°C.32°D.38°11、如图,直线l1∥l2,∠1=45°,∠2=75°,则∠3等于()A.55°B.60°C.65°D.70°12、如图,△ABC中,AB=AC,∠BAC=40°,D为△ABC内一点,如果将△ACD绕点A按逆时针方向旋转到△ABD′的位置,则∠ADD′的度数是()A.40°B.50°C.60°D.70°13、如图,直线AD∥BC,若∠1=74°,∠BAC=56°,则∠2的度数为()A.70°B.60°C.50°D.40°14、已知在△ABC中,∠C=90°,设sinB=n,当∠B是最小的内角时,n 的取值范围是()A.0<n<B.0<n<C.0<n<D.0<n<15、在△ABC中,BC=a ,AB=c,AC=b,则不能作为判定△ABC是直角三角形的条件的是()A. B.∠A∶∠B∶∠C=1∶4∶3 C.a∶b∶c =7∶24∶25 D.a∶b∶c =4∶5∶6二、填空题(共10题,共计30分)16、如图,将一个正三角形纸片剪成个全等的小正三角形,再将其中的一个按同样的方法剪成个更小的全等正三角形如此下去,次后得到的正三角形的总个数为________.第一次第二次第三次17、如图,AD平分∠BAC,E、F分别是AD、AC上的点,请你填写两个不一样的条件________或________,使EF∥AB.18、如图,D是AB边上的中点,将△ABC沿过D的直线折健,使点A落住BC上F处,若∠B =50 ,则∠ADE=________度.19、如图,将一副三角板如图摆放(一块三角板的直角边与另一块三角板的斜边在同一直线上),那么________.20、若:A32=3×2=6,A53=5×4×3=60,A54=5×4×3×2=120,A64=6×5×4×3=360,…,观察前面计算过程,寻找计算规律计算A73=________(直接写出计算结果),并比较A103________A104(填“>”或“<”或“=”)21、如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是________.22、如图,四边形内接于⊙,为⊙的直径,点为的中点.若,则________.23、如图,已知点O是△ABC内一点,且点O到三边的距离相等,∠A=40°,则∠BOC=________.24、观察下面一列数:﹣1,2,﹣3,4,﹣5,6,﹣7,…将这列数排成下列形式:按照上述规律排下去,那么第10行从左边数第9个数是________;数﹣201是第________行从左边数第________个数.25、已知________.三、解答题(共5题,共计25分)26、如图,直线a∥b,△DCB中,AB与DC垂直,点A在线段BC上,直线b经过点C.若∠1=73°﹣∠B,求∠2的度数.27、如图所示,△ABC中∠C=∠ABC=2∠A,BD是边AC上的高,求∠DBC的度数.28、已知:如图,交于G,交于F,平分,交于H,.求:的度数.29、如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠B=60°,求∠A的度数.30、黑板上写有1,2,3,…,2019,2020这2020个自然数,对它们进行操作,每次操作规则如下:擦掉写在黑板上的三个数后,再添写上所擦掉三个数之和的个位数字,例如:擦掉5,13和2010后,添加上8;若再擦掉8,8,38,添上4,等等.如果经过1004次操作后,发现黑板上剩下两个数,一个是29,求另一个数.参考答案一、单选题(共15题,共计45分)1、D2、C3、B4、C5、A6、A7、B9、B10、B11、B12、D13、C14、A15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、28、29、30、。
第七章 平行线的证明数学八年级上册-单元测试卷-北师大版(含答案)

第七章平行线的证明数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题,共计45分)1、如图,已知∠B+∠DAB=180°,AC平分∠DAB,如果∠C=50°,那么∠B等于( )A.50°B.60°C.70°D.80°2、如图,△ABC中,∠A=75°,∠B=50°,将△ABC绕点C按逆时针方向旋转,得到△A’B’ C,点A的对应点A'落在AB边上,则∠BCA'的度数为()A.20°B.25°C.30°D.35°3、如图, AB=AC ,BD=BC,若∠A=50°,则∠ABD=度数是()A.15°B.20°C.25°D.30°4、三角形的一个外角小于与它相邻的内角,这个三角形是()A.直角三角形B.钝角三角形C.锐角三角形D.不确定5、直线a∥b,一块含60°角的直角三角尺(∠A=60°)按如图所示放置.若∠1=45°,则∠2=()A.100°B.105°C.120°D.135°6、如图,AB∥CD,点E在BC上,且CD=CE,∠D=74°,则∠B的度数为()A.68°B.32°C.22°D.16°7、在△ABC中,若∠A:∠B:∠C=1:3:5,则△ABC是()A.锐角三角形B.直角三角形C.钝角三角形D.无法确定8、若,,为的三边长,则下列条件中不能判定是直角三角形的是()A. ,,B.C.D.9、如图,△ABC中,AB=AC,点D在AC上,点E在AB上,且BC=BD,AD=DE=EB,则∠A的度数是()A.30°B.36°C.45°D.54°10、如图,AE‖BD,∠1=120°,∠2=40°,则∠C的度数是()A.10°B.20°C.30°D.40°11、由下列条件不能判定△ABC为直角三角形的是()A. A十B= CB.a=5,b=12,c=13C.D. ,,12、已知等腰三角形的一个内角等于50º,则该三角形的一个底角的余角是()A.25ºB.40º或30ºC.25º或40ºD.50º13、如图所示,AD是△ABC的角平分线,点O在AD上,且OE⊥BC于点E.若∠BAC = 60°,∠C = 80°,则∠EOD的度数为 ( )A.20°B.30°C.10°D.15°14、在一个直角三角形中,有一个锐角等于,则另一个锐角的度数是()A. B. C. D.15、一个三角形的3个内角度数之比为5:3:1,则与之对应的3个外角的度数之比为()A.4:3:2B.2:3:4C.3:2:4D.3:1:5二、填空题(共10题,共计30分)16、如图,在中,AB=AC,,// ,则的度数是________°.17、如图,将三角板的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3=________°.18、以线段AC为对角线的四边形ABCD(它的四个顶点A,B,C,D按顺时针方向排列),已知AB=BC=CD,∠ABC=100°,∠CAD=40°,则∠BCD的度数为________.19、古希腊数学家把数1,3,6,10,15,……做三角形数,其中1是第一个三角形数,3是第2个三角形数,6是第3个三角形数,……依此类推,第20个三角形数是________.20、下列命题中,①对顶角相等;②两条直线被第三条直线所截,同旁内角互补;③在同一平面内,垂直于同一条直线的两条直线互相平行;④经过一点,有且只有一条直线与这条直线平行;⑤若一个角的两边分别与另一个角的两边平行,那么这两个角相等或互补,其中假命题是________.21、已知:,,,,,,试猜想的末位数字是________.22、如图,三角板的直角顶点在直线a上,已知∠1=25°,则∠2的度数为 ________°.23、如图,在中,,平分,交于点、过点作,交于点,那么图中等腰三角形有________个.24、某数学活动小组的20位同学站成一列做报数游戏,规则是:从前面第一位同学开始,每位同学依次报自己顺序数的倒数加1,第1位同学报,第2位同学报,第3位同学报……这样得到的20个数的积为________.25、如图,若l1∥l2,∠1=x°,则∠2=________ .三、解答题(共5题,共计25分)26、请先阅读下列一组内容,然后解答问题:因为:所以:请你计算:①;②27、如图,AD是△ABC的高,BE平分∠ABC交AD于点E,∠C=70º,∠BED=64º,求∠BAC 的度数.28、已知:如图,在△BAC中,AB=AC,D,E分别为AB,AC边上的点,且DE∥BC,求证:△DAE是等腰三角形.29、如图,AD平分∠BAC,AD⊥BD,垂足为点D,DE∥AC.求证:△BDE是等腰三角形.30、如图,点D是△ABC的边AB上一点,点E为AC的中点,过点C作CF∥AB交DE延长线于点F.求证:点E平分DF.参考答案一、单选题(共15题,共计45分)1、D2、B3、A4、B5、B6、B7、C8、D9、C10、B11、D12、C13、A14、A15、B二、填空题(共10题,共计30分)16、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、30、。
第七章 平行线的证明数学八年级上册-单元测试卷-北师大版(含答案)

第七章平行线的证明数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题,共计45分)1、如右图,在△ABC中,线段BC的垂直平分线交线段AB于点D,若AC=CD,∠A=50°,则∠ACB的度数为()A.90°B.95°C.100°D.105°2、如图,四边形的外接圆为⊙O,,,,则的度数为()A. B. C. D.3、在下列条件中,①∠A+∠B=∠C;②∠A:∠B:∠C=1:2:3;③∠A=∠B=∠C;④∠A=∠B=2∠C;⑤∠A=2∠B=3∠C,能确定△ABC为直角三角形的条件有()A.2个B.3个C.4个D.5个4、下列说法中错误的是()A.三角形的中线、角平分线、高线都是线段B.任意三角形的内角和都是180°C.三角形一个外角的大于任何一个内角D.三角形的三条高至少有一条高在三角形的内部5、如图,在△ABD中,AB的垂直平分线DE交BC于点D,∠B=30°,AD=AC,∠BAC 的度数为()A.80°B.85°C.90°D.105°6、如图,△ABC中,∠A=45°,I是内心,则∠BIC=()A.112.5°B.112°C.125°D.55°7、等腰三角形的一个底角是30°,则它的顶角是()A.30°B.40°C.75°D.120°8、如图,在△ABC中,点D、E分别在边AB、AC上,如果∠A=50°,那么∠1+∠2的大小为()A.130°B.180°C.230°D.260°9、如图,∠A=50°,P 是△ABC 内一点,BP 平分,CP 平分∠ACB,则∠BPC 的度数为( )A.100°B.115°C.130°D.140°10、在△ABC中,已知∠ABC=66°,∠ACB=54°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,∠EHF的度数是()A.50°B.40°C.130°D.120°11、在直角△ABC中,∠B是直角,∠C=22°,则∠A等于().A.22°B.68°C.78°D.112°12、等腰三角形的一个外角是80°,则其底角是().A.100°B.100°或40°C.40°D.80°13、一个三角形三个内角的度数之比为2∶3∶7,这个三角形一定是()A.直角三角形B.等腰三角形C.锐角三角形D.钝角三角形14、如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于()A.30°B.40°C.45°D.36°15、已知△ABC内接于⊙O,连接AO并延长交BC于点D,若∠B=62°,∠C=50°,则∠ADB的度数是()A.68°B.72°C.78°D.82°二、填空题(共10题,共计30分)16、在的方格纸上,有7格点已标记,分别为,,,,,,,从中找出4个点,两个点连一条线,另外两点连一条线,使两条连线平行,则所构造的平行连线可记作:________(格式如:,用图中的字母表示)17、命题“如果a>0,那么a2>0”的逆命题为________.18、如图,△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把△ABC 绕着点D逆时针旋转m (0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m 的值为________.19、如图,在△ABC中D、E两点分别在BC、AC边上,若BD=CD,∠B=∠CDE,DE=2,则AB 的长度是________.20、如图,在平面直角坐标系中,点,点,其中,,点是轴负半轴上一点,点是在直线与直线之间的一点,连接、,平分,平分,交于,则与之间可满足的数量关系式为________.21、如图,在△ADC中,B是AC上一点,AD=BD=BC.若∠C=25°,则∠ADB的度数是________°.22、如图,在△ABC中,过点B作EB⊥AB,交AC于点E,BE平分∠CBD,90°+∠C=∠BDC,则∠A的度数为________.23、如图,一把直尺的边缘AB经过一块三角板DCB的直角顶点B,交斜边CD于点A,直尺的边缘EF分别交CD,BD于点E,F,若∠D=60°,∠ABC=20°,则∠1的度数为________.24、1955年,印度数学家卡普耶卡()研究了对四位自然数的一种变换:任给出四位数,用的四个数字由大到小重新排列成一个四位数,再减去它的反序数(即将的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数,然后继续对重复上述变换,得数,…,如此进行下去,卡普耶卡发现,无论是多大的四位数,只要四个数字不全相同,最多进行次上述变换,就会出现变换前后相同的四位数,这个数称为变换的核.则四位数9631的变换的核为________.25、等边三角形的每个内角为________度。
八年级数学上册《第七章平行线的证明》单元测试卷及答案-北师大版

八年级数学上册《第七章平行线的证明》单元测试卷及答案-北师大版一、选择题1.下列说法正确的是( )A .过直线上一点有且只有一条直线与已知直线平行B .不相交的两条直线叫做平行线C .直线外一点到该直线的所有线段中垂线最短D .过直线外一点有且只有一条直线与已知直线平行2.下列语句是命题的是( )A .作直线AB 的垂线 B .在线段AB 上取点C C .垂线段最短吗?D .同旁内角互补3.如图,直线a 、b 被直线c 所截,下列条件不能判定直线a 与b 平行的是( )A .∠1=∠3B .∠2+∠4=180°C .∠1=∠4D .∠1+∠4=180°4.如图a b 和158∠=︒,则2∠的度数为( )A .58°B .112°C .120°D .132°5.在Rt ABC 中90C ∠=︒和25B ∠=︒,则A ∠的度数是( )A .75︒B .65︒C .55︒D .45︒6.下列说法正确的个数有( )①有两组边对应相等,一组角对应相等的两个三角形全等;②垂直于同一条直线的两直线平行;③三角形的中线把三角形的面积平分;④等腰三角形高所在的直线是对称轴. A .1个B .2个C .3个D .4个7.下列命题中是假命题的是( ).A .同旁内角互补,两直线平行B .直线a b ⊥,则a 与b 相交所成的角为直角C .如果两个角互补,那么这两个角是一个锐角,一个钝角D .若a b ,a c ⊥那么b c ⊥8.下列画出的直线a 与b 不一定平行的是( )A .B .C .D .9.如图AOB ADC ≌且90O D ∠∠︒==,记αOAD ∠=,βABO ∠=当BC OA 时,α与β之间的数量关系为( )A .αβ=B .α2β=C .αβ90+︒=D .α2β180+︒=10.如图,∠ABC∠∠DEF ,若∠A=100°,∠F=47°,则∠E 的度数为( )A .100°B .53°C .47°D .33°二、填空题11.在说明命题“若|a|>3,则a >3”是假命题的反例中,a 的值可以是 . 12.如图,AB∠CD ,点P 到AB ,BC ,CD 的距离相等,则∠P =13.如图,已知 AB//CF ,E 为DF 的中点,若AB=13cm ,CF=7cm ,则BD= cm .14.已知等腰三角形的顶角是底角的4倍,则顶角的度数为 .三、解答题15.以下是两位同学在复习不等式过程中的对话:小明说:”不等式a> 2a 永远都不会成立,因为如果在这个不等式两边同时除以a ,就.会出现1>2这样的错误结论!”小丽说:“如果a>b ,c>d ,那么一定会得出a-c>b-d ."你认为小明的说法 (填“正确”或“不正确”);小丽的说法 (填“正确”或“不正确”),并选择其中一个人判断阐述你的理由(若认为正确,则进行证明;若认为不正确,则给出反例).16.如图,C 为∠AOB 平分线上一点,点D 在射线OA 上,且OD =CD.求证:CD∠OB.17.已知,如图AB AE =,AB DE 和ACB D ∠=∠,求证:ABC EAD ≌.18.如图,在ABC 中36A ∠=︒,AB AC =且BM 平分ABC ∠交AC 于点M ,求证:AM BM =四、综合题19.探究问题:已知∠ABC ,画一个角∠DEF ,使DE ∠AB ,EF ∠BC ,且DE 交BC 于点P .∠ABC 与∠DEF 有怎样的数量关系?(1)我们发现∠ABC 与∠DEF 有两种位置关系:如图1与图2所示.①图1中∠ABC 与∠DEF 数量关系为 ;图2中∠ABC 与∠DEF 数量关系为 ; 请选择其中一种情况说明理由. ②由①得出一个真命题(用文字叙述): . (2)应用②中的真命题,解决以下问题:若两个角的两边互相平行,且一个角比另一个角的2倍少30°,请直接写出这两个角的度数.20.如图,AE 平分∠BAC ,∠CAE =∠CEA.(1)AB 与CD 有怎样的位置关系?为什么? (2)若∠C=50°,求∠CEA 的度数.21.如图,在四边形ABCD 中,P 为CD 边上的一点BCAD AP 、BP 分别是BAD ∠、ABC∠的角平分线.(1)若70BAD ∠=︒,则ABP ∠的度数为 ,APB ∠的度数为 ; (2)求证:AB BC AD =+(3)设3BP a =,4AP a =过点P 作一条直线,分别与AD ,BC 所在直线交于点E 、F ,若AB EF = 直接写出AE 的长(用含a 的代数式表示)22.如图,在ABC 中AB AC =,AB 的垂直平分线DE 分别交AC ,AB 于点D ,E.(1)若50A ∠=︒,求C ∠的度数:(2)若7AB =且CBD 周长为12,求BC 的长.23.问题情境在综合与实践课上,同学们以“一个含30︒的直角三角尺和两条平行线”为背景开展数学活动如图1,已知两直线a ,b 且a b 和直角三角形ABC 90BCA ∠=︒ 30BAC ∠=︒ 60ABC ∠=︒(1)在图1中146∠=︒,求2∠的度数;(2)如图2,创新小组的同学把直线a 向上平移,并把2∠的位置改变,发现21∠-∠是一个定值,请写出这个定值,并说明理由;(3)缜密小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,AC 平分BAM ∠ 此时发现1∠与2∠又存在新的数量关系,请直接写出1∠与2∠的数量关系.参考答案与解析1.【答案】D【解析】【解答】解:A、过直线外一点有且只有一条直线与已知直线平行,故该选项错误;B、在同一平面内,不相交的两条直线叫做平行线,故该选项错误;C、直线外一点到该直线的所有线段中垂线段最短,故该选项错误;D、过直线外一点有且只有一条直线与已知直线平行,故该选项正确.故答案为:D.【分析】根据平行线的定义:在同一平面内,不相交的两条直线叫平行线;平行公理:经过直线外一点,有且只有一条直线与这条直线平行;垂线段的性质可得答案.2.【答案】D【解析】【解答】解:A.作直线AB的垂线为描述性语言,它不是命题,所以A选项不符合题意;B.在线段AB上取点C为描述性语言,它不是命题,所以B选项不符合题意;C.垂线段最短吗为疑问句,它不是命题,所以C选项不符合题意;D.同旁内角互补为命题,所以D选项符合题意.故答案为:D.【分析】判断一件事情的语句叫做命题,据此判断即可.3.【答案】D【解析】【解答】解:A.由∠1=∠3,可得直线a与b平行,故A能判定;B. 如下图,由∠2+∠4=180°,∠5+∠4=180°,可得∠2=∠5,故直线a与b平行,故B能判定;C.由∠1=∠4,∠4=∠3,可得∠1=∠3,故直线a与b平行,故C能判定;D.由∠1+∠4=180°,不能判定直线a与b平行故答案为:D.【分析】根据平行线的判定方法逐项判断即可。
第七章 平行线的证明数学八年级上册-单元测试卷-北师大版(含答案)

第七章平行线的证明数学八年级上册-单元测试卷-北师大版(含答案)一、单选题(共15题,共计45分)1、如图,BC为直径,若,,则图中灰色区域的面积为()A. B. C. D.2、满足下列条件的△ABC中,不是直角三角形的是()A.∠B+∠A=∠CB.∠A:∠B:∠C=2:3:5C.∠A=2∠B=3∠C D.一个外角等于和它相邻的一个内角3、如图,AB∥CD,EF⊥AB于E,EF交CD于F,己知∠2=20°,则∠1等于()A.30°B.50°C.70°D.45°4、如图,AB是⊙O的直径,点C、D在⊙O上,∠BOC=110°,AD//OC,则∠ABD等于( )A. B. C. D.5、若等腰三角形的顶角为,则它的底角度数为()A. B. C. D.6、已知等腰三角形的一个内角等于30°则它的顶角等于()A.30°B.60°C.120°D.30°或120°7、如图,直线l1 ∥ l2 , CD⊥AB于点D ,∠1=50°,则∠BCD的度数为()A.40°B.45°C.50°D.30°8、小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于()A.180B.210C.360D.2709、一个三角形的三个内角之比为,则这个三角形是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形10、△ABC中,∠A=∠B,若与△ABC全等的三角形中有一个角为90°,则△ABC中等于90°的角是()A.∠AB.∠BC.∠CD.∠B或∠C11、如图,在平行四边形中,对角线与相交于点,是边的中点,连接.若,,则的度数为()A. B. C. D.12、如下图,在△ABC中,AD平分外角∠CAE,∠B=30°,∠CAD=65°,则∠ACD等于()A.50°B.65°C.80°D.95°13、在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,以下命题是假命题的是()A.若∠B+∠C=∠A,则△ABC是直角三角形B.若a 2=(b+c)(b﹣c),则△ABC是直角三角形C.若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形D.若a=3 2, b=4 2, c=5 2,则△ABC是直角三角形14、△ABC中,AB=AC,BD平分∠ABC交AC边于点D,∠BDC=75°,则∠A的度数为()A.35°B.40°C.70°D.110°15、在中,若,,则的度数为()A.65°B.70°C.75°D.80°二、填空题(共10题,共计30分)16、已知中,,,满足,则该三角形必为________三角形.17、如图,直线,等边的顶点B在直线m上,边与直线m所夹锐角为,则的度数为________.18、如图,已知,点D、C分别是EM、BN上的点,连接BD、CE交于点F,满足,,过点F作交BN于点G,若,则________ .19、如图,a∥b,∠1=70°,∠2=50°,∠3=________20、有一数值转换器,原理如图所示,若开始输入的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2020次输出的结果是________.21、如图,△ABC≌△ADE,∠BAE=110°,∠CAD=10°,∠D=40°.则∠BAC=________度,∠E=________度.22、己知如图,平分,当,且时,的度数为________.23、如图,△OAD≌△OBC,且∠O=72°,∠C=20°,则∠AEB=________度.24、一列数按某规律排列如下:,,,,,,,,,,…,可写为:,(,),(,,),(,,,),…,若第n个数为,则n=________.25、如图,点O是△ABC的两条角平分线的交点,若∠BOC=118°,则∠A的大小是________.三、解答题(共5题,共计25分)26、如图,D是AB上的一点,E是AC上的一点,BE、CD相交于一点F,∠A=63°,∠ACD=34°,∠ABE=20°,求∠BDC和∠BFC的度数.27、如图,已知平分.求的度数.28、如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=50°,∠C=70°,求∠DAC及∠BOA.29、如图,,直线分别交,于E、F两点,且平分,,求的度数.30、填写推理理由,将过程补充完整:如图,,.求证:.证明:∵(已知),∴().∵(已知),∴(如果两条直线都与第三条直线平行,那么这两条直线也互相平行). ∴= ()参考答案一、单选题(共15题,共计45分)1、C2、C3、C4、A6、D7、A8、B9、C10、C11、A12、C13、D14、B15、A二、填空题(共10题,共计30分)16、17、18、19、20、22、23、24、25、三、解答题(共5题,共计25分)26、28、29、30、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行线的证明(A)一、选择题1.下列语句:①钝角大于90°;②两点之间,线段最短;③明天可能下雨;④作AD⊥BC;⑤同旁内角不互补,两直线不平行.其中是命题的是( )A.①②③ B.①②⑤ C.①②④⑤ D.①②④2.如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )A.只有①正确 B.只有②正确 C.①和③正确 D.①②③都正确第2题图第3题图第4题图第5题图3.如图,在△ABC中,∠B=55°,∠C=63°,DE∥AB,则∠DEC等于( ) A.63° B.62° C.55° D.118°4.如图,在锐角△ABC中,CD和BE分别是AB和AC边上的高,且CD和BE交于点P,若∠A=50°则∠BPC的度数是( )A.150° B.130° C.120° D.100°5.如图,AB∥CD,AE交CD于点C,∠A=34°,∠DEC=90°,则∠D的度数为( ) A.17° B.34° C.56° D.124°6.如图,AB∥CD,∠A=45°,∠C=28°,则∠AEC的大小为( )A.17° B.62° C.63° D.73°第6题图第7题图第8题图第9题图7.如图,已知DE∥AB,那么表示∠3的式子是( )A.∠1+∠2-180° B.∠1-∠2C.180°+∠1-∠2 D.180°-2∠1+∠28.如图,在△ABC中,AB=AC,BC=BD,AD=DE=EB,则∠A的度数是( ) A.30° B.36° C.45° D.54°9.如图,把长方形ABCD沿EF对折后,使四边形ABFE与四边形HGFE重合,若∠1=50°,则∠AEF的度数为( )A.110° B.115° C.120° D.130°10.根据下图及已知条件,下列判断错误的是( )A.由∠1=∠2,得AB∥CD B.由∠1+∠3=∠2+∠4,得AE∥CHC.由∠5=∠6,∠3=∠4,得AB∥CD D.由∠SAB=∠SCD,得AB∥CD第10题图第11题图第12题图11.在满足“三线八角”的情况下,同位角、内错角、同旁内角的对数分别为( )A. 4,2,2B. 2,4,2C. 2,2,4D. 都有可能12.如图,在长方形ABCD中AB=3cm,BC=2cm,则AB与CD之间的距离为( )A. 2 cmB. 3 cmC. 5 cmD. 不能确定二、填空题13.如图,已知∠1=∠2=∠3=59°,则∠4=_________.第13题图第14题图第15题图14.如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=110°,则∠EAB=______度.15.如图,直线l1∥l2, ∠1=40°,∠2=75°,则∠3等于_______.16.已知三条不同的直线a,b,c在同一平面内,下列四个命题:①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.其中真命题的是_____________.(填序号)三、解答题17.直线AB,CD与GH交于点E,F,EM平分∠BEF,FN平分∠DFH,∠BEF=∠DFH,求证:EM∥FN.18.已知:△ABC中∠B的平分线与∠ACD的平分线交于点P.求证:2∠P=∠A.19.如图,已知:AB∥DE,∠1+∠3=180°,求证:BC∥EF.20.如图,BE,CD相交于点A,∠DEA、∠BCA的平分线相交于点F.(1)探求∠F与∠B、∠D有何等量关系?(2)当∠B∶∠D∶∠F=2∶4∶x时,x为多少?21.已知:如图,AD⊥BC,EF⊥BC,垂足为D,F,∠4=∠C.求证:∠1=∠2.22.已知,如图,∠XOY=90°,点A,B分别在射线OX,OY上移动,BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠AC B的大小是否发生变化?如果保持不变,请给出证明;如果随点A,B移动发生变化,请求出变化范围.参考答案一、选择题1.下列语句:①钝角大于90°;②两点之间,线段最短;③明天可能下雨;④作AD⊥BC;⑤同旁内角不互补,两直线不平行.其中是命题的是( B )A.①②③ B.①②⑤ C.①②④⑤ D.①②④2.如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( A )A.只有①正确 B.只有②正确 C.①和③正确 D.①②③都正确,第2题图) ,第3题图) ,第4题图) ,第5题图)3.如图,在△ABC中,∠B=55°,∠C=63°,DE∥AB,则∠DEC等于( B ) A.63° B.62° C.55° D.118°4.如图,在锐角△ABC中,CD和BE分别是AB和AC边上的高,且CD和BE交于点P,若∠A=50°则∠BPC的度数是( B )A.150° B.130° C.120° D.100°5.如图,AB∥CD,AE交CD于点C,∠A=34°,∠DEC=90°,则∠D的度数为( C ) A.17° B.34° C.56° D.124°6.如图,AB∥CD,∠A=45°,∠C=28°,则∠AEC的大小为( D )A.17° B.62° C.63° D.73°,第6题图) ,第7题图) ,第8题图) ,第9题图)7.如图,已知DE∥AB,那么表示∠3的式子是( A )A.∠1+∠2-180° B.∠1-∠2C.180°+∠1-∠2 D.180°-2∠1+∠28.如图,在△ABC中,AB=AC,BC=BD,AD=DE=EB,则∠A的度数是( C ) A.30° B.36° C.45° D.54°9.如图,把长方形ABCD沿EF对折后,使四边形ABFE与四边形HGFE重合,若∠1=50°,则∠AEF的度数为( B )A.110° B.115° C.120° D.130°10.根据下图及已知条件,下列判断错误的是( C )A.由∠1=∠2,得AB∥CD B.由∠1+∠3=∠2+∠4,得AE∥CHC.由∠5=∠6,∠3=∠4,得AB∥CD D.由∠SAB=∠SCD,得AB∥CD第10题图第11题图第12题图11.在满足“三线八角”的情况下,同位角、内错角、同旁内角的对数分别为( A )A. 4,2,2B. 2,4,2C. 2,2,4D. 都有可能12.如图,在长方形ABCD中AB=3cm,BC=2cm,则AB与CD之间的距离为( A )A. 2 cmB. 3 cmC. 5 cmD. 不能确定二、填空题13.如图,已知∠1=∠2=∠3=59°,则∠4=__121°__.第13题图)第14题图)第15题图) 14.如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=110°,则∠EAB=__40__度.15.如图,直线l1∥l2, ∠1=40°,∠2=75°,则∠3等于__65°__.16.已知三条不同的直线a,b,c在同一平面内,下列四个命题:①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.其中真命题的是__①②④__.(填序号)三、解答题17.直线AB,CD与GH交于点E,F,EM平分∠BEF,FN平分∠DFH,∠BEF=∠DFH,求证:EM∥FN.证明:∵EM 平分∠BEF,FN 平分∠DFH,∴∠BEF =2∠MEF,∠DFH =2∠NFH,∵∠BEF =∠DFH,∴∠MEF =∠NFH,∴EM ∥FN.18.已知:△ABC 中∠B 的平分线与∠ACD 的平分线交于点P.求证:2∠P=∠A.证明:在△ABC 中,∠A =180°-∠ABC-∠ACB,在△PCB 中∠P=180°-12∠ABC-∠ACB-12(180°-∠ACB)=90°-12(∠ABC+∠ACB)=12∠A ∴2∠P=∠A19.如图,已知:AB∥DE,∠1+∠3=180°,求证:B C∥EF.证明:∵AB ∥DE ,∴∠1=∠2,∵∠1+∠3=180°,∴∠2+∠3=180°,∴BC ∥EF.20.如图,BE ,CD 相交于点A ,∠DEA 、∠BCA 的平分线相交于点F. (1)探求∠F 与∠B、∠D 有何等量关系? (2)当∠B∶∠D∶∠F=2∶4∶x 时,x 为多少?证明:(1)连CE ,记∠AEC=∠1,∠ACE =∠2,∴∠D +∠2+∠1+∠DEA=180°,∠B +∠1+∠2+∠BCA=180°,∠F +∠1+∠2+12∠DEA+12∠BCD=180°,由∠D+∠2+∠1+∠DEA+∠B+∠1+∠2+∠BCA=360°. ∴12(∠D+∠B)+∠1+∠2+12∠BCA+12∠DEA=180°.∴∠1+∠2+12∠BCA+12∠DEA=180°-12(∠D+∠B),即∠F+180°-12(∠D+∠B)=180°,∴∠F =12(∠B+∠D) (2)设∠B=2α,则∠D=4α,∴∠F = 12(∠B+∠D)=3α,又∠B∶∠D∶∠F=2∶4∶x,∴x =3.21.已知:如图,AD ⊥BC ,EF ⊥BC ,垂足为D ,F ,∠4=∠C.求证:∠1=∠2.证明:∵AD⊥BC,EF ⊥BC ,∴∠ADF =∠EFC=90°,∴AD ∥EF ,∴∠2=∠DAC,又∵∠4=∠C,∴DG ∥AC ,∴∠1=∠DAC,∴∠1=∠222.已知,如图,∠XOY =90°,点A ,B 分别在射线OX ,OY 上移动,BE 是∠ABY 的平分线,BE 的反向延长线与∠OAB 的平分线相交于点C ,试问∠ACB 的大小是否发生变化?如果保持不变,请给出证明;如果随点A ,B 移动发生变化,请求出变化范围.解:∠C 的大小保持不变.理由:∵∠ABY =90°+∠OAB ,AC 平分∠OAB,BE 平分∠ABY,∴∠ABE =12∠ABY=12(90°+∠OAB)=45°+12∠OAB,即∠ABE=45°+∠CAB,又∵∠ABE=∠C +∠CAB ,∴∠C =45°,故∠ACB 的大小不发生变化,且始终保持45°.。
