2013年余姚中学自主招生数学模拟卷(一)
【推荐下载】浙江省余姚三中2013届高三月考数学试题

[键入文字]
的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 显示解析 3.在由正数组成的等比数列{an}中,a1+a2=1,a3+a4=4,则 a4+a5=( ) A.6B.8C.10D.12 显示解析 4.已知| a |=2| b |≠0,且关于 x 的方程 x2+| a |x+ a
4
ห้องสมุดไป่ตู้
[键入文字]
=(m,n), b =(p,q),令 a * b =mq-np.给出以下四个命题:(1)若 a 与 b 共线,则 a *
5
[键入文字]
b =0;(2) a * b = b * a ;(3)对任意的λ∈R,有(λ a )*
2
[键入文字]
• b =0 有实根,则 a 与 b 的夹角的取值范围是( ) A.[0,π 6 ]B.[π 3 ,π]C.[π
3
[键入文字]
3 ,2π 3 ]D.[π 6 ,π] 显示解析 5.若将一个真命题中的平面换成直线、直线换成平面后仍是真命题,则该 命题称为可换命题下列四个命题,其中是可换命题的是( ) ①垂直于同一平面的两直线平行; ②垂直于同一平面的两平面平行; ③平行于同一直线的两直线平行; ④平行于同一平面的两直线平行. A.①②B.①④C.①③D.③④ 显示解析 6.定义平面向量之间的一种运算*如下:对任意的 a
12
[键入文字]
11. 一个五面体的三视图如下,正视图与侧视图是等腰直角三角形,俯视图为直角梯 形,部分边长如图所示,则此五面体的体积为 1 显示解析 12.函数 f(x)=ax+loga(x+1)在 [0,1]上的最大值和最小值之和为 a,则 a 的值为 1 2 . 显示解析 13.设 Sn 为等比数列{an} 的前 n 项和,已知 3S3=a4-2,3S2=a3-2,则公 比 q=4. 显示解析 14.满足不等式 x2-(a+1)x+a 小于 0 的所有整数解之和为 27,则实数 a 的取值范围是(7,8]. 显示解析 15.在边长为 1 的正三角形 ABC 中, BD =1 2
2013年全国高校自主招生数学模拟试卷及答案

2013年全国高校自主招生数学模拟试卷一 参考答案一、选择题(本题满分36分,每小题6分)1. 如图,在正四棱锥P −ABCD 中,∠APC =60°,则二面角A −PB −C 的平面角的余弦值为( B ) A.71 B. 71-C.21 D. 21-解:如图,在侧面PAB 内,作AM ⊥PB ,垂足为M 。
连结CM 、AC ,则∠AMC 为二面角A −PB −C 的平面角。
不妨设AB =2,则22==AC PA ,斜高为7,故2272⋅=⨯AM ,由此得27==AM CM 。
在△AMC 中,由余弦定理得712cos 222-=⋅⋅-+=∠CM AM AC CM AM AMC 。
2. 设实数a 使得不等式|2x −a |+|3x −2a |≥a 2对任意实数x 恒成立,则满足条件的a 所组成的集合是( A)A. ]31,31[-B. ]21,21[-C. ]31,41[- D. [−3,3] 解:令a x 32=,则有31||≤a ,排除B 、D 。
由对称性排除C ,从而只有A 正确。
一般地,对k ∈R ,令ka x 21=,则原不等式为2|||34|||23|1|||a k a k a ≥-⋅+-⋅,由此易知原不等式等价于|34|23|1|||-+-≤k k a ,对任意的k ∈R 成立。
由于⎪⎪⎪⎩⎪⎪⎪⎨⎧<-<≤-≥-=-+-125334121134325|34|23|1|k k k k k k k k ,所以31|}34|23|1{|min R =-+-∈k k k ,从而上述不等式等价于31||≤a 。
3. 将号码分别为1、2、…、9的九个小球放入一个袋中,这些小球仅号码不同,其余完全相同。
甲从袋中摸出一个球,其号码为a ,放回后,乙从此袋中再摸出一个球,其号码为b 。
则使不等式a −2b +10>0成立的事件发生的概率等于( D ) A.8152 B.8159 C.8160 D.8161 解:甲、乙二人每人摸出一个小球都有9种不同的结果,故基本事件总数为92=81个。
2013余姚中学自主招生数学试卷

2013余姚中学自主招生数学试卷一、择选题(每小题4分,共32分)1.已知a 是实数,下列选项正确的是( )A.a = B .32a a ≥C.2a = D=时,1a =±2.如图BG ,BF ,CE 切⊙O 于G 、F 、D ,那么,下列结论正确的是( ) ①BG+BF=BC+CE+BE , ②BD ·BH=BF ·BG , ③△BDE ∽△BFHA .3B .2C .1D .03.某班有54名学生,其中会打篮球的有36人,会打排球的有40人,这两种球都不会打的人数比都会打的人数41还少1人,问既会打篮球又会打排球的人数是( )A .26 B.27 C.28 D.294.如图所示,在正三棱柱ABC -111C B A 中,已知AB=BC=CA=2,A 1A =4,一只蚂蚁从A 点出发绕三棱柱侧面两圈到达1A ,则蚂蚁爬行的最短距离为( )A .132B .1022+C .134D .1045.已知,BD 为△ABC 的中线,E 为BD 的中点,连接AE 并延长交BC 于点F ,若BC 长为7,则BF 的长为( )A .37B .47C .57D .676.若c bx ax y ++=2是关于x 的二次函数,其中a 是整数,并有不等式)1(2422+≤++≤x c bx ax x 在实数范围内恒成立,则二次函数的解析式为( )A .122++x xB .222++x x C.2221x x ++ D. 2222x x ++7.函数 y=2()()x a x b --(0a b <<),则函数的图象大致为( )C .8.如图所示,在Rt △ABC 中,∠B=90º,△ABC 的内切圆⊙O 切AC 于D ,过点D 作BC 的垂线交BC 于E ,设AD=a ,CD=b ,则△DEC 的面积为( )A .232()a b a b +B .2()a b a b +C . 22()a b a b +D . 32()a b a b +二、填空题(每小题4分,共32分)9.已知一个一元两次方程为x ²-7x+1=0,设方程的两个根为为1,2x x , 则12x x -= .10.若某抛物线的解析式为c bx ax y ++=2,已a 、b 为正整数,c 为整数,2b a >且当11≤≤-x 时,有24≤≤-y 成立,则抛物线的解析式为 .11.当(x+20≥时,x 的取值范围是 .12.如图所示,两个直角三角形叠放在一起,已知AB=AC=4,AE=3,CD=2,则FD 的长度为 .13.如图所示,在圆形转盘中,∠AOB=∠BOC=90º,拨动指针,指针指向区域a 的概率为1P ;在矩形转盘中,CD=1,BD=2,拨动指针,指针指向a 区域的概率为2P ,则12P P + = .14.某学校组织高二年级全体学生外出旅游,租了若干辆大巴车。
2013年余姚中学自主招生数学模拟卷(一)
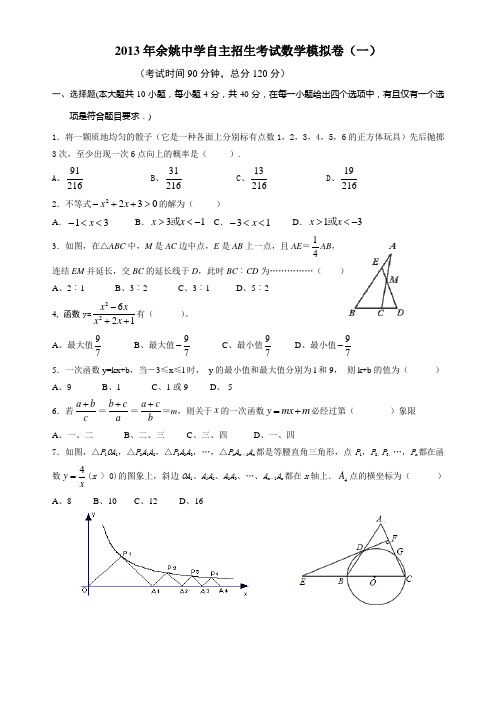
2013年余姚中学自主招生考试数学模拟卷(一)(考试时间90分钟,总分120分)一、选择题(本大题共10小题,每小题4分,共40分,在每一小题给出四个选项中,有且仅有一个选项是符合题目要求.)1.将一颗质地均匀的骰子(它是一种各面上分别标有点数1,2,3,4,5,6的正方体玩具)先后抛掷3次,至少出现一次6点向上的概率是( ).A 、91216B 、31216C 、13216D 、192162.不等式0322>++-x x 的解为( )A .31<<-xB .13-<>x x 或C .13<<-xD .31-<>x x 或3.如图,在△ABC 中,M 是AC 边中点,E 是AB 上一点,且AE =41AB , 连结EM 并延长,交BC 的延长线于D ,此时BC ︰CD 为……………( )A 、2︰1B 、3︰2C 、3︰1D 、5︰24, 函数y=22621x x x x -++有( )。
A 、最大值97 B 、最大值97- C 、最小值97 D 、最小值97- 5.一次函数y=kx+b ,当-3≤x ≤l 时, y 的最小值和最大值分别为l 和9, 则k+b 的值为( )A 、9B 、1C 、1或9D 、-56.若c b a +=a c b +=bc a +=m ,则关于x 的一次函数y mx m =+必经过第( )象限 A 、一、二 B 、二、三 C 、三、四 D 、一、四7.如图,△P 1OA 1,△P 2A 1A 2,△P 3A 2A 3,…,△P n A n -1A n 都是等腰直角三角形,点P 1,P 2,P 3,…,P n 都在函数xy 4=(x > 0)的图象上,斜边OA 1、A 1A 2、A 2A 3、…、A n -1A n 都在x 轴上.4A 点的横坐标为( ) A 、8 B 、10 C 、12 D 、168.如图,等腰三角形ABC 中,AC=BC=10,AB=12.以BC 为直径作⊙O 交AB 于点D ,交AC 于点G ,DF ⊥AC ,垂足为F ,交CB 的延长线于点E .则sin ∠E 的值为( ). A 、725 B 、925 C 、1425D 、2425 9.将一正五边形纸片沿其对称轴对折.旋转放置, 做成科学方舟模型.如图所示,该正五边形的边心距OB 长为10,AC 为科学方舟船头A 到船底的距离,则12AC AB +的值为( ) A 、5 B 、10 C 、25 D 、5010.在直角坐标系中,O 为原点,点A 坐标为(1,2),则直线31y x =+ 沿射线OA 后的解析式为()。
余姚中学2012-2013学年高一下学期期中考试数学试题及答案

浙江省余姚中学2012-2013学年高一下学期期中一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只 有一项是符合题目要求的) 1.在等比数列{}n a 中,已知3231891===q a a n ,,,则n 为 ( ) A .2 B .3C .4D .52.等差数列{}n a 的前n 项和为n S ,且3S =6,1a =4, 则公差d 等于 ( )A .1 B53C .- 2D 33.已知a ,b ,c 为△ABC 的三个内角A ,B ,C 的对边,若B b A a cos cos =,则ABC ∆的形 状为 ( ) A .等腰三角形 B .直角三角形C .等边三角形D .等腰或直角三角形4.已知数列1111{},,1(2)4n n n a a a n a -==-≥,则4a = ( ) A .45B .14C .14-D .155.数列{}n a 的通项公式11++=n n a n ,则该数列的前( )项之和等于9 ( ) A .98 B .99C .96D .976.在∆ABC中,若222()sin a c b B +-=,则角B 的值为 ( )A . 63ππ或 B . 3π C . 6π D. 233ππ或7.已知{}n a 是等差数列,124a a +=,7828a a +=,则该数列前8项和nS 等于 ( )A .72B . 64C .100D .1208.在数列{}n a 中,12a =, 11ln(1)n n a a n+=++,则n a = ( )A .2ln n n +B .2(1)ln n n +-C .2ln n +D . 1ln n n ++9.设y x ,满足约束条件组360200,0x y x y x y --≤⎧⎪-+≥⎨⎪≥≥⎩,若目标函数(0,0)z ax by a b =+>>的最大值为24,则46a b+的最小值为 ( )A .83 B . 276 C . 4 D. 256332220122012201310{},(201220111)1)sin ,1)320111)cos,6((2012(()n n a n S a a a a S ππ--=-=++-.等差数列的前项和则为已知等于A . 2013B . 4026C . 0 D.二.填空题 (本大题共7小题,每小题4分,共28分.请将答案填在相对应空格.) 11.若0x >,则2x x+的最小值为 . 12.已知数列}{n a 的前n 项的和n S 满足n S n =+)1(log 2,则n a = .13.若关于x 的不等式2122x x mx -+>-的解集为 {|02}x x <<,则m = .14.设1010101111112212221A =++++++-,则A 与1的大小关系是_____________.15.数列{a n }的通项公式为a n =2n-49,S n 达到最小时,n 等于_______________.16.把正偶数数列{2}n 的数按上小下大,左小右大的原则排列 成如图“三角形”所示的数表,设ij a *(,)i j ∈N 是位于这个三 角形数表中从上往下数第i 行,从左往右数第j 个数,若mn a =2014,则m n += .17.在锐角三角形ABC ,A 、B 、C 的对边分别为a 、b 、c ,7cos b aC a b+=,则tan C tan C+=tanA tanB______三.解答题(共5题,第18、19 、20小题14分,第21、22小题15分,共72分) 18.等比数列{}n a 中, 252,128a a ==.(1)求数列{}n a 的通项公式;(2)令4log n n b a =,求数列{}n b 的前n 项和。
浙江余姚第五中学13-14学年高一上摸底考试-数学

余姚市第五中学2013-2014学年高一上学期摸底考试数学试题有一个是正确的. 1. 下列各组数可能是一个三角形的边长的是()的对称轴为(直线x= — 1 6.若函数y=]—「.的图象在其所在的每一象限内,函数值y 随自变量x 的增大而增大,则 m的取值范围是() A . m v-2B . m v 0C . m >- 2D . m> 0 7.将一个有45°角的三角板的直角顶点放在一张宽为3cm 的纸带边沿上.另一个顶点在纸.选择题(本题有10个小题,每小题5分,共50分)下面每题给出的四个选项中,只A . 1, 2, 45, 112. 若 a+b=3, a — b=7,则 ab=(A . — 10B . — 40 3. 下面简单几何体的左视图是(B . 4, 5, 9C . 4, 6, 8D . 5,)C . 10D . 40)B. m C4. 为支援雅安灾区,小慧准备通过爱心热线捐款,他只记得号码的前 2这三个数字组成,但具体顺序忘记了.他第一次就拨通电话的概率是5位,后三位由5, 1,A . 1B . 1D . 15.若一次函数 y=ax+b (a 老)的图象与 x 轴的交点坐标为(-22, 0),则抛物线 y=ax +bx直线x=1B .直线x= — 2C .直线x= — 4ZE面带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为(A. 3cmB. 6cmC. :「cmD. I*.:: -cm8如图,OO的半径OD丄弦AB于点C,连结AO并延长交O O于点E,连结EC.若AB=8 ,CD=2,贝U EC的长为()A. 2 —B. 8C. 2 不 D . 2 —9. 如图,正方形 ABCD 的边长为4, P 为正方形边上一动点,沿 A T D ^B ^A 的路径匀速移动,设P 点经过的路径长为 x , △ APD 的面积是y ,则下列图象能大致反映10. 对于点 A (X 1, y i ) , B (X 2, y 2),定义一种运算:A ® B= ( X 1+X 2)+ (y i +y 2).例如, A (- 5, 4), B (2,- 3), A ® B= (- 5+2) + (4 - 3) =- 2•若互不重合的四点 C , D , E , F ,满足 C ® D=D ® E=E ® F=F ® D ,贝U C , D , E , F 四点()A . 在同一条直线上B .在同一条抛物线上C . 在同一反比例函数图象上D .是同一个正方形的四个顶点二、填空题(本大题共 7小题,每小题4分,共28分)11. ------------------------- 二次根式 ___________________ 中,x 的取值范围是 .12. _____________________________ 因式分解:ab 2- a= .13.我国古代数学名著《孙子算经》中有这样一题,今有鸡兔同笼,上有 35头,下有94 足,问鸡兔各几何?此题的答案是:鸡有23只,兔有12只,现在小敏将此题改编为:今有鸡兔同笼,上有33头,下有88足,问鸡兔各几何?则此时的答案是:鸡有 _________________ 只, 兔有 ___________ 只.14•如图,在O O 中,过直径AB 延长线上的点C 作O O 的一条切线,切点为D .若AC=7 ,) 函数关系的是(AB=4,贝U sinC的值为15.如图,在Rt △ ABC 中,/ A=Rt Z, / ABC则厶BDC的面积是的平分线BD交AC于点D, AD=3 , BC=10 ,16•将连续正整数按以下规律排列,则位于第7行第7列的数x是______________ ft-?:第三為乍-丸■七列…・M-H13$.1521 28師二行■591420£1 2 4S1926—7r IS策五行111724 1623篇切17•任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[二]=1 •现对72进行如下操作:72心[.[.,]=8〉.:—[;]=2丸二.’[.]=1,这样对72只需进行3次操作后变为1, 类似的,①对81只需进行______________ 此操作后变为1;②只需进行3次操作后变为1的所有正整数中,最大的是__________ •三、解答题(本题有5小题,第18〜20题每题14分,第21、22题每题15分,共72分)218•当x满足条件G+l<3z- 3 时,求出方程x - 2x - 4=0的根.U(X-4) <4(X-4)L匕J19. 如图,在△ ABC中,AB=AC,/ BAC=54 °以AB为直径的O O分别交AC, BC于点D, E,过点B作O O的切线,交AC的延长线于点F.1求证:BE=CE ;2求/ CBF的度数;(3 )若AB=6,求小的长.920. —个不透明的袋中装有 5个黄球,13个黑球和22个红球,它们除颜色外都相同. (1 )求从袋中摸出一个球是黄球的概率;(2)现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是 黄球的概率不小于 4,问至少取出了多少个黑球?921•为迎接中国森博会,某商家计划从厂家采购 A , B 两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数•下表提供了部分采购数据.(1 )设A 产品的采购数量为 x (件),采购单价为y i (元/件),求y 1与x 的关系式;(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的11,且A产品采购单价不低于1200元.求该商家共有几种进货方案;(3)该商家分别以1760元/件和1700元/件的销售单价售出A, B两种产品,且全部售完.在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.922.抛物线y (x - 3) (x+1 )与x轴交于A, B两点(点A在点B左侧),与y轴交于点C, 点D为顶点.(1)求点B及点D的坐标.(2)连结BD , CD,抛物线的对称轴与x轴交于点E .①若线段BD上一点P,使/ DCP= / BDE,求点P的坐标.②若抛物线上一点M ,作MN丄CD,交直线CD于点N,使/ CMN= / BDE,求点M的坐标.2013年余姚五中高一新生入学测试卷答案一.选择题(本题有10个小题,每小题 5分,共50分)下面每题给出的四个选项中,只 有一个是正确的.123 4 5 6 7S 9 10cABCDA DDBA、填空题 (本大题共7小题,每小题4分,共28分)x>31 区a(d-l)(i+l)13、2211 14. 27—15^1516、851?>3 255、解答题 (本题有 5小题,第18〜20题每题14分,第21、 22题每题15 分・共? /、72分)解方程 x :-2x-4-0 可得 Xi-1-^* x :=l -后*/2<V5<3s /.3<1-75<4,符合题意 /.x=l+V5- .... ..... ..... 4’19、解答:解:(1)连接AE , •/ AB 是O O 直径,•••/ AEB=90 ° 即 AE 丄 BC ,•/ AB=AC ,• BE=CE . .................................... 4'(2)•••/ BAC=54 ° AB=AC ,•/ ABC=63 ° •/ BF 是O O 切线,•/ ABF=90 °•••/ CBF= / ABF -Z ABC=27(3)连接OD , •/ OA=OD , Z BAC=54 ° AOD=72 °18^解答:解*由"1(z - 4)<4 (x- 4)则 2<x<4,•/ AB=6 ,••• 0A=3 ,•••弧AD的长是广厂”--=卜…T - ................... 14'180 r20、解答;(1)T一个不透胡的袋中爰有5个黄13个黒球和22个红琳二摸出一个球摸至債球的概率为.一I—=-, .................. T5+13+22 6(2)设取走x个黒球,则放丸x个黄球,由题意,得-5+^>-,解得’丘旦,5+13+22 9 3答’至少取走了9个黒球. ................... 14-2k解答:⑴ V, ^-20x+1500(0 <jc<20r jc^J整数)(不写取值范II扣1分)(2)根据题意可得'4分x>—(20-x)9-20x4-1500^1200 £15分解得U<x<15X为整数:* x可取的值为>1 tnaii 4,15 二该商家共有弗进货方案(3)解令总利润为.......... ………g 分则W=3D J T-54D X+12000=30(x-9)3 + 9570va = 30 >0二当x>90t,即随舶增大而增大12分14分也弋=10650答:采购A产品15件时总利润最尢最犬利润为10650元.解法二:根据题意可得B产品的采购单价可表示为:讨2 - -10(20 -x) 1300 = 10x 1100则A、B两种产品的每件利润可分别表示为:1760 - y i =20x 260 ..............................1700「y 2= -10x 600则当20x 26^ -10x 600时,A 产品的利润高于B 产品利润,11 _x _15.当x =15时,总利润最高 ....................... 9分此时总利润为(20 X 15+260)X 15+ (-10 X 15+600)X 5=10650 ........................ 10 分 答:略.解法三:列举法(过程2分,5个全算对2分,有部分错误1分,结果给出对应的 x 的值且最大利润正确各1分)x11 12 13 14 15 总利润(元)96909840100501032010650答:略.(其他解法酌情给分)22、解答:(1)v 抛物线y= (x -3) (x+1)与x 轴交于A , B 两点(点A 在点B 左侧), •••当 y=0 时,(x - 3) (x+1 ) =0, 解得x=3或-1,••点 B 的坐标为(3, 0).■/ y= (x - 3) (x+1 ) =x 2 - 2x - 3= (x - 1) 2 - 4,•• •对称轴为直线 x=1, •点E 的坐标为(1, 0).连接BC ,过点C 作CH 丄DE 于H ,贝U H 点坐标为(1,- 3),34即x 34时, 3A 产品越多,总利润越高•顶点D•- C 点坐标为(0,- 3).••• CH=DH=1 , •••/ CDH= / BCO= / BCH=45 °•CD= -, CB=3匚,△ BCD为直角三角形.分别延长PC、DC,与x轴相交于点Q, R.•••/ BDE= / DCP= / QCR ,/ CDB= / CDE+ / BDE=45 ° / DCP ,/ QCO= / RCO+ / QCR=45 ° / DCP,•••/ CDB= / QCO,•••△ BCD QOC ,•—严|i=,OQ CB•OQ=3OC=9,即Q (- 9, 0).•直线CQ的解析式为y= - x - 3,直线BD的解析式为y=2x - 6.由方程组j 1 ,解得f _9 .y=2x - 68'•••点P的坐标为(9,7②(I)当点M在对称轴右侧时.若点N在射线CD上,如备用图1,延长MN交y轴于点F,过点M作MG丄y轴于点G .•••△ MCN s\ DBE ,•••「]=」=,m DE•MN=2CN .设CN=a,贝U MN=2a .•••/ CDE= / DCF=45 °•△ CNF , △ MGF均为等腰直角三角形,•NF=CN=a , CF=匚a,•MF=MN+NF=3a ,•MG=FG= ~a,•CG=FG - FC= ,a,•M(一了—3+ -a).~ ~2代入抛物线y (x- 3) (x+1),解得玄十典,二M(,一2『;备用图2若点N在射线DC上,如备用图2, MN交y轴于点F,过点M作MG丄y轴于点G. •••/ CMN= / BDE,/ CNM= / BED=90 °MCN DBE ,•••':「=,m DE••• MN=2CN .设CN=a,贝V MN=2a .•••/ CDE=45 °•△ CNF , △ MGF均为等腰直角三角形,•NF=CN=a , CF= .:C a,•MF=MN - NF=a,MG=FG= . :■ :■、a,T--CG=FG+FC= >a,•M(-.j :a,- 3+:;..&).55<K C M N d N B D E A 4r:-l\M C N Y 5J刮詳替®w 潼m M ——^K」ssd N K CV门 43J ■.•亦 M m N m -酣H回岂:曲黑礙梦甘广—圄常0一匕-。
数学文卷·2013届浙江省宁波市余姚中学等十校高三3月联考(2013.03)扫描版

2013年宁波市高三“十校”联考数学(文科)参考答案1 2 3 4 5 6 7 8 9 10B A D B BC A C B C二、填空题(11)20 (12)(22,)(13)30 (14)4025(15)1 (16)34(17) ①②③ 三、解答题 18.解:(1)sin 2sin C B =即2c b =, (2分)又ABC ∆中,222cos 2b c a A bc +-=,得2221524b a b-= (5分)解得:ab(7分)(2)115sin sin (0,),(0,)(,)2266B C B πππ=∈∴∈⋃ (9分)23()cos(2)2cos cos221)1326f B B B B B B ππ=++=-+++(12分)所以值域为55(1,)(1)22⋃ (14分)19.解:(1)121112323()5311a a a a d a d +=++=+=,32624a a a =+-,即1112(2)54a d a d a d +=+++-,得2d =,11a =, (5分)1(1)1(1)221n a a n d n n =+-=+-⨯=-.(7分)⑵2111(1)1(1)222n S na n n d n n n n =+-=⨯+-⨯= (9分)2211111111()1(1)12(2)22n n b S n n n n n n n +=====--+-+++,(11分)11111111111(...)2132435112n T n n n n =-+-+-++-+--++111113()212124n n =+--<++ *()n N ∈. (14分)20、(1)解://,AD AEDE BC DE AD DE BD AB ACλ==⇒⇒⊥⊥,ADB ∴∠为二面角A DE B --平面角,2ADB π∠=。
(2分),,AD BCD BE BCD AD BE ∴⊥⊂∴⊥Q 面又面 (4分)又当12λ=时,1,1,,2BD BC BD DE BC BDE DBC DE BD ===∴∆∆:即,EBD DCB BE DC ∴∠=∠∴⊥ (6分),,BE ADC BE ABE ABE ADC∴⊥⊂∴⊥面又面面面(7分)(2)连结BE,过点D作DH BE⊥于H,连结AH过点D作DO AH⊥于O。
2013高中自主招生考试选拔试题(含答案)

(2)根据对对阵形式的分析可以知道:天忌赢得比赛的概率为 (得4分)
解(115、(本小题满分10分)
解:解:(1)集合 不是好的集合, 是好的集合。(每个判断正确得2分)
(2)集合 、 、 、 等都可以举。(每举出一个得3分)
16、(本小题满分10分)
证明: ,且 为 三等分点, 为 中点
我们观察操作,将某次操作前的三个数记为 .因为 对称,不妨设操作 .则操作后的三个数为 , , .不难发现
也就是说,操作前后平方和不改变,所以经过有限此操作后,三个数的平方和为10不为2014.(得4分)
A.20分钟B.22分钟
C.24分钟D.26分钟
5.二次函数 的图象如何移动就得到 的图象( )
A. 向左移动1个单位,向上移动3个单位。
B. 向右移动1个单位,向上移动3个单位。
C. 向左移动1个单位,向下移动3个单位。
D. 向右移动1个单位,向下移动3个单位。
6.下列名人中:①比尔 盖茨②高斯③刘翔④诺贝尔⑤陈景润⑥陈省身⑦高尔基⑧爱因斯坦,其中是数学家的是()
13.如果有2007名学生排成一列,按1、2、3、4、5、4、3、2、1、2、3、4、5、4、3、2、1……的规律报数,那么第2007名学生所报的数是.
三、解答题:(本题有4个小题,共38分)解答应写出文字说明,证明过程或推演步骤。
14.(本小题满分8分)【田忌赛马】
齐王和他的大臣田忌均有上、中、下马各一匹,每场比赛三匹马各出场一次,共赛三次,以胜的次数多者为赢.已知田忌的马较齐王的马略有逊色,即:田忌的上马不敌齐王的上马,但胜过齐王的中马;田忌的中马不敌齐王的中马,但胜过齐王的下马; 田忌的下马不敌齐王的下马. 田忌在按图1的方法屡赛屡败后,接受了孙膑的建议,用图2的方法,结果田忌两胜一负,赢了比赛.假如在不知道齐王出马顺序的情况下:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年余姚中学自主招生考试数学模拟卷(一)姓名_________(考试时间90分钟,总分120分)一、选择题(本大题共12小题,每小题5分,共60分,在每一小题给出四个选项中,有且仅有一个选项是符合题目要求.)1.将一颗质地均匀的骰子(它是一种各面上分别标有点数1,2,3,4,5,6的正方体玩具)先后抛掷3次,至少出现一次6点向上的概率是( ). A 、91216 B 、31216 C 、13216 D 、192162.不等式0322>++-x x 的解为( ) A .31<<-xB .13-<>x x 或C .13<<-xD .31-<>x x 或3.如图,在△ABC 中,M 是AC 边中点,E 是AB 上一点,且AE =41AB , 连结EM 并延长,交BC 的延长线于D ,此时BC ︰CD 为……………( ) A 、2︰1 B 、3︰2 C 、3︰1 D 、5︰24, 函数22621x xy x x -=++有( )。
A 、最大值97 B 、最大值97- C 、最小值97 D 、最小值97- 5.一次函数y=kx+b ,当-3≤x ≤l 时, y 的最小值和最大值分别为l 和9, 则k +b 的值为( ) A 、9 B 、1 C 、1或9 D 、-5 6.若c b a +=a c b +=bc a +=m ,则关于x 的一次函数y mx m =+必经过第( )象限 A 、一、二 B 、二、三 C 、三、四 D 、一、四7.如图,△P 1OA 1,△P 2A 1A 2,△P 3A 2A 3,…,△P n A n -1A n 都是等腰直角三角形,点P 1,P 2,P 3,…,P n 都在函数)0x (x4y >=的图象上,斜边OA 1、A 1A 2、A 2A 3、…、A n -1A n 都在x 轴上.4A 点的横坐标为( ) A 、8 B 、10 C 、12 D 、168.如图,等腰三角形ABC 中,AC=BC=10,AB=12.以BC 为直径作⊙O 交AB 于点D ,交AC 于点G ,DF ⊥AC ,垂足为F ,交CB 的延长线于点E .则sin ∠E 的值为( ).A 、725 B 、925 C 、1425D 、24259.将一正五边形纸片沿其对称轴对折.旋转放置,做成科学方舟模型.如图所示,该正五边形的边心距OB 长为10,AC 为科学方舟船头A 到船底的距离, 则12AC AB +的值为( ) A 、5 B 、10 C 、25 D 、5010.在直角坐标系中,O 为原点,点A 坐标为(1,2),则直线31y x =+ 沿射线OA 后的解析式为()。
A 、3y x =B 、3y x =C 、31yx =- D 、3y x =11、在△ABC 中,∠A =0120,BC =6,若△ABC 的内切圆半径为r ,则r 的最大值为( ) A 、43- B 、23C 、324-D 、336- 12、已知函数)0x (2x )x (f 2>+=,则)2005(f )1003(f )1002(f N +++= 的整数部分为( ) A 、1506500 B 、1509514 C 、4010 D 、3013 二、填空题(本大题共6小题,每小题5分,共30分)13、抛物线221y x x =--关于点(2,3)对称的解析式为 。
14、如图,.在Rt △ABC 中,∠C=90°,BC=3,AC=4,M 为斜边AB 上一动点,过M 作MD ⊥AC,过M 作ME ⊥CB 于点E ,则线段DE 的最小值为______.15、如图,AB 为⊙O 的直径,AB =2BC =2,DE =DB,则DB = .16、抛物线2(21)1y x a x a =-++-与x 轴的两个交点分别位于点(1,0)的两旁,则a 的取值范围为______。
17、如图,水平地面有一个面积为120πcm 2的灰色扇形OAB ,其中OA 的长度为12cm ,且OA 与地面垂直。
若在没有滑动的情况下,将图最左边的扇形向右滚动至点A再一次接触地面时,2则O 点移动的路径长为_____。
18、若A ,B 两点是抛物线10x 3x y 2--=与X 轴交点(A 左B 右),抛物线上一点P 的横坐标为4,在抛物线AP 段(不包括A ,P 点)上存在一点M ,使得△MAP 的面积最大,点M 的坐标为 。
三、解答题(本大题共5小题,共60分)19、(本题10分)已知二次函数c bx ax y 2++=的图像经过点(-1,2),开口向下,与x 轴交点的横坐标分别为21x ,x ,如果1x 0,1x 221<<-<<-,请问下列结论中,哪些是正确的?(1)0abc >;(2)0c b 2a 4<+-;(3)0b 2a <-;(4)ac 4a 8b 2>+。
20、(本题10分) 有一列数123,,,,n a a a a ,满足下列条件:10a =,211a a =+,3211,,1n n a a a a -=+=+.求证:123,,,,n a a a a 这n 个数的算术平均数不小于12-.21、(本题12分)已知点P 是抛物线2y x =上一点,过点M (0,2M ,(1)过点P 作⊙M 的两条切线1l 、2l ,若1l ⊥2l ,求点P 的坐标;(2)若过点Q(2,4)的直线l 与抛物线2y x =只有一个公共点时,求出点M 与直线的距离.22、(本题14分)如图,O 是△ABC 的外心,D 、E 、F 分别在线段BC 、CA 、AB 上,使得DE ⊥CO ,DF ⊥BO ,设K 是△AFE 的外心。
证明:DK ⊥BC 。
23、(本题12分)求所有使z1y 1x 1,xyz ,z y x ++++均为整数的正有理数组)z y x )(z ,y ,x (≤≤。
2013年余姚中学自主招生考试数学模拟卷(一)参考答案一、选择题:作A M ⊥BC 于点M ,连结ID 、IE 、IF ,IA 。
易得AE =r 33,AI =r 332, AM 3r )CA BC AB (21S ABC =++=Δ, 故336r r r 332ID AI r )r 932(AM -≤⇒+=+≤+=,故选C 。
12、解:注意到:0x 2x x )x (f 2>-+=-, ∴x1x x 2x2x 2x 2x x )x (f 22=+<++=-+=-,于是x 1x 2x 02<-+<,由上知200510031002N +++> ,且+-++-+=+++-)100321003()100221002()200510031002(N 22)200522005(2-++1100241002998200511003110021=+<+++<, 因此,N 的整数部分为1509514200510031002=+++ ,故选B 。
二、填空题:13、261y x x =-+- 14、512 15、2216、1a -> 17、π22 18、)12,1(- 三、解答题(本大题共5小题,共52分)19、解: a-b+c=2 ,f(-2)=4a-2b+c<0,4a-2(a+c-2)+c<0,2a-c+4<02a<c-4<-2,a<-1,b=a+c-2 ,b2+8a-4ac. =(a+c-2)^-4a(c-2) =a^+2a(c-2)+(c-2)^)-4a(c-2) =a^-2a(c-2)+(c-2)^ =(a-c+2)^2 -2〈x1<-1,0<x2<1. 抛物线的对称轴-1<-b/2a<0抛物线的开口向下:a<0 ,0>b>2a ,a+c-2>2aa-c+2<0 ,所以(a-c+2)^2>0 ,即:b ^2+8a-4ac >0 ,b ^2+8a >4ac a-b+c=2;(1);4a-2b+c <0;(2);a+b+c <0。
(3)(1)与(2)得2a-c <-4;(4);(1)与(3)得a+c<1.(5) (4)与(5)得a <-119. 提示:已知式两边平方分别相加解:a1=0,a2=-|a1+1|=-|0+1|=-1,a3=-|a2+2|=-|-1+2|=-1,a4=-|a3+3|=-|-1+3|=-2, a5=-|a4+4|=-|-2+4|=-2,…,所以,n 是奇数时,an=-(n-1)/ 2 ,n 是偶数时,an=-n/ 2 , a2012=-2012 /2 =-1006. 故选B .20、解:考虑以z ,y ,x 为根的多项式)z t )(y t )(x t ()t (f ---=xyz t )zx yz xy (t )z y x (t 23++++++-=。
注意到zx yz xy )z1y 1x 1(xyz ++=++为整数,所以)t (f 是首一的整系数多项式,又其根均为有理数,其根的分母为首项系数的约数,故其根为整数,即z ,y ,x 均为整数。
设k z1y 1x 1=++,因为z y x ≤≤,所以3x 1k z 1y 1x 1x 3≤⇒≥=++≥。
(1)当1x =时,z1y 1+为整数,若1y =,则只能是1z =,得)1,1,1()z ,y ,x (=; 若2y =,由z 3z y x +=++为整数,知z 为整数,故2z =, 所以)2,2,1()z ,y ,x (=;若3y ≥,则3131z 1y 1+≤+,矛盾。
(2)当2x =时,2121121k z 1y 1y 2=-≥-=+≥4y ≤⇒。
若2y =,只能是1z =与2y z =≥矛盾; 若3y =,则6z =,所以)6,3,2()z ,y ,x (=; 若4y =,则4z =,所以)4,4,2()z ,y ,x (=。
(3)当3x =时,3y 3231131k z 1y 1y 2≤⇒=-≥-=+≥,又3x y =≥,则3z ,3y ==,故)3,3,3()z ,y ,x (=。
综上,)3,3,3(),4,4,2(),6,3,2(),2,2,1(),1,1,1()z ,y ,x (=。
(本题10.20.21、证明:过点C 作△ABC 的外接圆⊙O 的切线CH 。
则CH ⊥CO ,∴D E ∥CH 。
从而,∠CDE =∠BCG =∠BAC , 所以,A 、B 、D 、E 四点共圆, 同理,C 、D 、F 、A 四点共圆, 故∠CDE =∠BCG =∠FDB ,又K 是△AFE 的外心,∴∠EDF =0180-2∠FAE =0180-∠FKE , 即∠ED F +∠FKE =0180,从而,E 、D 、F 、K 四点共圆, 故∠EDK =∠EFK =∠KEF =∠KDF ,又由∠CDE =∠FDB ,从而,DK ⊥BC 。
