数值计算方法-第7章-数值微分与数值积分-part-2

合集下载

数值计算_第7章数值微分和数值积分

数值计算_第7章数值微分和数值积分数值微分和数值积分是数值计算中的两个重要内容，它们在科学、工程和经济等领域有着广泛的应用。

本文将详细介绍数值微分和数值积分的概念、方法和应用，并分析其优缺点。

数值微分是通过数值方法来近似计算函数的导数。

在实际问题中，往往很难直接计算函数的导数，因此需要使用数值方法来进行近似计算。

常用的数值微分方法有中心差分法、向前差分法和向后差分法。

中心差分法是一种通过利用函数在特定点两侧的数据点来计算函数的导数的方法。

具体方法是用函数在该点两侧的差值来估计导数。

中心差分法具有较高的精度和稳定性，适用于函数光滑的情况。

向前差分法和向后差分法是一种通过利用函数在该点的数据点来计算函数的导数的方法。

向前差分法用函数在该点的后一点数据来估计导数，向后差分法用函数在该点的前一点数据来估计导数。

这两种方法的精度相对较低，但计算简单，适用于函数不太光滑的情况。

数值微分方法的优点是计算简单、直观易懂、易于实现。

缺点是对函数的平滑性和间隔大小要求较高，误差较大。

数值积分是通过数值方法来近似计算函数的积分。

在实际问题中，往往很难直接计算函数的积分，因此需要使用数值方法来进行近似计算。

常用的数值积分方法有梯形法则、辛普森法则和数值积分公式。

梯形法则是一种通过将区间划分为多个小区间，在每个小区间上用梯形面积来近似计算积分的方法。

辛普森法则是一种通过将区间划分为多个小区间，在每个小区间上用抛物线面积来近似计算积分的方法。

这两种方法的精度较高，适用于函数较光滑的情况。

数值积分公式是通过选取节点和权重，将积分转化为对节点函数值的加权求和。

常用的数值积分公式有高斯求积公式和牛顿-寇茨公式。

这些公式具有较高的精度和稳定性，适用于计算复杂函数的积分。

数值积分方法的优点是适用范围广、精度较高、计算稳定。

缺点是计算量较大、计算复杂、需要选取合适的节点和权重。

数值微分和数值积分在科学、工程和经济等领域有着广泛的应用。

数值积分与数值微分

Remark：定出 Ak (k 0,1, , n) ，则求积公式至少具有n 次代数精度，但并不一定它具有n次代数精度,要将 xn1代入求积公式，如果等式不准确成立，即求积公式具有n次代数精度，否则代数精度将大于n。
2019/6/1
8
求积公式的代数精确度（续）
Remark1：代数精度越高，求积公式的适应性越强。
一个求积公式首先应该是收敛的，其次应该是稳定的。
2019/6/1
13
收敛性与稳定性（续）
设计算 f (xk ) 时有绝对误差 k ，即 f * (xk ) f (xk ) k .
n
n
则 e(In ) Ak f *(xk ) Ak f (xk )
k 0
k 0
n
n
Akk Ak k
Ak f (xk ) R[ f ] In R[ f ]
k 0
其中R[f]称为求积公式的余项，xk (k 0,1,2,n)
称为求积节点，Ak (k 0,1,2,n) 称为求积系数。
Ak 仅与求积节点 xk 的选取有关，而不依赖与被积
函数f(x)的具体形式。
2019/6/1
3
二.求积公式的代数精确度
衡量一个求积公式好坏的标准。
定义：如果求积公式
b
n
f (x)dx
a
Ak f (xk )
k 0
对于一切不高于m次的代数多项式准确成立，
而对于某个m+1次多项式并不准确成立，
则称上述求积公式具有m次代数精确度，或称为具有m次代数精度。
2019/6/1
4
求积公式的代数精确度（续）
如果要构造具有m次代数精度的求积公式，

数值计算方法-第7章+数值微分与数值积分-part-1

积分误差:
已知在[a,b]中连续,
由积分第一中值定理:
其中,
在[a,b]中不变号,
共四十页
证毕 #
➢ 定理(dìnglǐ)7.3
若
第7章数值(shùzí)微分与数值
(shùzí)积分
, 则Simpson公式的误差为:
其中,
【证明】Simpson公式是2阶N-C公式, 由定理7.1, 它具有2n+1 (这里n=1) 阶
1.151 3.1613527
1.1499 3.1578771
0.0001 1.1500 3.1581929
3.158
3.158 1.9290E-04 1.9290E-04
1.1501 3.1585087
1.149999 3.1581897
1.00E-06 1.150000 3.1581929
3.2
1.14 3.1267684
0.01
1.15 3.1581929 3.17404 3.158245 1.5847E-02 5.2100E-05
1.16 3.1899333
1.149 3.1550363
0.001 1.150 3.1581929
3.1598
3.1582 1.6071E-03 7.1000E-06
代数精度. 即对任意3次多项式, Simpson公式精确成立. 构造f(x)的三次(sān cì)插值多项式 H3(x), 满足:
由第五章中Hermite 插值的余项 (对应n=2, m=0):
共四十页
➢ 定理(dìnglǐ)7.3 证明 (续) 对上式积分(jīfēn),
Simpson积分误差: 在[a,b]上连续作变量代换, 由积分第一中值定理:

第七章数值积分与数值微分 PPT

a
2
b
梯形公式
b
a
f
( x)dx
1 2
(b
a)
f
(a)
f
(b)
3
一般形式
数值积分公式得一般形式
一般地,用 f(x) 在 [a, b] 上得一些离散点
a x0 < x1 < ···< xn b
上得函数值得加权平均作为 f () 得近似值,可得
b
n
f ( x)dx
a
Ai f ( xi )
29
复合梯形公式
将 [a, b] 分成 n 等分 [xi , xi+1] ,其中
xi a i h,
h
b
a n
(i = 0, 1, …, n)
复合梯形公式
b
n1
f ( x) dx
a i0
xi 1 xi
f (x)
dx
n1 i0
h[ 2
f
(
xi
)
f ( xi1)]
余项
h 2
f (a)
n
Ai =A0 A1 An b a
i0
9
大家学习辛苦了，还是要坚持
继续保持安静
插值型求积公式
设求积节点为:a x0 < x1 < ···< xn b
n
若 f (xi) 已知,则可做 n 次多项式插值: Ln( x) li ( x) f ( xi )
i0
b
b
n
b
n
a f ( x)dx a Ln( x) dx f ( xi ) a li ( x) dx Ai f ( xi )
代数精度的验证方法

数值计算第7章数值微分和数值积分

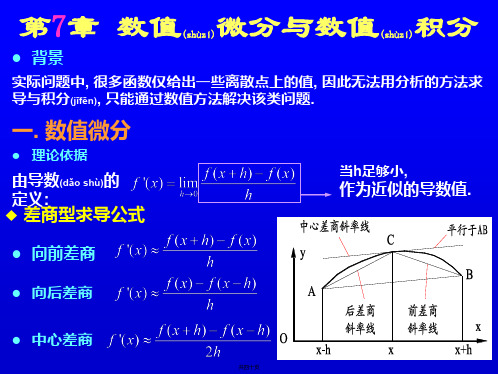
第7章数值微分和数值积分7.1 数值微分差商与数值微分当函数是以离散点列给出时，当函数的表达式过于复杂时，常用数值微分近似计算的导数。

在微积分中，导数表示函数在某点上的瞬时变化率，它是平均变化率的极限；在几何上可解释为曲线的斜率；在物理上可解释为物体变化的速率。

以下是导数的三种定义形式：（7.1）在微积分中，用差商的极限定义导数；在数值计算中返璞归真，导数取用差商（平均变化率）作为其近似值。

最简单的计算数值微分的方法是用函数的差商近似函数的导数，即取极限的近似值。

下面是与式（7.1）相应的三种差商形式的数值微分公式以及相应的截断误差。

向前差商用向前差商（平均变化率）近似导数有：（7.2）其中的位置在的前面，因此称为向前差商。

同理可得向后差商、中心差商的定义。

由泰勒展开得向前差商的截断误差：向后差商用向后差商近似导数有：（7.3）与计算向前差商的方法类似，由泰勒展开得向后差商的截断误差：中心差商用中心差商（平均变化率）近似导数有：（7.4）由泰勒展开得中心差商的截断误差：差商的几何意义微积分中的极限定义，表示在的斜率；差商表示过和两点直线的斜率，是一条过的割线。

可见数值微分是用近似值内接弦的斜率代替准确值切线的斜率。

图7.1 微商与差商示意图给出下列数据，计算，解：（(0.10) －设定最佳步长在计算数值导数时，它的误差由截断误差和舍入差两部分组成。

用差商或插值公式近似导数产生截断误差，由原始值的数值近似产生舍入误差。

在差商计算中，从截断误差的逼近值的角度看，越小，则误差也越小；但是太小的会带来较大的舍入误差。

怎样选择最佳步长，使截断误差与舍入误差之和最小呢？一般对计算导数的近似公式进行分析可得到误差的表示式，以中心差商为例，截断误差不超过而舍入误差可用量估计（证明略），其中是函数的原始值的绝对误差限，总误差为当时，总误差达到最小值，即（*）可以看到用误差的表达式确定步长，难度较大，难以实际操作。

数值方法中的数值微分和数值积分

泰勒展开法：将函数在某点处展开成泰勒级数，然后利用级数的各项系数计算数值微分
牛顿插值法：利用牛顿插值多项式计算数值微分，其思想是通过构造插值多项式ห้องสมุดไป่ตู้ 逼近导数函数
数值微分的误差分析
数值微分的基本概念
数值微分误差的来源
数值微分误差的估计
减小误差的方法
数值微分的应用
计算物理量的变化率
应用领域的比较
数值微分的应用领域：主要应用于求解微分方程的近似解，例如在物理学、工程学和经济学等领域。
数值积分的应用领域：主要应用于求解定积分、不定积分等积分问题，例如在计算面积、体积、物理实验数据处理等领域。
比较：数值微分和数值积分在应用领域上存在差异，但两者都是数值计算中的重要工具，可以相互补充。
矩形法：将积分区间划分为若干个小的矩形，用矩形面积的和近似积分
梯形法：将积分区间划分为若干个小的梯形，用梯形面积的和近似积分
辛普森法：将积分区间划分为若干个等分的子区间，用抛物线面积的和近似积分
牛顿-莱布尼茨法：利用定积分的定义和牛顿-莱布尼茨公式，通过求和的方式计算定积分
预测函数的变化趋势
优化问题中的梯度计算
机器学习中的梯度下降算法
Part Three
数值积分
数值积分的概念
数值积分定义：用数值方法近似计算定积分的值常用方法：矩形法、梯形法、辛普森法等近似误差：与使用的数值方法有关，通常误差随迭代次数增加而减小应用领域：科学计算、工程、数学建模等
数值积分的计算方法
数值积分的误差分析
算法稳定性：数值积分方法的稳定性和误差控制步长选择：步长对误差的影响和最佳步长选择收敛性：数值积分方法的收敛速度和误差收敛性误差来源：数值积分中误差的来源和减小误差的方法

数值计算方法第07章数值微分与数值积分方案

(n 1)!

(
xi
)
10
下面仅仅考察节点处的导数值。为简化讨论，假定所给
的节点是等距的，设步长为 h 。
(1)两点公式：两节点 x0 , x1 x0 h 的函数值 f ( x0 ), f ( x1) 。则线性插值函数
L1( x)
x x1 x0 x1
f
( x0 )
x x0 x1 x0
n
次插值多项式 Ln( x) f ( xk )lk ( x), 即得到
k0
b
n
b
f ( x)dx
a
f ( xk ) a lk ( x)dx
Ak
k0
插值型求积公式
Ak
b n ( x x j ) dx a j0, jk ( xk x j )
由节点决定, 与 f (x) 无关.
f ( x1 )
x x1 h
f ( x0 )
x x0 h
f ( x1 )
则
L1( x)

1 [ h
f
( x0 )
f
( x1 )]
(7.1)
L1( x0 )

1 [ h
f
( x0 )
f
( x1 )],
L1( x1 )

1 [ h
f
( x0 )
f
( x1)]
11
(2) 三点公式 : 已知 x0 , x1 x0 h,, x2 x0 2h 的函数值 f (x0 ), f (x1), f (x2 ) ,
本章主要介绍数据微积分的基本思想方法及常用的数值微分与数值积分公式。

数值微分与数值积分

数值微分与数值积分数值微分和数值积分是数值分析中两个重要的概念和技术。

它们在数学与工程领域中都有着广泛的应用。

本文将介绍数值微分和数值积分的概念、原理和应用。

1. 数值微分数值微分是指通过数值计算方法来逼近函数的导数。

在实际计算中，我们常常需要求解某一函数在特定点的导数值，这时数值微分就能派上用场了。

一种常用的数值微分方法是有限差分法。

它基于函数在离给定点很近的两个点上的函数值来逼近导数。

我们可以通过选取合适的差分间距h来求得函数在该点的导数值。

有限差分法的一般形式可以表示为：f'(x) ≈ (f(x+h) - f(x))/h其中，f'(x)是函数f(x)在点x处的导数值，h是差分间距。

数值微分方法有很多种，比如前向差分、后向差分和中心差分等。

根据实际需求和计算精度的要求，我们可以选择合适的数值微分方法来进行计算。

2. 数值积分数值积分是指通过数值计算方法来近似计算函数的定积分。

在实际问题中，我们经常需要求解函数在某一区间上的积分值，而数值积分可以提供一个快速而准确的近似。

一种常见的数值积分方法是复合梯形法。

它将积分区间分割成若干个小区间，然后在每个小区间上应用梯形面积的计算公式。

最后将所有小区间上的梯形面积相加，即可得到整个积分区间上的积分值。

复合梯形法的一般形式可以表示为：∫[a, b] f(x)dx ≈ h/2 * [f(a) + 2∑(i=1 to n-1)f(x_i) + f(b)]其中，[a, b]是积分区间，h是分割的小区间宽度，n是划分的小区间个数，x_i表示第i个小区间的起始点。

除了复合梯形法，还有其他常用的数值积分方法，比如复合辛普森法、龙贝格积分法等。

根据被积函数的性质和计算精度要求，我们可以选择合适的数值积分方法来进行计算。

3. 数值微分和数值积分的应用数值微分和数值积分在科学研究和工程实践中具有广泛的应用。

以下是一些常见的应用领域：3.1 物理学在物理学中，我们经常需要对物体的位置、速度和加速度进行计算。

数值微分与积分算法

数值微分与积分算法数值微分和积分算法是计算数学中常用的数值计算方法，它们通过离散化数学函数来估计导数和定积分的值。

本文将介绍数值微分和积分的基本概念，并介绍几种常用的数值方法。

1. 数值微分数值微分是计算函数导数的数值方法。

导数表示了函数在某一点的斜率或变化率。

常见的数值微分方法有：向前差分、向后差分和中心差分。

1.1 向前差分向前差分计算导数的方法是通过近似函数在某一点的切线斜率。

假设有函数f(x)，可选取小的增量h，并使用如下公式计算导数：f'(x) ≈ (f(x+h) - f(x)) / h1.2 向后差分向后差分与向前差分类似，也是通过近似函数在某一点的切线斜率。

使用如下公式计算导数：f'(x) ≈ (f(x) - f(x-h)) / h1.3 中心差分中心差分是向前差分和向后差分的结合，计算导数时使用函数在点前后进行采样。

使用如下公式计算导数：f'(x) ≈ (f(x+h) - f(x-h)) / (2h)2. 数值积分数值积分是计算函数定积分的数值方法。

定积分表示函数在某一区间上的面积。

常见的数值积分方法有：矩形法、梯形法和辛普森法则。

2.1 矩形法矩形法是通过将函数曲线分割成若干个矩形，然后计算每个矩形的面积之和来近似定积分。

常见的矩形法有：左矩形法、右矩形法和中矩形法。

2.2 梯形法梯形法是通过将函数曲线分割成若干个梯形，然后计算每个梯形的面积之和来近似定积分。

使用如下公式计算：∫[a,b] f(x)dx ≈ (h/2) * [f(x0) + 2f(x1) + 2f(x2) + ... + 2f(x(n-1)) + f(xn)]2.3 辛普森法则辛普森法则是通过将函数曲线分割成若干个抛物线来近似定积分。

使用如下公式计算：∫[a,b] f(x)dx ≈ (h/3) * [f(x0) + 4f(x1) + 2f(x2) + 4f(x3) + ... + 4f(x(n-1))+ f(xn)]3. 总结数值微分和积分是实际计算中常用的数值方法，它们通过将连续的数学问题离散化来进行数值计算。

数值微分与数值积分的计算方法

数值微分与数值积分的计算方法数值微分和数值积分是数学中一种非常重要的方法。

在实际生活和科学研究中，很多情况下，需要对函数进行微分或积分的计算。

然而，由于很多函数的解析式很难或者根本不能求出，因此需要采用一些数值方法来近似计算。

本文将讨论数值微分和数值积分的计算方法。

一、数值微分在数值计算中，常常会遇到需要求函数在某个点处的导数的问题。

这时候，我们就需要用到数值微分。

数值微分主要有三种方法：前向差分、后向差分和中心差分。

（一）前向差分前向差分是一种用来计算函数在某个点处导数的方法。

其基本思想是求函数在当前点和向前一点的斜率，即：$$f'(x_i)=\frac{f(x_{i+1})-f(x_i)}{h}$$其中，$h$表示步长。

（二）后向差分后向差分是一种用来计算函数在某个点处导数的方法。

其基本思想是求函数在当前点和向后一点的斜率，即：$$f'(x_i)=\frac{f(x_i)-f(x_{i-1})}{h}$$（三）中心差分中心差分是一种用来计算函数在某个点处导数的方法。

其基本思想是求函数在当前点左右两个点的平均斜率，即：$$f'(x_i)=\frac{f(x_{i+1})-f(x_{i-1})}{2h}$$对于三种方法，其截断误差的阶分别为 $\mathcal{O}(h)$、$\mathcal{O}(h)$ 和 $\mathcal{O}(h^2)$。

二、数值积分数值积分是指用数值方法对某个函数在某一区间上的定积分进行近似计算的过程。

常见的数值积分方法有梯形法、辛普森法和龙贝格法。

下面将分别介绍这三种方法。

（一）梯形法梯形法是一种比较简单的数值积分方法。

其基本思想是将积分区间分成若干个小梯形，然后求出这些小梯形面积的和。

具体地，假设我们要对函数 $f(x)$ 在区间 $[a,b]$ 上进行积分，将该区间分成 $n$ 个小区间，步长为 $h=(b-a)/n$，则梯形法的计算公式为：$$\int_{a}^{b}f(x)dx\approx\frac{h}{2}\left[f(a)+2\sum_{i=1}^{n-1}f(a+ih)+f(b)\right]$$梯形法的截断误差的阶为 $\mathcal{O}(h^2)$。

第7章数值积分与数值微分

当步长h充分小时，有
f ( x) f ( x) h f ( x ) f ( x) h f ( x) f ( x) h
分别称为函数在x点处以h(h>0)为步长的向前差商、向后差商和中心差商。当步长h(h>0)充分小时，函数f 在点x的微分接近于函数在该点的任意一种差分，而f 在点x的导数接近于函数在该点的任意一种差商。
7.2.2 数值微分的实现
计算任意函数f(x)在给定点x处数值导数的方式有两种，一种是用多项式或样条函数g(x)对f(x)进行逼近（插值或拟合），然后用逼近函数g(x)在点 x处的导数作为f(x)在点x处的导数；另一种是用f(x)在点x处的某种差商作为其导数。
在MATLAB中，没有直接提供求数值导数的函数，只有计算向前差分的函数diff，其调用格式为： DX=diff(X)：计算向量X的向前差分 DX(i)=X(i+1)-X(i)，i=1,2,…,n-1。 DX=diff(X,n)：计算X的n阶向前差分例如，diff(X,2)=diff(diff(X))。 DX=diff(A,n,dim)：计算矩阵A的n阶差分 dim=1时(缺省状态)，按列计算差分；dim=2，按行计算差分。
[S,n]=quad(‘fesin’,0,3*pi) 或者@fesin S= 0.9008 n= 77

也可不建立关于被积函数的函数文件，而使用语句函数（内联函数）求解，命令如下： g=inline('exp(-0.5*x).*sin(x+pi/6)'); %定义语句函数 [S,n]=quad(g,0,3*pi) %注意函数名不加‘号或@符号 S= 0.9008 n= 77
2.5
1

数值计算方法第07章数值微分与数值积分

h
2
f '( x) f ( x) f ( x h) f ''( x 2h) h O(h)
h
2
f '( x) f ( x h) f ( x h) 2h
f (3)( x 3h) f (3)( x 3h) h2 O(h2 )
12
心差商公式
sin x2 , cos x2 , sin x , 1 , 1 x3 , ex2 x ln x
17
2. 有些被积函数其原函数虽然可以用初等函数表示,但表达式相当复杂,计算极不方便.
x x1 x0 x1
f
( x0 )
x x0 x1 x0
f
(
x1
)@
x
h
x1
f
( x0 )
x
x0 h
f ( x1 )
则
L1( x)
1 [ h
f
( x0 )
f
( x1 )]
(7.1)
L1( x0 )
1 [ h
f
( x0 )
f
( x1 )],
L1( x1 )
1 [ h
f
( x0 )
f
x0 )( x x2 ) x0 )( x1 x2 )
f
( x1)
(x (x2
x0 )( x x1 ) x0 )( x2 x1 )
f
(x2 )
(x
x1 )( x 2h2
x2 )
f
( x0 )
(x
x0 )( x h2
x2 )
f
(x ( x1 )
x0 )( x 2h2
x1 )
f (x2 )

数值分析中的数值微分与数值积分

数值分析中的数值微分与数值积分数值微分和数值积分是数值分析领域中两个重要的概念。

它们在计算机科学、工程学和物理学等领域中有广泛的应用。

本文将介绍数值微分和数值积分的概念、原理以及一些常用的方法和技巧。

一、数值微分数值微分是通过数值方法来计算函数的导数。

导数是描述函数变化率的工具，它在物理学、经济学和生物学等领域中具有重要的作用。

1. 前向差分法（Forward Difference）前向差分法是一种简单而常用的计算导数的方法。

它利用函数在某一点上的值与函数在该点附近的一个点上的值之间的差异来估计导数。

具体公式如下：f'(x) ≈ (f(x+h) - f(x))/h其中，h为步长，为了提高精度，需要选择足够小的步长。

2. 后向差分法（Backward Difference）后向差分法与前向差分法类似，不同之处在于它利用函数在某一点上的值与函数在该点附近的一个点上的值之间的差异来估计导数。

具体公式如下：f'(x) ≈ (f(x) - f(x-h))/h同样地，步长h需要选择足够小。

3. 中心差分法（Central Difference）中心差分法是一种更加准确的数值微分方法，它利用函数在某一点上的前后两个点的值来估计导数。

具体公式如下：f'(x) ≈ (f(x+h) - f(x-h))/(2h)中心差分法相对于前向差分法和后向差分法而言，具有更高的精度。

二、数值积分数值积分是通过数值方法来计算函数的积分。

积分在物理学、经济学和统计学等领域中起着重要的作用，它可以用来计算面积、体积以及概率等。

1. 矩形法（Rectangle Method）矩形法是一种简单的数值积分方法，它利用多个矩形来逼近曲线下的面积。

具体来说，将积分区间等分为若干子区间，然后在每个子区间上选择一个点作为高度，从而构造出多个矩形。

最后，将各个矩形的面积相加，即可得到近似的积分值。

2. 梯形法（Trapezoidal Method）梯形法是一种更加准确的数值积分方法，它利用多个梯形来逼近曲线下的面积。

《数值计算方法》课程思政教学大纲

《数值计算方法》课程思政教学大纲数值计算方法课程思政教学大纲1. 课程概述- 课程名称：数值计算方法- 课程性质：专业核心课- 学时分配：理论授课 X 学时，实践操作 X 学时- 先修课程：高等数学、线性代数、数据结构- 课程目标：掌握数值计算的基本理论和方法，培养学生的计算机编程和问题解决能力。

2. 主要内容- 数值计算的概念与原理- 线性方程组的数值解法- 非线性方程的数值解法- 插值与逼近- 数值微积分- 数值积分和数值微分- 常微分方程的数值解法- 偏微分方程的数值解法- 矩阵计算与特征值问题- 数值优化方法3. 教学目标- 了解数值计算方法的发展历程和基本理论- 掌握常见的数值计算方法及其适用范围- 研究并掌握计算机编程语言在数值计算中的应用- 培养学生的计算思维和问题解决能力- 培养学生的实践动手能力和团队合作精神4. 教学方法- 理论授课与案例分析相结合，引导学生理解数值计算的基本原理和方法- 实践操作，编程实现数值计算算法并解决相关问题- 课堂讨论，提供解决数值计算问题的思路和方法- 阶段测验和课程项目，检验学生对数值计算方法的掌握程度和应用能力5. 评分方式- 平时成绩：包括课堂表现、作业和实验报告等- 期末考试：考察学生对数值计算方法的理解和应用能力6. 参考教材- 《数值计算方法导论》（第三版），华中科技大学出版社，作者：刘维等- 《数值计算方法及其MATLAB编程》，机械工业出版社，作者：刘明等该教学大纲旨在为学生提供系统的数值计算方法知识体系，并通过理论和实践相结合的教学方式，培养学生的计算和解决问题的能力。

同时通过评分方式的设置，鼓励学生在日常学习中积极参与、主动思考。

希望学生能够掌握基本的数值计算方法，并能运用所学知识解决实际问题，为将来的学术和职业发展打下坚实基础。

数值分析中的数值微分与数值积分

数值分析中的数值微分与数值积分数值分析是一门重要的数学分支，用于研究如何使用计算机来求解各种数学问题。

数值微分和数值积分是数值分析中的两个基本概念，它们在科学计算和工程应用中具有广泛的应用。

一、数值微分数值微分是通过数值方法来近似计算函数的导数。

在实际计算中，往往很难直接求得函数的导数表达式，这时候数值微分方法就派上用场了。

1. 前向差分公式前向差分公式是最简单的数值微分方法之一，它基于导数的定义，用函数值的差商来近似计算导数。

假设函数f(x)在点x0处可导，则其导数f'(x0)可以近似表示为：f'(x0) ≈ (f(x0 + h) - f(x0)) / h其中h是一个足够小的正数，通常称为步长。

通过取不同的步长h，可以得到不同精度的数值微分结果。

2. 中心差分公式中心差分公式是数值微分中较为常用的方法，它利用了函数值的前向和后向差商来近似计算导数。

假设函数f(x)在点x0处可导，则其导数f'(x0)可以近似表示为：f'(x0) ≈ (f(x0 + h) - f(x0 - h)) / (2h)与前向差分公式相比，中心差分公式的精度更高，但计算量稍大一些。

二、数值积分数值积分是通过数值方法来近似计算函数在某个区间上的定积分值。

定积分在数学、物理等领域中具有广泛的应用，尤其是对于无法用解析方法求解的积分问题，数值积分提供了可行的解决办法。

1. 矩形法则矩形法则是最简单的数值积分方法之一，它将函数在积分区间上分成若干个小矩形，然后计算这些小矩形的面积之和。

假设函数f(x)在区间[a, b]上积分，则其定积分值可以近似表示为：∫[a,b] f(x)dx ≈ (b - a) * f(x)其中x是[a, b]上的随机点。

2. 梯形法则梯形法则是数值积分中较常用的方法，它将函数在积分区间上分成若干个小梯形，然后计算这些小梯形的面积之和。

假设函数f(x)在区间[a, b]上积分，则其定积分值可以近似表示为：∫[a,b] f(x)dx ≈ (b - a) * (f(a) + f(b)) / 2梯形法则的精度要比矩形法则要高一些。

数值积分与数值微分

数值积分与数值微分数值积分和数值微分是数值计算中重要的概念和方法，它们在科学、工程和统计等领域有广泛的应用。

本文将介绍数值积分和数值微分的基本概念、原理和方法，并对其在实际问题中的应用进行讨论。

一、数值积分数值积分是求解定积分的数值近似值的方法。

定积分是函数在给定区间内的面积，表示为∫f(x)dx。

在实际计算中，由于很多函数的原函数求解十分困难或不可求得，因此需要借助数值积分方法来进行求解。

1.1 矩形法矩形法是最基本的数值积分方法之一。

它将积分区间等分为若干小区间，并在每个小区间上取一点，然后用这些小区间上的函数值的平均值来近似积分值。

具体而言，对于等分为n个小区间的积分，矩形法可以表示为：∫f(x)dx ≈ Δx * (f(x0) + f(x1) + ... + f(xn-1))其中，Δx为每个小区间的长度，xi为每个小区间上的取点。

矩形法的计算简单，但精度较低。

1.2 梯形法梯形法是另一种常用的数值积分方法，它通过用梯形面积来逼近积分值。

类似于矩形法，梯形法将积分区间等分为若干小区间，并在每个小区间上取两个点，然后用这些小区间上的梯形面积之和来逼近积分值。

具体而言，梯形法可以表示为：∫f(x)dx ≈ Δx/2 * (f(x0) + 2f(x1) + 2f(x2) + ... + 2f(xn-1) + f(xn))其中，Δx为每个小区间的长度，xi为每个小区间上的取点。

梯形法相对于矩形法有更高的精度，但计算复杂度也相应提高。

1.3 辛普森法则辛普森法则是一种更加精确的数值积分方法，它利用三次多项式来逼近积分值。

辛普森法则将积分区间等分为若干小区间，并在每个小区间上取三个点，然后通过构造一个三次多项式，利用多项式的积分近似面积来逼近积分值。

具体而言，辛普森法则可以表示为：∫f(x)dx ≈ Δx/3 * (f(x0) + 4f(x1) + 2f(x2) + 4f(x3) + ... + 2f(xn-2) +4f(xn-1) + f(xn))其中，Δx为每个小区间的长度，xi为每个小区间上的取点。

计算方法课件第七章数值积分与数值微分.ppt

在[a,b]上存在一点，使
b f (4) ( )(x a)(x b)(x c)2 dx a
f (4) () b (x a)(x c)2 (x b)dx a
R[ f ] 1 f (4) ()(b a)(b a )4
180
2
1 f (4) ()(b a)5 (a b)
总存在求积系数 A0, A1,An，使求积公式至少有n次代数精度。
事实上，只要令求积公式对于 f (x) 1, x, x2,, xn
都能准确成立即可得到下式：
b
n
dx
a
Ak
k 0
b
n
xdx
a
Ak xk
k 0
b xndx a
n
Ak xkn
k 0
则可通过给定的n+1个节点得到上述含n+1 个未知数、n+1个方程的方程组。
分近似值
b
n
I f (x)dx a
Ak f (xk ) In
b
n
k 0
I f (x)dx a
Ak f (xk ) R[ f ] In R[ f ]
k 0
其中R[f]称为求积公式的余项。xk (k 0,1,2,n)称为求
积节点。Ak (k 0,1,2,n)称为求积系数。Ak 仅与求积节点 xk 的选取有关，而不依赖与被积函数f(x)
第七章数值积分与数值微分
§7.0 §7.1
§7.2 §7.3 §7.4 §7.5
数值积分概述 Newton Cotes 公式
复化求积公式 Romberg求积法 Gauss型求积公式数值微分
§7.0 数值积分概述
由积分学基本定理知
b