三年级奥数学练习试卷思维培训资料数阵图 (3)
三年级奥数之数阵图习题
数阵图
1、把1到6这六个数分别填入下图的六个圈内,使得每个正方形顶点上的数的和都为13。
2、将2到7这六个数,填入上图的圈中,使得每条线上的三个数的和相等。
练习:请将1到7这7个数填入下图中,使得每条线上的三个数的和相等。
3、将1到9这九个数填入下图,使得从中心出发的每条线段上的三个数的和相等。
练习:将1到8填入下图,使两个正方形顶点上的数的和相等,并且用斜线连接的4对数的和也都相等。
4、将1到5这五个数填入上图中,使得圆周上四个数的和与每条直线上的三个数的和都相等。
练习:在图中填上7、8、10、12,使得每个圆内的四个数的和相等。
5、将1到16填入4*4(16格)的正方形中,使每行、每列、每条对角线的和都相等。
数阵图练习
1、将6到10这五个数填入下图,使得每条边上的三个数的和相等。
2、将2到11填入下图,使得每条线段上的三个数之和相等。
3、将2到10填入下图,使得每条线上的四个数的和相等。
. .
.。
小学三年级奥数 第39讲:数阵图

【例4】(★★★★★) 将1~7七个数字填入下图的七个○内,使每个圆周和每条直线上的 三个数之和都相等。
【例5】(★★★★) 将1~6这六个数字分别填入下图的六个○内,使得三条直线上的数 字之和都相等。
【例6】(★★★★★) 如图所示,大三角形被分成了9个小三角形。试将1,2,3,4,5,6, 7,8,9分别填入这9个小三角形内,每个小三角形内填一个数,要 求靠近大三角形3条边的每5个数相加的和相等,问这5个数的和最大 可能是多少?
数阵图
数阵图:将一些数字按照一定的要求排列而成的某些 图形。
数阵图的分类:
辐射型
பைடு நூலகம்封闭型
复合型
【例1】(★★) 将1~7这七个数字,分别填入图中各个○内,使每条线段上的 三个○内数的和都等于14。
【例2】(★★★) 将1~11填入下图的各个圆圈内,使每条线段上三个圆圈内的数之和相 等。
1
【例3】(★★★) 你能把1~6六个数字分别填入下图的六个圆圈中,使每一边三个数相 加的和都等于11吗?
2
【本讲总结】 数阵图 一、分类
辐射型
封闭型
复合型
二、基本关系 各数之和+重叠数×重叠次数=线和×线数
三、辐射型数阵图 窍门:掐头、去尾、取中间
四、注意事项 (a)关键点:特殊位置 (b)(b) 复合型:在调整的时候,不能改变原有边和
3
三年级数阵图

word格式-可编辑-感谢下载支持
1.将1~7这七个数分别填入左下图中的○里,使每条直线上的三个数之和都等于12。
如果每条直线上的三个数之和等于10,那么又该如何填?
9
(第1题)(第2题)
2.将1~9这九个数分别填入右上图中的○里(其中9已填好),使每条直线上的三个数之和都相等。
如果中心数是5,那么又该如何填?
3将1~9这九个数分别填入右图中的小方格里,
使横行和竖列上五个数之和相等。
(至少找出两
种本质上不同的填法)
4.将3~9这七个数分别填入左下图的○里,使(第3题)
每条直线上的三个数之和等于20。
(第4题)(第5题)
5.将1~11这十一个数分别填入右上图的○里,使每条直线上的三个数之和相等,并且尽可能大。
6.将1~7这七个数分别填入右图的○里,
使得每条直线上三个数之和与每个圆圈
上的三个数之和都相等。
小学奥数5-1-3-3 数阵图(三).专项练习

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格); 第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.数阵图与数论【例 1】 把0—9这十个数字填到右图的圆圈内,使得五条线上的数字和构成一个等差数列,而且这个等差数列的各项之和为55,那么这个等差数列的公差有 种可能的取值.【例 2】 将1~9填入下图的○中,使得任意两个相邻的数之和都不是3,5,7的倍数.例题精讲知识点拨教学目标5-1-3-3.数阵图【例 3】在下面8个圆圈中分别填数字l,2,3,4,5,6,7,8(1已填出).从1开始顺时针走1步进入下一个圆圈,这个圆圈中若填n(n≤8)。
则从这个圆圈开始顺时针走n步进入另一个圆圈.依此下去,走7次恰好不重复地进入每个圆圈,最后进入的一个圆圈中写8.请给出两种填法.【例 4】在圆的5条直径的两端分别写着1~10(如图)。
现在请你调整一部分数的位置,但保留1、10、5、6不动,使任何两个相邻的数之和都等于直径另一端的相邻两数之和(画在另一个圆上)。
【例 5】图中是一个边长为1的正六边形,它被分成六个小三角形.将4、6、8、10、12、14、16各一个填入7个圆圈之中.相邻的两个小正三角形可以组成6个菱形,把每个菱形的四个顶点上的数相加,填在菱形的中心A、B、C、D、E、F位置上(例如:a b g f A+++=).已知A、B、C、D、E、F依次分别能被2、3、4、5、6、7整除,那么a g d⨯⨯=___________.【例 6】在如图所示的圆圈中各填入一个自然数,使每条线段两端的两个数的差都不能被3整除。
小学奥数:数阵图(三).专项练习及答案解析

1.了解数阵图的种类2.学会一些解决数阵图的解题方法3.能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1.定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2.数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图.3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手:第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.数阵图与数论【例 1】把0—9这十个数字填到右图的圆圈内,使得五条线上的数字和构成一个等差数列,而且这个等差数列的各项之和为55,那么这个等差数列的公差有种可能的取值.【考点】数阵图与数论【难度】3星【题型】填空【关键词】迎春杯,三年级,初赛,第8题【解析】设顶点分别为A、B、C 、D、E,有45+A+B+C+D+E=55,所以A+B+C+D+E=10,所以A、B、C、D、E分别只能是0-4中的一个数字.则除之外的另外5个数(即边上的)为45-10=35.设所形成的等差数列的首项为a1,公差为d.利用求和公式5(a1+a1+4d)2=55,得a1+2d=11,故大于等于0+1+5=6,且为奇数,只能取7、9或11,而对应的公差d分别为2、1和0.经试验都能填出来所以共有3中情况,公差分别为2、1、0.例题精讲知识点拨教学目标5-1-3-3.数阵图【答案】2种可能【例 2】将1~9填入下图的○中,使得任意两个相邻的数之和都不是3,5,7的倍数.【考点】数阵图与数论【难度】4星【题型】填空【解析】根据题意可知1的两边只能是3与7;2的两边只能是6与9;3的两边只能是1、5或8;4的两边只能是7与9.可以先将3—1—7--写出来,接下来7的后面只能是4,4的后面只能是9,9的后面只能是2,2的后面只能是6,可得:3—1—7—4—9—2—6--,还剩下5和8两个数.由于6814+=是7的倍数,所以接下来应该是5,这样可得:3—1—7—4—9—2—6—5—8—3.检验可知这样的填法符合题意.【答案】3—1—7—4—9—2—6—5—8—3【例 3】在下面8个圆圈中分别填数字l,2,3,4,5,6,7,8(1已填出).从1开始顺时针走1步进入下一个圆圈,这个圆圈中若填n(n≤8)。
2020~2021学年三年级奥数思维能力训练:数阵图初步
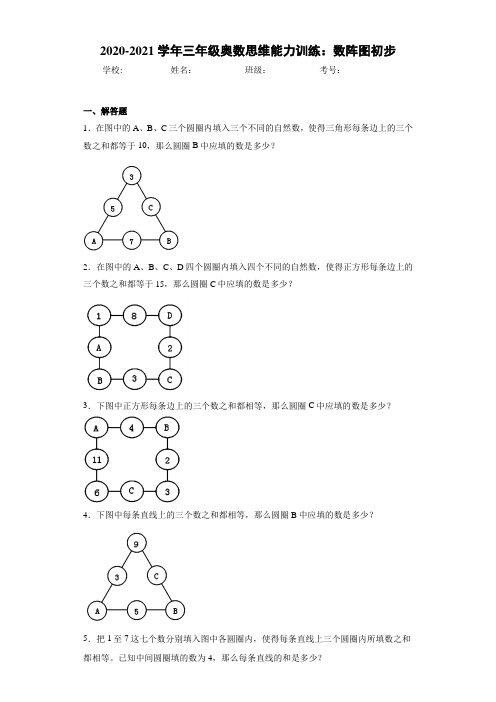
10.在图中的A、B、C三个圆圈内填入三个不同的自然数,使得正方形每条边上的三个数之和都相等,那么圆圈A中应填的数是多少?
参考答案
1.1
【解析】
【分析】
封闭型数阵图,线和是10,先求A,再求B,再求C。
【解析】
【分析】
辐射型数阵图问题,中间数是4,重复了2次,可利用数和、线和及中间数的关系进行求解。
【详解】
先求数和, ,中间数重复了2次,再求线和, ,所以每条直线的和是12,根据“4+1+7=12”,“4+2+6=12”,“4+3+5=12”,进行合理构造,完成数阵图。
【点睛】
辐射型数阵图,注意中间数的填法,考虑中间数除了4,还可以填多少。
【详解】
A=
B=
【点睛】
本题较为简单,根据数阵图的基本要求直接求解即可。
2.7
【解析】
【分析】
封闭型数阵图,1,B,C,D重复了1次,线和已知,按照D,C,B,A的顺序依次求解。
【详解】
D=
C=
【点睛】
本题较为简单,线和已经给出,按照线和相等这一基本原则,直接计算即可。
3.9
【解析】
【分析】
封闭型数阵图,根据线和相等,先求出B,然后求出线和,再求A和C。
8.
【解析】
【分析】
复合型数阵图问题,每块区域的数都重复了一次,利用数和、线和的关系进行求解。
【详解】
如图,
令 ;
已知a,b,c,d,e,f,g,h各自用了两次,计算数和, ;
(完整版)小学三年级奥数--数阵图

数阵图(一)在神奇的数学王国中,有一类非常有趣的数学问题,它变化多端,引人入胜,奇妙无穷。
它就是数阵,一座真正的数字迷宫,它对喜欢探究数字规律的人有着极大的吸引力,以至有些人留连其中,用毕生的精力来研究它的变化,就连大数学家欧拉对它都有着浓厚的兴趣。
那么,到底什么是数阵呢?我们先观察下面两个图:左上图中有3个大圆,每个圆周上都有四个数字,有意思的是,每个圆周上的四个数字之和都等于13。
右上图就更有意思了,1~9 九个数字被排成三行三列,每行的三个数字之和与每列的三个数字之和,以及每条对角线上的三个数字之和都等于15,不信你就算算。
上面两个图就是数阵图。
准确地说,数阵图是将一些数按照一定要求排列而成的某种图形,有时简称数阵。
要排出这样巧妙的数阵图,可不是一件容易的事情。
我们还是先从几个简单的例子开始。
例1 把1~5这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9。
同学们可能会觉得这道题太容易了,七拼八凑就写出了右上图的答案,可是却搞不清其中的道理。
下面我们就一起来分析其中的道理,只有弄懂其中的道理,才可能解出复杂巧妙的数阵问题。
分析与解:中间方格中的数很特殊,横行的三个数有它,竖列的三个数也有它,我们把它叫做“重叠数”。
也就是说,横行的三个数之和加上竖列的三个数之和,只有重叠数被加了两次,即重叠了一次,其余各数均被加了一次。
因为横行的三个数之和与竖列的三个数之和都等于9,所以(1+2+3+4+5)+重叠数=9+9,重叠数=(9+9)-(1+2+3+4+5)=3 。
重叠数求出来了,其余各数就好填了(见右上图)。
试一试:练习与思考第1 题。
例2 把1~5 这五个数填入下页左上图中的○里(已填入5),使两条直线上的三个数之和相等。
分析与解:与例1 不同之处是已知“重叠数”为5,而不知道两条直线上的三个数之和都等于什么数。
所以,必须先求出这个“和”。
根据例1 的分析知,两条直线上的三个数相加,只有重叠数被加了两遍,其余各数均被加了一遍,所以两条直线上的三个数之和都等于[(1+2+3+4+5)+5] ÷2=10。
三年级思维拓展- 数阵图

(2)要使每个五边形上的5个数和为20,那么2个五边形上的数的总和是:20×2=40.
(3)2个五边形上的数的总和比8个数的和多了:40-36=4
(4)多的6就是五边形交叉点重复计算了2次,即多算了1次。在1--8这8个数中有:1+3=4,所以中间位置填1和3.
思路点拨:观察发现中间的圆重复了3次,题目要求3条线上的和相等,那么,每条线上只要有两个数加起来和都相等,中间重复加任何一个数和也都相等。因为1+7=8,2+6=8,3+5=8,所以将4填在中间,再将分好的数填进圆内即可。
活学巧用:
1.,使每条边上的3个数之和都等于10。
活学巧用:
1.将2﹑3﹑4﹑5﹑6﹑7这6个数填在下面的圆圈里,使每条边上3个数的和等于15。
2.把数字1、2、3、4、5、6分别填入下图的圆圈内,使3条边上3个数字之和等于11。
3.将1——9这九个数填入下图中,使三角形每条边上四个数的和等于19
【例3】:将1--7这7个数填入○中,使每条线上三个数的和都相等。
2.计算出所给数的总和。
3.再计算出各个部分的总和。
4.两和之间找出“重复计算的数的和”,填出关键位置的数,再根据要求尝试,调整,填出其他位置上的数。
精选例题:
【例1】:将1、3、5、7、9这5个数分别填入□中,使每条线上的三个数的和都相等。
思路点拨:因为1、3、5、7、9中,一头一尾组合结果都为10,题目只要求每条线上三个数的和相等,那么,只要每条线上的两个数的和相等了,中间重复计算的数填任何一个,这两条线上的和也就相等了。
(5)先填被重复计算的数字,在通过计算填出其余的数字:2+6+8=16,4+5+7=16.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6
3
1
4
2
5
7
2
6
4
7
5
1
3
3
4
7
5
6
2
1
例3 (学而思题库)将 10~20 填入左下图的○内,其中 15 已填好,使得每条边上的三个数字之和
都相等.
15
分析:中间○内的 15 是重叠数,并且重叠了四次,所以每条边上的三个数字之和等于 [(10+11+…+ 20)+15×4]÷5=45.
学而思教育
08 年寒假
三年级
精英班
第六讲
教师版
Page 44
讲义是乐谱,学生是听众,老师是指挥家,每节课都是一篇乐章,老师您辛苦了! ——学而思小学奥数讲义组
专题精讲
到底什么是数阵呢?我们先观察右面两个图: 左图中有 3 个大圆,每个圆周上都有四个数字,有意思的是, 每个圆周上的四个数字之和都等于 13.右图就更有意思了,1~9 九个数字被排成三行三列,每行的三个数字之和与每列的三个数字 之和,以及每条对角线上的三个数字之和都等于 15.上面两个图就 是数阵图.准确地说,数阵图是将一些数按照一定要求排列而成的 某种图形,有时简称数阵.
在神奇的数学王国中,有一类非常有趣的数学问题,它变化多端,引人入胜, 奇妙无穷.它就是数阵,一座真正的数字迷宫,它对喜欢探究数字规律的人 有着极大的吸引力,以至有些人留恋其中,用毕生的精力来研究它的变化, 就连大数学家欧拉对它都有着浓厚的兴趣.到底什么是数阵呢? 下面我们一 起来研究吧.
学而思教育
08 年寒假
三年级
精英班
第六讲
教师版
Page 46
讲义是乐谱,学生是听众,老师是指挥家,每节课都是一篇乐章,老师您辛苦了! ——学而思小学奥数讲义组
剩下的十个数中,两两之和等于(45-15=)30 的有 10,20;11,19;12,18;13,17;14,16.
也可以这样求:五条边上两个数的和都是相等的,(10+11+…+20)÷5=
讲义是乐谱,学生是听众,老师是指挥家,每节课都是一篇乐章,老师您辛苦了! ——学而思小学奥数讲义组
第六讲 数字谜(二)—数阵图
教学目标
本讲通过对简单数阵的学习,让学生在数与数之间的变化中,感受到数字的奇妙,体会到数学思维 的乐趣
知识点:1.封闭型数阵图; 2.辐射型数阵图; 3.复合型数阵图.
想
挑
将 1、2、3、4、5、6 这六个数填在图中的空灯里,使
分析:在图中我们可以看出,中间圆圈里的数很特殊,横行的三个数有它,竖列的三个数也有它,我们 把它叫做“重叠数”.也就是说,横行的三个数之和加上竖列的三个数之和,只有重叠数被加了两次, 即重叠了一次,其余各数均被加了一次.我们可以得出: (1+2+3+4+5)+重叠数=每条直线上三数 之和×2,所以,每条直线上三数之和等于(15+重叠数)÷2. 因为每条直线上的三数之和是整数,所以重叠数只可能是 1,3 或 5. 若“重叠数”=1,则两条直线上三数之和为(15+1)÷2=8.填法见左下图; 若“重叠数”=3,则两条直线上三数之和为 (15+3)÷2=9.填法见下中图; 若“重叠数”=5,则两条直线上三数之和为 (15+5)÷2=10.填法见右下图.
2
1
2
3
1
4
2
3
4
1
5
4
5
5
3
[巩固]把 1~5 这五个数填入下图中的○里(已填入 5),使两条直线上的三个数之和相等.
1
5
2
5
3
学而思教育
08 年寒假
三年级
精英班
4
第六讲
教师版
Page 45
讲义是乐谱,学生是听众,老师是指挥家,每节课都是一篇乐章,老师您辛苦了! ——学而思小学奥数讲义组
分析:与例题不同之处是已知“重叠数”为 5,而不知道两条直线上的三个数之和都等于什么数.,其余各数均被加了一遍, 所以两条直线上的三个数之和都等于 [(1+2+3+4+5)+5]÷2=10.因此,两条直线上另两个数(非 “重叠数”)的和等于 10-5=5.非“重叠数”的和也可以这样求,因为 1~4 的和我们可以求,每条直 线上两端的数的和是:(1+2+3+4)÷2=5. 在剩下的四个数 1,2,3,4 中,只有 1+4=2+3=5.故有右上图的填法.
7 213 645
816 357 492
(一)辐射型数阵图
有一种数阵图,它们的特点是从一个中心出发,向外作了一些射线,我们把这种数阵图叫做辐射型 数阵图.填辐射型数阵图的关键是确定中心数以及每条线段上的几个数的和,然后通过对各数的分析, 进行试验填数求解.
例1 (学而思题库)把 1~5 这五个数填入下图中的○里,使每条直线上的三个数之和相等.
30,所以两两之和等于 30.
20
于是得到右图的填法.
[拓展]把 10~20 这 11 个数分别填入下图的圆圈内,使每条线段上三个圆圈内的数 的和都相等.请你把各种填法都写出来(中心圆圈内的数相同就视为一种填 法).(1993 年武汉市小学数学竞赛试题)
战
每个大圆上的四盏灯里的数相加都等于 14.
吗
?
分析:将三个大圆上的所有数字相加,中间三个灯笼上的数字被加了 2 遍, 其余三个灯笼上的数字只加了一遍,所以,中间三个数的和为(1+2+3 +4+5+6)-14=7,三个数相加等于 7 的情况只有 1+2+4,所以中间 的三个灯笼上的数为 1,2,4,这 6 个数中四个数相加等于 14 的组合有 (6521)(6431)(5432),就可以填出:
即:(28+中心数×2)÷3=每条线段上三个数的和. 用试验的方法,将 1~7 这七个数作中心数分别代入上述关系式中.可求出中心数及每条直线上三 个数的和.经试验,若中心数取 2、3、5、6,此题无解;中心数取 1、4、7 时该题数阵图成立. (1)(28+1×2)÷2=10,中间圆圈内填 1,各线段其他两数和为 10-1=9. (2)(28+4×2)÷3=12,中间圆圈内填 4,各线段其他两数和为 12-4=8. (3)(28+7×2)÷3=14,中间圆圈内填 7,各线段其他两数和为 14—7=7. 三种基本解法详见下图.
[注意] 求数阵问题的关键是找到关键数,也就是重复数,教会学生学会找关键数的方法是最重要的.
例2 (学而思题库)把 1~7 这七个数分别填入下图的○内,使每条线段上三个○内数的和相等.
分析:解这道题的关键是首先求出中心数.1~7 七个数的和是 28,而计算三条线段中数的和时,中心 圆的数要多加两次.因此可得如下关系式:28+(中心数)×2=每条线段上三个数的和×3.
