抛物线焦点弦性质总结
抛物线焦点弦的性质及应用

抛物线焦点弦的性质及应用抛物线是一种具有特殊性质的二次曲线,它的焦点弦性质是指过焦点parabola. 抛物线上任意一点的切线与从焦点引出的该点的法线的交点,这些交点都在焦点所在的直线上。
抛物线焦点弦的性质和应用如下:1. 焦点弦与顶点:抛物线的焦点弦通过抛物线的顶点,且与抛物线的对称轴垂直相交。
2. 焦点弦的长度:焦点弦的长度等于抛物线焦点到对称轴的距离的两倍。
3. 焦点弦的切线方程:焦点弦的切线方程可由抛物线的切线方程推导得到,即通过抛物线上一点(x1,y1)的切线方程为y = mx + (1 - m²) a/4,其中m为切线的斜率,a为焦点到对称轴的距离。
4. 焦点弦的法线方程:焦点弦的法线方程可由切线方程得到,即过抛物线上一点(x1,y1)的法线方程为y = -x/m + (x1/m + y1)。
5. 焦点弦的性质应用:抛物线焦点弦的性质在物理学、工程学和几何学等领域有广泛的应用。
在物理学中,抛物线焦点弦的性质可以用于描述光线的反射和聚焦。
例如,在反射望远镜中,抛物面用于反射并聚焦光线,使观察者能够看到远处的物体。
在工程学中,抛物线焦点弦的性质可以用于设计抛物面反射器、喇叭等产品。
抛物面反射器可以将声音或者电磁波线聚焦在焦点处,以达到提高功率传输效果的目的。
类似地,喇叭的设计也借鉴了抛物线焦点弦的性质,使声音能够更好地聚焦并扩散。
在几何学中,抛物线焦点弦的性质可以用于求解问题。
例如,已知抛物线上一点的坐标和抛物线焦点的坐标,可以通过焦点弦性质来求解该点在抛物线上的位置。
另外,抛物线焦点弦的性质还可以进一步推广到三维空间中的抛物面。
三维空间中的抛物面也具有焦点弦的性质,可以用于描述反射、聚焦和求解问题等。
综上所述,抛物线焦点弦是抛物线特有的性质之一,它的性质和应用在物理学、工程学和几何学等领域有重要的应用。
深入理解和应用这些性质可以帮助我们更好地解决各种问题,并且进一步推广到更高维度的几何形状中。
抛物线焦点弦的八大结论

抛物线焦点弦的八大结论
第一类是常见的基本结论;
第二类是与圆有关的结论;
第三类就是由焦点弦得出结论有关直线横向的结论;
第四类是由焦点弦得出有关直线过定点的结论。
1、以焦点弦为直径的圆与准线切线(用抛物线的定义与梯形的中位线定理融合证明)。
2、1/|af|+1/|bf|=2/p(p为焦点到准线的距离,下同)。
3、当且仅当焦点弦与抛物线的轴横向(此时的焦点弦称作“通径”)时,焦点弦的长度获得最小值2p。
4、如果焦点弦的两个端点是a、b,那么向量oa与向量ob的数量积是-0.75p^2。
抛物线具备这样的性质,如果它们由反射光的材料做成,则平行于抛物线的对称轴前进并喷发其凹面的光被散射至其焦点,而不管抛物线在哪里出现散射。
恰好相反,从焦点处的点源产生的光被散射成平行(“电子束”)光束,并使抛物线平行于对称轴。
声音和其他形式的能量也可以产生相同的效果。
这种散射性质就是抛物线的许多实际应用领域的基础。
证明抛物线焦点弦的18个结论

证明抛物线焦点弦的18个结论
抛物线是一种椭圆形的函数图形,它是由抛物线焦点弦决定的。
抛物线焦点弦是指抛物线的两个焦点和连接它们的弦段。
围绕抛物线焦点弦可以建立18个结论。
1. 两个焦点之间的距离与抛物线弦段长度相同,即它们之间的距离等于抛物线弦段的1倍。
2. 弦段连接抛物线的两个焦点,因此,任何一点的垂直距离都等于其焦点的距离。
3. 对抛物线的焦点取中对称,则其两点之间的距离一定是直线的1倍.
5. 相对于一个焦点而言,另一个焦点总是处于弦段的同一边,而且位于弦段上面。
6. 抛物线是对称的,即抛物线的对称轴是连接两个焦点的直线段。
8. 抛物线准线与切线交于抛物线的焦点。
12. 对任意点A而言,从A点向任意点B连线便构成一条直线,此直线连接A点和B 点的距离有正有负,正值表示线段到抛物线焦点的距离是它的弦段长度所乘以2倍的直线段距离,负值则表示抛物线焦点到线段的距离也是它的弦段长度乘以2倍的直线段距离。
17. 抛物线的对称轴与它的弦段垂直,因此它的弦段将对称轴分为2个相等的距离。
以上就是抛物线焦点弦的十八个结论,也是其对称性规律、准确性和完整性的总结。
抛物线焦点弦的这些结论,既给抛物线函数提供了数学化的更直观的解释,又为描述抛物线的属性提供了一定的参考依据。
抛物线焦点弦22条结论

抛物线焦点弦22条结论1、抛物线的焦点总是在数轴上的对称轴上。
2、抛物线的无穷近点总处在顶点上。
3、抛物线的顶点的坐标总是(h,k)的形式。
4、抛物线的斜率在顶点处最大,向两侧无穷远时最小。
5、抛物线不同于椭圆,即使在斜率为零时也不会平行于y轴。
6、抛物线焦点弦中椭圆内的焦点和斜率有关。
7、抛物线焦点弦中椭圆外的焦点和斜率有关。
8、抛物线焦点弦中椭圆内的线段始末点在椭圆上。
9、抛物线焦点弦中椭圆外的线段始末点在椭圆外。
10、抛物线焦点弦中,两个焦点分别对应一条双曲直线,而外圆的直径线段是两个焦点的连线。
11、抛物线的弦一定位于双曲线的两侧且是双曲线的垂直线段。
12、抛物线的焦点弦外圆的周长是抛物线的一象限周长的二倍。
13、抛物线焦点弦的另一圆的面积等于抛物线的一象限面积的两倍。
14、抛物线的焦点弦中,双曲线内外的直线段条数是一样多的。
15、抛物线焦点弦中,双曲线外的直线段总是比双曲线内的长。
16、抛物线焦点弦中,椭圆内及其外圆的线段总是一模一样的。
17、抛物线焦点弦中,双曲线外圆的形状是矩形,两个顶点在焦点上,其他两个顶点位于y轴上。
18、抛物线焦点弦中,双曲线内的所有线段的总长比双曲线外的总长要短。
19、抛物线焦点弦中,双曲线外的直线段均贯穿原点。
20、抛物线焦点弦中,两条分别从两个焦点开始,沿着双曲线直线段向原点靠近的线段,称为弦线。
21、抛物线焦点弦中,椭圆的焦点到顶点的距离,称为长轴半径的大小等于抛物线机小数a的值。
22、抛物线焦点弦中,椭圆的焦点到其他顶点的距离,称为短轴半径的大小等于抛物线机小数b的值。
焦点弦的八大结论

焦点弦的八大结论焦点弦是一种常见的数学问题,它的研究有助于我们更深入地理解数学中的一些重要概念和定理。
在这篇文章中,我们将讨论焦点弦的八大结论,了解它们分别是什么以及它们的意义。
最后,我们还将介绍焦点弦在实际应用中的一些例子。
一、焦点弦与抛物线的关系抛物线是一种经典的二次函数图像,它的形状是一个开口朝上或朝下的U字形曲线。
而焦点弦则是经过抛物线焦点的一条线段,根据抛物线的性质,焦点弦与抛物线的顶点在同一条直线上。
二、焦点弦的长度焦点弦的长度等于抛物线顶点到焦点的距离的两倍,这个结论很容易证明,只需要利用抛物线的定义式和距离公式即可得出。
三、焦点弦的中点焦点弦的中点恰好落在抛物线的准线上,这个结论也很容易证明,只需要利用抛物线的对称性即可。
四、焦点弦的垂线焦点弦的垂线恰好与抛物线相切,并且与抛物线准线垂直,这个结论涉及到了抛物线的切线和法线的概念。
五、抛物线对称性抛物线的对称轴恰好与焦点弦重合,这个结论是由于焦点弦的中点在对称轴上。
六、焦距的作用焦点弦和焦距有着密切的关系,焦点弦的长度等于焦距的两倍,这个结论是逆向推导出来的,也就是我们通过焦距来求出焦点弦的长度。
七、焦点弦的作用焦点弦在数学中有着重要的作用,它可以用来推导一些抛物线的性质,例如抛物线的切线和法线。
此外,在工程中,焦点弦也有广泛的应用,它可以用来设计一些光学系统和声学系统。
八、应用实例我们举个例子,考虑一个天线系统,它的辐射方向呈现出一条抛物线形状,我们可以通过焦点弦来设计这个天线系统的形状和大小,以达到最优的信号接收和传输效果。
类似的应用还包括椭圆镜头和声学降噪系统等。
综上所述,焦点弦是一个重要的数学问题,它在抛物线的研究和实际应用中有着广泛的应用。
理解焦点弦的八大结论有助于我们更深入地理解抛物线的概念和性质,同时也为我们提供了一些实际应用的思路和方法。
因此,学习和掌握焦点弦的八大结论是非常有益的。
抛物线经典性质总结30条
2124p x =;212y p =-;'90AC B ∠=; ''90A FB ∠=;6. 123222()2sin p pAB x x p x α=++=+=; 7.112AF BF P+=; 8. A 、O 、'B 三点共线; 9. B 、O 、'A 三点共线;10. 22sin AOB P S α=;11. 23()2AOB S PAB =〔定值〕; 12. 1cos P AF α=-;1cos PBF α=+;13. 'BC 垂直平分'B F ; 14. 'AC 垂直平分'A F ; 15. 'C F AB ⊥; 16. 2AB P ≥; 17. 11'('')22CC AB AA BB ==+; 18. AB 3P K =y ; 19. 2p 22ytan =x -α;20. 2A'B'4AF BF =⋅; 21. 1C'F A'B'2=. 22. 切线方程 ()x x m y y +=00性质深究一)焦点弦与切线1、 过抛物线焦点弦的两端点作抛物线的切线,两切线交点位置有何特殊之处?结论1:交点在准线上先猜后证:当弦x AB ⊥轴时,则点P 的坐标为⎪⎭⎫⎝⎛-0,2p 在准线上. 证明: 从略结论2 切线交点与弦中点连线平行于对称轴结论3 弦AB 不过焦点即切线交点P 不在准线上时,切线交点与弦中点的连线也平行于对称轴.2、上述命题的逆命题是否成立?结论4 过抛物线准线上任一点作抛物线的切线,则过两切点的弦必过焦点先猜后证:过准线与x 轴的交点作抛物线的切线,则过两切点AB 的弦必过焦点. 结论5过准线上任一点作抛物线的切线,过两切点的弦最短时,即为通径.3、AB 是抛物线px y 22=〔p >0〕焦点弦,Q 是AB 的中点,l 是抛物线的准线,l AA ⊥1,l BB ⊥1,过A ,B 的切线相交于P ,PQ 与抛物线交于点M .则有结论6PA ⊥PB . 结论7PF ⊥AB . 结论8 M 平分PQ .结论9 PA 平分∠A 1AB ,PB 平分∠B 1BA .结论2PF FB FA =结论11PAB S ∆2minp =二)非焦点弦与切线思考:当弦AB 不过焦点,切线交于P 点时, 也有与上述结论类似结果: 结论12 ①p y y x p 221=,221y y y p += 结论13 PA 平分∠A 1AB ,同理PB 平分∠B 1BA .结论14 PFB PFA ∠=∠ 结论15 点M 平分PQ结论162PF =相关考题1、已知抛物线y x 42=的焦点为F ,A ,B 是抛物线上的两动点,且FB AF λ=〔λ>0〕,过A ,B 两点分别作抛物线的切线,设其交点为M ,〔1〕证明:AB FM ⋅的值;〔2〕设ABM ∆的面积为S ,写出()λf S =的表达式,并求S 的最小值.2、已知抛物线C 的方程为y x 42=,焦点为F ,准线为l ,直线m 交抛物线于两点A ,B ; 〔1〕过点A 的抛物线C 的切线与y 轴交于点D ,求证:DF AF =;〔2〕假设直线m 过焦点F ,分别过点A ,B 的两条切线相交于点M ,求证:AM ⊥BM ,且点M 在直线l 上.3、对每个正整数n ,()n n n y x A ,是抛物线y x 42=上的点,过焦点F 的直线FA n 交抛物线于另一点()n n n t s B ,, 〔1〕试证:4-=⋅n n s x 〔n ≥1〕〔2〕取nn x 2=,并C n 为抛物线上分别以A n 与B n 为切点的两条切线的交点,求证:122121+-=++++-n n n FC FC FC 〔n ≥1〕抛物线的一个优美性质几何图形常常给人们带来直观的美学形象,我们在研究几何图形时也会很自然地想得到有关这个几何图形的美妙的性质,作为几何中的圆锥曲线的研究,正是这方面的一个典型代表,作为高中数学中的必修内容,对于培养学生对于数学美的认识,起着相当重要的作用。
抛物线焦点弦22条结论

抛物线焦点弦22条结论抛物线是一种经典的数学曲线,被广泛应用于物理学、工程学、计算机图形学等领域。
在研究抛物线的性质和应用过程中,焦点和弦是两个重要的概念。
本文将介绍抛物线焦点弦的22条结论。
1. 抛物线的焦点是由平行于抛物线的直线反射后汇聚而成的点。
2. 抛物线的焦点是离抛物线顶点等距离的点。
3. 抛物线的焦点是所有平行于抛物线的直线的交点。
4. 抛物线的焦点是所有过抛物线的顶点的对称轴的交点。
5. 抛物线的焦点是所有与抛物线相切的直线的交点。
6. 抛物线的焦点是所有过抛物线的顶点并且与抛物线平行的直线的交点。
7. 抛物线的焦点是所有过抛物线的顶点并且与抛物线垂直的直线的交点。
8. 抛物线的焦点是所有经过抛物线的两个端点并且与抛物线垂直的直线的交点。
9. 抛物线的焦点是所有过抛物线的顶点且与抛物线切线垂直的直线的交点。
10. 抛物线的焦点是所有过抛物线的顶点且与抛物线切线平行的直线的交点。
11. 抛物线的焦点是所有与抛物线相交的直线的交点。
12. 抛物线的焦点是所有通过抛物线的两个端点且与抛物线相交的直线的交点。
13. 抛物线的焦点是所有过抛物线的顶点且与抛物线切线相交的直线的交点。
14. 抛物线的焦点是所有过抛物线的顶点且与抛物线切线平行且相交于抛物线的焦点的直线的交点。
15. 抛物线的焦点是所有过抛物线的顶点且与抛物线切线垂直且相交于抛物线的焦点的直线的交点。
16. 抛物线的焦点是所有过抛物线的顶点并且与抛物线切线平行于抛物线的对称轴的直线的交点。
17. 抛物线的焦点是所有过抛物线的顶点并且与抛物线切线垂直于抛物线的对称轴的直线的交点。
18. 抛物线的焦点是所有过抛物线的顶点且与抛物线对称轴平行的直线的交点。
19. 抛物线的焦点是所有过抛物线的顶点且与抛物线对称轴垂直的直线的交点。
20. 抛物线的焦点是所有通过抛物线的两个端点且与抛物线对称轴平行的直线的交点。
21. 抛物线的焦点是所有通过抛物线的两个端点且与抛物线对称轴垂直的直线的交点。
焦点弦及其性质

焦点弦及其性质1.抛物线焦点弦的定义:过抛物线焦点的直线与抛物线交于两点这两点间的线段叫做抛物线的焦点弦。
2.抛物线焦点弦的性质:若抛物线的方程为y2=2px(p>0),过抛物线的焦点F(p2,0)的直线交抛物线与A(x1,y1)、B(x2,y2)两点,则①y1y2=-p2;②x1x2=p24;③|AB|=x1+x2+p;④|AB|=2psin2θ(其中θ为直线的倾斜角);⑤1|AF|+1|BF|=2p;⑥过A、B两点作准线的垂线,垂足分别为A/、B/,F抛物线的焦点,则∠A/FB/=900;⑦以弦AB为直径的圆与准线相切。
证明:①当直线过焦点且垂直于x轴时,A(p2,p)、B(p2,-p),因此y1y2=-p2成立;当直线过焦点且不与x轴垂直时,显然直线的斜率k≠0,直线AB的方程为:y=k(x-p2);由此的x=yk+p2;把x=yk+p2代入y2=2px消去x得:ky2-2py-kp2=0,∴y1y2=-p2②∵A(x1,y1)、B(x2,y2)两点都在抛物线y2=2px(p>0)上,∴y12=2px1,y22=2px2;两式相乘得(y1y2)2=2px1·2px2∴p4=4p2x1x2;从而x1x2=p2 4③过A、B两点作准线x=-p2的垂线,垂足分别为A/、B/,则|AB|=|AF|+|BF|=|AA/|+|BB/|=x1+p2+x2+p2=x1+x2+p④当θ=900时,显然成立;当θ≠900时,,则直线AB的方程为:y=k(x-p2);把y=k(x-p2)代入y2=2px消去y得:k2x2-p(k2+2)x+k2p24=0;x1+x2=p(k2+2)k2,x1x2=p24;|AB|=1+k2|x1-x2|=1+k2(x1+x2)2-4x1x2=2p(1+k2)k2=2p(1+tan2θ)tan2θ=2psin2θ。
⑤∵A(x1,y1)、B(x2,y2)∴1 |AF|+1|BF|=1x1+p2+1x2+p2=x 1+x 2+px 1x 2+p 2 (x 1+x 2)+p 24=x 1+x 2+pp 24+p 2 (x 1+x 2)+p24=x1+x2+pp 2(x1+x2+p)=2p⑥过A、B两点分别作准线的线,垂足分别为A/、B/,由于点A、B是抛物线上的点,F是抛物线的焦点,根据抛物线的定义可知,|AF|=|AA/|,|BF|=|BB/|∴∠B/BF=1800-2∠B/FB,∠A/AF=1800-2∠A/FA由∵AA/∥BB/∴∠B/BF+∠A/AF=1800即:1800-2∠B/FB+1800-2∠A/FA=1800∴∠B/FB+∠A/FA=900(7)N为线段AB的中点,过A、B、N分别作准线的垂线,垂足分别为A/、B/、N/,∵N为线段AB的中点,则|NN/|=|AA/|+|BB/|2=|AF|+|BF|2=|AB|2∴以AB为直径的圆与准线相切。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
抛
物线焦点弦性质总结
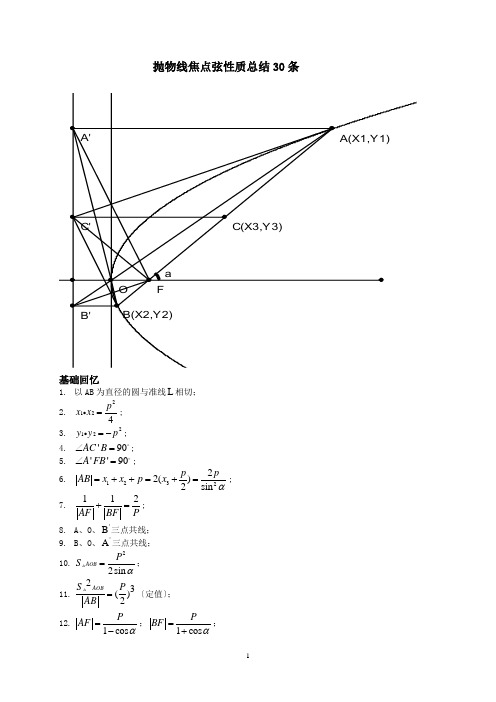
基本性质 已知抛物线22y px =的图像如图所示,
则有以下基本结论:
1、以AB 为直径的圆与准线L 相切;
2、2124p x x ⋅=且212y y p ⋅=-;
3、90AC B '∠=︒,90A FB ''∠=︒;
4、123222()2sin p p AB x x p x α=++=+=;
5、112AF BF P +=; 6A 、O 、B '三点共线,B 、O 、A '三点共线;
7、22sin AOB p S α=△,3
22AOB S p AB ⎛⎫= ⎪⎝⎭△(定值); 8、1cos p AF α=-,1cos p BF α=+; 9、BC '垂直平分B F ',AC '垂直平分A F ', C F AB '⊥;
10、2AB p ≥;
11、11()22CC AB AA BB '''==+; 12、3AB p k y =,22tan 2
y p x α=-; 13、24A B AF BF ''=⋅,12C F A B '''=. 14、切线方程:()x x m y y +=00
性质深究
一、焦点弦与切线
结论1、过抛物线焦点弦的两端点作抛物线的切线,两切线
交点在准线上.
特别地,当弦x AB ⊥轴时,则点P 的坐标为,02p ⎛⎫- ⎪⎝⎭
. 结论2、切线交点与弦中点连线平行于对称轴
结论3、弦AB 不过焦点即切线交点P 不在准线上时,切线交点与弦中点的连线也平行于对称轴.
结论4、过抛物线准线上任一点作抛物线的切线,则过两切点的弦必过焦点.
特别地,过准线与x 轴的交点作抛物线的切线,则
过两切点AB 的弦必过焦点.
结论5、过准线上任一点作抛物线的切线,过两切点
的弦最短时,即为通径.
AB 是抛物线px y 22=(p >0)焦点弦,Q 是AB 的
中点,l 是抛物线的准线,l AA ⊥1,l BB ⊥1,过A ,B
的切线相交于P ,PQ 与抛物线交于点M .则有
结论6、PA ⊥PB .
结论7、PF ⊥AB . 结论8、M 平分PQ . 结论9、PA 平分∠A 1AB ,PB 平分∠B 1BA .
结论102=
结论11、PAB S ∆2min p =
二、非焦点弦与切线 当弦AB 不过焦点,切线交于P 点时,也有与上述结论类似结果:
结论12、①p y y x p 221=,2
21y y y p += 结论13、PA 平分∠A 1AB ,同理PB 平分∠B 1BA .
结论14、PFB PFA ∠=∠
结论15、点M 平分PQ
结论162PF =。
