抛物线的焦点弦-经典性质及其证明过程
(完整版)抛物线的性质归纳及证明
抛物线的常见性质及证明概念焦半径：抛物线上一点与其焦点的连线段；焦点弦：两端点在抛物线上且经过抛物线的焦点线段称为焦点弦.性质及证明过抛物线y 2＝2px （p ＞0）焦点F 的弦两端点为),(11y x A ,),(22y x B ,倾斜角为α,中点为C(x 0,y 0), 分别过A 、B 、C 作抛物线准线的垂线，垂足为A ’、B ’、C ’. 1.求证：①焦半径αcos 12||1-=+=p p x AF ；②焦半径αcos 12||2+=+=pp x BF ; ③1| AF |＋1| BF |＝2p ； ④弦长| AB |＝x 1＋x 2＋p =α2sin 2p ；特别地，当x 1=x 2(α=90︒)时，弦长|AB|最短，称为通径，长为2p ；⑤△AOB 的面积S △OAB ＝αsin 22p .证明：根据抛物线的定义，| AF |＝| AD |＝x 1＋p 2，| BF |＝| BC |＝x 2＋p2，| AB |＝| AF |＋| BF |＝x 1＋x 2＋p如图2，过A 、B 引x 轴的垂线AA 1、BB 1，垂足为 A 1、B 1，那么| RF |＝| AD |－| FA 1 |＝| AF |－| AF |cos θ， ∴| AF |＝| RF |1－cos θ＝p1－cos θ同理，| BF |＝| RF |1＋cos θ＝p1＋cos θ∴| AB |＝| AF |＋| BF |＝p 1－cos θ＋p 1＋cos θ＝2psin 2θ.S △OAB ＝S △OAF ＋S △OBF ＝12| OF || y 1 |＋12| OF || y 1 |＝12·p2·(| y 1|＋| y 1 |)∵y 1y 2＝－p 2，则y 1、y 2异号，因此，| y 1 |＋| y 1 |＝| y 1－y 2 |∴S △OAB ＝p 4| y 1－y 2 |＝p 4(y 1＋y 2)2－4y 1y 2＝p 44m 2p 2＋4p 2＝p 221＋m 2＝p 22sin θ.2.求证：①2124p x x =；②212y y p =-；③ 1| AF |＋1| BF |＝2p .当AB ⊥x 轴时，有 AF BF p ==，成立； 当AB 与x 轴不垂直时，设焦点弦AB 的方程为：2p y k x ⎛⎫=-⎪⎝⎭.代入抛物线方程： 2222p k x px ⎛⎫-= ⎪⎝⎭.化简得：()()222222014p k x p k x k -++=∵方程（1）之二根为x 1，x 2，∴1224k x x ⋅=.(122111212111111222x x p p pp AF BF AA BB x x x x +++=+=+=+++()()121222121222424x x p x x p p p p p p x x p x x ++++===+++++. 3.求证：=∠=∠'''FB A B AC Rt ∠.先证明：∠AMB ＝Rt ∠【证法一】延长AM 交BC 的延长线于E ，如图3，则△ADM ≌△ECM ，∴| AM |＝| EM |，| EC |＝| AD | ∴| BE |＝| BC |＋| CE |＝| BC |＋| AD | ＝| BF |＋| AF |＝| AB |∴△ABE 为等腰三角形，又M 是AE 的中点， ∴BM ⊥AE ，即∠AMB ＝Rt ∠ 【证法二】取AB 的中点N ，连结MN ，则| MN |＝12(| AD |＋| BC |)＝12(| AF |＋| BF |)＝12| AB |，∴| MN |＝| AN |＝| BN |∴△ABM 为直角三角形，AB 为斜边，故∠AMB ＝Rt ∠.【证法三】由已知得C (－p 2，y 2)、D (－p 2，y 1)，由此得M (－p 2，y 1＋y 22).∴k AM ＝y 1－y 1＋y 22x 1＋p 2＝y 1－y 22·y 212p ＋p ＝p (y 1－y 2)y 21＋p 2＝p (y 1－－p 2y 1)y 21＋p 2＝p y 1，同理k BM ＝py 2 ∴k AM ·k BM ＝p y 1·p y 2＝p 2y 1y 2＝p 2－p 2＝－1∴BM ⊥AE ，即∠AMB ＝Rt ∠.【证法四】由已知得C (－p 2，y 2)、D (－p2，y 1)，由此得M (－p 2，y 1＋y 22). ∴MA →＝(x 1＋p 2，y 1－y 22)，MB →＝(x 3＋p 2，y 2－y 12)∴MA →·MB →＝(x 1＋p 2)(x 2＋p 2)＋(y 1－y 2)(y 2－y 1)4＝x 1x 2＋p 2(x 1＋x 2)＋p 24－(y 1－y 2)24＝p 24＋p 2(y 212p ＋y 222p )＋p 24－y 21＋y 22－2y 1y 24＝p 22＋y 1y 22＝p 22＋－p 22＝0 ∴MA →⊥MB →，故∠AMB ＝Rt ∠.【证法五】由下面证得∠DFC ＝90 ，连结FM ，则FM ＝DM .又AD ＝AF ，故△ADM ≌△AFM ，如图4 ∴∠1＝∠2，同理∠3＝∠4∴∠2＋∠3＝12×180︒＝90︒∴∠AMB ＝Rt ∠. 接着证明：∠DFC ＝Rt ∠【证法一】如图5，由于| AD |＝| AF |，AD ∥RF ，故可设∠AFD ＝∠ADF ＝∠DFR ＝α， 同理，设∠BFC ＝∠BCF ＝∠CFR ＝β， 而∠AFD ＋∠DFR ＋∠BFC ＋∠CFR ＝180︒ ∴2(α＋β)＝180︒，即α＋β＝90︒，故∠DFC ＝90︒ 【证法二】取CD 的中点M ，即M (－p 2，y 1＋y 22)由前知k AM ＝py 1，k CF ＝－y 2＋p 2＋p 2＝－y 2p ＝p y 1∴k AM ＝k CF ，AM ∥CF ，同理，BM ∥DF ∴∠DFC ＝∠AMB ＝90︒.【证法三】∵DF →＝(p ，－y 1)，CF →＝(p ，－y 2)，∴DF →·CF →＝p 2＋y 1y 2＝0 ∴DF →⊥CF →，故∠DFC ＝90︒.【证法四】由于| RF |2＝p 2＝－y 1y 2＝| DR |·| RC |，即| DR || RF |＝| RF || RC |，且∠DRF ＝∠FRC ＝90︒ ∴ △DRF ∽△FRC∴∠DFR ＝∠RCF ，而∠RCF ＋∠RFC ＝90︒ ∴∠DFR ＋∠RFC ＝90︒ ∴∠DFC ＝90︒4. C ’A 、C ’B 是抛物线的切线【证法一】∵k AM ＝p y 1，AM 的直线方程为y －y 1＝p y 1(x －y 212p)图6与抛物线方程y 2＝2px 联立消去x 得y －y 1＝p y 1(y 22p －y 212p)，整理得y 2－2y 1y ＋y 21＝0可见△＝(2y 1)2－4y 21＝0，故直线AM 与抛物线y 2＝2px 相切， 同理BM 也是抛物线的切线，如图8.【证法二】由抛物线方程y 2＝2px ，两边对x 求导，(y 2)'x＝(2px )'x ， 得2y ·y 'x＝2p ，y 'x ＝py，故抛物线y 2＝2px 在点A (x 1，y 1)处的切线的斜率为k 切＝y 'x | y ＝y 1＝p y 1. 又k AM ＝py 1，∴k 切＝k AM ，即AM 是抛物线在点A 处的切线，同理BM 也是抛物线的切线.【证法三】∵过点A (x 1，y 1)的切线方程为y 1y ＝p (x ＋x 1)，把M (－p 2，y 1＋y 22)代入左边＝y 1·y 1＋y 22＝y 21＋y 1y 22＝2px 1－p 22＝px 1－p 22，右边＝p (－p 2＋x 1)＝－p 22＋px 1，左边＝右边，可见，过点A 的切线经过点M ，即AM 是抛物线的切线，同理BM 也是抛物线的切线.5. C ’A 、C ’B 分别是∠A ’AB 和∠B ’BA 的平分线. 【证法一】延长AM 交BC 的延长线于E ，如图9，则△ADM ≌△ECM ，有AD ∥BC ，AB ＝BE ， ∴∠DAM ＝∠AEB ＝∠BAM ，即AM 平分∠DAB ，同理BM 平分∠CBA . 【证法二】由图9可知只须证明直线AB 的倾斜角α是直线AM 的倾斜角β的2倍即可，即α＝2β. 且M (－p 2，y 1＋y 22)图9∵tan α＝k AB ＝y 2－y 1x 2－x 1＝y 2－y 1 y 222p －y 212p＝2py 1＋y 2. tan β＝k AM ＝y 1－y 1＋y 22x 1＋p 2＝y 1－y 22·y 212p ＋p ＝p (y 1－y 2)y 21＋p 2＝p (y 1－－p 2y 1)y 21＋p 2＝py 1. ∴tan 2β＝2tan β1－tan 2β＝2py 11－(p y 1)2＝2py 1y 22－p 2＝2py 1y 22＋y 1y 2＝2py 1＋y 2＝tan α ∴α＝2β，即AM 平分∠DAB ，同理BM 平分∠CBA .6. AC ’、A ’F 、y 轴三线共点，BC ’、B ’F 、y 轴三线共点 【证法一】如图10，设AM 与DF 相交于点G 1，由以上证明知| AD |＝| AF |，AM 平分∠DAF ，故AG 1也是DF 边上的中线， ∴G 1是DF 的中点.设AD 与y 轴交于点D 1，DF 与y 轴相交于点G 2， 易知，| DD 1 |＝| OF |，DD 1∥OF ， 故△DD 1G 2≌△FOG 2∴| DG 2 |＝| FG 2 |，则G 2也是DF 的中点.∴G 1与G 2重合（设为点G ），则AM 、DF 、y 轴三线共点，同理BM 、CF 、y 轴也三线共点.【证法二】AM 的直线方程为y －y 1＝p y 1(x －y 212p)，令x ＝0得AM 与y 轴交于点G 1(0，y 12)，又DF 的直线方程为y ＝－y 1p (x －p 2)，令x ＝0得DF 与y 轴交于点G 2(0，y 12)∴AM 、DF 与y 轴的相交同一点G (0，y 12)，则AM 、DF 、y 轴三线共点，同理BM 、CF 、y 轴也三线共点H ．由以上证明还可以得四边形MHFG 是矩形.图107. A 、O 、B ’三点共线，B 、O 、A ’三点共线. 【证法一】如图11，k OA ＝y 1x 1＝y 1 y 212p＝2py 1，k OC ＝y 2 －p 2 ＝－2y 2p ＝－2py 2p 2＝－2py 2－y 1y 2＝2p y 1∴k OA ＝k OC ，则A 、O 、C 三点共线， 同理D 、O 、B 三点也共线.【证法二】设AC 与x 轴交于点O '，∵AD ∥RF ∥BC∴| RO ' || AD |＝| CO ' || CA |＝| BF || AB |，| O 'F || AF |＝| CB || AB |， 又| AD |＝| AF |，| BC |＝| BF |，∴| RO ' || AF |＝| O 'F || AF |∴| RO ' |＝| O 'F |，则O '与O 重合，即C 、O 、A 三点共线，同理D 、O 、B 三点也共线.【证法三】设AC 与x 轴交于点O '，RF ∥BC ，| O 'F || CB |＝| AF || AB |，∴| O 'F |＝| CB |·| AF || AB |＝| BF |·| AF || AF |＋| BF |＝1 1| AF |＋1| BF |＝p2【见⑵证】∴O '与O 重合，则即C 、O 、A 三点共线，同理D 、O 、B 三点也共线. 【证法四】∵OC →＝(－p 2，y 2)，OA →＝(x 1，y 1)，∵－p 2·y 1－x 1 y 2＝－p 2·y 1－y 212p y 2＝－py 12－y 1y 2y 12p ＝－py 12＋p 2y 12p ＝0∴OC →∥OA →，且都以O 为端点∴A 、O 、C 三点共线，同理B 、O 、D 三点共线.【推广】过定点P (m ，0)的直线与抛物线y 2＝2px （p ＞0）相交于点A 、B ，过A 、B 两点分别作直线l ：x ＝－m 的垂线，垂足分别为M 、N ，则A 、O 、N 三点共线，B 、O 、M 三点也共线，如下图：图118. 若| AF |：| BF |＝m ：n ，点A 在第一象限，θ为直线AB 的倾斜角. 则cos θ＝m －nm ＋n ；【证明】如图14，过A 、B 分别作准线l 的垂线，垂足分别为D ，C ，过B 作BE ⊥AD于E ，设| AF |＝mt ，| AF |＝nt ，则| AD |＝| AF |，| BC |＝| BF |，| AE |＝| AD |－| BC |＝(m －n )t ∴在Rt △ABE 中，cos ∠BAE ＝| AE || AB |＝ (m －n )t (m ＋n )t ＝m －nm ＋n∴cos θ＝cos ∠BAE ＝m －nm ＋n.【例6】设经过抛物线y 2＝2px 的焦点F 的直线与抛物线相交于两点A 、B ，且| AF |：| BF |＝3：1，则直线AB 的倾斜角的大小为 .则E 的坐标为( p2＋x 1 2，y 12)，则点E 到y 轴的距离为d ＝ p2＋x 1 2＝12| AF |故以AF 为直径的圆与y 轴相切， 同理以BF 为直径的圆与y 轴相切.【说明】如图15，设M 是AB 的中点，作MN ⊥准线l 于N ，则| MN |＝12(| AD |＋| BC |)＝12(| AF |＋| BF |)＝12| AB |则圆心M 到l 的距离| MN |＝12| AB |，故以AB 为直径的圆与准线相切. 10. MN 交抛物线于点Q ，则Q 是MN 的中点.【证明】设A (y 212p ，y 1)，B (y 222p ，y 1)，则C (－p 2，y 2)，D (－p 2，y 1)，M (－p 2，y 1＋y 22)，N (y 21＋y 224p ，y 1＋y 22)，设MN 的中点为Q '，则Q ' ( －p 2＋y 21＋y 224p 2，y 1＋y 22)∵ －p 2＋y 21＋y 224p 2＝ －2p 2＋y 21＋y 22 8p ＝ 2y 1y 2＋y 21＋y 228p ＝ ⎝⎛⎭⎫y 1＋y 222 2p∴点Q ' 在抛物线y 2＝2px 上，即Q 是MN 的中点.图16。
抛物线的性质归纳及证明
抛物线的常见性质及证明概念焦半径：抛物线上一点与其焦点的连线段；焦点弦：两端点在抛物线上且经过抛物线的焦点线段称为焦点弦.性质及证明过抛物线y 2＝2px （p ＞0）焦点F 的弦两端点为),(11y x A ,),(22y x B ,倾斜角为α,中点为C(x 0,y 0), 分别过A 、B 、C 作抛物线准线的垂线，垂足为A ’、B ’、C ’. 1.求证：①焦半径αcos 12||1-=+=p p x AF ；②焦半径αcos 12||2+=+=pp x BF ; ③1| AF |＋1| BF |＝2p ； ④弦长| AB |＝x 1＋x 2＋p =α2sin 2p ；特别地，当x 1=x 2(α=90)时，弦长|AB|最短，称为通径，长为2p ；⑤△AOB 的面积S △OAB＝αsin 22p . 证明：根据抛物线的定义，| AF |＝| AD |＝x 1＋p 2，| BF |＝| BC |＝x 2＋p2，| AB |＝| AF |＋| BF |＝x 1＋x 2＋p如图2，过A 、B 引x 轴的垂线AA 1、BB 1，垂足为A 1、B 1，那么| RF |＝| AD |－| FA 1 |＝| AF |－| AF|cos，∴| AF |＝| RF |1－cos ＝p1－cos同理，| BF |＝| RF |1＋cos ＝p1＋cos∴| AB |＝| AF |＋| BF |＝p 1－cos ＋p 1＋cos ＝2psin2 .S △OAB ＝S △OAF ＋S △OBF ＝12| OF || y 1 |＋12| OF || y 1 |＝12·p2·(| y 1 |＋| y 1 |)CDB (x 2，y 2) R A (x 1，y 1)xy O θA 1B 1 F 图2∵y 1y 2＝－p 2，则y 1、y 2异号，因此，| y 1 |＋| y 1 |＝| y 1－y 2 | ∴S △OAB ＝p 4| y 1－y 2 |＝p4(y 1＋y 2)2－4y 1y 2＝p44m 2p 2＋4p 2＝p 221＋m 2＝p 22sin.2.求证：①2124p x x =；②212y y p =-；③ 1| AF |＋1| BF |＝2p .当AB ⊥x 轴时，有 AF BF p ==，成立； 当AB 与x 轴不垂直时，设焦点弦AB 的方程为：2p y k x ⎛⎫=-⎪⎝⎭.代入抛物线方程： 2222p k x px ⎛⎫-= ⎪⎝⎭.化简得：()()222222014p k x p k x k -++=∵方程（1）之二根为x 1，x 2，∴1224k x x ⋅=.()12111212121111112224x x p p pAF BF AA BB x x x x x x +++=+=+=+++++ ()()121222121222424x x p x x p p p p p p x x p x x ++++===+++++. 3.求证：=∠=∠'''FB A B AC Rt ∠.先证明：∠AMB ＝Rt ∠DRA (x 1，y 1)xyOF N M xy C'CB'A'BO FK A【证法一】延长AM 交BC 的延长线于E ，如图3，则△ADM ≌△ECM ，∴| AM |＝| EM |，| EC |＝| AD | ∴| BE |＝| BC |＋| CE |＝| BC |＋| AD | ＝| BF |＋| AF |＝| AB |∴△ABE 为等腰三角形，又M 是AE 的中点， ∴BM ⊥AE ，即∠AMB ＝Rt ∠ 【证法二】取AB 的中点N ，连结MN ，则| MN |＝12(| AD |＋| BC |)＝12(| AF |＋| BF |)＝12| AB |，∴| MN |＝| AN |＝|BN |∴△ABM 为直角三角形，AB 为斜边，故∠AMB ＝Rt ∠.【证法三】由已知得C (－p 2，y 2)、D (－p 2，y 1)，由此得M (－p 2，y 1＋y 22).∴k AM ＝y 1－y 1＋y 22x 1＋p2＝y 1－y 22·y 212p＋p ＝p (y 1－y 2)y 21＋p 2＝p (y 1－－p 2y 1)y 21＋p 2＝p y 1，同理k BM ＝py 2 ∴k AM ·k BM ＝p y 1·p y 2＝p 2y 1y 2＝p 2－p 2＝－1∴BM ⊥AE ，即∠AMB ＝Rt ∠.【证法四】由已知得C (－p 2，y 2)、D (－p 2，y 1)，由此得M (－p2，y 1＋y 22).∴MA →＝(x 1＋p 2，y 1－y 22)，MB →＝(x 3＋p 2，y 2－y 12)∴MA →·MB →＝(x 1＋p 2)(x 2＋p 2)＋(y 1－y 2)(y 2－y 1)4＝x 1x 2＋p 2(x 1＋x 2)＋p 24－(y 1－y 2)24＝p 24＋p 2(y 212p ＋y 222p )＋p 24－y 21＋y 22－2y 1y 24＝p 22＋y 1y 22＝p 22＋－p 22＝0 ∴MA →⊥MB →，故∠AMB ＝Rt ∠. 【证法五】由下面证得∠DFC ＝90，连结FM ，则FM ＝DM .又AD ＝AF ，故△ADM ≌△AFM ，如图4 ∴∠1＝∠2，同理∠3＝∠4 ∴∠2＋∠3＝12×180＝90∴∠AMB ＝Rt ∠. 接着证明：∠DFC ＝Rt ∠【证法一】如图5，由于| AD |＝| AF |，AD ∥RF ，故可设∠AFD ＝∠ADF ＝∠DFR ＝， 同理，设∠BFC ＝∠BCF ＝∠CFR ＝， 而∠AFD ＋∠DFR ＋∠BFC ＋∠CFR ＝180∴2(＋)＝180，即＋＝90，故∠DFC ＝90【证法二】取CD 的中点M ，即M (－p 2，y 1＋y 22)图5CDB (x 2，y 2)R A (x 1，y 1)xyOF ( p 2，0)CDB (x 2，y 2)R A (x 1，y 1)xy O FM G H D 1由前知k AM ＝p y 1，k CF ＝－y 2＋p 2＋p2＝－y 2p＝p y 1∴k AM ＝k CF ，AM ∥CF ，同理，BM ∥DF ∴∠DFC ＝∠AMB ＝90.【证法三】∵DF →＝(p ，－y 1)，CF →＝(p ，－y 2)，∴DF →·CF →＝p 2＋y 1y 2＝0 ∴DF →⊥CF →，故∠DFC ＝90.【证法四】由于| RF |2＝p 2＝－y 1y 2＝| DR |·| RC |，即| DR || RF |＝| RF || RC |，且∠DRF ＝∠FRC ＝90∴ △DRF ∽△FRC∴∠DFR ＝∠RCF ，而∠RCF ＋∠RFC ＝90∴∠DFR ＋∠RFC ＝90∴∠DFC ＝904. C ’A 、C ’B 是抛物线的切线【证法一】∵k AM ＝p y 1，AM 的直线方程为y －y 1＝p y 1(x －y 212p)与抛物线方程y 2＝2px 联立消去x 得y －y 1＝p y 1(y 22p －y 212p)，整理得y 2－2y 1y ＋y 21＝0 可见△＝(2y 1)2－4y 21＝0，故直线AM 与抛物线y 2＝2px 相切， 同理BM 也是抛物线的切线，如图8.【证法二】由抛物线方程y 2＝2px ，两边对x 求导，(y 2)x ＝(2px )x ，N 1N MxyOF图7M 1l CDB (x 2，y 2)R A (x 1，y 1)xy OFM 图8D 1得2y ·y x ＝2p ，y x ＝py，故抛物线y 2＝2px 在点A (x 1，y 1)处的切线的斜率为k 切＝yx| y ＝y 1＝p y 1.又k AM ＝py 1，∴k 切＝k AM ，即AM 是抛物线在点A 处的切线，同理BM 也是抛物线的切线.【证法三】∵过点A (x 1，y 1)的切线方程为y 1y ＝p (x ＋x 1)，把M (－p 2，y 1＋y 22)代入左边＝y 1·y 1＋y 22＝y 21＋y 1y 22＝2px 1－p 22＝px 1－p 22，右边＝p (－p 2＋x 1)＝－p 22＋px 1，左边＝右边，可见，过点A 的切线经过点M ，即AM 是抛物线的切线，同理BM 也是抛物线的切线.5. C ’A 、C ’B 分别是∠A ’AB 和∠B ’BA 的平分线.【证法一】延长AM 交BC 的延长线于E ，如图9，则△ADM ≌△ECM ，有AD ∥BC ，AB ＝BE ， ∴∠DAM ＝∠AEB ＝∠BAM ，即AM 平分∠DAB ，同理BM 平分∠CBA . 【证法二】由图9可知只须证明直线AB 的倾斜角是直线AM 的倾斜角的2倍即可，即＝2. 且M (－p 2，y 1＋y 22)CDB (x 2，y 2) R A (x 1，y 1)xyO FNM图9∵tan ＝k AB ＝y 2－y 1x 2－x 1＝y 2－y 1 y 222p －y 212p ＝2py 1＋y 2. tan ＝k AM ＝y 1－y 1＋y 22x 1＋p2＝y 1－y 22·y 212p＋p ＝p (y 1－y 2)y 21＋p 2＝p (y 1－－p 2y 1)y 21＋p 2＝py 1. ∴tan 2＝2tan1－tan 2＝2py 11－(p y 1)2＝2py 1y 22－p 2＝2py 1y 22＋y 1y 2＝2py 1＋y 2＝tan∴＝2，即AM 平分∠DAB ，同理BM 平分∠CBA .6. AC ’、A ’F 、y 轴三线共点，BC ’、B ’F 、y 轴三线共点 【证法一】如图10，设AM 与DF 相交于点G 1，由以上证明知| AD |＝| AF |，AM 平分∠DAF ，故AG 1也是DF 边上的中线， ∴G 1是DF 的中点.设AD 与y 轴交于点D 1，DF 与y 轴相交于点G 2， 易知，| DD 1 |＝| OF |，DD 1∥OF ， 故△DD 1G 2≌△FOG 2∴| DG 2 |＝| FG 2 |，则G 2也是DF 的中点. ∴G 1与G 2重合（设为点G ），则AM 、DF 、y 轴三线共点，同理BM 、CF 、y 轴也三线共点.【证法二】AM 的直线方程为y －y 1＝p y 1(x －y 212p)，令x ＝0得AM 与y 轴交于点G 1(0，y 12)，又DF 的直线方程为y ＝－y 1p (x －p 2)，令x ＝0得DF 与y 轴交于点G 2(0，y 12)CDB (x 2，y 2)R A (x 1，y 1)xy O FM 图10G H D 1∴AM 、DF 与y 轴的相交同一点G (0，y 12)，则AM 、DF 、y 轴三线共点，同理BM 、CF 、y 轴也三线共点H ．由以上证明还可以得四边形MHFG 是矩形. 7. A 、O 、B ’三点共线，B 、O 、A ’三点共线.【证法一】如图11，k OA ＝y 1x 1＝y 1 y 212p＝2py 1，k OC ＝y 2 －p 2＝－2y 2p ＝－2py 2p 2＝－2py 2－y 1y 2＝2p y 1∴k OA ＝k OC ，则A 、O 、C 三点共线， 同理D 、O 、B 三点也共线. 【证法二】设AC 与x 轴交于点O，∵AD ∥RF ∥BC∴| RO || AD |＝| CO || CA |＝| BF || AB |，| O F || AF |＝| CB || AB |，又| AD |＝| AF |，| BC |＝| BF |，∴| RO || AF |＝| O F || AF |∴| RO|＝| OF |，则O 与O 重合，即C 、O 、A 三点共线，同理D 、O 、B 三点也共线.【证法三】设AC 与x 轴交于点O，RF ∥BC ，| O F || CB |＝| AF || AB |，∴| O F |＝| CB |·| AF || AB |＝| BF |·| AF || AF |＋| BF |＝1 1| AF |＋1| BF |＝p2【见⑵证】∴O 与O 重合，则即C 、O 、A 三点共线，同理D 、O 、B 三点也共线.【证法四】∵OC →＝(－p 2，y 2)，OA →＝(x 1，y 1)，CDB (x 2，y 2)R A (x 1，y 1)xy OF 图11∵－p2·y 1－x 1 y 2＝－p2·y 1－y 212p y 2＝－py 12－y 1y 2y 12p ＝－py 12＋p 2y 12p＝0∴OC →∥OA →，且都以O 为端点∴A 、O 、C 三点共线，同理B 、O 、D 三点共线.【推广】过定点P (m ，0)的直线与抛物线y 2＝2px （p ＞0）相交于点A 、B ，过A 、B 两点分别作直线l ：x ＝－m 的垂线，垂足分别为M 、N ，则A 、O 、N 三点共线，B 、O 、M 三点也共线，如下图：OyNMBAPx Oy NM BAP x8. 若| AF |：| BF |＝m ：n ，点A 在第一象限，为直线AB 的倾斜角. 则cos＝m －n m ＋n； 【证明】如图14，过A 、B 分别作准线l 的垂线，垂足分别为D ，C ，过B 作BE ⊥AD于E ，设| AF |＝mt ，| AF |＝nt ，则| AD |＝| AF |，| BC |＝| BF |，| AE |＝| AD |－| BC |＝(m －n )t∴在Rt △ABE 中，cos ∠BAE ＝| AE || AB |＝ (m －n )t (m ＋n )t ＝m －nm ＋n∴cos＝cos ∠BAE ＝m －nm ＋n.【例6】设经过抛物线y 2＝2px 的焦点F 的直线与抛物线相交于两点A 、B ，且| AF |：| BF |＝3：1，则直线AB 的倾斜角的大小为 . 【答案】60或120.C DB R Axy OEF 图14l则E 的坐标为( p2＋x 12，y 12)，则点E 到y 轴的距离为d ＝ p2＋x 12＝12| AF |故以AF 为直径的圆与y 轴相切， 同理以BF 为直径的圆与y 轴相切.【说明】如图15，设M 是AB 的中点，作MN ⊥准线l 于N ，则| MN |＝12(| AD |＋| BC |)＝12(| AF |＋| BF |)＝12| AB |则圆心M 到l 的距离| MN |＝12| AB |，故以AB 为直径的圆与准线相切. 10. MN 交抛物线于点Q ，则Q 是MN 的中点.【证明】设A (y 212p ，y 1)，B (y 222p ，y 1)，则C (－p 2，y 2)，D (－p 2，y 1)，图16xy M'A'MOFAxy C'CB'A'BO FK Axy C'CB'A'BO FK A精品----精品 M (－p 2，y 1＋y 22)，N (y 21＋y 224p ，y 1＋y 22)， 设MN 的中点为Q ，则Q ( －p 2＋y 21＋y 224p 2，y 1＋y 22)∵ －p 2＋y 21＋y 224p 2＝ －2p 2＋y 21＋y 22 8p ＝ 2y 1y 2＋y 21＋y 22 8p ＝ ⎝ ⎛⎭⎪⎫y 1＋y 222 2p∴点Q 在抛物线y 2＝2px 上，即Q 是MN 的中点.。
抛物线焦点弦性质及推导过程
抛物线焦点弦性质及推导过程抛物线是一种二次曲线，具有许多重要的性质。
其中一个重要的性质是焦点弦性质。
接下来，我将介绍焦点弦性质的定义、推导过程以及将该性质应用于实际问题的例子。
1.焦点弦性质的定义：考虑一个抛物线和其焦点上的两个点A和B，连接AB，然后过抛物线上的其他点C，将CA和CB分别延长，与抛物线相交于D和E。
焦点弦性质指出，点D和E的中点M一定位于直线AB上。
2.推导过程：首先，我们需要了解抛物线的标准方程是什么。
假设抛物线的焦点位于原点上方，其焦半径为p。
那么，抛物线的标准方程为y² = 4px。
接下来，设焦点F的坐标为 (0, p)，则点A的坐标为 (a, 2ap)，点B的坐标为 (-a, 2ap)。
由于点C(x,y)位于抛物线上，我们可以将其坐标带入抛物线的方程中得到：y² = 4px(x,y)²=4p(x,y)x² + y² = 4px我们知道直线CA的方程为 y - 2ap = (x - a)(2ap - a)。
以此类推，直线CB的方程为 y - 2ap = (x + a)(2ap + a)。
将以上两个直线方程与抛物线方程联立，我们可以求出点D和点E的坐标。
设点D的坐标为(x₁,y₁)和点E的坐标为(x₂,y₂)。
即有：x₁² + y₁² = 4px₁x₂² + y₂² = 4px₂求解出x₁和x₂，我们可以得到点D和点E的坐标。
然后，我们将点D和点E的坐标带入直线AB的方程中：y - 2ap = (x - a)(2ap - a)y - 2ap = (x + a)(2ap + a)联立以上两个方程，我们可以求解出直线AB的方程。
最后，我们求出点M的坐标，并将其带入直线AB的方程中：y - 2ap = (x - a)(2ap - a)若点M的坐标满足该方程，则说明点M位于直线AB上，证明了焦点弦性质。
抛物线焦点弦的八大结论推导过程
抛物线焦点弦的八大结论推导过程抛物线焦点弦是一个重要研究课题，它可以帮助我们理解抛物线的切线、焦点、双曲线、点到弦距离等微积分概念。
抛物线焦点弦推导过程通常被认为是一个好方向，它具有很多有益的特点，例如微积分知识的运用。
该过程包括以下步骤：一、首先，要确定抛物线的方程，它可以是一元二次方程，也可以是一般的双曲线方程。
二、然后，求解出抛物线的焦点和弦长，可以利用不同的函数求解方法来求解，或者可以利用几何的推导原理。
三、然后，可以运用微积分来求解抛物线的切线，可以利用极限的方法来求解抛物线的切线，同时也可以利用微分形式来求解抛物线的切线。
四、然后，可以利用数学分析的方法，用一元二次型或者双曲线型去绘制抛物线的切线，来求解抛物线焦点弦。
五、接着可以利用微积分中的定义来计算抛物线焦点弦的弧长，可以利用定积分的方法来计算抛物线弦的长度。
六、然后，利用向量的知识来求解抛物线焦点弦的方向，即利用向量的几何性质，推导出抛物线焦点弦的方向。
七、最后，可以利用抛物线焦点弦的方向和弦长，来进一步检验焦点弦是否符合抛物线的法则。
八、完成全部推导后，可以得到抛物线焦点弦的八个结论：1）抛物线的焦点和弦长可以用一元二次方程或者双曲线函数来求解。
2）抛物线的切线可以通过极限的方法和微分来求解。
3）焦点弦的长度可以通过定积分的方法来求解。
4）焦点弦的方向可以通过向量的几何性质来求解。
5）焦点弦的长度与抛物线的焦点和切线总是垂直。
6）距离抛物线在不同点上的距离是固定的，与抛物线的焦点和弦长相关。
7）抛物线在每个焦点点处均有弦，其长度总是相等的。
8）抛物线的弦长和焦点会满足正弦和余弦函数方程的要求。
(完整版)抛物线的焦点弦_经典性质及其证明过程
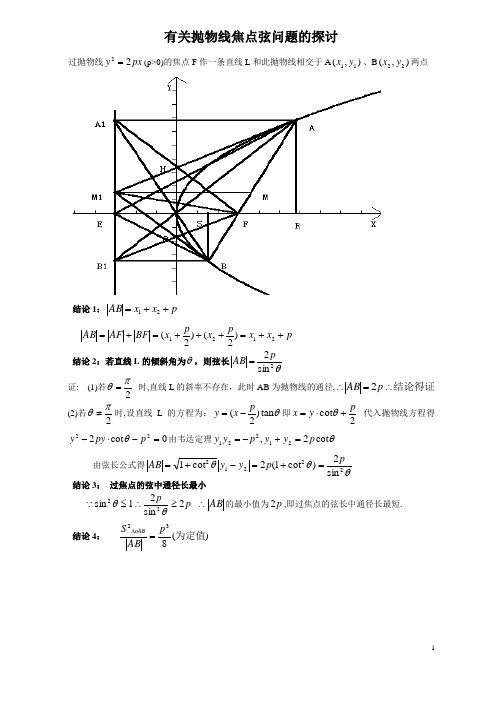
有关抛物线焦点弦问题的探讨过抛物线px y 22=(p>0)的焦点F 作一条直线L 和此抛物线相交于A ),(11y x 、B ),(22y x 两点结论1：p x x AB ++=21p x x px p x BF AF AB ++=+++=+=2121)2()2( 结论2：若直线L 的倾斜角为θ，则弦长θ2sin 2pAB =证: (1)若2πθ= 时,直线L 的斜率不存在，此时AB 为抛物线的通径,结论得证∴=∴p AB 2(2)若2πθ≠时,设直线L 的方程为：θtan )2(p x y -=即2cot py x +⋅=θ 代入抛物线方程得0cot 222=-⋅-p py y θ由韦达定理θcot 2,21221p y y p y y =+-=由弦长公式得θθθ22212sin 2)cot 1(2cot1pp y y AB =+=-+= 结论3： 过焦点的弦中通径长最小p p2sin 21sin 22≥∴≤θθ ∴AB 的最小值为p 2,即过焦点的弦长中通径长最短. 结论4： )(832为定值p AB S oAB =∆()8sin 2sin sin 2221sin 21sin 21sin 21sin 2132220P AB S p p p AB OF BF AF OF AF OF BF OF S S S OAB AF OBF OAB =∴=⋅⋅⋅=⋅⋅=+⋅=⋅⋅+⋅⋅=+=∆∆∆∆θθθθθϑθ结论5： (1) 221p y y -= (2) x 1x 2=42p证44)(,2,22222121222211P Py y x x p y x p y x ==∴== 结论6：以AB 为直径的圆与抛物线的准线相切证：设M 为AB 的中点，过A 点作准线的垂线AA 1， 过B 点作准线的垂线BB 1， 过M 点作准线的垂线MM 1，由梯形的中位线性质和抛物线的定义知 222111AB BFAF BB AA MM =+=+=故结论得证结论7：连接A 1F 、B 1 F 则 A 1F ⊥B 1FFA A FO A FO A F AA OF AA AFA F AA AF AA 11111111//,∠=∠∴∠=∠∴∠=∠∴=同理︒=∠∴∠=∠901111FB A FB B FO B ∴A 1F ⊥B 1 F 结论8：（1）AM 1⊥BM 1 （2）M 1F ⊥AB （3）BF AF FM ⋅=21（4）设AM 1 与A 1F 相交于H ，M 1B 与 FB 1相交于Q 则M 1，Q ，F ，H 四点共圆 （5）2121214M M B M AM =+证：由结论（6）知M 1 在以AB 为直径的圆上∴ AM 1⊥BM 111FB A ∆为直角三角形， M 1 是斜边A 1 B 1 的中点111111111AFA F AA F A M FA M F M M A ∠=∠∠=∠∴=∴︒=∠=∠+∠9011111M AA M FA F AA ︒=∠+∠∴90111FM A AFA∴M 1F ⊥ABBF AF F M ⋅=∴21 AM 1⊥BM 1 F B F A 90111⊥︒=∠∴ 又B AM︒=∠∴90FB A 11 所以M 1，Q ，F,H 四点共圆，22121AB B M AM =+()()()2121211242MM MM BB AABFAF ==+=+=结论9： （1）、A O 、B 1 三点共线 （2）B ，O ，A 1 三点共线（3）设直线AO 与抛物线的准线的交点为B 1，则BB 1平行于X 轴（4）设直线BO 与抛物线的准线的交点为A 1，则AA 1平行于X 轴证：因为p y p y k y p p y y x y k oB oA 2212111122,221-=-====，而221p y y -=所以122222oB oA k p y y ppk =-=-=所以三点共线。
抛物线的焦点弦性质
法二：由题知AB不与x轴平行 p 设AB方程为x my ，（m R） 2 y 2 2 px p 2 p y 2 p (my ) 2 x my 2 y
即：y 2 pmy p 0
2 2
A
y1 y2 p （定值）
2
O
F B
1 当AB x轴时，
O B
F
x
20 AB斜率存在时设为k，（k 0）
2
y p 2 py 2 消元得y 2 （ p ）即y p2 0 k 2 k 2 2 2 y1 y1 p 2 y1 y2 - p ；x1 x2 2 p 2 p 4
p 则直线AB方程为y=k（x- ） 代入抛物线方程y2 2 px 2
1 同理， k
以代k得B(2pk2, -2pk) .
1 2 x p ( k ) 0 k2 y p( 1 k ) 0 k
1 1 2 k 2 (k ) 2 k k
2
x0 y0 2 ( ) 2 p p
即 y02 = px0-2p2，
2 px y1 2 px1 y1 y2 2 px 2 px1 y y y1 y1 y2 y1 y2 y1 y2 y1 y2
2 2 px 4 p 2 y1 2 px1 , y1 y2 4 p2 y y1 y2 y1 y2
2 p | y1 y2 | 4 p2
当且仅当|y1|=|y2|=2p时，等号成立.
例3. A、B是抛物线 y2 = 2px(p>0)上的两点，且OA⊥OB， (5)求O在AB上的射影M轨迹方程. y (5)法一：设M(x3, y3), 则 kOM 3 x3 x
抛物线焦点弦性质2
y A F B x
联想 : 在同样的条件下， 注意到 y1 y2 p 2 , 那么x1 x2 ________?
O 2 变题1 : 过抛物线y 2 px( p 0)焦点 F的直线， 交抛物线于点A( x1 , y1 )、
p B( x2 , y2 ), 则有x1 x2 . 4
顶点
焦半径
（0,0）
p x0 2
（0,0）
p x0 2
（0,0）
p y0 2
（0,0）
p y0 2
p ( y1 y2 )
焦点弦 的长度
p x1 x2
p ( x1 x2 )
p y1 y2
二、抛物线的焦点弦：
如图所示，弦AB过抛物线y 2 px( p 0)的焦点F，
y12 2 px1 y1 y2 2 px1 2 px 2 px ∴ y ∴ y y1 y1 y2 y1 y2 y1 y2 y1 y2
2 px 4 p2 ∵ y12 2 px1 , y1 y2 4 p2 ∴ y y1 y2 y1 y2 2p ∴ y ( x 2 p) ∴ AB 过定点（2p,0）. y1 y2
p2 A、 4
B、 p 2
p2 C、－ 4
D、 p 2
思考题: 3、 、B 是抛物线 y 2 2 px( p 0) 上的两点,满足 A OA OB ( O 为坐标原点). 求证:⑴ A 、B 两点的横坐标之积,纵坐标之积分 别为定值; ⑵直线 AB 经过一个定点.
设 A（x1,y1） ，B（x2,y2） ，中点 P（x0,y0） y y ⑴ kOA 1 , kOB 2 ∵ OA⊥OB ∴ kOAkOB=-1∴ x1x2+y1y2=0 x1 x2
抛物线的焦点弦经典性质及其证明过程
抛物线的焦点弦经典性质及其证明过程抛物线所示的是具有经典性质的几何图形，其定义为一个特别的二次函数：当其焦点在原点上时，抛物线形式为y = ax2；当其焦点在非原点处时，抛物线形式为 y = a(x - h)\pt2 + k，其中h是抛物线的焦点的横坐标位置，k是焦点的纵坐标位置，a是抛物线的斜率系数。
抛物线具有许多经典性质，最为重要的是焦点弦性质，它是抛物线的几何和数学基础。
焦点弦的定义是连接抛物线上任意两点的直线都与焦点构成直角，或者说从焦点连接到抛物线上任意点都构成直角三角形。
证明抛物线经典性质焦点弦证明：抛物线具有经典性质焦点弦可以应用三角函数定理证明。
设点P(x,y)位于抛物线上，则有 y = a(x - h)² + k；设F为抛物线的焦点，则有 F (h,k) ；∠FPQ 为钝角，则有：tan∠FPQ = /FP/ \cos∠FPQ/PQ/即 /FP/\ G(x-h, y-k)/PQ/由已知：FP：((h - x), (k - y))PQ：((x' - x), (y' - y))可得：/(h-x)(y'-y)-(k-y)(x'-x)\tan∠FPQ = ----------------------/(x'-x)²+(y'-y)²\\式子两边同乘以(x'-x)²+(y’-y)²即 /(h-x)(y'-y)-(k-y)(x'-x)(x'-x)²+(y'-y)²\t an∠FPQ = ------------------------------------/ (x'-x)²+(y'-y)²)²\\即/(h-x)y'+(k-y)x'-(h-x)y-(k-y)x\tan∠FPQ = -----------------------------------/ (x'-x)²+(y'-y)²\\将已知带入即可得tan∠FPQ = 0即点F、P、Q三点构成的三角形为钝角，即证明了抛物线具有经典性质的焦点弦性质。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
有关抛物线焦点弦问题的探讨过抛物线px y 22=(p>0)的焦点F 作一条直线L 和此抛物线相交于A ),(11y x 、B ),(22y x 两点结论1：p x x AB ++=21p x x px p x BF AF AB ++=+++=+=2121)2()2( 结论2：若直线L 的倾斜角为θ，则弦长θ2sin 2pAB = 证: (1)若2πθ= 时,直线L 的斜率不存在，此时AB 为抛物线的通径,结论得证∴=∴p AB 2(2)若2πθ≠时,设直线L 的方程为：θtan )2(p x y -=即2cot py x +⋅=θ 代入抛物线方程得0cot 222=-⋅-p py y θ由韦达定理θcot 2,21221p y y p y y =+-=由弦长公式得θθθ22212sin 2)cot 1(2cot1pp y y AB =+=-+= 结论3： 过焦点的弦中通径长最小p p2sin 21sin 22≥∴≤θθΘ ∴AB 的最小值为p 2,即过焦点的弦长中通径长最短.结论4： )(832为定值p AB S oAB =∆()8sin 2sin sin 2221sin 21sin 21sin 21sin 2132220P AB S p p p AB OF BF AF OF AF OF BF OF S S S OAB AF OBF OAB =∴=⋅⋅⋅=⋅⋅=+⋅=⋅⋅+⋅⋅=+=∆∆∆∆θθθθθϑθ结论5： (1) 221p y y -= (2) x 1x 2=42p证44)(,2,22222121222211P P y y x x p y x p y x ==∴==Θ 结论6：以AB 为直径的圆与抛物线的准线相切证：设M 为AB 的中点，过A 点作准线的垂线AA 1， 过B 点作准线的垂线BB 1， 过M 点作准线的垂线MM 1，由梯形的中位线性质和抛物线的定义知 222111AB BFAF BB AA MM =+=+=故结论得证结论7：连接A 1F 、B 1 F 则 A 1F ⊥B 1FFA A FO A FO A F AA OF AA AFA F AA AF AA 11111111//,∠=∠∴∠=∠∴∠=∠∴=ΘΘ同理︒=∠∴∠=∠901111FB A FB B FO B ∴A 1F ⊥B 1 F 结论8：（1）AM 1⊥BM 1 （2）M 1F ⊥AB （3）BF AF FM ⋅=21（4）设AM 1 与A 1F 相交于H ，M 1B 与 FB 1相交于Q 则M 1，Q ，F ，H 四点共圆 （5）2121214M M B M AM =+证：由结论（6）知M 1 在以AB 为直径的圆上∴ AM 1⊥BM 1Θ11FB A ∆为直角三角形， M 1 是斜边A 1 B 1 的中点111111111AFA F AA F A M FA M F M M A ∠=∠∠=∠∴=∴Θ︒=∠=∠+∠9011111M AA M FA F AA Θ ︒=∠+∠∴90111FM A AFA∴M 1F ⊥ABBF AF F M ⋅=∴21 Θ AM 1⊥BM 1 F B F A 90111⊥︒=∠∴Θ又B AM︒=∠∴90FB A 11 所以M 1，Q ，F,H 四点共圆，22121AB B M AM =+()()()2121211242MM MM BB AABFAF ==+=+=结论9： （1）、A O 、B 1 三点共线 （2）B ，O ，A 1 三点共线（3）设直线AO 与抛物线的准线的交点为B 1，则BB 1平行于X 轴（4）设直线BO 与抛物线的准线的交点为A 1，则AA 1平行于X 轴证：因为p y p y k y p py y x y k oB oA 2212111122,221-=-====，而221p y y -=所以122222oB oA k p y y p pk =-=-=所以三点共线。
同理可征（2）（3）（4） 结论10：pFB FA 211=+ 证：过A 点作AR 垂直X 轴于点R ，过B 点作BS 垂直X 轴于点S ，设准线与x 轴交点为E,θ的倾斜角为因为直线L 则θθcos 1cos -=∴=+=+=PAF AF AF P FR EF ER P AF θcos 11-=∴ 同理可得P BF θcos 11+= ∴pFB FA 211=+ 结论11：证:AA B B EA E B A A FA B B BF FABF EA E B AA EF BB 1111111111,////=∴===∴ΘΘEB B EA A EB B 90111111∠∠∴∆∆∴︒=∠=∠＝相似于EA A E BB E AA ΘPEQEF BEF AEF 90EB B BEF EA A AEF 11∠∠∠∴︒∠∠∠∠平分角即＝＝＋＝＋Θ0K K X BE AE BEAE BFAF BE AE ＝＋轴对称关于和直线直线∴=∴Θ(4) 90AEB FB EF AF 2︒∠∴=＝＝＝时，当πθ2px y 2p -x k y L 2 2=⎪⎭⎫⎝⎛=≠将其代入方程的方程为时，设直线当πθ ()k2k p x x )y ,B(x ),y ,A(x 04p k 2)x p(k -x k 2221221122222+=+=++则设得 x 1x 2=4p 2假设122y 1K K BE AE 2211BE AE -=+⋅+∴⋅⊥p x y p x ＝－则AE BE AF AE(1)PEQ (2) (3) K K 0BF BE(4) AE BE , AE BE22EF ππθθ∠=+==⊥≠线段平分角当时当时不垂直于p21|CD |1|AB |1=+⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛∴⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=2p x 2p x -2p -x k 2p -x k 2p x 2p x -y y 21212121即()()()()()()()222222222212122121k 2p 01k 4p 1k x x 2p x x 1k k k k p -+=+∴=++-+-+∴结论得证假设错误不可能∴∴∴=-∴02结论12：过抛物线的焦点作两条互相垂直的弦AB 、CD ，则推广与深化：深化 1：性质5中，把弦AB 过焦点改为AB 过对称轴上一点E （a,0），则有pa 2y y 21-=．证：设AB 方程为my=x-a ，代入px 2y 2=．得：0ap 2pmy 2y 2=--，∴pa 2y y 21-=． 深化2： 性质12中的条件改为焦点弦AB 不垂直于x 轴，AB 的中垂线交x 轴于点R ，则21|AB ||FR |=证明：设AB 的倾斜角为a ，直线AB 的方程为：)2px (tga y -=， 代入px 2y 2=得：px 2)4p px x (a tg 222=+-，即：04p )a pctg 2p (x x 222=++-．由性质1得a sin p2a pctg 2p 2p x x |AB |2221=+=++=，又设AB 的中点为M ，则|a cos a pctg ||a cos 2p2x x ||FM |221=-+=， ∴a sin p |a cos a pctg ||a cos ||FM ||FE |222===， ∴21|AB ||FR |=．深化3：过抛物线的焦点F 作n 条弦n n 2211B A B A B A ⋯、、，且它们等分周角2π，则有（1）∑=⋅n1i i i |FB ||F A |1为定值； （2）∑=n1i i i |B A |1为定值．证明：（1）设抛物线方程为aFx A ,cos 1p1=∠θ-=λ．由题意π-+=∠⋯π+=∠π+=∠n 1n a Fx A n 2a Fx A ,n a Fx A n 32，所以222211p a sin p a cos 1p )a cos(1p a cos 1|FB ||F A |1=-=+π-⋅-=⋅， 同理22n n 2222p )n 1n a (sin |FB ||F A |1,,p )n a (sin |FB ||F A |1π-+=⋅⋯π+=⋅易知2n)n 1n a (sin )n 2a (sin )n a (sin a sin 2222=π-++⋯+π+π++， ∴222n1i 2222i i p 2n p )n 1n a (sin p )n a (sin p a sin |FB ||F A |1=π-++⋯+π++=⋅∑=．（2）∵a sin p2a cos 1p 2)a cos(1p a cos 1p |B A |2211=-=+π-+-=，∴p 2)n 1n a (sin |B A |1,,p 2a sin |B A |12n n 211π-+=⋯=，∴p 4n p 2)n 1n a (sin p 2)n a (sin p 2a sin |B A |12n1i 22i i =π-++⋯+π++=∑=．。