基于顺序栈实现的四则算术表达式计算
C++实例（表达式求值（栈的应用））
表达式求值： 设计⼀个程序实现输⼊⼀个表达式如3*(3+4)，以”#”结尾，求出其值。
分析： 先分析⼀下四则运算的规则： 1. 先乘除后加减； 2. 从左到右计算； 3. 先括号内后括号外； 于是我们要把运算符的优先级确定清楚。
这⾥我只⽤这⼏个运算符：+-*/()， 可以知道+-的优先级低于*/，⽽对于()，当第⼀次遇到’(‘时，’(‘后⾯的就优先计算，直到遇到’)’为⽌，可以先把’(’的优先级定为⽐其它⼏个都⾼，然后遇到’)’时把⾥⾯的先算出来，再算括号外⾯的，具体实现在代码中会表现得很清楚。
考试2⼤提⽰这个程序还是⽤栈来实现，具体代码如下。
代码： #include #include using namespace std; const int STACK_INIT_SIZE=100; //The maximize length of stack template class Stack //A class of stack { public: Stack() //Constructor function { base = new int[STACK_INIT_SIZE]; if (!base) { cerr< exit(-1); } top=base; stacksize=STACK_INIT_SIZE; } ~Stack() //Destructor function { if (base) delete[] base; } T GetTop() { if (top==base) { cerr< exit(-1); } return *(top-1); } void Push(T e) { if (top-base>=stacksize) { base=new int[STACK_INIT_SIZE]; if(!base) { cerr< exit(-1); } top=base+STACK_INIT_SIZE; stacksize+=STACK_INIT_SIZE; } *top++=e; } void Pop(T& e) { if (top==base) { cerr< exit(-1); } e=*--top; } private: int *base; int *top; int stacksize; }; string op("+-*/()#"); //The set of operator bool In(char c,string op) //Judge the character whether belong to the set of operator { string::iterator iter=op.begin(); for (;iter!=op.end();++iter) if (*iter==c) return true; return false; } char Precede(char top,char c) //Confirm the precedence of operator { int grade_top=0,grade_c=0; switch (top) { case '#':grade_top=0;break; case ')':grade_top=1;break; case '+':grade_top=2;break; case '-':grade_top=2;break; case '*':grade_top=3;break; case '/':grade_top=3;break; case '(':grade_top=4;break; } switch (c) { case '#':grade_c=0;break; case ')':grade_c=1;break; case '+':grade_c=2;break; case '-':grade_c=2;break; case '*':grade_c=3;break; case '/':grade_c=3;break; case '(':grade_c=4;break; } if (grade_top>=grade_c) { if (top=='('&&c!=')') return ' else if (top=='('&&c==')') return '='; return '>'; } else if (top=='#'&&c=='#') return '='; else return ' } int Operate(int a,char theta,int b) //Calculate { if (theta=='+') return a+b; else if (theta=='-') return a-b; else if (theta=='*') return a*b; else if (theta=='/') return a/b; return 0; } int EvaluateExpression(Stack& OPTR,Stack& OPND) { int a=0,b=0,n=0; char x; char theta; string c; cin>>c; OPTR.Push('#'); while (c[0]!='#'||OPTR.GetTop()!='#') { if (!In(c[0],op)){ n=atoi(&c[0]); OPND.Push(n); cin>>c; } else switch (Precede(OPTR.GetTop(),c[0])) { case ' OPTR.Push(c[0]); cin>>c; break; case '=': OPTR.Pop(x); cin>>c; break; case '>': OPTR.Pop(theta); OPND.Pop(b); OPND.Pop(a); OPND.Push(Operate(a,theta,b)); break; } } return OPND.GetTop(); } int main() { Stack OPTR; Stack OPND; cout< cout< return 0; }。
利用栈来实现算术表达式求值的算法
利用栈来实现算术表达式求值的算法利用栈来实现算术表达式求值的算法算术表达式是指按照一定规则组成的运算式，包含数字、运算符和括号。
在计算机中，求解算术表达式是一项基本的数学运算任务。
根据算术表达式的性质，我们可以考虑利用栈这一数据结构来实现求值算法。
一、算法思路首先，我们需要明确一个重要概念——逆波兰表达式（ReversePolish notation）。
逆波兰表达式是一种没有括号的算术表达式，其运算规则是先计算后面的数字和运算符，再计算前面的数字和运算符。
例如，对于算术表达式“3+4*5-6”，其对应的逆波兰表达式为“3 45 * +6 -”。
那么，我们可以利用栈来实现将中缀表达式转化为逆波兰表达式的过程，具体步骤如下：1. 创建两个栈——操作数栈和操作符栈。
2. 从左到右扫描中缀表达式的每一个数字和运算符，遇到数字则压入操作数栈中，遇到运算符则进行如下操作：（1）如果操作符栈为空或当前运算符的优先级大于栈顶运算符的优先级，则将当前运算符压入操作符栈中。
（2）如果当前运算符的优先级小于或等于栈顶运算符的优先级，则将栈顶运算符弹出并加入操作数栈中，重复此过程直到遇到优先级较低的运算符或操作符栈为空为止，然后将当前运算符压入操作符栈中。
3. 扫描完中缀表达式后，若操作符栈不为空，则将其中所有运算符弹出并加入操作数栈中。
4. 最终，操作数栈中存放的就是逆波兰表达式，我们可以按照逆波兰表达式的计算规则来计算其结果。
二、算法优点利用栈来实现算术表达式求值的算法具有以下优点：1. 代码简洁易懂，易于实现和维护。
2. 由于将中缀表达式转化为逆波兰表达式后，可以减少运算符的优先级关系而消除括号，从而减少求值的复杂度，提高程序的执行效率。
三、代码实现下面是利用栈来实现算术表达式求值的算法的Python代码实现：```pythonclass Stack:def __init__(self):self.items = []def push(self, item):self.items.append(item)def pop(self):return self.items.pop()def peek(self):return self.items[-1]def is_empty(self):return len(self.items) == 0def size(self):return len(self.items)def calculate(op_num1, op_num2, operator):if operator == "+":return op_num1 + op_num2elif operator == "-":return op_num1 - op_num2elif operator == "*":return op_num1 * op_num2elif operator == "/":return op_num1 / op_num2def infix_to_postfix(infix_expr):opstack = Stack()postfix_expr = []prec = {"+": 1, "-": 1, "*": 2, "/": 2, "(": 0} token_list = infix_expr.split()for token in token_list:if token.isdigit():postfix_expr.append(token)elif token == '(':opstack.push(token)elif token == ')':top_token = opstack.pop()while top_token != '(':postfix_expr.append(top_token)top_token = opstack.pop()else:while (not opstack.is_empty()) and(prec[opstack.peek()] >= prec[token]):postfix_expr.append(opstack.pop())opstack.push(token)while not opstack.is_empty():postfix_expr.append(opstack.pop())return " ".join(postfix_expr)def postfix_eval(postfix_expr):opstack = Stack()token_list = postfix_expr.split()for token in token_list:if token.isdigit():opstack.push(int(token))else:op_num2 = opstack.pop()op_num1 = opstack.pop()result = calculate(op_num1, op_num2, token) opstack.push(result)return opstack.pop()infix_expr = "3 + 4 * 5 - 6"postfix_expr = infix_to_postfix(infix_expr)print(postfix_expr)print(postfix_eval(postfix_expr))```四、总结算术表达式求值是一项常见的数学运算任务，利用栈这一数据结构来实现求值算法是一种简单有效的方法，它将中缀表达式转化为逆波兰表达式后，可以消除括号并减少运算符的优先级关系，从而提高程序的执行效率。
用堆栈实现四则运算c语言
用堆栈实现四则运算c语言堆栈是一种常见的数据结构，它符合先进后出的原则。
在四则运算中，我们可以借助堆栈这种数据结构实现运算，方便高效，不易出错。
堆栈的实现包括两个基本操作：Push（入栈）和Pop（出栈）。
我们可以以此设计四则运算。
首先，我们需要将输入的四则运算表达式转换成后缀表达式。
后缀表达式也叫逆波兰表达式，相对于中缀表达式而言，运算符在后面，操作数在前面，这样方便计算机进行读取和计算。
例如：中缀表达式：5+3*2后缀表达式：5 3 2 * +将中缀表达式转换成后缀表达式，我们需要用到堆栈。
具体的实现方法是，从左向右遍历表达式，如果是数字，则直接输出；如果是符号，则将其与堆栈顶的符号进行比较，如果优先级高就入栈，否则不断将符号出栈并输出，直到当前符号优先级大于堆栈顶符号优先级，最后将当前符号入栈。
例如：表达式：5+3*2堆栈操作：1.将5输出，堆栈为空2.遇到+号，入栈3.将3输出，堆栈顶为+号4.遇到*号，入栈5.将2输出，堆栈顶为*号6.输出*号，堆栈顶为+号7.输出+号，堆栈为空得到后缀表达式：5 3 2 * +有了后缀表达式，我们可以用堆栈进行计算。
具体方法是，从左向右遍历后缀表达式，如果是数字则入栈，如果是符号则将栈顶两个数字出栈并进行计算，将结果入栈，最终得到最终的计算结果。
例如：后缀表达式：5 3 2 * +堆栈操作：1.将5入栈2.将3入栈3.遇到*号，出栈3和2，进行计算得到6，将6入栈4.将栈顶元素5出栈5.遇到+号，出栈6和5，进行计算得到11，将11入栈得到计算结果：11通过堆栈实现四则运算，可以有效简化我们的计算流程，避免复杂的优先级判断和计算错误。
同时，堆栈为我们提供了一种更加高效的数据结构，不仅在四则运算中可以发挥作用，在其他应用中也很常见。
当然，在实际应用中，我们需要考虑到多种情况的处理，例如负数、小数、括号等，以及错误处理等细节问题，才能保证算法的正确性和可靠性。
双栈 四则运算
双栈四则运算
双栈四则运算系统是一个基于栈结构的计算器系统，用于处理四则运算。
这个系统包含两个栈：操作数栈和运算符栈。
操作数栈用于存储待计算的数字，运算符栈用于存储待执行的运算符号。
在双栈四则运算系统中，用户可以输入一串数字和运算符，系统会将数字压入操作数栈，将运算符压入运算符栈。
当用户按下等号时，系统会从操作数栈中弹出两个数字，从运算符栈中弹出运算符号，然后进行相应的运算，并将结果压入操作数栈。
双栈四则运算系统的核心算法包括以下步骤：
初始化两个空栈：操作数栈和运算符栈。
循环执行以下步骤，直到用户按下等号或退出程序：
读取用户输入的数字，并将其压入操作数栈。
读取用户输入的运算符，并将其压入运算符栈。
如果用户按下等号，则执行以下步骤：
弹出运算符栈中的运算符。
弹出操作数栈中的两个数字。
进行相应的运算，并将结果压入操作数栈。
如果用户没有按下等号，则继续等待用户输入。
程序结束。
需要注意的是，为了避免精度误差和溢出问题，双栈四则运算系统需要进行相应的处理。
例如，可以使用高精度算法来处理大数运算，或者使用浮点数运算来处理小数运算。
四则运算解析及计算
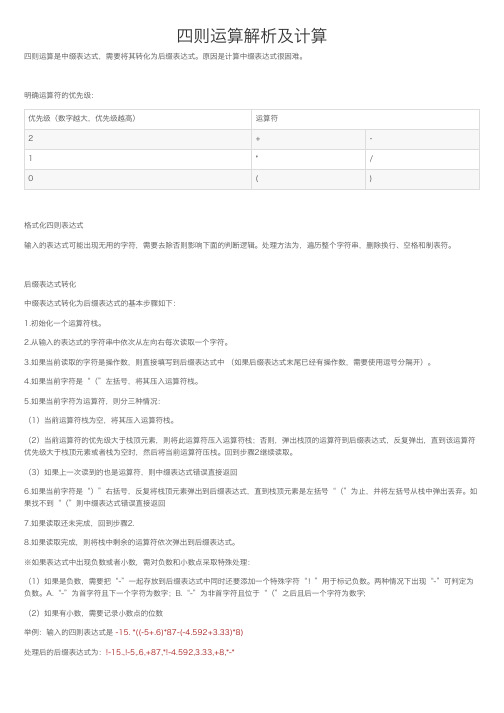
四则运算解析及计算四则运算是中缀表达式，需要将其转化为后缀表达式。
原因是计算中缀表达式很困难。
明确运算符的优先级：优先级（数字越⼤，优先级越⾼）运算符2+-1*/0()格式化四则表达式输⼊的表达式可能出现⽆⽤的字符，需要去除否则影响下⾯的判断逻辑。
处理⽅法为，遍历整个字符串，删除换⾏、空格和制表符。
后缀表达式转化中缀表达式转化为后缀表达式的基本步骤如下：1.初始化⼀个运算符栈。
2.从输⼊的表达式的字符串中依次从左向右每次读取⼀个字符。
3.如果当前读取的字符是操作数，则直接填写到后缀表达式中 （如果后缀表达式末尾已经有操作数，需要使⽤逗号分隔开）。
4.如果当前字符是“（”左括号，将其压⼊运算符栈。
5.如果当前字符为运算符，则分三种情况：（1）当前运算符栈为空，将其压⼊运算符栈。
（2）当前运算符的优先级⼤于栈顶元素，则将此运算符压⼊运算符栈；否则，弹出栈顶的运算符到后缀表达式，反复弹出，直到该运算符优先级⼤于栈顶元素或者栈为空时，然后将当前运算符压栈。
回到步骤2继续读取。
（3）如果上⼀次读到的也是运算符，则中缀表达式错误直接返回6.如果当前字符是“）”右括号，反复将栈顶元素弹出到后缀表达式，直到栈顶元素是左括号“（”为⽌，并将左括号从栈中弹出丢弃。
如果找不到“（”则中缀表达式错误直接返回7.如果读取还未完成，回到步骤2.8.如果读取完成，则将栈中剩余的运算符依次弹出到后缀表达式。
※如果表达式中出现负数或者⼩数，需对负数和⼩数点采取特殊处理：（1）如果是负数，需要把“-”⼀起存放到后缀表达式中同时还要添加⼀个特殊字符“！”⽤于标记负数。
两种情况下出现“-”可判定为负数。
A.“-”为⾸字符且下⼀个字符为数字；B.“-”为⾮⾸字符且位于“（”之后且后⼀个字符为数字;（2）如果有⼩数，需要记录⼩数点的位数举例：输⼊的四则表达式是 -15. *((-5+.6)*87-(-4.592+3.33)*8)处理后的后缀表达式为：!-15.,!-5,.6,+87,*!-4.592,3.33,+8,*-*后缀表达式求值：从左到右读取1、设置⼀个栈，开始时，栈为空；2、然后从左到右读取后缀表达式，若遇操作数，则进栈；3、若遇运算符，则从栈中退出两个元素，先退出的放到运算符的右边，后退出的放到运算符左边，运算后的结果再进栈，直到后缀表达式扫描完毕；4、最后，栈中仅有⼀个元素，即为运算的结果。
C语言简单计算器实现四则运算可带括号
C语言简单计算器实现四则运算可带括号```c#include <stdio.h>#include <stdlib.h>int priority(char op)if (op == '+' ， op == '-')return 1;else if (op == '*' ， op == '/')return 2;else if (op == '(')return 0;elsereturn -1;void calculate(char op, int *numStack, int *top, char *opStack, int *opTop)int num2 = numStack[(*top)--];int num1 = numStack[(*top)--];switch (op)case '+':numStack[++(*top)] = num1 + num2; break;case '-':numStack[++(*top)] = num1 - num2; break;case '*':numStack[++(*top)] = num1 * num2; break;case '/':numStack[++(*top)] = num1 / num2; break;}int eval(char *expr)int numStack[100];char opStack[100];int numTop = -1;int opTop = -1;int num = 0;int sign = 1;while (*expr != '\0')if (*expr >= '0' && *expr <= '9')num = num * 10 + (*expr - '0');} else if (*expr == '+' ， *expr == '-')numStack[++numTop] = num * sign;num = 0;sign = (*expr == '+') ? 1 : -1;} else if (*expr == '*' ， *expr == '/')while (opTop >= 0 && priority(*expr) <=priority(opStack[opTop]))calculate(opStack[opTop--], numStack, &numTop, opStack, &opTop);}opStack[++opTop] = *expr;} else if (*expr == '(')opStack[++opTop] = '(';} else if (*expr == ')')while (opStack[opTop] != '(')calculate(opStack[opTop--], numStack, &numTop, opStack, &opTop);}opTop--;}expr++;}numStack[++numTop] = num * sign;while (opTop >= 0)calculate(opStack[opTop--], numStack, &numTop, opStack, &opTop);}return numStack[0];int maichar expr[100];printf("请输入表达式：");scanf("%s", expr);int result = eval(expr);printf("计算结果：%d\n", result);return 0;```以上是一个简单的C语言四则运算计算器的实现。
运用栈方法的四则运算法
int Empty_SeqStack(PSeqStack S)
{
if(S->top1==-1)
return 1;
else
return 0;
}
int Pop_SeqStack(PSeqStack S,char *x)
{/*出栈*/
if(Empty_SeqStack(S))
s->top=-1;
k->top1=-1;
push1(k,'#');
while(a[i]!='='||(ch=get_top(k))!='#')
{
if(Isnum(a[i])) /*当前字符为数字*/
{
x=0;Int_part=0;float_part=0;
{
case '+':c=d+b;break;
case '-':c=d-b;break;
case '*':c=d*b;break;
S->top2++;
S->data[S->top2]=x;
return 1;
}
}
char GetTop_SeqStack(PSeqStack S,float *x)
{
if(Empty_SeqStack(S))
return 0;
else
*x=S->data[S->top2];
ch=pop1(k); /*从数据栈压出两个数,并从字符栈压出一个运算符进行计算*/
b=pop(s);
Java实现四则运算表达式
四则混合运算的算符优先算法Java实现它们都是对表达式的记法，因此也被称为前缀记法、中缀记法和后缀记法。
它们之间的区别在于运算符相对与操作数的位置不同：前缀表达式的运算符位于与其相关的操作数之前；中缀和后缀同理。
举例：(3 + 4) × 5 - 6 就是中缀表达式- × + 3 4 5 6 前缀表达式3 4 + 5 × 6 - 后缀表达式中缀表达式（中缀记法）中缀表达式是一种通用的算术或逻辑公式表示方法，操作符以中缀形式处于操作数的中间。
中缀表达式是人们常用的算术表示方法。
虽然人的大脑很容易理解与分析中缀表达式，但对计算机来说中缀表达式却是很复杂的，因此计算表达式的值时，通常需要先将中缀表达式转换为前缀或后缀表达式，然后再进行求值。
对计算机来说，计算前缀或后缀表达式的值非常简单。
前缀表达式（前缀记法、波兰式）前缀表达式的运算符位于操作数之前。
前缀表达式的计算机求值：从右至左扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（栈顶元素op 次顶元素），并将结果入栈；重复上述过程直到表达式最左端，最后运算得出的值即为表达式的结果。
例如前缀表达式“- × + 3 4 5 6”：(1) 从右至左扫描，将6、5、4、3压入堆栈；(2) 遇到+运算符，因此弹出3和4（3为栈顶元素，4为次顶元素，注意与后缀表达式做比较），计算出3+4的值，得7，再将7入栈；(3) 接下来是×运算符，因此弹出7和5，计算出7×5=35，将35入栈；(4) 最后是-运算符，计算出35-6的值，即29，由此得出最终结果。
可以看出，用计算机计算前缀表达式的值是很容易的。
将中缀表达式转换为前缀表达式：遵循以下步骤：(1) 初始化两个栈：运算符栈S1和储存中间结果的栈S2；(2) 从右至左扫描中缀表达式；(3) 遇到操作数时，将其压入S2；(4) 遇到运算符时，比较其与S1栈顶运算符的优先级：(4-1) 如果S1为空，或栈顶运算符为右括号“)”，则直接将此运算符入栈；(4-2) 否则，若优先级比栈顶运算符的较高或相等，也将运算符压入S1；(4-3) 否则，将S1栈顶的运算符弹出并压入到S2中，再次转到(4-1)与S1中新的栈顶运算符相比较；(5) 遇到括号时：(5-1) 如果是右括号“)”，则直接压入S1；(5-2) 如果是左括号“(”，则依次弹出S1栈顶的运算符，并压入S2，直到遇到右括号为止，此时将这一对括号丢弃；(6) 重复步骤(2)至(5)，直到表达式的最左边；(7) 将S1中剩余的运算符依次弹出并压入S2；(8) 依次弹出S2中的元素并输出，结果即为中缀表达式对应的前缀表达式。
简单的四则运算(栈+逆波兰)
逆波兰利用栈实现简单的四则运算一．逆波兰表达式引自/blog/472070逆波兰表达式解决四则运算逆波兰表达式又叫做后缀表达式，它将复杂表达式转换为可以依靠简单的操作得到计算结果的表达式，解决了四则运算中括号改变运算符优先级的问题。
四则运算的表达式一般都是中缀表达式如1+2*(3-4)+5，即操作符在两个操作数之间。
四则运算需要两个步骤，一是把中缀表达式转为后缀表达式，二是由后缀表达生成结果中缀表达式转为后缀表达式算法描述：(1)首先有个包含中缀表达式元素列表sourceList,然后创建一个符号列表destList保存最终后缀表达式,创建一个操作符堆栈opStack(2)从sourceList取出一个元素A(3a)如是数字则加入到destList中(3b)如果元素A是运算符，将操作符A与操作符堆栈opStack栈顶的运算符的优先关系相比较。
如果，优先关系高于opStack栈顶的运算符，则将该运算符压入操作符堆栈opStack。
倘若不是(低于或等于)的话，则将运算符栈opStack栈顶的运算符从栈中弹出保存到destList，重复此步骤,直到作符A压入操作符堆栈opStack。
(3c)若元素A是左括号"("，则压入操作符堆栈opStack(3d)若元素B是右括号")",则操作符堆栈opStack弹出操作符并加入到destList中，直到弹出左括号"("。
(5)从步骤2重复上述操作，所有元素处理完毕后将操作符堆栈opStack弹出操作符并加入到destList中，这样中缀式表示的简单算术表达式转化为逆波兰表示的简单算术表达式。
示例：中缀表达式如1+2*(3-4)+5，构造元素列表1,+,2,*,(,3,-,4,),5,构造一个空最终后缀表达式destList，一个操作符堆栈opStack1、取出“1”，destList【1】，opStack【】2、取出“+”，destList【1】，opStack【+】3、取出“2”，destList【1,2】，opStack【+】4、取出“*”，destList【1,2】，opStack【+,*】5、取出“(”，destList【1,2】，opStack【+,*,(】6、取出“3”，destList【1,2,3】，opStack【+,*,(】7、取出“-”，destList【1,2,3】，opStack【+,*,(,-】8、取出“4”，destList【1,2,3,4】，opStack【+,*,(,-】9、取出“)”，destList【1,2,3,4,-】，opStack【+,*】//操作符堆栈opStack弹出操作符并加入到destList中，直到弹出左括号"("10、取出“+”，destList【1,2,3,4,-,*,+】，opStack【+】//加号优先级不大于【+,*】11、取出“5”，destList【1,2,3,4,-,*,+,5】，opStack【+】12、处理完毕，destList【1,2,3,4,-,*,+,5,+】，opStack【】后缀表达式到计算结果算法描述：遍历储存后缀表达式的列表，将元素依次进栈，当遇到操作符时，连续出栈两个元素，进行运算，再将结果进栈，最后栈内留下的元素就是计算结果示例：后缀表达式destList【1,2,3,4,-,*,+,5,+】，结果堆栈resultStatck【】格式输入-->:结果[1,2,3,4]-->:resultStatck【1,2,3,4】[-]-->:resultStatck【1,2,3-4】[ * ]-->:resultStatck【1,2*(3-4)】[+]-->:resultStatck【1+2*(3-4)】[5]-->:resultStatck【1+2*(3-4),5】[+]-->:resultStatck【1+2*(3-4)+5】举例：正常的表达式逆波兰表达式a+b ---> a,b,+a+(b-c) ---> a,b,c,-,+a+(b-c)*d ---> a,b,c,-,d,*,+a+d*(b-c) ---> a,d,b,c,-,*,+a=1+3 ---> a=1,3 +二．自己写的简单四则运算的程序。
利用栈实现数据的四则运算c语言并构造哈夫曼树
为了实现数据的四则运算并构造哈夫曼树，我们可以先定义一个栈结构，然后实现四则运算的函数。
接下来，我们需要构建哈夫曼树。
以下是一个简单的实现：1. 定义栈结构：```c#include <stdio.h>#include <stdlib.h>typedef struct Stack {int top;unsigned capacity;int* array;} Stack;Stack* createStack(unsigned capacity) {Stack* stack = (Stack*)malloc(sizeof(Stack));stack->capacity = capacity;stack->top = -1;stack->array = (int*)malloc(stack->capacity * sizeof(int));return stack;}int isFull(Stack* stack) {return stack->top == stack->capacity - 1;}int isEmpty(Stack* stack) {return stack->top == -1;}void push(Stack* stack, int item) {if (isFull(stack)) return;stack->array[++stack->top] = item;}int pop(Stack* stack) {if (isEmpty(stack)) return INT_MIN;return stack->array[stack->top--];}int peek(Stack* stack) {if (isEmpty(stack)) return INT_MIN;return stack->array[stack->top];}void freeStack(Stack* stack) {free(stack->array);free(stack);}```2. 实现四则运算的函数：```cint add(int a, int b) {return a + b;}int subtract(int a, int b) {return a - b;}int multiply(int a, int b) {return a * b;}int divide(int a, int b) {if (b == 0) {printf("除数不能为0");return INT_MIN;}return a / b;}```3. 构建哈夫曼树（这里仅给出一个简单的示例，实际应用中需要根据具体需求实现）：```ctypedef struct HuffmanNode {char data;unsigned freq;struct HuffmanNode* left;struct HuffmanNode* right;} HuffmanNode;HuffmanNode* createNode(char data, unsigned freq) {HuffmanNode* node = (HuffmanNode*)malloc(sizeof(HuffmanNode));node->left = NULL;node->right = NULL;node->data = data;node->freq = freq;return node;}```4. 使用栈实现四则运算：```cint main() {Stack* stack = createStack(100);// 假设我们已经有了两个操作数和操作符，将它们压入栈中int operand1 = 10;int operand2 = 5;char operator = '+';push(stack, operand1);push(stack, operand2);push(stack, operator);// 从栈中弹出操作数和操作符，执行四则运算int result = 0;while (!isEmpty(stack)) {char op = pop(stack);if (op == '+') {result = add(pop(stack), pop(stack));} else if (op == '-') {result = subtract(pop(stack), pop(stack));} else if (op == '*') {result = multiply(pop(stack), pop(stack));} else if (op == '/') {result = divide(pop(stack), pop(stack));} else {printf("无效的操作符：%c", op);return 1;}push(stack, result);}printf("结果：%d", result);freeStack(stack);return 0;}```这个示例仅用于演示如何使用栈实现四则运算，实际应用中可能需要根据具体需求进行修改。
四则运算表达式计算前序遍历
四则运算表达式计算前序遍历前序遍历是二叉树遍历的一种方式，它的遍历顺序是根节点->左子树->右子树。
在四则运算表达式中，我们可以通过前序遍历的方式来计算表达式的结果。
四则运算表达式由操作数和操作符组成，操作数表示参与运算的数字，而操作符表示运算的方式（如加、减、乘、除等）。
在前序遍历中，我们首先遇到的是根节点，在四则运算表达式中根节点即为操作符。
根据前序遍历的顺序，我们可以得到以下算法来计算前序遍历的四则运算表达式：1.初始化一个操作数栈和一个操作符栈。
2.从右向左遍历表达式，逐字符读入。
3.如果当前字符是操作数，将其放入操作数栈中。
4.如果当前字符是操作符，将其放入操作符栈中。
5.如果当前字符是右括号')',则将操作符栈中的操作符弹出，直到遇到左括号'('.弹出后，将弹出的操作符和操作数栈中的两个操作数进行计算，并将结果加入操作数栈中。
6.继续遍历表达式的下一个字符，直到表达式中的所有字符都遍历完毕。
7.最后，操作数栈中剩余的操作数即为表达式的计算结果。
下面以一个具体的表达式为例，来说明如何通过前序遍历计算四则运算表达式：表达式：(+ (* 4 5) (- 6 3))1.初始化操作数栈和操作符栈为空。
2.从右向左遍历表达式，首先遇到的是右括号')',压入操作符栈中。
3.继续遍历，遇到左括号'(',压入操作符栈中。
4.下一个字符是操作符'*',压入操作符栈中。
5.继续遍历，下一个字符是操作数'4',压入操作数栈中。
6.继续遍历，下一个字符是操作数'5',压入操作数栈中。
7.继续遍历，下一个字符是右括号')',弹出操作符栈中的操作符'*'。
8.弹出操作数栈中的两个操作数，即为'4'和'5'，进行计算，得到结果'20'，将结果'20'压入操作数栈中。
顺序栈基本运算算法运行
顺序栈基本运算算法运行
顺序栈（Sequential Stack）是一种基于数组实现的栈，它具有后进先出（LIFO）的特点。
以下是顺序栈的基本运算算法运行过程：
1. 初始化顺序栈
- 创建一个固定长度的数组，用于存储栈中的元素。
- 定义一个指针top，初始值为-1，表示栈为空。
2. 判断栈是否为空（isEmpty）
- 判断top是否等于-1，如果是，则表示栈为空；否则，表示栈非空。
3. 入栈（push）
- 判断栈是否已满，即top是否等于数组的最大长度-1。
如果是，则表示栈已满，无法进行入栈操作；否则，执行以下步骤：
- 将要入栈的元素放入数组中top+1的位置，即数组[top+1] = 元素。
- 将top的值加1，即top = top + 1。
4. 出栈（pop）
- 判断栈是否为空，如果是，则表示栈为空，无法进行出栈操作；否则，执行以下步骤：
- 将数组中top位置的元素取出并保存到一个临时变量中，即临时变量 = 数组[top]。
- 将top的值减1，即top = top - 1。
- 返回临时变量，即为出栈的元素。
5. 获取栈顶元素（getTop）
- 判断栈是否为空，如果是，则表示栈为空，无法获取栈顶元素；否则，返回数组中top位置的元素。
以上是顺序栈的基本运算算法运行过程，其中包括初始化栈、判断栈是否为空、入栈、出栈和获取栈顶元素等操作。
栈 四则运算
栈四则运算
本文将介绍栈在四则运算中的应用。
栈是一种线性数据结构，具有后进先出（LIFO）的特点。
在四则运算中，我们可以使用栈来实现中缀表达式的转换和计算。
首先，我们需要了解中缀表达式和后缀表达式。
中缀表达式是人类常用的表达式形式，例如：2+3*4。
而后缀表达式是一种更适合计
算机处理的表达式形式，例如：234*+。
中缀表达式需要考虑运算符
优先级和括号等因素，而后缀表达式则不需要考虑这些因素。
转换中缀表达式为后缀表达式的方法是使用栈。
我们从左到右遍历中缀表达式，遇到数字时直接输出，遇到运算符时则需要将其与栈顶运算符比较优先级，如果栈顶运算符优先级高，则将栈顶运算符弹出并输出，直到栈顶运算符优先级低于当前运算符或者栈为空。
最后将当前运算符入栈。
遍历完中缀表达式后，如果栈中还有运算符，则将它们全部弹出并输出。
计算后缀表达式同样可以使用栈。
我们从左到右遍历后缀表达式，遇到数字时将其入栈，遇到运算符时则弹出栈顶的两个数字进行计算，并将结果入栈。
遍历完后缀表达式后，栈中的唯一元素即为表达式的结果。
以上就是栈在四则运算中的应用。
通过栈，我们可以将中缀表达式转换为后缀表达式并进行计算，这种方法在计算机科学中有着广泛的应用。
- 1 -。
堆栈 实现四则运算,直接能跑
#include<stdio.h>#include<string.h>#define MaxSize 100typedef struct{int data[MaxSize];int top;}DataStack;int InitStack(DataStack *S){S->top = -1;memset(S->data, '\0', sizeof(int) * MaxSize);return 1;}int StackEmpty(DataStack S){return S.top == -1;}int Push(DataStack *S, char e){if (S->top >= MaxSize - 1) {printf("Stack is full!\n");return 0;} else {S->data[++S->top] = e;return 1;}}int Pop(DataStack *S){if (S->top >= 0) {return S->data[S->top--];} else {printf("Stack is empty!\n");return 0;}}int trans(DataStack *S,char *exp,char postexp[]) {int i=0;while(*exp!='\0'){switch(*exp){case '(':Push(S,*exp);exp++;break;case ')': while(S->data[S->top]!='('){postexp[i++]=Pop(S);}Pop(S);exp++;break;case '+':case '-':Push(S,*exp);while(S->top!=-1&&S->data[S->top]!='('){postexp[i++]=Pop(S);}exp++;break;case '*':case '/':Push(S,*exp);while(S->data[S->top]=='*'||S->data[S->top]=='/'){postexp[i++]=Pop(S);}exp++;break;case ' ': break;default : while(*exp>='0' && *exp<='9'){postexp[i++]=*exp;exp++;postexp[i++]='#';}}while(S->top!=-1){postexp[i++]=Pop(S);}postexp[i]='\0';}float compvalue(DataStack *S,char *postexp) {float a,b,c,d;float value;while(*postexp!='\0'){switch(*postexp){case '+':a=Pop(S);b=Pop(S);c=a+b;Push(S,c);break;case '-':a=Pop(S);b=Pop(S);c=b-a;Push(S,c);break;case '*':a=Pop(S);b=Pop(S);c=a*b;Push(S,c);break;case '/':a=Pop(S);b=Pop(S);if(a!=0){Push(S,c);}else{printf("零不能作除数\n");return ;}break;default :d=0;while(*postexp>='0'&&*postexp<='9'){d=10*d+*postexp-'0';postexp++;}Push(S,d);break;}postexp++;}return Pop(S);}int main(){DataStack S;InitStack(&S);char exp[20];scanf("%s",exp);char postexp[MaxSize];float value;trans(&S,exp,postexp);printf("后缀表达式的值：%s\n",postexp);value=compvalue(&S,postexp);printf("表达式的值：%.2f\n",value);}。
栈实现计算器（简单四则运算）
栈实现计算器（简单四则运算）主要是通过定义⼀个数栈和⼀个符号栈，并根据给出的计算式进⾏拆分，循环判断是数字还是符号，考虑数字的连续性和符号计算的优先级，具体实现如下：package com.pangzi.stucture;public class calculator {public static void main(String[] args) {String expression = "50+9*9-7";//定义⼀个需要被扫描的表达式//创建两个栈，⼀个数栈，⼀个符号栈ArrayStack2 numStack = new ArrayStack2(10);ArrayStack2 operStack = new ArrayStack2(10);//定义需要的变量int index = 0;//定义⼀个指向数字和运算符的索引,扫描栈中的内容int num1 = 0;//定义第⼀个数字int num2 = 0;//定义第⼆个数字int oper = 0;//定义操作符int res = 0;//定义运算结果char ch = ' ';//将每次扫描得到的char保存⾄ch⾥⾯String keepNum = "";//⽤于拼接多位数//开始扫描表达式while(true){//依次得到expression中的每⼀个字符ch = expression.substring(index, index+1).charAt(0);//⽤substr获取长度为1的⼀个个字符串，然后通过charat转换为字符。
//判断字符是数字还是运算符,然后进⾏处理if(operStack.isOper(ch)){//如果ch是⼀个符号//判断符号栈是否为空if(!operStack.isEmpty()){//如果符号栈不为空，⽤ch和符号栈存在的运算符进⾏⽐较，如果ch的优先级⼩于等于栈中符号的优先级//就从数栈中弹出两个数字，进⾏运算并将得到的结果放⼊数栈，然后将ch⼊符号栈if(operStack.priority(ch) <= operStack.priority(operStack.peek())){num1 = numStack.pop();num2 = numStack.pop();oper = operStack.pop();res = numStack.cal(num1, num2, oper);numStack.push(res);operStack.push(ch);}else{//如果当前操作符的优先级⼤于符号栈中的优先级，直接⼊符号栈operStack.push(ch);}}else{//如果符号栈为空，进⾏⼊栈操作operStack.push(ch);//将ch⼊符号栈}}else{//如果ch是数据的话,则直接⼊数栈//numStack.push(ch - 48);//根据ascii表换算//当处理多位数时，不能扫描到数字时就⽴即⼊栈，因为有可能是多位数//在处理时，应该在expression的表达式后⾯在扫描⼀位，如果是数继续扫描，如果是符合则停⽌。
栈实现四则运算
栈实现四则运算休息一会儿。
来恒为的第三天了，到目前为止做的事情就是把四则运算的栈实现完成的差不多了，说差不多是因为对输入会出错的判断和输出还没有实现。
来说说这个程序吧。
首先，对输入的表达式是以字符为单位读入的，对每个读入的字符进行判断，数字放到character栈中，算符放到operator栈中，另外定义了push和pop的函数进行进栈和出栈的操作，（大二学数据结构的时候对各种结构一直没有清晰的认识，现在觉得结构的特性取决于对结构的操作，也就是他的行为决定了他的特性，然后才有栈，队列等名字）。
初始化的时候先将‘#’字符压到operator栈中，此时其优先级是最低的，方便对以后读入的算符进行比较和处理。
优先级的判断是通过定义了两个数组实现的。
当后来读入的算符的优先级低于已经在operator中栈顶的算符时就弹出operator中的算符以及character中的两个数字用operate函数进行运算，运算的数值push 到character栈中，继续进行算符的判断看是否需要继续进行运算。
表达式必须是以‘#’结尾的，当operator中的栈顶和最后读入的字符都是‘#’时就结束循环，返回character中栈顶元素，这就是最后的结果。
整体的思路就是对输入表达式的依次读入和处理，对一开始就出现的‘+’和‘-’要进行特殊的处理，设置一个标志位对负数进行标记，正数直接覆盖。
由于是一位一位读取的，对多位数的处理要用求和的方式。
难点是对运算符优先级的判断，特别是括号的处理，这也是我觉得最为巧妙的地方。
设置两个整型数组，分别对应栈内和栈外的算符优先级。
对括号的处理上，栈外的‘）’应该与栈内的‘(’优先级相同，把两者之间的运算解决之后要将栈内的‘(’pop出来，以免影响后续的操作。
清单：mystack栈，in[7],out[7]优先级数组，ch[7]保存算符对应的数字。
函数：push，pop，gettop，initstack，compare，evaluate对输入格式的错误处理还没有具体实现。
c++实现四则运算
c++实现四则运算
描述：读⼊⼀个只包含 +, -, *, / 的⾮负整数计算表达式，计算该表达式的值。
输出：计算结果，保留两位⼩数。
程序任务分为两部分：
⼀。
将输⼊的中缀表达式转换为后缀表达式，实现过程：
1.准备队列保存后缀表达式（计算后缀表达式时，需要从队⾸读取数据）
准备栈保存计算符，使⽤找调整计算顺序
2.读输⼊字符串，如果是数字，直接⼊后缀表达式队列；
如果是计算符号，当计算符号栈为空或当前符号优先级⼤于栈顶符号优先级，直接⼊栈。
否则依次弹出栈顶符号⼊后缀表达式队列，直到遇到优先级不⼩于当前的符号或栈空。
如果是(直接⼊栈，如果是)弹出符号栈中符号⼊后缀表达式队列，直到(（不⼊队）
3.反复2过程直到读完所有字符串，若符号栈不为空，弹出其中所有元素⼊队
⼆。
计算后缀表达式：
计算栈
1.弹出队列元素，如果是数字，直接⼊栈，如果是操作符号，弹出栈顶两个数字计算。
P.S.第⼀个弹出数字是第⼆个数字，第⼆个弹出数字是第⼀个数字。
|temp1| 栈顶 temp2 - temp1 注意这⼀点，容易在减和除运算中出错
|--------|
|temp2|
|--------|。
栈 四则运算
栈四则运算
栈四则运算是计算机科学中的一个基本算法，它利用栈来实现表达式的计算。
在栈四则运算中，我们需要将表达式中的数字和运算符依次入栈，并在遇到运算符时弹出相应的数字进行计算，最终得到表达式的结果。
这种算法的优点在于它能够处理复杂的表达式，并且具有较高的运算效率。
同时，栈四则运算也是许多计算机程序设计语言的基础之一，例如C语言中的表达式计算、Java中的算术运算等。
然而，在实际应用中，栈四则运算也存在一些问题。
例如，当表达式中存在括号时，需要进行额外的处理才能得到正确的结果。
由于计算机存储空间的限制，对于过于复杂的表达式，栈的深度可能会超过系统所能承受的范围，从而导致程序崩溃。
总的来说，栈四则运算是计算机科学中一项重要的算法，它在实际应用中具有广泛的应用。
然而，在使用时需要注意其局限性，以保证程序的正确性和稳定性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1
概要详细
程序组织结构
排错程序
排错程序
1、遍历数组 2、括号匹配 3、条件判断“/” 4、条件判断“%”
1、记录出错索引 2、打印“^”标示
中序表达式转后缀表达式程序
1、操作数排入数组 2、操作符标识优先级入栈 3、操作符根据优先级出栈 排入数组
后缀表达式计算程序
1、操作数入栈 2、条件判断操作符 3、操作数出栈计算 4、计算结果入栈 5、判断栈长度为1出栈
2
概要详细
平台选择
用户普及度高，操作熟悉，易移植
简单直接，一直在学在用
功能熟悉，操作简便
3
目录
需求分析
Demand Analysis
概要详细
Outline&Detail
算法设计
Algorithm Design
编码测试
Encoding&Test
算法设计 1 2 3
算法统计
算式排错算法
中序转后缀 表达式算法
基于顺序栈实现的 四术算数表达式计算
指导老师：杜晓凤 汇报人：黄成旺
目录
需求分析
Demand Analysis
概要详细
Outline&Detail
算法设计
Algorithm Design
编码测试
Encoding&Test
目录
需求分析
Demand Analysis
概要详细
Outline&Detail
^
^
3
算法设计
中序表达式转后后缀表达式算法
puts(a);
3
+
(
3
+
2
*
3
)
\0
char ch[100]；
3 op
3 level
2
3
*
+
+
\0
stack st; * + ( + 2 1 -1
1
4
算法设计
算式排错算法
char ch[100]；
3
3
2
3
*
+
+
\0
stack numstack 9 + 3
3 6 2 3 9 12 3 3 6
12
6 9
+ *
32
5
目录
需求分析
Demand Analysis
概要详细
Outline&Detail
算法设计
Algorithm Design
编码测试
Encoding&Test
编码测试
容错测试：
1
编码测试
计算测试：
2
后话
1
后话
2
3
1、一个人做很累
2、一个人做很累
编码测试
Encoding&Test
概要详细
排错理
判断是否 缺少括号， 操作数是否 符合标准
基本处理流程
输入一则 四则运算， 可带括号， 可以是浮点 数
算式处理 排错处理
错误提示 算式输入
错误提示
发现错误 用“^”标 出位置
调用函数， 计算结果
正确计算
算式分析
算式修改
正确计算
算式修改
根据提示 重新输入算 式
后缀表达 式计算算法
1
算法设计
算式排错算法
puts(a); stack che；
3 (（
+
(
3
+
2
）
+
3
\0
puts(b); char c[100]={‘ ’}; c[i]='^';
3
+
（
3
+
2
+
3
\0
^
2
算法设计
算式排错算法
puts(a); stack che；
3 (
+
(
3
/
0
）
%
3.1
\0
c[i]='^';
3、一个人做很累
3
谢谢聆听！
Thanks for listening！
指导老师：杜晓凤
汇报人：黄成旺
算法设计
Algorithm Design
编码测试
Encoding&Test
需求分析
功能需求
（
%整数
+&-
*&/
浮点 运算
%
四 则 运 算
算 数 排 错
缺少括号
除数为0？
缺少运算 符
1
目录
需求分析
Demand Analysis
概要详细
Outline&Detail
算法设计
Algorithm Design