第五章残差与误差检验
第五章抗差估计RobustEstimation

Z 0.463 0.435 0.457 0.462
Sum 0.715 0.679 0.682 0.670
X 5.334 5.335 5.248 0.720
Y 4.661 4.661 4.629 1.077
Z 5.367 5.367 5.193 0.420
Sum 5.131 5.131 5.031 0.787
三、应用实例——基准转换
背景
➢ 基准转换一般通过公共点坐标求转换参数; ➢ 公共点坐标难免有误差,甚至有异常误差; ➢ 我国经典大地基准是通过三角测量、导线测量传算
的,累积误差明显——边远地区误差达数米或数十 米; ➢ 利用公共点坐标求解转换参数必然歪曲坐标基准间 的真正关系; ➢ 进而扭曲转换后的大地网。
➢ 再用效率高的权函数进行迭代计算,提高转换参数效 率。
第五章 抗差估计(Robust Estimation)
三、应用实例——基准转换
参数初值
tˆx0 med (Wxi ) tˆy0 med (Wyi )
tˆz0 med (Wzi )
0 wx
med
(
e
0 xi
) / 0.6745
e0 xi
tˆx0
X=[
1 5
(
13 i9
X
2 i
)]
1
2
sum= [
1 15
13 i9
(X
2 i
Yi2
Z
2 i
1
)] 2
1
0,8
0,6
0,4
0,2
0
1
2
3
4
5
6
7
无额外粗差情形中误差
LS LS+Test
第五章线性回归模型的假设与检验

⎟⎟⎠⎞
于是
βˆ1 = ( X1′X1)−1 X1′y1 , βˆ2 = ( X 2′ X 2 )−1 X 2′ y2
应用公式(8.1.9),得到残差平方和
和外在因素.那么我们所要做的检验就是考察公司效益指标对诸因素的依赖关系在两个时间 段上是否有了变化,也就是所谓经济结构的变化.又譬如,在生物学研究中,有很多试验花费 时间比较长,而为了保证结论的可靠性,又必须做一定数量的试验.为此,很多试验要分配在 几个试验室同时进行.这时,前面讨论的两批数据就可以看作是来自两个不同试验室的观测 数据,而我们检验的目的是考察两个试验室所得结论有没有差异.类似的例字还可以举出很 多.
而刻画拟合程度的残差平方和之差 RSSH − RSS 应该比较小.反过来,若真正的参数不满足
(5.1.2),则 RSSH − RSS 倾向于比较大.因此,当 RSSH − RSS 比较大时,我们就拒绝假设(5.1.2),
不然就接受它.在统计学上当我们谈到一个量大小时,往往有一个比较标准.对现在的情况,我
们把比较的标准取为 RSS .于是用统计量 (RSSH − RSS) RSS 的大小来决定是接受假设
(5.1.2),还是拒绝(5.1.2). 定理 5.1.1 对于正态线性回归模型(5.1.1)
(a )
RSS
σ2
~
χ2 n− p
(b )
若假设(8.1.2)成立,则 (RSSH
− RSS)
σ2
~
χ2 n− p
得愈好.现在在模型(5.1.1)上附加线性假设(5.1.2),再应用最小二乘法,获得约束最小二乘估计
βˆH = βˆ − ( X ′X )−1 A′( A( X ′X )−1 A′)−1 ( Aβˆ − b)
残差检验-误差检验

2 2 n
0
S0 0.8154 ; n 1
2
3)计算残差
i 1 0
的均值为: 0 0.00524 ;
S1 0.06128 ; n 1
2
4)计算残差的均方差为: S1 其中: S1 0 i 0
2 i 1 n
ቤተ መጻሕፍቲ ባይዱ
2
S1 0.075 ; S0 6)进行检验:根据残差检验规定预测精度等级表(见表 1)
5)计算方差比为: c
c值 <0.35 <0.50 <0.65 <0.65
预测精度等级 好 合格 勉强合格 不合格
表 1 预测精度等级划分 则可知该模型的预测等级为:“好” 。
报告中的误差项和残差分析

报告中的误差项和残差分析一、误差项和残差的概念和区别误差项和残差是统计学中常用的两个概念,它们在数据分析和建模中起着重要的作用。
误差项指的是观测值与真实值之间的差异,而残差则是观测值与模型预测值之间的差异。
在实践中,误差项和残差往往被用来描述数据的随机性和模型的拟合程度。
二、误差项和残差的计算方法计算误差项和残差的方法主要有最小二乘法和最大似然估计法。
最小二乘法是一种常见的参数估计方法,它通过最小化观测值与模型预测值之间的差异来确定模型的参数。
最大似然估计法则是在给定观测数据时,寻找使得观测数据在给定模型下的概率最大的参数值。
三、误差项和残差的意义和应用误差项和残差的存在使得我们能够对数据和模型进行有效的分析和评估。
通过对误差项和残差的研究,我们可以了解数据中的随机噪声,评估模型的拟合优度,检验模型的假设,识别异常值等。
四、误差项和残差的检验方法误差项和残差的检验方法包括正态性检验、异方差性检验和独立性检验。
正态性检验用于检验误差项或残差是否满足正态分布的假设,常用的方法有正态概率图和K-S检验。
异方差性检验用于检验误差项或残差的方差是否与自变量或因变量相关,常用的方法有方差齐性检验和异方差鉴别。
独立性检验用于检验误差项或残差是否具有独立性,常用的方法有自相关检验和Durbin-Watson检验。
五、误差项和残差的解释和汇报在报告中,正确解释和汇报误差项和残差的结果对于研究人员和决策者具有重要意义。
我们应该通过描述统计量和图表,结合领域知识和背景信息,解释误差项和残差的含义和影响。
此外,还可以通过引用相关文献和研究成果,对结果进行进一步的解释和讨论。
六、误差项和残差的应对和改进方法当我们遇到误差项或残差偏离预期时,应该及时采取相应的应对和改进方法。
对于异常值和离群点的处理,我们可以考虑删除、修复或调整这些数据。
对于异方差或自相关的问题,我们可以进行变量转换、加权最小二乘法或时间序列分析等处理方法。
计量经济学 第五章习题答案
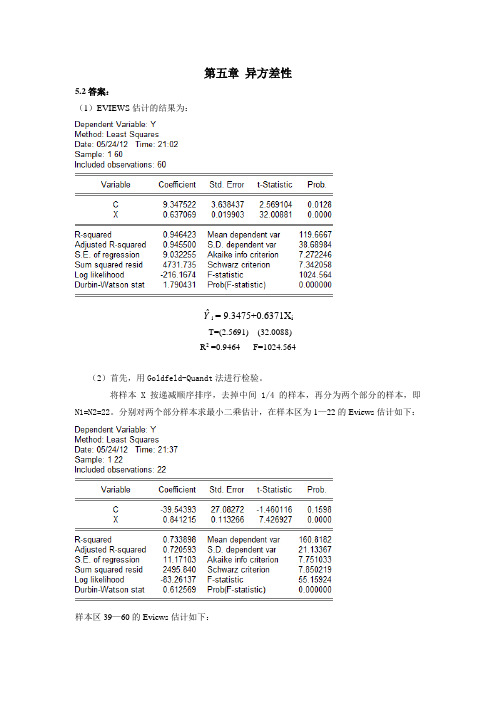
第五章异方差性5.2答案:(1)EVIEWS估计的结果为:Yˆi= 9.3475+0.6371X iT=(2.5691) (32.0088)R2 =0.9464 F=1024.564(2)首先,用Goldfeld-Quandt法进行检验。
将样本X按递减顺序排序,去掉中间1/4的样本,再分为两个部分的样本,即N1=N2=22。
分别对两个部分样本求最小二乘估计,在样本区为1—22的Eviews估计如下:样本区39—60的Eviews估计如下:得到两个部分各自的残差平方和,即∑e 12 =2495.840∑e 22 =603.0148求F 统计量为: F=∑∑e e 2221=2495.840/603.0148=4.1390给定α=0.05,查F 分布表,得临界值为F 0.05=(20,20)=2.12.比较临界值与F 统计量值,有F =4.1390>F 0.05=(20,20)=2.12,说明该模型的随机误差项存在异方差。
其次,用White 法进行检验结果如下:给定α=0.05,在自由度为2下查卡方分布表,得χ2=5.9915。
比较临界值与卡方统计量值,即nR2=10.8640>χ2=5.9915,同样说明模型中的随机误差项存在异方差。
(2)用权数W1=1/X,作加权最小二乘估计,得如下结果用White法进行检验得如下结果:F-statistic 3.138491 Probability 0.050925Obs*R-squared 5.951910 Probability 0.050999。
比较临界值与卡方统计量值,即nR2=5.9519<χ2=5.9915,说明加权后的模型中的随机误差项不存在异方差。
其估计的结果为:Yˆi= 10.3705+0.6309X iT=(3.9436) (34.0467)R2 =0.21144 F=1159.176 DW=0.95855.3答案:(1)EVIEWS估计结果:Yˆi= 179.1916+0.7195X iT=(0.808709) (15.74411)R2 =0.895260 F=247.8769 DW=1.461684 (2)利用White方法检验异方差,则White检验结果见下表:由上述结果可知,该模型存在异方差。
第05章多元时间序列分析方法

第05章多元时间序列分析⽅法142第五章多元时间序列分析⽅法[学习⽬标]了解协整理论及协整检验⽅法;掌握协整的两种检验⽅法:E-G 两步法与Johansen ⽅法; ? 熟悉向量⾃回归模型VAR 的应⽤; ? 掌握误差修正模型ECM 的含义及检验⽅法; ? 掌握Granger 因果关系检验⽅法。
第⼀节协整检验前⾯介绍的ARMA 模型要求时间序列是平稳的,然⽽实际经济运⾏中的⼤多数时间序列都是⾮平稳的,通常采取差分⽅法消除时间序列中的⾮平稳趋势,使得序列平稳后建⽴模型,这就是第四章所介绍的ARIMA 模型。
但是,变换后的时间序列限制了所要讨论问题的范围,并且有时变换后的序列由于不具有直接的经济意义,从⽽使得转换为平稳后的序列所建⽴的时间序列模型的解释能⼒⼤⼤降低。
1987年,Engle 和Granger 提出的协整理论及其⽅法,为⾮平稳时间序列的建模提供了另⼀种重要途径。
①⽬前,协整问题研究已经成为20世纪80年代末到90年代以来经济计量学建模理论的⼀个重⼤突破,在分析变量之间的长期均衡关系中得到⼴泛应⽤。
⼀、协整概念与定义在经济运⾏中,虽然⼀组(两个或两个以上)时间序列变量(例如⼈民币汇率与外汇储备、货币供应量和股票指数)都是随机游⾛,但它们的某个线性组合却可能是平稳的,在这种情况下,我们称这两个变量是平稳的,既存在协整关系。
其基本思想是,如果两个(或两个以上)的时间序列变量是⾮平稳的,但它们的某种线性组合却表现出乎稳性,则这些变量之间存在长期稳定关系,即协整关系。
根据以上叙述,我们将给出协整这⼀重要概念。
⼀般⽽⾔,协整(cointegration)是指两个或两个以上同阶单整的⾮平稳时间序列的组合是平稳时间序列,则这些变量之间的关系的就是协整的。
为何会有协整问题存在呢?这是因为许多⾦融、经济时间序列数据都是不平稳的,但它们可能受到某些共同因素的影响,从⽽在时间上表现出共同趋势,即变量之间存在⼀定稳定关系,他们的变化受到这种关系的制约,因此它们的某种线性组合可能是平稳的,即存在协整关系。
实用回归分析课件 (残差与残差图)

5.3 异常值与强影响值
一、关于因变量y的异常值
在残差分析中,认为超过 3ˆ 的残差为异常值。
标准化残差
ZREi
ei
ˆ
学生化残差
SREi ˆ
ei 1 hii
ZREi / SREi 3 观测数据判定为异常值
存在y的异常观测值,普通/标准化/学生化残差都不适用
5.3 异常值与强影响值
当数据中存在关于 y 的异常观察值时,异常值把回归线拉向 自己,使异常值本身的残差减少,而其余观察值的残差增大,这时 回归标准差ˆ 也会增大,因而用“3σ”准则不能正确分辨出异常值。 解决这个问题的方法是改用删除残差。
其中, hii
1 n
(xi x)2 Lxx
称为杠杆值
靠近x附近的点相应的残差方 差较大,
远离x附近的点相应的残差方 差较小.
5.2 残差的性质
一、残差的性质
性质3. 残差满足约束条件:
n
ei 0
i 1 n
xiei 0
i 1
5.2 残差的性质
二、改进的残差
5.3 异常值与强影响值
异常值分为两种情况: 一种是关于因变量y异常; 另一种是关于自变量x异常。
第三步,做等级相关系数的显著性检验。在n>8的情况下, 用下式对样本等级相关系数rs进行t检验。检验统计量为:
t n 2 rs 1 rs2
如果t≤tα/2(n-2)可认为异方差性问题不存在, 如果t>tα/2(n-2),说明xi与|ei|之间存在系统关系,异方差性 问题存在。
违背基本假设的情况
第六章 关于异方差性问题 第七章 关于自相关性问题 第八章 关于多重共相关问题
第六章 关于异方差性问题
var(i ) var( j ), i j
残差与误差的区别复习进程

残差与误差的区别残差与误差的区别误差与残差,这两个概念在某程度上具有很大的相似性,都是衡量不确定性的指标,可是两者又存在区别。
误差与测量有关,误差大小可以衡量测量的准确性,误差越大则表示测量越不准确。
误差分为两类:系统误差与随机误差。
其中,系统误差与测量方案有关,通过改进测量方案可以避免系统误差。
随机误差与观测者,测量工具,被观测物体的性质有关,只能尽量减小,却不能避免。
残差――与预测有关,残差大小可以衡量预测的准确性。
残差越大表示预测越不准确。
残差与数据本身的分布特性,回归方程的选择有关。
随机误差项Ut反映除自变量外其他各种微小因素对因变量的影响。
它是Y t 与未知的总体回归线之间的纵向距离,是不可直接观测的。
残差e t 是Yt 与按照回归方程计算的Yt 的差额,它是Yt 与样本回归线之间的纵向距离,当根据样本观测值拟合出样本回归线之后,可以计算et 的具体数值。
利用残差可以对随机误差项的方差进行估计。
随机误差是方程假设的,而残差是原值与拟合值的差。
实践中人们经常用残差去估计这个随机误差项。
意义不一样哈,残差一般只的是在计算近似值过程中某一步与真实值得差值,而误差指的的是最终近似值与真实值得差值残差就是回归所得的估计值与真值(实际值)之间的误差;修正的R square就是剔出了数据量影响后的R23.4.3 测量不确定度评定方法参考公式及其详解参考:/sfzx/sy3.docISO发布的“测量不确定度表示指南”是测量数据处理和测量结果不确定度表达的规范,由于在评定不确定度之前,要求测得值为最佳值,故必须作系统误差的修正和粗大误差(异常值)的剔除。
最终评定出来的测量不确定度是测量结果中无法修正的部分。
测量不确定度评定总的过程如图3-3所示的流程。
具体的方法还要有各个环节的计算。
图3-3 测量不确定度评定流程图1、标准不确定度的A类评定此法是通过对等精度多次重复测量所得数据进行统计分析评定的,正如前面介绍的随机误差的处理过程,标准不确定度u(xi)=s(xi),是用单次测量结果的标准不确定度算出:(3-20)其单次测量结果的标准不确定度可用贝塞尔法求得,即:= (3-21)其实,单次测量结果的标准不确定度还有如下求法:①最大残差法: = ,系数如表3-2所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ui ˆ
vi
Qii 1
hii
;
Q(ui ) 1;
Q(uiu j ) ˆ 2
Q(viv j )
QiiQjj (1 hii )(1 hjj ) ˆ 2
hij Qjj
QiiQjj (1 hii )(1 hjj ) ˆ 2
(n t)
{V T PV 2 ~ 2 (n t)}
4,
ui2 nt
vi2 Qvi ˆ 2 (n t)
vi2 Qvi 2 V T PV 2
~ 1 , n t 1 2 2
X1
~ (n 1);
n
1
n
X
2 i
1
n
Xi ~ N (0, 2 );
X
2 i
/
2
~
2(n)
1
Z X ~ (m, n);
(3)
Q(vi ) (1 hii )Qii riiQii
当 hii 1 时, rii 0 (rii:多余观测分量)
Q(vi ) 0 强权 (高杠杆) 观测值 (抵抗粗差能力最差)
当 hii 0(rii 1) 时, Q(vi ) 1 完全"多余"的观测值;
(4) QXˆV N 1AT PQ(I PAN1AT ) 0; QLˆV 0.
4,
ˆ
2与ˆ
2 (i
的关
)
系
vi
vi 近似 t(n t 1)
Qii 1 hii
ˆ(i) Qvi
VT (i)
P(
i
)V(i
)
LT(i) P(i) L(i)
( A(Ti) P(i) L(i) )T
Xˆ (i)
(LT PL
Pi L2i ) {(AT PL)T
( AiT Pi Li )T }(Xˆ
{ ~ N(0, 02Q)} , Q为对角阵.
2, 平差因子( 帽子矩阵,投影矩阵)
H AN 1 AT P
(1)H是幂等阵
H * H AN 1AT PAN1AT P AN 1AT P H ;
n
hij hik hkj k 1
(2)令 R I H ,
则R 也是为幂等阵;且 HR H (I H ) 0;
2, δi与 vi的关系
因 Xˆ (i) (N AiT Pi Ai )1( AT PL AiT Pi Li )
{N
1
N
1
AiT
( Pi 1
Ai
N
A 1 T i
)1
Ai
N
1} ( AT
PL
AiT
Pi
Li
)
Xˆ
1
1 hii
N 1 AiT Pi
Ai Xˆ
N 1 AiT Pi Li
hii 1 hii
N 1 AiT Pivi 1 hii
)
LT PL ( AT PL)T
Xˆ
Pi Li Ai Xˆ
Pi L2i
Xˆ T AiT Pivi 1 hii
Lihii Pivi 1 hii
V T PV Pivi2 1 hii
(n t)ˆ 2 ui2ˆ 2
(n t ui2 )ˆ 2
即:
(n
t
N 1 AiT Pi Li
Xˆ
1 1 hii
N 1 AiT Pi
( Ai Xˆ
Li )
Xˆ
1 1 hii
N 1 AiT Pivi
所以
i
Ai Xˆ (i)
Li
vi
Ai 1 hii
N 1 AiT Pivi
vi
hii 1 hii
vi
vi 1 hii
即:
i
vi 1 hii
Qii 1 hii
(3)Rank(QvvP) Rank(R) tr(R)
tr( I ) n,n
tr(
N
1
AT
P A)t ,t
nt
r
n
4)令 ri Rii (QvvP)ii , 则 ri tr(R) r; (称ri为多余观测分量)
1
(5) Li Lˆi Vi , QLˆV 0, Qii QLˆi Lˆi QViVi
5, 残差与误差检验
5.1 残差 5.2 粗差与数据探测 5.3 模型误差及其检验 5.4 稳健估计 5.5 基于相关分析的粗差检验
5.1 残 差
1) 普通残差及其性质
1, 普通残差的定义
观测方程:
L = AX - Δ
回归模型: y = xβ- e
误差方程:
V A Xˆ L
n,1 n,t t,1
1)
ˆ
2 (i
)
(n
t
ui2 )ˆ 2
4) 不相关残差
1, 普通残差的相关性
Qvv Q AN1AT (I H )Q RQ; 当Q是对角阵时, QVi (1 hii )Qii ;
2, 标准化残差的相关性
Rank(Qvv) n t r QViVj hijQii hjiQjj 0
X Y
22
X ~ 2(m); Y ~ 2(n)
3) 预测残差δi 与学生化残差
1,定义: 在 观测值 L 中 去掉 Li 后 , 有:
V(i) A(i) Xˆ (i) L(i) ;
可解得 :
Xˆ (i)
(
AT (i)
P(i) A(i) )1 A(Ti) P(i) L(i)
则称 i Ai Xˆ (i) Li 为预测残差.
ui ~
N (0, 2Qii ); 1 hii
Var(i )
Var(vi ) (1 hii )2
2Qii 1 hii
.
3, 标准化预测残差与学生化残差
ui
i
Qii /(1 hii )
vi
Qii 1
hii
~
N 0,1
用
ˆ
(i
代
)
替
,
有学生化残差:
ui* ˆ(i)
i
Qii /(1 hii ) ˆ(i)
2) 标准化残差
1,
定义
ui
vi
vi
vi Qvi
vi
;
Qii (1 hii )
ui
vi
ˆ vi
ˆ
vi Qvi
ˆ 2 1 V T PV
nt
2, E(ui ) 0; D(ui ) 1;
Cov(ui , u j ) 0
往往未知.
3,
ui
vi
ˆ vi
vi
V T PV
2
Qvi
~ (n t 1);
则
0 QViVi Qii QLˆi Lˆi Qii
所以 0 ri Q P ViVi i Qii Pi 1 , 即0 ri 1
由Qii QLˆi Lˆi QViVi 还可得: QLˆiLˆi Qii 可见平差后观测值的精度比平差前是提高了。
3,普通残差的性质
(1) V QvvP( AX ) QvvP R
上式中: QvvPA (I AN 1AT P) A 0
所以:
vi (1 hii )Li hij Lj (1 hii )i hij j
ji
ji
(2) E(V ) 0, D(V ) Qvv 2
Qvv (I AN1AT P)Q(I PAN1AT ) Q AN1AT (I H )Q RQ
