深圳市龙华中英文实验学校高二数学选修1-1
深圳宝安区龙华中英文实验学校选修二第一单元《数列》测试题(答案解析)

一、选择题1.若数列{}n a 满足12a =,23a =,12n n n a a a --=(3n ≥且*N n ∈),则2018a 等于( ) A .12B .2C .3D .232.已知数列{}n a 满足25111,,25a a a ==且*121210,n n n n a a a ++-+=∈N ,则*n N ∈时,使得不等式100n n a a +≥恒成立的实数a 的最大值是( ) A .19B .20C .21D .223.已知数列{}n a 满足2122111,16,2n n n a a a a a ++===则数列{}n a 的最大项为( ) A .92B .102C .8182D .1124.数列{}n a 的通项公式为12n n a +=,其前n 项和为n T ,若不等式()2log 4(1)73n n T n n λ+-++对任意*n N ∈恒成立,则实数λ的取值范围为( )A .3λB .4λC .23λ D .34λ5.已知等差数列{}n a 的前n 项和n S 满足:21<<m m m S S S ++,若0n S >,则n 的最大值为( ) A .2mB .21m +C .22m +D .23m +6.定义:在数列{}n a 中,若满足211n n n na a d a a +++-=(n N +∈,d 为常数),称{}n a 为“等差比数列”。
已知在“等差比数列”{}n a 中,1231,3a a a ===则20152013a a =( ) A .2420151⨯- B .2420141⨯- C .2420131⨯-D .242013⨯7.已知等比数列{}n a 的前n 项和为S n ,则下列命题一定正确的是( ) A .若S 2021>0,则a 3+a 1>0 B .若S 2020>0,则a 3+a 1>0 C .若S 2021>0,则a 2+a 4>0D .若S 2020>0,则a 2+a 4>08.已知函数()()633,7,,7.x a x x f x a x -⎧--≤=⎨>⎩令()()n a f n n *=∈N 得数列{}n a ,若数列{}n a 为递增数列,则实数a 的取值范围为( ) A .()1,3B .()2,3C .9,34⎛⎫ ⎪⎝⎭D .92,4⎛⎫ ⎪⎝⎭9.设n S 是等差数列{}n a 的前n 项和,若535,9a a =则95SS =( )A .1B .1-C .2D .1210.已知数列{}n a 的前n 项和为n S ,且21n n S a =-,则66(S a = ) A .6332B .3116C .12364 D .12712811.已知数列{a n }是等比数列,S n 为其前n 项和,若a 1+a 2+a 3=4,a 4+a 5+a 6=8,则S 12= A .40 B .60 C .32D .5012.定义12...nnp p p +++为n 个正数12,,......n p p p 的“均倒数”,若已知正整数数列{}n a 的前n 项的“均倒数”为121n +,又14n n a b +=,则12231920111b b b b b b +++=( ) A .1920 B .120C .1011 D .111二、填空题13.数列{}n a 满足2121231722222n n a a a a n n -+++⋅⋅⋅+=-,若对任意0λ>,所有的正整数n 都有22n k a λλ-+>成立,则实数k 的取值范围是_________.14.设n S 是数列{}n a 的前n 项和,若点(),n n S a 在直线21y x =+上,则5a =__________. 15.设数列{}n a 的前n 项和为n S ,若()*11111n n n n N S S a +⎛⎫-=∈ ⎪⎝⎭,且112a =-,则20191S =_______.16.中国排球超级联赛争冠总决赛采用七场四胜制,即若有一队先胜四场,则此队为总冠军,比赛就此结束.现甲、乙两支球队进行总决赛,因两队实力相当,每场比赛两队获胜的可能性均为12.据以往资料统计,第一场比赛可获得门票收入500万元,以后每场比赛门票收入比上一场增加100万元.则总决赛中获得门票总收入恰好为4500万元的概率是_____. 17.数列{}n a 中,11a =,121n n a a n +=++,则数列{}n a 的通项公式为______. 18.设等比数列{}n a 的公比为q ,其前n 项之积为n T ,并且满足条件:11a >,201620171a a >,20162017011a a -<-,给出下列结论:①01q <<;②2016201810a a ->;③2016T 是数列{}n T 中的最大项;④使1n T >成立的最大自然数等于4031;其中正确结论的序号为______.19.已知n S 为等差数列{}n a 的前n 项和,且675S S S >>,给出下列说法: ①6S 为n S 的最大值;②110S >;③120S <;④850S S ->.其中正确的是______. 20.等比数列{}n a 中,11a =,且2436a a a +=,则5a =________.三、解答题21.已知数列{}n a 的前n 项和*41,()3n n n S S n N -=∈.(1)求数列{}n a 的通项公式; (2)设2log n b =n n b a ⎧⎫⎨⎬⎩⎭的前n 项和n T .22.已知数列{}n a 的前n 项和为n S ,且n a 是n S 与2的等差中项,数列{}n b ,11b =,点()1,n n P b b +直线20x y -+=上.(1)求1a 值;(2)求数列{}{},n n a b 的通项公式; (3)设n n n c a b =,求数列{}n c 的前n 项和n T .23.已知数列{a n }的前n 项和S n 和通项a n 满足2S n +a n =1,数列{b n }中,b 1=1,212b =,12n b +211n n b b +=+,(n ∈N *). (1)求数列{a n },{b n }的通项公式; (2)数列{c n }满足n n n a c b =,求证:12334n c c c c ++++<…. 24.设数列{}n a 的前n 项和2*,n S n n N =∈.(1)求数列{}n a 的通项公式; (2)若不等式1122318111log n n a a a a a a λ++++≥对任意*n N ∈恒成立,求实数λ的取值范围.25.已知数列{}n a 的前n 项和为n S ,且对任意*n N ∈,n a ,n S ,2n 成等差数列. (1)求数列{}n a 的通项公式;(2)设数列n b 是首项为1,公比为q 的正项等比数列. (i )求数列{}n b 的前n 项和n T .(ii )若数列1{2}n n b a +-为单调递增数列,求q 的取值范围.26.已知正项数列{}n a 满足2220n n a na n --=,数列(){}12nnn a a -⋅+的前n 项和为n S .(1)求数列{}n a 的通项公式; (2)求n S .【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】先由题设求得数列{}n a 的前几项,然后得到数列{}n a 的周期,进而求得结果. 【详解】因为12a =,23a =,12n n n a a a --=(3n ≥且*N n ∈), 所以23132a a a ==,34231232a a a ===, 453112332a a a ===, 564123132a a a ===,67523213a a a ===,7862323a a a ===,,所以数列{}n a 是周期为6的周期数列, 所以20183366223a a a ⨯+===, 故选:C. 【点睛】思路点睛:该题考查的是有关数列的问题,解题方法如下: (1)根据题中所给的前两项以及递推公式,逐项写出数列的前几项; (2)根据规律判断出数列的周期;(3)根据所求的数列的周期,求得20182a a =,进而求得结果.2.B解析:B 【分析】由等差数列的性质可得数列1n a ⎧⎫⎨⎬⎩⎭为等差数列,再由等差数列的通项公式可得1n n a ,进而可得1n a n=,再结合基本不等式即可得解. 【详解】因为*121210,n n n n a a a ++-+=∈N ,所以12211n n n a a a ++=+, 所以数列1n a ⎧⎫⎨⎬⎩⎭为等差数列,设其公差为d , 由25111,25a a a ==可得25112,115a a a ==⋅, 所以111121145d a d a a ⎧+=⎪⎪⎨⎪+=⋅⎪⎩,解得1111a d ⎧=⎪⎨⎪=⎩,所以()1111n n d n a a =+-=,所以1n a n=,所以不等式100n n a a +≥即100n a n+≥对任意的*n N ∈恒成立,又10020n n +≥=,当且仅当10n =时,等号成立, 所以20a ≤即实数a 的最大值是20. 故选:B. 【点睛】关键点点睛:解决本题的关键是构造新数列求数列通项及基本不等式的应用.3.B解析:B 【分析】本题先根据递推公式进行转化得到21112n n n n a a a a +++=.然后令1n n na b a +=,可得出数列{}n b 是等比数列.即11322nn n a a +⎛⎫= ⎪⎝⎭.然后用累乘法可求出数列{}n a 的通项公式,根据通项公式及二次函数的知识可得数列{}n a 的最大项. 【详解】解:由题意,可知: 21112n n n na a a a +++=. 令1n n n ab a +=,则112n n b b +=.21116a b a ==, ∴数列{}n b 是以16为首项,12为公比的等比数列. 111163222n nn b -⎛⎫⎛⎫∴== ⎪⎪⎝⎭⎝⎭.∴11322nn n a a +⎛⎫= ⎪⎝⎭. ∴1211322aa ⎛⎫= ⎪⎝⎭, 2321322a a ⎛⎫= ⎪⎝⎭,111322n n n a a --⎛⎫= ⎪⎝⎭.各项相乘,可得: 12111111(32)222n n na a --⎛⎫⎛⎫⎛⎫=⋯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.(1)2511()22n n n --⎛⎫= ⎪⎝⎭ 2115(1)221122n n n ---⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭211552212n n n --+⎛⎫= ⎪⎝⎭21(1110)212n n -+⎛⎫= ⎪⎝⎭.令2()1110f n n n =-+,则,根据二次函数的知识,可知:当5n =或6n =时,()f n 取得最小值. ()2551151020f =-⨯+=-,()2661161020f =-⨯+=-,()f n ∴的最小值为20-.∴211(1110)(20)1022101112222n n -+⨯--⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.∴数列{}n a 的最大项为102.故选:B .本题主要考查根据递推公式得出通项公式,构造新数列的方法,累乘法通项公式的应用,以及利用二次函数思想求最值;4.A解析:A 【分析】将不等式()2log 4(1)73n n T n n λ+-++对任意*n N ∈恒成立,转化为271n n n λ-++对任意*n N ∈恒成立,由2min71n n n λ⎛⎫-+ ⎪+⎝⎭求解.【详解】 依题意得,()24122412n n nT +-==--,∴不等式()2log 4(1)73n n T n n λ+-++可化为22log 2(1)73n n n n λ+-++,即27(1)n n n λ-++.又*n N ∈,∴271n n n λ-++对任意*n N ∈恒成立.只需满足2min71n n n λ⎛⎫-+ ⎪+⎝⎭即可.设1n t +=,则*t N ∈,2t ,∴27931n n t n tλ-+=+-+.∵993233t t t t+-⋅-=,当且仅当3t =,即2n =时等号成立, ∴2min731n n n ⎛⎫-+= ⎪+⎝⎭. ∴3λ,故选:A. 【点睛】方法点睛:恒(能)成立问题的解法:若()f x 在区间D 上有最值,则()()min ,00x D f x f x ∀∈>⇔>;()()max ,00x D f x f x ∀∈<⇔<;若能分离常数,即将问题转化为:()a f x >(或()a f x <),则()()max a f x a f x >⇔>;()()min a f x a f x <⇔<. 5.C【分析】首先根据数列的通项n a 与n S 的关系,得到10m a +>,2<0m a +,12+>0m m a a ++,再根据选项,代入前n 项和公式,计算结果. 【详解】由21<<m m m S S S ++得,10m a +>,2<0m a +,12+>0m m a a ++. 又()()()1212112121>02m m m m a a S m a +++++==+,()()()1232322323<02m m m m a a S m a +++++==+,()()()()122221222102m m m m m a a S m a a ++++++==++>.故选:C. 【点睛】关键点睛:本题的第一个关键是根据公式11,2,1n n n S S n a S n --≥⎧=⎨=⎩,判断数列的项的正负,第二个关键能利用等差数列的性质和公式,将判断和的正负转化为项的正负.6.C解析:C 【分析】利用定义,可得1n n a a +⎧⎫⎨⎬⎩⎭是以1为首项,2为公差的等差数列,从而121n n a n a +=-,利用201520152014201320142013a a a a a a =⋅,可得结论. 【详解】121a a ==,33a =,32212a a a a ∴-=, 1n n a a +⎧⎫∴⎨⎬⎩⎭是以1为首项,2为公差的等差数列, 121n na n a +∴=-, ()()20152015201420132014201322014122013140274025a a a a a a ∴=⋅=⨯-⨯-=⨯ 22(40261)(40261)40261420131=+-=-=⨯-.故选:C.数列的递推关系是给出数列的一种方法,根据给出的初始值和递推关系可以依次写出这个数列的各项,由递推关系求数列的通项公式,常用的方法有:①求出数列的前几项,再归纳猜想出数列的一个通项公式;②将已知递推关系式整理、变形,变成等差、等比数列,或用累加法、累乘法、迭代法求通项.7.A解析:A 【分析】根据等比数列的求和公式及通项公式,可分析出答案. 【详解】等比数列{}n a 的前n 项和为n S ,当1q ≠时,202112021(1)01a q S q-=>-,因为20211q-与1q -同号,所以10a >,所以2131(1)0a a a q +=+>,当1q =时,2021120210S a =>,所以10a >,所以1311120a a a a a +=+=>, 综上,当20210S >时,130a a +>, 故选:A 【点睛】易错点点睛:利用等比数列求和公式时,一定要分析公比是否为1,否则容易引起错误,本题需要讨论两种情况.8.B解析:B 【分析】由()()633,7,,7.x a x x f x a x -⎧--≤=⎨>⎩,()()n a f n n N *=∈得数列{}n a ,根据数列{}n a 为递增数列,联立方程组,即可求得答案. 【详解】()()633,7,,7.x a x x f x a x -⎧--≤=⎨>⎩令()()n a f n n N *=∈得数列{}n a∴()633,7,7n n a n n a a n -⎧--≤=⎨>⎩()n N *∈且数列{}na 为递增数列,得()230,1,733,a a a a ⎧->⎪>⎨⎪--<⎩解得23a <<. 即:()2,3a ∈ 故选:B. 【点睛】本题主要考查了根据递增数列求参数范围问题,解题关键是掌握递增数列的定义,考查了分析能力和计算能力,属于中档题.9.A解析:A 【分析】利用等差数列的前n 项和公式和等差数列的性质可得结果. 【详解】在等差数列{a n }中,由5359a a =,得()()9955115392199555952a a S a a a S a +==⨯=⨯=+ 故选:A 【点睛】本题考查等差数列的性质,考查等差数列的前n 项和,是基础题.10.A解析:A 【分析】利用数列递推关系:1n =时,1121a a =-,解得1a ;2n 时,1n n n a S S -=-.再利用等比数列的通项公式与求和公式即可得出. 【详解】21n n S a =-,1n ∴=时,1121a a =-,解得11a =;2n 时,1121(21)n n n n n a S S a a --=-=---,化为:12n n a a -=.∴数列{}n a 是等比数列,公比为2.56232a ∴==,66216321S -==-.则666332S a =. 故选:A . 【点睛】本题考查数列递推关系、等比数列的通项公式与求和公式,考查推理能力与计算能力,属于中档题.11.B解析:B 【解析】由等比数列的性质可知,数列S 3,S 6−S 3,S 9−S 6,S 12−S 9是等比数列,即数列4,8,S 9−S 6,S 12−S 9是等比数列,因此S 12=4+8+16+32=60,选B .12.A解析:A 【分析】首先根据新定义求得()21n S n n =+,再求数列{}n a 的通项公式,以及求得n b n =,最后利用裂项相消法求和. 【详解】由已知可得数列{}n a 的前n 项的“均倒数”为1211..21n n n a a a S n ==++++,可得()21n S n n =+,则2n ≥时,()()212111231n S n n n n -=-+-=-+⎡⎤⎣⎦,∴ 141n n n a S S n -=-=-,当1n =时,113a S ==,满足41n a n =-,41n a n ∴=-,又14n n a b +=,故n b n =, 12231920111111 (12231920)b b b b b b ∴+++=+++⨯⨯⨯ 111111191..122319202020⎛⎫⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选:A 【点睛】本题考查新定义数列的理解,考查裂项相消法求和,以及已知n S 求n a ,属于基础题型,本题的关键是理解新定义.,并能抽象为121n n S n =+. 二、填空题13.【分析】记设根据即可求出从而得到再根据题意可得分参利用基本不等式即可求出实数k 的取值范围【详解】记设当时;当时当时也满足上式所以即显然当时当时因此的最大值若存在必为正值当时因为当且仅当时取等号所以的解析:,2⎛-∞ ⎝⎭【分析】记12n n n b a -=,设21212317222222n n n S a a a a n n -=+++⋅⋅⋅+=-, 根据1112n n n S n b S S n -=⎧=⎨-≥⎩即可求出n b ,从而得到n a ,再根据题意可得()m 2ax 2n k a λλ-+>,分参利用基本不等式即可求出实数k 的取值范围.【详解】记12n n n b a -=,设21212317222222n n n S a a a a n n -=+++⋅⋅⋅+=-, 当1n =时,117322b =-=-; 当2n ≥时,()()21217171142222n n n b S n S n n n n -⎡⎤-----=-⎢⎥⎣⎦=-=. 当1n =时,13b =-也满足上式,所以()*4n b n n N =-∈,即142n n n a --=. 显然当3n ≤时,0n a <,40a =,当5n ≥时,0n a >,因此n a 的最大值若存在,必为正值.当5n ≥时,()1324n n a n a n +-=-,因为()151024n n a na n +--=≤-,当且仅当5n =时取等号. 所以n a 的最大值为116.故()m 2ax 1126n k a λλ>=-+,变形得,3116k λλ<+,而31162λλ+≥=,当且仅当λ=时取等号,所以k <.故答案为:,2⎛-∞ ⎝⎭.【点睛】本题主要考查n S 与n a 的关系1112n nn S n a S S n -=⎧=⎨-≥⎩应用,不等式恒成立问题的解法应用,以及基本不等式的应用,意在考查学生的转化能力和数学运算能力,属于中档题.解题关键是记12n n n b a -=,设21212317222222n n n S a a a a n n -=+++⋅⋅⋅+=-,利用通项n b 与前n 项和n S 的关系1112n n n Sn b S S n -=⎧=⎨-≥⎩求出通项n b ,再利用数列的单调性进而求出数列中的最大值,由基本不等式解出.14.【分析】由得两式相减得时然后利用等比数列的定义求解【详解】由题意知当时两式相减得即当时所以数列是首项为公比为的等比数列则故答案为:-1【点睛】本题主要考查数列的递推关系还考查了运算求解能力属于中档题 解析:1-【分析】由21n n a S =+,得1121n n a S --=+,两式相减得1n n a a -=-,1n =时,11a =-,然后利用等比数列的定义求解. 【详解】由题意知21n n a S =+, 当2n ≥时,1121n n a S --=+, 两式相减,得12n n n a a a --=, 即1n n a a -=-, 当1n =时,11a =-,所以数列{}n a 是首项为1-,公比为1-的等比数列, 则()()45111a =-⨯-=-. 故答案为:-1 【点睛】本题主要考查数列的递推关系,还考查了运算求解能力,属于中档题.15.【分析】用代入已知等式得变形可得说明是等差数列求其通项公式可得的值【详解】整理可得则即所以是以为公差的等差数列又则故答案为:【点评】本题考查数列递推式考查等差数列的判定训练了等差数列通项公式的求法是 解析:2020-【分析】用11n n n a S S ++=-,代入已知等式,得11n n n n S S S S ++-=⋅,变形可得1111n nS S +-=-,说明1n S ⎧⎫⎨⎬⎩⎭是等差数列,求其通项公式,可得20191S 的值.【详解】11n n n a S S ++=-,1111111n n n n nS S a S S ++⎛⎫∴-== ⎪-⎝⎭,整理可得11n n n n S S S S ++-=⋅, 则111111n n n n n n S S S S S S +++-=-=,即1111n nS S +-=-, 所以,1n S ⎧⎫⎨⎬⎩⎭是以1-为公差的等差数列,又11112S a ==-, ()()()12111nn n S ∴=-+-⋅-=-+,则201912020S =-.故答案为:2020-. 【点评】本题考查数列递推式,考查等差数列的判定,训练了等差数列通项公式的求法,是中档题.16.【分析】构造等差数列求得比赛场次再利用概率公式即可求得结果【详解】根据题意每场比赛的没票收入构成首项为公差为的等差数列设该数列为即可得由可得或(舍)故该比赛共比赛了场前场比赛比分是且第6场比赛是领先 解析:516【分析】构造等差数列,求得比赛场次,再利用概率公式,即可求得结果. 【详解】根据题意,每场比赛的没票收入,构成首项为500,公差为100的等差数列, 设该数列为{}n a ,即可得1500a =,100d =, 由4500n S =,可得6n =或15n =-(舍),故该比赛共比赛了6场,前5场比赛比分是2:3,且第6场比赛是领先队获胜.故其概率为53515216C ⎛⎫=⎪⎝⎭. 故答案为:516. 【点睛】本题考查等差数列前n 项和基本量的计算,以及n 次独立重复试验的概率求解,属综合中档题.17.【分析】根据累加法求通项公式即可【详解】解:因为所以所以……累加得:由于所以显然当时满足所以故答案为:【点睛】本题考查累加法求数列的通项公式数列前项和公式考查数学运算能力是中档题解析:2n a n =【分析】根据累加法求通项公式即可.【详解】解:因为121n n a a n +=++,所以121n n a a n +-=+, 所以()1211n n a a n --=-+,()12221n n a a n ---=-+, ()23231n n a a n ---=-+,……21211a a -=⨯+,累加得:()()211=212112112n n n a a n n n n --++-+-=⨯+-=-⎡⎤⎣⎦,*2,n n N ≥∈,由于11a =,所以2n a n =,*2,n n N ≥∈ 显然当1n =时,11a =满足2n a n =,所以2n a n =,*n N ∈. 故答案为:2n a n =【点睛】本题考查累加法求数列的通项公式,数列前n 项和公式,考查数学运算能力,是中档题.18.①③【分析】分别讨论和找到矛盾可判断①通过以及可得到则通过可判断②通过时时可判断③算出可判断④【详解】解:∵若则此时与矛盾故不成立若此时与矛盾故不成立∴故①正确;因为由得故②不正确;因为所以当时当时解析:①③ 【分析】分别讨论1q ≥和0q <,找到矛盾,可判断①,通过01q <<以及20162017011a a -<-可得到20171a <,则通过2201620182017a a a =可判断②,通过2016,n n N *≤∈时,1n a >,2016,n n N *>∈时,01n a <<,可判断③,算出4032T ,4033T 可判断④.【详解】 解:∵11a >,若1q ≥,则2015201620161201711,1a a qa a q =>=>, 此时20162017011a a ->-,与20162017011a a -<-矛盾,故1q ≥不成立, 若0q <,2015201620161201710,0a a qa a q =<=>, 此时201620170a a <,与201620171a a >矛盾,故0q <不成立,∴01q <<,故①正确;因为11a >,01q <<,20162017a a >, 由20162017011a a -<-得201620171,01a a ><<22016201820171a a a ∴=<,故②不正确;因为11a >,01q <<,201620171,01a a ><<,所以当2016,n n N *≤∈时,1n a >,当2016,n n N *>∈时,01n a <<,所以2016T 是数列{}n T 中的最大项,故③正确;()()2016201640321240304031403214032201620171a a a a a a a a T a =⋅⋯⋅⋅==>,()201624033124030403140324033201720171T a a a a a a a a =⋅⋯⋅⋅⋅=⨯<,∴使1n T >成立的最大自然数等于4032,故④不正确. 故答案为:①③. 【点睛】本题考查了等比数列的通项公式及其性质、递推关系、不等式的性质,考查了推理能力与计算能力,属于中档题.19.①②【分析】利用前项和公式得可得最大即可判断出正确命题【详解】化为:最大①为的最大值正确;②正确;③所以③不正确;④所以不正确综上可得:①②正确故答案为:①②【点睛】本题考查命题的真假判断与应用等差解析:①② 【分析】675S S S >>,利用前n 项和公式得7670,0a a a <+>,可得67670,,0a a a a d >>><,6S 最大, ()11111611110.2a a S a +==>即可判断出正确命题.【详解】675S S S >>116576546175222a d a d a d ⨯⨯⨯∴+>+>+, 化为:7670,0a a a <+>67670,,0a a a a d ∴>>>∴<6S 最大, ①6S 为n S 的最大值,正确; ()11111611110.2a a S a +==>②110S >正确;③()126760S a a =+>,所以③120S <不正确;④85678730S S a a a a -=++=<,所以850S S ->不正确. 综上可得:①②正确.故答案为: ①②. 【点睛】本题考查命题的真假判断与应用,等差数列的前n 项和公式,难度一般.20.4【分析】在等比数列中将已知转化为首项和公比求得再将其带入通项公式中求得答案【详解】因为所以在等比数列中所以或-3(舍)故故答案为:4【点睛】本题考查等比数列中知三求二由已知转化为首项和公比进而表示解析:4 【分析】在等比数列中,将已知转化为首项和公比求得2q ,再将其带入通项公式中,求得答案. 【详解】因为11a =,所以在等比数列中32422431116a a a a q a q a q q q +=⋅+=+=所以22q =或-3(舍),故425124a a q ===故答案为:4 【点睛】本题考查等比数列中知三求二,由已知转化为首项和公比,进而表示所求问题,属于简单题.三、解答题21.(1)14n n a -=;(2)11643994n n -+-⨯. 【分析】(1)2n 时,1n n n a S S -=-,1n =时,111a S ==.即可得出n a . (2)22log 2nn b log n ===,14n n n b n a -=.利用错位相减法即可得出. 【详解】解:(1)2n 时,1114141433n n n n n n a S S -----=-=-=,1n =时,111a S ==.综上可得:14n n a -=.(2)22log 2n n b log n ===,∴14n n n b na -=. ∴数列n nb a ⎧⎫⎨⎬⎩⎭的前n 项和21231444n n n T -=+++⋯⋯+.21112144444n n n n nT --=++⋯⋯++,相减可得:2111311141144444414n n n n n n n T --=+++⋯⋯+-=--. 11643994n n n T -+∴=-⨯.【点睛】本题考查了数列递推关系、等比数列的通项公式求和公式、错位相减法,考查了推理能力与计算能力,属于中档题.根据和求通项时,一定要注意1n =时的检验,利用错位相减求和法时,运算容易出错,一定要仔细准确运算,注意检查,必要时用10110,b T T a ==检验一下.22.(1)12a =;(2)2nn a =,21n b n =-;(3)1(23)26n nT n +=-⋅+.【分析】(1)由题意得出22n n a S =+,令1n =可求得1a 的值;(2)当2n ≥时,由22n n a S =+可得出1122n n a S --=+,两式作差可得出12nn a a -=,可得出数列{}n a 是等比数列,确定该数列的首项和公比,可求得数列{}n a 的通项公式,由题意可推导出数列{}n b 为等差数列,确定该数列的首项和公差,可求得数列{}n b 的通项公式;(3)求得12n n c n +=⋅,然后利用错位相减法可求得n T . 【详解】(1)由22n n a S =+得:1122a S =+ 即1122a a =+解得12a = (2)由22n n S a =-1122(2)n n S a n --=-≥①-②1122n n n n n a S S a a --=-=-12(2)nn a n a -=≥ 所以数列{}n a 是以2为首项,以2为公比的等比数列,则2nn a =又由数列{}bn 中,12b =,点()1,n n P b b +在直线20x y -+=上 得1:20n n b b +-+=且11b = 所以:12(1)21n b n n =+-=- (2)(21)2nn n n c a b n ==-数列{}n C 的前n 项和23412325272(21)2nTn n =⨯+⨯+⨯+⨯+⋯+-⋅23451212325272(21)2n n T n +=⨯+⨯+⨯+⨯+⋯+-⋅()23411222222222(21)2n n n T n +∴-=⨯+⨯+⨯+⨯+⋯+⋅--⋅可得:1(23)26n n T n +=-⋅+【点睛】解答特殊数列(等差数列与等比数列)的问题时,根据已知条件构造关于基本量的方程,解方程求出基本量,再根据定义确定数列的通项公式,当数列表示为等差和等比数列之积时,利用错位相减法求其前n 项和. 23.(1)1()3nn a =;1n b n=;(2)证明见解析. 【分析】(1)当1n =时,代入条件,可求得1a 的值,当n ≥2时,根据1n n n a S S -=-,结合等比数列的定义,即可求得数列{a n }的通项公式,根据等差中项的性质,可得1{}nb 为等差数列,代入数据,求得首项11b 和公差d ,即可求得数列{b n }的通项公式;(2)根据(1),可得1()3n n n n a c n b ==⋅,利用错位相减求和法,即可求得数列{c n }的前n 项和,根据表达式,即可得证. 【详解】(1)由2S n +a n =1,得1(1)2n n S a =-,当1n =时,111(1)2S a =-,∴113a =,当n ≥2时,11(12)n n n n a S S a -=-=--1(12)1n a --,∵10n a -≠,∴113n n a a -=, ∴{a n }是首项为13,公比为13的等比数列, ∴1()3nn a =. ∵*12211()n n n n N b b b ++=+∈,∴1{}nb 为等差数列, 由b 1=1,212b =,得111b =,212b =,21111d b b =-=,∴1{}nb 是首项为1,公差为1的等差数列, ∴11(1)1nn n b =+-⨯=,∴1n b n=. (2)1()3n n n n a c n b ==⋅, 设T n =c 1+c 2+c 3+…+c n ,则21112()()3331nn T n =⋅+⋅++⋅…①,13n T =2311111()2()()333n n +⋅+⋅++⋅…②,①-②得231211111()()()()333333n n n T n +=+++⋅⋅⋅+-⋅ 111[1()]2111133()()()133223313n n n n n T n +-=-⋅=-+-, ∴323134434n n n T +=-⨯<. 【点睛】当题中出现n S 与n a 关系时,解题的方法是利用1n n n a S S -=-求解,并检验n=1时是否满足题意,证明数列为等差、等比数列时,①可以用等差、等比数列的定义证明,②可以利用等差中项、等比中项证明,考查学生对基础知识的掌握程度,属中档题.24.(1)*21,n a n n N =-∈;(2)1,2⎡⎫+∞⎪⎢⎣⎭.【分析】(1)直接利用11,1,2n nn S n a S S n -=⎧=⎨-≥⎩,求出数列的通项公式;(2)利用(1)的结论和裂项相消法求和得到12231111+++⋯+n n a a a a a a ,再根据不等式恒成立,得到关于λ的方程,然后求出参数λ的取值范围. 【详解】解:(1)当2n ≥时,()221121n n n a S S n n n -=-=--=-,在2n S n =中,令1n =,则111a S ==,满足21n a n =-, 故数列{}n a 的通项公式是*21,n a n n N =-∈;(2)因为一般项()()111111212122121n n a a n n n n +⎛⎫==- ⎪-+-+⎝⎭,所以12231111111111111233557212121n n n a a a a a a n n n +⎛⎫+++=-+-+-++-= ⎪-++⎝⎭ 1122318111log n n a a a a a a λ++++≥对任意*n N ∈恒成立, 也就是18log 21n n λ≤+对任意*n N ∈恒成立,1min 8log 21n n λ⎛⎫≤ ⎪+⎝⎭, 因为121111*********n n n n n +-⎛⎫==- ⎪+++⎝⎭是增函数,其最小值是11112213⎛⎫-= ⎪+⎝⎭, 于是181log 3λ≤,12λ≥.故实数λ的取值范围是1,2⎡⎫+∞⎪⎢⎣⎭. 【点睛】数列求和的方法技巧(1)倒序相加:用于等差数列、与二项式系数、对称性相关联的数列的求和.(2)错位相减:用于等差数列与等比数列的积数列的求和.(3)分组求和:用于若干个等差或等比数列的和或差数列的求和.25.(1)n a n =;(2)(i ),11,11n n n q T q q q =⎧⎪=-⎨≠⎪-⎩;(ii )2q >.【分析】(1)根据对任意*n N ∈,n a ,n S ,2n 成等差数列得到22n n S a n =+,然后利用数列通项与前n 项和的关系得到()11n n a n a n -⎡⎤-=---⎣⎦求解.(2)(i )根据数列n b 是首项为1,公比为q 的正项等比数列,分 1q =, 1q ≠利用等比数列的前n 项和公式求解.(ii )令122n n n n c b a q n +==--,根据数列1{2}n n b a +-为单调递增数列,转化为10n n c c +->,对*n N ∈恒成立求解.【详解】(1)因为对任意*n N ∈,n a ,n S ,2n 成等差数列,所以22n n S a n =+,当2n ≥时,由22n n S a n =+,得()12121n n a n S --=+-, 两式相减得:121n n a a n -=-+-,即()11n n a n a n -⎡⎤-=---⎣⎦, 当1n =时,11a =,则110a -= ,所以0n a n -=,即 n a n =.(2)(i )因为数列n b 是首项为1,公比为q 的正项等比数列.当 1q =时, n T n =,当 1q ≠时, 11nn q T q-=-, 所以数列{}n b 的前n 项和,11,11nn n q T q q q =⎧⎪=-⎨≠⎪-⎩. (ii )令122n n n n c b a q n +==--,因为数列1{2}n n b a +-为单调递增数列,所以()11212(1)20n n n n n q n q n c q q c ++=-+-+=-->-,对*n N ∈恒成立, 当 1q =时, 不成立;当 01q <<时,(1)20n q q --< 不成立;当1q >时,令()(1)2nf n q q =--,()f n 递增, 只需()1(1)20f q q =-->,解得2q >所以q 的取值范围2q >.【点睛】方法点睛:数列的通项a n 与前n 项和S n 的关系是11,1,2n nn S n a S S n -=⎧=⎨-≥⎩,当n =1时,a 1若适合S n -S n -1,则n =1的情况可并入n ≥2时的通项a n ;当n =1时,a 1若不适合S n -S n -1,则用分段函数的形式表示.当数列是数列{}n a 递增数列,则数列10n n a a +->对*n N ∈恒成立;当数列是数列{}n a 递减数列,则10n n a a +-<对*n N ∈恒成立,26.(1)2n a n =;(2)()()123?216n n S n n n +=-+++. 【分析】(1)由已知得()()20n n a n a n -+=且0n a >,即可得通项公式. (2)由(1)有()()122122n nn n a a n n -⋅+=-⋅+,利用分组、错位相减法求n S . 【详解】(1)由2220n n a na n --=得()()20n n a n a n -+=,又{}n a 为正项数列, ∴2n a n =.(2)由(1)知()()122122n nn n a a n n -⋅+=-⋅+, 令n T 为数列(){}212nn -⋅的前n 项和,则()123123252212n n T n =⨯+⨯+⨯+⋅⋅⋅+-⨯,∴()23412123252212n n T n +=⨯+⨯+⨯+⋅⋅⋅+-⨯, 两式相减,得()123112222222212n n n T n +-=⨯+⨯+⨯+⋅⋅⋅+⨯--⨯,所以()()2112212221212n n n T n ++⨯⨯--=+--⨯-, 所以()12326n n T n +=-⨯+,令n B 为数列{}2n 的前n 项和,则()()1212n n n B n n +=⨯=+, 所以()()123216n n n n S T B n n n +=+=-⨯+++.【点睛】关键点点睛: (1)由已知方程,将n a 作为未知数求正解,即为数列通项公式. (2)将所得数列分为(){}212n n -⋅、{}2n 两组分别求和,应用错位相减、等差数列前n 项和公式求n S .。
深圳宝安区龙华中英文实验学校选修一第一单元《空间向量与立体几何》测试题(答案解析)
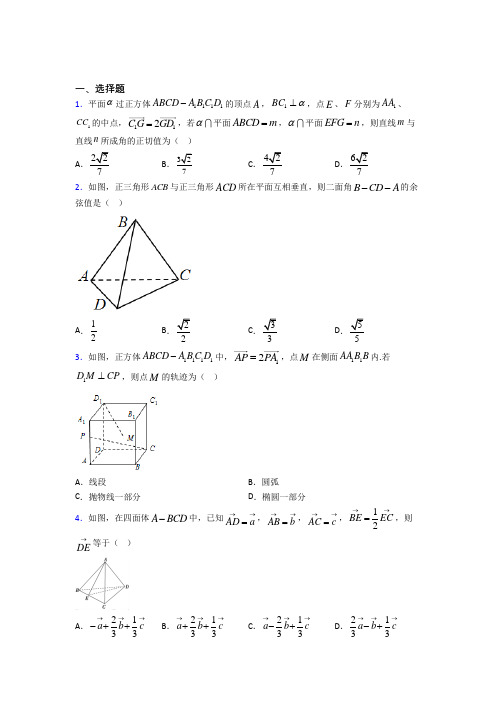
一、选择题1.平面α过正方体1111ABCD A B C D -的顶点A ,1BC α⊥,点E 、F 分别为1AA 、1CC 的中点,112C G GD =,若α平面ABCD m =,α平面EFG n =,则直线m 与直线n 所成角的正切值为( ) A .227B .327C .427D .6272.如图,正三角形ACB 与正三角形ACD 所在平面互相垂直,则二面角B CD A --的余弦值是( )A .12B .22C .33D .553.如图,正方体1111ABCD A B C D -中,12AP PA =,点M 在侧面11AA B B 内.若1D M CP ⊥,则点M 的轨迹为( )A .线段B .圆弧C .抛物线一部分D .椭圆一部分4.如图,在四面体A BCD -中,已知AD a →→=,AB b →→=,AC c →→=,12BE EC →→=,则DE →等于( )A .2133a b c →→→-++B .2133a b c →→→++C .2133a b c →→→-+D .2133a b c →→→-+5.如图,正四棱锥P ABCD -中,已知PA a =,PB b =,PC c =,12PE PD =,则BE =( )A .131222a b c -+ B .111222a b c --- C .131222a b c --+ D .113222a b c --+ 6.如图,三棱锥S ﹣ABC 中,SA =SB =SC ,∠ABC =90°,AB >BC ,E ,F ,G 分别是AB ,BC ,CA 的中点,记直线SE 与SF 所成的角为α,直线SG 与平面SAB 所成的角为β,平面SEG 与平面SBC 所成的锐二面角为γ,则( )A .α>γ>βB .α>β>γC .γ>α>βD .γ>β>α7.如图,在四面体O ABC -中,1G 是ABC 的重心,G 是1OG 上的一点,且12OG GG =,若OG xOA yOB zOC =++,则(,,)x y z 为( )A .111(,, )222B .222(, , )333C .111(, , )333D .222(,, )9998.已知(),(3,0,1),(131,2,3,1),55a b c =-==--给出下列等式:①a b c a b c ++=--;②()()a b c a b c +⋅=⋅+;③2222()a b c b c a =++++ ④()()a b c a b c ⋅⋅=⋅⋅.其中正确的个数是 A .1个B .2个C .3个D .4个9.四棱锥P ABCD -中,底面ABCD 为直角梯形,AB AD ⊥,//BC AD ,且2AB BC ==,3AD =,PA ⊥平面ABCD 且2PA =,则PB 与平面PCD 所成角的正弦值为( )A .427B 3C 7D 6 10.在棱长为1的正方体1111ABCD A B C D -中,M ,N ,H 分别在棱1BB ,BC ,BA 上,且满足134BM BB =,12BN BC =,12BH BA =,O 是平面1B HN ,平面ACM 与平面11B BDD 的一个公共点,设BO xBH yBN zBM =++,则3x y z ++=( ) A .105B .125C .145D .16511.以下四个命题中正确的是( )A .空间的任何一个向量都可用其他三个向量表示B .若{},,a b c 为空间向量的一组基底,则{},,a b b c c a +++构成空间向量的另一组基底 C .ABC ∆为直角三角形的充要条件是0AB AC ⋅= D .任何三个不共线的向量都可构成空间向量的一个基底12.如图在一个120︒的二面角的棱上有两点,A B ,线段,AC BD 分别在这个二面角的两个半平面内,且均与棱AB 垂直,若2AB =,1AC =,2BD =,则CD 的长为( ).A .2B .3C .23D .413.在正方体1111ABCD A B C D -中,点E ,F 分别是AB ,1CC 的中点,则直线1A E 与平面11B D F 所成角的正弦值是( ) A .155B .15 C .5 D .3010第II 卷(非选择题)请点击修改第II 卷的文字说明参考答案二、填空题14.在三棱锥P -ABC 中,PA ,AB ,AC 两两垂直,D 为棱PC 上一动点,2PA AC ==,3AB =.当BD 与平面PAC 所成角最大时,AD 与平面PBC 所成角的正弦值为________.15.已知直二面角l αβ--的棱l 上有A ,B 两个点,AC α⊂,AC l ⊥,BD β⊂,BD l ⊥,若4AB =,3AC =,5BD =,则CD 的长是______.16.已知正三棱柱111ABC A B C -的所有棱长都相等,则1AC 与平面11BB C C 所成角的余弦值为_________.17.如图:二面角α﹣l ﹣β等于120°,A 、B 是棱l 上两点,AC 、BD 分别在半平面α、β内,AC ⊥l ,BD ⊥l ,AB =AC =BD =1,则CD 的长等于__.18.如图所示,在正方体1111ABCD A B C D -中,M 为棱1CC 的中点,则异面线1BD 与AM 所成角的余弦值为________.19.已知向量(1,2,1)a =-,(2,2,0)b =-,则a 在b 方向上的投影为________. 20.已知A(1,2,0),B(0,1,-1),P 是x 轴上的动点,当0AP BP ⋅=取最小值时,点P 的坐标为__________.21.在空间直角坐标系中, ()()()2,1,1,3,4,,2,7,1,A B C AB CB 若λ-⊥,则λ=____ 22.在直三棱柱111ABC A B C -中,90BAC ∠=︒,14AA AB AC ===,点E 为棱1CC 上一点,且异面直线1A B 与AE 所成角的余弦值为130,则CE 的长为______. 23.如图,在棱长为2的正方体中,点P 在正方体的对角线AB 上,点Q 在正方体的棱CD 上,若P 为动点,Q 为动点,则PQ 的最小值为_____.24.如图,在平行六面体1111ABCD A B C D -中,以顶点A 为顶点的三条棱的长均为2,且两两所成角均为60°,则1||AC =__________.25.在△ABC 中,A (1,﹣1,2),B (2,1,1),C (﹣1,2,3),若向量n 与平面ABC 垂直,且n =15,则n 的坐标为_____.26.点(1,A 2,1),(3,B 3,2),(1,C λ+4,3),若,AB AC 的夹角为锐角,则λ的取值范围为______.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】以1D 为原点,11D A 为x 轴,11DC 为y 轴,1D D 为z 轴建立空间直角坐标系,用向量法计算即可. 【详解】不妨设AB =2, 以1D 为原点,11D A 为x 轴,11DC 为y 轴,1D D 为z 轴建立空间直角坐标系,则()()()()()()()1110,0,02,0,02,0,22,0,10,2,00,2,20,2,1D A A E C C F ,,,,,,, ()()()12,2,22,2,0,2,0,2,B EF C B =-=-,112420,,00,,133C G GD G GF ⎛⎫⎛⎫=∴∴= ⎪ ⎪⎝⎭⎝⎭设平面EFG 的一个法向量()1,,n x y z =,则11·2204·03n EF x y n GF y z ⎧=-+=⎪⎨=+=⎪⎩,不妨令x =1,则141,1,3n ⎛⎫= ⎪⎝⎭ 易知平面ABCD 的一个法向量为()20,0,1n =,设直线m ,n 的方向向量分别为()0000,,m x y z =,()0222,,n x y z = 因为α平面ABCD m =,1BC α⊥,所以0100020·220·0m C B x z m n z ⎧=+=⎪⎨==⎪⎩不妨令0y =1,则()00,1,0m =同理可求071,,13n ⎛⎫=--⎪⎝⎭设直线m 与直线n 所成角为θ,则0000007||||7673cos |cos ,|||||491114m n m n m n θ-====⨯⨯++所以227673134 sin1cos16767θθ⎛⎫=-=-=⎪⎪⎝⎭3134sin3267tancos 767θθθ===故选:B【点睛】向量法解决立体几何问题的关键:(1)建立合适的坐标系;(2)把要用到的向量正确表示;(3)利用向量法证明或计算.2.D解析:D【分析】取AC的中点E,连接BE,DE,证明BE垂直于平面ACD,以点E为原点建立空间直角坐标系,分别求出平面BCD和平面CDA的法向量,利用空间向量公式即可求出所求二面角的余弦.【详解】如图示,取AC中点E,连结BE、DE,在正三角形ACB与正三角形ACD中,BE⊥AC,DE⊥AC,因为面ACB⊥面ACD,面ACB面=ACD AC,所以BE⊥面ADC,以E 为原点,ED为x轴正方向,EC为y轴正方向,EB为z轴正方向,建立空间直角坐标系,设AC=2,则())()()(0,0,0,3,0,0,0,1,0,0,1,0,3E D C A B-,平面ACD的一个法向量为(3EB=而()()0,1,3,3,1,0CB CD=-=-,设(),,n x y z=为面BCD的一个法向量,则:·0·0n CB n DC ⎧=⎨=⎩即 3030y z y x ⎧-+=⎪⎨-+=⎪⎩,不妨令x =1,则()1,3,1n = 设二面角B CD A --的平面角为θ,则θ为锐角, 所以35cos |cos ,|||||5||||35EB n EB n EB n θ⋅====⨯. 故选:D 【点睛】向量法解决立体几何问题的关键: (1)建立合适的坐标系; (2)把要用到的向量正确表示; (3)利用向量法证明或计算.3.A解析:A 【分析】首先建立空间直角坐标系,利用向量数量积的坐标表示求点M 的轨迹. 【详解】如图建立空间直角坐标系,设棱长为3,()3,0,2P ,()0,3,0C,()10,0,3D ,()3,,M y z ,()13,,3D M y z =-,()3,3,2CP =-, ()193230D M CP y z ⋅=-+-=,整理为:3230y z --=,点M 的轨迹方程是关于,y z 的二元一次方程,所以轨迹是平面11ABB A 平面内,直线3230y z --=内的一段线段.故选:A 【点睛】关键点点睛:本题考查利用几何中的轨迹问题,本题的关键是解题方法,建立空间直角坐标系后,转化为坐标运算,根据方程形式判断轨迹.4.A解析:A 【分析】利用向量三角形法则与向量共线定理可得:DE BE BD →→→=-,13BE BC →→=,BC AC AB →→→=-,BD AD AB →→→=-,代入即可得出.【详解】解:已知AD a →→=,AB b →→=,AC c →→=,12BE EC →→=,利用向量三角形法则和向量共线定理得出:DE BE BD →→→=-,13BE BC →→=,BC AC AB →→→=-,BD AD AB →→→=-,∴112()()333DE AC AB AD AB c a b →→→→→→→→=---=-+,即:2133DE a b c →→→→=-++.故选:A. 【点睛】本题考查向量的三角形法则和向量基本定理的应用,考查了推理能力.5.A解析:A 【分析】连接AC BD 、交点为O ,根据根据向量加法运算法则1122PO PA PC =+,1122PO PD PB =+,求得PD ,然后由BE BP PE =+求解. 【详解】 如图所示:连接AC BD 、交点为O ,则1122PO a c =+, 又1122PO PD PB =+, 所以PD a c b =+-,又11112222PE PD a c b ==+-, 所以131222BE BP PE a b c =+=-+. 故选:A. 【点睛】本题主要考查空间向量基本定理,还考查了数形结合的思想和运算求解的能力,属于中档题.6.A解析:A 【分析】根据题意可知,G 作SE 的垂线l ,显然l 垂直平面SAB ,故直线SG 与平面SAB 所成的角为β=∠GSE ,同理,平面SEG 与平面SBC 所成的锐二面角为γ=∠FSG ,利用三角函数结合几何性质,得出结论. 【详解】因为AB ⊥BC ,SA =SB =SC ,所以AB ⊥SE ,所以AB ⊥平面SGE ,AB ⊥SG , 又SG ⊥AC ,所以SG ⊥平面ABC , 过G 作SE 的垂线l ,显然l 垂直平面SAB , 故直线SG 与平面SAB 所成的角为β=∠GSE ,同理,平面SEG 与平面SBC 所成的锐二面角为γ=∠FSG ,由tanγ=tan FG EGSG SGβ>=,得γ>β,γ也是直线SF 与平面SEG 所成的角, 由cosα=cosβ•cosγ<cosγ,则α>γ,所以α>γ>β, 故选:A .【点睛】本题考查了异面直线夹角,线面夹角,二面角,意在考查学生的空间想象能力和计算能力.7.D解析:D根据空间向量线性运算进行计算,用,,OA OB OC 表示出OG . 【详解】因为E 是BC 中点,所以1()2OE OB OC =+, 1G 是ABC 的重心,则123AG AE =, 所以122()33AG AE OE OA ==-, 因为12OG GG = 所以112224()()3339OG OG OA AG OA OE OA ==+=+-2422222()9999999OA OE OA OB OC OA OB OC =+=++=++, 若OG xOA yOB zOC =++,则29x y z ===. 故选:D . 【点睛】本题考查空间的向量的线性运算,掌握向量线性运算的运算法则是解题关键.8.D解析:D 【详解】由题设可得197(,3,)55a b c ++=,则63525a b c ++== 923(,1,)55a b c --=-,63525a b c --=,则①正确;因1346()(4,2,2)(,1,)205555a b c +⋅=⋅--=-+-=, 1481424()(1,2,3)(,1,)205555a b c ⋅+=⋅-=+-=,故②正确;又因2635127()255a b c ++==,而22235714,10,255a b c ====, 所以22271272455a b c ++=+=,即③正确; 又3030a b ⋅=+-=,则()0a b c ⋅⋅=, 而330055b c ⋅=-++=,故()0a b c ⋅⋅=,也即④正确.9.C解析:C 【分析】以A 为坐标原点建立空间坐标系,进而求得PB 和平面PCD 的法向量,再由向量的数量积即可求得PB 与平面PCD 所成角的正弦值. 【详解】依题意,以A 为坐标原点,分别以,,AB AD AP 为,,x y z 轴建立空间直角坐标系O xyz -,2,3,2AB BC AD PA ====,则()()()()0,0,2,2,0,0,2,2,0,0,3,0P B C D , 从而()()()2,0,2,2,2,2,0,3,2PB PC PD =-=-=-设平面PCD 的法向量为(),,n a b c =,00n PC n PD ⎧⋅=⎨⋅=⎩,即2220320a b c b c +-=⎧⎨-=⎩,不妨取3c =c=3,则1,2a b ==,所以平面PCD 的一个法向量为()1,2,3n =, 所以PB 与平面PCD 所成角的正弦值 ()22222267sin cos ,22123PB n θ-===+-++, 故选C. 【点睛】本题主要考查了线面所成的角, 其中求解平面的法向量是解题的关键,着重考查了推理与计算能力,属于中档试题.10.C解析:C 【分析】根据条件确定O 点位置,再根据向量表示确定,,x y z 的值,即得结果.如图,Q 为AC 与BD 交点,P 为BQ 中点,O 为MQ 与1B P 的交点.过P 作PT 平行MQ 交1BB 于T .如图,则T 为BM 中点,所以1111131334224242MT BM BB MB MB ==⨯=⨯⨯=. 所以123B O OP =, 因此1323421411()555352555BO BB BP BM BH BN BM BH BN =+=⋅+⋅+=++, 因为BO xBH yBN zBM =++,所以411,,555z x y ===,1435x y z ∴++=. 故选:C 【点睛】本题考查平面向量基底表示,考查综合分析求解能力,属中档题.11.B解析:B 【分析】根据空间向量基底的定义:任何三个不共面的向量都可构成空间向量的一组基底,逐一分析A ,B ,D 可判断这三个结论的正误;根据向量垂直的充要条件,及直角三角形的几何特征,可判断C 的真假. 【详解】对A ,空间的任何一个向量都可用其他三个不共面的向量表示,A 中忽略三个基底不共面的限制,故A 错误;对B ,若{},,a b c 为空间向量的一组基底,则,,a b c 三个向量互不共面;则,,a b b c c a +++,也互不共面,故{,,}a b b c c a +++可又构成空间向量的一组基底,故B 正确;对C ,0AB AC ABC ⋅=⇔∆的A ∠为直角ABC ⇒∆为直角三角形,但ABC ∆为直角三角形时,A ∠可能为锐角,此时0AB AC ⋅>,故C 错误;对D ,任何三个不共面的向量都可构成空间向量的一组基底,三个向量不共线时可能共面,故D 错误; 故选:B . 【点睛】本题以命题的真假判断为载体考查空间向量的基底概念、向量垂直的充要条件,考查对概念的理解与应用,属基础题.12.B解析:B 【分析】由CD CA AB BD =++,两边平方后展开整理,即可求得2CD ,则CD 的长可求. 【详解】 解:CD CA AB BD =++,∴2222222CD CA AB BD CA AB CA BD AB BD =+++++,CA AB ⊥,BD AB ⊥,∴0CA AB =,0BD AB =,()1||||cos 1801201212CA BD CA BD =︒-︒=⨯⨯=.∴2124219CD =+++⨯=,||3CD ∴=,故选:B . 【点睛】本题考查了向量的多边形法则、数量积的运算性质、向量垂直与数量积的关系,考查了空间想象能力,考查了推理能力与计算能力,属于中档题.13.D解析:D 【分析】设正方体棱长为2,以1,,AD AB AA 为,,x y z 轴建立空间直角坐标系,求得1(0,1,2)A E =-和平面11B D F 的一个法向量为(1,1,2)n =,利用向量的夹角公式,即可求解. 【详解】设正方体棱长为2,分别以1,,AD AB AA 为,,x y z 轴建立空间直角坐标系, 则111(0,0,2),(0,1,0),(0,2,2),(2,0,2),(2,2,1)A E B D F , 所以1111(0,1,2),(2,2,0),(2,0,1)A E B D B F =-=-=-.设平面11B D F 的法向量为(,,)n x y z =,则1110,0,n B D n B F ⎧⋅=⎪⎨⋅=⎪⎩即220,20,x y x z -=⎧⎨-=⎩令1x =,则1,2y z ==, 即平面11B D F 的一个法向量为(1,1,2)n =. 设直线1A E 与平面11B D F 所成角为θ, 则1130sin 30n A E n A Eθ⋅===⋅ 故选D. 【点睛】本题主要考查了利用空间向量求解直线与平面所成的角,根据几何体的结构特征,建立适当的空间直角坐标系,求得直线的方向向量和平面的一个法向量,利用向量的夹角公式,准确计算是解答的关键,着重考查了推理与运算能力,属于基础题.二、填空题14.【分析】首先可证平面PAC 则BD 与平面PAC 所成角为所以当D 为PC 的中点时取得最大值如图建立空间直角坐标系利用空间向量法求出线面角的正弦值;【详解】解:因为PAABAC 两两垂直所以平面PAC 则BD 与 311【分析】首先可证AB ⊥平面PAC ,则BD 与平面PAC 所成角为ADB ∠,所以当D 为PC 的中点时ADB ∠取得最大值,如图建立空间直角坐标系,利用空间向量法求出线面角的正弦值; 【详解】解:因为PA ,AB ,AC 两两垂直,PA AC A =所以AB ⊥平面PAC ,则BD 与平面PAC 所成角为ADB ∠, 所以3tan AB ADB AD AD∠==, 当AD 取得最小值时,ADB ∠取得最大值在等腰Rt PAC △中, 当D 为PC 的中点时,AD 取得最小值,以A 为坐标原点, 建立如图所示的空间直角坐标系A -xyz ,则(0,0,0)A ,(3,0,0)B ,(0,2,0)C ,(0,0,2)P ,(0,1,1)D , 则(0,1,1)AD =,(0,2,2)PC=-,(3,2,0)BC =-,设平面PBC 的法向量为(,,)n x y z =,则0n PC n BC ⋅=⋅=,即220320y z x y -=⎧⎨-+=⎩,令3y =,得(2,3,3)n =. 因为311cos ,222n AD 〈〉==⨯ 所以AD 与平面PBC 311. 故答案为:31111【点睛】(1)求直线与平面所成的角的一般步骤:①找直线与平面所成的角,即通过找直线在平面上的射影来完成; ②计算,要把直线与平面所成的角转化到一个三角形中求解.(2)作二面角的平面角可以通过垂线法进行,在一个半平面内找一点作另一个半平面的垂线,再过垂足作二面角的棱的垂线,两条垂线确定的平面和二面角的棱垂直,由此可得二面角的平面角.15.【分析】首先然后利用向量数量积表示向量的模计算的长度【详解】由条件可知故答案为:【点睛】关键点点睛:本题考查空间几何中长度的计算本题的关键点是分析出从而利用数量积表示比较容易计算结果解析:52【分析】首先CD CA AB BD =++,然后利用向量数量积表示向量的模,计算CD 的长度. 【详解】CD CA AB BD =++, ()()22222CD CA AB BDCA AB BD CA AB CA BD AB BD ∴=++=+++⋅+⋅+⋅由条件可知CA AB ⊥,CA BD ⊥,AB BD ⊥,()22229162552CD CA AB BD CA AB BD ∴=++=++=++=.故答案为:52 【点睛】关键点点睛:本题考查空间几何中长度的计算,本题的关键点是分析出CA AB ⊥,CA BD ⊥,ABBD ⊥,从而利用数量积表示CD ,比较容易计算结果.16.【分析】取BC 的中点E 连接AE 证明面可得就是与平面所成的角解直角三角形即可【详解】如上图取BC 的中点E 连接AE 则∵正三棱柱中面面面面∴面∴就是与平面所成的角不妨设正三棱柱的所有棱长都为2则在中故答案 解析:104【分析】取BC 的中点E ,连接1C E ,AE ,证明AE ⊥面11BB C C ,可得1E AC ∠就是1AC 与平面11BB C C 所成的角,解直角三角形1AC E 即可.【详解】如上图,取BC 的中点E ,连接1C E ,AE ,则AE BC ⊥, ∵正三棱柱111ABC A B C -中,面ABC ⊥面11BB C C ,面ABC 面11BB C C BC =,∴AE ⊥面11BB C C ,∴1E AC ∠就是1AC 与平面11BB C C 所成的角,不妨设正三棱柱111ABC A B C -的所有棱长都为2,则15C E =122AC =在1Rt AC E ∆中,111cos C E AC E AC ∠===.【点睛】本题考查直线与平面所成的角,考查空间想象能力和计算能力,属于常考题.17.2【分析】求CD 的长即为由向量的加法可得利用向量的数量积运算即可得出答案【详解】∵AB 是棱l 上两点ACBD 分别在半平面αβ内AC ⊥lBD ⊥l 因为所以因为所以故答案为:2【点睛】本题主要考查空间向量的解析:2 【分析】求CD 的长即为CD ,由向量的加法可得CD CA AB BD =++,利用向量的数量积运算即可得出答案. 【详解】∵A 、B 是棱l 上两点,AC 、BD 分别在半平面α、β内,AC ⊥l ,BD ⊥l ,0,0∴⋅=⋅=CA AB BD AB ,,60︒<>=CA BD因为1AB AC BD ===,所以111cos602︒⋅=⨯⨯=CA BD , 因为CD CA AB BD =++, 所以2()12=++==CD CA AB BD故答案为:2 【点睛】本题主要考查空间向量的加法,减法及几何意义和空间向量的数量积,考查了运算求解能力和转化的数学思想,属于一般题目.18.【分析】建立空间直角坐标系以的方向为x 轴y轴z 轴的正方向不妨设正方体的棱长为1则异面线与AM 所成角的余弦值转化为求向量的夹角的余弦值利用向量夹角公式即得【详解】分别以的方向为x 轴y 轴z 轴的正方向建立 【分析】建立空间直角坐标系,以1,,DA DC DD 的方向为x 轴,y 轴,z 轴的正方向,不妨设正方体的棱长为1,则异面线1BD 与AM 所成角的余弦值,转化为求向量1,BD AM 的夹角的余弦值,利用向量夹角公式即得. 【详解】分别以1,,DA DC DD 的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系,不妨设正方体的棱长为1,则11(1,0,0),(1,1,0),(0,1,),(0,0,1)2A B M D ,可得11(1,1,1),(1,1,)2BD AM =--=-,则11111132cos ,||||13114BD AMBD AM BD AM -+⋅<>===⋅++,即异面直线1BD 与AM 所成角的余弦值为3. 故答案为:3【点睛】本题考查利用空间向量求异面直线的夹角,运用了向量夹角公式.19.【分析】根据向量投影的计算公式计算出在方向上的投影【详解】依题意在方向上的投影为【点睛】本小题主要考查向量在另一个向量上的投影的计算考查空间向量的数量积的坐标运算属于基础题 解析:322-【分析】根据向量投影的计算公式,计算出a 在b 方向上的投影. 【详解】依题意a 在b 方向上的投影为()223222222a b b⋅===-+-.【点睛】本小题主要考查向量在另一个向量上的投影的计算,考查空间向量的数量积的坐标运算,属于基础题.20.(00)【分析】设P(x00)求出·=x(x -1)+2=(x -)2+再利用二次函数求出函数的最小值和此时点P 的坐标【详解】设P(x00)则=(x -1-20)=(x -11)·=x(x -1)+2=(x -解析:(12,0,0) 【分析】设P (x,0,0),求出·=x (x -1)+2=(x -)2+,再利用二次函数求出函数的最小值和此时点P 的坐标. 【详解】 设P (x,0,0),则=(x -1,-2,0),=(x ,-1,1),·=x (x -1)+2=(x -)2+, ∴当x =时,·取最小值,此时点P 的坐标为(,0,0).故答案为(12,0,0) 【点睛】(1)本题主要考查空间向量的坐标表示和数量积的计算,意在考查学生对这些知识的掌握水平和分析推理能力.(2) 111222121212(,,),(,,),a x y z b x y z a b x x y y z z ==⋅=++.21.【分析】利用空间向量的结论将垂直的问题转化为向量数量积等于零的问题然后利用向量的数量积坐标运算计算的值即可【详解】又即解得故答案为【点睛】本题主要考查空间向量的应用向量垂直的充分必要条件等知识意在考 解析:3±【分析】利用空间向量的结论将垂直的问题转化为向量数量积等于零的问题,然后利用向量的数量积坐标运算计算λ的值即可. 【详解】()()()2,1,1,3,4,,2,7,1A B C λ-, ∴AB ()1,3,1,λ=+CB ()1,3,1λ=--,又,AB CB ⊥0AB CB ∴⋅=,即()()()1133110λλ⨯+⨯-++-=,解得3λ=±, 故答案为3±. 【点睛】本题主要考查空间向量的应用,向量垂直的充分必要条件等知识,意在考查学生的转化能力和计算求解能力.22.【分析】利用基向量表示出结合异面直线所成角确定点E 的位置从而可求的长也可以建立空间坐标系利用空间向量坐标求解【详解】设则因为异面直线与所成角的余弦值为所以解得所以故答案为:【点睛】关键点睛:利用空间 解析:12【分析】利用基向量表示出1,A B AE,结合异面直线所成角,确定点E 的位置,从而可求1C E 的长,也可以建立空间坐标系,利用空间向量坐标求解.【详解】设1CE C C λ= ,则11A B AB AA =-,11AE AC CE AC CC AC AA λλ=+=+=+, 142A B =,21616AE λ=+,111()()16A B AE AB AA AC AA λλ⋅=-⋅+=-. 1121cos ,22A B AEA B AE A B AE λ⋅==+,因为异面直线1A B 与AE 所成角的余弦值为130,所以200213213λ=+. 解得18λ=,所以12CE =. 故答案为:12.【点睛】关键点睛:利用空间向量解决异面直线所成角的问题,注意向量夹角与异面直线所成角的范围的不同.23.【分析】建立空间直角坐标系利用三点共线设出点P(λλ2﹣λ)0≤λ≤2以及Q(02μ)0≤μ≤2根据两点间的距离公式以及配方法即可求解【详解】建立如图所示空间直角坐标系设P(λλ2﹣λ)Q(02μ)2【分析】建立空间直角坐标系,利用,,A B P 三点共线设出点P (λ,λ,2﹣λ),0≤λ≤2,以及Q (0,2,μ),0≤μ≤2,根据两点间的距离公式,以及配方法,即可求解.【详解】建立如图所示空间直角坐标系,设P (λ,λ,2﹣λ),Q (0,2,μ)(0≤λ≤2且0≤μ≤2),可得PQ =22222(2)(2)2(1)(2)2λλλμλλμ+-+--=-+--+,∵2(λ﹣1)2≥0,(2﹣λ﹣μ)2≥0,∴2(λ﹣1)2+(2﹣λ﹣μ)2+2≥2,当且仅当λ﹣1=2﹣λ﹣μ=0时,等号成立,此时λ=μ=1,∴当且仅当P 、Q 分别为AB 、CD 的中点时,PQ 的最小值为2. 故答案为:2.【点睛】本题考查空间向量法求两点间的距离,将动点用坐标表示是解题的关键,考查配方法求最值,属于中档题.24.【分析】设且利用数量积运算即得解【详解】设故答案为:【点睛】本题考查了空间向量的模长数量积运算考查了学生空间想象数学运算能力属于中档题解析:6【分析】设1,,AB a AD b AA c ===,且1|||++|AC a b c =,利用数量积运算即得解. 【详解】设1,,||||||2,,,60o AB a AD b AA c a b c a b a c c b ===∴===<>=<>=<>=, 222221|||++|||||||22224AC a b c a b c a b a c c b ==+++⋅+⋅+⋅=||26AC ∴=故答案为:26【点睛】 本题考查了空间向量的模长,数量积运算,考查了学生空间想象,数学运算能力,属于中档题.25.(57)或(﹣5﹣7)【分析】求出23设向量与平面垂直列出方程组能求出结果【详解】∵在△ABC 中A (1﹣12)B (211)C (﹣123)∴(12﹣1)(﹣231)设∵向量与平面ABC 垂直∴解得∵∴1解析:n =(33,3n =(﹣3,3,﹣3【分析】求出(1AB =,2,1)-,(2AC =-,3,1),设(n x =,y ,)z ,向量n 与平面ABC 垂直,15n =,列出方程组能求出结果.【详解】∵在△ABC 中,A (1,﹣1,2),B (2,1,1),C (﹣1,2,3),∴AB =(1,2,﹣1),AC =(﹣2,3,1),设(),,n x y z =∵向量n 与平面ABC 垂直,∴20230n AB x y z n AC x y z ⎧⋅=+-=⎨⋅=-++=⎩,解得57x y z y=⎧⎨=⎩,∵15n =,∴=15,解得3y =,x = 73z =或y =x =- z =-∴(53,n =或(53,n =--.【点睛】本题考查向量的坐标的求法,考查向量与平面垂直、向量的模等基础知识,考查运算求解能力,属于中档题. 26.【分析】根据的夹角为锐角可得且不能同向共线解出即可得出【详解】12的夹角为锐角且不能同向共线解得则的取值范围为故答案为【点睛】本题主要考查了向量夹角公式向量共线定理考查了推理能力与计算能力属于中档题 解析:()()2,44,∞-⋃+【分析】根据,AB AC 的夹角为锐角,可得0AB AC ⋅>,且不能同向共线.解出即可得出.【详解】(2,AB =1,1),(,AC λ=2,2),,AB AC 的夹角为锐角,2220AB AC λ∴⋅=++>,且不能同向共线.解得2λ>-,4λ≠.则λ的取值范围为()()2,44,∞-⋃+.故答案为()()2,44,∞-⋃+.【点睛】本题主要考查了向量夹角公式、向量共线定理,考查了推理能力与计算能力,属于中档题.。
深圳菁华中英文实验中学高中数学选修2-1第一章《常用逻辑用语》检测(包含答案解析)

一、选择题1.下列命题中,真命题是( ) A .命题“若a b >,则22ac bc >” B .命题“若a b =,则a b =”的逆命题 C .命题“当2x =-时,2560x x ++=”的否命题D .命题“终边相同的角的同名三角函数值(三角函数值存在)相等”的逆否命题 2.已知1:12p x ≥-,:2q x a -<,若p 是q 的充分不必要条件,则实数a 的取值范围为( ) A .(],4-∞B .[]1,4C .(]1,4D .()1,43.下列命题中为真命题的是( )A .若命题p :“2,10x R x x ∃∈-->”,则命题p 的否定为:“2,10x R x x ∀∈--≤”B .直线,a b 为异面直线的充要条件是直线,a b 不相交C .“1a =”是“直线0x ay -=与直线0x ay +=互相垂直”的充要条件D .0x ≠则12x x+≥ 4.已知命题p :在ABC 中,若A B >,则cos cos A B <,命题q :()0,x ∃∈+∞,sin x x >,则下列命题中为真命题的是( )A .p q ∧B .()p q ⌝∧C .()p q ∨⌝D .()()p q ⌝∧⌝5.下列说法中错误的是( )A .命题“1x ∀>,20x x ->”的否定是“01x ∃>,2000x x -≤”.B .在ABC 中,sin sin cos cos A B A B A B <⇔<⇔>.C .已知某6个数据的平均数为3,方差为2,现又加入一个新数据3,则此时这7个数的平均数和方差不变.D .从装有完全相同的4个红球和2个黄球的盒子中任取2个小球,则事件“至多一个红球”与“都是红球”互斥且对立.6.命题:p 关于x 的不等式2240x ax ++>对一切x ∈R 恒成立,:q 函数()()32xf x a =-是增函数,若“p q ∨”为真命题,“p q ∧”为假命题,则实数a 取值范围为( ) A .()(),22,-∞-+∞B .(][),21,2-∞-C .(](],21,2-∞-D .(][),22,-∞-+∞7.下列说法正确的是( )A .命题“,0x x R e ∀∈>”的否定是“,0x x R e ∃∈>”B .命题“已知,x y R ∈,若3,x y +≠则2x ≠或1y ≠”是真命题C .命题“若1,a =-则函数2()21f x ax x =+-只有一个零点”的逆命题为真命题D .“22x x ax +≥在[]1,2x ∈上恒成立”2min min (2)()x x ax ⇔+≥在[]1,2x ∈上恒成立8.下列四种说法中,错误的个数是( )①命题“x ∃∈R ,20x x ->”的否定是“x ∀∈R ,20x x -≤”; ②命题“p q ∨为真”是命题“p q ∧为真”的必要不充分条件; ③“若22am bm <,则a b <”的逆命题为真; ④若实数x ,[]0,1y ∈,则满足221x y +>的概率为4π. A .0个B .1个C .2个D .3个9.下列说法错误的是( )A .“若2560x x -+=,则2x =”的逆否命题是“若2x ≠,则2560x x -+≠”B .“2x >”是“2230x x +->”的充分不必要条件C .“x R ∀∈,2650x x -+≠”的否定是“0x R ∃∈,200650x x -+=”D .若“p q ∧”为假命题,则,p q 均为假命题10.已知条件p :()()30x m x m --->;条件q :2340x x +-<,若q 是p 的充分不必要条件,则实数m 的取值范围是( ) A .(,7)(1,)-∞-+∞B .(],7[1,)-∞-+∞C .()7,1-D .[]7,1-11.已知x 、y R ∈,则“221x y +<”是“()()110x y -->”成立的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分又不必要条件12.设:22x p ≤,2:log 0q x <,则p 是q 的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件二、填空题13.若不等式21x m -<成立的一个充分不必要条件为1<x <2,则实数m 的取值范围为________.14.已知2:230p x x --<,:1q m x m <<+,若p 是q 的必要不充分条件,则实数m 的取值范围是________.15.若0, 0a >b >,则“4a b +≤”是 “4ab ≤”的_____条件16.设x ∈R ,则“1x <”是“20x x -<”的__________条件.(填“充分必要”、“充分不必要”、“必要不充分”、“既不充分也不必要”)17.若命题“存在实数x ,使得()222(2)40a x a x -+--≥成立”是假命题,则实数a 的取值范围是________.18.已知命题P :“1a ≠或2b ≠”,Q :“3a b +≠”,则P 是Q 成立的______ 19.下列是有关△ABC 的几个命题:① 若tan tan tan 0A B C ++>,则△ABC 是锐角三角形;② 若cos cos a A b B =,则△ABC 是等腰三角形;③ 若cos cos a B b A b +=,则△ABC 是等腰三角形;④ 若cos sin A B =,则△ABC 是直角三角形,其中所有正确命题的序号是________20.已知命题p :存在[]0,1x ∈,使得0x a e -≥成立,命题:q 对任意x ∈R ,240x x a ++> 恒成立,若命题p q ∧⌝是真命题,则实数a 的取值范围是______________.三、解答题21.已知命题:“{}|11x x x ∃∈-<<,使等式220x x m --=成立”是真命题. (1)求实数m 的取值集合M ;(2)设不等式()()20x a x a -+-<的解集为N ,若x ∈N 是x M ∈的必要条件,求a 的取值范围.22.已知命题p :(x +1)(x -5)≤0,命题q :1-m ≤x ≤1+m (m >0). (1)若p 是q 的充分条件,求实数m 的取值范围;(2)若m =5,p ∨q 为真命题,p ∧q 为假命题,求实数x 的取值范围.23.已知{}2|8200A x x x =--≤,{}|2B x x m =-≤(1)若“∃x ∈A ,使得x ∈B ”为真命题,求m 的取值范围;(2)是否存在实数m ,使“x ∈A ”是“X ∈B ”必要不充分条件,若存在,求出m 的取值范围;若不存在,请说明理由.24.给定两个命题P :对任意实数x 都有210ax ax ++>恒成立;Q :关于x 的方程20x x a -+=有实数根;(1)“0a =”是P 的什么条件?(2)如果P 与Q 中有且仅有一个为真命题,求实数a 的取值范围. 25.已知命题p :实数x 满足245220x x ⋅-⋅+≥,命题q :实数x 满足2(21)(1)0x m x m m -+++≥.(1)求命题p 为真命题,求实数x 的取值范围;(2)若命题q 是命题p 的必要不充分条件,求实数m 的取值范围.26.设命题:p 对任意[]0,1x ∈,不等式2234x m m -≥-恒成立,命题:q 存在[]1,1x ∈-,使得不等式2210x x m -+-≤成立. (1)若p 为真命题,求实数m 的取值范围;(2)若p ,q 有且只有一个为真,求实数m 的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】根据不等式的性质和四种命题的关系判断各选项. 【详解】 A .当0c时,22ac bc >不成立,A 错;B .命题“若a b =,则a b =”的逆命题是若a b =,则a b =,错误,也可能是=-a b ;C .命题“当2x =-时,2560x x ++=”的否命题是若2x ≠-,则2560x x ++≠,错误,3x =-时,也有2560x x ++=;D .命题“终边相同的角的同名三角函数值(三角函数值存在)相等”是真命题,逆否命题也是真命题. 故选:D . 【点睛】关键点点睛:本题考查命题真假的判断,四种命题之间互为逆否的命题同真假,因此原命题的为真只能判断逆否命题为真,而逆命题和否命题的真假不确定,需写出逆命题,否命题进行判断.这也告诉我们当一个命题难以判断真假时可考虑判断其逆否命题的真假.2.C解析:C【分析】求出p 、q 中的不等式,根据p 是q 的充分不必要条件可得出关于实数a 的不等式组,由此可解得实数a 的取值范围. 【详解】 解不等式112x ≥-,即131022x x x --=≤--,解得23x <≤, 解不等式2x a -<,即22x a -<-<,解得22a x a -<<+, 由于p 是q 的充分不必要条件,则(]2,3()2,2a a -+,所以2223a a -≤⎧⎨+>⎩,解得14a <≤.因此,实数a 的取值范围是(]1,4. 故选:C. 【点睛】本题考查利用充分不必要条件求参数,同时也考查了分式不等式和绝对值不等式的求解,考查计算能力,属于中等题.3.A解析:A 【分析】A ,根据一个是特称命题的否定,变为全称命题,即可判断;B ,根据空间中两条直线的位置关系得到结果;C ,根据两条直线垂直的条件得到a 的值;D 、根据基本不等式得到,这个不等式大于等于2或小于等于2-. 【详解】解:对于A ,根据特称命题的否定形式知道:命题p :“x R ∃∈,210x x -->”,则命题p 的否定为:“x R ∀∈,210x x --”,故A 是真命题;对于B ,直线a ,b ,为异面直线的充要条件是直线a ,b 不相交且不平行,故B 为假命题;对于C ,“直线0x ay -=与直线0x ay +=互相垂直” ⇔ “1a =±”,故“1a =”是“直线0x ay -=与直线0x ay +=互相垂直”的充分不必要条件,故C 为假命题;对于D ,若0x >,则12x x+,或若0x <,则12x x +-,故D 为假命题. 故选:A . 【点睛】本题考查命题的否定,考查函数的值域,考查空间中两条直线的位置关系,考查特称命题和全称命题的否定,属于中档题.4.C解析:C 【分析】由函数cos y x =在(0,)π上的单调性即可判断p 为真命题;当(0,)2x π∈时,令()sin f x x x =-,利用导数判断函数()f x 在(0,)2π上的单调性从而证明sin x x <,当[,)2x π∈+∞时,根据图象判断sin x x <,即可确定q 为假命题,利用复合命题的真假判断规则进行判断即可. 【详解】命题p :在ABC 中,,(0,)A B π∈,因为函数cos y x =在(0,)π上单调递减,所以若A B >,则cos cos A B <,命题p 为真命题.命题q :令()sin f x x x =-,当(0,)2x π∈时,cos 10y x '=-<,函数()sin f x x x=-在(0,)2π上单调递减,所以()(0)0f x f <=,即sin x x <;当[,)2x π∈+∞时,由下图可知sin x x <,所以q 为假命题.所以()p q ∨⌝为真命题. 故选:C 【点睛】本题考查复合命题的真假判断,涉及正、余弦函数的图象与性质,利用导数证明不等式,属于中档题.5.C解析:C 【分析】选项A 根据命题的否定判断,选项B 根据正弦定理及两角和的余弦公式判定即可,选项C 可根据均值及方差的性质判断,选项D 根据互斥事件与对立事件的定义判断即可. 【详解】A 中根据命题的否定可知,命题“1x ∀>,20x x ->”的否定是“01x ∃>,2000x x -≤”正确;B 中A B <可知a b <,根据正弦定理可得sin sin A B <,同理可知由sin sin A B <可得a b <,可得A B <,即sin sin A B A B <⇔<,因为cos y x =在(0,)x π∈上单调递减,且(0,),(0,)A B ππ∈∈,所以cos cos A B A B <⇔>,故正确;C 中设原数据中方差为2s ,则加入一个新数据3后平均值为63337⨯+=,方差为2226(33)677s s ⨯+-=,故不正确;D 中,事件“至多一个红球”与“都是红球”不能同时发生,而且在一次试验中有且只有一个事件发生, 故互斥且对立正确. 故选:C 【点睛】本题主要考查了命题的否定,三角形中的充要条件,平均值与方差,互斥与对立事件,属于中档题.6.B解析:B 【分析】先求得命题,p q 为真命题时,a 的取值范围.根据“p q ∨”为真命题,“p q ∧”为假命题可知,p q 一真一假,由此进行分类讨论,求得a 的取值范围.【详解】当p 为真命题时,24160a ∆=-<,解得22a -<<. 当q 为真命题时,321,1a a -><.由于“p q ∨”为真命题,“p q ∧”为假命题,所以,p q 一真一假. 当p 真q 假时,221a a -<<⎧⎨≥⎩,解得12a ≤<;当p 假q 真时,221a a a ≤-≥⎧⎨<⎩或,解得2a ≤-.综上所述,实数a 的取值范围是(][),21,2-∞-.故选:B 【点睛】本小题主要考查一元二次不等式恒成立问题,考查根据含有逻辑联结词命题的真假性求参数的取值范围,考查分类讨论的数学思想方法,属于基础题.7.B解析:B 【分析】A .注意修改量词并否定结论,由此判断真假;B .写出逆否命题并判断真假,根据互为逆否命题同真假进行判断;C .写出逆命题,并分析真假,由此进行判断;D .根据对恒成立问题的理解,由此判断真假. 【详解】A .“,0x x R e ∀∈>”的否定为“,0x x R e ∃∈≤”,故错误;B .原命题的逆否命题为“若2x =且1y =,则3x y +=”,是真命题,所以原命题是真命题,故正确;C .原命题的逆命题为“若函数2()21f x ax x =+-只有一个零点,则1a =-”, 因为0a =时,()21f x x =-,此时也仅有一个零点,所以逆命题是假命题,故错误;D .“22x x ax +≥在[]1,2x ∈上恒成立”⇔“min2x a x ⎛⎫+≥ ⎪⎝⎭在[]1,2x ∈上恒成立”,故错误. 故选:B. 【点睛】本题考查命题真假的判断,涉及到函数零点、含一个量词的命题的真假判断、不等式恒成立问题的理解等内容,难度一般.注意互为逆否命题的两个命题真假性相同.8.C解析:C【分析】根据题意,①②说法正确,若0m =③错误,根据古典概型④概率应该为14π-.【详解】命题“x ∃∈R ,20x x ->”的否定是“x ∀∈R ,20x x -≤”,所以①正确; 命题“p q ∨为真”即p ,q 至少有一个为真,不能推出命题“p q ∧为真”,命题“p q ∧为真”则p ,q 全为真,能够推出命题“p q ∨为真”,所以命题“p q ∨为真”是命题“p q ∧为真”的必要不充分条件,所以②正确;“若22am bm <,则a b <”的逆命题是:若a b <,则22am bm <,当0m =时不成立,所以该逆命题不是真命题,所以③不正确;若实数x ,[]0,1y ∈,有序数对(),x y 对应平面内的点形成的区域面积为1,如图:其中扇形区域不满足221x y +>,面积为4π,深色区域符合题意, 则满足221x y +>的概率为14π-,所以④不正确.故选:C 【点睛】此题考查命题的真假判断,涉及全称命题的否定,含有逻辑连接词的命题真假判断,不等式的性质辨析,求几何概型,涉及知识面比较广.9.D解析:D 【分析】根据逆否命题的定义、集合间的关系、全称命题的否定、p q ∧为假命题的定义,对选项进行一一验证,即可得答案. 【详解】对A ,根据逆否命题的定义可知命题正确,故A 正确;对B ,若2230x x +->,则1x >或3x <-,所以“2x >”是“2230x x +->”的充分不必要条件,故B 正确;对C ,因为全称命题的否定是特称命题,且将结论否定,故C 正确;对D ,若“p q ∧”为假命题,则p 、q 中只要有一个为假命题,故D 错误. 故选:D. 【点睛】本题考查命题真假性的判断,考查对概念的理解与应用,属于基础题.10.B解析:B 【分析】解一元二次不等式求得条件q 中x 的范围,解一元二次不等式求得条件p 中x 的范围,根据q 是p 的充分不必要条件列不等式组,解不等式组求得m 的取值范围. 【详解】对于条件q ,()()234410x x x x +-=+-<,解得41x -<<.对于条件p ,由()()30x m x m --->,解得x m <或3x m >+.由于q 是p 的充分不必要条件,所以34m +≤-或m 1≥,解得(],7[1,)m ∈-∞-+∞. 故选:B 【点睛】本小题主要考查一元二次不等式的解法,考查根据充分不必要条件求参数的取值范围,属于中档题.11.A解析:A 【分析】根据充分条件、必要条件的定义结合不等式的性质判断即可. 【详解】由221x y +<,可得11x -<<,且11y -<<,则可得到()()110x y -->,故充分性成立;反之若()()110x y -->,可取2x y ==,显然得到不等式221x y +<不成立,故必要性不成立. 故选:A . 【点睛】本题考查充分不必要条件的判断,同时也涉及了不等式基本性质的应用,考查推理能力,属于中等题.12.B解析:B 【分析】先化简两个命题,再根据充分必要条件的定义分析判断得解. 【详解】由题得:1p x ≤,:01q x <<,设(,1],B (0,1)A =-∞=,所以B 是A 的真子集,所以p 是q 的必要非充分条件. 故选:B 【点睛】本题主要考查指数对数不等式的解法,考查充分必要条件的判断,意在考查学生对这些知识的理解掌握水平.二、填空题13.【分析】根据不等式的性质以及充分条件和必要条件的定义即可得到结论【详解】解:由题意不等式的解为且1<x<2是的充分不必要条件所以且等号不能同时取得则故答案为:【点睛】结论点睛:本题考查由充分不必要条解析:112⎡⎤⎢⎥⎣⎦, 【分析】根据不等式的性质,以及充分条件和必要条件的定义即可得到结论. 【详解】解:由题意不等式21x m -<的解为2121m x m -<<+,且1<x <2是2121m x m -<<+的充分不必要条件,所以211212m m -≤⎧⎨+≥⎩,且等号不能同时取得,则112m ≤≤, 故答案为:112⎡⎤⎢⎥⎣⎦,. 【点睛】结论点睛:本题考查由充分不必要条件求参数的范围,一般可根据如下规则建立不等式组:(1)若p 是q 的必要不充分条件,则q 对应集合是p 对应集合的真子集; (2)p 是q 的充分不必要条件, 则p 对应集合是q 对应集合的真子集; (3)p 是q 的充分必要条件,则p 对应集合与q 对应集合相等;(4)p 是q 的既不充分又不必要条件, q 对的集合与p 对应集合互不包含.14.【分析】解一元二次不等式求得根据是的必要不充分条件求得的取值范围【详解】由解得所以由于是的必要不充分条件所以解得所以的取值范围是故答案为:【点睛】本小题主要考查根据必要不充分条件求参数考查一元二次不 解析:[]1,2-【分析】解一元二次不等式求得p ,根据p 是q 的必要不充分条件求得m 的取值范围. 【详解】由()()223310x x x x --=-+<,解得13x .所以:p ()1,3-.由于p 是q 的必要不充分条件,所以113m m ≥-⎧⎨+≤⎩, 解得12m -≤≤.所以m 的取值范围是[]1,2-.故答案为:[]1,2-【点睛】本小题主要考查根据必要不充分条件求参数,考查一元二次不等式的解法,属于中档题. 15.充分不必要【分析】根据题意利用基本不等式可判定充分性是成立的可举出反例说明必要性不成立即可得到答案【详解】当时由基本不等式可得当时有解得充分性是成立的;例如:当时满足但此时必要性不成立综上所述是的充 解析:充分不必要【分析】根据题意,利用基本不等式,可判定充分性是成立的,可举出反例,说明必要性不成立,即可得到答案.【详解】当0,0a b >>时,由基本不等式,可得a b +≥,当4a b +≤时,有4a b ≤+≤,解得4ab ≤,充分性是成立的;例如:当1,4a b ==时,满足4ab ≤,但此时=5>4a+b ,必要性不成立,综上所述,“4a b +≤”是“4ab ≤”的充分不必要条件.故答案为充分不必要条件.【点睛】本题主要考查了充分不必要条件的判定,其中解答中熟记充分条件、必要条件的判定方法,以及合理利用基本不等式求解是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.16.充分不必要【分析】先化简不等式再根据两集合包含关系确定充要关系【详解】或或因为所以是的充分不必要条件故答案为:充分不必要【点睛】本题考查解含绝对值不等式以及充要关系的判定考查基本分析求解判断能力属基 解析:充分不必要【分析】 先化简不等式20x x -<,再根据两集合包含关系确定充要关系.【详解】202020x x x x ≥⎧-<∴⎨-<⎩或20020x x x <⎧∴≤<⎨--<⎩0x x <∴<因为(,1)-∞(-∞,所以“1x <”是“20x x -<”的充分不必要条件故答案为:充分不必要【点睛】本题考查解含绝对值不等式以及充要关系的判定,考查基本分析求解判断能力,属基础题. 17.(﹣22【分析】由原命题的否定为真命题得到∀实数x 使得(a ﹣2)x2+2(a ﹣2)x ﹣4<0成立然后分二次项系数为0和不为0讨论当二次项系数不为0时需要二次项系数小于0且判别式小于0求解【详解】命题解析:(﹣2,2].【分析】由原命题的否定为真命题得到∀实数x ,使得(a ﹣2)x 2+2(a ﹣2)x ﹣4<0成立,然后分二次项系数为0和不为0讨论,当二次项系数不为0时,需要二次项系数小于0,且判别式小于0求解.【详解】命题“存在实数x ,使得(a ﹣2)x 2+2(a ﹣2)x ﹣4≥0成立”是假命题,则其否定为“∀实数x ,使得(a ﹣2)x 2+2(a ﹣2)x ﹣4<0成立”是真命题,当a =2时,原不等式化为﹣4<0恒成立;当a ≠2时,则()2204(2)1620a a a -⎧⎨=-+-⎩<<,解得﹣2<a <2. 综上,实数a 的取值范围是(﹣2,2].故答案为:(﹣2,2].【点睛】本题考查命题的真假判断与应用,考查了复合命题的真假判断,训练了不等式恒成立的解法,是中档题.18.必要非充分条件【分析】可以考虑逆否命题的充分必要性即得解【详解】先考虑充分性即考虑是否成立其逆否命题为::且显然不成立所以P 是Q 成立的非充分条件;再考虑必要性即考虑是否成立其逆否命题为::且显然成立 解析:必要非充分条件【分析】可以考虑逆否命题的充分必要性,即得解.【详解】先考虑充分性,即考虑P Q ⇒是否成立,其逆否命题为:Q P ⌝⇒⌝,:Q ⌝“3a b +=”,P ⌝:“1a =且2b =”,显然Q P ⌝⇒⌝不成立,所以P 是Q 成立的非充分条件;再考虑必要性,即考虑Q P ⇒是否成立,其逆否命题为:P Q ⌝⇒⌝,:Q ⌝“3a b +=”,P ⌝:“1a =且2b =”,显然P Q ⌝⇒⌝成立,所以P 是Q 成立的必要条件.所以P 是Q 成立必要非充分条件.故答案为必要非充分条件【点睛】本题主要考查充分必要条件的判断,考查逆否命题,意在考查学生对这些知识的理解掌握水平.19.①③【分析】根据正弦定理三角形内角正切关系以及诱导公式进行判断选择【详解】因为△中所以若则因此必有即△是锐角三角形;若则或;若则所以△是等腰三角形;若则所以或即或;综上正确命题的序号是①③【点睛】本 解析:①③【分析】根据正弦定理、三角形内角正切关系以及诱导公式进行判断选择.【详解】因为△ABC 中tan tan tan tan tan tan A B C A B C ++=,所以若tan tan tan 0A B C ++>,则tan tan tan 0A B C >,因此必有tan 0,tan 0,tan 0A B C >>>,即△ABC 是锐角三角形; 若cos cos a A b B =,则cos cos sinA A sinB B =, 22,A B sin A sin B ==或A B 2π+=; 若cos cos a B b A b +=,则cos cos sinA B sinB A sinB +=, ()sin A B sinB +=,sinC sinB =,C B =,所以△ABC 是等腰三角形;若cos sin A B =,则sin sin 2A B π⎛⎫-= ⎪⎝⎭,所以2A B π-=或2A B ππ-+=,即2A B π+=或2A B π-+=;综上正确命题的序号是①③.【点睛】本题考查正弦定理、三角形内角正切关系以及诱导公式,考查基本转化与判断化简能力,属中档题.20.【分析】先确定各命题为真时实数的取值范围再根据复合命题真假得各命题真假最后求交集得结果【详解】命题:存在使得成立所以最小值1即所以;命题对任意恒成立所以;因为命题是真命题所以是真命题是假命题即【点睛 解析:[]1,4a ∈【分析】先确定各命题为真时实数a 的取值范围,再根据复合命题真假得各命题真假,最后求交集得结果.【详解】命题p :存在[]0,1x ∈,使得0x a e -≥成立,所以x a e ≥的最小值1,即所以1a ≥; 命题:q 对任意x R ∈,240x x a ++> 恒成立,所以24404a a ,-; 因为命题p q ∧⌝是真命题,所以p 是真命题,q 是假命题,即14a ≤≤【点睛】本题考查命题真假以及不等式恒成立与存在性问题,考查基本分析转化与求解能力,属中档题.三、解答题21.(1)1,38M ⎡⎫=-⎪⎢⎣⎭(2)3a ≥或1a ≤- 【分析】(1)利用参数分离法将m 用x 表示,结合二次函数的性质求出m 的取值范围,从而可求集合M ;(2)若x ∈N 是x M ∈的必要条件,则M N ⊆分类讨论①当2a a >-即1a >时,{|2}N x a x a =-<<,②当2a a <-即1a <时,{|2}N x a x a =<<-,两种情况进行求解;【详解】解:(1)由题意,方程22m x x =-在(1,1)-上有解令2()2f x x x =-(11)x -<<.只需m 在()f x 值域内易知()f x 值域为1,38⎡⎫-⎪⎢⎣⎭.m ∴的取值集合1,38M ⎡⎫=-⎪⎢⎣⎭(2)由题意,M N ⊆,显然N 不为空集.①当2a a >-即1a >时,(2,)N a a =-. 12831a a a ⎧-<-⎪⎪∴≥⎨⎪>⎪⎩3a ∴≥ ②当2a a <-即1a <时,(,2)N a a =-.23181a a a -≥⎧⎪⎪∴<-⎨⎪<⎪⎩1a ∴≤-. 综合:3a ∴≥或1a ≤-【点睛】本题主要考查了二次函数在闭区间上的值域的求解,集合之间包含关系的应用,体现了分类讨论思想的应用.22.(1)[4,+∞);(2)[4,1)(5,6]--⋃.【分析】(1)设使命题p 成立的集合为A ,命题q 成立的集合为B ,由题意可得A ⊆B ,根据集合的包含关系,列出方程,即可求得结果;(2)由题意可得:p ,q 命题,一真一假,分别求得当p 真q 假时、 p 假q 真时x 的范围,即可得结果.【详解】(1)设使命题p 成立的集合为A ,命题q 成立的集合为B ,则A ={x |-1≤x ≤5},B ={x |1-m ≤x ≤1+m },由题意得:A ⊆B , 所以01511m m m >⎧⎪+≥⎨⎪-≤-⎩,解得m ≥4,故m 的取值范围为[4,+∞).(2)根据条件可得:p ,q 命题,一真一假,当p 真q 假时,156?4x x x -≤≤⎧⎨><-⎩或,无解; 当p 假q 真时,5?146x x x ><-⎧⎨-≤≤⎩或,解得-4≤x <-1或5<x ≤6. 故实数x 的取值范围为[4,1)(5,6]--⋃.【点睛】本题考查根据充分条件求参数范围、利用复合命题真假求参数范围,考查分析理解,计算求值的能力,属中档题.23.(1)412m -≤≤;(1)存在,08m ≤≤【分析】(1)根据题意转化为集合A 、B 存在公共元素,求出A 、B 无公共元素时,实数m 的取值范围,取补集即可.(2)由题意转化为B A ⊆,再根据集合的包含关系可得22210m m -≥-⎧⎨+≤⎩,解不等式组即可. 【详解】 {}()(){}{}2|82001020210A x x x x x x x x =--≤=-+≤=-≤≤,{}{}{}|22222B x x m x x m x m x m =-≤=-≤-≤=-≤≤+(1)若“∃x ∈A ,使得x ∈B ”为真命题,即集合A 、B 存在公共元素,假设A 、B 无公共元素,则210m ->或22m +<-,解得12m >或4m <-,则集合A 、B 存在公共元素时,实数m 的取值范围412m -≤≤.(2)存在实数m ,使“x ∈A ”是“X ∈B ”必要不充分条件,若 “x ∈A ”是“X ∈B ”必要不充分条件,则B A ,所以22210m m -≥-⎧⎨+≤⎩,解得08m ≤≤, 所以m 的取值范围为08m ≤≤.【点睛】本题考查了充分条件、必要条件的集合思想,考查了转化与化归的思想,属于中档题. 24.(1)充分不必要条件;(答充分条件也对);(2)()1,0,44⎛⎫-∞ ⎪⎝⎭ 【分析】(1)若a =0,求出P 成立的等价条件,根据充分条件和必要条件的定义进行判断. (2)根据复合命题之间的关系分P 真Q 假和P 假Q 真,进行求解即可.【详解】(1)若0a =,210ax ax ++>等价于10>恒成立,若0a ≠,则210ax ax ++>恒成立等价于判别式240a a ∆=-<,且0a >,则04a <<,综上,P :04a ≤<,即“0a =”是P 的充分不必要条件;(答充分条件也对)(2)对任意实数x 都有210ax ax ++>恒成立,可得0a =或00a >⎧⎨∆<⎩,可得04a ≤<; 关于x 的方程20x x a -+=有实数根,可得140,a -≥14a ≤; 如果P 正确,且Q 不正确,有04a ≤<,且14a >,144a ∴<<; 如果Q 正确,且P 不正确, 有0a <或4a ≥,且14a ≤,0a ∴<. 所以实数a 的取值范围为()1,0,44⎛⎫-∞ ⎪⎝⎭. 【点睛】本题考查必要条件、充分条件与充要条件的判断及根据命题真假求参数,必要条件、充分条件与充要条件的判断一般利用定义或集合进行判断,根据命题真假求参数一般是列不等式求解即可,属于中等题.25.(1){1x x ≤-或}1x ≥;(2)[]1,0-.【分析】(1)根据题意得(22)(221)0x x -⋅-≥,进而得122x ≤或22x ≥,即可得{1x x ≤-或}1x ≥(2)解不等式2(21)(1)0x m x m m -+++≥得{B x x m =≤或}1x m ≥+,结合(1)得{1A x x =≤-或}1x ≥,根据题意得A B ,进而根据集合关系即可得答案.【详解】(1)由命题p 为真命题,则245220x x ⋅-⋅+≥可化为(22)(221)0x x -⋅-≥ 解得122x ≤或22x ≥,所以实数x 的取值范围是{1x x ≤-或}1x ≥ (2)命题q :由2(21)(1)0x m x m m -+++≥,得[]()(1)0x m x m --+≥,解得x m ≤或1x m ≥+. 设{1A x x =≤-或}1x ≥,{B x x m =≤或}1x m ≥+因为命题q 是命题p 的必要不充分条件,所以A B 111m m ≥-⎧⎨+≤⎩,解得10m -≤≤, 所以实数m 的取值范围为[]1,0-.【点睛】结论点睛:本题考查充分不必要条件的判断,一般可根据如下规则判断:(1)若p 是q 的必要不充分条件,则q 对应集合是p 对应集合的真子集;(2)若p 是q 的充分不必要条件, 则p 对应集合是q 对应集合的真子集;(3)若p 是q 的充分必要条件,则p 对应集合与q 对应集合相等;(4)若p 是q 的既不充分又不必要条件, 则q 对的集合与p 对应集合互不包含.26.(1)13m ≤≤;(2)1m <或23m <≤【分析】(1)p 为真命题时,任意[]0,1x ∈,不等式2234x m m -≥-恒成立可转化为()2min 234x m m -≥-,求解即可(2)由题可得,p q 一真一假,结合(1),再化简命题q ,即可求出m 的取值范围.【详解】对于p :()2min 234x m m -≥-成立,而[]0,1x ∈,有()min 233x -=-, ∴234m m -≥-,∴13m ≤≤.q :存在[]1,1x ∈-,使得不等式2210x x m -+-≤成立,只需()2min 210x x m -+-≤, 而()2min 212x x m m -+-=-+,∴20m -+≤,∴2m ≤;(1)若p 为真,则13m ≤≤;(2)若p ,q 有且只有一个为真,则,p q 一真一假.若q 为假命题,p 为真命题,则132m m ≤≤⎧⎨>⎩,所以23m <≤;若p 为假命题,q 为真命题,则132m m m ⎧⎨≤⎩或,所以1m <.综上,1m <或23m <≤.【点睛】 思路点睛:本题考查根据命题的真假求参数,解决此类问题一般先求出命题为真时对应的参数范围,再结合命题的真假或复合命题的真假列出对应的不等式求解.。
深圳宝安区龙华中英文实验学校选修一第三单元《圆锥曲线的方程》测试题(答案解析)

一、填空题1.已知A 为椭圆22221(0)x y a b a b+=>>的左顶点,O 为坐标原点,若直线:2l x c =上存在点P 使得45APO ∠=︒,则椭圆离心率的最大值为__________.2.P 是非等轴双曲线222:116x y C a -=上的一点,12,F F 分别是双曲线C 左、右焦点,若1122,12PF F F PF ⊥=,则双曲线C 的渐近线方程是__________.3.已知双曲线22:221(0,0)x y C a b a b -=>>的左、右焦点分别为12,F F ,过原点O 作斜率3的直线交C 的右支于点A ,若1223F AF π∠=,则双曲线的离心率为__________. 4.已知点1,0A ,直线l :1x =-,两个动圆均过点A 且与l 相切,其圆心分别为1C 、2C ,若动点M 满足22122C M C C C A =+,则M 的轨迹方程为______.5.若椭圆22221(0)x y a b a b+=>>与双曲线()2211221110,0x y a b a b -=>>有相同的焦点12,F F ,点P 是两条曲线的一个交点,122F PF π∠=,椭圆的离心率为1e ,双曲线的离心率为2e ,122e e ,则2212e e +=__________.6.如图所示,抛物线形拱桥的跨度是20米,拱高是4米,在建桥时,每隔4米需要用一支柱支撑,则其中最长的支柱的长度为____________米.7.已知椭圆的方程为2212516x y +=,1F ,2F 分别是椭圆的左、右焦点,A 点的坐标为(2,1),P 为椭圆上一点,则2||||PA PF +的最大值是___________.8.已知抛物线24y x =的焦点为F ,P 为抛物线上一动点,定点()1,1A ,当PAF △周长最小时,PF 所在直线的斜率为______.9.若抛物线22y px =的焦点与双曲线22145x y -=的右焦点重合,则实数p 的值为____.10.已知椭圆()222210x y a b a b+=>>的左、右焦点分别为1F ,2F ,若椭圆上存在一点P使12PF e PF =,则该椭圆的离心率e 的取值范围是______.11.已知椭圆2222:1(0)x y C a b a b+=>>的左,右焦点分别为1F ,2F ,过1F 的直线交椭圆C 于A ,B 两点,若290ABF ∠=︒,且2ABF 的三边长2BF 、||AB 、2AF 成等差数列,则C 的离心率为___________.12.已知双曲线221124x y -=的右焦点为F ,若过点F 的直线与双曲线的右支有且只有一个交点,则此直线的斜率的取值范围是______.13.设D 为椭圆2215y x +=上任意一点,()0,2A -,()0,2B ,延长AD 至点P ,使得PD BD =,则点P 的轨迹方程为______. 二、解答题14.已知抛物线2:2C y px =过点()1,2A . (1)求抛物线C 的方程;(2)求过点()3,2P -的直线与抛物线C 交于M 、N 两个不同的点(均与点A 不重合).设直线AM 、AN 的斜率分别为1k 、2k ,求证:12k k ⋅为定值.15.如图,在平面直角坐标系xoy 中,已知椭圆C :22221x ya b+=(0)a b >>的离心率1,2e =左顶点为(2,0)A -,过点A 作斜率为(0)k k ≠的直线l 交椭圆C 于点D ,交y 轴于点E .(Ⅰ)求椭圆C 的方程;(Ⅱ)已知P 为AD 的中点,是否存在定点Q ,对于任意的(0)k k ≠都有OP EQ ⊥,若存在,求出点Q 的坐标;若不存在说明理由;(III )若过O 点作直线l 的平行线交椭圆C 于点M ,求AD AEOM+的最小值. 16.已知椭圆()222210x y a b a b+=>>中,短轴的一个端点与两个焦点的连线互相垂直,且焦距为22(1)求椭圆的标准方程.(2)如图,已知椭圆的左顶点为A ,点M 在圆2289x y +=上,直线AM 与椭圆相交于另一点B ,且AOB 的面积是AOM 的面积的2倍,求直线AB 的方程.17.已知A ,B 分别为椭圆2222:+=1(>>0)x y E a b a b的左右项点,G 为E 的上顶点,直线AG ,BG 的斜率之积为34-,且点3(1,)2P 在椭圆上. (1)求椭圆E 的方程;(2)过点(1,0)F 的直线l 交椭圆E 于C ,D 两点,交直线=4x 点Q .设直线,,PC PD PQ的斜率分别为123,,.k k k 问:是否存在常数λ,使得123+=k k k λ?若存在求λ的值;若不存在,说明理由.18.在①01PF x =+,②0022y x ==,③PF x ⊥轴时,2PF =这三个条件中任选一个,补充在下面的问题中,并回答.问题:已知抛物线2:3(0)C y px p =>的焦点为F ,点()00,P x y 在抛物线C 上,且______,(1)求抛物线C 的标准方程;(2)若直线:20l x y --=与抛物线C 交于A ,B 两点,求ABF 的面积.19.已知椭圆()2222:10x y C a b a b+=>>的右焦点为()2,0F ,且右焦点到左准线的距离为10.(1)求椭圆C 的方程;(2)O 为坐标原点,过点F 且斜率为1的直线与椭圆交于A ,B 两点,求△AOB 的面积.20.已知椭圆M :22213x y a +=()0a >的一个焦点为()1,0F -,左右顶点分别为A ,B .经过点F 的直线l 与椭圆M 交于C ,D 两点. (Ⅰ)求椭圆M 方程;(Ⅱ)当直线l 的倾斜角为45时,求线段CD 的长;(Ⅲ)记△ABD 与△ABC 的面积分别为1S 和2S ,求12S S -的最大值.21.已知双曲线1C 的方程为22143x y -=,椭圆2C 与双曲线有相同的焦距,1F ,2F 是椭圆的上、下两个焦点,已知P 为椭圆上一点,且满足12PF PF ⊥,若12PF F △的面积为9. (1)求椭圆2C 的标准方程;(2)点A 为椭圆的上顶点,点B 是双曲线1C 右支上任意一点,点M 是线段AB 的中点,求点M 的轨迹方程.22.已知椭圆C :22221x y a b+=(a >b >0), 直线330x y +-=经过椭圆的上顶点和右焦点.(1)求椭圆C 的方程;(2)过右焦点2F 的直线l 与椭圆C 相交于A , B 两点.若OAB 的面积为265,求直线l 的方程.23.已知P 是圆22:4O x y +=上一动点,P 点在x 轴上的射影是D ,点M 满足12DM DP =. (1)求动点M 的轨迹曲线C 的方程;(2)若点(2,)N t 在曲线C 上,求12F NF △的面积.24.已知椭圆2222:1(0)x y C a b a b+=>>的左、右顶点分别为,A B ,||4AB =.过右焦点F 且垂直于x 轴的直线交椭圆C 于,D E 两点,且||1DE =.(1)求椭圆C 的方程;(2)斜率大于0的直线l 经过点(4,0)P -,且交椭圆C 于不同的两点,M N (M 在点,P N 之间).记PNA 与PMB △的面积之比为λ,求实数λ的取值范围.25.已知椭圆2222:1(0)x y C a b a b+=>>经过点(2,0),一个焦点为(3,0).(Ⅰ)求椭圆C 的方程;(Ⅱ)若直线(1)(0)y k x k =-≠与x 轴交于点P ,与椭圆C 交于,A B 两点,线段AB 的垂直平分线与x 轴交于点Q ,求||||AB PQ 的取值范围. 26.已知椭圆的中心在坐标原点,右焦点F 的坐标为()3,0,直线l :220x y +-=交椭圆于A 、B 两点,线段AB 的中点为11,2M ⎛⎫⎪⎝⎭.(1)求椭圆的方程;(2)动点N 满足0NA NB ⋅=,求动点N 的轨迹方程.参考答案【参考答案】***试卷处理标记,请不要删除一、填空题1.【分析】设则利用直线倾斜角及两角差的正切可得在上有解该分式方程可转化为一元二次方程利用判别式可得的不等式从而可求离心率的最大值【详解】设右焦点为则故因为直线上存在点P 使得故在上有解即在上有解所以即故解析:14【分析】设()2,P c t ,则利用直线,AP OP 倾斜角及两角差的正切可得()2122att c c a =++在R 上有解,该分式方程可转化为一元二次方程,利用判别式可得,a c 的不等式,从而可求离心率的最大值. 【详解】设()2,P c t ,右焦点为F , 则tan 2t PAO c a ∠=+,tan 2tPOF c∠=, 故()()2222tan 22122t tat c c a APO t t c c a c c a -+∠==++++,因为直线:2l x c =上存在点P 使得45APO ∠=︒,故()2122att c c a =++在R 上有解即()2220t at c c a -++=在R 上有解, 所以()2820a c c a -+≥即216810e e +-≤,故104e <≤.故离心率的最大值为14.故答案为:14. 【点睛】方法点睛:离心率的取值范围的计算,则需要利用坐标的范围、几何量的范围或点的位置关系构建关于,,a b c 的不等式或不等式组,有时也可以根据题设条件构建关于,,a b c 的等量关系,可根据方程有解得到基本量的不等式.2.【分析】由双曲线定义可得根据已知可解得再由渐近线方程是可得答案【详解】因为所以又因为所以即解得或(舍去)所以双曲线C 的渐近线方程是故答案为:【点睛】本题考查了双曲线的定义焦点三角形的问题关键点是焦点 解析:2y x =±【分析】由双曲线定义可得212PF PF a -=,根据112PF F F ⊥、已知可解得2a =,再由渐近线方程是by x a=±可得答案. 【详解】因为2122,12PF PF a PF -==,所以122122PF PF a a =-=-, 又因为112PF F F ⊥,2222212444464F F c a b a ==+=+,所以2221122PF F F PF +=,即()222212412a c -+=,解得2a =或4a =(舍去), 所以双曲线C 的渐近线方程是422y x x =±=±. 故答案为:2y x =±. 【点睛】本题考查了双曲线的定义、焦点三角形的问题,关键点是焦点三角形中112PF F F ⊥,考查了分析问题、解决问题的能力.3.【分析】由题意知结合已知条件可证明利用可计算在中利用余弦定理可计算出由即可求得离心率【详解】由题意知直线的斜率为所以所以又因为所以所以即可得在中由余弦定理可得解得:故双曲线的离心率为故答案为:【点睛【分析】由题意知123FOA π∠=,结合已知条件可证明112FOA F AF ,利用11112F O F AF A F F =可计算1F A =,在12F AF中,利用余弦定理可计算出22AF c =,由 121222F F ce a AF AF ==-即可求得离心率. 【详解】由题意知直线OA23AOF π∠=,所以123FOA π∠=,又因为1223F AF π∠=,121AFO F F A ∠=∠, 所以112FOA F AF ,所以11112F O F A F A F F =,即112F cc A F A =可得1F A =, 在12F AF 中,由余弦定理可得22212121222cos3F F AF AF AF AF π=+-⋅,解得:2AF =,故双曲线的离心率为121222F F c e a AF AF ====-. 【点睛】123FOA π∠=,结合1223F AF π∠=可得112FOA F AF,即可求出1F A =,在12F AF 中,再利用余弦定理,可求出2AF ,由双曲线的定义可计算122a AF AF =-,121222F F c e a AF AF ==-即可. 4.【分析】由抛物线的定义得动圆的圆心轨迹方程设根据可得利用可求得结果【详解】由抛物线的定义得动圆的圆心轨迹是以为焦点直线:为准线的抛物线其方程为设因为动点满足所以即所以因为所以所以即的轨迹方程为故答案 解析:221y x =-【分析】由抛物线的定义得动圆的圆心轨迹方程24y x =,设()1,C a b ,()2,C m n ,(),M x y ,根据22122C M C C C A =+可得21a x =-,2b y =,利用24b a =可求得结果. 【详解】由抛物线的定义得动圆的圆心轨迹是以1,0A 为焦点,直线l :1x =-为准线的抛物线,其方程为24y x =,设()1,C a b ,()2,C m n ,(),M x y ,因为动点M 满足22122C M C C C A =+, 所以()()()2,,1,x m y n a m b n m n --=--+--,即21x a =+,2y b =, 所以21a x =-,2b y =,因为24b a =,所以()()22421y x =-,所以221y x =-,即M 的轨迹方程为221y x =-. 故答案为:221y x =- 【点睛】关键点点睛:由抛物线的定义得动圆的圆心轨迹方程24y x =是解题关键.5.【分析】设PF1=sPF2=t 由椭圆的定义可得s+t =2a 由双曲线的定义可得s ﹣t =2a1利用勾股定理和离心率公式得到化简计算即可得出结论【详解】不妨设P 在第一象限再设PF1=sPF2=t 由椭圆的定 解析:8【分析】设PF 1=s ,PF 2=t ,由椭圆的定义可得s +t =2a ,由双曲线的定义可得s ﹣t =2 a 1,利用勾股定理和离心率公式得到2212224e e =+,化简计算即可得出结论. 【详解】不妨设P 在第一象限,再设PF 1=s ,PF 2=t ,由椭圆的定义可得s +t =2a , 由双曲线的定义可得s ﹣t =2a 1, 解得s =a +a 1,t =a ﹣a 1, 由∠F 1PF 22π=,在三角形F 1PF 2中,利用勾股定理可得22222221114()()22c s t a a a a a a =+=++-=+. ∴2212224e e =+, 化简221222221212121=e e e e e e ++=,又由e 1e 2=2,所以22221212=28e e e e +=. 故答案为:8. 【点睛】本题考查椭圆和双曲线的定义、方程和性质,主要考查离心率的求法,考查运算能力,属于中档题.在解题的过程中要合理的利用平面几何的思想,适当利用勾股定理,建立离心力的关系式,在化简的过程中根据题目的条件和结论合理构造和变形,这样解题会轻松一点.6.(或)【分析】以抛物线的顶点为坐标原点抛物线的对称轴所在直线为轴建立平面直角坐标系设所求抛物线的方程为由题意可得出点在该抛物线上可求得的值然后将代入抛物线的方程进而可求得结果【详解】以抛物线的顶点为解析:9625(或3.84)【分析】以抛物线的顶点为坐标原点,抛物线的对称轴所在直线为y 轴建立平面直角坐标系,设所求抛物线的方程为22x py =-,由题意可得出点()10,4A --在该抛物线上,可求得p 的值,然后将2x =代入抛物线的方程,进而可求得结果. 【详解】以抛物线的顶点O 为坐标原点,抛物线的对称轴所在直线为y 轴建立平面直角坐标系,设抛物线的方程为22x py =-,由题意可知点()10,4A --在该抛物线上,所以,()10024p =-⨯-,解得252p =,所以,抛物线的方程为225x y =-, 当2x =时,2242525y =-=-,因此,最长的支柱的长度为49642525-=(米). 故答案为:9625(或3.84). 【点睛】利用解析法解决平面几何问题的步骤如下: (1)建立合适的坐标系;(2)将几何元素用代数形式加以表示; (3)将几何关系转化为数学运算; (4)将数学结果转化为实际结论.7.【分析】本题先根据已知求出再求最后转化即可解题【详解】解:∵椭圆的方程为∴则∵∴∵∴故答案为:【点睛】本题考查椭圆上点到焦点与定点距离的和的最值椭圆的标准方程求是中档题 解析:1026+【分析】本题先根据已知求出2a 、c ,再求1||AF 、12||||10PF PF +=,最后转化2||||PA PF +即可解题. 【详解】解:∵椭圆的方程为2212516x y +=,∴225a =,2229c a b =-=,则210a =,3c =,∵(2,1)A ,1(3,0)F -,∴221||(23)(10)26AF =++-=,∵12||||210PF PF a +==,∴211||||10||||10||1026PA PF PA PF AF +=+-≤+=+ 故答案为:1026+ 【点睛】本题考查椭圆上点到焦点与定点距离的和的最值、椭圆的标准方程求a ,b ,c ,是中档题.8.【分析】过点向准线作垂线垂足为由抛物线定义得周长等于易得共线时取得最小值【详解】抛物线的焦点为准线为从点向准线作垂线垂足为从点向准线作垂线垂足为则周长当且仅当三点共线时取到最小值此时故答案为:【点睛解析:43- 【分析】过点P 向准线作垂线,垂足为B ,由抛物线定义得PF PB =,PAF △周长等于1PB PA ++,易得,,B P A 共线时,取得最小值.【详解】抛物线24y x =的焦点为()1,0F ,准线为1x =-,从点P 向准线作垂线,垂足为B ,从点A 向准线作垂线,垂足为1A ,则PAF △周长1113PF PA AF PB PA AA =++=++≥+=,当且仅当A ,P ,1A 三点共线时,取到最小值,此时1,14P ⎛⎫ ⎪⎝⎭,43PF k =-.故答案为:43-. 【点睛】本题考查抛物线的点到定点与到焦点的距离之和的最小值问题,解题关键是利用定义把抛物线上的点以焦点的距离转化为到准线的距离.9.6【解析】因为双曲线的右焦点为所以解析:6 【解析】因为双曲线22145x y -=的右焦点为(3,0) ,所以3,62p p ==10.【分析】由椭圆的定义可得解得由椭圆的性质可得解不等式求得离心率的取值范围【详解】设点的横坐标为则由椭圆的定义可得由题意可得则该椭圆的离心率的取值范围是故答案为:【点睛】本题考查椭圆的定义以及简单性质解析:)1,1【分析】由椭圆的定义可得22()()a a e x e e x c c +=⨯-,解得(1)c a x e e -=+,由椭圆的性质可得(1)c aaa e e --+,解不等式求得离心率e 的取值范围.【详解】设点P 的横坐标为x ,12PF e PF =,则由椭圆的定义可得22()()a a e x e e x c c +=⨯-,(1)c a x e e -∴=+,由题意可得(1)c a a a e e --+, 111(1)e e e -∴-+,∴2211e e e e e e⎧--⎨-+⎩,∴11e <,则该椭圆的离心率e 的取值范围是1,1),故答案为:1,1). 【点睛】本题考查椭圆的定义,以及简单性质的应用,由椭圆的定义可得22()()a a e x e e x c c+=⨯-,是解题的关键.11.【分析】由已知设据勾股定理有;由椭圆定义知的周长为4a 由勾股定理可得选项【详解】由已知设所以根据勾股定理有解得;由椭圆定义知所以的周长为4a 所以有;在直角中由勾股定理∴离心率故答案为:【点睛】本题考解析:22【分析】由已知,设2BF x =,||AB x d =+,22AF x d =+,据勾股定理有3x d =;由椭圆定义知2ABF 的周长为4a ,由勾股定理,2224a c =,可得选项. 【详解】由已知,设2BF x =,||AB x d =+,22AF x d =+,所以根据勾股定理有()()222+2++x d x x d =,解得3x d =;由椭圆定义知1212++2AF AF BF BF a ==,所以2ABF 的周长为4a ,所以有3a d =,21BF a BF ==;在直角2BF F △中,由勾股定理,2224a c =,∴离心率22e =. 故答案为:22. 【点睛】本题考查椭圆离心率,椭圆的定义,重在对问题的分析,抓住细节,同时考查计算能力,属于中档题.12.【分析】由双曲线方程求得渐近线方程当过焦点的两条直线与两条渐近线平行时这两条直线与双曲线右支分别只有一个交点利用数形结合可求出符合条件直线的斜率取值范围【详解】双曲线的渐近线方程当过焦点的直线与两条解析:33,⎡⎤-⎢⎥⎣⎦【分析】由双曲线方程求得渐近线方程33y x =±,当过焦点的两条直线与两条渐近线平行时,这两条直线与双曲线右支分别只有一个交点,利用数形结合,可求出符合条件直线的斜率取值范围. 【详解】双曲线221124x y -=的渐近线方程33y x =±,当过焦点的直线与两条渐近线平行时, 直线与双曲线右支分别只有一个交点(因为双曲线正在与渐近线无限接近中),由图可知,斜率不在33,⎡⎤-⎢⎥⎣⎦的所有直线与双曲线右支有两点交点(如图中直线2l ),斜率在33,33⎡⎤-⎢⎥⎣⎦的所有直线都与双曲线右支只有一个交点(如图中直线m ). 所以此直线的斜率的取值范围33,.⎡⎤-⎢⎥⎣⎦故答案为33,.⎡⎤-⎢⎥⎣⎦【点睛】本题主要考查双曲线的几何性质以及直线与双曲线的位置关系,属于中档题.求解与双曲线性质有关的问题时要结合图形进行分析,既使不画出图形,思考时也要联想到图形,当涉及顶点、焦点、实轴、虚轴、渐近线等双曲线的基本量时,要理清它们之间的关系,挖掘出它们之间的内在联系.13.【分析】由已知可得为椭圆两焦点再由已知结合椭圆定义可得点的轨迹是以为圆心以为半径的圆写出圆的标准方程得答案【详解】如图由椭圆方程得所以则为椭圆两焦点所以由于则所以点的轨迹是以为圆心以为半径的圆其方程 解析:()22220x y ++=【分析】由已知可得,(0,2)A -,(0,2)B 为椭圆两焦点,再由已知结合椭圆定义可得点P 的轨迹是以A 为圆心,以25为半径的圆,写出圆的标准方程得答案. 【详解】 如图,由椭圆方程2215y x +=,得25a =,21b =,所以2c ==,则(0,2)A -,(0,2)B 为椭圆两焦点,所以||||2DA DB a +== 由于||||PD BD =,则||||||||||PA PD DA BD DA =+=+=所以点P 的轨迹是以A为圆心,以22(2)20x y ++=. 故答案为:22(2)20x y ++=. 【点睛】本题考查轨迹方程的求法,运用了椭圆的标准方程、椭圆定义和焦点坐标,同时考查数学转化思想方法,是中档题.二、解答题14.(1)24y x =;(2)证明见解析. 【分析】(1)本题可将()1,2A 代入抛物线方程中求出p 的值,即可得出结果; (2)本题首先可设()11,M x y 、()22,N x y 以及直线MN 的方程23xt y ,然后通过联立直线MN 的方程与抛物线方程即可得出124y y t +=、12812y y t =--,最后通过1212122211y y k k x x 并化简即可得出结果.【详解】(1)因为抛物线2:2C y px =过点()1,2A , 所以42p =,2p =,抛物线方程为24y x =.(2)设()11,M x y ,()22,N x y ,直线MN 的方程为23x t y ,联立()2234x t y y x⎧=++⎨=⎩,整理得248120y ty t ---=,21632480t t ∆=++>,124y y t +=,12812y y t =--,则1212122212122222111144y y y y k k y y x x 1212161622481284y y y y t t ,故12k k ⋅为定值2-.【点睛】关键点点睛:本题考查抛物线方程的求法以及抛物线与直线相交的相关问题的求解,通过联立直线的方程与抛物线方程以及韦达定理得出12y y +、12y y 的值是解决本题的关键,考查计算能力,考查化归与转化思想,是中档题.15.(Ⅰ)22143x y +=;(Ⅱ)存在,3(,0)2-;(III)【分析】(Ⅰ)根据离心率和顶点求出,a c ,再求出b 即可得出方程;(Ⅱ)联立直线与椭圆方程求出点D 坐标,进而得出点P 坐标,再利用1OP EQ k k ⋅=-即可求出定点;(III )设OM 的方程为y kx =,与椭圆联立,得出M 横坐标,利用D AE AMx x x x AD AE OM x -+-+=表示出,即可求出最值.【详解】解:(Ⅰ)因为椭圆C :22221x y a b+=0a b >>()的离心率1,2e =左顶点为(2,0)A -, 所以2a =,又12e =,所以1c =,可得2223b a c =-=, 所以椭圆C 的标准方程为22143x y +=;(Ⅱ)直线l 的方程为(2)y k x =+,由22143(2)x y y k x ⎧+=⎪⎨⎪=+⎩,可得:22(2)(43)860x k x k ⎡⎤+++-=⎣⎦,所以12x =-,2228643k x k -+=+, 当 228643k x k -+=+时,2228612(2)4343k ky k k k -+=+=++, 所以2228612(,)4343k kD k k -+++,因为点P 为AD 的中点,所以P 点坐标为22286(,)4343k kk k -++,则3(0)4OP k k k-=≠, 直线l 的方程为(2)y k x =+,令0x =,得E 点坐标为(0,2)k , 假设存在定点(,)(0)Q m n m ≠使得OP EQ ⊥,则1OP EQ k k ⋅=-,即3214n kk m -⎛⎫-⋅=- ⎪⎝⎭恒成立, 所以(46)30m k n +-=,所以46030m n +=⎧⎨-=⎩,即320m n ⎧=-⎪⎨⎪=⎩,所以定点Q 的坐标为3(,0)2-.(III )因为//OM l ,所以OM 的方程可设为y kx =,和22143x y +=联立可得M点的横坐标为x =, 由//OM l可得:22D A E A D A M M x x x x x x AD AE OM x x -+--+===≥,即k =时取等号,所以当k =AD AE OM +的最小值为.【点睛】方法点睛:解决直线与圆锥曲线相交问题的常用步骤: (1)得出直线方程,设交点为()11A x y ,,()22B x y ,; (2)联立直线与曲线方程,得到关于x (或y )的一元二次方程; (3)写出韦达定理;(4)将所求问题或题中关系转化为1212,x x x x +形式; (5)代入韦达定理求解.16.(1)22142x y +=;(2)220x y ++=或220x y .【分析】(1)由已知即可得b c ==2a =,写出椭圆方程即可.(2)由面积关系知M 为AB 的中点,法一:()2,0A -设()00,M x y 有()0022,2B x y +,由M 在圆上,B 在椭圆上,代入求00,x y ,进而得到直线方程;法二:设直线AB 的方程为()2y k x =+,联立抛物线方程求得B 的横坐标,即可得到M 的坐标,由M 在圆上求k 值,即可得直线方程.【详解】(1)由短轴的一个端点与两个焦点的连线互相垂直且焦距为易得:b c ==2a =,即椭圆的方程为22142x y +=.(2)因为2AOB AOM S S =△△,所以2AB AM =,即M 为AB 的中点,方法一:根据椭圆的方程22142x y +=,有()2,0A -,设()00,M x y ,则()0022,2B x y +,∴22089x y +=①,()()2200222142x y ++=②,得200918160x x --=,解得023x =-,083x =(舍去),把023x =-代入①,得023y =±,有12AB k =±. 因此,直线AB 的方程为()122y x =±+,即220x y ++=或220x y . 方法二: 设直线AB 的方程为()2y k x =+,由()221422x y y k x ⎧+=⎪⎨⎪=+⎩,得()2222128840k xk x k +++-=,∴()()22212420x k x k ⎡⎤+++-=⎣⎦,解得222412B k x k -=+, ∴()2224212B M x k x k+--==+,()22212M M ky k x k =+=+, 代入2289x y +=,得2222242812129k k k k ⎛⎫-⎛⎫+= ⎪ ⎪++⎝⎭⎝⎭,化简得422820k k +-=,即()()2272410kk +-=,解得12k =±,所以,直线AB 的方程为()122y x =±+,即220x y ++=或220x y . 【点睛】 关键点点睛:(1)根据已知确定,,a b c 关系并求值,写出椭圆方程即可.(2)由直线与圆、椭圆的关系,以及三角形面积的数量关系确定M 为AB 的中点,通过设点或直线方程,结合点在曲线上求参数,即可得到直线方程.17.(1)22143x y +=;(2)存在实数2λ=.【分析】(1)由椭圆方程确定A ,B ,G 的坐标,再由已知条件有22191344AG BG a b k k +⎧⋅=-⎪⎪⎨=⎪⎪⎩即可求得2a ,2b ,写出椭圆E 的方程;(2)由题意有直线l 的方程为(1)y k x =-,联立椭圆方程、设11(,)C x y ,22(,)D x y ,()4,3Q k ,结合根与系数关系有12x x +,12x x ⋅,由斜率的两点公式可证1232k k k +=,即可确定λ的值; 【详解】解:(1)由题意,(),0A a -,(),0B a ,()0,G b ,22341914AG BG a b b b k k a a ⎧⋅=⋅=-⎪⎪-⎨+=⎪⎪⎩,解得24a =,23b =, 故椭圆E 的方程为:22143x y +=.(2)存在实数2λ=满足题意;由(1)知椭圆E 的方程:2234120x y +-=,直线l 的方程为(1)y k x =-,代入椭圆方程并整理,得2223484120()k x k x k +-+-=,设11(,)C x y ,22(,)D x y ,()4,3Q k 则有2122834kx x k +=+,212241234k x x k-⋅=+, ()()121212121233331122221111y y k x k x k k x x x x ------+=+=+----22122212122282233342241282()12131234k x x kk k k k x x x x k k -+-+=-⋅=-⋅-⋅-++-+-+22222386822412834k k k k k k --=-⋅--++21k =-, 3332222141k k k -=⋅=--,即1232k k k +=, 故存在实数2λ=满足题意. 【点睛】关键点点睛:由直线斜率关系,椭圆过定点,应用待定系数法求2a ,2b ,写出椭圆E 的方程;根据直线与椭圆关系,联立方程由根与系数关系有12x x +,12x x ⋅,再由斜率的两点公式确定123,,k k k 的数量关系.18.(1)任选一个条件,抛物线方程都为24y x =;(2) 【分析】(1)选①:由抛物线的性质可得02pPF x =+,即可求出p ;选②:由题将点P 代入抛物线即可求出p ;选③:由题可得222p pPF p =+==;(2)联立直线与抛物线方程,利用弦长公式求出AB ,利用点到直线距离公式求出高,即可得出面积. 【详解】解:(1)若选①:由抛物线的性质可得02p PF x =+ 因为01PF x =+,所以0012px x +=+,解得2p =. 故抛物线C 的标准方程为24y x =. 若选②:因为0022y x ==所以002,1y x ==,因为点()00,P x y 在抛物线C 上,所以2002y px =,即24p =,解得2p =, 故抛物线C 的标准方程为24y x =. 若选③:因为PF x ⊥轴,所以22p pPF p =+=, 因为2PF =,所以2p =. 故抛物线C 的标准方程为24y x =.(2)设()()1122,,,A x y B x y 由(1)可知(1,0)F .联立2204x y y x--=⎧⎨=⎩,整理得2480y y --=,则1212124,8,y y y y y y +==--===故12AB y y =-==因为点F 到直线l 的距离2d ==,所以ABF的面积为11222AB d ⋅=⨯= 【点睛】方法点睛:解决直线与圆锥曲线相交问题的常用步骤: (1)得出直线方程,设交点为()11A x y ,,()22B x y ,; (2)联立直线与曲线方程,得到关于x (或y )的一元二次方程; (3)写出韦达定理;(4)将所求问题或题中关系转化为1212,x x x x +形式; (5)代入韦达定理求解.19.(1)2211612x y +=;(2【分析】(1)由题得2c =,210a c c+=,联解可得.(2)写出:2AB y x =-,与椭圆方程联解,利用根与系数关系及求得三角形面积得解.【详解】解(1)设椭圆的半焦距为c ,()2,0F2c ∴=,210a c c+=,216a ∴= 22216412b a c ∴=-=-=∴椭圆C 的方程为2211612x y +=(2):2AB y x =-22211612y x x y =-⎧⎪⎨+=⎪⎩2712360y y ∴+-= 设()11,A x y ,()22,B x y1212127367y y y y ⎧+=-⎪⎪∴⎨⎪⋅=-⎪⎩127y y ∴-==△AOB的面积121122277S OF y y =-=⨯⨯=【点睛】直线与圆锥曲线的位置关系通常是直线方程与圆锥曲线方程联解,利用根与系数关系求解,达到设而不求,简化运算.20.(Ⅰ)22143x y +=;(Ⅱ)247;(Ⅲ)12||S S -【分析】(Ⅰ)根据椭圆的几何性质求出,a b 可得结果; (Ⅱ)联立直线与椭圆,根据弦长公式可求得结果;(Ⅲ)设直线l :1x ty =-(0)t ≠,11(,)C x y ,22(,)D x y ,联立直线l 与椭圆M 的方程,利用韦达定理求出12y y +,12||S S -=212||34t t +,变形后利用基本不等式可求得最大值. 【详解】(Ⅰ)因为椭圆的焦点为()1,0F -,所以1c =且23b =,所以222314a b c =+=+=,所以椭圆M 方程为22143x y +=.(Ⅱ)因为直线l 的倾斜角为45,所以斜率为1,直线l 的方程为1y x =+,联立221143y x x y =+⎧⎪⎨+=⎪⎩,消去y 并整理得27880x x +-=,设11(,)C x y ,22(,)D x y , 则1287x x +=-,1287x x =-,所以||CD =247=. (Ⅲ)由(Ⅰ)知(2,0),(2,0)A B -,设直线l :1x ty =-(0)t ≠,11(,)C x y ,22(,)D x y ,联立221143x ty x y =-⎧⎪⎨+=⎪⎩,消去x 并整理得22(34)690t y ty +--=,则122634ty y t +=+,123934y y t =-+0<,所以12,y y 异号, 所以121211|||4||4|||22S S y y -=⨯-⨯⨯122||||||y y =-122||y y =+212||34t t =+ 1243||||t t =+≤==当且仅当||3t =时,等号成立.所以12||S S -. 【点睛】关键点点睛:第(Ⅲ)问中将三角形面积用,C D 两点的纵坐标表示,并利用韦达定理和基本不等式解决是解题关键.21.(1)221169y x +=;(2)()222413y x --=(1≥x ). 【分析】(1)根据条件先求解出双曲线的半焦距c ,然后结合三角形的面积、勾股定理、椭圆的定义求解出椭圆方程中2a 的值,从而椭圆方程可求;(2)设(),M x y ,()00,B x y ,根据条件用M 点的坐标表示出B 点的坐标,再根据B 在双曲线上求解出,x y 满足的等式即为轨迹方程. 【详解】(1)设双曲线的半焦距为c ,由题2437c =+=,设椭圆方程22221y xa b+=(0a b >>).∴1222212121924282PF PF PF PF c PF PF a⎧=⎪⎪⎪+==⎨⎪+=⎪⎪⎩,∴2221212142+4=64a PF PF PF PF ⎛⎫ ⎪⎝⎭=+∴216a =,∴2221679b a c =-=-=,∴2:C 221169y x +=;(2)由题点()0,4A .设双曲线右支上任意一点B 的坐标为()00,x y ,AB 中点M 的坐标为(),x y ,则00242x x y y ⎧=⎪⎪⎨+⎪=⎪⎩,∴00224x xy y =⎧⎨=-⎩, 又点B 在双曲线上,∴2200143x y -=∴()222413y x --=(1≥x ).【点睛】结论点睛:椭圆或双曲线的焦点三角形的顶点为P ,焦点为12,F F ,且12F PF θ∠=,则有:(1)椭圆的焦点三角形的面积为:2tan2b θ(b 为短轴长度一半);(2)双曲线的焦点三角形的面积为:2tan2bθ(b为虚轴长度一半).22.(1)2214xy+=;(2)0x y--=或0x y+=或20x--=或20x-=.【分析】(1)由直线方程,求出椭圆的上顶点和右焦点,可得出a、b的值,进而可求出椭圆C的方程;(2)设直线l的方程为x my=,设点()11,A x y、()22,B x y,于是得出OAB的面积为1212OABS OF y y=⋅-,将直线l的方程与椭圆C的方程联立,将韦达定理代入OAB的面积表达式可求出m的值,从而可得出直线l的方程.【详解】(1)由0x-=,令0x=可得1y=;令0y=可得x=因为直线0x+-=经过椭圆的上顶点和右焦点,所以半焦距为c=1b=,因此2a==,所以,椭圆C的方程为2214xy+=;(2)由(1)可得)2F,设过)2F的直线方程为x my=,由2214x myxy⎧=⎪⎨+=⎪⎩消去x,整理得()22410m y++-=,显然22124164280m m∆=++=+>.设12(,)A x x,12(,)B x x,则12y y+=,12214y ym-=+,从而1224y ym-=+.所以121122OABS OF y y=⋅-==,解得1m=±或2m=±所以直线l的方程为0x y-=或0x y+=,20x--=或20x-=.【点睛】思路点睛:求解椭圆中三角形(或四边形)面积相关问题时,一般需要联立直线与椭圆方程,结合韦达定理,以及弦长公式等,表示出三角形(或)四边形的面积,结合题中条件列出方程求解即可.23.(1)2214x y +=;(2 【分析】(1)设(),M x y ,利用已知条件得到(),2P x y ,代入圆的方程整理即可得出结果;(2)由(1)得12F F =)N t 在曲线C 上,可得2t =,利用三角形的面积公式求解即可. 【详解】(1)设(),M x y ,则(),0D x , 由12DM DP =, 知(),2P x y ,因为点P 在圆224x y +=上, 所以2244x y +=,故动点M 的轨迹C 的方程为2214x y +=;(2)由(1)得曲线C 的方程为:2214x y +=,得122F F c ====又点)N t 在曲线C 上,得22142t t +=⇒=,所以1212112222F NF S F F t ==⨯=.所以12F NF △的面积为2. 【点睛】方法总结:求点的轨迹方程的方法:(1)定义法;(2)直接法;(3)代入法;(4)参数法.24.(1)2214x y +=;(2)1,13⎛⎫ ⎪⎝⎭.【分析】(1)由椭圆性质结合通径运算即可得解;(2)设直线l 的方程为4,0x my m =->,()()1122,,,M x y N x y ,联立方程组结合韦达定理得1221102,3y y y y ⎛⎫+∈ ⎪⎝⎭,再由三角形的面积公式即可得解. 【详解】(1)因为||4AB =,所以24a =即2a =, 设椭圆右焦点(),0F c ,当x c =时,2by a=±=±,所以221b a =,1b =, 所以椭圆C 的方程为2214x y +=;(2)设直线l 的方程为4,0x my m =->,()()1122,,,M x y N x y ,则120y y <<,由22414x my x y =-⎧⎪⎨+=⎪⎩,整理可得()2248120m y my +-+=, ()22264484161920m m m ∆=-+=->,解得212m >,所以12284m y y m +=+,122124y y m =+, 则()()22221212221122816422212344m y y y ym m y y y y m m ⎛⎫⎪++⎝⎭+=-=-=-++ 2161022,4331m ⎛⎫=-∈ ⎪⎛⎫⎝⎭+ ⎪⎝⎭, 所以()211,3y y ∈, 所以2211112,11332PNA PMBPA y S y S y PB y λ⋅⎛⎫==⎪⎭=∈ ⎝⋅△△.【点睛】关键点点睛:解决本题的关键是将三角形的面积比转化为213y y ,结合韦达定理即可得解. 25.(Ⅰ)2214x y +=;(Ⅱ)(4,.【分析】(Ⅰ)依题意2a =,c =222a c b -=求解b 的值,则椭圆方程可求;(Ⅱ)联立直线和椭圆方程,利用根与系数关系求出A ,B 横纵坐标的和与积,进一步求得AB 的垂直平分线方程,求得Q 的坐标,由两点间的距离公式求得||PQ ,由弦长公式求得||AB ,作比后求得||||AB PQ 的取值范围. 【详解】解:(Ⅰ)由题意得2a =,c =因为222a cb -=,即2222b -=,所以1b =.所以椭圆C 的方程是2214x y +=.(Ⅱ)由22(1),1,4y k x x y =-⎧⎪⎨+=⎪⎩得2222(14)8440k x k x k +-+-=. 设1122(,),(,)A x y B x y ,则有2122814k x x k +=+,21224414k x x k -=+, 121222(2)14ky y k x x k -+=+-=+.所以线段AB 的中点坐标为2224(,)1414k kk k-++, 所以线段AB 的垂直平分线方程为22214()1414k k y x k k k --=--++. 于是,线段AB 的垂直平分线与x 轴的交点Q 223(,0)14kk+,又点(1,0)P , 所以22223111414k k PQ k k +=-=++.又AB ==.于是,22||141||14AB k k PQ k +===++ 因为0k ≠,所以221331k<-<+. 所以||||AB PQ的取值范围为(4,.【点睛】(1)解答直线与椭圆的题目时,时常把两个曲线的方程联立,消去x (或y )建立一元二次方。
深圳华南中英文学校高中数学选修2-1第一章《常用逻辑用语》测试题(答案解析)

一、选择题1.下列命题错误的是( )A .命题“若0m >,则方程20x x m +-=有实数根”的逆否命题为:“若方程20x x m +-=无实数根,则0m ≤”B .“6πθ=”是“()1sin 22k θπ+=”的充分不必要条件 C .若p q ∧为假命题,则,p q 均为假命题 D .对于命题:p x R ∃∈,使得210x x ++<,则:p x R ⌝∀∈,均有210x x ++≥ 2.下列命题错误的是( )A .命题“若p 则q ”与命题“若q ⌝,则p ⌝”互为逆否命题B .命题“x ∃∈R, 20x x ->”的否定是“R ∀∈,20x x -≤”C .∀ 0x >且1x ≠,都有12x x+> D .“若22am bm <,则a b <”的逆命题为真3.下列4个命题中正确命题的个数是( )①已知a ,b 表示直线,α表示平面,若//a α,//b α,则//a b ;②ABC 中,若A B >,则sin sin A B >;③若平面向量a ,b ,c ,满足//a b ,//b c ,则存在a ,c 不共线;④等差数列{}n a 中,n a m =,()m a n m n =≠,则0m n a +=.A .4个B .3个C .2个D .1个4.给出如下四个命题:①若“p 且q ”为假命题,则,p q 均为假命题;②命题“若a b >,则221a b >-”的否命题为“若a b <,则221a b ≤-”;③“x ∀∈R ,211x +≥”的否定是“x ∃∈R ,211x +<”;其中正确的命题的个数是( )A .0B .1C .2D .3 5.已知三个正数a ,b ,c 满足3a b c a ≤+≤,()2235b a a c b ≤⋅+≤,则以下四个命题正确的是( )1p :对任意满足条件的a ,b ,c ,均有b c ≤;2p :存在一组实数a ,b ,c ,使得b c >;3p :存在满足条件的a ,b ,c ,使得64b a c ≤+;4p :对任意满足条件的a ,b ,c ,均有64b a c >+.A .1p ,3pB .1p ,4pC .2p ,3pD .2p ,4p 6.已知0a b >>,给出下列命题:①1=,则1a b -<; ②若331a b -=,则1a b -<;③若1a b e e -=,则1a b -<; ④若ln ln 1a b -=,则1a b -<.其中真命题的个数是( )A .1B .2C .3D .4 7.命题:p 关于x 的不等式2240x ax ++>对一切x ∈R 恒成立,:q 函数()()32x f x a =-是增函数,若“p q ∨”为真命题,“p q ∧”为假命题,则实数a 取值范围为( )A .()(),22,-∞-+∞B .(][),21,2-∞-C .(](],21,2-∞-D .(][),22,-∞-+∞ 8.设0a >,0b >.下列说法正确的是( ) A .2ln 2ln a b a b +<+则a b >B .2ln 2ln a b a b +<+则a b <C .2ln 2ln a b a b -<-则a b >D .2ln 2ln a b a b -<-则a b < 9.已知命题():0,p x ∀∈+∞,1102x m ⎛⎫+-> ⎪⎝⎭;命题():0,q x ∃∈+∞,2410mx x +-=,则命题p 是命题q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件10.若命题“0x R ∃∈,200230x mx m ++-<”为假命题,则实数m 的取值范围是( )A .[]2,6B .()2,6C .(][),26,-∞+∞D .()(),26,-∞+∞11.已知命题p :23100x x -->,命题q :23x m m +>﹣,若p ⌝是q ⌝的充分不必要条件,则实数m 的取值范围是( )A .[﹣1,2]B .(﹣∞,﹣1]∪[2,+∞)C .(﹣∞,﹣1)∪(2,+∞)D .(﹣1,2) 12.下列说法中正确的是( )A .命题“若21x =,则1x =”的否命题是“若21x =,则1x ≠”B .“1x =-”是“220x x --=”的必要不充分条件C .命题“若x y =,则sin sin x y =”的逆否命题是真命题D .“tan 1x =”是“4x π=”的充分不必要条件二、填空题13.已知命题p :实数x 满足不等式2212x x -<-;命题q :实数x 满足不等式223(1)230x m x m m -+++≤,若命题q 是命题p 的必要不充分条件,则实数m 的取值范围是________.14.若“x ∀∈R ,使210x ax ++≥”为假命题,则实数a 的取值范围为______.15.命题p :(x ﹣m )2>3(x ﹣m )是命题q :x 2+3x ﹣4<0成立的必要不充分条件,则实数m 的取值范围为____.16.在下列给出的命题中,所有正确命题的序号为__________.①函数3231y x x =-+的图象关于点()0,1成中心对称;②对,x y R ∀∈若0x y +≠,则1x ≠或1y ≠-;③若实数x ,y 满足221x y +=,则2y x +的最大值为3;④若ABC ∆为钝角三角形,则sin cos A B <.17.设2:8120x x α-+>,2:x m m β-≤,若β是α的充分非必要条件,则实数m 的取值范围是_______________.18.在整数集Z 中,被5除所得余数为k 的所有整数组成一个“类”,记为[]k ,即[]{}5,0,1,2,3,4k n k n Z k =+∈=.给出如下四个结论:①[]20111∈,②[]33-∈,③[][][][][]01234Z =⋃⋃⋃⋃,④整数,a b 属于同一类的充要条件是[]0a b -∈.其中正确的个数是___________19.已知集合{}|A x x a =>,{}|22,B x x x R =-<∈,若“x A ∈”是“x B ∈”的必要不充分条件,则a 的取值范围_________.20.已知m ∈R ,命题p :对∀x ∈[0,1],不等式2x ﹣2≥2m ﹣3m 恒成立;命题q :∃x ∈[﹣1,1],使得m≤ax 成立,当a =1时,若p ∧q 假,p ∨q 为真,求m 的取值范围_____. 三、解答题21.已知命题:“{}|11x x x ∃∈-<<,使等式220x x m --=成立”是真命题.(1)求实数m 的取值集合M ;(2)设不等式()()20x a x a -+-<的解集为N ,若x ∈N 是x M ∈的必要条件,求a 的取值范围.22.已知{}2|8200A x x x =--≤,{}|2B x x m =-≤ (1)若“∃x ∈A ,使得x ∈B ”为真命题,求m 的取值范围;(2)是否存在实数m ,使“x ∈A ”是“X ∈B ”必要不充分条件,若存在,求出m 的取值范围;若不存在,请说明理由.23.设a 是实数,命题p :函数22()233f x x x a a =-++-的最小值小于0,命题q :不等式23610ax x +-≤在R 上恒成立,命题r :11m a m -≤≤+.(1)若p 是真命题、q 是假命题,求实数a 的取值范围;(2)若p 是r 的充分不必要条件,求实数m 的取值范围.24.已知命题甲:对任意实数x ∈R ,不等式223022ax ax x x -+-+≥恒成立;命题乙:已知*x y R ∈,满足3x y xy +=-,且a xy ≤恒成立.(1)分别求出甲、乙为真命题时,实数a 的取值范围;(2)求实数a 的取值范围,使命题甲、乙中有且只有一个真命题.25.已知a R ∈,命题:p “[]21,2,0x x a ∀∈-≤”,命题:q “2,220x R x ax a ∃∈++-=”. (1)若命题p 是真命题,求实数a 的取值范围;(2)若p q 、有且只有一个真命题,求实数a 的取值范围.26.已知{}{}222210,3100.:;:A xx x a B x x x p x A q x B =-+-=-->∈∈∣∣,若p 是q 的必要不充分条件,求实数a 的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】对于A ,命题的逆否命题,既要交换条件、结论,又要否定条件及结论,所以‘命题“若m >0,则方程x 2+x-m=0有实数根”的逆否命题为:“若方程x 2+x-m=0无实数根,则m≤0”,故正确;对于B “6πθ=”⇒“()1sin 22k θπ+=” 但“()1sin 22k θπ+=” 不能推出“6πθ=” 故正确;对于C ,p ∧q 为假命题,则p ,q 有一个为假命题即可,故错误;对于D ,命题的否定先换量词,再否定结论,故正确.故选C . 2.D解析:D【分析】对给出的四个选项分别进行判断可得结果.【详解】对于选项A ,由逆否命题的定义可得,命题“若p 则q ”的逆否命题为“若q ⌝,则p ⌝”,所以A 正确.对于选项B ,由含量词的命题的否定可得,命题“x ∃∈R, 20x x ->”的否定是“R ∀∈,20x x -≤”,所以B 正确.对于选项C ,当0x >且1x ≠时,由基本不等式可得12x x+>.所以C 正确. 对于选项D ,命题“若a b <,则22am bm <”当0m =时不成立,所以D 不正确. 故选D .【点睛】由于类似问题考查的内容较多,解题的关键是根据每个命题对应的知识解决,要求对相关知识要有一个整体性的掌握,本题考查综合运用知识解决问题的能力.3.B解析:B【分析】对于①由线面平行的性质知:a 与b 不一定平行,故①错误;对于②,运用三角形的边角关系和正弦定理可判断②正确;对于③,由于向量的平行不满足传递性,故③正确;对于④,由等差数列的性质和通项公式可知④正确.从而得到正确的答案.【详解】对于①,当//a α,//b α时,a 与b 也可能相交或异面,故①错误;对于②,在ABC 中,2sin 2sin sin sin (A B a b R A R B A B R >⇔>⇔>⇔>为ABC 的外接圆的半径),故②正确;对于③,若平面向量a ,b ,c ,满足//a b ,//b c ,当0b =时,a 与c 可以不共线,故③正确;对于④,由n a m =,()m a n m n =≠⇒公差1n m a a m n d n m n m--===---,0m n m a a nd n n +∴=+=-=,故④正确.故选:B .【点睛】本题主要考查线面平行的性质、正弦定理与三角形的边角关系、向量共线及等差数列的性质、通项公式等知识点,属于中档题.4.B解析:B【分析】结合命题相关知识,对选项逐个分析即可得到答案.【详解】对于①,,p q 可能为一真一假也可能两个都为假,故①错误;对于②,命题“若a b >,则221a b >-”的否命题为“若a b ≤,则221a b ≤-”,故②错误;对于③,“x ∀∈R ,211x +≥”的否定是“x ∃∈R ,211x +<”,正确.故只有③正确,答案为B.【点睛】本题考查了复合命题的性质,考查了命题的否定、原命题的否命题,属于基础题. 5.C解析:C【分析】取特殊值,结合原命题与否定的真假关系,即可得出答案.【详解】取2,1,3b c a ===,满足条件3a b c a ≤+≤,()2235b a a c b ≤⋅+≤,此时b c > 则2p 为真命题,由于2p 的否定为1p ,则1p 为假命题取1,2a b c ===,满足条件3a b c a ≤+≤,()2235b a a c b ≤⋅+≤,此时也满足64b a c ≤+,则3p 为真命题,由于3p 的否定为4p ,则4p 为假命题故选:C【点睛】本题主要考查了判断命题的真假,属于中档题.6.B解析:B【分析】①1=1=,然后两边平方,再通过作差法即可得解; ②若331a b -=,则331a b -=,然后利用立方差公式可知23(1)(1)a a a b -++=,再结合0a b >>以及不等式的性质即可判断;③若1a b e e -=,则111a b a b b b b e e ee e e -+===+,再利用0b >,得出1b e >,从而求得a b e -的范围,进而判断;④取特殊值,a e =,1b =即可判断.【详解】解:①1=,1=,所以1a b =++所以11a b -=+,即①错误;若331a b -=,则331a b -=,即23(1)(1)a a a b -++=,因为0a b >>,所以22a b >,所以221a a b ++>,所以1a b -<,即1a b -<,所以②正确;若1a b e e -=, 则111a b a b b b b e e e e e e-+===+,因为0b >,所以12a b e e -<<<,所以1a b -<,即③正确;④取a e =,1b =,满足1lna lnb -=,但1a b ->,所以④错误;所以真命题有②③,故选:B .【点睛】本题考查命题真假的判断,涉及根据不等式的性质证明不等式、指对运算法则、立方差公式等,考查学生的分析能力和运算能力.7.B解析:B【分析】先求得命题,p q 为真命题时,a 的取值范围.根据“p q ∨”为真命题,“p q ∧”为假命题可知,p q 一真一假,由此进行分类讨论,求得a 的取值范围.【详解】当p 为真命题时,24160a ∆=-<,解得22a -<<.当q 为真命题时,321,1a a -><.由于“p q ∨”为真命题,“p q ∧”为假命题,所以,p q 一真一假.当p 真q 假时,221a a -<<⎧⎨≥⎩,解得12a ≤<; 当p 假q 真时,221a a a ≤-≥⎧⎨<⎩或,解得2a ≤-. 综上所述,实数a 的取值范围是(][),21,2-∞-.故选:B【点睛】 本小题主要考查一元二次不等式恒成立问题,考查根据含有逻辑联结词命题的真假性求参数的取值范围,考查分类讨论的数学思想方法,属于基础题.8.B解析:B【分析】举反例说明C,D 不成立,再根据函数2ln x y x =+单调性,进而确定选项.【详解】 因为311123112ln12ln 2,2ln 2ln ,ee e e -<--<-所以CD 不成立; 因为2ln xy x =+在(0,)+∞上单调递增,所以由2ln 2ln a b a b +<+得a b <, 故选:B【点睛】本题考查利用函数单调性判断命题真假,考查基本分析判断能力,属基础题.9.A解析:A【分析】分别计算得到m 1≥和4m ≥-,根据范围大小判断得到答案.【详解】():0,p x ∀∈+∞,1102x m ⎛⎫+-> ⎪⎝⎭,即112x m ⎛⎫>- ⎪⎝⎭,易知函数()112xf x ⎛⎫=- ⎪⎝⎭单调递增,故m 1≥. 命题():0,q x ∃∈+∞,2410mx x +-=, 2214124m x x x ⎛⎫=-=-- ⎪⎝⎭,故4m ≥-. 故命题p 是命题q 的充分不必要条件.故选:A .【点睛】本题考查了根据命题求参数,充分不必要条件,意在考查学生的推断能力.10.A解析:A【分析】因为原命题是假命题,其否定为真命题,问题可转化为0x R ∀∈,200230x mx m ++-≥恒成立,故由0∆≤即可求出m 的取值范围.【详解】因为命题“0x R ∃∈,200230x mx m ++-<”为假命题,故其否定:“0x R ∀∈,200230x mx m ++-≥”为真命题,故224(23)8120m m m m ∆=--=-+≤,解得26m ≤≤,故实数m 的取值范围是[2,6].故选:A【点睛】本题原命题是存在性命题且为假命题,它的否定是全称命题且为真命题,进而将问题转化为恒成立处理,采用正难则反的思想进行求解,同时考查命题的等价性和转化的思想. 11.B解析:B【分析】由p ⌝是q ⌝的充分不必要条件,则q 是p 的充分不必要条件, 由23100x x -->得5x >或2x <-,只需235m m -+≥,即可.【详解】由23100x x -->得5x >或2x <-,因为p ⌝是q ⌝的充分不必要条件,所以q 是p 的充分不必要条件,所以235m m -+≥,解得2m ≥或1m ≤-.故选:B .【点睛】本题考查充分必要条件求参数取值范围问题,难度一般.12.C解析:C【分析】对选项逐个进行判断,即可得出结论.【详解】A :命题“若21x =,则1x =”的否命题是“若21x ≠,则1x ≠”,故A 不正确;B :“1x =-”是“220x x --=”的充分不必要条件,故B 不正确;C :命题“若x y =,则sin sin x y =”是真命题,所以命题“若x =y ,则sinx =siny ”的逆否命题是真命题,故C 正确;D : “tan 1x =”是“4x π=”的必要不充分条件,故D 不正确.故选:C .【点睛】本题考查命题的真假判断与应用,考查四种命题,考查充要条件,属于中档题. 二、填空题13.【分析】首先求出命题为真时的的范围然后根据必要不充分条件确定参数的范围【详解】命题:命题当时当时命题是命题的必要不充分条件即但不能推出不合题意时解得故答案为:【点睛】思路点睛:本题考查由必要不充分条 解析:1[,0]2- 【分析】首先求出命题,p q 为真时的x 的范围,然后根据必要不充分条件确定参数m 的范围.【详解】命题p :2212x x -<-0(2)0022x x x x x ⇒<⇒-<⇒<<-, 命题:q 223(1)230x m x m m -+++≤,()(23)0x m x m ---≤,当3m ≥-时,23m x m ≤≤+,当3m <-时,23m x m +<<,命题q 是命题p 的必要不充分条件,即p q ⇒,但q 不能推出p ,3m <-不合题意,3m ≥-时,0232m m ≤⎧⎨+≥⎩,解得102m -≤≤, 故答案为:1,02⎡⎤-⎢⎥⎣⎦.【点睛】思路点睛:本题考查由必要不充分条件求参数,解题时首先求出命题,p q 为真时变量的范围,然后根据必要不充分条件的定义得出参数的关系.也可根据充分必要条件与集合包含之间的关系求解.14.【分析】根据 是假命题得出它的否定命题是真命题求出实数a 的取值范围【详解】∵命题 是假命题∴是真命题即使不等式有解;所以解得:或∴实数a 的取值范围是故答案为:【点睛】关键点点睛:根据特称命题与全称命 解析:(,2][2,)-∞-+∞【分析】根据“R x ∀∈,210x ax ++> ”是假命题,得出它的否定命题是真命题,求出实数a 的取值范围.【详解】∵命题“R x ∀∈,210x ax ++> ”是假命题,∴R x ∃∈,210x ax ++≤是真命题,即R x ∃∈使不等式210x ax ++≤有解;所以240a ∆=-≥,解得:2a ≤-或2a ≥.∴实数a 的取值范围是(,2][2,)-∞-+∞.故答案为:(,2][2,)-∞-+∞.【点睛】关键点点睛:根据特称命题与全称命题的真假求参数,转化为一元二次不等式能成立问题是解题的关键,属于中档题.15.m≥1或m≤﹣7【分析】先求出命题p 和命题q 中不等式的解再根据必要不充分条件列不等式求解【详解】解:由x2+3x ﹣4<0得﹣4<x <1由(x ﹣m )2>3(x ﹣m )得(x ﹣m ﹣3)(x ﹣m )>0即x >解析:m ≥1或m ≤﹣7【分析】先求出命题p 和命题q 中不等式的解,再根据必要不充分条件列不等式求解.【详解】解:由x 2+3x ﹣4<0得﹣4<x <1,由(x ﹣m )2>3(x ﹣m )得(x ﹣m ﹣3)(x ﹣m )>0,即x >m +3或x <m ,若p 是q 的必要不充分条件,则1≤m 或m +3≤﹣4,即m ≥1或m ≤﹣7,故答案为:m ≥1或m ≤﹣7.【点睛】本题考查二次不等式的求解,考查充分性,必要性的应用,是中档题.16.①②③【分析】我们可以根据对称性等函数的性质对四个结论逐一进行判断可以得到正确的结论【详解】解:①函数可得所以函数关于点成中心对称成立故①正确;②对若且则即有若则或故②正确;③若实数满足可设则设为可解析:①②③【分析】我们可以根据对称性等函数的性质对四个结论逐一进行判断,可以得到正确的结论.【详解】解:①函数()3231y f x x x ==-+可得()()2f x f x +-=()()3323123112x x x x -++-++=.所以函数关于点()0,1成中心对称成立.,故①正确;②对x ∀,y R ∈.若1x =且1y =-,则0x y +=.即有若0x y +≠,则1x ≠或1y ≠-.故②正确;③若实数x ,y 满足221x y +=,可设cos x α=,sin (02)y ααπ=<, 则sin 22cos y x αα=++,设为t ,可得sin cos 2t t αα-=22||t, 解得33t ,则2y x +③正确; ④若ABC ∆为钝角三角形,若A 为锐角,B 为钝角,则sin cos A B >,故④错误. 故答案为:①②③【点睛】本题考查的知识点是判断命题真假,比较综合的考查了函数的性质,属于中档题, 17.【分析】根据是的充分非必要条件可知集合是集合的真子集由集合之间的包含关系再求参数范围即可【详解】对集合:解得;对集合:解得;因为是的充分非必要条件可知集合是集合的真子集故可得或解得或故故答案为:【点 解析:21m -<<【分析】根据β是α的充分非必要条件,可知集合β是集合α的真子集,由集合之间的包含关系,再求参数范围即可.【详解】对集合α:28120x x -+>,解得()(),26,x ∈-∞⋂+∞;对集合β:2x m m -≤,解得22,x m m m m ⎡⎤∈-++⎣⎦; 因为β是α的充分非必要条件,可知集合β是集合α的真子集,故可得22m m +<,或26m m -+>,解得()2,1m ∈-或m ∈∅,故()2,1m ∈-.故答案为:21m -<<.【点睛】本题考查由充分非必要条件,推出集合之间的关系,以及根据集合关系求参数范围的问题,属综合基础题.18.3【分析】根据2011被5除的余数为1可判断①;将=可判断②;根据整数集就是由被5除所得余数为01234可判断③;令根据类的定理可证明④的真假【详解】①由2011÷5=402…1所以2011∈1故①解析:3【分析】根据2011被5除的余数为1,可判断①;将3-=52-+,可判断②;根据整数集就是由被5除所得余数为0,1,2,3,4,可判断③;令115a n m =+,225b n m =+,根据“类”的定理可证明④的真假.【详解】①由2011÷5=402…1,所以2011∈[1],故①正确;②由()3512-=⨯-+ 所以[]33-∉,故②错误;③整数集就是由被5除所得余数为0,1,2,3,4的整数构成,③正确;④假设115a n m =+,225b n m =+,()12125a b n n m m -=-+-,,a b 要是同类. 则 12m m =,即120m m -=,所以[]0a b -∈,反之若[]0a b -∈,即120m m -=,所以12m m =,则,a b 是同类. ④正确;故答案为:3【点睛】本题考查的知识点是命题的真假判断与应用,正确理解新定义“类”是解答的关键,以及进行简单的合情推理.属中档题.19.【分析】根据必要不充分条件得到集合之间的关系从而求解出参数的取值范围【详解】因为是的必要不充分条件所以又因为所以因为所以即的取值范围是:【点睛】集合:若是的必要不充分条件则有:;若是的充分不必要条件 解析:0a ≤【分析】根据必要不充分条件得到集合,A B 之间的关系,从而求解出参数的取值范围.【详解】因为“x A ∈”是“x B ∈”的必要不充分条件,所以B A ,又因为{}|22,B x x x R =-<∈,所以()0,4B =,因为(),A a =+∞,所以0a ≤,即a 的取值范围是:0a ≤.【点睛】集合()(){|},{|}A x x p x B x x q x =∈=∈:若“x A ∈”是“x B ∈”的必要不充分条件,则有:B A ; 若“x A ∈”是“x B ∈”的充分不必要条件,则有:A B .20.(﹣∞1)∪(12【分析】先求解命题p 命题q 为真时m 的取值范围利用若p ∧q 假p ∨q 为真那么一真一假分类讨论(1)当为真为假;(2)当为真为假两种情况最后取并集【详解】命题p :对∀x ∈01不等式恒成立解析:(﹣∞,1)∪(1,2]【分析】先求解命题p ,命题q 为真时m 的取值范围,利用若p ∧q 假,p ∨q 为真,那么p,q 一真一假,分类讨论(1)当p 为真,q 为假;(2)当q 为真,p 为假两种情况,最后取并集.【详解】命题p :对∀x ∈[0,1],不等式22x 2m 3m -≥-恒成立,则2m 32m -≤-,解得1m 2≤≤;命题q :∃x ∈[﹣1,1],使得m≤ax 成立,当a =1时,那么m x ≤则m 1≤ 若p ∧q 假,p ∨q 为真,那么p,q 一真一假(1)当p 为真,q 为假时,解得1m 2<≤;(2)当q 为真,p 为假时,解得m 1<;由此解得m 的取值范围(﹣∞,1)∪(1,2]【点睛】已知命题的真假求参数的取值范围,先求解命题p ,命题q 为真时m 的取值范围,利用若p ∧q 假,p ∨q 为真,那么p,q 一真一假,分类讨论(1)当p 为真,q 为假;(2)当q 为真,p 为假两种情况,最后取并集.三、解答题21.(1)1,38M ⎡⎫=-⎪⎢⎣⎭(2)3a ≥或1a ≤- 【分析】(1)利用参数分离法将m 用x 表示,结合二次函数的性质求出m 的取值范围,从而可求集合M ;(2)若x ∈N 是x M ∈的必要条件,则M N ⊆分类讨论①当2a a >-即1a >时,{|2}N x a x a =-<<,②当2a a <-即1a <时,{|2}N x a x a =<<-,两种情况进行求解;【详解】解:(1)由题意,方程22m x x =-在(1,1)-上有解令2()2f x x x =-(11)x -<<.只需m 在()f x 值域内易知()f x 值域为1,38⎡⎫-⎪⎢⎣⎭.m ∴的取值集合1,38M ⎡⎫=-⎪⎢⎣⎭(2)由题意,M N ⊆,显然N 不为空集.①当2a a >-即1a >时,(2,)N a a =-. 12831a a a ⎧-<-⎪⎪∴≥⎨⎪>⎪⎩3a ∴≥ ②当2a a <-即1a <时,(,2)N a a =-.23181a a a -≥⎧⎪⎪∴<-⎨⎪<⎪⎩1a ∴≤-. 综合:3a ∴≥或1a ≤-【点睛】本题主要考查了二次函数在闭区间上的值域的求解,集合之间包含关系的应用,体现了分类讨论思想的应用.22.(1)412m -≤≤;(1)存在,08m ≤≤【分析】(1)根据题意转化为集合A 、B 存在公共元素,求出A 、B 无公共元素时,实数m 的取值范围,取补集即可.(2)由题意转化为B A ⊆,再根据集合的包含关系可得22210m m -≥-⎧⎨+≤⎩,解不等式组即可. 【详解】{}()(){}{}2|82001020210A x x x x x x x x =--≤=-+≤=-≤≤,{}{}{}|22222B x x m x x m x m x m =-≤=-≤-≤=-≤≤+(1)若“∃x ∈A ,使得x ∈B ”为真命题,即集合A 、B 存在公共元素,假设A 、B 无公共元素,则210m ->或22m +<-,解得12m >或4m <-,则集合A 、B 存在公共元素时,实数m 的取值范围412m -≤≤.(2)存在实数m ,使“x ∈A ”是“X ∈B ”必要不充分条件,若 “x ∈A ”是“X ∈B ”必要不充分条件, 则B A ,所以22210m m -≥-⎧⎨+≤⎩,解得08m ≤≤, 所以m 的取值范围为08m ≤≤.【点睛】本题考查了充分条件、必要条件的集合思想,考查了转化与化归的思想,属于中档题. 23.(1)()3,1-;(2)[)5,+∞【分析】(1)利用二次函数的性质求命题,p q 为真命题时,a 的取值范围,再根据条件求a 的取值范围;(2)由条件可知{}41a a -<<是集合{}11a m a m -≤≤+的真子集,利用包含关系求m 的取值范围.【详解】当命题p 为真时,∵()()2222233134f x x x a a x a a =-++-=-++-,∴函数()f x 的最小值为()2min 340f x a a =+-<,解得:41a -<<. 当命题q 为真时,3643(1)00a a ∆=-⨯⨯-≤⎧⎨<⎩,解得:3a ≤-. (1)因为p 为真命题,q 为假命题.∴413a a -<<⎧⎨>-⎩,∴31a -<<, ∴实数a 的取值范围是()3,1-. (2)若p 是r 的充分不必要条件,则1411m m -≤-⎧⎨≤+⎩,解得:5m ≥. 故实数m 的取值范围是[)5,+∞.【点睛】本题考查根据命题的真假,命题的充分必要条件求参数的取值范围,重点考查计算能力,属于基础题型.24.(1)甲为真命题时,012a ≤≤;乙为真命题时,9a ≤(2)912a <≤或0a <【分析】(1)甲为真命题时,先转化为一元二次不等式恒成立问题,根据二次函数图象解得实数a 的取值范围,乙为真命题时,利用基本不等式求得xy 最小值,再根据恒成立得实数a 的取值范围;(2)分类求交集:甲真乙假与乙真甲假,最后求并集得结果.【详解】(1)222303022ax ax ax ax x x -+∴-+-+≥≥ 当0a =时,03≥成立;当0a ≠时,要使230ax ax -+≥恒成立,需20012120a a a a >⎧∴<≤⎨-≤⎩综上,甲为真命题时,012a ≤≤;*33,9x y R x y xy xy ∈+=-≥≥,,(当且仅当3x y ==时取等号)a xy ≤恒成立,min )9a xy ∴=≤(综上, 乙为真命题时,9a ≤(2)命题甲、乙中有且只有一个真命题,即甲真乙假与乙真甲假,所以0129a a ≤≤⎧⎨>⎩或1209a a a ><⎧⎨≤⎩或 即912a <≤或0a <【点睛】本题考查不等式恒成立问题以及根据命题真假求参数范围,考查综合分析求解能力,属中档题.25.(1)[4,)+∞(2)2a ≤-或14a ≤<【分析】(1)令2()f x x a =-,只要[1,2]x ∈时,max ()0f x ≤即可;(2)命题q 为真命题时,24420a ∆=-⋅≥,解得a 的取值范围,再分析p q 、一真一假即可求解.【详解】(1)∵命题p :[]21,2,0x x a ∀∈-≤为真命题, 令2()f x x a =-所以只要x ∈[1,2]时,max ()0f x ≤即可,也就是40a -≤,解得4a ≤∴实数a 的取值范围是[4,)+∞.(2) 命题:q “2,220x R x ax a ∃∈++-=”为真时,244(2)0,a a ∆=--≥解得2a ≤-或 1.a ≥当命题p 为真,命题q 为假时,421a a ≤⎧⎨-<<⎩, 解得a φ∈当命题p 为假,命题q 为真时,421a a a <⎧⎨≤-≥⎩或, 解得2a ≤-或14a ≤<综上:2a ≤-或14a ≤<【点睛】方法点睛:该题考查的是命题的有关问题,一是需要注意命题为真时对应的参数的取值范围,二是根据这两个命题是一真一假,建立不等式组从而求得结果. 26.33a -≤≤【分析】若p 是q 的必要不充分条件,则B A ,然后根据集合间的关系分类讨论求解即可.【详解】解:因为{}22210A x x x a =-+-≥∣,{}{23100|5B x x x x x =-->=>∣或}2x <- ①当0a >时,集合{|1A x x a =≥+或}1x a ≤-,若B A ,则有1512a a +≤⎧⎨-≥-⎩,解得:03a <≤; ②当0a <时,{|1A x x a =≥-或}1x a ≤+,若B A ,则有1512a a -≤⎧⎨+≥-⎩,解得:30a -≤<;③当0a =时,A R =,B A 成立,综上所述:33a -≤≤.【点睛】本题考查根据必要不充分条件确定参数的取值范围问题,难度一般. 解答时,一般将问题转化为根据集合的包含关系求参问题,注意分类讨论思想的运用.。
深圳华南中英文学校高中数学选修2-1第二章《空间向量与立体几何》测试题(答案解析)

一、选择题1.如图,在三棱锥A BCD -中,平面ABC ⊥平面BCD ,BAC 与BCD △均为直角三角形,且90BAC BCD ∠=∠=︒,AB AC =,112CD BC ==,点P 是线段AB 上的动点,若线段CD 上存在点Q ,使得异面直线PQ 与AD 成30的角,则线段PA 长的取值范围是( )A .20,2⎛⎤ ⎥⎝⎦B .60,3⎛⎤⎥ ⎝⎦C .(0,1]D .(0,2⎤⎦2.如图,在几何体111ABC A B C -中,ABC ∆为正三角形,111////AA BB CC ,1AA ⊥平面ABC ,若E 是棱11B C 的中点,且1112AB AA CC BB ===,则异面直线1A E 与1AC 所成角的余弦值为( )A .1313B .21313C .2613D .226133.长方体12341234A A A A B B B B -的底面为边长为1的正方形,高为2,则集合12{|i j x x A B A B =⋅,{1,2,3,4},{1,2,3,4}}i j ∈∈中元素的个数为( )A .1B .2C .3D .44.阅读材料:空间直角坐标系O ﹣xyz 中,过点P (x 0,y 0,z 0)且一个法向量为=(a ,b ,c )的平面α的方程为a (x ﹣x 0)+b (y ﹣y 0)+c (z ﹣z 0)=0;过点P (x 0,y 0,z 0)且一个方向向量为d =(u ,v ,w )(uvw≠0)的直线l 的方程为000x x y y z z u v w---==,阅读上面材料,并解决下面问题:已知平面α的方程为x+2y ﹣2z ﹣4=0,直线l 是两平面3x ﹣2y ﹣7=0与2y ﹣z+6=0的交线,则直线l 与平面α所成角的大小为( ) A .arcsin 1414 B .arcsin 421C .arcsin51442D .arcsin123773775.正方体ABCD —A′B′C′D′中,AB 的中点为M ,DD′的中点为N ,则异面直线B′M 与CN 所成角的大小为 A .0°B .45°C .60 °D .90°6.如图,在正方体1111ABCD A B C D ﹣中,1A H ⊥平面11AB D ,垂足为H ,给出下面结论:①直线1A H 与该正方体各棱所成角相等; ②直线1A H 与该正方体各面所成角相等;③过直线1A H 的平面截该正方体所得截面为平行四边形; ④垂直于直线1A H 的平面截该正方体,所得截面可能为五边形, 其中正确结论的序号为( )A .①③B .②④C .①②④D .①②③7.如图,已知平行六面体1111ABCD A BC D -中,底面ABCD 是边长为1的正方形,12AA =, 011120A AB A AD ∠=∠=,则线段1AC 的长为( )A 2B .1C .2D 38.在四面体O-ABC 中,G 1是△ABC 的重心,G 是OG 1上的一点,且OG=3GG 1,若OG =x OA +y OB +z OC ,则(x ,y ,z )为( )A .111,,444⎛⎫⎪⎝⎭B .333,,444⎛⎫⎪⎝⎭ C .111,,333⎛⎫⎪⎝⎭D .222,,333⎛⎫⎪⎝⎭9.若向量(3,1,0)a =,(1,0,)b z =,,3a b π=,则实数z 的值为( )A .2B .2C .2±D .2±10.如图,在空间四边形OABC 中,点E 为BC 中点,点F 在OA 上,且2OF FA =, 则EF 等于( )A .121+232OA OB OC - B .211+322OA OB OC -+ C .111222OA OB OC +- D .211322OA OB OC -- 11.如图,在棱长都相等的正三棱柱111ABC A B C -中,D 是棱1CC 的中点,E 是棱1AA 上的动点.设AE x =,随着x 增大,平面BDE 与底面ABC 所成锐二面角的平面角是( )A .增大B .先增大再减小C .减小D .先减小再增大12.如图,四棱锥P ABCD -的底面是边长为2的正方形, Q 为BC 的中点,PQ ⊥面ABCD ,且2PQ =,动点N 在以D 为球心半径为1的球面上运动,点M 在面 ABCD内运动,且PM 5=,则MN 长度的最小值为( )A .352-B .23-C .25-+D .332-二、填空题13.若平面α的一个法向量为()n 122=,,,A(1,0,2),B(0,-1,4),A ∉α,B ∈α,则点A 到平面α的距离为__________.14.若非零向量,αβ满足αβαβ+=-,则α与β所成角的大小为___. 15.ABC △中,90C ∠︒=,60A ∠︒=,2AB =,M 为AB 中点,将BMC △沿CM 折叠,当平面BMC ⊥平面AMC 时,A ,B 两点之间的距离为_____.16.如图,在棱长为2的正方体1111ABCD A BC D -中,E ,F 分别为棱1AA 、1BB 的中点,M 为棱11A B 上的一点,且1(02)A M λλ=<<,设点N 为ME 的中点,则点N 到平面1D EF 的距离为________.17.在正方体1111ABCD A BC D -中,M 为棱11A B 的中点,则异面直线AM 与1BC 所成的角的大小为________(结果用反三角函数值表示).18.如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面互相垂直,,,M E F 分别为,,PQ AB BC 的中点,则直线ME 与平面ABCD 所成角的正切值为________;异面直线EM 与AF 所成角的余弦值是________.19.如图,直三棱柱111ABC A B C -中,12AA =,1AB BC ==, 90ABC ∠=︒,外接球的球心为O ,点E 是侧棱1BB 上的一个动点.有下列判断:① 直线AC 与直线1C E 是异面直线;②1A E 一定不垂直1AC ; ③ 三棱锥1E AAO -的体积为定值; ④1AE EC +的最小值为22. 其中正确的序号序号是______.20.如图,在四面体D ABC -中,5AD BD AC BC ====,6AB DC ==.若M 为线段AB 上的动点(不包含端点),则二面角D MC B --的余弦值取值范围是__________.三、解答题21.在三棱台ABC DEF -中,2,60AB BC DE DAB EBA ∠∠====,平面ABED ⊥平面,.ABC BC BE ⊥(1)求证:平面ABED ⊥平面BCFE ; (2)求直线DF 与平面ABF 所成角的正弦值. 22.如图,在四棱锥P ABCD -中,6π∠=CAD ,且321,2AD CD PA ABC ===,和PBC 均是等边三角形,O 为BC 的中点.(I )求证:PO ⊥平面ABCD ; (Ⅱ)求CB 与平面PBD 所成角的正弦值.23.如图,在四棱锥P ABCD -中,90BAD ∠=,//AD BC , PA AD ⊥,PA AB ⊥,122PA AB BC AD ====.(Ⅰ)求证://BC 平面PAD ;(Ⅱ)求平面PAB 与平面PCD 所成锐二面角的余弦值.24.如图,四边形ABCD 与四边形BDEF 均为菱形,60DAB DBF ∠=∠=︒,且FA FC =(1)求证:平面ACF ⊥平面ABCD ; (2)求二面角A FC B --的余弦值.25.如图,平面ABCD ⊥平面ABEF ,其中四边形ABCD 为正方形,四边形ABEF 为直角梯形,1//902AB AF BE AF BE BAF ==∠=︒,,,M 为线段CE 上一点,//MF 平面ABCD .(1)确定点M 的位置,并证明你的结论; (2)求直线DF 与平面BFM 所成角的正弦值.26.如图,在四棱锥P ABCD -中,平面PAB ⊥平面ABCD ,PA AB ⊥,4PA AD ==,//BC AD ,AB AD ⊥,2AB BC ==,()01PE PC λλ=≤<.(1)若12λ=,求直线DE 与平面ABE 所成角的正弦值; (2)设二面角B AE C --的大小为θ,若234cos θ=,求λ的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】以C 为原点,CD 为x 轴,CB 为y 轴,过C 作平面BCD 的垂线为z 轴,建立空间直角坐标系,利用向量法能求出PA 长的取值范围. 【详解】如图,以C 为原点,CD 为x 轴,CB 为y 轴,过C 作平面BCD 的垂线为z 轴,建立空间直角坐标系,则()()()()0,0,0,0,1,1,0,2,0,1,0,0C A B D ,设(),0,0Q q ()01q ≤≤,设()0,,AP AB λλλ==-()01λ<≤,则()(,0,0)(0,1,1)(0,,)(,1,1)PQ CQ CA AP q q λλλλ=-+=---=---,(1,1,1)AD =--,异面直线PQ 与AD 成30的角,22||3cos30||||223PQ AD PQ AD q λ⋅∴===⋅++⋅, 22182516q q λ∴+=-+, 201,516[0,11]q q q ≤≤∴-+∈,即22182018211λλ⎧+≥⎨+≤⎩,解得2222λ-≤≤, 201,02λλ<≤∴<≤, 可得2||||22(0,1]PA AP λλ===∈.故选:C. 【点睛】利用向量求解空间角的关键在于“四破”:第一,破“建系关”,构建恰当的空间直角坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求法向量关”,求出平面的法向量;第四,破“应用公式关”.2.C解析:C 【解析】 【分析】以C 为原点,在平面ABC 内过C 作BC 的垂线为x 轴,CB 为y 轴,CC 1为z 轴,建立空间直角坐标系,利用向量法能求出异面直线A 1E 与AC 1所成角的余弦值 【详解】以C 为原点,在平面ABC 内过C 作BC 的垂线为x 轴, CB 为y 轴,CC 1为z 轴,建立空间直角坐标系, 设AB =AA 1=CC 1=2BB 1=2,则A 1(3,1,2),A (310,,),C 1(0,0,2),B 1(0,2,1),E (0,1,32), 1A E =(3-,0,12-),1AC =(3-,﹣1,2),设异面直线A 1E 与AC 1所成角为θ,则cosθ1111226131384A E AC A E AC ⋅===⋅⋅. ∴异面直线A 1E 与AC 1所成角的余弦值为2613. 故选C .【点睛】本题考查异面直线所成角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是基础题.3.C解析:C 【分析】建立空间直角坐标系,结合向量的数量积的定义,进行计算,即可求解. 【详解】由题意,因为正方体12341234A A A A B B B B -的底面为班车为1的正方形,高为2, 建立如图所示的空间直角坐标系,则12341234(1,1,0),(0,1,0),(0,0,0),(1,0,0),(1,1,2),(0,1,2),(0,0,2),(1,0,2)A A A A B B B B , 则12(1,0,2)A B =-, 与11(0,0,2)A B =相等的向量为223344A B A B A B ==,此时1211224A B A B ⋅=⨯=, 与14(0,1,2)A B =-相等的向量为23A B ,此时1214224A B A B ⋅=⨯=, 与41(0,1,2)A B =相等的向量为32A B ,此时1241224A B A B ⋅=⨯=, 与21(1,0,2)A B =相等的向量为34A B ,此时1221143A B A B ⋅=-+=, 与12(1,0,2)A B =-相等的向量为43A B ,此时1212145A B A B ⋅=+=, 体对角线向量为13(1,1,2)A B =--,此时1213145A B A B ⋅=+=, 24(1,1,2)A B =-,此时1224143A B A B ⋅=-+=, 31(1,1,2)A B =,此时1231143A B A B ⋅=-+=, 42(1,1,2)A B =-,此时1242145A B A B ⋅=+=,综上集合11{|,{1,2,3,4},{1,2,3,4}}{3,4,5}i j x x A B A B i j =⋅∈∈=,集合中元素的个数为3个. 故选:C .【点睛】本题主要考查了集合的元素的计算,以及向量的数量积的运算,其中解答中建立恰当的空间直角坐标系,熟记向量的数量积的运算公式,准确计算是解答的关键,着重考查了推理与运算能力,属于基础题.4.B解析:B【分析】先根据两个平面的方程,求出平面交线的方向向量,结合已知平面的方程确定平面的法向量,然后求解.【详解】平面α的法向量为n =(1,2,﹣2),联立方程组3270260x y y z --=⎧⎨-+=⎩,令x =1,得y =﹣2,z =2,令x =3,得y =1,z =8, 故点P (1,﹣2,2)和点Q (3,1,8)为直线l 的两个点,∴PQ =(2,3,6)为直线l 的方向向量, ∵44cos ,3721||||PQ n PQ n PQ n ⋅-<>===-⨯ ,∴直线l 与平面α所成角的正弦值为421, 故选B .【点睛】本题主要考查直线和平面所成角的正弦,属于信息提供题目,理解题中所给的信息是求解关键. 5.D解析:D 【分析】以A 为原点,AB 为x 轴,AD 为y 轴,1AA 为z 轴建立空间直角坐标系,利用向量1(1,0,2)B M =--,(2,0,1)CN =-的数量积为0,即可求解.【详解】以A 为原点,AB 为x 轴,AD 为y 轴,1AA 为z 轴建立空间直角坐标系如图所示, 设正方体1111ABCD A BC D -的棱长为2,由图可知(1,0,0)M ,1(2,0,2)B ,(2,2,0)C ,(0,2,1)N , 所以1(1,0,2)B M =--,(2,0,1)CN =-所以1cos ,0B M CN 〈〉=所以异面直线B M '与CN 所成的角为90︒.故本题正确答案为D.【点睛】本题主要考查了异面直线所成角,属于基础题.6.D解析:D【解析】【分析】由A1C⊥平面AB1D1,直线A1H与直线A1C重合,结合线线角和线面角的定义,可判断①②;由四边形A1ACC1为矩形,可判断③;由垂直于直线A1H的平面与平面AB1D1平行,可判断④.【详解】如图,在正方体ABCD﹣A1B1C1D1中,A1H⊥平面AB1D1,垂足为H,连接A1C,可得A1C⊥AB1,A1C⊥AD1,即有A1C⊥平面AB1D1,直线A1H与直线A1C重合,直线A1H与该正方体各棱所成角相等,均为2①正确;直线A1H与该正方体各面所成角相等,均为arctan22,故②正确;过直线A1H的平面截该正方体所得截面为A1ACC1为平行四边形,故③正确;垂直于直线A1H的平面与平面AB1D1平行,截该正方体,所得截面为三角形或六边形,不可能为五边形.故④错误.故选:D.【点睛】本题考查线线角和线面角的求法,以及正方体的截面的形状,考查数形结合思想和空间想象能力,属于中档题.7.A解析:A【分析】由11AC AB BC CC =++,两边平方,利用数量积的运算法则及数量积公式能求出21AC 的值,从而可得结果.【详解】平行六面体1111ABCD A BC D -中,底面ABCD 是边长为1的正方形,1112,120AA A AB A AD =∠=∠=, 11AC AB BC CC ∴=++,()2211AC AB BC CC ∴=++222111222AB BC CC AB CC BC CC AB BC =+++⋅+⋅+⋅ 114212cos120212cos12002=+++⨯⨯⨯+⨯⨯⨯+=,∴线段1AC 的长为12AC = A.【点睛】 本题主要考查利用空间向量求线段的长,考查向量数量积的运算法则,属于中档题.向量数量积的运算主要掌握两点:一是数量积的基本公式cos a b a b θ⋅=;二是向量的平方等于向量模的平方22a a =. 8.A解析:A【分析】如图所示,连接AG 1交BC 于点E ,则E 为BC 中点,利用空间向量的运算法则求得131114444OG OG OA OB OC ===++,即得(x,y,z). 【详解】如图所示,连接AG 1交BC 于点E ,则E 为BC 中点,1(2AE AB AC =+)=1(2OB -2OA OC +), 121(33AG AE OB ==-2OA OC +). 因为OG =31GG =3(1OG OG -),所以OG=34OG 1. 则1133(44OG OG OA AG ==+)=31211114333444OA OB OA OC OA OB OC ⎛⎫+-+=++ ⎪⎝⎭ . 故答案为A【点睛】(1)本题主要考查空间向量的运算法则和基底法,意在考查学生对这些知识的掌握水平和分析推理能力.(2) 如果三个向量,,a b c 不共面,那么对于空间任意一个向量p ,存在一个唯一的有序实数组,,x y z 使p xa yb zc =++.我们把{},,x y z 叫做空间的一个基底,其中,,a b c 叫基向量.9.C解析:C【解析】 分析:根据两个向量的数量积的定义式,推导出其所成角的余弦公式,从而利用cos ,a ba b a b ⋅<>=,结合22a a =,将有关量代入求得z 的值,得到结果.详解:根据题意得31cos ,23a b ⨯===+,化简得22z =,解得z = C.点睛:该题考查的是有关向量夹角余弦公式的问题,在解题的过程中,需要把握住向量夹角余弦公式,再者就是向量的模的平方和向量的平方是相等的,还有就是向量的模的坐标运算式.10.D解析:D【解析】分析:利用向量多边形与三角形法则即可求出,首先分析题中各选项都是由从O 出发的三个向量表示的,所以将待求向量用从O 出发的向量来表示,之后借助于向量的差向量的特征以及中线向量的特征,求得结果.详解:由题意可得21()32EF OF OE OA OB OC =-=-+ 211322OA OB OC =--,故选D. 点睛:该题考查的是有关空间向量基本定理,考查了用向量表示几何的量,向量的线性运算,解题的关键是根据图形把所研究的向量用三个基向量表示出来,本题是向量的基础题. 11.D解析:D【分析】设正三棱柱111ABC A B C -棱长为2,设平面BDE 与底面ABC 所成锐二面角为α,,02AE x x =≤≤,以A 为坐标原点建立空间直角坐标系,确定出,,B D E 点的坐标,求出平面BDE 的法向量m ,底面ABC 的法向量坐标为(0,0,1)n =,将cos α表示为关于x 的函数,通过讨论cos α的增减变化,即可求出结论.【详解】设正三棱柱111ABC A B C -棱长为2,,02AE x x =≤≤,设平面BDE 与底面ABC 所成锐二面角为α,以A 为坐标原点,过点A 在底面ABC 内与AC 垂直的直线为x 轴,1,AC AA 所在的直线分别为,y z 轴建立空间直角坐标系, 则(3,1,0),(0,2,1),(0,0,),(3,1,1),(0,2,1)B D E x BD ED x =-=-,设平面BDE 的法向量(,,)m s t k =,则m BD m ED ⎧⊥⎨⊥⎩, 即302(1)0s t k t x k ⎧-++=⎪⎨+-=⎪⎩,令23k =,则33,1t x s x =-=+, 所以平面BDE 的一个法向量(1,33,23)m x x =+-,底面ABC 的一个法向量为(0,0,1)n =,222233cos |cos ,|115(1)3(1)12()24m n x x x α=<>==++-+-+ 当1(0,)2x ∈,cos α随着x 增大而增大,则α随着x 的增大而减小,当1(,2)2x ∈,cos α随着x 增大而减小,则α随着x 的增大而增大.故选:D.【点睛】本题考查空间向量法求二面角,应用函数思想讨论二面角的大小,考查直观想象、数学计算能力,素养中档题.12.C解析:C【分析】若要使MN 最短,点N 必须落在平面ABCD 内,且一定在DN 的连线上,此时应满足,,,D N M Q 四点共线,通过几何关系即可求解【详解】如图,当点N 落在平面ABCD 内,且,,,D N M Q 四点共线时,MN 距离应该最小,由PM 5=1MQ =,即点M 在以Q 为圆心,半径为1的圆上,由几何关系求得5DQ ,1DN MQ ==,故552NM DN MQ -=故答案选:C【点睛】本题考查由几何体上的动点问题求解两动点间距离的最小值,属于中档题二、填空题13.【分析】利用点到直线的距离公式借助平面的法向量利用公式即可求解【详解】由题意平面的一个法向量为且则所以点A 到平面的距离为【点睛】本题主要考查了点到平面的距离的求法其中解答中熟记空间向量在几何问题中的 解析:13【分析】利用点到直线的距离公式,借助平面的法向量,利用公式,即可求解.【详解】由题意,平面α的一个法向量为,,(1)22n =,且(1,0,2),(0,1,4),,A B A B αα-∉∈,则(1,1,2)BA =-,所以点A 到平面α的距离为12413144BA n d n ⋅+-===++. 【点睛】本题主要考查了点到平面的距离的求法,其中解答中熟记空间向量在几何问题中的应用,以及点到直线的距离公式,准确计算是解答的关键,着重考查了推理与计算能力,属于基础题.14.90°【分析】对该方程两边分别平方即可得到即可【详解】则∴α与β所成角的大小为90°故答案为90°【点睛】本题考查了向量模去绝对值问题可以通过对向量模平方去掉绝对值即可解析:90°【分析】对该方程两边分别平方,即可得到0αβ⋅=,即可.【详解】 αβαβ+=-222222ααββααββ∴+⋅+=-⋅+则0αβ⋅=∴α与β所成角的大小为90°故答案为90°【点睛】本题考查了向量模去绝对值问题,可以通过对向量模平方,去掉绝对值,即可. 15.【解析】【分析】取MC 中点O 连结AOBO 推导出AC =BM =AM =CM =1AO =BO =AO ⊥MCAO ⊥平面BMCAO ⊥BO 由此能求出AB 两点之间的距离【详解】取MC 中点O 连结AOBO ∵△ABC 中∠C =解析:102【解析】【分析】 取MC 中点O ,连结AO ,BO ,推导出AC =BM =AM =CM =1,AO =32,BO =72,AO ⊥MC ,AO ⊥平面BMC ,AO ⊥BO ,由此能求出A ,B 两点之间的距离.【详解】取MC 中点O ,连结AO ,BO ,∵△ABC 中,∠C =90°,∠A =60°,AB =2,M 为AB 中点,∴AC =BM =AM =CM =1,∴AOBO= AO ⊥MC ,将△BMC 沿CM 折叠,当平面BMC ⊥平面AMC 时,AO ⊥平面BMC ,∴AO ⊥BO ,∴A ,B 两点之间的距离|AB |2==,. 【点睛】 本题考查两点间距离的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.16.【分析】以为原点分别以所在的直线为轴建立空间直角坐标系利用向量法即可求解点N 到平面的距离得到答案【详解】由题意以为原点分别以所在的直线为轴建立空间直角坐标系则可得设平面的一个法向量为则令可得所以点N【分析】以D 为原点,分别以1,,DA DC DD 所在的直线为,,x y z 轴,建立空间直角坐标系,利用向量法,即可求解点N 到平面1D EF 的距离,得到答案.【详解】由题意,以D 为原点,分别以1,,DA DC DD 所在的直线为,,x y z 轴,建立空间直角坐标系, 则13(2,0,1),(2,,2),(2,,),(0,0,2),(2,2,1)22E M N D F λλ, 可得11(0,2,0),(0,,),(2,0,1)22EF EN ED λ===-, 设平面1D EF 的一个法向量为(,,)n x y z =,则12020n EF y n ED x z ⎧⋅==⎪⎨⋅=-+=⎪⎩,令1x =,可得(1,0,2)n =, 所以点N 到平面1D EF的距离155n ENd n ⋅===.故答案为:55.【点睛】本题主要考查了点到平面的距离的求法,以及空间中点、线、面的位置关系等知识的应用,着重考查了空间想象能力,以及推理与运算能力.17.【分析】以D 为原点DA 为x 轴DC 为y 轴DD1为z 轴建立空间直角坐标系利用向量法能求出异面直线AM 与B1C 所成的角【详解】以D 为原点DA 为x 轴DC 为y 轴DD1为z 轴建立空间直角坐标系设正方体ABCD ﹣ 解析:10 【分析】以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,利用向量法能求出异面直线AM 与B 1C 所成的角.【详解】以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,设正方体ABCD ﹣A 1B 1C 1D 1棱长为2,则A (2,0,0),M (2,1,2),B 1(2,2,2),C (0,2,0), AM =(0,1,2),1BC =(﹣2,0,2), 设异面直线AM 与B 1C 所成的角为θ, cosθ1141058AM B CAM B C ⋅===⨯⋅ ∴θ105arccos =. ∴异面直线AM 与B 1C 所成的角为10. 故答案为:10【点睛】本题考查异面直线所成角的求法,是基础题,解题时要认真审题,注意向量法的合理运用.18.【详解】试题分析:由两两垂直分别以所在的直线为轴建立如图所示的空间直角坐标系设则所以其中平面的一个法向量为所以与平面所成角的正弦值为所以;又向量与所成角的余弦值为又所以异面直线与所成角的余弦值是考点 230【详解】试题分析:由,,AB AD AQ 两两垂直,分别以,,AB AD AQ 所在的直线为,,x y z 轴建立如图所示的空间直角坐标系,设2AB =,则(0,0,0),(1,0,0),(2,1,0),(0,1,2)A E F M ,所以(1,1,2),(2,1,0)EM AF =-=,其中平面ABCD 的一个法向量为(0,0,1)n =,所以ME 与平面ABCD 所成角的正弦值为6sin 3EM n EM n α⋅==⋅,所以tan 2α=EM 与AF 所成角的余弦值为cos EM AFEM AFβ⋅=⋅ 3030=-,又(0,]2πβ∈,所以异面直线EM 与AF 所成角的余弦值是3030考点:空间向量的运算及空间角的求解.19.①③④【分析】由题意画出图形由异面直线的概念判断①;利用线面垂直的判定与性质判断②;找出球心由棱锥底面积与高为定值判断③;设BE =x 列出AE+EC1关于x 的函数式结合其几何意义求出最小值判断④【详解解析:①③④ 【分析】由题意画出图形,由异面直线的概念判断①;利用线面垂直的判定与性质判断②;找出球心,由棱锥底面积与高为定值判断③;设BE =x ,列出AE +EC 1关于x 的函数式,结合其几何意义求出最小值判断④. 【详解】 如图,∵直线AC 经过平面BCC 1B 1内的点C ,而直线C 1E 在平面BCC 1B 1内不过C , ∴直线AC 与直线C 1E 是异面直线,故①正确; 当E 与B 重合时,AB 1⊥A 1B ,而C 1B 1⊥A 1B , ∴A 1B ⊥平面AB 1C 1,则A 1E 垂直AC 1,故②错误;由题意知,直三棱柱ABC ﹣A 1B 1C 1的外接球的球心为O 是AC 1 与A 1C 的交点,则△AA 1O 的面积为定值,由BB 1∥平面AA 1C 1C ,∴E 到平面AA 1O 的距离为定值,∴三棱锥E ﹣AA 1O 的体积为定值,故③正确; 设BE =x ,则B 1E =2﹣x ,∴AE +EC 12211(2)x x =++-由其几何意义,即平面内动点(x ,1)与两定点(0,0),(2,0)距离和的最小值知,其最小值为22,故④正确. 故答案为①③④ 【点睛】本题考查命题的真假判断与应用,考查空间想象能力和思维能力,属于中档题20.【详解】以AB 的中点为原点建立如图所示的空间直角坐标系则平面的一个法向量为设平面的一个法向量为则则令所以平面的一个法向量为所以因为所以所以所以即二面角的余弦值的取值范围是点睛:本题主要考查了空间几何 解析:99(,)1616-【详解】以AB 的中点为原点,建立如图所示的空间直角坐标系,则163(0,,),(0,4,0),(,0,0)(33)22D C M a a --<<,平面MBC 的一个法向量为1(0,0,1)n =, 设平面DMC 的一个法向量为2(,,)n x y z =,则963(0,,),(,4,0)22DC MC a =-=-,则229630022040n DC y z n MC ax y ⎧⎧⋅=--=⎪⎪⇒⎨⎨⋅=⎪⎩⎪-+=⎩, 令4639,,63z x y a ===,所以平面DMC 的一个法向量为2463(,63,9)n a=, 所以122299cos ,166316636381144n n a a ==⨯⨯+++, 因为33a -<<,所以29<a ,所以2166316631441442569a ⨯⨯+>+=, 所以129cos ,16n n <,即二面角的余弦值的取值范围是99(,)1616-.点睛:本题主要考查了空间几何体的结构特征和二面角的计算问题,空间向量是解决空间几何问题的锐利武器,利用空间向量求解空间角的关键在于“四破”:第一、破“建系关”,构建恰当的空间直角坐标系;第二、破“求坐标关”,准确求解相关点的坐标;第三、破“求法向量关”,求出平面的法向量;第四、破“应用公式关”.三、解答题21.(1)证明见解析;(2)4214. 【分析】(1)过E 作EH AB ⊥于H ,由面面垂直得EH ⊥平面ABC ,从而有EH BC ⊥,再结合已知,BC BE ⊥可得线面垂直后得线线垂直;(2)将三棱台ABC DEF -补体成三棱锥P ABC -,以B 为原点建立空间直角坐标系(如图),设2AB =,得出各点坐标,求出平面ABF 的法向量,由空间向量法求得线面角的正弦值. 【详解】解:(1)过E 作EH AB ⊥于H ,因为面ABED ⊥面ABC ,面ABED ⋂面ABC BC =,所以EH ⊥平面ABC ,而BC ⊂平面ABC ,所以EH BC ⊥, 又,BC BE ⊥BEEH E =,,BE EH ⊂平面ABED ,所以BC ⊥面ABED ,又BC ⊂平面BCFE 所以平面ABED ⊥平面;BCFE(2)将三棱台ABC DEF -补体成三棱锥P ABC -,则,,D E F 分别是,,PA PB PC 的中点,PAB △是正三角形,设2AB =, 以B 为原点建立空间直角坐标系(如图),(()()13333,0,2,0,2,0,0,1,,0,22P A C F D ⎛⎛ ⎝⎭⎝⎭()()131,1,0,0,2,0,1,2DF BA BF ⎛∴=-== ⎝⎭设平面ABF 的法向量为,,,nx y z由00n AB n FB ⎧⋅=⎨⋅=⎩,有013022y x y z =⎧⎪⎨++=⎪⎩,令2z =得()3,0,2n =-. 42sin 14||||n DF n DF θ⋅∴==⋅∣.【点睛】方法点睛:本题考查证明面面垂直,求直线与平面所成的角.求线面角的常用方法 (1)定义法,作出直线在平面内的射影(主要过直线上一点作平面的垂线),由直线与射影的夹角得出直线与平面所成的角(注意证明),然后解三角形得结论;(2)空间向量法,建立空间直角坐标系,求出平面的法向量,由直线的方向向量与平面的法向量夹角余弦值的绝对值得线面角的正弦值. 22.(Ⅰ)证明见解析;(Ⅱ39【分析】(Ⅰ)根据题中的边长以及垂直关系,可求出,OA OP ,利用勾股定理判断OP OA ⊥,再根据等边三角形三线重合,判断OP BC ⊥,即可证明PO ⊥平面ABCD ;(Ⅱ)根据垂直关系,以O 为坐标原点,建立空间直角坐标系,利用向量的坐标公式求CB 与平面PBD 所成角的正弦值. 【详解】(Ⅰ)证明:在ACD △中,由已知得3AC =,ABC PBC 3O 为BC 的中点 ,OA BC OP BC ∴⊥⊥,且32OA OP ==. 在PAO 中,已知322PA =, 则有222,PO OA PA OP OA +=∴⊥. 又,OA BC O OA ⋂=⊂平面,ABCD BC ⊂平面,ABCD OP ∴⊥平面ABCD .(Ⅱ)以O 为坐标原点,,,OA OC OP 分别为x 轴,y 轴,z 轴的正方向,建立如图所示的空间直角坐标系,则3330,0,,0,,2P B C ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,3D ⎛⎫ ⎪ ⎪⎝⎭. (0,3,0)(1,3,0)BC BD ∴==,,3333)2BP ⎛⎫== ⎪ ⎪⎝⎭.设平面PBD 的法向量为(,,)n x y z =,则00n BP n BD ⎧⋅=⎨⋅=⎩即3030x y y z ⎧=⎪⎨=⎪⎩,令1z =.则3,3y x =-=. ∴平面PBD 的一个法向量为(3,3,1)n =-,39sin |cos ,|13BC n θ∴=<>=.39sin θ∴= 【点睛】方法点睛:1.利用面面垂直的性质定理,得到线面垂直,进而确定线面角中的垂足,明确斜线在平面内的射影,即可确定线面角;2.在构成线面角的直角三角形中,可利用等体积法解垂线段的长度h ,而不必画出线面角,利用sin h θ= /斜线段长,进行求角;3.建立空间直角坐标系,利用向量法求解,设a 是直线l 的方向向量,n 是平面的法向量,利用公式sin cos ,a n θ=<>求解. 23.(Ⅰ)证明见解析;(Ⅱ6【分析】(Ⅰ)解法1.利用线面平行的判定定理证明; 解法2.以A 为坐标原点,,,AB AD AP 所在直线分别为x 轴、y 轴、z 轴,建立如图所示空间直角坐标系A xyz -,利用空间向量证明直线BC 与平面PAD 的法向量垂直,从而证明结论.(Ⅱ)建立空间直角坐标系后,后利用空间向量的坐标运算求得两平面的法向量的坐标,进而计算. 【详解】 (Ⅰ)证明:解法1. 因为//BC ADBC ⊄平面PAD AD ⊂平面PAD 所以//BC 平面PAD解法2.因为PA AD ⊥,PA AB ⊥,AD AB ⊥,所以以A 为坐标原点,,,AB AD AP 所在直线分别为x 轴、y 轴、z 轴,建立如图所示空间直角坐标系A xyz -,则(0,0,0),(2,0,0),(0,4,0),(0,0,2),(2,2,0)A B D P C , 平面PAD 的法向量为(1,0,0)t, (0,2,0)BC = ,因为 0120000t BC ⋅=⨯+⨯+⨯= ,BC ⊄平面PAD ,所以//BC 平面PAD ;(Ⅱ)解:因为PA AD ⊥,PA AB ⊥AD AB ⊥, 所以以A 为坐标原点,,,AB AD AP 所在直线分别为x 轴、y 轴、z 轴,建立如图所示空间直角坐标系A xyz -,则(0,0,0),(2,0,0),(0,4,0),(0,0,2),(2,2,0)A B D P C所以平面PAB 的法向量为(0,1,0)n = , 设平面PCD 的法向量为(,,)m x y z =(2,2,2)PC =-,(0,4,2)PD =- ,所以2220042020x y z x y m PCm PC y z z y m PD m PD ⎧⎧+-==⎧⎧⊥⋅=⇒⇒⇒⎨⎨⎨⎨-==⊥⋅=⎩⎩⎩⎩ ,令1(1,1,2)y m ==得 ,16cos ,616n m n m n m⋅<>===⨯ 设平面PAB 与平面PCD 所成角为θθ,为锐角, 所以6cos 6θ=. 【点睛】本题考查利用空间向量证明线面垂直和求二面角问题,关键是平面的法向量的求解和夹角余弦值的计算,注意所求为两平面所成的锐二面角的余弦值,因此对两平面的法向量所成角的余弦值与两平面所成锐角的余弦值要注意区分与联系. 24.(1)证明见解析;(2)155. 【分析】(1)AC 与BD 交于点O ,连接FO 、FD ,证明FO AC ⊥,FO BD ⊥,然后得到FO ⊥平面ABCD 即可;(2)以O 为原点,OA 、OB 、OF 分别为x 、y 、z 轴建立空间直角坐标系,然后求出平面BFC 和平面ACF 的法向量,然后可算出答案.【详解】(1)证明:AC 与BD 交于点O ,连接FO 、FD ,∵FA FC =,O 是AC 中点,且O 是BD 中点,∴FO AC ⊥, ∵四边形BDEF 为菱形,60DBF ∠=︒, ∴FD FB =,∴FO BD ⊥, 又ACBD O =,∴FO ⊥平面ABCD ,∵FO ⊂平面ACF ,∴平面ACF ⊥平面ABCD (2)易知OA ,OB ,OF 两两垂直以O 为原点,OA 、OB 、OF 分别为x 、y 、z 轴建立如图所示的空间直角坐标系设2AB =,∵四边形ABCD 为菱形,60DAB ∠=︒ 则2BD =,∴1OB =,3OA OF ==故(0,0,0)O ,(0,1,0)B ,()3,0,0C -,()3F∴()3,0,3CF =,3,1,0CB,()0,1,0OB =设平面BFC 的一个法向量为(,,)n x y z =则33030n CF x z n CB x y ⎧⋅=+=⎪⎨⋅=+=⎪⎩,取1x =,得()1,3,1n =-- 显然,()0,1,0OB =为平面ACF 的一个法向量 ∴15cos ,5OB n OB n OB n⋅<>==-⋅ 由图知,二面角A FC B --的平面角为锐角 ∴二面角A FC B --的余弦值为155【点睛】关键点睛:用向量法求解空间角的问题时,解题的关键是建立适当的空间直角坐标系,准确地写出点的坐标和算出直线的方向向量、平面的法向量. 25.(1)点M 在CE 的中点处,证明见解析;(2)32. 【分析】(1)首先观察图形的特征,确定点M 的位置,之后利用线面平行的判定定理证明即可; (2)建立空间直角坐标系,设出边长,写出点的坐标,利用向量法求得线面角的正弦值. 【详解】(1)点M 在CE 的中点处,证明如下:取BC 中点P ,连接,BP AP , 根据题意,可知//,PM AF PM AF =,所以四边形AFMP 是平行四边形,所以//AP MF , 又因为FM ⊄平面ABCD ,AP ⊂平面ABCD , 所以//MF 平面ABCD ;(2)设1AF AB AD ===,如图建立空间直角坐标系,则有1(1,0,1),(1,1,0),(0,1,),(0,0,0)2D F M B , 所以(0,1,1)DF =-,1(1,1,0),(0,1,)2BF BM ==, 设平面BFM 的法向量为(,,)n x y z =,则有00n BF n BM ⎧⋅=⎨⋅=⎩,即0102x y y z +=⎧⎪⎨+=⎪⎩,取1y =,则有1,2x z =-=-, 所以平面BFM 的一个法向量为(1,1,2)n =--, 所以03cos ,226DF n DF n DF n⋅+<>===⋅, 所以直线DF 与平面BFM 所成角的正弦值32. 【点睛】思路点睛:该题考查的是有关立体几何的问题,解题思路如下:(1)首先根据图形的特征,判断出点的位置,之后利用线面平行的判定定理证明即可; (2)在证明的过程中,注意线在面外和线在面内的条件; (3)建立空间直角坐标系,求得平面的法向量和直线的方向向量; (4)利用向量所成角的余弦值得到线面角的正弦值. 26.(1470;(2)13λ=.【分析】(1)首先证明PA ⊥平面ABCD ,再以点A 为原点,{},,AB AD AP 为正交基底,建立空间直角坐标系,求平面ABE 的法向量,再求直线DE 与平面ABE 所成角的正弦值; (2)首先求平面ABE 和平面AEC 的法向量,利用法向量求二面角的余弦值,求λ的值. 【详解】解:因为平面PAB ⊥平面ABCD ,PA AB ⊥,平面PAB ⋂平面ABCD AB =,PA ⊂平面PAB ,所以PA ⊥平面ABCD .因为AD ⊂平面ABCD ,所以PA AD ⊥. 又AB AD ⊥,所以PA ,AB ,AD 两两互相垂直. 以{},,AB AD AP 为正交基底,建立如图所示的空间直角坐标系A xyz -.因为4PA AD ==,2AB BC ==,所以()0,0,0A ,()2,0,0B ,()2,2,0C ,()0,4,0D ,()0,0,4P ,(1)若12λ=,即E 为PC 中点,则()1,1,2E , 所以()1,3,2DE =-,()2,0,0AB =,()1,1,2AE =. 设平面ABE 的一个法向量为()111,,m x y z =,则00m AB m AE ⎧⋅=⎨⋅=⎩即111120,20.x x y z =⎧⎨++=⎩令11z =,得12y =-,所以平面ABE 的一个法向量为()0,2,1m =-. 设直线DE 与平面ABE 所成角为α, 则62470sin cos ,145DE m α+===⨯ (2)因为()01PE PC λλ=≤<,则()2,2,44E λλλ-. 设平面ABE 的一个法向量为()222,,n x y z =,则00n AB n AE ⎧⋅=⎨⋅=⎩即()222220,22440.x x y z λλλ=⎧⎨++-=⎩。
深圳公明中英文学校数学高二下期末经典练习(含答案)
一、选择题1.在四边形ABCD 中,AB DC =,且AC ·BD =0,则四边形ABCD 是( )A .菱形B .矩形C .直角梯形D .等腰梯形2.已知tan 2α=,则2cos α=( ) A .14B .34C .45D .153.将函数()sin 3f x x πω⎛⎫=+⎪⎝⎭的图象向左平移(0)ϕϕ>个单位长度后得到函数()cos2g x x =的图象,则ϕ的最小值为( )A .3π B .6π C .12πD .24π4.ABC ∆中,M 是AC 边上的点,2AM MC =,N 是边的中点,设1AB e =,2AC e =,则MN 可以用1e ,2e 表示为( )A .121126e e - B .121126e e -+ C .121126e e + D .121726e e + 5.已知函数()()π2cos 332f x x ϕϕ⎛⎫=++≤ ⎪⎝⎭,若ππ,612x ⎛⎫∀∈- ⎪⎝⎭,()f x 的图象恒在直线3y =的上方,则ϕ的取值范围是( ) A .ππ,122⎛⎫⎪⎝⎭ B .ππ,63⎡⎤⎢⎥⎣⎦C .π0,4⎡⎤⎢⎥⎣⎦D .ππ,63⎛⎫-⎪⎝⎭ 6.已知π(,π)2α∈,π1tan()47α+=,则sin cos αα+= ( ) A .17-B .25-C .15-D .157.已知P (14,1),Q (54,-1)分别是函数()()cos f x x ωϕ=+0,2πωϕ⎛⎫>< ⎪⎝⎭的图象上相邻的最高点和最低点,则ωϕ-=( ) A .54π-B .54πC .-34π D .34π 8.函数()sin()A f x x ωϕ=+(0,)2πωϕ><的部分图象如图所示,则()f π=( )A .4B .23C .2D .39.若将函数y =cos2x 的图象向左平移π12个单位长度,则平移后图象的对称轴为( ) A .x =kπ2−π6(k ∈Z ) B .x =kπ2+π6(k ∈Z )x C .x =kπ2−π12(k ∈Z )D .x =kπ2+π12(k ∈Z )10.设a ,b ,c 为同一平面内具有相同起点的任意三个非零向量,且满足a 与b 不共线,a ⊥c ,|a |=|c |,则|b ⋅c |的值一定等于 ( ) A .以a ,b 为邻边的平行四边形的面积 B .以b ,c 为两边的三角形面积 C .a ,b 为两边的三角形面积 D .以b ,c 为邻边的平行四边形的面积11.已知a ,b 是平面内两个互相垂直的单位向量,若向量c 满足()()0a c b c -⋅-=,则c 的最大值是( ) A .1B .2C .D .12.若O 为ABC ∆所在平面内一点,()()20OB OC OB OC OA -⋅+-=,则ABC ∆形状是( ). A .等腰三角形 B .直角三角形 C .正三角形D .以上答案均错13.已知向量(2,0)OB =,向量(2,2)OC =,向量(22)CA αα=,则向量OA 与向量OB 的夹角的取值范围是( ).A .π0,4⎡⎤⎢⎥⎣⎦B .π5π,412⎡⎤⎢⎥⎣⎦C .5ππ,122⎡⎤⎢⎥⎣⎦ D .π5π,1212⎡⎤⎢⎥⎣⎦ 14.已知f (x )=A sin(ωx+θ)(ω>0),若两个不等的实数x 1,x 2∈()2A x f x ⎧⎫=⎨⎬⎩⎭,且|x 1-x 2|min =π,则f (x )的最小正周期是( )A .3πB .2πC .πD .π215.在ABC ∆中,a b c 、、分别是内角A B C 、、所对的边,若2224ABCa b c S ∆+-=(其中)ABC S ABC ∆∆表示的面积,且0,AB AC BC AB AC ⎛⎫⎪+⋅= ⎪⎝⎭则ABC ∆的形状是( ) A .有一个角为30的等腰三角形 B .正三角形 C .直角三角形D .等腰直角三角形二、填空题16.已知12,e e 是夹角为3π的两个单位向量,1212,a e e b e e =-=+,则2a b +=___. 17.已知a ,b 是单位向量.若2a b b a +≥-,则向量a ,b 夹角的取值范围是_________.18.向量,a b 的夹角为60︒,且2,1a b ==则(2)a a b ⋅+=__________. 19.已知()1,3a =-,()1,b t =,若()2a b a -⊥,则b =_________. 20.已知4tan()5αβ+=,1tan 4β=,那么tan α=____.21.在平面上,12OB OB ⊥,122MB MB ==12OP OB OB =+.若1MP <,则OM 的取值范围是_______.22.若动直线x a =与函数()sin f x x =和()cos g x x =的图象分别交于M ,N 两点,则||MN 的最大值为__________.23.在平行四边形ABCD 中,E 为线段BC 的中点,若AB AE AD λμ=+,则λμ+=__________.24.已知平面向量a 、b 满足||3a =,||2b =,a 与b 的夹角为60,若(a mb -)a ⊥,则实数m 的值是___________ .25.已知已知sin π3()25α+=,α∈π(0,)2,则sin(π+α)等于__________三、解答题26.已知3sin 5α=-,,22ππα⎛⎫∈- ⎪⎝⎭. (1)求sin 2α的值; (2)求3tan 4πα⎛⎫-⎪⎝⎭的值. 27.已知点(2,0)A -,(1,9)B ,(,)C m n ,O 是原点. (1)若点,,A B C 三点共线,求m 与n 满足的关系式; (2)若AOC ∆的面积等于3,且AC BC ⊥,求向量OC .28.如图,在三棱柱111ABC A B C -中,D 、P 分别是棱AB ,11A B 的中点,求证:(1)1AC ∥平面1B CD ; (2)平面1APC 平面1B CD .29.已知α∈,2ππ⎛⎫⎪⎝⎭,且sin 2α +cos 2α 6(1)求cos α的值; (2)若sin(α-β)=-35 ,β∈,2ππ⎛⎫⎪⎝⎭,求cos β的值. 30.已知函数()3cos 22f x x x ππ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭. (1)求函数()f x 的最小正周期; (2)求函数()f x 的单调区间.【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题 1.A 2.D 3.C 4.A5.C6.C7.B8.A9.C10.A11.C12.A13.D14.A15.D二、填空题16.【解析】【分析】先计算得到再计算然后计算【详解】是夹角为的两个单位向量故答案为【点睛】本题考查了向量的计算和模属于向量的常考题型意在考查学生的计算能力17.【解析】【分析】设向量的夹角为在不等式两边平方利用数量积的运算律和定义求出的取值范围于此可求出的取值范围【详解】设向量的夹角为两边平方得都是单位向量则有得因此向量的夹角的取值范围是故答案为【点睛】本18.6【解析】【分析】由题意利用向量的数量积的运算可得即可求解【详解】由题意可知向量的夹角为且则【点睛】本题主要考查了平面向量的数量积的运算其中解答中熟记平面向量的数量积的运算公式准确计算是解答的关键着19.【解析】【分析】利用两个向量垂直的坐标表示列方程解方程求得的值进而求得【详解】由于故解得故【点睛】本小题主要考查向量减法的坐标运算考查两个向量垂直的坐标表示考查向量的模属于基础题20.【解析】【分析】根据题干得到按照两角和与差公式得到结果【详解】已知那么故答案为【点睛】这个题目考查了给值求值的问题常见的解题方式有:用已知角表示未知角再由两角和与差的公式得到结果21.【解析】【分析】本题可以通过建立平面直角坐标系将给的向量条件坐标化然后把所求的也用坐标表示出来最后根据式子采用适当的方法得出结果【详解】设则有因为所以①②③因为所以①+②得即由①②可知带入③中可知综22.【解析】所以的最大值为方法点睛:本题考查数形结合思想的应用根据两点间距离公式再根据辅助角公式转化为当时取得最大值23.【解析】分析:先根据三角形法则化为再根据分解唯一性求即得详解:因为所以因为不共线所以点睛:利用向量基本定理中唯一性可求参数:即若为不共线向量则24.3【解析】∵∴∴∴∴故答案为325.【解析】由题意得三、解答题26.27.28.29.30.2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1.A解析:A【解析】【分析】由AB DC可得四边形为平行四边形,由AC·BD=0得四边形的对角线垂直,故可得四边形为菱形.【详解】∵AB DC =,∴AB 与DC 平行且相等, ∴四边形ABCD 为平行四边形. 又0AC BD ⋅=, ∴AC BD ⊥,即平行四边形ABCD 的对角线互相垂直, ∴平行四边形ABCD 为菱形. 故选A . 【点睛】本题考查向量相等和向量数量积的的应用,解题的关键是正确理解有关的概念,属于基础题.2.D解析:D 【解析】 【分析】根据同角三角函数的基本关系,由2222cos cos cos sin αααα=+,化为正切即可求解. 【详解】22222cos 1cos cos sin 1tan ααααα==++, 且tan 2α=,∴211cos 145α==+, 故选:D 【点睛】本题主要考查了同角三角函数的基本关系,弦化切的思想,属于中档题.3.C解析:C 【解析】 【分析】根据题意得到变换后的函数解析式,利用诱导公式求得结果 【详解】由题,向左平移(0)ϕϕ>不改变周期,故2ω=,∴平移得到()sin 2sin 22cos 233x x x ππϕϕ⎡⎤⎡⎤⎛⎫++=++= ⎪⎢⎥⎢⎥⎣⎦⎝⎭⎣⎦ 2+=+232k ππϕπ∴,12k πϕπ∴=+0ϕ>,∴当0k =时,min 12πϕ=,故选C【点睛】本题考查函数()sin y A x ωϕ=+的图象变换规律,利用诱导公式完成正、余弦型函数的转化4.A解析:A 【解析】 【分析】利用向量的线性运算求解即可. 【详解】由题, ()12111111322626MN MC CN AC AB AC AB AC e e =+=+-=-=-.故选:A 【点睛】本题主要考查了平面向量的线性运算,属于基础题型.5.C解析:C 【解析】分析:根据函数()f x 的解析式,利用x 的取值范围,结合题意求出ϕ的取值范围. 详解:函数函数()()π2cos 332f x x ϕϕ⎛⎫=++≤⎪⎝⎭,ππ,612x ⎛⎫∈- ⎪⎝⎭时,324x ππϕϕϕ+∈-++(,),又()f x 的图象恒在直线3y =的上方,2223333042cos x cos x ππϕϕϕππϕ⎧-+≥-⎪⎪∴++∴+∴⎨⎪+≤⎪⎩()>,()>,,解得04πϕ≤≤;∴ϕ的取值范围是π0,4⎡⎤⎢⎥⎣⎦.故选C .点睛:本题考查了三角函数的图象与性质的应用问题,是基础题.6.C解析:C 【解析】 【分析】由两角和的正切公式得出3sin cos 4αα=-,结合平方关系求出43cos ,sin 55αα=-=,即可得出sin cos αα+的值. 【详解】1tan 1tan 41tan 7πααα+⎛⎫+== ⎪-⎝⎭3tan 4α∴=-,即3sin cos 4αα=-由平方关系得出223cos cos 14αα⎛⎫-+= ⎪⎝⎭,解得:43cos ,sin 55αα=-=341sin cos 555αα+=-=- 故选:C 【点睛】本题主要考查了两角和的正切公式,平方关系,属于中档题.7.B解析:B 【解析】 【分析】由点P,Q 两点可以求出函数的周期,进而求出ω,再将点P 或点Q 的坐标代入,求得ϕ,即求出ωϕ-. 【详解】因为512244πω⎛⎫-= ⎪⎝⎭,所以ωπ=,把1,14P ⎛⎫ ⎪⎝⎭的坐标代入方程()cos y x πϕ=+,得 ()24k k Z ϕππ=-+∈,因为2πϕ<,所以5,44ππϕωϕ=--=,故选B . 【点睛】本题主要考查利用三角函数的性质求其解析式.8.A解析:A 【解析】试题分析:根据题意,由于函数()sin()A f x x ωϕ=+(0,)2πωϕ><,那么根据图像可知周期为2π,w=4,然后当x=6π,y=2,代入解析式中得到22sin(4)6πϕ=⨯+,6πϕ=-,则可知()f π=4,故答案为A.考点:三角函数图像点评:主要是考查了根据图像求解析式,然后得到函数值的求解,属于基础题.9.C解析:C 【解析】 【分析】 【详解】试题分析:由题意得,将函数y =cos2x 的图象向左平移π12个单位长度,得到y =cos2(x +π12)=cos (2x +π6),由2x +π6=kπ,k ∈Z ,得x =kπ2−π12,k ∈Z ,即平移后的函数的对称轴方程为x =kπ2−π12(k ∈Z ),故选C .10.A解析:A 【解析】 【分析】 【详解】记OA =a ,OB =b ,OC =c ,记a 与b ,b 于c 夹角分别为,αθ,因为这三向量的起点相同,且满足a 与b 不共线,a ⊥c ,|a |=|c |,则cos sin θα=,利用向量的内积定义,所以|b c ⋅|=||b |•|c |cos <b ,c >|=||OB ||OC |cosθ|==||OB ||OA |sin α |,又由于12BOA S ∆=|OB ||OA |sin α,所以||OB ||OA |sin α |等于以a ,b 为邻边的平行四边形的面积,故选A 11.C解析:C 【解析】 【分析】 【详解】 试题分析:由于垂直,不妨设,,,则,,表示到原点的距离,表示圆心,为半径的圆,因此的最大值,故答案为C .考点:平面向量数量积的运算.12.A解析:A 【解析】 【分析】根据向量的减法运算可化简已知等式为()0CB AB AC ⋅+=,从而得到三角形的中线和底边垂直,从而得到三角形形状. 【详解】()()()20OB OC OB OC OA CB AB AC -⋅+-=⋅+= ()CB AB AC ∴⊥+∴三角形的中线和底边垂直 ABC ∆∴是等腰三角形本题正确选项:A 【点睛】本题考查求解三角形形状的问题,关键是能够通过向量的线性运算得到数量积关系,根据数量积为零求得垂直关系.13.D解析:D 【解析】 不妨设(0,0)O∵(2,2)OC =,(22)CA αα=. ∴(2,2)C 、(22,22)A cos αα+. ∴点A 在以(2,2)2的圆上. ∴OA 与OB 的夹角为直线OA 的倾斜角. 设:OA l y kx = ∴22121k d r k -=≤=+即2410k k -+≤,则[23,23]k ∈-+. 又∵π23tan12=,523tanπ12+=. ∴OA 、OB 夹角[23,23]θ∈.故选D .14.A解析:A 【解析】 【分析】 由题意可得123ππω⨯=,求得ω的值,可得()f x 的最小正周期是2πω的值 【详解】由题意可得()1sin 2x ωθ+=的解为两个不等的实数1x ,2x 且123ππω⨯=,求得23ω= 故()f x 的最小正周期是23ππω=故选A 【点睛】本题主要考查了的是三角函数的周期性及其图象,解题的关键根据正弦函数的图象求出ω的值,属于基础题15.D解析:D 【解析】试题分析:在边AB ,AC 上分别取点D ,E ,使,AB AC AD AE ABAC==,以AD ,AE 为邻边作平行四边形ADFE ,则:四边形ADFE 为菱形,连接AF ,DE ,AF ⊥DE ,且ABACAF AB AC=+;∵0,AB AC BC AB AC ⎛⎫⎪+⋅= ⎪⎝⎭; ∴·0AF BC =;∴AF ⊥BC ;又DE ⊥AF ;∴DE ∥BC ,且AD=AE ;∴AB=AC ,即b=c ;∴延长AF 交BC 的中点于O ,则:S △ABC =222221244a abc a c +--=,b=c ;∴22a a =∴=;∴2224c a a -=;∴22222a c b c ==+;∴∠BAC=90°,且b=c ;∴△ABC 的形状为等腰直角三角形. 考点:平面向量数量积的运算二、填空题16.【解析】【分析】先计算得到再计算然后计算【详解】是夹角为的两个单位向量故答案为【点睛】本题考查了向量的计算和模属于向量的常考题型意在考查学生的计算能力【解析】 【分析】 先计算得到1212e e ⋅=,再计算1223a b e e +=-,然后计算2(2)727a b a b +=⇒+=. 【详解】12,e e 是夹角为3π的两个单位向量1212e e ⇒⋅=12121222()3a b e e e e e e +=-++=-2222121122(2)(3)96931727a b e e e e e e a b +=-=-⋅+=-+=⇒+=【点睛】本题考查了向量的计算和模,属于向量的常考题型,意在考查学生的计算能力.17.【解析】【分析】设向量的夹角为在不等式两边平方利用数量积的运算律和定义求出的取值范围于此可求出的取值范围【详解】设向量的夹角为两边平方得都是单位向量则有得因此向量的夹角的取值范围是故答案为【点睛】本解析:0,3π⎡⎤⎢⎥⎣⎦【解析】 【分析】设向量a 、b 的夹角为θ,在不等式2a b b a +≥-两边平方,利用数量积的运算律和定义求出cos θ的取值范围,于此可求出θ的取值范围. 【详解】设向量a 、b 的夹角为θ,2a b b a +≥-,两边平方得2222244a a b b a a b b +⋅+≥-⋅+,a 、b 都是单位向量,则有22cos 54cos θθ+≥-,得1cos 2θ≥,0θπ≤≤,03πθ∴≤≤,因此,向量a 、b 的夹角的取值范围是0,3π⎡⎤⎢⎥⎣⎦, 故答案为0,3π⎡⎤⎢⎥⎣⎦.【点睛】本题考查平面数量积的运算,考查平面向量夹角的取值范围,在涉及平面向量模有关的计算时,常将等式或不等式进行平方,结合数量积的定义和运算律来进行计算,考查运算求解能力,属于中等题.18.6【解析】【分析】由题意利用向量的数量积的运算可得即可求解【详解】由题意可知向量的夹角为且则【点睛】本题主要考查了平面向量的数量积的运算其中解答中熟记平面向量的数量积的运算公式准确计算是解答的关键着解析:6 【解析】 【分析】由题意,利用向量的数量积的运算,可得2(2)2a a b a a b ⋅+=+⋅,即可求解. 【详解】由题意,可知向量,a b 的夹角为060,且2,1a b ==则221(2)22cos60422162a ab a a b a a b ⋅+=+⋅=+⋅=+⨯⨯⨯=. 【点睛】本题主要考查了平面向量的数量积的运算,其中解答中熟记平面向量的数量积的运算公式,准确计算是解答的关键,着重考查了推理与运算能力.19.【解析】【分析】利用两个向量垂直的坐标表示列方程解方程求得的值进而求得【详解】由于故解得故【点睛】本小题主要考查向量减法的坐标运算考查两个向量垂直的坐标表示考查向量的模属于基础题【解析】 【分析】利用两个向量垂直的坐标表示列方程,解方程求得t 的值,进而求得b . 【详解】()23,32a b t -=--,由于()2a b a -⊥,故()23960a b a t -⋅=+-=,解得2t =,故()221,212b b ==+=, 【点睛】本小题主要考查向量减法的坐标运算,考查两个向量垂直的坐标表示,考查向量的模,属于基础题.20.【解析】【分析】根据题干得到按照两角和与差公式得到结果【详解】已知那么故答案为【点睛】这个题目考查了给值求值的问题常见的解题方式有:用已知角表示未知角再由两角和与差的公式得到结果 解析:1124【解析】 【分析】根据题干得到an α=()tan αββ+-,按照两角和与差公式得到结果. 【详解】 已知()4tan 5αβ+=,1 tan 4β=, 那么tan α=()tan αββ+-()()tan tan 111tan tan 24αββαββ+-==++. 故答案为1124. 【点睛】这个题目考查了给值求值的问题,常见的解题方式有:用已知角表示未知角,再由两角和与差的公式得到结果.21.【解析】【分析】本题可以通过建立平面直角坐标系将给的向量条件坐标化然后把所求的也用坐标表示出来最后根据式子采用适当的方法得出结果【详解】设则有因为所以①②③因为所以①+②得即由①②可知带入③中可知综解析:2⎤⎦【解析】 【分析】本题可以通过建立平面直角坐标系,将给的向量条件坐标化,然后把所求的也用坐标表示出来,最后根据式子采用适当的方法得出结果. 【详解】设()()()120b 0B B a M x y ,,,,,,则有()P a b , 因为()()()12,,P b y MB x b y MB a x y M a x =--=--=--,,, 所以2222122MB x y by b =+-+= ①2222222MB x y ax a =+-+= ②22222P 221M x y ax a by b =+-+-+< ③因为222222by b y ax a y ,≤+≤+ 所以①+②得222222224x y by b x y ax a +-+++-+=即224x y +≤由①②可知2222222222by x y b ax x y a =++-=++-, 带入③中可知223x y +> 综上可得2234x y <+≤所以,OM 的取值范围是2⎤⎦.【点睛】在做向量类的题目的时候,可以通过构造直角坐标系,用点的坐标来表示向量以及向量之间的关系,借此来得出答案.22.【解析】所以的最大值为方法点睛:本题考查数形结合思想的应用根据两点间距离公式再根据辅助角公式转化为当时取得最大值【解析】sin cos )4MN a a a π=-=-≤MN .方法点睛:本题考查数形结合思想的应用,(),sin M a a ,(),cos N a a ,根据两点间距离公式sin cos MN a a ==-,再根据辅助角公式转化为sin cos )4a a a π-=-,当()42k k Z ππαπ-=+∈时,MN 取得最大值.23.【解析】分析:先根据三角形法则化为再根据分解唯一性求即得详解:因为所以因为不共线所以点睛:利用向量基本定理中唯一性可求参数:即若为不共线向量则解析:12. 【解析】分析:先根据三角形法则化AE 为12AB AD +,再根据分解唯一性求λμ,,即得.λμ+ 详解:因为12AE AB AD =+,所以2AB AB AD λλμ⎛⎫=++ ⎪⎝⎭, 因为,AB AD 不共线,所以111=1+=0=-,+=.222λλμμλμ∴, 点睛:利用向量基本定理中唯一性可求参数:即若,a b 为不共线向量,1122+y +y c x a b x a b ==,则1212y =y .x x =,24.3【解析】∵∴∴∴∴故答案为3解析:3 【解析】 ∵()a mb a -⊥∴()0a mb a -⋅=∴2cos ,0a m a b a b -⋅⋅〈〉= ∴932cos600m -⨯⨯⨯︒= ∴3m = 故答案为325.【解析】由题意得解析:4-5【解析】 由题意得3π44cos ,(0,)sin ,sin(π)sin 5255ααααα=∈∴=+=-=-三、解答题 26.(1)2425-;(2)17- 【解析】 【分析】(1)根据同角三角函数关系求出4cos 5α==,根据二倍角公式即可得解;(2)结合(1)求出3tan 4α=-,利用两角差的正切公式求解. 【详解】 (1)3sin 5α=-,,22ππα⎛⎫∈- ⎪⎝⎭, 所以4cos 5α==,所以24sin 22sin cos 25ααα==-; (2)由(1)可得3tan 4α=-, 3131tan 14tan 341tan 714πααα-+--⎛⎫-===- ⎪-⎝⎭+ 【点睛】此题考查根据已知三角函数值求三角函数值,关键在于熟练掌握同角三角函数基本关系,二倍角公式以及和差公式.27.(1)360n m --=(2)()4,3OC =或()5,3OC =- 【解析】 【分析】(1)由题意结合三点共线的充分必要条件确定m ,n 满足的关系式即可; (2)由题意首先求得n 的值,然后求解m 的值即可确定向量的坐标. 【详解】(1)()3,9AB =,()2,AC m n =+, 由点A ,B ,C 三点共线,知AB ∥AC , 所以()3920n m -+=,即360n m --=; (2)由△AOC 的面积是3,得1232n ⨯⨯=,3n =±, 由AC BC ⊥,得0AC BC ⋅=,所以()()2,1,90m n m n +⋅--=,即22920m n m n ++--=, 当3n =时,2200m m +-=, 解得4m =或5m =-, 当3n =-时,2340m m ++=,方程没有实数根, 所以()4,3OC =或()5,3OC =-. 【点睛】本题主要考查三点共线的充分必要条件,向量垂直的充分必要条件等知识,意在考查学生的转化能力和计算求解能力.28.(1)见证明;(2)见证明 【解析】 【分析】(1)设1BC 与1B C 的交点为O ,连结OD ,证明1OD AC ,再由线面平行的判定可得1AC ∥平面1B CD ;(2)由P 为线段11A B 的中点,点D 是AB 的中点,证得四边形1ADB P 为平行四边形,得到1APDB ,进一步得到AP ∥平面1B CD .再由1AC ∥平面1B CD ,结合面面平行的判定可得平面1APC 平面1B CD .【详解】证明:(1)设1BC 与1B C 的交点为O ,连结OD , ∵四边形11BCC B 为平行四边形,∴O 为1B C 中点, 又D 是AB 的中点,∴OD 是三角形1ABC 的中位线,则1OD AC ,又∵1AC ⊄平面1B CD ,OD ⊂平面1B CD ,∴1AC ∥平面1B CD ;(2)∵P 为线段11A B 的中点,点D 是AB 的中点, ∴1AD B P 且1AD B P =,则四边形1ADB P 为平行四边形, ∴1APDB ,又∵AP ⊄平面1B CD ,1DB ⊂平面1B CD , ∴AP ∥平面1B CD . 又1AC ∥平面1B CD ,1AC AP P =,且1AC ⊂平面1APC ,AP ⊂平面1APC ,∴平面1APC 平面1B CD .【点睛】本题考查直线与平面,平面与平面平行的判定,考查空间想象能力与思维能力,是中档题.29.(1)3cos α=;(2)cos β=433+【解析】试题分析:(1)把已知条件平方可得sin α=12,再由已知α∈,2ππ⎛⎫⎪⎝⎭,可得cos α的值. (2)由条件可得-2π<α-β<2π, cos(α-β)=45,再根据cos β=cos[α-(α-β)],利用两角和差的余弦公式,运算求得结果.试题解析: (1)已知sin 2α+cos2α=62,两边同时平方, 得1+2sin 2αcos 2α=32 ,则sin α=12. 又2π<α<π,所以cos α21sin α-3 (2)因为2π<α<π,2π <β<π,所以-2π<α-β<2π.又sin(α-β)=-35 ,所以cos(α-β)=45. 则cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)×45 +12 ×35⎛⎫- ⎪⎝⎭点睛: 本题考查的是三角函数式化简中的给值求值问题,看“角”,这是最重要的一环,通过看角之间的区别和联系,把角进行合理的拆分β=[α-(α-β),从而正确使用公式;由条件可得-2π<α-β<2π, cos(α-β)=45,再根据cos β=cos[α-(α-β)],利用两角和差的余弦公式,运算求得结果.30.(1) ()f x 的最小正周期为2π (2) ()f x 的单调增区间为()72,266k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦【解析】试题分析:(1)化简函数的解析式得()2sin 3f x x π⎛⎫=+ ⎪⎝⎭,根据周期公式求得函数的周期;(2)由()22232k x k k Z πππππ-+≤+≤+∈,求得x 的取值范围即为函数的单调增区间,由()322232k x k k Z ,πππππ+≤+≤+∈求得x 取值范围即为函数的单调减区间。
深圳宝安区龙华中英文实验学校选修二第二单元《一元函数的导数及其应用》测试题(答案解析)
一、选择题1.下列不等式错误的是( ) A .ln 33ln 2<B .3ln 242e <C .ln eππ<D .21515<2.已知定义在()0,∞+上的函数()f x 满足()()0xf x f x '-<,其中()f x '是函数()f x 的导函数,若()()()201920191f m m f ->-,则实数m 的取值范围为( ) A .()0,2020B .()2019,+∞C .()2020,+∞D .()2019,20203.已知函数()f x 与()f x '的图象如图所示,则函数()()x f x g x e=(其中e 为自然对数的底数)的单调递减区间为( )A .()0,4B .()4,1,43⎛⎫-∞⋃⎪⎝⎭ C .40,3⎛⎫ ⎪⎝⎭D .()0,1,()4,+∞4.某堆雪在融化过程中,其体积V (单位:3m )与融化时间t (单位:h )近似满足函数关系:31()1010V t H t ⎛⎫=- ⎪⎝⎭(H 为常数),其图象如图所示.记此堆雪从融化开始到结束的平均融化速度为()3m /h v .那么瞬时融化速度等于()3m /h v 的时刻是图中的( ).A .1tB .2tC .3tD .4t5.已知函数f (x )(x ∈R )满足(1)1f =,且()f x 的导数f ′(x )>12,则不等式1()22x f x <+的A .(-∞,1)B .(1,+∞)C .(-∞,-1]∪[1,+∞)D .(-1,1)6.已知函数()f x 的图象如图所示,则()f x 可以为( )A .()3x x f x e=B .()x x xf x e e -=- C .()xx f x e = D .()xf x xe =7.设函数()e 3x f x x a =+-若曲线sin y x =上存在点()00,x y ,使得()()00f f y y =,则实数a 的取值范围是( )A .[]1,2e +B .13,1e -⎡⎤-⎣⎦C .[]1,1e +D .13,1e e --⎡⎤+⎣⎦8.已知定义在R 上的函数()f x 满足(3)16f =,且()f x 的导函数'()41f x x <-,则不等式2()21f x x x <-+的解集为( )A .{}|33x x -<<B .{}|3x x >-C .{}|3x x >D .{|3x x <-或3x9.已知函数()y f x =对任意的(,)22x ππ∈-满足()cos ()sin 0f x x f x x '+>(其中()'f x 是函数()f x 的导函数),则下列不等式成立的是( ) A .(0)2()4f π>B 2()()34f ππ< C .(0)2()3f f π>D 2()()34f ππ-<-10.函数f (x )=x ﹣g (x )的图象在点x =2处的切线方程是y =﹣x ﹣1,则g (2)+g '(2)=( ) A .7B .4C .0D .﹣411.已知函数()ln f x x x =,则()f x ( ) A .在()0,∞+上递增 B .在()0,∞+上递减 C .在10,e ⎛⎫⎪⎝⎭上递增 D .在10,e ⎛⎫⎪⎝⎭上递减 12.已知定义在[),e +∞上的函数()f x 满足()()ln 0f x xf x x '+<且()40f =,其中fx 是函数()f x 的导函数,e 是自然对数的底数,则不等式()0f x >的解集为( )A .[),4eB .[)4,+∞C .(),e +∞D .[),e +∞13.函数2()ln(3)f x x ax =--在(1,)+∞上单调递增,则实数a 的取值范围是______. 14.已知函数()332f x x x =+,()2,2x ∈-,如果()()1120f a f a -+-<成立,则实数a 的取值范围为__________.15.设(1+ax )2020=a 0+a 1x +a 2x 2+……+a 2019x 2019+a 2020x 2020,若a 1+2a 2+3a 3+…+2019a 2019+2020a 2020=2020a ,则实数a =_______. 16.已知位移和时间的关系是321()2533s t t t t =++-,则2t =时的瞬时速度是_______ 17.已知抛物线2y ax bx c =++过点()1,1,且在点()2,1-处与直线3y x =-相切,则a =__________,b =____________,c =_________________.18.函数()1ln(12)2xf x x x-=+-的导函数是()f x ',则()f x '=______________. 19.若曲线21()ln 2f x x a x =-在点(1,(1))f 处的切线与直线310x y ++=垂直,则常数a =___.20.已知函数()f x 的导函数为'()f x ,且满足()2'(1)ln f x xf x =+,则'(1)=f ________三、解答题21.已知函数2()ln f x x x =-,()g x kx =. (1)求函数()f x 的最小值;(2)若()g x 是()f x 的切线,求实数k 的值;(3)若()f x 与()g x 的图象有两个不同交点A (1x ,1y ),B (2x ,2y ),求证:121x x >. 22.设函数()(1)ln(1)f x x x x =-++ (1)求函数()f x 的极值; (2)若方程()f x t =在1,12⎡⎤-⎢⎥⎣⎦有两个实数解,求t 的取值范围; (3)证明:当0m n >>时,(1)(1)n mm n +<+.23.已知函数()ln f x a x ax =+,2()2g x x x =+,其中a R ∈. (1)求函数()()()h x f x g x =+的极值; (2)若()g x 的图像在()()11,A x g x ,()()()2212,0B x g x xx <<处的切线互相垂直,求21x x -的最小值.24.已知函数()xaf x x e =+,其中a R ∈,e 是自然对数的底数. (1)当1a =-时,求函数() f x 在区间[0,)+∞的零点个数;(2)若()2xe f x <对任意[1,)x ∈-+∞恒成立,求实数a 的取值范围.25.已知函数321()23f x x bx x a =-++,2x =是()f x 的一个极值点. (1)求()f x 的单调递增区间; (2)若当[1,3]x ∈时,22()3f x a ->恒成立,求实数a 的取值范围. 26.已知集合M 是同时满足下列两个性质的函数()f x 的全体①函数()f x 在其定义域上是单调函数;②()f x 的定义域内存在区间[]a b ,,使得()f x 在[]a b ,上的值域为22a b ⎡⎤⎢⎥⎣⎦,.(1)判断()3g x x =是否属于M ,若是,求出所有满足②的区间[]a b ,,若不是,说明理由;(2)若()h x t M =∈,求实数t 的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】 引入函数()ln xf x x=,利用导数确定它的单调性,然后由单调性判断各选项. 【详解】 考查函数()()2ln 1ln ,x xf x f x x x -='=由()0f x '>,得0x e << 由()0f x '<得x e >,所以()f x 在()0,e 上单调递增,在(),e +∞上单调递减, 选项:32A e <<,()2ff <ln 22<,ln 32∴<故本选项正确,不符合题意; 选项B :22e <()(f e f ∴>即lne e >3ln 2e ∴<故本选项正确,不符合题意; 选项:C e e π<<ff ∴<<ln π∴>故本选项错误,符合题意; 选项D154e << 154e <<()4ff ∴>2ln >=15∴>故本选项正确,不符合题意. 故选:C . 【点睛】关键点点睛:本题考查实数的比较大小.解题关键是引入函数ln ()xf x x=,由导数确定它的单调性,由单调性可判断各选项.2.D解析:D 【分析】构造函数()()f x h x x =,根据导数可判断函数单调递减,由()()2019120191f m f m ->-,结合函数定义域可解得. 【详解】令()()f x h x x =,()0,x ∈+∞,则()()()2xf x f x h x x'-'=,因为()()0xf x f x '-<,所以()0h x '<,所以函数()h x 在()0,∞+上单调递减. 因为()()()201920191f m m f ->-,20190m ->,所以()()2019120191f m f m ->-,即()()20191h m h ->,所以20191m -<且20190m ->,解得20192020m <<, 所以实数m 的取值范围为()2019,2020. 故选D . 【点睛】易错点点睛,本题的容易忽略定义域20190m ->,切记解函数抽象不等式要优先考虑定义域.3.D解析:D 【分析】利用图象求得不等式()()0f x f x '-<的解集,求得()()()xf x f xg x e'-'=,解不等式()0g x '<即可得出函数()g x 的单调递减区间.【详解】由图象可知,不等式()()0f x f x '-<的解集为()()0,14,+∞,因为()()x f x g x e =,所以,()()()()()()2x x x x f x e f x e f x f x g x e e ''--'==, 解不等式()0g x '<,可得()()0f x f x '-<,解得()()0,14,x ∈+∞,因此,函数()g x 的单调递减区间为()0,1,()4,+∞. 故选:D. 【点睛】易错点睛:本题考查利用导数求解函数的单调递减区间,通过解不等式()0g x '<得到()()0,14,x ∈+∞,但需要注意的是,函数()g x 的两个单调递减区间不能取并集,而应分开表示.4.C解析:C 【分析】根据题意可知,平均融化速度为(100)(0)1000V V v -=-,反映的是()V t 图象与坐标轴交点连线的斜率,通过观察某一时刻处瞬时速度(即切线的斜率),即可得到答案. 【详解】解:平均融化速度为(100)(0)1000V V v -=-,反映的是()V t 图象与坐标轴交点连线的斜率,观察可知3t 处瞬时速度(即切线的斜率)为平均速度一致, 故选:C .【点睛】本题考查了图象的识别,瞬时变化率和切线斜率的关系,理解平均速度表示的几何意义(即斜率)是解题的关键.5.A解析:A 【分析】 根据f ′(x )>12,构造函数 ()()122x g x f x =-- ,又()()1111022=--=g f ,然后将不等式1()22x f x <+,转化为1()022--<x f x ,利用单调性的定义求解. 【详解】 因为f ′(x )>12, 所以()102f x '-> 所以()()()()()110222x g x f x g x f x g x =--⇒=->⇒'' 在R 上递增, 又()()1111022=--=g f , 所以不等式1()22x f x <+,即为1()022--<x f x , 即为:()()1g x g <, 所以1x <, 故选:A 【点睛】本题主要考查函数的单调性与导数以及单调性的应用,还考查了构造转化求解问题的能力,属于中档题.6.A解析:A 【分析】由图象可知,函数()y f x =为R 上的奇函数,且在()0,∞+上先增后减,然后逐项分析各选项中函数()y f x =的定义域、奇偶性及其在区间()0,∞+上的单调性,结合排除法可得出正确选项. 【详解】由图象可知,函数()y f x =为R 上的奇函数,且在()0,∞+上先增后减. 对于A 选项,函数()3x x f x e =的定义域为R ,()()x xx xf x f x e e---==-=-,该函数为奇函数,当0x >时,()xx f x e =,()1x xf x e -'=. 当01x <<时,()0f x '>,此时函数()y f x =单调递增;当1x >时,()0f x '<,此时函数()y f x =单调递减,合乎题意; 对于B 选项,函数()x xxf x e e-=-的定义域为{}0x x ≠,不合乎题意; 对于C 选项,函数()xx f x e=的定义域为R ,()1f e -=-,()11f e =,()()11f f -≠-,该函数不是奇函数,不合乎题意;对于D 选项,函数()xf x xe =的定义域为R ,当0x >时,()xf x xe =,()()10x f x x e '=+>,该函数在区间()0,∞+上单调递增,不合乎题意.故选:A. 【点睛】本题考查函数图象的识别,一般从函数的定义域、奇偶性、单调性、零点以及函数值符号来判断,结合排除法求解,考查分析问题和解决问题的能力,属于中等题.7.A解析:A 【分析】由题意可得存在0[0y ∈,1],使00()f y y =成立,即()f x x =在[0,1]上有解,即23x a e x x =+-,[0x ∈,1].利用导数可得函数的单调性,根据单调性求函数的值域,可得a 的范围.【详解】由题意可得00sin [1y x =∈-,1],0()f y 曲线sin y x =上存在点0(x ,0)y 使得00(())f f y y =,∴存在0[0y ∈,1],使00()f y y =成立.函数()f x = 下面证明00()f y y =.假设00()f y c y =>,则0(())f f y f =(c )00()f y c y >=>,不满足00(())f f y y =. 同理假设00()f y c y =<,则不满足00(())f f y y =. 综上可得:00()f y y =.则问题等价于方程()f x x =,[0,1]x ∈有解,即23x x e x a =+-在[0,1]x ∈有解,分离参数可得23x a e x x =+-,令2()3x g x e x x =+-,∵()320,[0,1]x g x e x x '=+->∈,所以函数()g x 在[0,1]上单调递增, 所以1(0)()(1)2g g x g e =≤≤=+,所以12a e ≤≤+. 故选:A. 【点睛】本题主要考查正弦函数的图象和性质,利用导数研究函数的单调性,由单调性求函数的值域,体现了转化的数学思想,属于中档题.8.C解析:C 【分析】根据题意,设2()()21g x f x x x =-+-,求导分析可得()0g x '<,即函数()g x 在R 上为减函数,则原不等式可以转化为()()3g x g <,结合函数的单调性分析可得答案. 【详解】解:根据题意,设2()()21g x f x x x =-+-,其导数()()41g x f x x '='-+, 又由()41f x x '<-,即()410f x x '-+<, 则()0g x '<,即函数()g x 在R 上为减函数,又由f (3)16=,则g (3)f =(3)18310-+-=, ()()22()21()2103f x x x f x x x g x g <-+⇒-+-<⇒<,又由函数()g x 为减函数,则有3x >,则不等式2()21f x x x <-+的解集为{|3}x x >; 故选:C . 【点睛】本题考查函数的导数与函数单调性的关系,涉及不等式的求解,根据条件构造函数,利用函数的单调性和导数之间的关系是解决本题的关键,属于中档题.9.D解析:D 【分析】 构造函数()()cos f x F x x=,利用函数()'F x 导数判断函数()F x 的单调性,将ππππ0,,,,3434x =--代入函数()F x ,根据单调性选出正确的选项.【详解】构造函数()()cos f x F x x=,依题意()()()2cos sin 0cos f x x f x xF x x+='>',故函数在定义域上为增函数,由()π04F F ⎛⎫< ⎪⎝⎭得()π04πcos 0cos4f f ⎛⎫ ⎪⎝⎭<,即()π04f ⎛⎫< ⎪⎝⎭,排除A 选项. 由ππ34F F ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭得ππ34ππcos cos34f f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭>ππ34f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭,排除B 选项.由()π03F F ⎛⎫< ⎪⎝⎭得()π03πcos 0cos3f f ⎛⎫ ⎪⎝⎭<,即()π023f f ⎛⎫< ⎪⎝⎭,排除C ,选项. 由ππ34F F ⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭得ππ34ππcos cos 34f f ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭<⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭ππ34f ⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭,D 选项正确,故选D. 【点睛】本小题主要考查构造函数法比较大小,考查函数导数的概念,考查函数导数运算,属于基础题.10.A解析:A 【解析】()()()(),'1'f x x g x f x g x =-∴=-,因为函数()()f x x g x =-的图像在点2x =处的切线方程是1y x =--,所以()()23,'21f f =-=-,()()()()2'2221'27g g f f ∴+=-+-=,故选A . 11.D解析:D 【分析】确定函数的定义域,求导函数,根据导函数的正负确定函数的单调性. 【详解】函数的定义域为(0,+∞) 求导函数,可得f′(x )=1+lnx令f′(x )=1+lnx=0,可得x=1e, ∴0<x <1e 时,f′(x )<0,x >1e时,f′(x )>0 ∴在10,e ⎛⎫ ⎪⎝⎭上递减, 在1,e ⎛⎫+∞ ⎪⎝⎭上递增故选D . 【点睛】这个题目考查了导数在函数的单调性中的应用,判断函数的单调性常用的方法是:求导,根据导函数的正负得到函数的单调区间.导函数为正的区间是增区间,导函数为负的区间是减区间.12.A解析:A 【分析】根据条件构造函数()()g x f x lnx =,求函数的导数,研究函数的单调性,将不等式()0f x >等价为()()4g x g >,进行求解即可.【详解】 解:x e ,1lnx ∴,则不等式()()0f x xf x lnx '+<等价为()()0f x f x lnx x'+<, 设()()g x f x lnx =, 则()()()0f x g x f x lnx x'='+<, 即()g x 在[e ,)+∞上为减函数,f (4)0=,g ∴(4)f =(4)40ln =,则不等式()0f x >等价为()0lnxf x >, 即()()04g x g >=,()g x 在[e ,)+∞上为减函数,4e x ∴<,即不等式()0f x >的解集为[e ,4), 故选:A . 【点睛】本题主要考查不等式 的求解,根据条件构造函数,通过导数研究函数的单调性是解决本题的关键.属于中档题.二、填空题13.【分析】结合复合函数增减性和二次函数单调性及对数函数真数的定义域列出不等式组即可求解【详解】由在上单调递增可知即设则即解得综上所述故答案为:【点睛】本题考查由复合函数在定区间的单调性求解参数取值范围 解析:(],2-∞-【分析】结合复合函数增减性和二次函数单调性及对数函数真数的定义域列出不等式组,即可求解 【详解】由2()ln(3)f x x ax =--在(1,)+∞上单调递增可知12ax =≤,即2a ≤ 设()23g x x ax =--,则()10g ≥,即20a --≥,解得2a ≤- 综上所述,2a ≤- 故答案为:(],2-∞- 【点睛】本题考查由复合函数在定区间的单调性求解参数取值范围,易错点为忽略对数函数中真数的取值范围,属于中档题14.【详解】因为恒成立所以在R 上递增又所以为奇函数则可化为由递增得解得:0<a <故答案为解析:3(0,)2【详解】因为23+6x 0f x '=()>恒成立,所以f x ()在R 上递增,又f x f x =(﹣)﹣(),所以f x ()为奇函数,则1120f a f a +(﹣)(﹣)<,可化为121f a f a (﹣)<(﹣), 由f x ()递增,得1212122212a a a a --⎧⎪--⎨⎪--⎩<<<<<,解得:0<a <32,故答案为302⎛⎫⎪⎝⎭,.15.0【分析】结合所求式子与已知的式子特点可以对原函数求导然后利用赋值法求解即可【详解】对已知的式子两边同时求导可得:2020a (1+ax )2019令x =1则:2020a (1+a )2019=a1+2a2解析:0 【分析】结合所求式子与已知的式子特点,可以对原函数求导,然后利用赋值法求解即可. 【详解】对已知的式子两边同时求导可得:2020a (1+ax )2019220191232020232020a a x a x a x =++++,令x =1则:2020a (1+a )2019=a 1+2a 2+3a 3+…+2020a 2020, 又因为:a 1+2a 2+3a 3+…+2019a 2019+2020a 2020=2020a , 所以(1+a )2019=1,所以a =0.故答案为:0. 【点睛】本题考查了二项式定理的系数的性质、赋值法的应用.同时考查了学生的运算能力,属于中档题.16.17【分析】先求导再根据导数的定义求得时的瞬时速度是得解【详解】则时的瞬时速度故答案为:17【点睛】本题考查导数的定义在物理中的应用函数在处的瞬时变化率称函数在处的导数解析:17 【分析】先求导,再根据导数的定义求得2t =时的瞬时速度是(2)s ',得解. 【详解】321()2533s t t t t =++-,22()45=(2)1s t t t t '∴=++++则2t =时的瞬时速度2(2)(22)117v s '==++= 故答案为:17 【点睛】本题考查导数的定义在物理中的应用函数(=)y f x 在0=x x 处的瞬时变化率称函数(=)y f x 在0=x x 处的导数.17.3-119【分析】先求函数的导函数再由题意知函数过点且在点处的切线的斜率为1即分别将三个条件代入函数及导函数解方程即可【详解】解:由于抛物线过点则又因为点处与直线相切即切线的斜率为1即又因为切点为把解析:3 -11 9 【分析】先求函数2y ax bx c =++的导函数'()f x ,再由题意知,函数过点(1,1),(2,1)-,且在点(2,1)-处的切线的斜率为1,即()'21f =,分别将三个条件代入函数及导函数,解方程即可. 【详解】解:由于抛物线2y ax bx c =++过点()1,1,则()11f =,1a b c ∴++=, 又'()2f x ax b =+,因为2y ax bx c =++点()2,1-处与直线3y x =-相切,即切线的斜率为1,即()21f '=, 41a b ∴+=.又因为切点为(2,1)-,421a b c ∴++=-.把①②③联立得方程组14142 1.a b c a b a b c ++=⎧⎪+=⎨⎪++=-⎩,解得:3119a b c =⎧⎪=-⎨⎪=⎩,即3a =,11b =-,9c =. 故答案为:3,-11,9. 【点睛】本题考查导数的几何意义及其应用,利用方程的思想求参数的值,考查计算能力.18.【分析】利用基本函数求导公式和导数运算法则求出导数然后代入求值【详解】解:因为由于且解得:且即的定义域为:即:故答案为:【点睛】本题考查基本函数求导公式和导数运算法则以及复合函数求导考查计算能力解析:23242142x x x x -+--+ 【分析】利用基本函数求导公式和导数运算法则,求出导数,然后代入求值. 【详解】 解:因为()1ln(12)2xf x x x-=+-, 由于20x ≠且120x ->,解得:12x <且0x ≠, 即()f x 的定义域为:()1,00,2⎛⎫-∞⋃ ⎪⎝⎭, ()()11()ln 12()ln 1222x x f x x x x x '--⎡⎤''∴=+-='+-⎡⎤⎣⎦⎢⎥⎣⎦2223222(1)14214122122242x x x x x x x x x x -----+-=-+=+=-+---,即:()23242142x x f x x x -+-'=-+. 故答案为:23242142x x x x -+--+.【点睛】本题考查基本函数求导公式和导数运算法则,以及复合函数求导,考查计算能力.19.-2【分析】利用导数的几何意义求得在点处的切线斜率为再根据两直线的位置关系即可求解【详解】由题意函数可得所以即在点处的切线斜率为又由在点处的切线与直线垂直所以解得【点睛】本题主要考查了利用导数的几何解析:-2【分析】利用导数的几何意义,求得在点(1,(1))f 处的切线斜率为1k a =-,再根据两直线的位置关系,即可求解. 【详解】由题意,函数21()ln 2f x x a x =-,可得()af x x x'=-,所以(1)1f a '=-, 即在点(1,(1))f 处的切线斜率为1k a =-,又由在点(1,(1))f 处的切线与直线310x y ++=垂直,所以1(1)()13a -⨯-=-, 解得2a =-. 【点睛】本题主要考查了利用导数的几何意义求解参数问题,其中解答中利用导数的几何意义求得切线的斜率,再根据两直线的位置关系是解答的关键,着重考查了推理与运算能力,属于基础题.20.-1【解析】【分析】首先对函数求导然后利用方程思想求解的值即可【详解】由函数的解析式可得:令可得:则【点睛】本题主要考查导数的运算法则基本初等函数的导数公式方程的数学思想等知识意在考查学生的转化能力解析:-1 【解析】 【分析】首先对函数求导,然后利用方程思想求解()'1f 的值即可. 【详解】由函数的解析式可得:()()1'2'1f x f x=+, 令1x =可得:()()1'12'11f f =+,则()'11f =-. 【点睛】本题主要考查导数的运算法则,基本初等函数的导数公式,方程的数学思想等知识,意在考查学生的转化能力和计算求解能力.三、解答题21.(1)11ln 222+;(2)1;(3)证明见解析. 【分析】(1)利用导数求出其单调性,即可得出函数()f x 的最小值;(2)利用导数的几何意义得出切线方程20000121ln y x x x x x ⎛⎫=--+- ⎪⎝⎭,再由2000012,1ln 0x k x x x -=-+-=求出k 的值; (3)将22111222ln ,ln x x kx x x kx -=-=两式相加相减化简得出2121212211ln 2ln x x x x x x x x x x ++=-,令211x t x =>,构造函数2(1)()ln (1)1t F t t t t -=->+,利用单调性证明2(1)ln 1t t t ->+,从而得出1212ln 22x x x x +>,再由令()ln 2G x x x =+的单调性得出12()(1)G x x G >,从而得出121x x >. 【详解】解:(1)∵2()ln f x x x =-,∴2121()2(0)x f x x x x x-'=-=>当0,2x ⎛⎫∈ ⎪ ⎪⎝⎭时,()0f x '<,∴()f x在2⎛ ⎝⎭上单调递减;当,2x ⎛⎫∈+∞ ⎪ ⎪⎝⎭时,()0f x '>,∴()f x在2⎛⎫+∞ ⎪ ⎪⎝⎭上单调递增. 故函数()f x的最小值为211ln ln 222222f ⎛⎫⎛⎫=-=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭(2)若()g x 是()f x 的切线,设切点为00(,())x f x 则过点00(,())x f x 的切线方程为000()()()y f x x x f x '=-+ 即20000012()ln y x x x x x x ⎛⎫=--+- ⎪⎝⎭,即20000121ln y x x x x x ⎛⎫=--+- ⎪⎝⎭ 由题意知2000012,1ln 0x k x x x -=-+-= 令2()1ln (0)h x x x x =-+->,则0x >时,1()20h x x x'=--< ∴2()1ln h x x x =-+-在(0,)+∞上单调递增,又(1)0h =∴2001ln 0x x -+-=有唯一的实根01x =,则0012211k x x =-=-=. (3)由题意知22111222ln ,ln x x kx x x kx -=-=两式相加得22121212ln ()x x x x k x x +-=+两式相减得22221211ln ()x x x k x x x --=-,即212121ln x x x x k x x +-=-∴22211212211221ln ln ()x x x x x x x x x x x x ⎛⎫ ⎪ ⎪+-=+-+- ⎪ ⎪⎝⎭,即2121212211ln 2ln x x x x x x x x x x ++=- 不妨令120x x <<,记211x t x =>,则2121212211ln 2ln x x xx x x x x x x ++==-1ln 1t t t +- 令2(1)()ln (1)1t F t t t t -=->+,则2(1)()0(1)t F t t t -'=>+∴2l ())1n 1(t F t t t -=-+在(1,)+∞上单调递增,则2(1)()ln (1)01t F t t F t -=->=+ ∴2(1)ln 1t t t ->+,因而1212ln 2x x x x +=112(1)ln 2111t t t t t t t ++->⋅=--+ 令()ln 2G x x x =+,则0x >时,1()20G x x'=+>,∴()G x 在(0,)+∞上单调递增∵121212()ln 22(1)G x x x x x x G =+>=,∴121x x >. 【点睛】在处理极值点偏移问题时,关键是构造新函数,结合单调性解决极值点偏移问题. 22.(1)0;(2)11[ln 2,0)22-+;(3)证明见详解. 【分析】(1)首先明确定义域,再求导()ln(1)f x x '=-+,所以()f x 在()1,0-上单调递增,在()0,∞+上单调递减,即可得解;(2)实际研究直线x t =与函数()y f x =图像交点有两个的情况,由(1)知()f x 在1[,0]2-上单调递增,在[0,1]上单调递减,且1(1)()2f f <-,所以当11[,ln 2,0)22t ∈-+时,方程()f x t =有两解.(3)首先将两变量分离,这要用到取对数,即ln(1)ln(1),n m m n +<+因此只需证ln(1)ln(1)m n m n++<,即证ln(1)(),(0)x g x x x+=>为单调减函数,可利用导数2ln(1)1()xx x g x x-+'+=,再结合(1)的结论可证. 【详解】(1)由()(1)ln(1)f x x x x =-++,定义域为()1,-+∞,()ln(1)f x x '=-+,()ln(1)00f x x x '=-+=⇒=,当10x -<<时,()()0,f x f x '>单调递增,当0x >时,()()0,f x f x '<单调递减, 所以0x =为函数的极大值点,则函数()f x 的极值为(0)0(01)ln(01)0f =-++=. (2)由(1)知,()f x 在1[,0]2-上单调递增, 在(]0,1上单调递减,又111(0)0,(1)1ln 4,()ln 2222f f f ==--=-+, ∴ 135(1)()ln 20222f f --=-<. ∴ 当11[ln 2,0)22t ∈-+时,方程()f x t =有两解. (3)∵ 0m n >>.∴ 要证:(1)(1)n m m n +<+只需证ln(1)ln(1)n m m n +<+, 只需证:ln(1)ln(1)m n m n ++<. 设ln(1)(),(0)x g x x x+=>, 则22ln(1)(1)ln(1)1()(1)xx x x x x g x x x x -+-+++=+'=. 由(1)知()(1)ln(1)f x x x x =-++在(0,)+∞单调递减, 又()00f =,∴ (1)ln(1)0x x x -++<, 即()g x 是减函数,而m n >. ∴ ()()g m g n <,故原不等式成立. 【点睛】关键点睛:要证:(1)(1)n mm n +<+只需证ln(1)ln(1)n m m n +<+,只需证:ln(1)ln(1)m n m n ++<,构造函数ln(1)(),(0)x g x x x +=>是解决本题的关键. 23.(1)答案见解析;(2)1. 【分析】(1)求导2(1)2()2(2)a x x a h x x a x x⎛⎫++ ⎪⎝⎭'=+++=,然后分0a ≥,0a <讨论求解. (2)求导()22g x x '=+,根据()g x 的图像在()()11,A x g x ,()()22,B x g x 处的切线互相垂直,得到()()1222221x x ++=-,即 ()121141x x =--+,然后由()21221141x x x x -=+++,利用基本不等式求解.【详解】(1)函数2()ln (2)h x a x x a x =+++的定义或为(0,)+∞,2(1)2()2(2)a x x a h x x a x x⎛⎫++ ⎪⎝⎭'=+++=, 若0a ≥,()0h x '>恒成立,此时()h x 在(0,)+∞上单调递增,无极值;若0a <时,()0h x '=,解得2a x =-, 当02ax <<-时,()0h x '<,()h x 单调递减; 当2ax >-时,()0h x '>,()h x 单调递增. ∴当2a x =-时,()h x 有极小值2ln 224a a ah a a ⎛⎫⎛⎫-=--- ⎪ ⎪⎝⎭⎝⎭,无极大值.(2)()22g x x '=+,则()()1222221x x ++=-,其中,120x x <<,1222022x x ∴+<<+,且()121141x x =--+,210x -<<,()212211141x x x x ∴-=++≥=+,当且仅当21(1,0)2x =-∈-时取等号, ∴当212x =-,132x =-时,21x x -取最小值1.【点睛】结论点睛:(1)可导函数y =f (x )在点x 0处取得极值的充要条件是f ′(x 0)=0,且在x 0左侧与右侧f ′(x )的符号不同.(2)若函数y =f (x )在区间(a ,b )内有极值,那么y =f (x )在(a ,b )内绝不是单调函数,即在某区间上单调函数没有极值.24.(1)1个;(2)2122e e a --+<.【分析】(1)求导得到函数的单调性,再利用零点存在性定理得解 (2)分离参变量,不等式恒成立转化为求函数的最值得解 【详解】(1)()x f x x e -=-,0x ≥,()10x f x e '-=+> 故()f x 在[0,)+∞递增,又(0)1f =-,1(1)10f e -=->(0)(1)0f f <,故()f x 在(0,1)上存在唯一零点因此()f x 在区间[0,)+∞的零点个数是1个; (2)1x ∀≥-,2x xe x ae-+<恒成立,即1x ∀≥-,2e 2x x a xe <-恒成立 令2()2xx e g x xe =-,1x ≥-,则min ()a g x <()()1x x g x e x e '=--,令()1x h x e x =--,1x ≥-()1x h x e '=-,[1,0)x ∈-时,()0h x '<,0x >时,()0h x '>故()h x 在[1,0)-递减,(0,)+∞递增,因此()(0)0h x h ≥= 所以,()0g x '≥,故 ()g x 在[1,)-+∞递增 故21min 2()(1)2e e g x g --+=-=,因此2122e e a --+<. 【点睛】不等式恒成立问题解决思路:一般参变分离、转化为最值问题. 25.(1)(,1)-∞,(2,+)∞;(2)01a <<. 【分析】(1)根据2x =是()f x 的一个极值点,2x =是2()220f x x bx '=-+=方程的一个根,解得b ,然后令()0f x '>求解. (2)将 [1,3]x ∈时,22()3f x a ->恒成立,转化为22()3f x a >+恒成立,只需2min 2()3f x a >+求解. 【详解】(1)2()22f x x bx '=-+.∵2x =是()f x 的一个极值点, ∴2x =是方程2220x bx -+=的一个根, 解得32b =. 令()0f x '>,则2320x x -+>, 解得1x <或2x >.∴函数()y f x =的单调递增区间为(,?1)-∞,(2,+)∞. (2)∵当(1,2)x ∈时()0f x '<,(2,3)x ∈时()0f x '>, ∴()f x 在(1,2)上单调递减,()f x 在(2,3)上单调递增.∴(2)f 是()f x 在区间[1,3]上的最小值,且 2(2)3f a =+. 若当[1,?3]x ∈时,要使22()3f x a ->恒成立, 只需22(2)3f a >+, 即22233a a +>+, 解得 01a <<.【点睛】方法点睛:恒(能)成立问题的解法:若()f x 在区间D 上有最值,则(1)恒成立:()()min ,00x D f x f x ∀∈>⇔>;()()max ,00x D f x f x ∀∈<⇔<; (2)能成立:()()max ,00x D f x f x ∃∈>⇔>;()()min ,00x D f x f x ∃∈<⇔<. 若能分离常数,即将问题转化为:()a f x >(或()a f x <),则(1)恒成立:()()max a f x a f x >⇔>;()()min a f x a f x <⇔<;(2)能成立:()()min a f x a f x >⇔>;()()max a f x a f x <⇔<.26.(1) ()g x 属于M ,且满足②的区间[a ,b ]为002222⎡⎤⎡⎡--⎢⎥⎢⎢⎣⎦⎣⎦⎣⎦,,,, ; (2) 102⎛⎤ ⎥⎝⎦, 【分析】(1)可以看出()g x 为增函数,满足条件①,而方程32x x =有三个不同的解,从而满足条件②,从而说明()g x 属于M ,且可写出所有满足②的区间[a ,b ];(2)()h x 属于M 2x t =至少有两个不同的实数根,从而得到2x t =-,两边平方并整理可得()221104x t x t -+++= 从而20t ∆=>,得到t >0,而02x t -≥即2x t ≤恒成立,且1≥x ,从而又得到12t ≤,这样便可得出实数t 的取值范围.【详解】 (1)()3g x x =在R 上为增函数,满足性质①;解32x x =得,x =0,或2x =± ;∴()g x 属于M ,且满足②的区间[a ,b ]为222200⎡⎤⎡⎤⎡⎤--⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,,,,,; (2)()1h x x t =-+在定义域内单调递增,满足①;∵h (x )∈M ;∴h (x )满足②;则方程12x x t -=-少有两个解; 即函数1y x =-与函数2x y t =-的图象有两个不同的交点. 如图当直线2x y t =-过点()1,0时,12t = 设直线2x y t =-与曲线1y x =-相切于点()00,A x y 由函数1y x =-的导函数为21'=-y x 所以01221k x ==-,所以02x =,则()2,1A 由()2,1A 在直线2x y t =-上,解得0t = 根据图象可得函数1y x =-与函数2x y t =-的图象有两个不同的交点,得102t <≤∴实数t 的取值范围为102⎛⎤ ⎥⎝⎦,.【点睛】考查函数单调性的定义,函数值域的定义,()f x 满足性质②便说明方程()2x f x =至少有两个不同解,即函数1y x =-2x y t =-的图象有两个不同的交点,数形结合可得出答案,属于中档题.。
深圳宝安区龙华中英文实验学校人教版高中化学选修1-第1章选择题专项经典练习卷(培优专题)
一、选择题1.强酸与强碱的稀溶液发生中和反应的热效应为:H+(aq)+OH-(aq)=H2O(l)△H =-57.3KJ·mol-1.分别向1L 0.5mol·L-1的Ba(OH)2的溶液中加入①浓硫酸;②稀硫酸;③稀硝酸,恰好完全反应的热效应分别为△H1、△H2、△H3,下列关系正确的是A.△H1>△H2>△H3B.△H1<△H2<△H3C.△H1>△H2=△H3D.△H1<△H2=△H3答案:B【详解】强酸与强碱的稀溶液发生中和反应热效应表示为:H+(aq)+OH-(aq)═H2O(l)△H=-57.3kJ•mol-1,分别向1L 0.5mol·L-1的Ba(OH)2的溶液中加入①浓硫酸;②稀硫酸;③稀硝酸至恰好完全反应,均生成1mol水,其中:①浓硫酸发生中和反应生成1mol水时,浓硫酸溶于水放热,且生成BaSO4沉淀也放出热量,则放出的热量最多,△H1最小;②稀硫酸在发生中和反应时生成1mol水,同时生成BaSO4沉淀也能放出热量,放出的热量要略大于中和热,即△H2略小于△H;③稀硝酸正常发生中和反应生成1mol水,中和热不变,即△H3=△H;则恰好完全反应时的放出的热量为:①>②>③,即△H1<△H2<△H3,故答案为B。
2.已知:2H2(g)+O2(g)=2H2O(l),ΔH=-572kJ/mol;H-H键的键能为436kJ/mol;O=O键的键能为498kJ/mol,则H2O分子中O-H键的键能为()A.485.5kJ/mol B.610kJ/mol C.917kJ/mol D.1220kJ/mol答案:A【详解】设H2O分子中O-H键的键能为x,则可建立如下等量关系式:2mol×436kJ/mol+1mol×498kJ/mol-4mol∙x=-572kJ,从而求出x=485.5kJ/mol,故选A。
3.下列热化学方程式中,正确的是A.甲烷的燃烧热△H=-890.3 kJ/mol,则甲烷燃烧的热化学方程式可表示为:CH4(g)+2O2(g)=CO2(g)+2H2O(g) △H=-890.3 kJ/molB.一定条件下,0.5 molN2与1.5molH2充分反应后放出35.5 kJ的热量:N2(g)+3H2(g)2NH3(g) △H=-71 kJ/molC.HCl和NaOH反应的中和热△H=-57.3 kJ/mol,则H2SO4和Ca (OH)2反应的中和热△H=2×(-57.3) kJ/molD.96 g O2的能量比96 gO3的能量低b kJ:3O2(g)2O3(g) △H=+b kJ/mol答案:D【详解】A.燃烧热表示1mol可燃物完全燃烧生成稳定的氧化物时放出的热量,表示甲烷燃烧热时,生成的水为液体,则甲烷燃烧的热化学方程式可表示为CH4(g)+2O2(g)=CO2(g)+2H2O(l) △H=-890.3 kJ/mol,故A错误;B.0.5 mol N2和1.5 mol H2充分反应生成NH3,放热35.5 kJ,合成氨为可逆反应,0.5 mol N2不能完全反应生成NH3,则1molN2(g)充分反应生成NH3(g)放热大于71kJ,放热反应的焓变为负值,则N2(g)+3H2(g)⇌2NH3(g) △H<-71kJ⋅mol−1,故B错误;C.中和反应为放热反应,焓变为负值,生成硫酸钙时也放出热量,由HCl和NaOH反应的中和热△H=−57.3 kJ⋅mol−1可知,H2SO4和Ca(OH)2反应的△H<2×(-57.3) kJ⋅mol−1,故C 错误;D.96 g O2的物质的量为:96g32g/mol=3mol,96 gO3的物质的量为:96g48g/mol=2mol,3mol O2的能量比2molO3的能量低b kJ,则3mol O2生成2molO3时吸收bkJ的热量,热化学方程式为:3O2(g)2O3(g) △H=+b kJ/mol,故D正确;答案选D。
广东省深圳市市龙华中英文实验学校高二化学下学期期末试卷含解析
广东省深圳市市龙华中英文实验学校高二化学下学期期末试卷含解析一、单选题(本大题共15个小题,每小题4分。
在每小题给出的四个选项中,只有一项符合题目要求,共60分。
)1. 下列说法正确的是()A.需要加热的化学反应都是吸热反应B.应用盖斯定律可以计算某些难以测量的反应焓变C.盐类的水解反应是放热反应D.在吸热反应中,反应物的总能量比产物的总能量高参考答案:B略2. 下列有关0.1 mol·L-1NaOH溶液的叙述正确的是A.1L该溶液中含有NaOH 40gB.100ml该溶液中含有OH-0.01molC.从1L该溶液中取出100mL,所取出的NaOH溶液的浓度为0.01 mol·L-1D.在1L水中溶解4g NaOH即可配制得0.1 mol·L-1 NaOH溶液参考答案:B3. 等物质的量浓度的下列五种溶液:①CH3COOH ②(NH4)2CO3③NaHSO4④NaHCO3 ⑤Ba(OH)2,溶液中水的电离程度由大到小排列正确的是()A.⑤③①④②B.⑤③①②④C.②④③①⑤D.②④①③⑤参考答案:D 向水中加酸、加碱,抑制水的电离,[H+]或[OH-]抑制程度相同,浓度越大,抑制程度越大;加入弱离子,促进水的电离,浓度越大,促进程度越大。
故答案D。
4. 下列关于药物的使用说法正确的是A.虽然药物能治病,但大部份药物有毒副作用B.使用青霉素时,不用进行试验直接静脉注射C.长期大量使用阿司匹林可预防疾病,没有副作用D.对于标记“OTC”的药物,必需在医生指导下使用参考答案:A略5. 一种适用于柑橘、苹果等作物的低毒杀螨剂“溴螨酯”,杀螨谱广、持续期长,对蜜蜂及作物均较安全,其结构为BrCOHCOOCH(CH3)2Br。
下列说法错误的是A.分子中至少只有4个原子位于同一平面上B.既能发生水解反应,又能发生酯化反应 C.不能与FeCl3溶液发生显色反应D.1 mol溴螨酯可与4 mol NaOH溶液反应参考答案:B略6. 下列叙述正确的是()A.根据非金属原子最外层电子数的多少,可判断两种元素得电子能力的强弱B.具有相同电子层结构的微粒,其化学性质是相似的C.某变化过程中发生共价键的断裂,则该过程中一定发生化学变化D.含金属元素的离子不一定是阳离子,不含金属元素的离子可能是阳离子参考答案:D略7. 在铁制品上镀上一定厚度的锌层,以下电镀方案中正确的是()A.锌作阳极,铁制品作阴极,溶液中含Fe2+B.锌作阴极,铁制品作阳极,溶液中含Zn2+C.锌作阴极,铁制品作阳极,溶液中含Fe3+D.锌作阳极,铁制品作阴极,溶液中含Zn2+参考答案:D略8. 在密闭容器中进行下列反应:M(g)+N(g)?R(g)+2L,此反应符合如图,下列叙述正确的是()A.正反应吸热,L是气体B.正反应吸热,L是固体C.正反应放热,L是气体D.正反应放热,L是固体或液体参考答案:C考点:化学平衡建立的过程;产物的百分含量随浓度、时间的变化曲线.专题:化学平衡专题.分析:由图象可知,温度为T1时,根据到达平衡的时间可知P2>P1,且压强越大,R的含量越低,说明平衡向逆反应方向移动,正反应为气体体积增大的反应;压强为P1时,根据到达平衡的时间可知T2>T1,且温度越高,R的含量越低,说明平衡向逆反应方向移动,则正反应为放热反应解答:解:由图象可知,温度为T1时,根据到达平衡的时间可知P2>P1,且压强越大,R的含量越低,说明平衡向逆反应方向移动,正反应为气体体积增大的反应,故L为气体;压强为P1时,根据到达平衡的时间可知T2>T1,且温度越高,R的含量越低,说明平衡向逆反应方向移动,则正反应为放热反应;由上述分析可知,该反应的正反应为放热反应,L是气体,故选C.点评:本题考查化学平衡图象问题,难度不大,本题注意根据图象判断温度、压强的大小,根据温度、压强对平衡移动的影响分析9. 下列各组物质中,属于同系物的是A.HCHO、CH3COOH B.、C.CH3COOH、CH3CH20H D.醋酸、硬脂酸参考答案:D10. 只用一种试剂,可区别Na2SO4、AlCl3、NH4Cl、MgSO4四种溶液,这种试剂是()A.HCl B.BaCl2 C.NaOH D.AgNO3参考答案:C略11. 下列各组有机物,无论以何种物质的量的比例混合,只要总物质的量一定,则完全燃烧消耗氧气的量为一恒定值的是()A.C3H6和C3H8 B.C2H6和C2H4O2 C.C5H10和C6H6 D.C2H6和C3H8参考答案:C12. 花青苷是引起花果呈现颜色的一种花色素,广泛存在于植物中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.已知双曲线 ,则双曲线右支上的点 到右焦点的距离与点 到右准线的距离之比等于()
A. B. C. 2 D. 4
3.方程 的两个根可分别作为()
A.一椭圆和一双曲线的离心率B.两抛物线的离心率
C.一椭圆和一抛物线的离心率D.两椭圆的离心率
4.若抛物线 的焦点与椭圆 的右焦点重合,则 的值为()
.联立方程组 ,消去y得, .
设A( ),B( ),AB线段的中点为M( )那么: , =
所以 = +2= .
也就是说线段AB中点坐标为(- , ).
15.解:设椭圆的方程为 ,双曲线得方程为 ,半焦距c=
由已知得:a1-a2=4
,解得:a1=7,a2=3
所以:b12=36,b22=4,所以两条曲线的方程分别为:
,
16.解:(1)由已知得椭圆的半长轴a=2,半焦距c= ,则半短轴b=1.
又椭圆的焦点在x轴上,∴椭圆的标准方程为
(2)设线段PA的中点为M(x,y) ,点P的坐标是(x0,y0),
由
x=
得
x0=2x-1
y=
y0=-
由,点P在椭圆上,得 ,
∴线段PA中点M的轨迹方程是 .
(2)顶点间的距离为6,渐近线方程为 .
14.(8分)已知椭圆C的焦点F1(- ,0)和F2( ,0),长轴长6,设直线 交椭圆C于A、B两点,求线段AB的中点坐标。
15.(12分)中心在原点,焦点在x轴上的一个椭圆与一双曲线有共同的焦点F1,F2,且 ,椭圆的长半轴与双曲线的半实轴之差为4,离心率之比为3:7。求这两条曲线的方程。
A. B. C. D.
7.曲线 与曲线 的()
A.焦距相等B.离心率相等C.焦点相同D.准线相同
8.已知双曲线 的实轴长、虚轴长、焦距长成等差数列,则双曲线的离心率e为( )
A.2 B.3C. D.
二、填空题(每题4分,共20分)。
9.焦点在直线 上,且顶点在原点的抛物线标准方程为________。
深圳市龙华中英文实验学校高二数学选修1-1圆锥曲线测试题
本试卷分第一卷和第二卷两部分,共3页,满分为100分。
第一卷(60分)
姓名班别成绩
一、选择题(每题5分,共40分)
题号
1
2
3
4
5
6
7
8
答案
1.已知△ABC的顶点B、C在椭圆 +y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是()
A. B. C. D.4
5.平面内有两定点A、B及动点P,设命题甲是:“|PA|+|PB|是定值”,命题乙是:“点P的轨迹是以A.B为焦点的椭圆”,那么()
A.甲是乙成立的充分不必要条件B.甲是乙成立的必要不充分条件
C.甲是乙成立的充要条件D.甲是乙成立的非充分非必要条件
6.已知双曲线 的一条渐近线方程为y= x,则双曲线的离心率为()
12.16,12
三13.解(1)焦点在x轴上,设所求双曲线的方程为 =1.
由题意,得 解得 , . ∴ .
所以焦点在x轴上的双曲线的方程为 .
(2)当焦点在x轴上时,设所求双曲线的方程为 =1
由题意,得 解得 , .
所以焦点在x轴上的双曲线的方程为 .
同理可求当焦点在y轴上双曲线的方程为 .
14.解:由已知条件得椭圆的焦点在x轴上,其中c= ,a=3,从而b=1,所以其标准方程是:
16.(12分)已知在平面直角坐标系 中的一个椭圆,它的中心在原点,左焦点为 ,右顶点为 ,设点 .
(1)求该椭圆的标准方程;
(2)若 是椭圆上的动点,求线段 中点 的轨迹方程;
答案:
一1. C 2 . C 3. A 4 . D 5 . B 6 . A 7 .A 8. D
二.9.y =16x或x =-12y 10.- 11. 或
10.双曲线 的虚轴长是实轴长的2倍,则 。
11.与椭圆 具有相同的离心率且过点(2,- )的椭圆的标准方程是________。
12、设 为椭圆 的焦点, 为椭圆上的一点,则 的周长是, 的面积的最大值是。
第二卷(40分)
三、解答题(共40分)。
13.(8分)求适合下列条件的双曲线的标准方程:
(1)焦点在x轴上,虚轴长为12,离心率为 ;
