2.3 传递函数的方块图表示及运算
合集下载
第2章(4)传递函数方块图及其化简

G(s) 1 G(s)H (s)
G(s) 1 Gk (s)
B(s)
H(s)
前向通道传递函数、
反馈通道传递函数、
开环传递函数、
正反馈、负反馈;
2.方框图的变换与化简:(1)串、并联的化简; (2)分支点跨过环节的移动规则; (3)相加点的拆并及跨过环节的移动规则; (4)反馈与并联交错的化简
Xo(s)
G1(S)
G2(S)
Xi(s) G1(S) G2(S)
Xo(s)
G(s)
X X
o(s) i(s)
X o(s) X (s)
X (s) Xi(s)
G2
(
s)G1(
s
)
n
G(s) Gi (s) i 1
负载效应问题
i1 R1 i2 R2
G1(s)
1 R1C1s
1
G2 (s)
Xo(s)
C
略
H1
jik 04
16
X (s) 0 求 Xo(s) 。令
Xi2(s)
i1
Xi 1(s)
H3
+
-
-
G1 B +
G2
,
Xi
2(
Xi1(s)处的相加点取消,
H1 变成(-H1)。原图改画成:
s)
Xi 2(s) +
G3
Xo(s)
+
+
-A +
+
-
G3 Xo(s) A +
H2
C
H2
G2
+
-
B G1
复习:
1.微分方程的拉氏算子解法; 2.系统的响应就是微分方程的解 总响应x(t) =零输入响应xZ(t)+零状态响应xs(t)
传递函数方块图及其等效变换

Xr(s) ±
W1(s)
W2(s)
仪表维修工
方块图
由图可得: 由图可得:
Xr(s) ±
E(s)
B(s)
X c ( s) = W1 ( s) E ( s ) E (s) = X r ( s) ± B( s) B( s ) = W2 ( s) X c( s)
W1(s)
W2(s)
Xc(s)
∴ X c ( s ) = W1 ( s )[ X r ( s ) ± 2 ( s ) X c ( s ) ] W W1 ( s ) X c (s) = X r ( s) 1 +W 1( s )W2 ( s )
Xi(s) A
W(s) X1(s)
B
X0(s)
1/W(s)
X2(s)
仪表维修工
方块图
②从输出端移动到输入端
当分支点在A点 当分支点在 点 处时, 处时,各分支的输 出分别为: 出分别为:
Xi(s)
W(s)
A
X0(s) X1(s)
X 0 ( s ) = X i ( s )W ( s ) X 1( s ) = X 0 ( s ) = X i ( s )W ( s )
仪表维修工
方块图
图中: 图中:指向方块单元的箭头表示 输入量的象函数X 离开方块单元 输入量的象函数 i(s),离开方块单元 的箭头表示输出量的象函数X 的箭头表示输出量的象函数 0(s),写 写 在方块单元中的是传递函数G(s)。 在方块单元中的是传递函数 。
注意:元件方块图具有单向性, 注意:元件方块图具有单向性,即输出对 输入没有反作用。 输入没有反作用。
仪表维修工
方块图
为了达到等效的目的, 为了达到等效的目的,则输出应 分别为: 分别为:
传递函数及方块图剖析

则G(s) = Uo s = RCS
(RC = T
K 1
Ui s RCS + 1
K = 1)
Gs k
4 积分环节
s
时间域方程
xo t k xi t dt
X o s
k
X i s
s
X o s X i s
k s
例9
i2(t)
i1(t) ui(t)
R
A
B
C
_
K0 +
uo(t)
ui (t) = -C duo (t)
传递函数及 典型环节的传递函数
一、传递函数定义:
在初始条件为零时,线性
定常系统输出象函数 Xo s与输 入象函数 Xi s 之比。
Gs
X o s Xi s
Xi s Gs Xo s
设线性定常系统的微分方程为:
a
0
xon
t
a1
x
n1
o
t
a
n1
x
o
t
a
n
x
o
t
b0
x
m
i
t
b1
x
m
i
1
t
bm 1
x i
t
则G(s) = Uo s =
1
Ui s RCS + 1
(RC = T)
例4
弹簧-阻尼系统
K
xi
t
xo
t
D
dxo
dt
t
KXi s KXo s DsXo s
Gs
Xo s Xi s
K Ds
K
D
1 s 1
K
Gs Ks
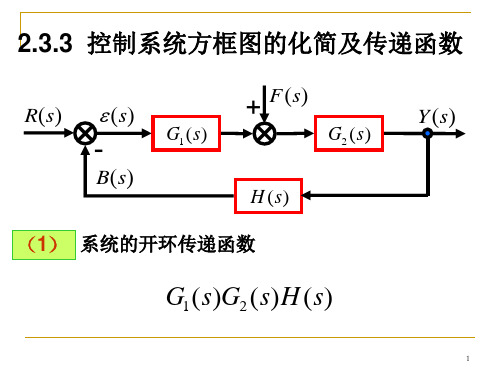
233控制系统方框图的化简及传递函数
U 2 ( s)
22
两个相加点互相交换移动
U1 ( s )
A
-
-
1 R1
1 sC1
1 R2C2 s 1
R1C2 s
U 2 ( s)
U1 ( s )
A
-
-
1 R1
1 sC1
1 R2C2 s 1
R1C2 s
U 2 ( s)
23
小回路化简
U1 ( s ) A
-
-
1 R1
1 sC1
1 R2C2 s 1
12
结论
下列闭环传递函数
(s)
F ( s)
(s)
F ( s )
具有相同的特征多项式
13
闭环特征多项式:
1 G1 (s)G2 (s) H (s)
14
G1 (s)G2 (s) (s) 1 G1 (s)G2 (s) H (s)
输出对输入 对 比
G2 (s) F ( s) 1 G1 (s)G2 (s) H (s)
R( s )
+
E ( s )
G1 ( s )
G2 (s)
Y ( s)
35
G3 ( s) G1 ( s)
R( s )
+
E ( s )
G1 ( s )
G2 (s)
Y ( s)
小回路化简
R( s )
G1 ( s) G3 ( s) G1 ( s)
G1 ( s)G2 ( s) 1 G1 ( s)G2 ( s)
1 G2 ( s)G3 ( s) 1 G1 ( s)G2 ( s)
E (s)
E ( s) 1 G2 (s)G3 (s) R(s) 1 G1 (s)G2 (s)
机械工程控制基础-第二章-传递函数

华中科技大学材料学院
典型环节
比例环节 惯性环节 微分环节 积分环节 振荡环节 延时节例
华中科技大学材料学院
比例环节
1、传递函数函:G(s) K (放大环节)
2、特性:输入输出成正比,无惯性,不失真, 无延迟 X(s) Y(s) K 3、参数:K 4、单位阶跃响应:输出按比值复现输入, 无过渡过程。
华中科技大学材料学院
4)方框图不唯一。由于研究角度不一样,传递函数 列写出来就不一样,方框图也就不一样。 5) 研究方便。对于一个复杂的系统可以画出它的方 框图,通过方框图简化,不难求得系统的输入、输出 关系,在此基础上,无论是研究整个系统的性能,还 是评价每一个环节的作用都是很方便的。
华中科技大学材料学院
n 2
2
p1 p2 n , p1 p2 2n 2 1
n e p t e p t y (t ) 1 ( ) 2 p1 p2 2 1
1 2
华中科技大学材料学院
p1 p2 ,当 1时, p1 p2
则
n e p t y (t ) 1 2 2 1 p2
华中科技大学材料学院
延迟环节
1. 传函
W ( s) e
s
x
y
1
t
1
(t ) 2.单位阶跃响应 y(t ) L1[es 1 s ] 1 3.参数 延迟时间 4.特性:能充分复现输入,只是相差 ,该环节
t
是线性的,他对系统稳定性不利。然而过程控制中,
系统多数都存在延迟环节,常用带延迟环节的一阶
x(t )
1
y(t )
K
t
t
比例环节实例
1)分压器
# 23传递函数方块图(系统动态结构图)及其等效变换

– F4(s)
1 F3(s) 1 Xo(s) X o (s) F3 ( s) — K2 K2
sf F4 ( s) sX o ( s) f F3 ( s) k2
F3(s)
S2f/k2 Sf/k2
F4(s)
Xi(s)
–
Sf2 F4(s) —— K2 – F1(s) F2(s) F(s) Sf1 1 Xo(s) —— — K1 K1 F3(s) K2 +
例一、直流电动机动态结构图的绘制 解: U ( s ) R i La dia E a a a b
dt
M m Cmia d m dm J f Mm ML 2 dt dt
2
dm Eb K b dt
求拉氏变换并用元件方块图表示出信号间的 关系得:
U a ( s) Ra I a ( s) La SIa ( s) Eb ( s) U a ( s) Eb ( s) I a ( s) Ra La S
U a K AU S dia U a Ra ia La Eb dt M m Cm ia
d 2m dm J f Mm ML 2 dt dt 1 c m i dm Eb K b dt
求它们的拉氏变换并用方块图表示得:
e (s) r (s) c (s)
U2(s)
–
1 I2(s) — R E0(s)
3
1 E0 ( s ) I 2 ( s ) CS
I2(s)
E0(s) 1 — CS
# 2—5 传递函数方块图(系统动态结构图) 及其等效变换 最后的方块图为: I2(s) Ei(s)
– U2(s)
1 — R1
I(s)
机械控制工程传递函数与方框图

则其传递函数为
G(s) Y (s) b0sm b1sm1 bm X (s) a0sn a1sn1 an
• 系统的传递函数是一种数学模型 • 传递函数适用于线性定常系统 • 传递函数是系统本身的一种属性 • 若传递函数已知,就可以针对不同输入,
研究系统的响应或输出
Y(s) G(s)X (s)
第 3 节 传递函数与方块图
1.传递函数 2.典型环节传递函数 3.方块图及其化简 4.系统方块图绘制
1. 传递函数
定义: 在全部初始条件为零的假设下,系
统输出量的拉氏变换与输入量的拉氏变 换之比
G(s) Y(s) X (s)
若系统由下列微分方程描述
(n)
( n 1)
(m)
( m 1)
a0 y a1 y an y b0 x b1 x bm x
•
11、一个好的教师,是一个懂得心理 学和教 育学的 人。21. 7.1410:33:1010 :33Jul- 2114-Ju l-21
•
12、要记住,你不仅是教课的教师, 也是学 生的教 育者, 生活的 导师和 道德的 引路人 。10:33:1010:3 3:1010:33Wed nesday , July 14, 2021
•
17、儿童是中心,教育的措施便围绕 他们而 组织起 来。上 午10时3 3分10 秒上午1 0时33 分10:33:1021.7. 14
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒,而是机会之杯。二〇二一年六月十七日2021年6月17日星期四
系统传递函数方框图及其简化

X1 X2
X1 X 2 X 3
分支点 系统方框图的建立步骤
同一信号向不同方向传递
建立系统各元部件的微分方程,明确信号的因果关系(输入/ 输出)。 对上述微分方程进行拉氏变换,绘制各部件的方框图。 按照信号在系统中的传递、变换过程,依次将各部件的方框 图连接起来,得到系统的方框图。
2
示例 无源RC网络
4
传递函数的等效 变化
1.串联传递函数等于各相串传函之积。
Xi(s) X(s)
G1(S)
G2(S)
X o(s)
X i(s)
G1(S) G2(S)
n
X o(s)
X ( s ) X o ( s ) X ( s ) G (s)G (s) G (s) o 2 1 X i (s) X (s) X i (s)
X1 +
+ (-)
G ( s)
1 G (s)
X3
X2
前移:从G(s)的输出端移到输入端;
后移:从G(s)的输入端移到输出端。
注意:分支 点和相加点 之间不能相 互移动。
9
例:求下图所示系统的传递函数。
H2(s) Xi(s)
+
B
G1(s)
H1(s)
G2(s)
G3(s)
A Xo(s)
H3(s)
X o (s)[1 G(s)H (s)] H (s) X i (s)
X o ( s) G( s) G( s) GB ( s) X i (s) 1 G ( s ) H ( s ) 1 Gk ( s )
7
讨论: 单位反馈:H(s)=1
Xi(s) + -
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.3.2 闭环控制系统的方块图
(4)误差传递函数 假设N(s)=0 误差信号E(s)与输入信号Xi(s)之比 。
X 0 (s) E(s)G(s) 代入上式,消去G(s)即得:
E ( s) 1 1 X i ( s) 1 H ( s)G( s) 1 开环传递函数
2.3.2 闭环控制系统的方块图
G2 ( s) G( s) X 0 ( s) X i ( s) N ( s) 1 G( s) H ( s) 1 G( s) H ( s)
G2 ( s) H ( s) 1 E (s) X i (s) N (s) 1 G( s) H (s) 1 G(s) H (s)
注意:由于N(s)极性的随机性,因而在路传递函数 假设N(s)=0
主反馈信号B(s) 与输出信号X0(s) 之比。 B( s) H ( s ) 当H(s)=1时,系统叫单位反馈系统。 X 0 (s)
(3)闭环系统的开环传递函数 假设N(s)=0 假设反馈通路断开,反馈信号B(s)与误差信号E(s) 之比。 B( s ) G1 ( s)G2 ( s) H ( s) G ( s) H ( s) E ( s)
反馈公式 G1G5 G1G6 1 G5 H 2 G1G5 G7 1 GHG 1 G5 H 2 G1 H 1G2 1 G1G6 H 1G2 1 1 1 2 G5 1 G5 H 2
R
i
(1) (2)
ui
i
C (a)
uo
(b)
U o ( s)
U i (s) - U o ( s)
I(s)
U o ( s)
I(s) (c)
U o ( s)
(d)
例:画出下列R-C网络的方块图
U r ( s ) U C1 ( s ) (1) I1 ( s ) R1 U ( s ) I1 ( s ) I 2 ( s ) ( 2) C1 sC1 U C1 ( s ) U c ( s ) I 2 (s) (3) R2 I 2 (s) ( 4) U c ( s ) sC 2
函数方块 函数方块 I( s)
Ui(s)
比较点U(s)
1 R
1 Cs
引出线 Uo(s)
方块图示例
2.3.2 闭环控制系统的方块图
闭环控制系统方块图
(1)前向通路传递函数--假设N(s)=0 打开反馈后,输出X0(s)与Xi(s)之比。等价于X0(s) 与误差E(s)之比 X 0 ( s) G1 ( s)G2 ( s) G( s) E ( s)
X i(s)
X o(s)
G( s ) 1 G( s) H ( s )
(b)
图2-24 环节的反馈连接
2.3.4 方块图的简化-等效变换 (3)反馈连接
X i(s)
G( s ) 1 G( s) H ( s )
X o(s)
(b)
负反馈时
X o ( s) G( s) X i ( s) 1 G( s) H ( s)
2.3.2 闭环控制系统的方块图
(4)闭环传递函数 假设N(s)=0 反馈通路接通时, 输出信号X0(s)与输 入信号Xi(s)之比。
**
X 0 (s) G1 (s)G2 (s) G( s) X i (s) 1 H (s)G(s) 1 H (s)G(s)
即 X ( s) 0
G( s) 前向通路传递函数 X i (s) 1 H (s)G( s) 1 开环传递函数
E ( s) G2 ( s) H ( s) G2 ( S ) H ( S ) M NE ( s) N ( s) 1 G1 ( s)G2 ( S ) H ( s) 1 G( S ) H ( S )
可得:
图2-29 误差对扰动的结构图
2.3.2 闭环控制系统的方块图
线性系统满足叠加原理,当控制输入Xi(s)与扰动N(s) 同时作用于系统时,系统的输出及误差可表示为:
G(s) R(s)
C(s) R(s)
C (s) R(s)G(s)
缩小放大
1 R( s) R( s)G( s) R( s ) G( s) 放大缩小
图2-27 分支点移动示意图
例2-10 用方块图的等效法则,求图2-30所示系统的传递函 数C(s)/R(s)。 解:这是一个具有交叉反馈的多回路系统,如果不对它作适当 的变换,就难以应用串联、并联和反馈连接的等效变换公式进 行化简。本题的求解方法是把图中的点A先前移至B点,化简 后,再后移至C点,然后从内环到外环逐步化简,其简化过程 如下图。
1 R2
④
-
A
1 sC 2
U c ( s)
U c ( s)
(c)方块图
2.3.3系统方块图的绘制
绘制方块图的步骤:
1、列出描述系统各个环节的微分方程式,要分清元件 的输入量、输出量; 2、假定初始条件为零,对方程式进行拉氏变换; 3、分别画出各环节的方块图; 4、按信号在系统中传递、变换的过程,依次将各环节的方 块图连接起来,系统输入量置于左端,输出量置于右端,组 成完整的系统方块图。
(5)输出对扰动的传递函数 假设Xi(s)=0
从上面的方框图可得:
图2-28 输出对扰动的结构图
X 0 ( s) G2 (s) G2 (s) GN (s) N (s) 1 G1 (s)G2 (s) H (s) 1 G( s) H ( S )
2.3.2 闭环控制系统的方块图
(7)误差对扰动的传递函数 假设Xi(s)=0
不能认为利用N(s)产生的误差可抵消Xi(s)产生的 误差。
2.3.3系统方块图的绘制
画出下列RC电路的方块图。 解:由图,利用基尔霍夫电压定律及电容元件特性可得:
ui u o U i ( s) U o ( s) i I ( s) 对其进行拉氏变换得: R R I ( s) idt U o ( s) u sC o c U ( s) I(s)
2.3 传递函数的方块图表示及运算
控制系统的方块图是系统各元件特性、系统结构和信号 流向的图解表示法。它清楚地表明系统中各个环节间地相互 关系,便于对系统进行分析和研究。
2.3.1 方块图组成
(1)方块:表示该环节的输入信号按照方框中的传递函数关 系变换成输出信号,具有单向性,即输出对输入无反作用。
X i ( s) G(s) X o ( s)
信号线
方块
信号线:带有箭头的直线,箭头 表示信号的传递方向,在直线旁 标记信号的时间函数或象函数。
图2-20 方块图中的方块
2.3.1 方块图组成
(2)比较点(合成点、综合点)
两个或两个以上的输入信号进行加减比较的元件。 “+”表示相加,“-”表示相减。“+”号可省略不 写。 注意:进行相加减的量,必须具有相同的量纲。
(4)比较点和分支点(引出点)的移动
有关移动中,“前”、“后”的定义:按信号 流向定义,也即信号从“前面”流向“后面”,而 不是位置上的前后。
2.4.4 方块图的简化-等效变换
C ( s) R( s)G ( s) Q( s) Q( s ) [ R( s) ]G ( s) G( s)
C (s) [ R(s) Q(s)]G(s) R(s)G(s) Q(s)G(s)
放大缩小 缩小放大 图2-25 比较点移动示意图
2.4.4 方块图的简化-等效变换
R(s) G(s) C(s) C(s)
分支点(引出点)前移
R(s)
G(s)
分支点(引出点)后移
R(s)
R(s) G(s) G(s) C(s) C(s)
(1)串联连接
X 1 ( s ) G1 ( s) R( s ) X 2 ( s ) G2 ( s ) X 1 ( s ) G2 ( s )G1 ( s ) R ( s ) C ( s ) G3 ( s ) X 2 ( s ) G3 ( s )G2 ( s )G1 ( s ) R ( s )
图2-30
G5 G2 G3 G4
R(s)
G7
串联和并联
G5
G6
G1
C(s)
-
H1G2
H2
1 G5
G5 G6 1 G5 H 2
G7 G1G5 G1 (G2 G3 G4 ) C ( s) G( s) R( s ) 1 G7 1 G5 H 2 G1 H1G2 G1G5 1 (G2 G3 G4 )(G1 H 2 ) G1 H1G2
2.3.4 方块图的简化-等效变换 (1)串联连接 特点:方框与方框首尾相连,前一方框的输出就是 后一方框的输入,前后方框之间无任何负载 效应。
R (s)
G1 (s)
X 1 ( s)
G2 (s)
X 2 ( s)
C ( s)
R(s)
G(s) (b)
C ( s)
G3 (s)
(a)
图2-23 环节的串联连接
表示信号测量或引出的位置和传递方向 P(s) P(s) P(s) P(s) P(s) P(s)
R(s)
G1 (s)
P(s)
引出线
C(s)
G2 (s) P(s)
注意:同一位置引出 的信号, 大小和性质 完全一样。
图2-21 分支点示意图
2.3.1 方块图组成 任何系统都可以由信号线、函数方块、信号引 出点及比较点组成的方块图来表示。
C ( s) G1 ( s)G2 ( s)G3 ( s) G(s) R ( s)
推广:任意个传递函数的串联。
G(s) Gi (s)
