试求图示有源网络的传递函数和Bode图.docx
2.2 传递函数

3、典型环节的形式
G (s) K
( s 1) (T s 1)
j 1 j i 1 n i
m
上式中 τi──分子各因子的时间常数 ; Tj──分母各因子的时间常数 ;
K ──时间常数形式传递函数的增益;通常称为传递系数。
五、传递函数的求取
1、解析法
建立微分方程,根据微分方程按定义求取
介绍一种方法:复阻抗法
i
U R
du iC dt
i
1 udt L
U (s) I (s) R
U (s) I (s) Z (s)
I ( s) CsU ( s) U ( s )
1 Cs
1 Cs
I (s)
U (s) Ls
R
Ls
1 , Ls 分别成为电阻、电容和电感的复阻抗 把 R, Cs
传递函数是经典控制理论中最重要的数学模型之 一。利用传递函数,在系统的分析和综合中可解决如 下问题:
不必求解微分方程就可以研究初始条件为零的系统在输 入信号作用下的动态过程。 可以研究系统参数变化或结构变化对系统动态过程的影 响,因而使分析系统的问题大为简化。 可以把对系统性能的要求转化为对系统传递函数的要求, 使综合问题易于实现。
11/17/2013 8:53:46 PM
3
一、定义
零初始条件下,线性定常系统输出量的拉氏变换 与输入量的拉氏变换之比,称为该系统的传递函数,
记为G(s),即:
L[ y (t )] Y ( s ) G( s) L[r (t )] R( s )
意义:
R( s )
G (s )
Y ( s)
Y (s) R(s)G(s)
1 1 Y ( s) G s) R s) ( ( Ts 1 s
自控控制原理习题 王建辉 第2章答案

2-1 什么是系统的数学模型?在自动控制系统中常见的数学模型形式有哪些? 用来描述系统因果关系的数学表达式,称为系统的数学模型。
常见的数学模型形式有:微分方程、传递函数、状态方程、传递矩阵、结构框图和信号流图。
2-2 简要说明用解析法编写自动控制系统动态微分方程的步骤。
2-3 什么是小偏差线性化?这种方法能够解决哪类问题?在非线性曲线(方程)中的某一个工作点附近,取工作点的一阶导数,作为直线的斜率,来线性化非线性曲线的方法。
2-4 什么是传递函数?定义传递函数的前提条件是什么?为什么要附加这个条件?传递函数有哪些特点?传递函数:在零初始条件下,输出量的拉氏变换与输入量的拉氏变换之比。
定义传递函数的前提条件:当初始条件为零。
为什么要附加这个条件:在零初始条件下,传递函数与微分方程一致。
传递函数有哪些特点:1.传递函数是复变量S 的有理真分式,具有复变函数的所有性质;n m ≤且所有系数均为实数。
2.传递函数是一种有系统参数表示输出量与输入量之间关系的表达式,它只取决于系统或元件的结构和参数,而与输入量的形式无关,也不反映系统内部的任何信息。
3.传递函数与微分方程有相通性。
4.传递函数)(s W 的拉氏反变换是系统的单位脉冲响应。
2-5 列写出传递函数三种常用的表达形式。
并说明什么是系统的阶数、零点、极点和放大倍数。
nn n n mm m m a s a s a s a b s b s b s b s W ++++++++=----11101110)( ()()∏∏==++=nj jmi i s T s T K s W 1111)( 其中nma b K =()()∏∏==++=nj jm i i g p s z s K s W 11)( 其中0a b K g =传递函数分母S 的最高阶次即为系统的阶数,i z -为系统的零点,j p -为系统的极点。
K 为传递函数的放大倍数,g K 为传递函数的根轨迹放大倍数。
《控制工程基础》课程作业习题(含解答)
第一章概论本章要求学生了解控制系统的基本概念、研究对象及任务,了解系统的信息传递、反馈和反馈控制的概念及控制系统的分类,开环控制与闭环控制的区别;闭环控制系统的基本原理和组成环节。
学会将简单系统原理图抽象成职能方块图。
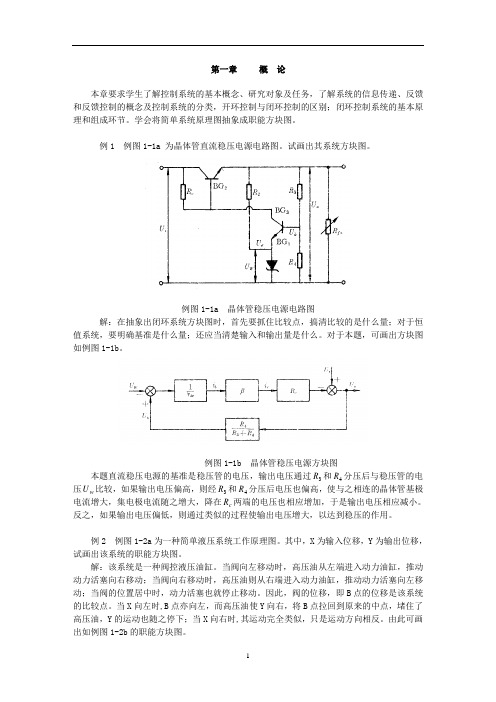
例1 例图1-1a 为晶体管直流稳压电源电路图。
试画出其系统方块图。
例图1-1a 晶体管稳压电源电路图解:在抽象出闭环系统方块图时,首先要抓住比较点,搞清比较的是什么量;对于恒值系统,要明确基准是什么量;还应当清楚输入和输出量是什么。
对于本题,可画出方块图如例图1-1b。
例图1-1b 晶体管稳压电源方块图本题直流稳压电源的基准是稳压管的电压,输出电压通过R和4R分压后与稳压管的电3压U比较,如果输出电压偏高,则经3R和4R分压后电压也偏高,使与之相连的晶体管基极w电流增大,集电极电流随之增大,降在R两端的电压也相应增加,于是输出电压相应减小。
c反之,如果输出电压偏低,则通过类似的过程使输出电压增大,以达到稳压的作用。
例2 例图1-2a为一种简单液压系统工作原理图。
其中,X为输入位移,Y为输出位移,试画出该系统的职能方块图。
解:该系统是一种阀控液压油缸。
当阀向左移动时,高压油从左端进入动力油缸,推动动力活塞向右移动;当阀向右移动时,高压油则从右端进入动力油缸,推动动力活塞向左移动;当阀的位置居中时,动力活塞也就停止移动。
因此,阀的位移,即B点的位移是该系统的比较点。
当X向左时,B点亦向左,而高压油使Y向右,将B点拉回到原来的中点,堵住了高压油,Y的运动也随之停下;当X向右时,其运动完全类似,只是运动方向相反。
由此可画出如例图1-2b的职能方块图。
例图1-2a 简单液压系统例图1-2b 职能方块图1.在给出的几种答案里,选择出正确的答案。
(1)以同等精度元件组成的开环系统和闭环系统,其精度比较为_______ (A )开环高; (B )闭环高; (C )相差不多; (D )一样高。
(2)系统的输出信号对控制作用的影响 (A )开环有; (B )闭环有; (C )都没有; (D )都有。
同济 自动控制原理 控制系统 答案 第二章例题
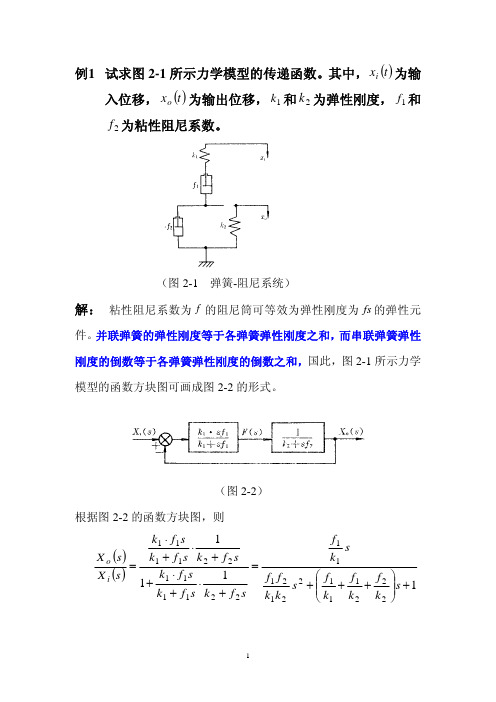
p1 = G1G2G3G4 G5 , Δ1 = 1
由梅逊公式可得:
G1G2 G3 G4 G5 C ( s) = R ( s ) 1 + G 2 H 2 + G 2 G 3 H 3 + G3 G 4 H 2 + G 4 G5 H 4 + G 2 G3 G 4 H 1 H 2 + G 2 G 4 G 5 H + + G 2 G3 G 4 G 5 H 3 H 4
4 3
k 2 (Bs + k1 ) M 1M 2 s + (M 1 + M 2 )Bs + (M 1k1 + M 1k 2 + M 2 k1 )s 2 + Bk 2 s + k1k 2
2)
Fs (s) k 2 M 1 M 2 s 2 + (M 1 + M 2 )Bs + (M 1 k1 + M 2 k1 ) s 2 = X i (s) M 1 M 2 s 4 + (M 1 + M 2 )Bs 3 + (M 1 k1 + M 1 k 2 + M 2 k1 )s 2 + Bk 2 s + k1 k 2
Gk ( s ) = G2 ( s ) +
G1 ( s )[(G2 ( s ) − 1)][(1 − G2 ( s )] 2G1 ( s )G2 ( s ) + G2 ( s ) − G1 ( s ) = 1 + G1 ( s )G2 ( s ) 1 + G1 ( s )G2 ( s )
因而,闭环传递函数
例7
图 2-11 为汽车在凹凸不平路上行驶时承载系统的简化力学模 型,路面不平度 xi (t ) 为激励源,由此造成汽车的垂向运动和轮 胎受力,画出框图,试求: 1)xi (t ) 作为输入,汽车质量垂直位移 x0 (t ) 作为输出的传递函数; 2) xi (t ) 作为输入,轮胎垂直受力 f s (t ) 作为输出的传递函数。
自控试题练习题集
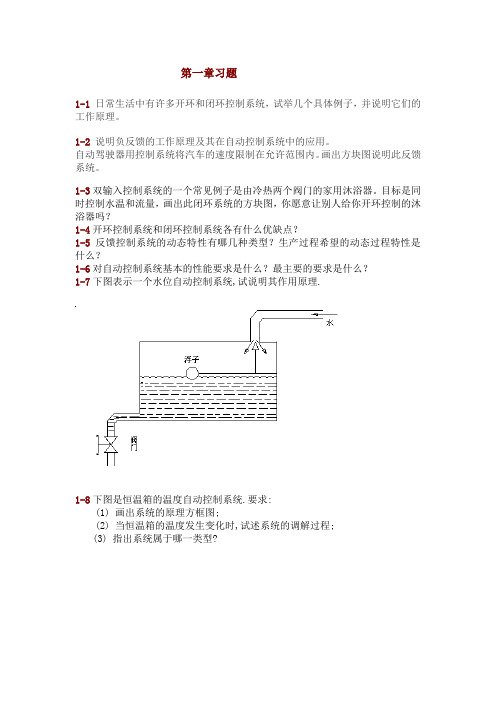
第一章习题1-1日常生活中有许多开环和闭环控制系统,试举几个具体例子,并说明它们的工作原理。
1-2说明负反馈的工作原理及其在自动控制系统中的应用。
自动驾驶器用控制系统将汽车的速度限制在允许范围内。
画出方块图说明此反馈系统。
1-3双输入控制系统的一个常见例子是由冷热两个阀门的家用沐浴器。
目标是同时控制水温和流量,画出此闭环系统的方块图,你愿意让别人给你开环控制的沐浴器吗?1-4开环控制系统和闭环控制系统各有什么优缺点?1-5反馈控制系统的动态特性有哪几种类型?生产过程希望的动态过程特性是什么?1-6对自动控制系统基本的性能要求是什么?最主要的要求是什么?1-7下图表示一个水位自动控制系统,试说明其作用原理.1-8下图是恒温箱的温度自动控制系统.要求:(1) 画出系统的原理方框图;(2) 当恒温箱的温度发生变化时,试述系统的调解过程;(3) 指出系统属于哪一类型?1-9 下图为位置随动系统,输入量为转角r θ,输出量为转角c θ,p R 为圆盘式滑动电位器,s K 为功率放大器SM 为伺服电动机.要求: (1)说明系统由哪几部分组成,各起什么作用? (2)画出系统原理方框图;(3)说明当r θ 变化时, c θ的跟随过程.1-10 位置随动系统如下图所示,回答以下问题 1.说明该系统的以下(1)-(10)各是什么:(1)被控制对象 (2)被控制量 (3)给定元件 (4)给定量 (5)主反馈元件 (6)主反馈量 (7)误差量 (8)负载 (9)积分元件 (10)执行元件. 2.画出系统作用方框图,表出个环节的输入输出量。
3.判断(在括号内对的上面打"对号")(1)该系统是(按偏差;按扰动)原则的控制系统; (2)该系统是(有差;无差)系统; (3)该系统是(0型,1型,2型)系统; (4)该系统的输入量是(rr U Q 、);(5)该系统的输出量是(c c U Q 、)。
1-11下图为温度自动控制系统,改变a 点位置可以改变恒温温度.试说明该系统的工作原理和性能,并指出它属何种类型?1-12如题图(a )、(b )所示两水位控制系统,要求∙ 画出方块图(包括给定输入量和扰动输入量); ∙ 分析工作原理,讨论误差和扰动的关系。
自动操纵历年考试题

试卷一一、填空题(每空1分,共15分)自动操纵是在___________情形下,利用___________使___________的被控量自动地按预先给定的规律去运动。
对操纵系统的大体要求是___________、___________和___________。
线性定常系统的传递函数概念为:初始条件___________时,系统___________拉式变换与系统___________拉式变换之比。
在频率域中表征系统稳固程度的指标是:___________和___________。
假设环节的传递函数为s K,那么其对数幅频特性L ()在零分贝点处的频率数值为______________。
Bode 图中对数相频特性图上的-180o 线对应于奈奎斯特图中的___________。
标志着系统最终可能达到的操纵精度,它既与系统的结构及参数有关,也取决于___________的形式及大小。
二、简答题(此题15分,其中第1小题10分,第2小题5分) 试求出以下图无源网络的传递函数)(/)(s U s U r c已知系统的闭环特点方程为0)3)(2)(1(=++++k s s s 试确信系统稳固时K 的取值范围 三、计算题(此题40分,其中第一、3小题15分,第2小题10分) 已知系统的结构图如以下图所示。
假设)(1)(t t r =时,试求 (1)当0=f K 时,求系统超调量%σ及调剂时刻s t。
(2)当0≠f K 时,假设要使超调量%σ=20%,试求f K 应为多大?并求出此刻的调剂时刻s t 的值。
(3)比较上述两种情形,说明内反馈s K f 的作用是什么?R (s )C (s )-2K sN(s )1K系统结构图如以下图所示。
当输入信号)(1)(t t r =,干扰信号)(1)(t t n =时,求系统总的稳态误差系统结构图假设以下图所示,求传递函数)(/)(s R s C ,)(/)(s R s E四、图解题(此题30分,其中第1小题20分,第2小题10分) 已知某最小相位系统开环对数幅频特性如下图。
自动控制原理 第3章习题解答
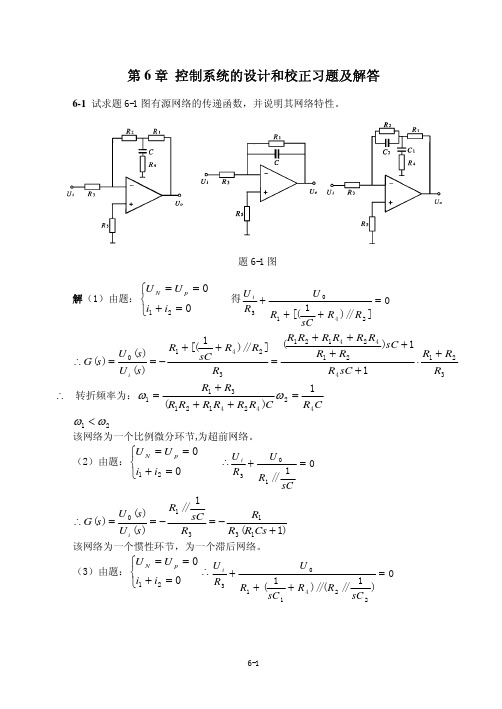
系统的 Bode 图为图 6-2-1(b)。
图 6-2-1(b)
6-2
2( s + 1) 时,则校正后系统的开环传递函数为: (10 s + 1) 10 2( s + 1) 20( s + 1) G" ( s ) = G ( s )Gc ( s ) = ⋅ = s (0.2s + 1) (10 s + 1) s (0.2 s + 1)(10 s + 1) ∴ 系统的 Bode 图为图 6-2-2。
ϕ c = ±(2k + 1)π − ∠G0 ( s1 ) = −180° − [−∠s1 − ∠( s1 + 1)] = 72.6° (4)由校正后系统的幅值条件,求校正装置的零极点位置及参数 α 和 T
由 K v = lim sG0 ( s ) = lim
s →0 s →0
K = K = 2即K = 2 s +1
该网络为一个比例微分环节,为超前网络。 (2)由题:
U N = U p = 0 i1 + i2 = 0
R1 //
∴U i + U 0 =0 1 R3 R1 // sC
∴ G ( s) =
U 0 ( s) =− U i ( s)
R3
1 sC = −
R1 R3 ( R1Cs + 1)
U0 1 1 R1 + ( + R 4 ) //( R 2 // ) sC 1 sC 2 =0
第 6 章 控制系统的设计和校正习题及解答
6-1 试求题 6-1 图有源网络的传递函数,并说明其网络特性。
题 6-1 图 解(1)由题:
U N = U p = 0 i1 + i2 = 0
典型环节传递函数及伯德图
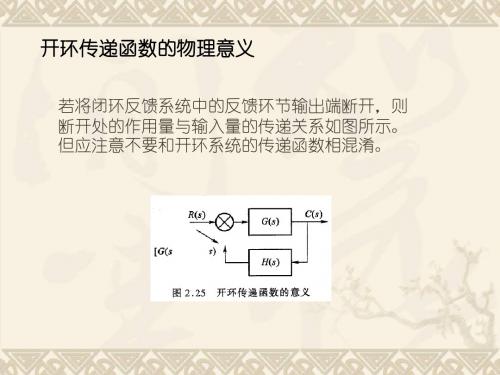
j
20
20dB / dec
0
0 0.01
0.1
1
10
( )()
0 0.01 -30 -60 -90
0.1
1
10
3. 理想微分环节
微分环节的特点:输出量与输入量的微分成正比例,即输出量与输入 量无关而与输入量的变化率正比例。 微分环节的微分方程:
微分环节的传递函数
3. 理想微分环节
1.比例环节(放大环节)
比例环节的特点:输出量与输入量之间的关系是一种固定 的比例关系,也就是输出量能无失真、无滞后地按一定比 例复现输入量。 比例环节的微分方程:
比例环节的传递函数:
比例环节的单位阶跃响应:
比例环阶的单位阶响应跃
1.比例环节(放大环节)
比例环节是自动控制系统中使用最多的一种,例如电子放大器、 齿轮减速器、杠杆、弹簧、电阻、质量等,如图所示。
说明 ω ω n
180 0.1
0.2
0.4
0.6 0.8
1
2
4
6
8
10
产生谐振峰值,阻尼比的大小决定了谐振峰值的幅值。
1 为二阶系统(振荡环节)的转折频率。 T
/ n
7. 二阶微分环节
二阶微分环节的传递函数是振荡环节的倒数。
特点:输出与输入及输入一阶、二阶导数都有关。
方块图为:
1 T
10 T
比例环节功能框图
1.比例环节(放大环节)
G( j ) K , L( ) 20lg G( j ) 20lg K G( s) K G( j ) K G( j ) K 0 ( ) G( j ) 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6-1试求图示有源网络的传递甫数和Bode 图,并说明其网络特性。
6-2已知单位反馈控制系统的开环传递函数为
G(f)二 10
5(0.25 +1)
当串联校正装置的传递函数G c ($)如下所示时:
(1) G c (5)= 0.2s +1
0.05s +1 2($ +1) (10s+ 1)
1・试绘出两种校正时校正前和校正后系统Bode 图;
2.试比较两种校正方案的优缺点。
6-3已知单位反馈系统的对数幅频特性Illi 线如图屮厶)@),
串联校正装置G c (s)的对
数幅频特性如图中&9),要求: 1. 在图小画出系统校止后的对数幅频特性厶(e);
2. 写出校正后系统的开环传递函数;
3. 分析校止装置G c (5)对系统的作用。
6-4系统的结构图如图所示,试利用根轨迹法设计超前校止装置,使系统满足下列性 能指标:=0.7 , t s =1.45, K v = 。
6—5已知一单位反馈系统的开环传递函数为
习题6— 1图
试设计一•校正装置,使系统的相角裕量厂> 45° ,剪切频率0. > 50$ j 0
6-6单位反馈系统的开环传递函数为
设计一串联滞后校正装置,使系统相角裕量/ > 40° ,并保持原有的开环增益。
6-7设单位反馈系统的开环传递函数为
G(s)= --------------- ------------ 5(0.15 + 1)(0.255 + 1)
试设计--校正装置,使系统满足下列性能指标,速度误差系数K,, 相角裕量 / > 40° ,剪切频率 > 0.5s~} o
6-8单位反馈系统的开环传递函数为
若耍求校正后系统的谐振峰值=1.4,谐振频率> lor 1,试确定校正装置的形 式与参数。
6-9单位反馈系统的结构如图所示,现用速度反馈来校正系统,校正后系统具有临界 G(s) =
200
5(0.15 + 1) G() =
4 s(2s +1) G(s)=
10 5(0.255 +1)(0.055 +1)
习题6 —3图
阻尼比< 试确定校正装置参数K,。
6-10己知系统如图所示,要求闭环回路的阶跃响应无超调,并且系统跟踪斜坡信号时 无稳态误差,试确定K 值及前馈校正装置G c ($) o
6-11已知系统如图所示,试确定G lc Cs )和G2C ($)使系统输出量完全不受T •扰信号 呛)的影响,R 单位阶跃响应的超调量等于25%,峰值时间等于2$。
瓦中G (s ) = K, \G2C ^)\ GicW
习题6 — 11图
6-12如图所示,试采用串联校止和复合
控制两种方法,消除系统跟踪斜坡信号时的稳
态误差,分别计算出校正装置的传递函数。
6-13己知某系统的传递函数为
G 102)(*01)_
(? + 2s + 2)(52 + 0.025 + 0」001)
试采用超而校正和滞后校正,借用MATLAB 设计校正网络,使系统的单位阶跃响应的 调节吋间小于2s,超调量小于20%o
6-14系统的传递函数为
5 :金
144
3 号 $(0.1$+1) 1 ----------- Kts ----- C(s) Gc®
习题6-12图 习题6—9图
(s 、+ l)(0.5s + l)
为使系统阶跃响应的稳态误差为零,将校止装置G (.(s)选为Pl 控制器。
试采丿IJ MATLAB 设计G,$),使系统阶跃响应的超调量小于5%,调节时间小于6s,速度误差系数K,,大于0.9o 6-15系统的传递函数为
试用MATLAB 来设计合适的校止装置,使系统剪切频率©55(),相角裕度/>50% 6-16设单位负反馈系统的开环传递函数为
若要是系统的速度误差系数K v > 5s~l ,相角裕M/>40°,幅值裕量KClOdB 。
设 计滞后校正装置,并MATLAB 用来验证设计结果. G (5)= 100 $(s +1)(0.0125$+ 1)
G($) = K
$(s + l)(0.5$ + l)。
