理论力学教程
理论力学教程 (周衍柏)(第四版)
理论力学教程 (周衍柏)(第四版)介绍《理论力学教程》是中国科学技术大学教授周衍柏先生编写的理论力学教程的第四版。
本教程系统地介绍了力学的基本原理、定律和方法，旨在帮助读者深入理解和掌握理论力学的核心概念，培养分析和解决力学问题的能力。
目录1.力学的基本概念–力学的起源和发展–力学的基本假设–物体的受力分析2.动力学–一维运动学–牛顿定律–静力学–动力学定律的应用3.连续体力学–连续体的基本概念–物质点系和质点系的运动方程–连续体的动力学方程4.运动学的数学方法–坐标系和位置矢量–速度和加速度–运动学定理–曲线运动的描述5.动力学的数学方法–牛顿第二定律的矢量形式–动量和动量守恒定律–力矩和力矩定律–统一的动力学方法6.力学系统的理论–多体系统的动力学–质点系和刚体系的力学–力学系统的能量和能量守恒定律7.外力作用下的刚体运动–刚体的运动学–刚体受力和动力学–刚体运动的定理和方法–刚体系统动力学的能量和能量守恒定律8.振动–简谐振动–非简谐振动–耦合振动–振动的应用内容概述《理论力学教程》共分为八个章节，包含了力学的基本概念、动力学、连续体力学、运动学的数学方法、动力学的数学方法、力学系统的理论、外力作用下的刚体运动以及振动等内容。
在力学的基本概念部分，教程介绍了力学的起源和发展，以及力学的基本假设和物体的受力分析方法，为后续章节的学习奠定了基础。
动力学部分介绍了一维运动学、牛顿定律、静力学以及动力学定律的应用。
读者可以学习如何利用牛顿定律分析力学问题，并应用其定律解决实际问题。
连续体力学部分讲解了连续体的基本概念、物质点系和质点系的运动方程，以及连续体的动力学方程。
通过学习这一章节，读者可以了解连续体力学的基本理论和应用。
运动学的数学方法一章介绍了坐标系和位置矢量的概念，以及速度和加速度的定义与计算方法。
运动学定理和曲线运动的描述也是本章的重要内容。
动力学的数学方法部分将牛顿第二定律推广到矢量形式，详细介绍了动量和动量守恒定律以及力矩和力矩定律的应用。
理论力学教程周衍柏
理论力学教程周衍柏《理论力学教程》是由周衍柏编写的一本力学学科的教材。
该教程主要涵盖了力学的基本概念、原理和计算方法，适用于大学力学课程的教学和学习。
第一章介绍了力学的基本概念和研究对象。
力学研究物体在力的作用下的运动规律，分为静力学和动力学两部分。
静力学研究物体平衡的条件和平衡状态，动力学研究物体在力的作用下的运动规律和能量变化。
第二章详细介绍了质点的运动规律。
讨论了质点的位移、速度和加速度的定义和计算方法，以及质点在直线上的运动和曲线上的运动。
介绍了质点的直线运动中的均匀运动和变速运动，以及曲线运动中的圆周运动。
第三章讨论了刚体的运动规律。
刚体是指无论在受力作用下还是不受力作用下，各部分之间的相对位置和相互间的距离保持不变的物体。
详细介绍了刚体的平动和转动，以及刚体的匀速旋转和变速旋转。
第四章介绍了力的作用、合力和力矩的概念。
力是产生物体运动或形变的原因，合力是多个力合成后的结果，力矩是力对物体产生转动的效果。
讨论了力的叠加原理和解析法，以及力的平衡条件和平衡的判定方法。
第五章讨论了静力学力学系的平衡条件和平衡的判定方法。
静力学力学系指在静止时，物体所受到的各个力及其力矩之间的平衡关系。
介绍了力的杠杆原理和力的分解原理，以及力矩的计算方法和力的平衡条件。
第六章介绍了动力学力学系的平衡条件和平衡的判定方法。
动力学力学系指在运动时，物体所受到的各个力及其力矩之间的平衡关系。
讨论了动力学力学系中的杠杆原理和力的合成原理，以及动力学平衡条件的计算方法。
第七章讨论了万有引力和弹性力的性质和计算方法。
介绍了万有引力的概念和计算公式，以及弹性力的概念和弹性势能的计算方法。
讨论了物体在重力和弹性力作用下的平衡位置和平衡条件，以及重心和回复力的概念。
第八章介绍了刚体的平衡条件和平衡的判定方法。
讨论了刚体在力和力矩作用下的平衡关系，以及刚体平衡条件和刚体静力学平衡的判定方法。
详细介绍了刚体平衡的三个条件和平衡关系的计算方法。
理论力学教程(第一章)
约束结构：两个物体2、3上钻同样大小 的圆孔，并用圆柱销钉1 穿入圆孔，将 两个物体连接起来。（轴向与径向）
约束特性：物体只能绕销钉轴线相对转动， 但不能在与销钉轴线相垂直的方向上有任 何相对位移。
约束力：在垂直于销钉轴线的平面内并 通过圆心，但方位和指向不能确定。通 常将其表示为大小未知的两个正交分力，
若刚体受三个力作用而处于平衡，且其中二力作用线 相交于一点，则这三个力必位于同一平面内，且它们的 作用线必定汇交于一点。
公理4 作用与反作用定律
两物体间的相互作用力，大小相等，方向相反，作 用线沿同一直线。
F = -F'
·此公理概括了物体间相互作用的关系，表明作用力与 反作用力成对出现，并分别作用在不同的物体上。
材料力学
高等数学 大学物理
理论力学
结构力学 水力学
机械原理
其他专业课程
学习理论力学的目的
理论力学是现代工程技术的重要基础理论之一 理论力学研究力学的最基本规律，是学习一系列后续课
程的重要基础 有助于我们树立辩证唯物主义的世界观，提高分析问题
和解决问题的能力
理论力学的学习方法
学习理论力学必须反复地理解它的基本概念和公理或定律,以及由 这些定理和结论引出的基本方法。 掌握抽象化的方法，理论联系实际，要逐步培养把具体实际问题 抽象成为力学模型的能力 独立做大量的习题和思考题。
例1-1
碾子重为 P，拉力为F ，A, B处光 滑接触，画出碾子的受力图。
解：画出简图
画出主动力 画出约束力
C
例1-2 受AB杆力分析
D
A
B
FAx FAx A
FB
D
B
A
FA
p
理论力学自学全部教程
(yFz zFy )i ( zFx xFz ) j ( xFy yFx )k
M Ox ( F ) = yFz zFy M Oy ( F ) = zFx xFz M Oz ( F ) = xFy yFx
1.1.3 力对轴的矩
力对轴的矩(moment of a force about an axis) 用来量度力对其所作 用的刚体绕某固定轴 转动的效应。
已知力F在各坐标轴上的投影，则可求得力F的大 小和它相对于各轴的方向余弦，即
cos( F , i ) Fx / F cos( F , j ) Fy / F cos( F , k ) Fz / F
1.1.2 力对点的矩
力矩(moment of a force)是用来量度力使物体 产生转动效应的概念。 ● 力对点的矩的概念 作用于刚体的力 F 对空间任意一点 O 的力矩 定义为
k
Fxy
y
O
h
rxy
x
力矩的单位在国际单位制(SI)中为牛顿· 米 (N· m)或千牛顿· 米(kN· m)。
● 力对点的矩在坐标轴上的投影
z MO(F) k r
F
i
x
O
j
y
F Fx i Fy j Fz k
r xi yj zk
i
j y Fy
k z Fz
MO (F ) r F x Fx
z
z
M z (F) > 0
M z (F) < 0
• 当力的作用线与 z 轴平行 (Fxy = 0) 或相交 (h=0) 时，或概括起来讲，当力与轴共面时， 力对轴的矩等于零。
力对轴之矩 M z (F ) = MO (Fxy ) = (rxy Fxy ) k
理论力学完整讲义
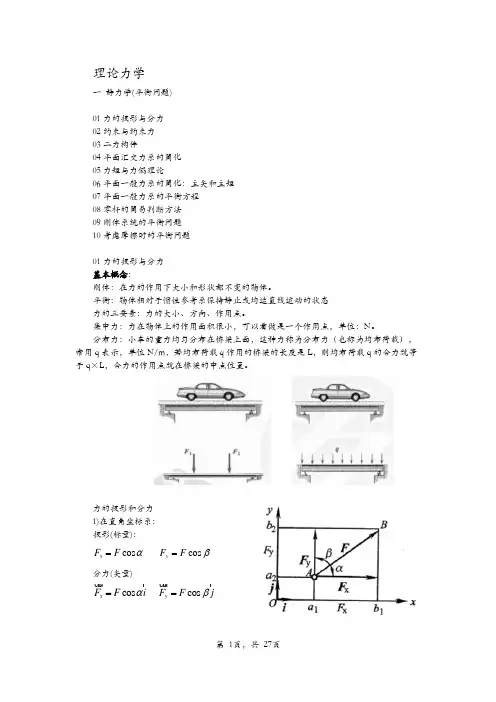
理论力学一 静力学(平衡问题)01力的投影与分力 02约束与约束力 03二力构件04平面汇交力系的简化 05力矩与力偶理论06平面一般力系的简化：主矢和主矩 07平面一般力系的平衡方程 08零杆的简易判断方法 09刚体系统的平衡问题 10考虑摩擦时的平衡问题01力的投影与分力 基本概念：刚体：在力的作用下大小和形状都不变的物体。
平衡：物体相对于惯性参考系保持静止或均速直线运动的状态 力的三要素：力的大小、方向、作用点。
集中力：力在物体上的作用面积很小，可以看做是一个作用点，单位：N 。
分布力：小车的重力均匀分布在桥梁上面，这种力称为分布力（也称为均布荷载），常用q 表示，单位N/m ，若均布荷载q 作用的桥梁的长度是L ，则均布荷载q 的合力就等于q ×L ，合力的作用点就在桥梁的中点位置。
力的投影和分力 1)在直角坐标系： 投影(标量)：cos x F F α= cos y F F β=分力(矢量)cos x F F i α=u u r r cos y F F j β=u u r r2)在斜坐标系： 投影(标量)：cos x F F α= cos()y F F ϕα=-分力(矢量)(cos sin cot )x F F F i ααϕ=-u u r rsin sin y F F j αβ=u u r r02约束与约束力约束：对于研究对象起限制作用的其他物体。
约束力方向：总是与约束所能阻止物体运动的方向相反，作用在物体和约束的接触点处。
约束力大小：通常未知，需要根据平衡条件和主动力求解。
(1)柔索约束：柔索约束：由绳索、皮带、链条等各种柔性物体所形成的约束，称为柔索约束。
特点：只能承受拉力，不能承受压力。
约束力：作用点位接触点，作用线沿拉直方向，背向约束物体。
(2)光滑面约束光滑面约束：由光滑面所形成的约束称为光滑面约束。
约束性质：只能限制物体沿接触面公法线趋向接触面的位移。
特点：只能受压不能受拉，约束力F 沿接触面公法线指向物体。
理论力学自学全部教程
○集中力—集中作用于物体上一点的力.
中新口腔
分 布 力
中新口腔
F1
F2
集 中 力
中新口腔
实际上要经一个几何点来传递作用力是不可能 的，集中力只是作用于一个小区域上的分布力， 一切真实力都是分布力。
P
A
B
C
集中力只是分布力在一定条件下的理想化模 型。能否进行这种简化主要取决于我们所研究的 问题的性质。
h
Plane determined by O and F
MO (F)通常被看作为一个定位矢量，习惯 上总是将它的起点画在矩心O处，但这并不 意味着O就是MO (F)的作用点。
中新口腔
力矩矢的三要素
力矩矢的三要素为大小、方向和矩心。 MO (F)的大小即它的模
MO(F) = r F Frsin Fh
O●
h r
MO(F) Fh
F 中新口腔
O●
h
MO(F) = ± Fh
F
正负号通常规定为:
+
逆时针为正
–
顺时针为负
中新口腔
平面问题 —矢量表达式
z
MO(Fxy)=(rxy× Fxy) ·k
k
Fxy
y
O
h
rxy
x
中新口腔
力矩的单位在国际单位制(SI)中为牛顿·米 (N·m)或千牛顿·米(kN·m)。
中新口腔
吊车梁的变形
δ
• 吊车梁在起吊重 物时所产生的最 大挠度 δ 一般不 超过梁的跨度的 1/500
中新口腔
这种小变形对于两端支承力的影响是微不足 道的，因此在计算两端的支承力时，吊车梁可 简化为刚体。
但在研究吊车梁的强度问题时，就不能这 样简化了。
理论力学教程知识点总结
理论力学教程知识点总结一、基本概念1.1 质点：质点是理论力学研究的对象之一，它是一个没有体积的点，只有质量和位置。
在质点运动的研究中，忽略了质点的大小和形状，只关心质点的位置和速度。
1.2 力：力是导致物体产生运动、变形或改变物体的运动状态的原因。
在理论力学中，力是一个基本概念，是对物体产生影响的原因。
根据牛顿第二定律，力是导致物体加速度改变的原因，与物体质量和加速度成正比。
1.3 运动：运动是物体在空间中位置随时间变化的过程。
物体的运动可以是直线运动、曲线运动或者是平面运动等。
在理论力学中，研究物体的运动规律和运动状态的改变。
1.4 动力学：动力学是研究物体运动规律的科学，包括物体的运动状态、位置、速度、加速度等方面的研究。
动力学是理论力学的核心内容之一，是理解物体运动规律和力的作用关系的基础。
1.5 动力学方程：动力学方程是描述物体运动规律的方程，根据牛顿第二定律，动力学方程描述了物体的运动状态和受到的力之间的关系。
动力学方程包括牛顿第二定律 F=ma，它表示物体受到的外力等于质量与加速度的乘积。
二、运动方程2.1 牛顿第一定律：牛顿第一定律也称为惯性定律，它指出物体在不受外力作用时，会保持静止或匀速直线运动的状态。
牛顿第一定律是动力学方程的基础，它表明物体的运动状态需要受到外力的作用才会发生改变。
2.2 牛顿第二定律：牛顿第二定律是理论力学的基本定律之一，它描述了物体受到外力作用时的运动规律。
根据这个定律，物体受到的外力等于质量与加速度的乘积，即F=ma。
物体的质量越大，相同的力引起的加速度越小；物体的质量越小，相同的力引起的加速度越大。
2.3 牛顿第三定律：牛顿第三定律也称为作用与反作用定律，它指出作用在物体上的力总有一个与之相等的反作用力。
即使两个物体之间产生相互作用的力，这两个力的大小相等，方向相反。
牛顿第三定律描述了物体之间力的作用关系，是理论力学中一个重要的定律。
2.4 弹簧力：弹簧力是一种常见的力，当物体受到弹簧的拉伸或压缩时，会产生弹簧力。
理论力学教程周衍柏第三版课件_图文
9
§0.4 力学单位制
• 物理理论组成：概念、概念的数学表示假定、方程组（物理 量的关系） 单位制通过以
[P]
X X a1 a2 12
X
am m
上式取对数
ln[P] a1lnX1 a 2lnX2 amlnXm
把lnX1, lnX2, …,lnXm看做m维空间的“正交基矢”，则 （a1,a2,…,am）相当于“矢量”ln[P]在基矢上的投影.
22
定理
设某物理问题内涉及n个物理量(包括物理常量) P1, P2 ,, Pn, 而我们所选的单位制中有m个基本量(n>m),则由此可以组成n-m
• 在力学中CGS和MKS单位制的基本量是长度、质量和 来自间, 它们的量纲分别为L、M和T.
• 任何力学量Q的量纲为[Q]=LαMβTγ，式中, ,
为量纲指数.
21
量纲分析—— 定理
设我们在选定单位制中的基本量数目为m，它们的量纲 为X1，X2，…，Xm. 用[P]代表导出量P的量纲,则
由A=A1+A2得
c2Φ() a2Φ() b2Φ()
消去(),即得 c2 a2 b2
a
c
b
这样我们就利用量纲分析定量的得到了勾股定理.
27
§0.6 微积分预备知识
1 常见函数的导数
y xn
y' dy dxn nx n1 dx dx
y sin x
理论力学教程(第四章)
静滑动摩擦力的特点
1 方向：沿接触处的公切线，
与相对滑动趋势反向；
2 大小：
3
（库仑摩擦定律）
④静摩擦系数的测定方法(倾斜法)
两种材料做成物体
和可动平面测沿下面滑
动时的 。
p
F=mgsin =fmgcos
2)、动滑动摩擦
tg f
两物体接触表面有相对运动时,沿接触面产生的切向 阻力称为动滑动摩擦力。
1)、静滑动摩擦
① 定义 两相接触物体虽有相对运动趋势，但仍保持相对静止F时，
给接触面产生的切向阻力，称为静滑动摩擦力或简称静摩 擦力。
满足
0 F Fmax (最大静摩擦力)
当 F Fmax时,则物体处于临界平衡状态
F
P Fmax f N (库仑静摩擦定律)
若物体静止，则 F P
摩擦的现象和概念
在大学物理已经讲到什么是摩擦：当物体与另一物体 沿接触面的切线方向运动或有相对运动的趋势时，在两物 体的接触面之间有阻碍它们相对运动的作用力，这种力叫 摩擦力。接触面之间的这种现象或特性叫“摩擦”。这里 来作更深入的研究，首先来看它的分类：滑动摩擦和滚动 摩擦。
滑动摩擦：相对运动为滑动或具有滑动趋势时的摩擦。
第四章 摩擦
欢迎加入湖 工大考试资
料群：
引言
前几章我们把接触表面都看成是绝对光滑的，忽略了物体 之间的摩擦，事实上完全光滑的表面是不存在的，一般情况下 都存在有摩擦。 [例]
平衡必计摩擦 3
摩擦
☆§4–1 滑动摩擦 ☆§4–2 摩擦角和自锁现象 ☆§4–3 考虑摩擦时物体的平衡问题 ☆§4–4 滚动摩阻的概念
性质：当物体静止在支承面时，支承面的总反力的偏角
理论力学教程哈工大
绪论 (2)第一章静力学公理和物体的受力分析 (3)§1-1 刚体和力的概念 (3)§1-2 静力学公理 (4)§1-3 约束和约束反力 (8)§1-4 物体的受力分析和受力图 (13)第二章平面汇交力系与平面力偶系 (20)§2-1 平面汇交力系合成与平衡的几何法 (20)§2-2 平面汇交力系合成与平衡的解析法 (25)§2-3 平面力对点之矩的概念及计算 (30)§2-4 平面力偶理论 (34)第三章平面任意力系 (41)§3-1 平面任意力系向作用面内一点简化 (41)§3-2平面任意力系的简化结果分析 (45)§3-3 平面任意力系的平衡条件和平衡方程 (48)§3-4 平面平行力系的平衡方程 (54)§3-5 物体系的平衡.静定和静不定问题 (56)§3-6 平面简单桁架的内力计算 (63)第四章空间力系 (69)§4-1 空间汇交力系 (69)§4-2 力对点的矩和力对轴的矩 (75)§4-3 空间力偶 (81)§4-4 空间任意力系向一点的简化.主矢和主矩 (85)§4-5 空间任意力系的简化结果分析 (87)§4-6 空间任意力系的平衡方程 (89)§4-7 空间约束的类型举例 (90)§4-8 空间力系平衡问题举例 (92)§4-9重心 (98)第五章摩擦 (109)§5-1 滑动摩擦 (109)§5-2 考虑摩擦时物体的平衡问题 (111)§5-3 摩擦角和自锁现象 (120)§5-4 滚动摩阻的概念 (124)小结 (128)绪论一、理论力学的研究对象和内容理论力学是研究物体机械运动一般规律的科学。
物体在空间的位置随时间的改变，称为机械运动。
理论力学教程 (周衍柏)(第四版)
理论力学教程 (周衍柏)(第四版)介绍《理论力学教程 (周衍柏)(第四版)》是一本经典的力学教材，由著名力学学者周衍柏编写。
本教程系统讲解了理论力学的基本概念、原理和方法，是理论力学领域的入门教材。
本文档将对该教程的主要内容进行介绍，并以Markdown文本格式输出。
第一章：基本概念1.1 力学的研究对象力学是研究物体运动规律的科学，它将物体分为质点和刚体两个研究对象。
质点被简化为没有具体形状和大小的点，刚体则具有固有形状和大小。
1.2 运动的描述运动可以通过位置、速度和加速度等量来描述。
位置是描述物体在空间中的位置关系，速度是位置随时间的变化率，加速度是速度随时间的变化率。
1.3 牛顿力学的三大定律牛顿力学的三大基本定律为惯性定律、动量定律和作用反作用定律。
惯性定律描述了物体在无外力作用下保持匀速直线运动的性质，动量定律描述了物体受力作用下速度发生变化的规律，作用反作用定律描述了力的相互作用导致的物体运动规律。
第二章：质点运动学2.1 一维直线运动一维直线运动是质点只沿一条直线方向运动的情况。
可以通过物体的位移、速度和加速度来描述其一维直线运动规律。
2.2 二维平面运动二维平面运动是质点在平面内任意方向上运动的情况。
可以通过物体的平面位置、速度和加速度来描述其二维平面运动规律。
2.3 相对运动相对运动是指两个运动物体相对于彼此的运动情况。
可以通过相对速度来描述两个物体之间的相对运动规律。
第三章：质点动力学3.1 牛顿第二定律牛顿第二定律描述了质点受力作用下速度的变化规律，即力等于质量乘以加速度。
3.2 动量定理动量定理描述了质点受力作用下动量的变化规律，即力是动量随时间的变化率。
3.3 机械能守恒定律机械能守恒定律适用于只受重力和弹性力作用的质点，描述了质点机械能（动能和势能之和）在运动过程中的守恒性质。
第四章：刚体静力学4.1 刚体的概念刚体是指形状和大小在运动过程中保持不变的物体。
刚体静力学研究的是刚体受力平衡时的性质和规律。
理论力学自学全部教程课件
边界条件：描述物体表 面受力情况的方程，根 据外力条件建立。
通过学习和掌握这些基 本概念、应力与应变的 关系以及基本方程，可 以对弹性力学有更深入 的理解，为后续的学习 和应用打下坚实的基础 。
06
理论力学应用案例
机械结构设计中的理论力学应用
强度分析
利用理论力学原理，对机械设备的零部件进行应力、应变 和位移分析，确保其在工作条件下不发生破坏或塑性变形 。
析物体的稳定性等。
03
运动学基础
点的运动学
01
02
03
矢量法
通过矢量来描述点的运动 ，包括位移、速度和加速 度的矢量表示和计算。
直角坐标法
在直角坐标系中研究点的 运动，通过位移、速度和 加速度的分量来表示点的 运动状态。
自然法
借助自然坐标系研究点的 运动，用切向加速度和法 向加速度描述点的曲线运 动。
力对点的矩
力对某点的矩等于力的大小与力 臂（力作用线到该点的垂直距离 ）的乘积，表示力使物体绕该点
转动的效应。
合力矩定理
在平面汇交力系中，各力对某点 的矩的代数和等于该力系的合力 对同一点的矩。该定理可用于求
解物体的平衡问题。
矩的应用
利用矩的概念和合力矩定理，可 以方便地解决物体在平面内的平 衡问题，如确定物体的重心、分
刚度分析
通过对机械结构进行刚度分析，可以确定结构在受力时的 变形程度，为设计提供优化建议，保证机械设备的精度和 稳定性。
动力学设计
理论力学可用于研究机械设备的动态特性，如振动、冲击 等，以合理设计机械设备的动力学性能，降低噪音，提高 使用寿命。
航空航天领域中的理论力学应用
飞行器结构设计
运用理论力学方法，对飞行器的机翼、机身等结构进行强度、刚度 和稳定性分析，确保飞行器在不同飞行条件下的安全性。
理论力学教程 (周衍柏)(第三版)
理论力学教程 (周衍柏)(第三版)一、引言理论力学是物理学的基础学科之一，它研究物体在力的作用下的运动规律。
本教程以周衍柏教授的《理论力学教程》第三版为蓝本，系统介绍了理论力学的基本概念、基本原理和常见的力学问题求解方法。
本教程主要面向物理学及相关专业的本科生，以系统、简明的方式解析力学理论，帮助读者建立起对力学问题的基本认知。
二、基本概念2.1 点、质点、物体点是一种没有大小和形状的基础几何概念，也是力学中的基本研究对象。
质点是一个研究物体运动时常用的模型，它假设物体可以看作是质量集中在一个点上的粒子。
而物体则表示具有一定体积和形状的物质实体。
2.2 粒子系粒子系是由多个质点组成的系统。
在粒子系中，每个质点的运动状态都可以用力学中的基本物理量表示，如质量、位置矢量和速度矢量等。
2.3 音速和光速音速是指声波在介质中传播的速度，而光速则是指光在真空中传播的速度。
它们是两个重要的物理量，对于理论力学的研究具有重要意义。
三、基本原理3.1 牛顿第一定律牛顿第一定律，也称为“惯性定律”，指出在没有外力或合力为零的情况下，物体维持静止或匀速直线运动的状态。
这一定律是理论力学研究的基础。
3.2 牛顿第二定律牛顿第二定律描述了物体在外力作用下的运动规律。
它表达了力与物体的质量和加速度之间的关系，可以用等式F=FF表示，其中F是合力，F是物体的质量，F是物体的加速度。
3.3 牛顿第三定律牛顿第三定律即“作用-反作用定律”，指出任何两个物体之间的相互作用力都是同等大小、相反方向的力。
这一定律充分体现了力的相互作用性质。
四、力学问题求解方法4.1 动力学方法动力学方法是研究力学问题的一种常见方法，它通过建立物体的运动方程和受力分析，求解物体的运动规律和相关物理量。
4.2 势能法势能法是一种基于能量守恒原理的力学分析方法。
通过定义系统的势能函数，可以将力学问题转化为求解势能函数的极值问题，从而得到物体的运动规律。
4.3 矢量法矢量法是一种运用矢量运算和矢量代数求解力学问题的方法。
lxy理论力学教程(第十章)
p=∑mivixi+∑miviy j
p m Av A mB v B =∑mivixi+∑miviy j 2ml (- sin t i cos t j )
11
解：第二种方法：先确定系统的质心，以及质心的速度，然 后计算系统的动量。 质点系的质心在C处，其速度矢量垂直于OC，数值为：
求：图示位置时，系统的总动量。 vA A
vC 解：第一种方法：先计算各个质点的动量， 再求其矢量和。 D
AB
p mAv A mB v B
AB =
O
C t vB B
v A AB DA 2l cos t vB AB DB 2l sin t
10
p=pxi+py j
23
§10-2 动量定理
一．质点的动量定理
dv ma m F dt
d ( mv ) F dt
d ∴ ( mv ) F dt
质点的动量对时间的导数等于作用于质点的力 —质点的动量定理 (1)微分形式：
（动量的微分等于力的元冲量）
t2 t1
(2)积分形式： mv2 - mv1 F dt I 质点动量定理的积分形式：质点在 t1 至 t2 时间内动量的改 变量等于作用于质点的合力在同一时间内的冲量。
1．力 F 是常矢量： S F (t2 - t1 )
20
2．力 F 是变矢量：（包括大小和方向的变化） 元冲量： 冲量：
dS Fdt
S
t2
F dt
t1
3．合力的冲量：等于各分力冲量的矢量和．
S Rdt F dt Fdt Si
t1 t1 t1
t2
2023大学_理论力学教程第三版(周衍柏著)课后答案下载
2023理论力学教程第三版(周衍柏著)课后答案下载理论力学教程第三版内容简介绪论第一章质点力学1.1 运动的描述方法1.2 速度、加速度的分量表示式1.3 平动参考系1.4 质点运动定律1.5 质点运动微分方程1.6 非惯性系动力学(一)1.7 功与能1.8 质点动力学的基本定理与基本守恒定律1.9 有心力小结补充例题思考题习题第二章质点组力学2.1 质点组2.2 动量定理与动量守恒定律2.3 动量矩定理与动量矩守恒定律 2.4 动能定理与机械能守恒定律 2.5 两体问题2.6 质心坐标系与实验室坐标系 2.7 变质量物体的运动2.8 位力定理小结补充例题思考题习题第三章刚体力学3.1 刚体运动的分析3.2 角速度矢量3.3 欧拉角3.4 刚体运动方程与平衡方程3.5 转动惯量3.6 刚体的平动与绕固定轴的.转动 3.7 刚体的平面平行运动3.8 刚体绕固定点的转动__3.9 重刚体绕固定点转动的解__3.10 拉莫尔进动小结补充例题思考题习题第四章转动参考系4.1 平面转动参考系4.2 空间转动参考系4.3 非惯性系动力学(二)__4.5 傅科摆小结补充例题思考题习题第五章分析力学5.1 约束与广义坐标5.2 虚功原理5.3 拉格朗日方程5.4 小振动5.5 哈密顿正则方程5.6 泊松括号与泊松定理5.7 哈密顿原理5.8 正则变换__5.9 哈密顿-雅可比理论__5.10 相积分与角变数__5.11 刘维尔定理小结补充例题思考题习题附录主要参考书目理论力学教程第三版目录本书是在第二版的基础上修订而成的，适用于高等学校物理类专业的理论力学课程。
本书与第二版相比内容保持不变，仅将科学名词、物理量符号等按照国家标准和规范作了更新。
本书内容包括质点力学、质点组力学、刚体力学、转动参考系及分析力学等，每章附有小结、补充例题、思考题及习题。
理论力学教程(第三版)第二章 周衍柏编
v2 = U −
所以落地时水平距离之差 Δs
Δs = s1 − s2 = v1t − v2t =
⎛ 1 V 1 ⎞ ⎟ 2E⎜ + ⎟ ⎜ g ⎝ M1 M 2 ⎠
y
m
V
M
θ
O
当 m 沿半圆球 M 下滑时，M 将以 V 向所示正方向的反向运动。以 M 、m 组成系 统为研究对象，系统水平方向不受外力，动量守恒，即
I
2
2.13 长为 l 的均匀细链条伸直地平放在水平光滑桌面上，其方向与桌边缘垂直，此时链条的
2.15 机枪质量为M，放在水平地面上，装有质量为 M ′ 的子弹。机枪在单位时间内射出的质 量为m.其相对地面的速度则为 u ，如机枪与地面的摩擦系数为 μ ，试证当 M ′ 全部射出后， 机枪后退的速度为
P
等，则两球碰撞后的速度互相垂直，试证明之。
2.9 一光滑小球与另一相同的静止小球相碰撞。在碰撞前，第一小球运动的方向与碰撞时两 球的联心线成 α 角。求碰撞后第一小球偏过的角度 β 以及在各种 α 值下 β 角的最大值。设 恢复系数 e 为已知。 2.10 质量为 m 的光滑球用一不可伸长的绳系于固定点 A 。另一质量为 m 的球以与绳成 θ 2 1 角的速度 v 与 m 正碰。试求 m 与 m 碰后开始运动的速度 v′ 及 v′ 。设恢复系数 e 为已知。 1 2 1 2 1 2
建立如图 2.4.1 图所示的水平坐标。
′ a1
P
H
Δs = s2 − s1 =
S
w uv0 sin α (W + w) g
• O
水平距离
I
w u W +w
可知道
x
v1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
6
讨论
I P
视频：动量 定理的应用
1）定理的形式特征
(过程量)=(状态量的增量)
2）估算平均作用力
将积分用平
t Fdt Ft
均力代替 t0
动量定 理写为
平均力 写为
F
P
t
Ft P
思考：为什么向水泥墙内钉钉子要用锤子呢？大力士除7 外
例：动量定理解释了“逆风行舟”
t1, t2, ti tn
则在t 间隔内力的冲量为
n
I fiti
f1t1
f2t2
f3t3
i 1
f4t4
I
若力的变
化连续
tt I fdt
矢量 冲量 过程量
t
4
二、质点运动的动量定理
由牛顿第 二定律
F
dP dt
(Fdt dP)
13
一、质点系 N个质点组成的系统-- 研究对象
内力 internal force
质点系
系统内部各质点间的相互作用力
特点： 成对出现； 大小相等方向相反
结论：质点系的内力之和为零 fi 0
i
质点系中的重要结论之一
14
外力 external force 系统外部对质点系内部质点的作用力
约定：
y
所受到的平均冲力．
10
解 由动量定理得：
Fxt mv2x mv1x
x
mv cos (mv cos)
2mvcos
mv1
mv2 O
Fyt mv2y mv1y
mvsin mvsin 0
F
Fx
2mv cos
t
14.1 N
方向与Ox 轴正向相同．
第3章 动量守恒定律与角动量守恒定律 §1 质点运动的动量定理 §2 质点系的动量定理 动量守恒定律 §3 质心 质心运动定理 §4 角动量定理 角动量守恒定律 §5 质心参考系
1
§1 质点运动的动量定理 一、力的冲量 二、 质点运动的动量定理
2
§1 质点运动的动量定理
一、力的冲量定义：力f 作 Nhomakorabea时间为t
y
F' F
11
3、质量为m，速率为v的小球，以入射角α斜向与墙壁相碰，又 以原速率沿反射角方向从墙壁弹回．设碰撞时间为⊿t，求墙壁受 到的平均冲力．
m v
解：方法一：建立图示坐标，以vx 、vy表示小球反射速度的x和 y分量，则由动量定理，小球受到的冲量的x，y分量 的表达式如下：
m
t PP
Fdt dP
t0
P
微分形式
质点运动的 动量定理
I P
积分形式
5
分量表示 说明
Ix
t2 t1
Fxdt
mv2x
mv1x
I y
t2 t1
Fydt
mv2 y
mv1y
I z
t2 t1
Fzdt
mv2z
mv1z
某方向受到冲量，该方向上动量就增加．
系 写统成内任一质Fi 点 受fi 力之和
质点系 F
外力之和
内力之和
15
二、 质点系的动量定理 动量守恒定律
方法:对每个质点分别使用牛顿定律,然后利用质 点系内力的特点加以化简 到 最简形式。
第1步，对 mi 使用动量定理：
fi
t2
t2
Fidt fidt Pi Pi0
演示
前 进 方 向
0
风吹来
P0
P
I P
船
前 进 方 向
取一小块风dm为研究对象
初 末
P0 P
0dm dm
由牛顿第 三定律
I P
风对帆的冲量大小
I P
方向与 P相反
P
F t 8
动量定F理常t1t应2 F用dt于碰m撞v2问题mv1
t2 t1
t2 t1
注意 在 p一定时
t越小，则 F 越大
mv
mv1
mv2
F
9
例1 一质量为0.05 kg、 速率为10 m·s-1的刚球，以与
x
mv1
钢板法线呈45º角的方向撞击 在钢板上，并以相同的速率
mv2 O
和角度弹回来．设碰撞时间
为0.05 s．求在此时间内钢板
i t1
t1
i
第3步，化简上式：
t2
先看外力冲量之和 Fidt
i t1
由于每个质点的受力时间dt 相同
所以：
t2
t2
Fidt ( Fi )dt
i t1
t1 i
t2
t2
写成： Fidt F外dt
i t1
t1
fi
mi
质点系 Fi
F外 Fi
t1
t1
mi
Fi
Pi
mii
Pi0
mii0
第2步，
t2
t2
( Fidt fidt) (Pi Pi0 )
对所有质
i t1
t1
i
点求和： 外力冲量之和 内力冲量之和
16
t2
t2
( Fidt fidt) (Pi Pi0 )
，
则ft
称为力 f
在 t时间间隔内的冲量， 记作
I ft
SI
I
F t
MLT1
m
单位 Ns
f
I
I ft
3
定义式 I ft
若在t 间隔内物体受力依次为 f1, f2, fi fn
相应作用时间依次为
v
x方向：Fxt mvx (mvx ) 2mvx (1) m
y
y方向：Fyt mvy (mvy ) 0 (2)
F Fx 2mvx / t v x=v cos a
O
x
F 2mv cos / t 方向沿x正向。
m
根据牛顿第三定律，墙受的平均冲力F F，方向垂直墙面向内。
方法二：作动量矢量图，由图知 (mvv) 2mv cos
方向垂直于墙向外 由动量定理： Ft (mvv)
mv
mv
a
a
得：F 2mv cos / t 不计小球重力，F即为墙对球的冲力，
(mv)
由牛顿第三定律，墙受的平均冲力F F，方向垂直墙面向内。
12
§2 质点系的动量定理 动量守恒定律 一、质点系 二、质点系的动量定理 动量守恒定律 三、火箭飞行原理-- 变质量问题
i
将所有的外力
共点Fc1力相FF21加37
t2
t2
( Fidt fidt) (Pi Pi0 )
i
t1
t1
i
t2
再看内力冲量之和 fidt