莱斯利Leslie种群模型
数学模型在《线性代数》教学中的应用实例(一)

数学模型在《线性代数》教学中的应用实例(一) 课 程: 线性代数 教 学 内 容: 矩阵数 学 模 型:生态学:海龟种群统计数据该模型在高等数学教学应用的目的:1. 通过生动有趣的实例激发学生的学习积极性,在分析问题和解决问题的过程中培养学生的创新意识。
2. 使学生掌握建立矩阵代数模型的基本过程,能熟练地将矩阵的知识应用于实际问题。
培养学生将实际问题抽象成数学模型,又用数学模型的结果解释实际现象的能力。
3. 巩固矩阵的概念和计算。
生态学:海龟种群统计数据管理和保护许多野生物种,依赖于我们建立种群的动态模型的能力。
一个常规的建模技术是,把一个物种的生命周期划分为几个阶段。
该模型假设:每阶段的种群规模只依赖于母海龟的种群数;每只母海龟能够存活到下一年的概率依赖于其处在生命周期的那个阶段,而与个体的具体年龄无直接关系。
举例来说,可以用一个四阶段的模型来分析海龟种群的动态。
如果d i 表示第i 个阶段的持续时间,s i 表示该阶段的每年存活率,那么可以证明,在第i 阶段可以存活到下一年的比例是111i i d i i id i s p s s -⎛⎫-= ⎪-⎝⎭种群可以存活且在次年进入下一阶段的比例是()11i i d i i i d is s q s-=-如果用e i 表示第i 阶段的成员1年内产卵的平均数,构造矩阵123412233400000p e e e q p L q p q p ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭那么L 可以用来预测未来几年每阶段的种群数。
上述形式的矩阵称为Leslie (莱斯利)矩阵,相应的种群模型有时也称为莱斯利种群模型。
根据前面表格数据,我们模型的莱斯利矩阵是0127790.670.73940000.000600000.810.8077L ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭假设每阶段的初始种群数分别是200000、300000、500和1500,用向量x 0来表示,1年后每阶段的种群数可以如下计算1000127792000001820000.670.73940030000035582000.000600500180000.810.807715001617x Lx ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪⎪ ⎪=== ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭(这里的计算进行了四舍五入)。
莱斯利Leslie种群模型

2 A1 A2 0 , 3 A 2 A 0 ,
3
()
t A t 1 At 0 .
4
§4.5 应 用(一) ———————————————————— 由此可预测该地区t年后的环境污染水平和经济发 — 展水平.下面作进一步地讨论:
水平与经济发展水平, 则经济发展与环境污染 的增长 模型为 xt 3xt 1 yt 1 yt 2 xt 1 2 yt 1
(t 1,2,, k )
3
§4.5 应 用(一) ———————————————————— 令 — xt t y t 则上述关系的矩阵形式为
1
§4.5 应 用(一) ———————————————————— 设x0 , y0分别为改地区目前的环 水 — 境污染水平与经济发展
平, x1 , y1分别为改地区若干年后 的环境污染水平与经济 发展水平, 且有如下关系: x1 3 x0 y 0 y1 2 x0 2 y 0
0不是特征值, 不能类似分析 . 但是 0可以由 1,2唯一线性表出为
0 31 22
由(*)及特征值与特征向量的性质
8
§4.5 应 用(一) ———————————————————— t t t At 0 At (31 2— ) 3 A 2 A 2 2 1
10
§4.5 应 用(一) ———————————————————— 4.5.2莱斯利(— Leslie)种群模型
莱斯利种群模型研究动物种群中雌性动物的年龄分 布与数量增长之间的关系.
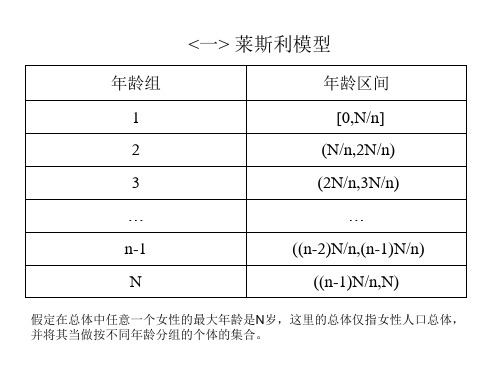
设某动物种群中雌性动物的最大生存年龄为L(单位: 年),将区间[0,L]作n等分得n个年龄组
Leslie矩阵模型预测人口

L e s l i e矩阵模型预测人口4.1Leslie矩阵模型的基本概念4.1.1参数定义[11]我们将中国人口按年龄段分成数段,因此当段数到达一定大小的时候就能包含全部年龄层的人。
再将时间序列也分割成数段(一年为一段即可研究年度人口总数),得到:——在时间周期k第i个年龄段的人数注:这里的;一定存在整数n 使得表示的是年龄最高的人的人数,如“100岁以上的人”的数量。
其他关于人口的参数:1)——在时间周期k第i年龄组的女性的生育率,即女性生的孩子的人数与女性数的比例,我们也称其为年龄别生育率2)——在时间周期k第i年龄组的死亡率,即死亡人数除以这一年龄组总人数,我们也称其为年龄别死亡率4.1.2Leslie矩阵1.转移过程在一个时间周期内里的人数转移到里,考虑死亡的人数我们得到如下式子:11(1)()(1()),1,2,k k kx i x i d i i n--+=-=(4-1)下面来讨论的情况,即新生儿人数,在这里我们做了一个假设,女性人口大致占总人口的一半(通过以往的人口普查可以得到证实),因此在时间周期k的第个i年龄段的女性人数为1()2kx i,则可以通过女性的年龄别生育率预测第一个递推关系如下:1111()()()2nk k kix i b i x i--==∑(4-2) 2.人口发展模型111111111111(0)(1)(1)()22221(0)00001(1)0001(1)0k k k kkk kkkb b b n b ndx xdd n--------⎛⎫-⎪⎪-⎪=⨯⎪-⎪⎪⎪--⎝⎭(4-3) 其中(0)(1)()k k k k x x x x n ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭1111(0)(1)()k k k k x x x x n ----⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭(4-4)为了化简,我们记:11111111111(0)(1)(1)()22221(0)00001(1)00001(1)0k k k k k k k b b b n b n d L d d n -------⎛⎫- ⎪⎪- ⎪=⎪- ⎪ ⎪⎪--⎝⎭(4-5)则有简写:1k k x L x -=(4-6)则有递推公式:10k kk x L x L x -==(4-7)通过这种方法,我们把人口预测问题的重点落到了一个n 维矩阵运算上。
leslie模型matlab程序

leslie模型matlab程序Leslie 模型是一种用于描述种群动态变化的数学模型,特别被广泛应用于生态学和人口学领域。
本文将介绍如何使用 MATLAB 编程实现 Leslie 模型,并提供一个完整的 MATLAB 程序。
Leslie 模型是由生物学家 Patrick Leslie 在 1945 年提出的,它利用年龄结构矩阵来描述一个种群中不同年龄段的个体数量。
该模型假设种群的年龄结构在各个时间段内保持不变,并且个体之间的交互仅通过生育和死亡来实现。
在 Leslie 模型中,种群的每个年龄段都有一个特定的存活率和生育率。
假设一个种群的年龄段从 0 到 k,种群的存活率可以用一个长度为 k+1 的向量 s 表示,其中 s(i) 表示年龄段 i 的存活率。
种群的生育率可以用一个长度为 k 的向量 b 表示,其中 b(i) 表示年龄段 i 的生育率。
为了计算种群在下一个时间段的年龄结构,我们需要将当前时间段的年龄结构向量乘以一个称为 Leslie 矩阵的矩阵 A。
Leslie 矩阵的第一行是生育率向量 b,其余行是存活率向量 s,只是向上移动了一格。
因此,Leslie 矩阵的维度为(k+1)×k。
现在我们将以 MATLAB 编程实现 Leslie 模型。
首先,我们需要确定种群的年龄段数目和初始年龄结构向量。
这里假设种群的年龄段从 0 到 9,初始年龄结构向量为一个10×1 的列向量,每个元素都为 100。
```matlabk = 9; % 年龄段数目x0 = zeros(k+1, 1); % 初始年龄结构向量x0(1) = 100; % 年龄 0 的个体数量为 100```接下来,我们需要定义存活率向量和生育率向量。
对于这里的示例,我们假设存活率向量是一个长度为 10 的向量,并且每个年龄段的存活率都为 0.8。
生育率向量是一个长度为 9 的向量,并且每个年龄段的生育率都为 2。
莱斯利模型
表示每一个女性在第i年龄组期间生育儿女的平均数。
表示第i年龄组的女性可望活到第(i+1)年龄组的分数。
显然 ai 0(i 1, 2,, n),0 b 1(i 1, 2,, n 1). 不允许任何bi等于0, 否则就没有一个没有女性会活到超过第i年龄组。
同样,至少有一个 a i 是正的,这样就保证有n个女儿出生了。与正的 对应的年龄组称为生育年龄组。
1)如果 1 3)如果 1
1 ,总体最终是增长的; 1 ,总体整体是不变的。
2)如果 1 1 ,总体整体是减少的;
1 1 的情形有特殊意义,因为它决定了一个具有零增长的总体。
对于任何初始年龄分布,总体趋于一个是特征向量的某个倍数
由(5.6)和(5.7)式可看出,当且仅当
a1 a2b1 a3b1b2 ... anb1b2 ...bn1 1
t0 0, t1 N / n, t2 2N / n, , tk kN / n, .
这样,在时刻 tk 1 时于第(i+1)组中的所有女性在时刻是均在第i组中。
在两次连续的观察时间之间的出生和死亡过程,用下述人口学参数来描述:
ai (i 1, 2,, n)
b(i 1, 2,, n 1)
此等式两边除以
1k ,就得出
0 P 1 X (0) . (n / 1 ) k 0
(5.9)
k 1
1
k 1
X (k )
由于1 是严格主特征值,所以
| i / 1 | 1(i 2,3,, n), 当 k (i / 1 )k 0(i 2,3,, n), 这样就得到
aiBiblioteka 记xi(i ) 是在时刻个 年龄组中的女性数目,则称
莱斯利矩阵科学家LesliePH于1945年引进一种数学方法利用某一

莱斯利矩阵科学家Leslie PH.于1945年引进一种数学方法,利用某一初始时刻种群的年龄结构现状,动态地预测种群年龄结构及数量随时间的演变过程,目录1 莱斯利(Leslie)矩阵模型2 佛坪大熊猫种群动态发展趋势3 计算结果与分析1 莱斯利(Leslie)矩阵模型简介如下:依种群个体的生理特征,将其最大寿命年龄等距分成m个年龄组,然后讨论不同时间种群按年龄的分布,故时间也离散化为t=0,1,2,…其间隔与年龄组的间隔时间相同.t=0对应于初始时刻.设开始时(t=0)第i个年龄组内的个体数为ni(0),i=1,2,…,m.则向量N∼(0)=[n1(0),n2(0),…,nm(0)]T称为初始年龄结构向量.第i年龄组的生殖率为fi(≥0)i=1,2,…,m;生存率为Si(>0),i=1,2,…,m-1.则相临两个时段间,各年龄组个体数ni有如下的迭代关系:注1 fi中已扣除了在时段t内出生,但活不到t+1时段的新生个体.注2 通常在两性生殖的种群中,只计雌体数.作矩阵2 佛坪大熊猫种群动态发展趋势利用莱斯利模型,对佛坪自然保护区内大熊猫种群的发展变化作出预测分析.2.1 佛坪大熊猫种群现状佛坪自然保护区位于秦岭中段南坡,北纬32°32′~33°43′,东经107°40′~107°55′,最高海拔2904m,最低海拔1100m,总面积293km2.1974年以来,科学工作者多次对该区域内大熊猫的种群数量、年龄结构、分布等进行了大量观察研究,提供了如下数据[3].1990年该区域内观察到64只大熊猫,分布面积237/km2,密度为0.27/km2,年龄结构为未成年组 6岁以下 24只 37.5%成年组 6~15岁 31只 48.2%老年组 15岁以上 9只 14.3%2.2 等距年龄结构分析处理由于模型分析中要求等距年龄结构,现有的数据是不等距的,故需进行等距年龄结构分析处理.根据大熊猫的生长发育规律,其野外最大寿命年龄为26岁[2],按每3岁一个年龄段分成9个年龄组:0岁~2岁,3岁~5岁,…,24岁~26岁,分别记为第1,2,…,9年龄组.文[4]已据文[2]提供的大熊猫的有关生命数据,换算出大熊猫按三年段的等距年龄组的生殖率fi和生存率Si为表1.由于野外大熊猫的性别不易识别,调查数据往往无性别之分,大熊猫的雌雄比为1∶1[2],故上表为雌、雄合计的,而非一般的只考虑雌体.文[5]计算了大熊猫种群的稳定年龄结构向量为N∼(∞)=[101,41,37,33,27,15,8,4,1]t据此,可按比例将现有非等距年龄结构调整为等距年龄结构.0~5岁共24只属于第1、2年龄组.因0~2岁幼仔死亡率极高,加之9月以前的幼仔不能离窝,不可能见到它们的活动痕迹,故第一年龄组的个体数应增加,能被观察到的个体数量以三分之一计算[3].于是n13+n2=24;n1n2=10141,解得n1=33(只),n2=13(只).6岁至15岁31只,但分龄到14岁,尚多出1岁,故调出1只到下一组内,余下的30只仍按比例分配调整为n3=12只,n4=11只,n5=7只.16岁以上9只,调入一只后共10只,按比例分配调整为n6=4只,n7=3只,n8=2只,n9=1只.最后得到1990年(t=0)的初始年龄结构向量为N∼(0)=[33,13,12,11,7,4,3,2,1]’.莱斯利矩阵为3 计算结果与分析对t=1,2,…,10,11,按公式N∼(t)=MtN∼(0)的计算结果见表2.其中N∼(0)=[33,13,12,11,7,4,3,2,1]T表2 佛坪大熊猫种群发展趋势从计算结果可以看到,自1990年起的33年间,该种群数量共增加30.39只,为原来的1.353倍,增长率为35.3%.可见大熊猫的发展十分缓慢.不过,这一濒危动物尚能缓慢增长也算幸事了.为分析环境对大熊猫的影响,即因环境造成大熊猫个体的非正常的突发性死亡(如捕猎等).假设1990年内,第二、三、四、五年龄组分别有1只大熊猫非正常死亡,即按N∼(0)=[33,12,11,10,6,4,3,2,1]’计算,以后33年间该大熊猫种群按年龄结构的发展见表3由表2与表3对照表明,虽少量个体受损对种群的影响也是显著的,需经过近十年时间种群才能恢复到原有水平,而且对种群总量的影响还将长期持续下去,可见保护好大熊猫的生存环境,尽量杜绝和减少非正常死亡是十分重要的。
2第二章矩阵应用例子

第二章 矩阵应用例子矩阵的概念是从大量各种各样的实际问题中抽象出来的,是最基本的数学概念之一.矩阵概念贯穿线性代数的各方面,许多问题的数量关系都可以通过矩阵来描述,因而矩阵是科学研究的一个非常重要的工具.它在自然科学、工程技术、经济管理等领域有着广泛的应用. 本章主要列举了矩阵在经济、统计、信息技术等方面的应用.例1 生产成本某工厂生产三种产品. 它的成本分为三类. 每一类成本中,给出生产单个产品时估计需要的量. 同时给出每季度生产每种产品数量的估计. 这些估计在表2-1和表2-2中给出. 该公司希望在股东会议上用一个表格展示出每一季度三类成本中的每一类成本的数量:原料费、工资和管理费.表2-1 生产单位产品的成本(美元)成 本 产 品A B C 原料费 工资管理费和其他0.10 0.30 0.10 0.30 0.40 0.200.15 0.25 0.15表2-2 每季度产量产 品 季 度夏季 秋季 冬季 春季 A B C4 000 2 0005 8004 500 2 600 6 2004 500 2 400 6 0004 000 2 200 6 000解 我们用矩阵的方法考虑这个问题. 这两个表格中的每一个均可表示为一个矩阵.0.100.300.150.300.400.250.100.200.15M ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦及400045004500400020002600240022005800620060006000P ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦如果我们构造乘积MP ,则MP 的第一列表示夏季的成本.原料费: (0.10)(4000)(0.30)(2000)(0.15)(5800)1870++= 工资: (0.30)(4000)(0.40)(2000)(0.25)(5800)3450++= 管理费和其他:(0.10)(4000)(0.20)(2000)(0.15)(5800)1670++=MP 的第二列表示秋季的成本.原料费: (0.10)(4500)(0.30)(2600)(0.15)(6200)2160++=工资: (0.30)(4500)(0.40)(2600)(0.25)(6200)3940++=管理费和其他:(0.10)(4500)(0.20)(2600)(0.15)(6200)1900++=MP 的第三列和第四列表示冬季和春季的成本.187021602070196034503940381035801670190018301740MP ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦MP 第一行的元素表示四个季度中每一季度原料的总成本. 第二和第三行的元素分别表示四个季度中每一季度工资和管理的成本. 每一类成本的年度总成本可由矩阵的每一行元素相加得到. 每一列元素相加,即可得到每一季度的总成本. 表2-3汇总了总成本.表2-3季 度夏季 秋季 冬季 春季 全年 原料费工资管理费和其他 总计1 870 3 450 1 670 6 9902 1603 940 1 900 8 0002 0703 810 1 830 7 7101 960 3 580 1 740 7 2808 060 14 780 7 140 29 980例2 生态学:海龟的种群统计学管理和保护很多野生物种依赖于我们模型化动态种群的能力. 一个经典的模型化方法是将物种的生命周期划分为几个阶段. 该模型假设每一阶段种群的大小仅依赖于雌性的数量,并且每一个雌性个体从一年到下一年存活的概率仅依赖于它在生命周期中的阶段,而并不依赖于个体的实际年龄. 例如,我们考虑一个4个阶段的模型来分析海龟的动态种群. 在每一个阶段,我们估计出1年中存活的概率,并用每年期望的产卵量近似给出繁殖能力的估计. 这些结果在表2-4中给出. 在每一阶段名称后的圆括号中给出该阶段近似的年龄.表2-4 海龟种群统计学的4个阶段阶段编号描述(年龄以年为单位) 年存活率 年产卵量 12 3 4卵、孵化期(<1)幼年和未成年期(1~21) 初始繁殖期(22) 成熟繁殖期(23~54)0.67 0.74 0.81 0.810 0 127 79若i d 表示第i 个阶段持续的时间,i s 为该阶段每年的存活率,那么在第i 阶段中,下一年仍然存活的比例将为111i i d i i id i s p s s -⎛⎫-= ⎪-⎝⎭(1) 而下一年转移到第1i +个阶段时,可以存活的比例应为(1)1i id i i i d i s s q s -=- (2) 若令i e 表示阶段(2,3,4)i i =1年中平均的产卵量,并构造矩阵123412233400000p e e e q p L q p q p ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦(3) 则L 可以用于预测以后每阶段海龟的数量. 形如(3)的矩阵称为莱斯列(Leslie )矩阵,相应的种群模型通常称为莱斯利种群模型. 利用表1给出的数字,模型的莱斯利矩阵为0127790.670.73940000.000600000.810.8077L ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦假设初始时种群在各个阶段的数量分别为200 000,300 000,500和1 500. 若将这个初始种群数量表示为向量0x ,1年后各个阶段的种群数量可如下计算:1000127792000001820000.670.73940030000035582000.000600500180000.810.807715001617L ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦x x (上述结果已经四舍五入到最近的整数了.)为求得2年后种群数量向量,再次乘以矩阵L .2210L L ==x x x一般地,k 年后种群数量可通过计算向量0k k L =x x 求得. 为观察长时间的趋势,我们计算102550,,x x x . 结果归纳在表2-5中. 这个模型预测,繁殖期的海龟数量将在50年后减少80%.表2-5 海龟种群预测阶段编号初始种群数量10年 25年 50年 1 2 3 4200 000 300 000500 1 500114 264 329 212214 1 06174 039 213 669139 68735 966 103 79568 334例3 密码问题在密码学中,称原来的消息为明文,经过伪装了的明文则成了密文,由明文变成密文的过程称为加密. 由密文变成明文的过程称为译密. 明文和密文之间的转换是通过密码实现的.在英文中,有一种对消息进行保密的措施,就是把消息中的英文字母用一个整数来表示,然后传送这组整数. 如~A Z 的26个英文字母与1~26的数字一一 对应.例如,发送“SEND MONEY ”这九个字母就可用[19,5,14,4,13,15,14,5,25]这九个数来表示. 显然5代表E ,13代表M ,…这种方法很容易被破译. 在一个很长的消息中,根据数字出现的频率,往往可以大体估计出它所代表的字母. 例如,出现频率特别高的数字很可能对应出现频率特别高的字母.我们可以用矩阵乘法对这个消息进一步加密. 假如A 是一个对应行列式等于1±的整数矩阵,则1A -的元素也必定是整数. 可以用这样一个矩阵对消息进行变换,而经过这样变换的消息是较难破译的. 为了说明问题,设100315,201⎛⎫ ⎪= ⎪ ⎪-⎝⎭A则11001315.201-⎛⎫ ⎪=-- ⎪ ⎪⎝⎭A把编了码的消息组成一个矩阵194145135,141525⎛⎫ ⎪= ⎪ ⎪⎝⎭B乘积10019414194143155135132100172.2011415252473⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪== ⎪⎪ ⎪ ⎪⎪ ⎪---⎝⎭⎝⎭⎝⎭AB所以,发出去的消息为[19,132,24-,4,100,7,14,172,3-]. 这与原来的那组数字不大相同,例如,原来两个相同的数字5和14在变换后成为不同的数字,所以就难于按照其出现的频率来破译了. 而接收方只要将这个消息乘以1-A ,就可以恢复原来的消息.100194141941413151321001725135.2012473141525⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪--= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭ 要发送的信息可以按照两个或三个一组排序,如果是两个字母为一组,那么选二阶可逆矩阵,如果是三个字母为一组,则选三阶可逆矩阵. 在字母分组的过程中,如果最后一组字母缺码,则要用Z 或YZ 顶位.。
种群相互竞争模型

种群相互竞争模型种群相互竞争模型是一种描述不同物种之间相互作用的模型。
在这个模型中,物种之间存在着竞争关系,它们彼此争夺有限的资源,如食物、空间、水等。
这种竞争关系是一种自然选择,只有适应环境的物种才能生存下来。
本文将介绍种群相互竞争模型的基本概念和模型类型。
一、基本概念种群:指在一个生态系统中,属于同一物种的个体集合。
相互作用:指不同种群之间在一个生态系统中进行的各种生物和非生物之间的相互作用。
竞争:指不同物种之间为获得生存所需的资源而进行的相互斗争。
资源:指能够提供生存所需的物质和能量,如食物、水、空间等。
竞争系数:指物种之间通过竞争所占据的位置和利用资源的能力。
二、模型类型1. Lotka-Volterra 模型Lotka-Volterra 模型是经典的种群相互竞争模型,它假设两个物种之间的竞争是无限的。
该模型有两个方程,包括一个描述一种物种的增长率和一个描述两种物种之间的交互作用。
该模型的形式为:dN1/dt = r1N1 - a12N2N1dN2/dt = r2N2 - a21N1N2其中,N1 和 N2 分别是种群1和2的数量,r1和r2是它们的增长率,a12和a21 是它们之间的交互作用。
2. Gause 模型其中,Ntotal=N1+N2是两种物种的总数量,r1和r2分别是它们的增长率,K1和K2是种群1和2的最大容量。
c1和c2 是两个物种之间的竞争系数,它们表示在某个条件下,一个物种的存在要比另一个物种更具有竞争力。
3. Ricker模型Ricker模型是一种离散的种群相互竞争模型,它包含了两个方程,描述了一种物种的数量随时间变化的规律。
Ricker模型的形式为:Nt+1 = Nt*exp(r(1-Nt/K)-a*Nc)其中,Nt是种群数量,r是增长率,K是种群的最大容量,a是物种之间的竞争系数,Nc是与物种竞争的物种数。
dN/dt = rN/(1 + aN)总结:种群相互竞争模型是描述不同物种之间相互作用的模型,包括竞争、相互作用、竞争系数、资源等基本概念。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
令
—
t
xt yt
则上述关系的矩阵形式为
t At1, t 1,2, , k
由此,有
1 A0 ,
2 A1 A20 ,
3 A2 A30 ,
()
t At1 At0. 4
——————§—4—.5—应——用—(—一—)——————
由此可预测该地区t年后—的环境污染水平和经济发
展水平.下面作进一步地讨论:
经济发展与环境污染是当今世界亟待解决的两个突 出问题.为研究某地区的经济发展与环境污染之间的关 系,可建立如下数学模型:
1
——————§—4—.5—应——用—(—一—)——————
设x0, y0分别为改地区目前—的环境污染水平与经济发展水
平, x1, y1分别为改地区若干年后的环境污染水平与经济
发展水平, 且有如下关系:
环境污染也保持着同步恶化趋势.
则也是A 的属于特征值 的特征向量
k
k
一个性质:若是矩阵A的属于特征值的特征向量,
7
——————§—4—.5—应——用—(—一—)——————
Case2 0 2 12 —
y0 2 0,不讨论此种情况.
1
Case30 7
0不是特征值,不能类似分析. 但是0可以由1,2唯一线性表出为 0 31 22
令
x1(k )
X
(k)
x(k) 2
x(k) n
,
k 1,2,
13
向量—则.显—X(然k—)即,—为随—时着—§刻时—t4k间该—.5的动—应变物——化种—用,群—(该中—一动雌—物)性—种动—群物—的的—各年—年龄—龄分组布
中雌性动物的数目会发生变化. 易知,时刻tk该动物种群的第一个年龄组中雌性动物
——————§—4—.5—应——用—(—一—)——————
4.5.1 经济发展与—环境污染的增长模型 矩阵的特征值和特征向量理论在经济分析、生命 科学和环境保护等领域都有着广泛而重要的应 用.§4.5和§4.6两节就来介绍这方面的知识.
本节先来介绍下面的经济发展与环境污染的增长 模型.
[经济发展与环境污染的增长模型]
每个年龄组的长度为
L n
.
11
——————§—4—.5—应——用—(—一—)——————
设第i个年龄组
[i
1 n
L,
i n
L—] 的生育率(即每一雌性动物
平均生育的雌性幼体的数目)为ai,存活率(即第i个
年龄组中可存活到第i+1个年龄组的雌性动物的数目与
第i 个年龄组中雌性动物的总数之比)为bi .
由此可预测该地区年后的环境污染水平和经济发展 水平.
9
——————§—4—.5—应——用—(—一—)——————
— 2 因无实际意义而在Case 2中未作讨论,但在Case 3的讨论中仍起到了重要作用.
由经济发展与环境污染的增长模型易见,特征值 和特征向量理论在模型的分析和研究中获得了成功的 应用.
10
——————§—4—.5—应——用—(—一—)——————
4.5.2莱斯利(—Leslie)种群模型
莱斯利种群模型研究动物种群中雌性动物的年龄分 布与数量增长之间的关系.
设某动物种群中雌性动物的最大生存年龄为L(单位: 年),将区间[0,L]作n等分得n个年龄组
[i 1 L, i L], i 1,2, , n, nn
xy11
3x0 2x0
y0 2 y0
令
0
x0 y0
,1
x1 y1
A
3 2
12
则上述关系的矩阵形式为
1 A0.
此式反映了该地区当前和若干年后的环境污染水
平和经济发展水平之间的关系. 2
——————§—4—.5—应——用—(—一—)——————
如
0
x0 y0
11
—
则由上式得 3 11 4 1
1 A0 2 21 4 41 40
由此可预测该地区若干年后的环境污染水平和经济
发展水平. 一般地,若令xt , yt分别为该地区t年后的环境污染
水平与经济发展水平,则经济发展与环境污染的增长
模型为
xytt
3xt1 2xt1
yt 1 2 yt1
(t 1,2, , k)
3
——————§—4—.5—应——用—(—一—)——————
的数目等于在时段[tk-1,tk]内各年龄组中雌性动物生育的 雌性幼体的数目之和,即
x1(k )
x(k 1) 1
a1
x(k 1) 2
a2
xn(k1) an
a1x1(k1) a2 x2(k1) an xn(k1)
(2.1)
又tk时刻该动物种群的第i+1个年龄组中雌性动物的数 目等于tk-1 时刻第i个年龄组中雌性动物的存活量,即
x(k) i 1
x(k 1) i
bi
bi xi(k 1) ,
i 1,2, , n 1
(2.2)
14
§4.5 应 用(一) ———————————————————— 联立(2.1)和(2.2)—得
显然,1,2线性无关.
下面分三种情况分析:
Case 1 0 1 11
由(*)及特征值与特征向量的性质知,
t
At 0
At1
t 1
1
4t 11
6
——————§—4—.5—应——用—(—一—)——————
即
—
xt yt
4t
11
或
xt yt 4t
此式表明:在当前的环境污染水平和经济发展水平
的前提下,t 年后,当经济发展水平达到较高程度时,
由(*)及特征值与特征向量的性质
8
——————§—4—.5—应——用—(—一—)——————
t At 0 At (31 2—2 ) 3At1 2At2
3
t
112 2t2Fra bibliotek34t
11
2
1t
1 2
3 3
4 4
t t
2 4
,
即
xt yt
3 3
4 4
t t
2 4
,
xt 3 4t 2, yt 3 4t 4
令
x (0) 1
X (0)
x (0) 2
x (0) n
12
§4.5 应 用(一) ————————————————————
X (0) 即为初始时刻该动—物种群中雌性动物的年龄分
布向量.
取
tk
k n
L, k
1,2,
,
设在时刻tk该动物种群的第i个年龄组中雌性动物的
数目为 xi(k), i 1,2, , n
由矩阵A 的特征多项式
3 1
| E A |
( 4)( 1)
2 2
得A 的特征值为
1 4, 2 1
对1 4,解方程组 (4E A)X 0得特征向量 1 11
5
——————§—4—.5—应——用—(—一—)——————
对1 1,解方程组 (E —A) X 0得特征向量
2 12
