多指标席位分配模型的研究
席位分配问题数学建模

席位分配问题是一个常见的实际问题,涉及到资源的分配和管理。
为了解决这个问题,我们可以使用数学建模的方法,通过建立数学模型来分析和优化席位的分配方案。
一、问题描述假设有一个大型会议,需要分配给不同的参与者席位。
每个参与者可能有不同的资格和需求,我们需要根据一定的规则来分配席位。
具体问题包括:1. 参与者数量和席位数量2. 参与者的资格和需求3. 席位分配的规则和标准二、数学建模为了解决席位分配问题,我们可以使用以下数学模型:1. 参与者集合P:表示所有的参与者。
2. 席位集合S:表示所有的席位。
3. 资格矩阵A:表示每个参与者的资格情况,每一行表示一个参与者,每一列表示一个资格类型(例如,专业、身份等)。
4. 需求矩阵D:表示每个参与者对席位的需求情况,每一行表示一个参与者,每一列表示一个席位类型(例如,地点、时间等)。
5. 分配规则R:表示席位的分配规则和标准,如按照资格优先、按照需求优先、按照公平分配等。
根据以上描述,我们可以建立如下的数学模型:目标函数:最小化席位浪费(即席位数与参与者需求之差)约束条件:1. 资格约束:每个参与者的资格必须满足分配规则的要求。
2. 需求约束:每个参与者所需席位类型必须得到满足。
3. 数量约束:总的席位数必须不超过总席位数量。
4. 可行性约束:分配的席位必须是有效的,即不存在冲突和重复的情况。
三、求解方法根据上述数学模型,我们可以使用以下方法进行求解:1. 枚举法:逐个尝试所有可能的席位分配方案,找到满足约束条件的方案。
这种方法需要大量的计算时间和空间,但在某些情况下可能找到最优解。
2. 优化算法:使用优化算法如遗传算法、粒子群算法等,通过不断迭代找到最优解。
这种方法需要一定的编程知识和技能,但通常能够快速找到满意的解。
3. 启发式算法:使用启发式算法如模拟退火、蚁群算法等,通过不断尝试找到满意解。
这种方法相对简单易行,但可能无法找到最优解。
4. 数学软件求解:使用专门的数学软件如Matlab、Python等,通过编程求解上述数学模型。
高中宿舍席位分配数学模型

科学咨询/教育科研
本刊特稿
高中宿舍席位分配数学模型
付潇靓
(山东省枣庄市第八中学 山东枣庄 277000)
摘 要:我们在日常生活中会遇到很多分配问题,例如对 于企业、公司、学校等部门的职位分配都是需要解决的实际问 题。本文讨论了席位分配问题,在以下的分析中,会先按照按 比例分配方法进行分配,然后采用Q值法与D’hondt方法进行 分配[1],最后再采用二者相结合的方法进行分配,从而使分配 达到相对公平的状态。
A
B
(1)如果
>
决定名额分给A宿舍或B宿舍。
> ,通过Q值法的运算
(2)如果
>>
且A宿舍的Q值比B
宿舍大,根据D’hondt方法,应将名额分给A宿舍。
根据表格内计算数据可得,N1=2,N2=4,N3=5。 (四)模型四求解
先将第一个名额分配给人最多的宿舍,C宿舍。然后根据
d'Hondt方法进行分配,直到第二个宿舍有分配名额。由模型
即有不公平的定义为:若有 是不公平的。
成立,则席位分配
此时若有
,则对A不公平,此时定义
为对A的绝对不公平度,
(N1,N2)为对A的相对不公平度;
若有
,则对B不公平,此时定义
B的绝对不公平度,
为对
(N1,N2)为对B的相对不公平度。
不妨假设A方与B方都已分配得到了N1、N2个名额,我
们可以根据相对不公平度r (N ,N )与r (N ,N ),计算
1
2
3.当有
时,说明给B增加1个名
额,将对A不公平,此时对A的相对不公平值为r A
(N1,N2+1) ………………………………………………[2]
席位分配问题的D’hondt模型和相对尾数模型

席位分配问题的D’hondt模型和相对尾数模型席位分配问题的D’hondt模型和相对尾数模型摘要:讨论公平席位分配的模型已有很多。
本文首先用比例加惯例法、Q值法、D’hondt法对问题中名额进行了分配,再对D’hondt法的合理性进行了分析,并在Q值法对绝对尾数(绝对不公平度)的处理方式基础上,提出了相对尾数模型,并讨论了其满足Young公理的1,3,4条;在模型求解上,全部由MATLAB程序来实现名额分配。
关键词:相对尾数 Balinsky & Young不可能定理 MATLAB正文1 问题复述公平的席位分配问题是一个非常有趣而重要的问题,它在政治学、管理学和对策论等领域具有广泛的应用价值。
处理这个问题的最早的方法是Hamilton法,即比例加惯例法;后来出现了Q值法;1974年M.L.Balinski和H.P.Young引入了席位分配问题的公理体系研究方法,并于1982年证明了同时满足五个公理的席位分配方法是不存在的;因此,我们只能根据实际建立在一定公平准则下成立并尽量多的满足Young公理的算法。
这里,我们需要理解并运用比例加惯例法、Q值法、D’hondt法对宿舍委员会名额进行分配,继而提出更优的公平分配席位的方法。
2 模型假设2.1合理假设2.1.1 比例加惯例法、Q值法等分配模型均为已知;2.1.2 各个宿舍相互独立互不影响,人数保持不变;2.1.3 委员分配以各宿舍人数为唯一权重。
2.2 符号约定符号意义Q第个宿舍的Q值 iin第个宿舍的人数 iim第个宿舍分配的名额 iin总人数m总名额数p 第个宿舍的理想分配名额 ii,个宿舍的理想分配名额总席位增加一个时第ip iniq 第个宿舍的分配比例,即 miins 第个宿舍的绝对尾数值 iir 第个宿舍的相对尾数值 ii,个宿舍的相对尾数值总席位增加一席时第ir it按比例分配后剩余名额3 模型的建立与求解3.1按比例加惯例模型分配根据比例加惯例分配模型的原理,编写MATLAB程序实现(附录-程序1,2,3,附录-输入及运行结果1),结果如表所示:表1(比例加惯例法分配结果):10个席位的分配 15个席位的分配宿舍学生人数比例分配惯例分配比例分配惯例分配的席位的结果的席位的结果A 235 2 3 3 4B 333 3 3 4 5C 432 4 4 6 6总数 1000 9 10 13 153.2按Q值法模型分配2ni首先用比例分配法对名额进行初步分配,再根据表达式 i,A,B,CQ,im(m,1)ii对剩下的名额进行分配,编写MATLAB程序实现求解(附录-程序4,5,附录-输入及运行结果2):表2(Q值法分配结果):10个席位的分配 15个席位的分配宿舍学生人数比例分配最终分配比例分配最终分Q值 Q值名额名额名额配名额A 235 2 9204.17 2 3 4602.08 4B 333 3 9240.75 3 4 5544.45 5C 432 4 9331.2 5 6 4443.43 6 总数 1000 9 10 13 153.3 D’hondt模型3.3.1 模型建立设,分别表示宿舍总人数和总分配席位数,()表示各宿舍人数,令nnmi,1,2,3iniaa,(),则得到一个数列,将该数列按递减顺序重新排列,得ij,,1,2,3,1,2,...,,ijijj()k()k()k()kaaa到,其中表示中第大的项。
基于变权综合的多指标席位分配模型

榆 林 学 院 学 报
J OURNAL OF YUU N UNBr ERS I rY
第2 卷 l
第 2期
Ma . 01 r2 l V0 . 1 NO 2 12 .
基 于 变权 综 合 的 多指 标席 位分 配模 型
杨昔阳 王 , 韵
( . 州师 范学 院 数 学与计算机 科 学学 院 , 建 泉 州 320 ; 1泉 福 6 00
标优化算法等 ] 。所有这些经典的算法都存在一
个 局限性 ,即只能 根 据 某 单 一指 标 进 行 席 位 分 配 。
而在实际的席位分配场合 , 决策者往往需要考虑多
个指 标 。解 决 这个 问 题 的 方 法 之 一 是 通 过 加 权 平 均, 综合各 方面 因素得 到 唯一 一 个综 合 指 标 ,再利
∞ , 是单位 i 于 的综 合成绩 可 以表示 为
用 各种经 典的席位 分配 方法进 行分 配 。常用 的普通 线 性加权综 合 ,只考 虑 到 了各 因素 数 值 上 的 大小 ,
忽略 了各 因素 是否 均 衡 发 展 这 一 问题 。而 实 际 上 , 决 策者也很 关心各个 单位 的均衡 发展性 。为 了解决 这个 问题 , 本文 提出 了一种 基于 变权 综合 的多 指标
杨昔阳 , 王
韵: 基于变权综合 的多指标席位分配模型
・l ・ 7
均 ,应 当让 甲 ,乙得 到 的席 位数 一 样 多 , 在 大 多 但 数情 况下 ( 为均衡 发展 更重 要 的场合 ) 认 ,甲应 得的 席位 数应该 多于 乙 。汪培庄 教授 提 出 的变 权综 合 方
法 是 解决这 类 问题 的有 效手 段 ,文献 提 出的权 重 公理 化设计 方法 丰富 了这种 思想 。
数学建模论文-席位公平分配问题

数学建模论文-席位公平分配问题数学建模论文(席位公平分配问题)席位公平分配问题摘要本文讨论了席位公平分配问题以使席位分配方案达到最公平状态。
我主要根据了各系人数因素对席位获得的影响,首先定义了公平的定义及相对不公平的定义,采用了比例模型、汉丁顿模型和Q值模型制定了一个比较合理的分配方案。
首先,我根据相关资料的查阅,定义了公平的定义和不公平的定义以及不公平程度的定义和相对不公平数的定义以便来检验模型的公平性程度。
其次,我建立了一个比例模型,采用了比例相等的方法,列出一个关于所获席位与总席位数和各系人数与各系总人数的等式,进而求得所获席位数。
同时我建立了一D+Q值模型,通过汉丁顿模型和Q值模型的结合,最终得出一个比较合理的分配方案。
最后,我用相对不公平数来检验两个模型的公平性程度。
关键词:数学建模公平定义 Q值模型 d'Hondt(汉丁顿)模型1目录一、问题重述与分析: ................................... 3 1.1问题重述: ........................................ 3 1.2问题分析: ........................................ 3 二、模型假设 .......................................... 4 三、符号说明 .......................................... 4 四、模型建立: ........................................ 5 4.1公平的定义: ...................................... 5 4.2不公平程度的表示: ................................ 5 4.3相对不公平数的定义: .............................. 5 4.4模型一的建立:(比例分配模型) ...................... 6 4.5模型二的建立:(d'hondt模型和Q值模型) (6)五、模型求解 .......................................... 8 5.1模型一求解: ...................................... 8 5.2模型二的求解: .................................... 8 六、模型分析与检验 ..................................... 9 七、模型的评价: ...................................... 11 7.1、优点: ......................................... 11 7.2、缺点: ......................................... 11 7.3、改进方向: ..................................... 11 八、模型优化 ......................................... 11 九、参考文献 (12)2一、问题重述与分析:1.1问题重述:三个系学生共200名(甲系100,乙系60,丙系40),代表会议共20席,按比例分配,三个系分别为10,6,4席。
席位分配模型
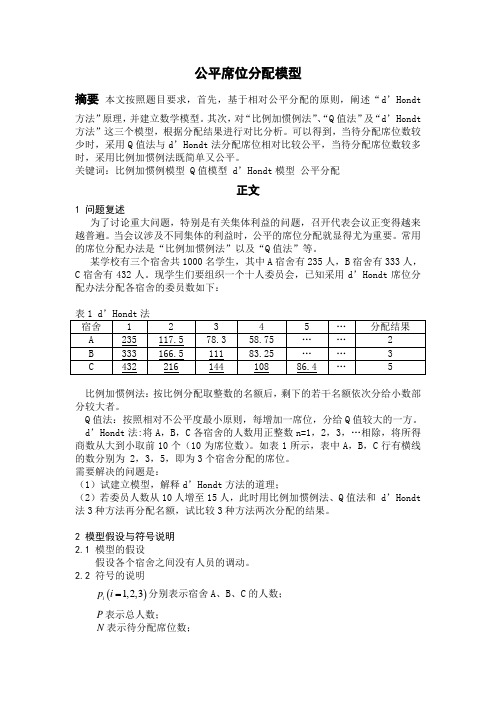
公平席位分配模型摘要本文按照题目要求,首先,基于相对公平分配的原则,阐述“d’Hondt方法”原理,并建立数学模型。
其次,对“比例加惯例法”、“Q值法”及“d’Hondt 方法”这三个模型,根据分配结果进行对比分析。
可以得到,当待分配席位数较少时,采用Q值法与d’Hondt法分配席位相对比较公平,当待分配席位数较多时,采用比例加惯例法既简单又公平。
关键词:比例加惯例模型 Q值模型 d’Hondt模型公平分配正文1 问题复述为了讨论重大问题,特别是有关集体利益的问题,召开代表会议正变得越来越普遍。
当会议涉及不同集体的利益时,公平的席位分配就显得尤为重要。
常用的席位分配办法是“比例加惯例法”以及“Q值法”等。
某学校有三个宿舍共1000名学生,其中A宿舍有235人,B宿舍有333人,C宿舍有432人。
现学生们要组织一个十人委员会,已知采用d’Hondt席位分配办法分配各宿舍的委员数如下:表1 d’Hondt法宿舍 1 2 3 4 5 …分配结果A 235 117.5 78.3 58.75 (2)B 333 166.5 111 83.25 (3)C 432 216 144 108 86.4 (5)比例加惯例法:按比例分配取整数的名额后,剩下的若干名额依次分给小数部分较大者。
Q值法:按照相对不公平度最小原则,每增加一席位,分给Q值较大的一方。
d’Hondt法:将A,B,C各宿舍的人数用正整数n=1,2,3,…相除,将所得商数从大到小取前10个(10为席位数)。
如表1所示,表中A,B,C行有横线的数分别为 2,3,5,即为3个宿舍分配的席位。
需要解决的问题是:(1)试建立模型,解释d’Hondt方法的道理;(2)若委员人数从10人增至15人,此时用比例加惯例法、Q值法和 d’Hondt 法3种方法再分配名额,试比较3种方法两次分配的结果。
2 模型假设与符号说明2.1 模型的假设假设各个宿舍之间没有人员的调动。
数学建模论文 - 席位公平分配问题1

数学建模论文(席位公平分配问题)席位公平分配问题摘要本文讨论了席位公平分配问题以使席位分配方案达到最公平状态。
我主要根据了各系人数因素对席位获得的影响,首先定义了公平的定义及相对不公平的定义,采用了比例模型、汉丁顿模型和Q值模型制定了一个比较合理的分配方案。
首先,我根据相关资料的查阅,定义了公平的定义和不公平的定义以及不公平程度的定义和相对不公平数的定义以便来检验模型的公平性程度。
其次,我建立了一个比例模型,采用了比例相等的方法,列出一个关于所获席位与总席位数和各系人数与各系总人数的等式,进而求得所获席位数。
同时我建立了一D+Q值模型,通过汉丁顿模型和Q 值模型的结合,最终得出一个比较合理的分配方案。
最后,我用相对不公平数来检验两个模型的公平性程度。
关键词:数学建模公平定义 Q值模型 d'Hondt(汉丁顿)模型目录一、问题重述与分析: (3)1.1问题重述: (3)1.2问题分析: (3)二、模型假设 (4)三、符号说明 (4)四、模型建立: (5)4.1公平的定义: (5)4.2不公平程度的表示: (5)4.3相对不公平数的定义: (5)4.4模型一的建立:(比例分配模型) (6)4.5模型二的建立:(d'hondt模型和Q值模型) (6)五、模型求解 (8)5.1模型一求解: (8)5.2模型二的求解: (8)六、模型分析与检验 (9)七、模型的评价: (11)7.1、优点: (11)7.2、缺点: (11)7.3、改进方向: (11)八、模型优化 (11)九、参考文献 (12)一、问题重述与分析:1.1问题重述:三个系学生共200名(甲系100,乙系60,丙系40),代表会议共20席,按比例分配,三个系分别为10,6,4席。
现因学生转系,三系人数为103, 63, 34, 问20席如何分配。
若增加为21席,又如何分配。
因此存在席位公平分配问题,以下针对各系自身人数对所获席位数目的影响建立相关模型,解得最优的席位公平分配方案。
数学建模论文:席位分配问题例题

席位分配问题例题:有一个学校要召开一个代表会议,席位只有20个,三个系总共200人,分别是甲系100,乙系60,丙系40.如果你是会议的策划人,你要合理的分配会议厅的20个座位,既要保证每个系部都有人参加,最关键的就是要对个公平都公平,保证三个系部对你所安排的位置没有异议。
如何分配最为恰当?问题:(1)问20席该如何分配,如果有三名学生转系该怎样分配?(2)若增加21席又如何分配?问题的分析:一、20席分配情况:系名甲乙丙总数学生数100 60 40 200学生人数比例100/200 60/200 40/200席位分配10 6 4 20如果有三名学生转系,分配情况:系名甲乙丙总数学生数103 63 34 200学生人数比例103/200 63/200 34/200按比例分配席位10.3 6.3 3.4 20按惯例席位分配10 6 4 20二、21席位分配情况:系名甲乙丙总数学生数103 63 34 200学生人数比例103/200 63/200 34/200按比例分配席位10.815 6.615 3.57 21按惯例席位分配11 7 3 21 这个分配结果出现增加一席后,丙系比增加席位前少一席的情况,这使人觉得席位分配明显不公平。
要怎样才能公平呢?模型的建立:假设由两个单位公平分配席位的情况,设单位人数席位数单位A p1 n1单位B p2 n2要公平,应该有p1/n1 = p2/n2,但这一般不成立。
注意到等式不成立时有若p1/n1 >p2/n2 ,则说明单位A吃亏(即对单位A不公平)若p1/n1 <p2/n2 ,则说明单位B 吃亏(即对单位B不公平)因此可以考虑用算式p=|p1/n1-p2/n2|来作为衡量分配不公平程度,不过此公式有不足之处(绝对数的特点),如:某两个单位的人数和席位为n1 =n2 =10 ,p1 =120,p2=100,算得p=2另两个单位的人数和席位为n1 =n2 =10 ,p1 =1020,p2=1000, 算得p=2虽然在两种情况下都有p=2,但显然第二种情况比第一种公平。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多指标席位分配模型的研究
The Mathematical Model about Multi-Criteria Distribution of Seats Number
赵洋阮小军
Zhao YangRuan Xiaojun
(南昌大学数学系, 江西南昌330031)
(Department of Mathematics, Nanchang University, Jiangxi Nanchang330031)
摘要: 针对经典席位分配模型在解决一些分配问题时的局限性,提出了多指标席位分配问题的数学模型,指出该模型是对经典席位分配模型的一个推广,并通过实例说明该模型在处理一些分配问题时更具公平合理性。
关键词: 席位分配问题; 多指标决策
中图分类号:F224文献标识码:A文章编号:1671-4792-(2008)3-0068-03
Abstract: In order to discard the requirement for many problems to be solved by classical distribution ofseats number, an evolutionary program method is proposed. The mathematical model about multi-criteria distri-bution of seats number is a generalization of the classical one. An example is shown that this model dealingwith some problems of distribution is more fair and reasonable than that classical one.Keywords: Distribution of Seats Number; Multi-Criteria Decision Making
0引言
席位分配模型[1,2]处理和研究的是人类社会生活中相当
普遍的一类资源分配问题,其目标是试图在一个大集体对小
集体进行某种资源分配时尽可能做到公平合理。
但在经典席
位分配模型中只考虑了参加分配的各单位成员数这一唯一指
标,而在解决实际的资源分配问题时,由于参加分配的各单
位情况的复杂性,往往使得做出分配决策的影响因素是多方
面的。
如果此时只考虑参加分配各单位的成员数这一个指
标,可能会导致做出的分配决策在某种程度上不能很好的体
现公平合理性。
因此,本文提出一种综合考虑多方面影响因
素,使得席位分配更加公平合理的数学模型,即多指标席位
分配模型。
1建立模型
在多指标席位分配问题中,设有m个单位参加分配,记
为I={1,2,…,m},第i个单位的人数为a
i(i=1,2,…,m),总
人数
15
16
科技广场2008.3。
1.3
计算各单位的综合指标值
对第i个单位的各指标值进行加权求和,
计算出该单位
的综合指标值为
:
(
1)
并记总体的综合指标值为
(2)
其中xi(i=1,2,L,m)为非负整数
Pi按前面的
(1)式计算
性质1 当指标个数n=1时,多指标席位分配模型即为
经典席位分配模型。
易见当
n=1时,多指标席位分配模型只考虑单位成员数
的这一个影响因素,而一个指标就不存在数量级和纲量不
同,这时令单位成员数这一影响因素的指标值就是各单位参加分配的人数,显然它的权重
w=1,则该模型就是经典席位
分配模型。
2
实例应用
(奖学金名额分配问题)某系进行年终奖学金评定工作,经系领导商议决定从该系
176名学生中选取
60名同学分别授
予一等、二等、三等奖学金。
奖学金的分配方案遵循鼓励在校学生刻苦学习、
奋发向上,
在德、智、体等方面全面发展的原则。
系领导综合考虑以下
7个影响因素
(见表一),
将这
60个名额公平合理分配到
A,B,C,D,E五个班上。
表一
各项测评的人数分布情况
(单位:人)
根据多指标席位分配模型计算出各班分得的奖学金名额数,并用只考虑各班学生人数这一指标的经典席位分配模型求出每个班分得的奖学金名额数,然后将这两种模型的计算
结果进行比较
(见表二)。
表二
各班分得的奖学金名额
(单位:人)从表一和表二不难看出,学生人数最多的C班在德、智、体方面优秀的学生很少而不合格的学生很多,
学生人数最少
的A班在德、智、体方面优秀的学生很多而不合格的学生很少。
若采用经典席位分配模型,由于只考虑了学生人数这一
影响因素,
使得C班分得的名额最多而
A班分得的名额最少,
这时就会导致
A班有许多各方面都非常优秀的学生得不到奖
学金,而C班那些各方面都很普通的学生却能够很容易就得
到奖学金。
当采用多指标席位分配模型进行奖学金的名额分
配时,不仅考虑到各班的学生人数,
还综合考虑了各班学生德、智、体等方面全面发展的情况,
这就使得学生整体综合
素质较好的A班分得的奖学金名额相对多一些,而学生整体综合素质不是很高的C班分得的奖学金名额相对少一些。
因此,本着鼓励在校学生刻苦学习、奋发向上,在德、智、体等方面全面发展的原则,这里采用多指标席位分配模型比采用经典席位分配模型进行奖学金的名额分配是更为公平合理的。
3结束语
在实际中遇到的很多资源分配问题是相当复杂的,如果采用经典席位分配模型,此时只考虑了参加分配的单位成员数这一个影响因素,往往使得分配不能够做到“真正的”公平合理。
针对该局限性,本文在经典席位分配模型的基础上综合考虑了多个影响因素,较全面地兼顾到参加分配各单位的实际情况,提出了一种新的解决资源分配问题的建模方法——多指标席位分配模型。
并通过奖学金名额分配这一实际问题,说明了多指标席位分配模型较经典席位分配模型更为公平合理一些。
另外,性质1表明了经典席位分配模型就是多指标席位分配模型的一种特殊情况。
由于多指标席位分配模型是对经典席位分配模型的推广,因此它在解决资源分配问题时适用范围更为广泛。
参考文献
[1]姜启源. 数学模型[M]. 北京: 高等教育出版社,
1987.
[2]M. L. Balinski, H. P. Young. The Quota Method
of Apportionment[J], American Mathematical Monthly,
Vol. 82, No. 7 (Aug. - Sep., 1975): 701-730.
[3]C. v. Altrock and B. Krause. Multi-Criteria
decision-making in German automotive industry using
fuzzy logic[J], Fuzzy Sets and Systems. Vol. 63(1994):
375-380.
[4]D.Diakoulaki, G.Mavrotas and L.Papayannakis.
Determining objective weights in multiple criteria
problem: The CRITIC method[J], Computer Ops Res, Vol.
22(1995): 763  ̄ 770.
作者简介
赵洋(1981—),男,湖北宜昌人,硕士,助教,主要
从事时间序列分析及数学模型的研究。
多
指
标
席
位
分
配
模
型
的
研
究
17。
