最新初中数学中的几道变式训练题
人教版初中数学中考 练本 中考真题中的教材变式题(一题多变)
（2）解：连接AQ，CQ.
∵四边形ABCD是正方形，
∴BA＝BC，∠ABQ＝∠CBQ＝45°，∠ABF＝90°.
∵BQ＝BQ，∴△ABQ≌△CBQ（SAS），
∴QA＝QC，∠BAQ＝∠BCQ.
∵EQ垂直平分线段AF，∴QA＝QF，
∴QC＝QF，∴∠QFC＝∠QCF，
∴∠QFC＝∠BAQ.
∵∠QFC＋∠BFQ＝180°，
∴AB＝BC，
∠B＝∠BCD＝90°.
∵CF平分∠DCH，
∴∠ECF＝135°.
∵AG＝CE，∴BG＝BE，
∴△BGE是等腰直角三角形，
∴∠BGE＝∠BEG＝45°，∴∠AGE＝135°＝∠ECF.
∵AE⊥EF，∴∠AEB＋∠FEC＝90°.
∵∠BAE＋∠AEB＝90°，∴∠FEC＝∠BAE，
∴△GAE≌△CEF，∴AE＝EF.
的中点G，连接EG.）
变式1：（2022·泸州）如图，在边长为3的正方形ABCD中，E是边AB上的点，且
BE＝2AE，过点E作DE的垂线，交正方形外角∠CBG的平分线于点F，交边BC于
点M，连接DF，交边BC于点N，则MN的长为（
B ）
D.1
变式2：（2022·呼和浩特）下面图片是八年级教科书中的一道题.
∵CE⊥BF，∴∠BOE＝90°，
∴∠2＋∠3＝90°，∴∠1＝∠3.
∵∠DAB＝90°＝∠CME，
∵AB＝BC，∠ABC＝60°，
变式3：（2020·鞍山）在矩形ABCD中，E是射线BC上一动点，连接AE，过点B作
BF⊥AE于点G，交直线CD于点F.
（1）当矩形ABCD是正方形时，以点F为直角顶点在正方形ABCD的外部作等腰
变式3：（2022·兰州）综合与实践
初中数学变式训练
初中数学教学变式训练题1、一膄快艇与孟关良的皮艇同在起点，快艇以每秒5米的速度先行了20米孟关良为了追上快艇，必须奋力前划，他如果以每秒6米的速度划行多少秒才能追上快艇？变式1：一膄快艇与孟关良的皮艇同在起点，快艇以每秒5米的速度先行了20秒，孟关良为了追上快艇，必须奋力前划，同学们，请你想一想他如果以每秒6米的速度划行多少秒才能追上快艇？（从先行20米改为先行了20秒）变式2：我们学校有一块300米的跑道在比赛跑步时经常会涉及到相遇问题和追及问题现有甲、乙两人比赛跑步，甲的速度是10米/秒，乙的速度是8米/秒，他们两人同地出发（1）两人同时相向而行经过几秒两人相遇。
（2）两人同时同向而行经过几秒两第一次相遇。
（3）乙先出发5秒，然后甲开始出发，问甲经过几秒两人第一次相遇。
变式3：一膄快艇与孟关良的皮艇同在起点，快艇以每秒5米的速度先行了10秒，教练要求他用45秒追上快艇，孟关良为了追上快艇，必须奋力前划，他以每秒6米的速度划行，划了5秒后他发现用这样的速度不能在规定的时间内追上，请问他的想法用45秒不能追上快艇对不对？如果他要追上请你算一算孟关良后来要用多少速度才能在规定的时间内追上快艇？2、16的算术平方根是。
变式1：16的平方根是。
变式2：的平方根是。
变式3：已知a的算术方根是2，则a= 。
3、“求证：顺次连结四边形各边中点所得的四边形是平行四边形.”变式1：顺次连结梯形各边中点所得的四边形是什么四边形?变式2：顺次连结矩形各边中点所得的四边形是什么四边形?变式3：顺次连结菱形各边中点所得的四边形是什么四边形?变式4：顺次连结正方形各边中点所得的四边形是什么四边形?变式5：顺次连结什么四边形中点可以得到平行四边形?变式6：顺次连结什么四边形中点可以得到矩形?4、例题：如图1，在平行四边形ABCD中，E、F分别是OB、OD的中点，四边形AECF是平行四边形吗？请说明理由。
图1变式训练：变式1:若将例题中的已知条件E、F分别是OB、OD的中点改为点E、F三等分对角线BD，其它条件不变，问上述结论成立吗？为什么？变式2:若将例题中的已知条件E、F分别是OB、OD的中点改为BE=DF，其它条件不变，结论成立吗？为什么？变式3:若将例题中的已知条件E、F分别是OB、OD的中点改为E、F为直线BD上两点且BE=DF，结论成立吗？为什么？5、如图14，已知，是一次函数的图象和反比例函数的图象的两个交点．求反比例函数和一次函数的解析式；变式一、求直线与轴的交点的坐标及△的面积；变式二、求方程的解（请直接写出答案）；变式三、求不等式的解集（请直接写出案）.6、已知正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A旋转．（1）发现：当E点旋转到DA的延长线上时（如图1），△ABE与△ADG的面积关系是： ____________．（2）引申：当正方形AEFG旋转任意一个角度时（如图2），△ABE与△ADG的面积关系是：____________．并证明你的结论（3）运用：已知三角形ABC，AB=5cm,AC=3cm,分别以AB、BC、CA为边作正方形（如图3），则图中阴影部分的面积和最大值是. ____________7、正方形ABCD与正方形CEFG的位置如图所示，点G在线段CD或CD的延长线上．分别连接BD、BF、FD，得到△BFD．(1)在图①～图③中，若正方形CEFG的边长分别为1、3、4，且正方形ABCD的边长均为3，请通过计算填写下表：正方形CEFG的边长 1 3 4△BFD的面积(2)若正方形CEFG的边长为a，正方形ABCD的边长为b，猜想S△BFD的大小，并结合图③证明你的猜想．8、如图（1），四边形ABCD内部有一点P，使得S△APD +S△BPC=S△PAB+S△PCD填空或解答：点B、C、E在同一直线上，点A、D在直线CE的同侧，AB＝AC，EC＝ED，∠BAC＝∠CED，直线AE、BD交于点F。
初中数学中的几道变式训练题
初中数学中的几道变式训练题一、已知：点O是等边△ABC内一点,OA=4，OB=5，OC=3求∠AOC的度数。
变式1：在△ABC中，AB=AC，∠OA=4，OB=6，OC=2求∠AOC的度数。
变式2：如图,点O是等边△ABC内一点,∠AOB=110°, ∠BOC=135°试问:(1)以OA、OB、OC为边能否构成一个三角形?若能,请求出三角形各内角的度数;若不能,请说明理由.(2)如果∠AOB的大小保持不变,那么当∠BOC等于多少度时, 以OA、OB、OC为边的三角形是一个直角三角形?二、已知：C为AB上一点，△ACM和△CBN为等边三角形（如图所示）求证：AN=BMAB COACAB CO（分析：如对此题多做一些引申，既可以培养学生的探索能力，又可培养学生的创新素质）探索一：设CM 、CN 分别交AN 、BM 于P 、Q ，AN 、BM 交于点R 。
问此题中还有其他的边相等以及特殊角、特殊图形吗？给予证明。
探索二：△ACM 和△BCN 如在AB 两旁，其它条件不变，AN=BM 成立吗？探索三：△ACM 和△BCN 分别为以AC 、BC 为底且顶角相等的等腰三角形，其它条件不变，AN=BM 成立吗？探索四：A 、B 、C 三点不在一条直线上时，其它条件不变，AN=BM 成立吗？三、轴对称：已知直线l 及同侧两点A 、B ，试在直线l 上选一点C ，使点C 到点A 、B 的距离和最小。
变式1：如图，请你设计出两种方案的路线和最短的行走路线（画图并说明理由）方案1：小华由家先去河边，再去姥姥家；MACBBAl方案2：小华由家先去姥姥家，再去河边；变式2：已知: AB 、AC 表示两条交叉的小河, P 点是河水化验室, 现想从P 点出发, 先到AB 河取点水样, 然后再到AC 河取点水样, 最后回到P 处化验河水, 怎么走路程最短呢？实验员小王说:“我从P 点笔直向A 走, 同时取好两河水样再原路返回, 这样走, 路最近。
初中数学变式训练题2
初中数学变式教学研究-----------10道变式题1：平面直角坐标系中，已知A(4,0)，B （0,3），点C 是坐标轴上的点，并且△ABC 为直角三角形，请求出满足要求的所有点C 的坐标 .答案（0，0）（49-，0）（0，316-） 变式1：平面直角坐标系中，已知A(6,3)，B （1,3），点C 是坐标轴上的点，并且△ABC 为直角三角形，请求出满足要求的所有点C 的坐标 .答案（1，0）（6，0）变式2：平面直角坐标系中，已知A(0,2)，B （5, 2），点C 是x 轴上的点，并且△ABC 为直角三角形，请求出满足要求的所有点C 的坐标 .答案（0，0）（1，0）（4，0）（5，0）变式3：平面直角坐标系中，已知A(2,2)，B （-2,2），点C 是坐标轴上的点，若△ABC 为直角三角形，则满足要求的所有点C 有 个.答案 8个2.平面直角坐标系中，已知A(4,0)，B （0,3），点C 是坐标轴上的点，并且△ABC 为直角三角形，请求出满足要求的所有点C 的坐标 .答案（0，0）（49-，0）（0，316-） 变式1：平面直角坐标系中，已知A(1,0)，B （5, 0），点C 是直线2y x =-上的点，若△ABC 为直角三角形，则点C 的坐标为 .答案（1，-1）（5，3）（275-，271-）（275+，271+） 变式2：平面直角坐标系中，已知A(-2,0)，B （2, 0），点C 是双曲线 上的点，若△ABC 为直角三角形，则满足要求的点C 的个数为 个.答案 3变式3：平面直角坐标系中，已知A(3,0)，B （0, 4），点C 是抛物线 的对称轴上的点，若△ABC 为直角三角形，则点C 的坐标为 .答案（4，2）（4，7）（4， ）3．平面直角坐标系中，已知A(4,0)，B （0,3），点C 是坐标轴上的点，并且△ABC 为直x y 2=1682+-=x x y 43角三角形，请求出满足要求的所有点C 的坐标 .答案（0，0）（49-，0）（0，316-）变式1：平面直角坐标系中，已知A(4,0)，B （0,3），点C 是坐标轴上的点，点D 在平面直角坐标系内，使 A 、B 、C 、D 为矩形，则点C 的坐标为 .答案（0，0）（49-，0）（0，316-） 变式2：平面直角坐标系中，已知A(0,2)，B （5, 2），点C 是x 轴上的点，点D 在第一象限内，使 A 、B 、C 、D 为矩形，则点D 的坐标为 .答案（1，4）（4，4）变式3：平面直角坐标系中，已知A(1,0)，B （5, 0），点C 是直线2y x =-上的点，点C 是坐标轴上的点，点D 在平面内，使 A 、B 、C 、D 为顶点的四边形为矩形，则点C 的坐标为 .答案（1，-1）（5，3）（275-，271-）（275+，271+）4：直角梯形ABCD 中，AD=1， BC=4 ， DC =4。
最新初中数学一题多变、一题多解
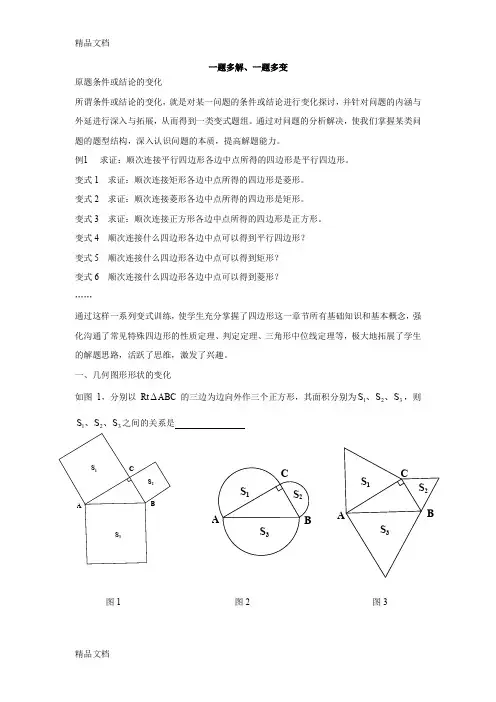
CBAS 2S 3S 1CBAS 3S 2S 1S 3S 2S 1CBA一题多解、一题多变原题条件或结论的变化所谓条件或结论的变化，就是对某一问题的条件或结论进行变化探讨，并针对问题的内涵与外延进行深入与拓展，从而得到一类变式题组。
通过对问题的分析解决，使我们掌握某类问题的题型结构，深入认识问题的本质，提高解题能力。
例1 求证：顺次连接平行四边形各边中点所得的四边形是平行四边形。
变式1 求证：顺次连接矩形各边中点所得的四边形是菱形。
变式2 求证：顺次连接菱形各边中点所得的四边形是矩形。
变式3 求证：顺次连接正方形各边中点所得的四边形是正方形。
变式4 顺次连接什么四边形各边中点可以得到平行四边形？ 变式5 顺次连接什么四边形各边中点可以得到矩形？ 变式6 顺次连接什么四边形各边中点可以得到菱形？ ……通过这样一系列变式训练，使学生充分掌握了四边形这一章节所有基础知识和基本概念，强化沟通了常见特殊四边形的性质定理、判定定理、三角形中位线定理等，极大地拓展了学生的解题思路，活跃了思维，激发了兴趣。
一、几何图形形状的变化如图1，分别以Rt ABC 的三边为边向外作三个正方形，其面积分别为321S S S 、、，则321S S S 、、之间的关系是图1 图2 图3E S 3S 2S 1DCBAS 3S 2S 1ABCDABCD S 3S 2S 1变式1：如图2，如果以Rt ∆ABC 的三边为直径向外作三个半圆，其面积分别为321S S S 、、，则321S S S 、、之间的关系是变式2：如图3，如果以Rt ∆ABC 的三边为边向外作三个正三角形，其面积分别为321S S S 、、，则321S S S 、、之间的关系是变式3：如果以Rt ∆ABC 的三边为边向外作三个一般三角形，其面积分别为321S S S 、、，为使321S S S 、、之间仍具有上述这种关系，所作三角形应满足什么条件？证明你的结论。
中考数学试题变式 变式训练
D3
C
O
x
D3 （ -
D2
等腰三角形的分类讨论
腰 一边
底
顶角 一角 底角 一腰上的高
形内 形外
一高
底边上的高
简解：过点A作AE⊥PB于E，过点C作CF⊥PB，交BP延 长线于F，由PB=5，S△PBC=5，得CF=2，由 PB=5，S△PAB=10， 得AE=4，易证 ∴BE=CF=2，∴S正ABCD=AB2=BE2+AE2=20
3、如图6，P是正方形ABCD外一点，PB=5， S△PAB=10，AM上是否存在点C，使 △ABC是等腰三角形
3 10 C1（ 3 10 - 6,） - 6 - 3 10） ,- 3 10 C 2（ 12 , 18 C 3（ ） - 1 , 5） C 4（
变式二
平行四边形中点的存在性问题
如图，在平面直角坐标系中，函数y＝2x＋ 12的图象分别交x轴、y轴于A、B两点．过 点A的直线交y轴正半轴于点M，且点M为 线段OB的中点。
变式一
三角形中的点的存在性问题
如图，在平面直角坐标系中，函数y＝2x＋12的图象分别交x轴、y轴于A、 B两点．过点A的直线交y轴正半轴于点M，且点M为线段OB的中点。 在坐标轴上是否存在点C，使以A,B,C为顶点的三角形是等腰三角形？
如图，在平面直角坐标系中，函数y＝2x＋12的图 象分别交x轴、y轴于A、B两点．过点A的直线交y轴 正半轴于点M，且点M为线段OB的中点。
如图，在平面直角坐标系中，函数y＝2x＋12的图 象分别交x轴、y轴于A、B两点．过点A的直线交y 轴正半轴于点M，且点M为线段OB的中点。
在平面内是否存在点C，使以 A,B,M,C为顶点的四边形是等腰梯形？
初中数学中的几道变式训练题
初中数学中的几道变式训练题一、 已知：点O 是等边△ABC 内一点,OA=4，OB=5，OC=3 求∠AOC 的度数。
变式1： 在△ABC 中，AB=AC ，∠ OA=4，OB=6，OC=2 求∠AOC 的度数。
变式2：如图,点O 是等边△ABC 内一点,∠AOB=110°, ∠BOC=135° 试问:(1)以OA 、OB 、OC 为边能否构成一个三角形?若能,请求出三角形各内角的度数;若不能,请说明理由.(2)如果∠AOB 的大小保持不变,那么当∠BOC 等于多少度时, 以OA 、OB 、OC 为边的三角形是一个直角三角形?二、已知：C 为AB 上一点，△ACM 和△CBN 为等边三角形（如图所示）求证：AN=BM（分析：如对此题多做一些引申，既可以培养学生的探索能力，又可ABC O A C A BC OMACB培养学生的创新素质）探索一：设CM、CN分别交AN、BM于P、Q，AN、BM交于点R。
问此题中还有其他的边相等以及特殊角、特殊图形吗？给予证明。
探索二：△ACM和△BCN如在AB两旁，其它条件不变，AN=BM成立吗？探索三：△ACM和△BCN分别为以AC、BC为底且顶角相等的等腰三角形，其它条件不变，AN=BM成立吗？探索四：A、B、C三点不在一条直线上时，其它条件不变，AN=BM 成立吗？三、轴对称：已知直线l及同侧两点A、B，试在直线l上选一点C，使点C到点A、B的距离和最小。
变式1：如图，请你设计出两种方案的路线和最短的行走路线（画图并说明理由）方案1：小华由家先去河边，再去姥姥家；方案2：小华由家先去姥姥家，再去河边；小华家河流BAl变式2：已知: AB 、AC 表示两条交叉的小河, P 点是河水化验室, 现想从P 点出发, 先到AB 河取点水样, 然后再到AC 河取点水样, 最后回到P 处化验河水, 怎么走路程最短呢？实验员小王说:“我从P 点笔直向A 走, 同时取好两河水样再原路返回, 这样走, 路最近。
全等三角形中的变式训练题
全等三角形中的变式训练题
设计者：海林市二道镇中学刘明玺
基本图形
习题：已知如图，AB⊥DC于B，且BD=BA，BE=BC。
求证：⑴DE=AC ⑵DE⊥AC
变式一、将上题中的△DBE沿DC方向平移至下图中的各种情况时，还有DE=AC、DE⊥AC吗？为什么？
变式二：已知：如图，△ABC中，AC=BC，AC⊥BC，直线EF交AC于F，交AB于E，交BC的延长线于D，且CF=CD，连结AD、BF，则BF与AD有何关系？试证明你的结论。
变式三：如图所示，在正方形ABCD中，E是正方形边AD上一点，F是BA延长线上一点，并且AF=AE，已知△ABE≌△ADF。
⑴在图中，可以通过平移、翻折、旋转中的哪一种方法，使△ABE与△ADF完全重合；
⑵指出图中线段BE与DF之间的关系。
变式四：已知：如图，AD为△ABC的高，E为AC上一点，BE交AD于F，且有BE⊥AC，FD=CD，求证：BF=AC
变式五：△ABC中，∠A=90°，AB=AC，BD平分∠ABC交AC于点D，CE⊥BD于E，若BD=m，EC=n，试探m、n之间的关系式。
初中数学之变式训练
初中数学之变式训练 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN【模拟试题】一、选择题1. “x 的2倍与3的差不大于8”列出的不等式是（ ） A. 2x －3≤8 B. 2x －3≥8 C. 2x －3＜8 D. 2x －3＞82.下列不等式一定成立的是（ ）A. 5a ＞4aB. x +2＜x +3C. －a ＞－2aD.a a 24> 3. 如果x ＜－3，那么下列不等式成立的是（ ）A. x 2＞－3xB. x 2≥－3xC. x 2＜－3xD. x 2≤－3x 4. 不等式－3x +6＞0的正整数有（ ）A. 1个B. 2个C. 3个D. 无数多个 5. 若m 满足|m |＞m ，则m 一定是（ ）A. 正数B. 负数C. 非负数D. 任意有理数 6. 在数轴上与原点的距离小于8的点对应的x 满足（ ） A. －8＜x ＜8 B. x ＜－8或x ＞8 C. x ＜8 D. x ＞87. 若不等式组⎩⎨⎧>≤11x m x 无解，则m 的取值范围是（ ） A. m ＜11 B. m ＞11 C. m ≤11 D. m ≥118. 要使函数y =（2m －3）x +（3n +1）的图象经过x 、y 轴的正半轴，则m 与n 的取值应为（ ）A. m ＞23，n ＞－31B. m ＞3，n ＞－3C. m ＜23，n ＜－31D. m ＜23，n ＞－31二、填空题9. 不等式6－2x ＞0的解集是________.10. 当x ________时，代数式523--x 的值是非正数.11. 当m ________时，不等式（2－m ）x ＜8的解集为x ＞m -28.12. 若x =23+a ，y =32+a ，且x ＞2＞y ，则a 的取值范围是________. 13. 已知三角形的两边为3和4，则第三边a 的取值范围是________.14. 不等式组⎩⎨⎧-<+<212m x m x 的解集是x ＜m －2，则m 的取值应为________.15. 已知一次函数y =（m +4）x －3+n （其中x 是自变量），当m 、n 为________时，函数图象与y 轴的交点在x 轴下方.16. 某种商品的价格第一年上升了10%，第二年下降了（m －5）%（m ＞5）后，仍不低于原价，则m 的值应为________.三、解答题17. 解不等式（组）（1）－2（x －3）＞1 （2）⎪⎩⎪⎨⎧-<-+≤-3314)3(265x x x x18. 画出函数y =3x +12的图象，并回答下列问题： （1）当x 为什么值时，y ＞0（2）如果这个函数y 的值满足－6≤y ≤6，求相应的x 的取值范围.19. 已知方程组⎩⎨⎧=+-=+2212y x m y x 的解x 、y 满足x +y ＞0，求m 的取值范围.120. 某批发商欲将一批海产品由A 地运往B 地.汽车货运公司和铁路货运公司均开办海产品运输业务.已知运输路程为120千米，汽车和火车的速度分别为60千米/时、100千米/时.小时的冷藏费.（1）设该批发商待运的海产品有x （吨），汽车货运公司和铁路货运公司所要收取的费用分别为y 1（元）和y 2（元），试求y 1和y 2与x 的函数关系式；（2）若该批发商待运的海产品不少于30吨，为节省运费，他应选择哪个货运公司承担运输业务？21. 某童装厂，现有甲种布料38米，乙种布料26米，现计划用这两种布料生产L 、M 两种型号的童装共50套.已知做一套L型号的童装需用甲种布料0.5米，乙种布料1米，可获利45元，做一套M型号的童装需用甲种布料0.9米，乙种布料0.2米，可获利30元，设生产L型号的童装套数为x（套），用这些布料生产两种型号的童装所获得利润为y（元）.（1）写出y（元）关于x（套）的代数式，并求出x的取值范围.（2）该厂生产这批童装中，当L型号的童装为多少套时，能使该厂的利润最大最大利润是多少玩数学------------变式训练一1、（2008山东模拟）如图所示，等腰Rt△ABC中，P是斜边BC的中点，以P 为顶点的直角边分别与边AB、AC交于点E、F，连结EF.当∠EPF绕顶点P旋转时（点E不与A、B重合），△PEF也始终是等腰直角三角形，请说明理由.2、一位同学拿了两块45三角尺MNK△，ACB△做了一个探究活动：将MNK△的直角顶点M放在ABC△的斜边AB的中点处，设4AC BC==．ANAMAMD（1）如图（1），两三角尺的重叠部分为ACM△，则重叠部分的面积为，周长为．（2）将图（1）中的MNK△绕顶点M逆时针旋转45，得到图26（2），此时重叠部分的面积为，周长为．（3）如果将MNK△绕M旋转到不同于图（1）和图（2）的图形，如图（3），请你猜想此时重叠部分的面积为。
初中数学改编题
解 (3 )点 ： B 能叠M 在 上 D . .直 . ....线 ............................1 ...分 ..... 由2 ） （得 P M ， ∽ B NM ; B NM D NM N 沿直 M折 N 线 叠纸 B 能 片 叠 ， M 在 上 点 D . .直 . ....2 线 .分 ....
证:( 明 1 ) PN M BN 1 Q 8 0 0 90 0 90 0 PN M PM 9N 0 0 ; BN Q PM ...N .......2 .分 ... 又 NP M BQ 9 N 0 0 ; NM ∽ B PN ...Q ....3 .分 ...
片展开
(2)再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得
编
到折痕BM。同时得到了线段BN。
变式一：
沿MN线折叠得折痕MH，点B在直线MD上，利用展开图探究：
题
△BMH是什么三角形并证明你的结论．
一
改编目的：通过对原题的
引申，培养了学生的发散
性思维，识图能力和灵活
运用数学知识解决实际问
题的能力。
原
题
原题出自：人教版八 年级（下册）课本115 页教学活动1
大家好
1
原题：如果我们身旁没有量角器或三角尺，需要做600,300,150
课
的角等大小的角，可以采用下面的方法： (1)对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸
片展开
(2)再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得
片展开
(2)再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得
编
到折痕BM。同时得到了线段BN。
变式三：
乘法变式练习题
乘法变式练习题一、基础乘法变式1. 计算下列乘法并写出变式：- 3 × 4 = 12- 4 × 3 = 12- 12 ÷ 3 = 4- 12 ÷ 4 = 32. 完成以下乘法并找出乘法的变式：- 5 × 6 = 30- 6 × 5 = 30- 30 ÷ 5 = 6- 30 ÷ 6 = 5二、乘法与加法的变式1. 将下列乘法表达式转换为加法表达式：- 4 × 7 = 4 + 4 + 4 + 4 + 4 + 4 + 42. 完成以下乘法并转换为加法：- 8 × 9 = 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8三、乘法与除法的变式1. 将下列乘法表达式转换为除法表达式：- 6 × 8 = 48 → 48 ÷ 6 = 8- 9 × 5 = 45 → 45 ÷ 9 = 52. 完成以下乘法并找出对应的除法：- 7 × 11 = 77 → 77 ÷ 7 = 11- 12 × 3 = 36 → 36 ÷ 12 = 3四、乘法的逆运算1. 给定乘法结果，找出乘法的两个因数：- 24 ÷ 3 = ?- 56 ÷ 7 = ?2. 根据乘法结果找出可能的乘法表达式：- 36 ÷ 4 可能的乘法表达式是4 × 9 或9 × 4五、乘法的应用题1. 一个班级有4个小组，每个小组有8名学生。
这个班级总共有多少名学生？2. 一个果园里有5排苹果树，每排有12棵。
这个果园里总共有多少棵苹果树？六、乘法的拓展练习1. 计算下列乘法表达式，并找出它们的变式：- 7 × 13 = ?- 13 × 7 = ?2. 计算下列乘法表达式，并将其转换为加法表达式：- 9 × 14 = ?结束语通过以上乘法变式练习题，学生可以加深对乘法运算规则的理解，提高解决实际问题的能力。
数学九年级教材下册变式题
=BD·AE +BD·CF =BD〔AE + CF〕=BD〔AO· sinα + CO· sinα〕=BD〔AO + CO〕sinα =BD·AC·sinα，∴当BD = AC =m时，S最大，为．题目抛物线y = ax2 + bx + c与x轴的公共点是A〔－1，0〕、B〔3，0〕，求这条抛物线的对称轴．〔人教课本P23 4题〕解∵抛物线y = ax2 + bx + c与x轴的公共点是A〔－1，0〕、B〔3，0〕，∴解得∴抛物线的方程为y = ax2－2ax－3a = a〔x2－2x－3〕=a〔x－1〕2－4a〔a≠0〕，因此，所求抛物线的对称轴为x = 1．另法∵抛物线y = ax2 + bx + c与x轴的公共点是A〔－1，0〕、B〔3，0〕，∴抛物线的方程可设为y = a〔x + 1〕〔x－3〕，a≠0，即y =－a〔x2－2x－3〕=a〔x－1〕2－4a〔a≠0〕，所以，抛物线的对称轴为x = 1．法三x = h与x轴垂直，∴对称轴必过点A〔－1，0〕、B〔3，0〕的中点，为h－〔－1〕= 3－h，得．点评a＞0和a＜0讨论．适当改变条件，可得出许多新颖的题目来〔如变式4这种开放题〕．演变变式1抛物线y = ax2 + bx + c与x轴的公共点是A〔－1，0〕、B〔3，0〕，与y轴的公共点是C，顶点是D．〔1〕假设△ABC是直角三角形，那么a =；〔2〕假设△ABD 是直角三角形，那么a =．解在草稿纸上画出大致图象，可知〔1〕假设△ABC是直角三角形，那么直角顶点只能是C，∴C〔0，c〕，即C〔0，－3a〕，于是〔－3a〕2 = 1×3，解得a =±1．〔2〕假设△ABD是直角三角形，那么直角顶点只能是D，∴D〔0，－4a〕，于是由2︱〔－4a〕︱= 4，解得a =±．变式2抛物线y = ax2 + bx + c与x轴的公共点是A〔－1，0〕、B〔3，0〕，与y轴的公共点是C，顶点是D．问是否存在非零常数a，使A、B、C、D在一个圆上？解假设存在非零常数a，使A、B、C、D在一个圆上，那么圆心E必在抛物线的对称轴xE〔1，m〕，那么︱DE︱=︱m + 4a︱，︱AE︱=︱BE︱=，︱CE︱=．由E到A、B、C、D的距离相等，得︱m + 4a︱==，经求解知，不存在非零常数a，使上式成立，因此说明，不存在非零常数a，使A、B、C、D在一个圆上．变式3抛物线y = ax2 + bx + c与x轴的公共点是A〔－1，0〕、B〔3，0〕，与y轴的公共点是C，顶点是D．假设四边形ABDC的面积为2，求抛物线的解析式．解作出示意图，设对称轴与x轴的交点为E．那么△BDE的面积为EB·DE =×2×︱4a︱= 4︱a︱；△AOC的面积为AO·CO =×1×︱3a︱=︱a︱；直角梯形OCDE的面积为〔CO + DE〕·OE =〔︱3a︱+︱4a︱〕· 1 =︱a︱；从而四边形ABDC的面积等于4︱a︱+︱a︱+︱a︱= 9︱a︱= 18，∴a =±2．因此，抛物线的解析式为y = 2x2－4x－6 或y =－2x2 + 4x + 6．变式4 y = ax 2 + bx + c 〔a ≠0〕的图象如图， 你能根据图象所提供的信息得出哪些结论呢？试一试．〔1〕〔2021丽水y = ax 2 + bx + c 〔a ≠0〕 的图象如下图，给出以下结论：① a ＞0 ②x = 1对称③ 当x =－1或x = 3时，y 的值都等于0 其中正确结论的个数是〔 〕．BA ．3B ．2C ．1D ．0〔2〕〔2021南充〕抛物线y = a 〔x + 1〕〔x －3〕〔a ≠0〕的对称轴是直线〔 〕．A A ．x = 1 B ．x =－1 C ．x =－3 D ．x = 3 〔3〕〔2021南宁〕y = ax 2 + bx + c 〔a ≠0〕的图象如下图，有以下四个结论：① b ＜0 ② c ＞0 ③ b 2－4ac ＞0 ④ a －b +c ＜0 其中正确的个数有〔 〕．CA ．1个B ．2个C ．3个D ．4个 〔4〕〔2021宁夏〕y = ax 2 + bx + c 〔a ≠0〕的图象如图 所示，对称轴是直线x = 1，那么以下四个结论错误的选项是．．．．．．〔 〕．A ．c ＞0 B ．2a + b = 0 C ．b 2－4ac ＞0 D ．a －b + c ＞〔5〕〔2021庆阳〕如y = ax 2 + bx + c 〔a ≠0〕 的图象，给出以下说法：① ab ＜0 ② 方程ax 2 + bx + c = 0的根为x 1 =－1，x 2 = 3③ a + b + c ＞0 ④ 当x ＞1时，y 随x 值的增大而增大 ⑤ 当y ＞0时，－1＜x ＜3其中，正确的说法有 ．①②④〔6〕〔2021内江〕如下图，点A 〔－1，0〕，B 〔3，0〕， C 〔0，t 〕，且t ＞0，tan ∠BAC = 3，抛物线经过A 、B 、C 三点，点P 〔2，m 〕是抛物线与直线l ：y = k 〔x + 1〕的一个交点．① 求抛物线的解析式；② 对于动点Q 〔1，n 〕，求PQ + QB 的最小值；③ 假设动点M 在直线l 上方的抛物线上运动，求△AMP 的边AP 上的高h 的最大值．〔限于篇幅，解答略去，下同〕〔7〕〔2021武汉〕如图，抛物线y = ax 2 + bx －4a 经过A 〔－1，0C 〔0，4〕两点，与x 轴交于另一点B ．① 求抛物线的解析式；② 点D 〔m ，m + 1〕在第一象限的抛物线上， 求点DBC 对称的点的坐标； ③ 在②的条件下，连接BD ，点P 为抛物线上一点，且∠DBP = 45 ，求点P 的坐标．〔8〕〔2021安顺〕如图，抛物线与x 交于A 〔－1，0〕、E 〔3，0〕两点，与y 轴交于点B 〔0，3〕．① 求抛物线的解析式；② 设抛物线顶点为D ，求四边形AEDB 的面积；③ △AOB 与△DBE 是否相似？如果相似，请给以证明；如果不相似，请说明理由．〔9〕〔2021威海〕如图，在直角坐标系中，点A ，B ，C 的坐标分别为〔－1，0〕，〔3，0〕．〔0，3〕，过A ，B ，C 三点的抛物线的对称轴为直线l ，D 为对称轴l 上一动点．① 求抛物线的解析式；② 求当AD + CD 最小时点D 的坐标； ③ 以点A 为圆心，以AD 为半径作⊙A ．ⅰ〕证明：当AD + CD 最小时，直线BD 与⊙A 相切．ⅱ〕写出直线BD 与⊙A 相切时，D 点的另一个坐标：___________． 〔10〕〔2021牡丹江〕y = x 2 + bx + c 的图象经过A 〔－1，0〕和B 〔3，0〕两点，且交y 轴于点C ．① 试确定b 、c 的值；② 过点C 作CD ∥x 轴交抛物线于点D ，点M 为此抛 物线的顶点，试确定△MCD 的形状．〔11〕〔2021十堰〕如图，抛物线y = ax 2 + bx + 3〔a ≠0〕 与x 轴交于点A 〔1，0〕和点B 〔－3，0〕，与y 轴交于点C ．① 求抛物线的解析式；② 设抛物线的对称轴与x 轴交于点M ，问在对称轴上是否存在点P ，使△CMP 为等腰三角形？假设存在，请直接写出所有符合条件的点P 的坐标；假设不存在，请说明理由．③ 如图，假设点E 为第二象限抛物线上一动点，连接BE 、CE ，求四边形BOCE 面积的最大值，并求此时E 点的坐标．题目 某商品现在的售价为每件60元，每星期可卖出300件．市场调查反映：如调整价格，每涨价1元，每星期要少卖出10件；每降价1元，每星期可多卖出20件．商品的进价为每件40元，如何定价才能使利润最大？〔人教课本P 25探究1〕分析 调整价格包括涨价和降价两种情况．看看涨价的情况：设每件涨价x 元，那么每星期售出商品的利润y 随之变化．涨价x 元时，每星期少卖10x 件，实际卖出〔300－10x 〕件，销售额为〔60 + x 〕〔300－10x 〕元，买进商品需要付40〔300－10x 〕元，因此所得利润y =〔60 + x 〕〔300－10x 〕－40〔300－10x 〕．解 〔1〕设每件涨价x 元，每星期售出商品的利润y 随x 的变化为： y =〔60 + x 〕〔300－10x 〕－40〔300－10x 〕，自变量x 的取值范围是0≤x ≤30． ∴ y =－10x 2 + 100x + 6000 =－10〔x －5〕2 + 6250， 因此当x = 5时，y 的最大值为6250．〔2〕设每件降价x 元，每星期售出商品的利润y 随x 的变化为： y =〔60－x －40〕〔300 + 20x 〕，自变量x 的取值范围是0≤x ≤20． ∴ y =－20x 2 + 100x + 6000 =－20〔x －2.5〕2 + 6125， 因此当x = 2.5时，y 的最大值为6125． 〔3〕每件60元销售〔即不涨不降〕，每星期可卖出300件，其利润y =〔60－40〕×300 = 6000元．综上所述，当商品卖价定位45元时，一周能获得最大利润6250． 点评 演变变式1 某宾馆有50个房间供游客居住，当每个房间的定价为每天180元时，房间会全部住满．当每个房间每天的定价增加10元时，就会有一个房间空闲．如果游客居住房间，宾馆需对每个房间每天支付20元的各种费用．房间定位多少时，宾馆利润最大？〔课本28页第6题〕解设每个房间每天的定价增加10x元，那么有x个房间空闲，于是宾馆利润y =〔180 + 10x〕〔50－x〕－20〔50－x〕，其中0≤x≤50．∴y =－10〔x2－34x－800〕=－10〔x－17〕2 + 10890．当x = 17时，y取得最大值10890元，即房价定为350元∕间时，宾馆利润最大．变式2〔2021绵阳〕青年企业家刘敏准备在北川禹里乡投资修建一个有30个房间供旅客住宿的旅游度假村，并将其全部利润用于灾后重建．据测算，假设每个房间的定价为60元∕天，房间将会住满；假设每个房间的定价每增加5元∕天时，就会有一个房间空闲．度假村对旅客住宿的房间将支出各种费用20元∕天·间〔没住宿的不支出〕．问房价每天定为多少时，度假村的利润最大？解设每天的房价为60 + 5x元，那么有x个房间空闲，已住宿了30－x个房间．于是度假村的利润y =〔30－x〕〔60 + 5x〕－20〔30－x〕，其中0≤x≤30．∴y =〔30－x〕· 5 ·〔8 + x〕= 5〔240 + 22x－x2〕=－5〔x－11〕2 + 1805．因此，当x = 11时，y取得最大值1805元，即每天房价定为115元∕间时，度假村的利润最大．另法设每天的房价为x元，利润y元满足=〔60≤x≤210，是5的倍数〕．法三设房价定为每间增加x元，利润y元满足=〔0≤x≤150，是5的倍数〕．变式3〔2021武汉〕某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品的售价每上涨1元，那么每个月少卖10件〔每件售价不能高于65元〕．设每件商品的售价上涨x元〔x为正整数〕，每个月的销售利润为y元．〔1〕求y与xx的取值范围；〔2〕每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？〔3〕每件商品的售价定为多少元时，每个月的利润恰为2200元？根据以上结论，请你直接写出售价在什么范围时，每个月的利润不低于2200元？解〔1〕y =〔210－10x〕〔50 + x－40〕=－10x2 + 110x + 2100〔0＜x≤15且x为整数〕．〔2〕y =－10〔x－5.5〕2 + 2402.5，∴当x = 5.5时，y有最大值2402.5．∵0＜x≤15，且x为整数，当x = 5或x = 6时，y = 2400〔元〕．∴当售价定为每件55或56元，每个月的利润最大，最大的月利润是2400元．〔3〕当y = 2200时，－10x2 + 110x + 2100 = 2200，解得x = 1或x = 10．∴当售价定为每件51或60元，每个月的利润为2200元．当售价不低于51或60元，每个月的利润为2200元．当售价不低于51元且不高于60元且为整数时，每个月的利润不低于2200元〔或当售价分别为51，52，53，54，55，56，57，58，59，60元时，每个月的利润不低于2200元〕．变式4〔2021黔东南州〔1〕设每间包房收费提高x〔元〕，那么每间包房的收入为y1〔元〕，但会减少y2间包房租出，请分别写出y1、y2与x〔2〕为了投资少而利润大，每间包房提高x〔元〕后，设酒店老板每天晚餐包房总收入为y〔元〕，请写出y与x解〔1〕y1 = 100 + x，．〔2〕y =〔100 + x〕〔100－〕，即y =－〔x－50〕2 + 11250，因为提价前包房费总收入为100×100 = 10000．当x= 50时，可获最大包房收入11250元，因为11250＞10000．又因为每次提价为20元，所以每间包房晚餐应提高40元或60元．变式5 〔2021烟台〕“家电下乡〞〔1〕假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x〔2〕商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？〔3〕每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？解〔1〕根据题意，得，即．〔2〕由题意，得，整理，得x2－300x + 20000 = 0．解这个方程，得x1 = 100，x2 = 200．要使百姓得到实惠，取x = 200，所以，每台冰箱应降价200元．〔3〕=，当每台冰箱的售价降价150元时，商场的利润最大，最大利润是5000元．变式6 〔2021济宁〔1〕求商家降价前每星期的销售利润为多少元？〔2〕降价后，商家要使每星期的销售利润最大，应将售价定为多少元？最大销售利润是多少？解〔1〕〔130－100〕×80 = 2400〔元〕．〔2〕设应将售价定为x元，那么销售利润=－4x2 + 1000x－60000 =－4〔x－125〕2 + 2500．当x = 125时，y有最大值2500，∴应将售价定为125元，最大销售利润是2500元．变式7 〔2021滨州〕某商品的进价为每件40元．当售价为每件60元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件．在确保盈利的前提下，解答以下问题：〔1〕假设设每件降价x元、每星期售出商品的利润为y元，请写出y与xx的取值范围；〔2〕当降价多少元时，每星期的利润最大？最大利润是多少？27.1 图形的相似题目如图，将一张矩形纸片沿较长边的中点对折，如果得到的两个矩形都和原来的矩形相似，那么原来矩形的长宽比是多少？将这张纸再如此对折下去，得到的矩形都相似吗？〔人教课本P41 8题〕解设矩形纸片的较长边为a，较短边为b，那么a＞b，且b＞．沿较长边的中点对折，得到了两个矩形都和原来的矩形相似，从而有两个小矩形是全等的，和原来的矩形相似的比为:b = b:a，所以a:b =:1，为原来矩形的长宽比．再折下去，得到的矩形都相似．点评矩形是有一个角为直角的平行四边形〔长方形〕．它具有平行四边形的所有性质〔它既然是特殊的平行四边形，那么它就应该有自己特有的性质〕；矩形是轴对称图形，有2条对称轴〔非正方形〕；矩形的四个角都是直角；矩形的对角线相等且互相平分．演变变式1 一个矩形长与宽的比为，如果将矩形沿较长边的中点对折，得到的两个全等的小矩形，那么它们都和原来的矩形相似．变式2 将一张矩形纸片沿过其中心的直线对折，得到两个图形〔直角三角形或直角梯形〕全等〔相似，相似比等于1〕．说明 此种情况的折法不需要长宽比的限制． 变式3 〔2021济宁〕如图，在长为8 cm 、宽为4 cm 的矩形 中，截去一个矩形，使得留下的矩形〔图中阴影局部〕与原矩形 相似，那么留下矩形的面积是〔 〕．CA ．2 cm 2B ．4 cm 2C ．8 cm 2D ．16 cm 2变式4 〔2021山西〕如图〔1〕，把一个长为m 、宽为n 的长方形〔m ＞n 〕沿虚线剪开，拼接成图〔2〕，成为在一角去掉一个小正方形后的一个大正方形，那么去掉的小正方形的边长为〔 〕．AA ．B ．m －nC ．D ．变式5 〔2021济南〕如图，矩形ABCD 中，AB = 3，BC = 5．过对角线交点O 作OE ⊥AC 交AD 于E ，那么AE 的长是〔 D〕．A ．1.6B ．2.5C ．3D ．3.4 变式6 〔2021凉山〕如图，将矩形ABCD 沿对角线BD 折叠，使C 落在C ′ 处，BC ′ 交AD 于E ，那么以下结论不一定成立的是〔 C 〕．A ．AD = BC ′B ．∠EBD =∠EDBC ．△ABE ∽△CBD D ． 变式7 〔〕如图，过P 点的两直线将矩形ABCD分成甲、乙、丙、丁四个矩形，其中P 在AC 上，且AP :PC = AD :AB = 4:3．以下对于矩形是否相似的判断，何者正确？〔 〕．A A ．甲、乙不相似 B ．甲、丁不相似 C ．丙、乙相似 D ．丙、丁相似变式8 〔2021杭州〕如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3和4及x ， 那么x 的值〔 〕．B A ．只有1个 B ．可以有2个 C ．有2个以上但有限 D ．有无数个 变式9 〔2021安徽〕如图，将正方形沿图中虚线〔其中x ＜y 〕 剪成①②③④四块图形，用这四块图形恰能拼成一个．．．．．．矩形〔非正方形〕． 〔1〕画出拼成的矩形的简图；〔2〕求的值．解 〔1〕yx③④① ② mn nnAB CDP甲乙丙 丁 O BA E C DB AEC DC ′说明：其它正确拼法可相应赋分． 〔2〕由拼图前后的面积相等得：， 因为y ≠0，整理，得 ，解得 〔负值不合题意，舍去〕．另法 由拼成的矩形，可知，以下同解法一．27．2 相似三角形题目 如图，Rt △ABC 中，CD 是斜边上的高，△ACD 和△CBD 都和△ABC本49页练习第2题〕分析利用它们的对应角分别相等，证明它们相似． 证明 略．点评 这个问题可以表述为：直角三角形被斜边上的高分成的该图形是平面几何中最根本的图形之一，称为母子三角形． 演变变式1如原题目和图形，求证：． 解 由 Rt △ACD ∽Rt △ABC ∽Rt △CBD 得 AC 2 = AD · AB ，BC 2 = BD · AB ，CD 2 = AD · BD ， ∴ ，因此 ．变式2 如图，△ABC 中，CD 是边AB 上的高，且，求∠C 的大小．〔课本P 57页15题〕解 由条件可得 Rt △ACD ∽Rt △CBD ，从而∠A 与∠BCD 互余，∠BCD 与∠ACD 互余，故 ∠C = 90︒． 变式3 如图，CD 是⊙O 的弦，AB 是直径，CD ⊥AB ，垂足为P ，求证：页8题〕证明 连结AC ，BC ， ∵ AB 是⊙O 的直径，CD ⊥AB ， ∴ △CP A ∽△BPD ，可得 ，从而 PC 2 = P A · PB ．变式4 〔2021牡丹江〕如图，△ABC 中，CD ⊥AB 于D ， 一定能确定△ABC 为直角三角形的条件的个数是〔 〕．C① ∠1 =∠A ② ③ ∠B +∠2 = 90︒ ④ BC :AC :AB = 3:4:5 ⑤ AC · BD = BC · ADA ．1B ．2C ．3D ．4变式5 〔2021梧州〕如图，正方形ABCD 中，E 为AB 的 中点，AF ⊥DE 于点O ，那么等于〔 〕．DA ．B ．C ．D ．变式6 〔2021山西〕在Rt △ABC 中，∠ACB = 90︒，BC = 3，AC = 4，AB 的垂直平分线DE 交BC的延长线于点E ，那么CE 的长为〔 〕．BA ．B ．C ．D ．2变式7 〔2021呼和浩特〕如图，AB 是⊙O 的直径，点C 在圆上， CD ⊥AB ，DE ∥BC ，那么图中与△ABC 相似的三角形的个数有〔 〕．AA ．4个B ．3个C ．2个D ．1个变式8 〔2021东营〕将三角形纸片〔△ABC 〕按如下图的方式折叠，使点B 落在边AC 上，记为点B ′，折痕为EF ．AB = AC = 3，BC = 4，假设以点B ′，F ，C 为顶点的三角形与△ABC 相似，那么BF 的长度是 ．或2变式9 〔2021长春〕如图，在矩形ABCD 中，点E 、F 分别在边AD 、DC 上，△ABE ∽△DEF ，AB = 6，AE = 9，DE = 2，求EF 的长．解 ∵ 四边形ABCD 是矩形，AB = 6， ∴ ∠A =∠D = 90︒，DC = AB = 6．又 ∵ AE = 9，∴ 在Rt △ABE 中，由勾股定理，得 BE =． ∵ △ABE ∽△DEF ， ∴ ，即 ， 解得 EF =．变式10 〔2021常德〕如图，△ABC 内接于⊙O ，AD 是△ABC 的边BC 上的高，AE 是⊙O 的直径，连接BE ，△ABE 与△ADC 相似吗？请证明你的结论．解 △ABE 与△ADC 相似． 在△ABE 与△ADC 中，∵ AE 是⊙O 的直径，∴ ∠ABE = 90︒，∵ AD 是△ABC 的边BC 上的高，∴ ∠ADC = 90︒，∴ ∠ABE =∠ADC ． 又 ∵ 同弧所对的圆周角相等，∴ ∠BEA =∠DCA ，∴ △ABE ∽△ADC ．变式11 〔2021泰安〕如图，△ABC 是直角三角形，∠ACB = 90︒，CD ⊥AB 于D ，E 是AC 的中点，OECDAFBB AED F CED 的延长线与CB 的延长线交于点F ．〔1〕求证：FD 2 = FB · FC ；〔2〕假设G 是BC 的中点，连接GD ，GD 与EF 垂直吗？并说明理由． 证明 〔1〕∵ E 是Rt △ACD 斜边中点， ∴ DE = EA ，∴ ∠A =∠ADE ． ∵ ∠BDF =∠ADE ，∴ ∠BDF =∠A ． ∵ ∠FDC =∠CDB +∠BDF = 90︒ +∠BDF ，∠FBD =∠ACB +∠A = 90︒ +∠A ，∴ ∠FDC =∠FBD ． ∵ F 是公共角，∴ △FBD ∽△FDC ，∴ ，∴ FD 2 = FB · FC ． 〔2〕GD ⊥EF ．∵ DG 是Rt △CDB 斜边上的中线，∴ DG = GC ，∴ ∠CDG =∠DCG ． 由〔1〕得 ∠DCG =∠BDF ，∴ ∠CDG =∠BDF ．∵ ∠CDG +∠BDG = 90︒，∴ ∠BDG +∠BDF = 90︒，∴ DG ⊥EF ．27.3 位似题目 如图，四边形ABCD 的坐标分别为A 〔－6，6〕，B 〔－8，2〕，C 〔－4，0〕，D 〔－2， 4〕，画出它的一个以原点O 为位似中心，相似比 为的位似图形．分析 问题的关键是要确定位似图形各个 顶点的坐标．根据位似图形的坐标规律性，点A 的对应点A ′ 的坐标为〔－6×，6×〕，即 〔－3，3〕．类似的，可以确定其它顶点的坐标．解 如图，利用位似图形中对应点的坐标的变化规律，分别取点A ′〔－3，3〕，B ′〔－4，1〕，C ′〔－2，0〕，D ′〔－1，2〕．依次连接点A ′、B ′、C ′、D ′，那么四边形A ′B ′C ′D ′就是要求四边形ABCD 的位似图形．点评 在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k ，那么位似图形对应点的坐标的比等于k 或－k ．演变变式1 试判断四边形ABCD 的形状，并说明理由．解 在平面直角坐标系中，作出四边形ABCD ，知点A 、B 、C 、D 分别在四条直线y = 6，x =－8，yG BEAD CF= 0，x =－2所构成的一个正方形四边上，且对应排列，可知四边形ABCD是正方形，边长为，中心在〔－5，5〕．变式2求四边形ABCD和四边形A1B1C1D1的面积．〔答案：20平方单位和5平方单位〕变式3求四边形ABCD的对角线的交点坐标到原点的距离？解四边形ABCD的对角线的交点的横坐标为－5，纵坐标为3，于是它到原点的距离为．变式4试作出四边形ABCDx轴、直线y = x的对称图形．〔略〕变式5求过点B、C答案：〕变式6求过点A、B、D答案：〕变式7求过点DBC的交点坐标．〔答案：〔，〕〕变式8〔2021舟山〕△ABC中，A，B两个顶点在x轴的上方，点C的坐标是〔－1，0〕．以点C 为位似中心，在x轴的下方作△ABC的位似图形，并把△ABC的边长放大到原来的2倍，记所得的象是△A′B′C．设点B的对应点B′的横坐标是a，那么点B的横坐标是〔〕．DA．B．C．D．变式9〔2021宜宾〕假设一个图形的面积为2，那么将它与成中心对称的图形放大为原来的两倍后的图形面积为〔〕．AA．8 B．6 C．4 D．2题目在Rt△ABC中，∠C = 90︒，BC = 5，sin A = 0.7，求cos A页8题〕P85解作出示意图，把和图形结合起来．∵∠C = 90︒，∴，即．从而，∴，．点评sin2A + cos2A = 1，，据此可立得结论．所以此题在锐角三角形前提下，条件∠C = 90︒，BC = 5是多余的．演变变式1 在Rt△ABC中，∠C = 90︒，BC = 5，sin A = 0.7，解这个直角三角形．〔见上〕变式2 △ABC是锐角三角形，且sin A = 0.7，求cos A、tan A的值．解画出满足sinA = 0.7一个△ABC〔示意图〕，在AB上取AD = 1，过D作DE⊥AC 于E，那么在Rt△ADE中，得DE = AD sin A = 0.7，∴，因此，．变式3 〔2021湖州〕在Rt△ABC中，∠ACB = Rt∠，BC = 1，AB正确的选项是〔〕．DA．B． C．D．变式4 〔2021益阳〕先锋村准备在坡角为α的山坡上栽树，要求相邻两树之间的水平距离为5米，那么这两树在坡面上的距离AB为〔〕．BA． B． C． D．变式5 〔2021温州〕△ABC中，∠C= 90︒，AB= 8，cos A=，那么AC的长是．628.2 解直角三角形题目多年来，很多船只、飞机都在大西洋的一个区域内神秘失踪，这个区域称为百慕大三角．根据图中标出的百慕大三角的位置，计算百慕大三角的面积〔精确到100 km2，sin64︒= 0.8988，cos64︒ = 0.4384〕〔课本97页第10题〕分析解决这个问题的难点在于如何构造直角三角形．结合文字和图形，理解、区分“百慕大岛〞与“百慕大三角〞，弄清楚方位角的大小和关联．解由图中所标的有关数据，可知，AB = 1700，AC = 2720，∠A = 62︒ + 54︒ = 116︒，延长CA，过B作BD⊥CA，D为垂足，那么∠BAD = 180︒－116︒ = 64︒．在Rt△ABD中，BD = AB sin∠BAD，∴百慕大三角ABC的面积== S△BCD－S△BAD==〔km2〕．另法同上法，延长BA，过C作CE⊥BA于E，那么 =ABCDABCE=．法三 过A 作FG 直于南北走向线〔如图〕，那么在Rt △ABG 中，AB = 1700，AC = 2720，∠ABG = 62︒，所以 AG = AB = sin 62︒，BG = AB cos 62︒．同理，AF = AC sin 54︒，CF = AC cos 54︒．于是百慕大三角ABC 的面积 S = S 直角梯形BCFG ―S Rt △ABG ―S Rt △ACF = = == ===〔km 2〕． 点评 演变变式1 如图，△ABC 的面积为 ，即三角形的面积等于任意两边与它们夹角的正弦的积的一半．解 作三角形的高BD ．在Rt △BDA 中，，那么 BD = AB sin A ． ∵ ， ∴ ． 同理，，．变式2 △ABC 中，两边AC = b ，BC = a 和夹角C ，试用a 、b 、C 来表示AB 2． 解 过B 作BD ⊥AC ，垂足为D ，那么D 在AC 或其延长线上．不妨设D 在AC 上． 在Rt △BCD 中，有 BD = a sin C ，CD = a cos C ， ∴ AD = b －a cos C ．在Rt △ABD 中，由勾股定理，得 AB 2 = AD 2 + BD 2， ∴ AB 2=〔b －a cos C 〕2+〔a sin C 〕2= b 2 + a 2〔cos 2C + sin 2C 〕－2ab cos C = a 2 + b 2－2ab cos C ．变式3 〔2021宁波〕在坡屋顶的设计图中，AB = AC ，屋顶的 宽度为10米，坡角α 这35︒，那么坡屋顶的高度h 为 米．3.5变式4 〔2021成都〕某中学九年级学生在学习“直角三角形的 边角关系〞一章时，开展测量物体高度的实践活动，他们要测ABCG FBACDa cbBACDab量学校一幢教学楼的高度．如图，他们先在点C测得教学楼AB 的顶点A的仰角为30︒，然后向教学楼前进60米到达点D，又测得点A的仰角为45︒．请你根据这些数据，求出这幢教学楼的高度．〔计算过程和结果均不取近似值〕〔答案：30 + 30〕变式5 〔2021江苏〕如图，在航线l的两侧分别有观测点A和B，点A到航线l的距离为2 km，点B位于点A北偏东60︒方向且与A相距10 km处．现有一艘轮船从位于点B南偏西76︒方向的C处，正沿该航线自西向东航行，5 min后该轮船行至点A的正北方向的D处．〔1〕求观测点B到航线l的距离；〔2〕求该轮船航行的速度〔结果精确到0.1 km∕h〕．〔答案：〔1〕3 km〔2〕40.6 km∕h〕变式6 〔2021洛江〕如图，一艘轮船位于灯塔P的北偏东60︒方向，与灯塔P的距离为80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45︒方向上的B处．求此时轮船所在的B处与灯塔P〔答案：40〕变式7 〔2021中山〕如下图，A、B两城市相距100 km．现方案在这两座城市间修筑一条高速公路〔即线段AB〕，经测量，森林保护中心P在A城市的北偏东30︒和B城市的北偏西45︒的方向上．森林保护区的范围在以P点为圆心，50 km为半径的圆形区域内．请问：方案修筑的这条高速公路会不会穿越保护区？为什么？〔答案：不会穿越保护区〕变式8 〔2021黄石〕三楚第一山——东方山是黄石地区的主峰ABBC，现在山脚P处测得峰顶的仰角为α，发射架顶端的仰角为β，其中，，求发射架高BC．〔答案：25 m〕30︒A BFEP45︒CBDA米29.2 三视图题目面积．〔课本121页例6〕分析 对于某些立体图形，沿着其中一些线〔例如棱柱 的棱〕剪开，可以把立体图形的外表展开成一个平面图形 —— 展开图．在实际的生产中，三视图和展开图往往结合在一起使用．解所需钢板的面积为6×50×50 + 2×6××50×50 sin 60 = 6×502〔1 +〕≈ 27990〔mm 2〕．点评 由主视图可知，物体正面是矩形及其组合体；由俯视图可知，由上向下看物体是正六边形；由左视图可知，物体的侧面是矩形及其组合体，综合各视图可知，物体是正六棱柱．所以由三视图想象立体图形时，要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面，然后再综合起来考虑整体图形．演变解 〔mm 3〕．变式2 假设该工厂现有每张面积为X 〔50×50〕的原材料板，共100张，…… ……变式4 制造一个这样的正六棱柱体罐子，需要多少本钱？变式5 〔2021芜湖〕如图，上下底面为全等的正六边形礼盒，其主视图与侧视图均由矩形构成，主视图中大矩形边长如下图，侧视图中包含两全等的矩形，如果用彩色胶带如图包扎礼盒，所需胶带长度至少为〔 〕．C实物图主视图 俯视图A ．320cmB ．395.24 cmC ．431.76 cmD ．480 cm变式6 〔2021南充〕如图，以下选项中不是正六棱柱三视图的是〔 〕．A变式7 〔2021钦州〕如图中物体的一个视图〔a 〕的名称为 ．〔答案：主视图〕变式8 〔2021临沂〕如图是一个包装盒的三视图， 那么这个包装盒的体积是〔 〕A ．192π cm 3B ．1152π cm 3C ．288cm 3D ．384cm 3D ．(a )。
初三数学变式训练标准版文档
人教版初中数学中考 练本 中考真题中的教材变式题(多题变一) 中考真题中的教材变式题(多题变一)
（人教九上P90习题T14）如图，A，P，B，C是☉O上的四个点，∠APC＝∠CPB ＝60°.判断△ABC的形状，并证明你的结论.
（人教九上P124复习题T13）如图，点E是△ABC的内心，AE的延长线和△ABC的 外接圆相交于点D.求证：DE＝DB.
多题变一：（潜江中考）已知△ABC内接于☉O，∠BAC的平分线交☉O于点D， 连接DB，DC.
（1）如图1，当∠BAC＝120°时，请直接写出线段AB，AC，AD之间满足的等量 关系式： AB＋AC＝AD ；
（2）如图2，当∠BAC＝90°时，试探究线段AB，AC，AD之间满足的等量关系， 并证明你的结论；
图1
图2
图3
∵四边形ABDC内接于☉O， ∴∠ABD＋∠ACD＝180°. ∵∠ABD＋∠MBD＝180°，
分两种情况讨论： ①当△PQD∽△ACO时，∠PQD＝∠ACO. 由（1）知∠ACO＝∠BOD， ∴∠PQD＝∠DOP，∴DQ＝DO， ∴∠PDO＝∠PDQ， ∴△DCQ≌△DCO，∴∠DCQ＝∠PCO. ∵∠ACO＋∠PCO＋∠DCQ＝180°， ∴∠ACO＝60°，∴∠BOD＝60°. 在Rt△ACO，Rt△BDO中，
多题变一：（潜江中考）如图1，半圆O的直径AB＝6，AM和BN是它的两条切 线，CP与半圆O相切于点P，并与AM，BN分别相交于C，D两点，连接OC，OD. （1）请直接写出∠COD的度数； （2）求AC·BD的值；
图1
图2
解：（1）∠COD＝90°.
（3）△PQD能与△ACO相似. ∵AC，CP是半圆O的切线， ∴AC＝CP，∠ACO＝∠PCO. ∵DB是☉O的切线， ∴DB＝DP，∠B＝∠OPD＝90°，OD＝OD， ∴Rt△ODB≌Rt△ODP，∴∠BOD＝∠DOP. ∵CP是半圆O的切线， ∴∠OPD＝90°，∴∠DPQ＝90°＝∠A.
全等三角形中的变式训练题+-2024-2025学年人教版数学八年级上册+
全等三角形中的变式训练题基本图形例：已知如图，AB⊥DC于B，且BD=BA，BE=BC。
求证：⑴DE=AC ⑵DE⊥AC变式一、将上题中的△DBE沿DC方向平移至下图中的各种情况时，还有DE=AC、DE⊥AC吗？为什么？变式二：已知：如图，△ABC中，AC=BC，AC⊥BC，直线EF交AC于F，交AB于E，交BC的延长线于D，且CF=CD，连结AD、BF，则BF与AD有何关系？试证明你的结论。
变式三：如图所示，在正方形ABCD中，E是正方形边AD上一点，F是BA延长线上一点，并且AF=AE，已知△ABE≌△ADF。
⑴在图中，可以通过平移、翻折、旋转中的哪一种方法，使△ABE与△ADF完全重合；⑵指出图中线段BE与DF之间的关系。
变式四：已知：如图，AD 为△ABC 的高，E 为AC 上一点，BE 交AD 于F ，且有BE ⊥AC ，FD=CD ，求证：BF=AC变式五：△ABC 中，∠A=90°，AB=AC ，BD 平分∠ABC 交AC 于点D ，CE ⊥BD 于E ，若BD=m ，EC=n ，试探m 、n 之间的关系式。
课后作业1.已知:AC=BC,D A ⊥AB,EB ⊥AB,求证: AE=BD2.已知:AC=BC,D A ⊥AC,EB ⊥CB,(1)求证: AE=BD(2)求证：CF 是∠ECD 的角平分线（1） （2） F CA F EDC A A CDE F3. 已知:AC=BC,D A⊥AC,EB⊥CB,求证: A E∥BD4.已知:AC=BC,D A⊥AC,EB⊥CB,求证: DF=EFCAFEDCA。
二元一次方程组变式训练
ax + by = 1 2x - y = 3 4、若方程组 、 的解与方程组 bx + 3y = a 3x + 2y = 8 的解相同， 的值. 的解相同，求a 、b的值 的值 2x - y = 3 2x - y = 3 ① 解： ∵ 方程组 3x + 2y = 8 的解与 3x + 2y = 8 ② ax + by = 1 方程组 bx + 3y = a 的解相同 由①得：y = 2x - 3 ③ 代入② 把③代入②得： x=2 ∴把 y = 1 代入方程组 3x + 2（2x – 3）= 8 （ ） 3x + 4x – 6 = 8 ax + by = 1 得： 3x + 4x = 8 + 6 bx + 3y = a 7x = 14 2a + b = 1 ④ x=2 2b + 3 = a ⑤ 代入③ 把x = 2 代入③，得： y = 2x - 3 = 2×2 - 3 =1 a=1 × 解得： 解得： x=2 ∴ b = -1 y=1
x = 4 2 x + (m − 1) y = 4 2、已知 是关于x、y的方程组 y = 2 nx + y = 2 的解，求(m + n )
2010
的值。
2 x + y = b x = 1 3、已知方程组 的解是 ，求 a − b 的值。 x − by = a y = 0
3 x − (m − 3) y m − 2 − 2 = 1 2、已知方程组 是关于x、y的 (m + 1)x = −2 二元一次方程组，求m的值。
3 5m+ 2n+ 2 3 3、若 x y 与 − 5 x 6 y 3m − 2 n −1是同类项， 4 求m、n的值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
初中数学中的几道变式训练题一、已知：点O是等边△ABC内一点,OA=4，OB=5，OC=3求∠AOC的度数。
变式1：在△ABC中，AB=AC，∠OA=4，OB=6，OC=2求∠AOC的度数。
变式2：如图,点O是等边△ABC内一点,∠AOB=110°, ∠BOC=135°试问:(1)以OA、OB、OC为边能否构成一个三角形?若能,请求出三角形各内角的度数;若不能,请说明理由.(2)如果∠AOB的大小保持不变,那么当∠BOC等于多少度时, 以OA、OB、OC为边的三角形是一个直角三角形?二、已知：C为AB上一点，△ACM和△CBN为等边三角形（如图所示）求证：AN=BMAB COACAB CO（分析：如对此题多做一些引申，既可以培养学生的探索能力，又可培养学生的创新素质）探索一：设CM 、CN 分别交AN 、BM 于P 、Q ，AN 、BM 交于点R 。
问此题中还有其他的边相等以及特殊角、特殊图形吗？给予证明。
探索二：△ACM 和△BCN 如在AB 两旁，其它条件不变，AN=BM 成立吗？探索三：△ACM 和△BCN 分别为以AC 、BC 为底且顶角相等的等腰三角形，其它条件不变，AN=BM 成立吗？探索四：A 、B 、C 三点不在一条直线上时，其它条件不变，AN=BM 成立吗？三、轴对称：已知直线l 及同侧两点A 、B ，试在直线l 上选一点C ，使点C 到点A 、B 的距离和最小。
变式1：如图，请你设计出两种方案的路线和最短的行走路线（画图并说明理由）方案1：小华由家先去河边，再去姥姥家；MACBBAl方案2：小华由家先去姥姥家，再去河边；变式2：已知: AB 、AC 表示两条交叉的小河, P 点是河水化验室, 现想从P 点出发, 先到AB 河取点水样, 然后再到AC 河取点水样, 最后回到P 处化验河水, 怎么走路程最短呢？实验员小王说:“我从P 点笔直向A 走, 同时取好两河水样再原路返回, 这样走, 路最近。
”化验员小吴否定了小王的路线, 提出了自己的想法, 请同学们想一想, 小吴走怎样的路线？小华家河流变式3：变式4：如图,在定直线XY 外有一点P,试于XY 上求两点A 、B,使PA+PB 为最短,而AB 等于定长a.aXY·PXY· ·P /·P //a aBAPAB CABPBCAD C变式5：如图，在河的两侧有A 、B 两个村庄，现要在河上修一座桥，规定桥必须与河岸垂直，要使A 村到B 村的路程最短，问桥应修在何处？(河宽为定长为m)解:(1)过B 作BC ⊥a,且使BC = m; (2)连接AC 交b 于P;(3)过点P 作PQ ⊥a,垂足为点Q,那么PQ 就是桥的位置.四、1、如图①，一架梯子长2.5米,顶端A 靠在墙AC 上,梯子下端B 与墙角C 相距1.5米. (1) 这架梯子的顶端距地面多高?(2)如果这架梯子滑动后停留在DE 位置(如图②所示),测得BD 长为0.5米,这时梯子顶端下落多少米?图① 图②变式：梯子靠在墙上，梯子的底端A 到墙根O 的距离2米，梯子的顶端B 到地面的距离为7米，现将梯子的底端向外移动到C ，使梯子底端C 到墙根O 的距离等于3米，同时梯子的顶端B 下降至D ，A ··Ba ba b·BA ·C PQAAC CBB DE那么BD （ ）A 、等于1米；B 、大于1米；C 、小于1米；D 、以上结果都不对。
四、1.小明把一根70cm 长的木棒放到一个长、宽、高分别为30cm 、40cm 、50cm 的木箱中，他能放进去吗？答：_______________（填“能”、或“不能”）2、有一个长、宽各2米，高3米且封闭的长方形纸盒，一只昆虫从顶点A 要爬到与A 点相对的顶点B ，那么这只昆虫爬行的最短路程为（ ）米。
A 、3；B 、4；C 、5；D 、6。
变式1：一个圆柱的高为36，底面圆的半径为5，一只蚂蚁从上底面的点A 处爬到与点A 相对应的下底面点B 处的最端路程是多少？Π值取3。
变式2：如图是一个三级台阶，它的每一级的长宽和高分别为20dm 、3dm 、2dm ，A 和B 是这个台阶两个相对的端点，A 点有一只蚂蚁，想到B 点去吃可口的食物，则蚂蚁沿着台阶面爬到B 点最短路程是_____________.变式3：如图，沿OA 将圆锥侧面剪开，展开成平面图形是扇形OAB.(1) 扇形的弧AB 的长与圆锥底面圆周的长是怎样的关系？点A 和点B 在圆锥的侧面上是怎样的位置关系？2032AB(2) 若角∠AOB=90°,则圆锥底面圆半径r 与扇形OAB 的半径R 之间有怎样的关系？(3) 若点A 在圆锥侧面上运动一圈后又回到原位，则点A 运动的最短路程应该怎样设计？若5.02=x ,且∠AOB=90°,求点A 运动的最短路程。
五、变式1：求下列不等式的解 (1)2X 〉3 （2）-4X 〉52,4____4;2____23,_______;,45X 2kx-1<2k-x x<1,K X 2kx-1<2k-x K a b a b a b x y ax ay a x y <--<<< 变式： 若则 变式： 若则中，应满足 若则ax>ay 中，a 应满足_______. 变式： 解不等式：（k+2)x>5变式： 若关于的不等式的解集为求的取值范围 若关于的不等式的解集为x>1,求的取值范围六、图1中，在ΔABC 中，∠C=90°在ΔABC 外，分别以AB 、BC 、CA 为边作正方形，这三个正方形的面积分别记为1,2,3s s s ，探索1,2,3s s s 之间的关系。
AOB图1 图2 图3变式1：如图2，在ΔABC中，∠C=90°在ΔABC外，分别以AB、BC、CA为边作正三角形，这三个正三角形的面积分别记为s s s，请探1,2,3索s s s之间的关系。
1,2,3变式2：如图3，在ΔABC中，∠C=90°在ΔABC外，分别以AB、BC、CA为直径作半圆，这三个半圆的面积分别记为s s s请探索1,2,3s s s之间的关系。
1,2,3变式3：你认为所作的图形具备什么特征时，s s s均有这样的关1,2,3系。
七、如图（1）A是CD上一点，⊿ABC、⊿ADE都是正三角形，求证CE=BD：如图2，⊿ABD、⊿ACE都是正三角形，求证CD=BE题3：如图3，分别以⊿ABC的边AB、AC为一边画正方形AEDB和正方形ACFG，连接CE、BG，求证BG=CE问题1：你能从（1），（2），（3）三题中选择一个进行证明吗？问题2：三个命题的证明方式为什么是一样的？用到了哪些知识点？问题3：这些命题在证明过程中哪些条件起到解决问题的决定性作用？变式1：如图4，有公共顶点的两个正方形ABCD、BEFG，连接AG、EC，求证AG=EC 对吗？变式2：在图4中，若将正方形BEFG 绕点B 旋转任意角度α，AG=EC 还成立吗？变式3：如图5，P 是正方形ABCD 内一点，⊿ABP 绕点B 顺时针方向旋转能与⊿CBP ’重合，若PB=3，求PP ’八、当x__________时，分式321-+x x 的值为零？变形1：当x__________时，分式3212--x x 的值为零？（分子为零时x=1±）变形2：当x__________时，分式112--x x 的值为零？（1=x 时分母为零因此要舍去）变形3：当x__________时，分式654322----x x x x 的值为零？（此时分母可以因式分解为)1)(6(+-x x ，因此x 的取值就不能等于6且不能等于-1）九、已知二次函数的图像经过A(-3,0)、B （1，0）、C （0，-3）三点，求这个二次函数的解析式。
变式1：已知二次函数的图像经过一次函数y=-x-3的图像与x 轴、y 轴的交点A 、C ，并且经过点B （1，0），求这个二次函数的解析式。
变式2：已知抛物线经过两点B （1，0）、C （0，-3）。
且对称轴是直线x=-1，求这条抛物线的解析式。
变式3：已知一次函数的图像经过点（1，0），且在y轴上的截距是-1，它与二次函数的图像相交于A（1，m）、B(n,4)两点，又知二次函数的对称轴是直线x=2，求这两个函数的解析式。
十、如图，在平行四边形ABCD中，E、F分别是OB、OD的中点，四边形AECF是平行四边形吗？请说明理由。
（引导学生分析，完成此例题）变式1:若将例题中的已知条件E、F分别是OB、OD的中点改为点E、F三等分对角线BD，其它条件不变，问上述结论成立吗？为什么？变式2:若将例题中的已知条件E、F分别是OB、OD的中点改为BE=DF，其它条件不变，结论成立吗？为什么？变式3:若将例题中的已知条件E、F分别是OB、OD的中点改为E、F为直线BD上两点且BE=DF，结论成立吗？为什么？变式4:如图7：在平行四边形ABCD中，H、G、E、F分别为线段BO、DO、AO、CO的中点，问四边形EGFH是平行四边形吗？为什么？精品文档若结论成立，那么直线EG、FH有什么位置关系？图7 图8变式5:如图8在平行四边形ABCD中，E、F是对角线AC上的两个点；G、H是对角线BD上的两点。
已知AE=CF，DG=BH，上述结论仍旧成立吗？精品文档。