圆轴扭转讲解
合集下载
《工程力学》课件——14 圆轴扭转

Iρ — 横截面对其形心极惯性矩(mm4),与截面形状 和大小有关的几何量
圆轴扭转的刚度条件:
max
Mn G I
180o
θ — 单位扭转角(θ = φ/l(°/m))
Mn — 横截面上的扭矩 G — 剪切弹性模量(Gpa)
Iρ — 横截面对其形心极惯性矩(mm4),与截面形状 和大小有关的几何量
X
Z
Y
《工程力学》
《 圆轴扭转 》
工程实际中受扭的零件
轴构件: 以扭转变形为主要变形形式的构件通常称为轴 工程上应用最广的多为圆截面轴,即圆轴
扭转受力的特点
BA
mc
mc
m
A
B
扭转受力的特点: 在构件两端作用两个大小相等、方向相反且作用面垂直于构件轴线的力偶矩 致使构件任意两个截面都发生绕构件轴线的相对转动,这种形式的变形即为扭转变形
φ — 扭转角(弧度)
Mn — 横截面上的扭矩 G — 剪切弹性模量(Gpa)
Iρ — 横截面对其形心极惯性矩(mm4),与截面形状和大小有关的几何量
圆轴扭转变形
单位扭转角:
max
Mn G I
θ — 单位扭转角(θ = φ/l(rad/m))
Mn — 横截面上的扭矩 G — 剪切弹性模量(Gpa)
扭矩确定
扭矩
• 圆轴扭转时其横截面上的内力为一力偶矩,称为扭矩(Mn) • 规定符号的正负按右手螺旋法则确定
正
m
T
Tm(a)m源自(b)TT
m
负
圆轴扭转强度计算
扭转的平面假设: 圆轴扭转变形后横截面保持平面,且形状、大小、间距不改变,半径仍为直线
结论: 圆轴扭转时横截面上无正应力,只有垂直于半径方向剪应力
圆轴扭转的刚度条件:
max
Mn G I
180o
θ — 单位扭转角(θ = φ/l(°/m))
Mn — 横截面上的扭矩 G — 剪切弹性模量(Gpa)
Iρ — 横截面对其形心极惯性矩(mm4),与截面形状 和大小有关的几何量
X
Z
Y
《工程力学》
《 圆轴扭转 》
工程实际中受扭的零件
轴构件: 以扭转变形为主要变形形式的构件通常称为轴 工程上应用最广的多为圆截面轴,即圆轴
扭转受力的特点
BA
mc
mc
m
A
B
扭转受力的特点: 在构件两端作用两个大小相等、方向相反且作用面垂直于构件轴线的力偶矩 致使构件任意两个截面都发生绕构件轴线的相对转动,这种形式的变形即为扭转变形
φ — 扭转角(弧度)
Mn — 横截面上的扭矩 G — 剪切弹性模量(Gpa)
Iρ — 横截面对其形心极惯性矩(mm4),与截面形状和大小有关的几何量
圆轴扭转变形
单位扭转角:
max
Mn G I
θ — 单位扭转角(θ = φ/l(rad/m))
Mn — 横截面上的扭矩 G — 剪切弹性模量(Gpa)
扭矩确定
扭矩
• 圆轴扭转时其横截面上的内力为一力偶矩,称为扭矩(Mn) • 规定符号的正负按右手螺旋法则确定
正
m
T
Tm(a)m源自(b)TT
m
负
圆轴扭转强度计算
扭转的平面假设: 圆轴扭转变形后横截面保持平面,且形状、大小、间距不改变,半径仍为直线
结论: 圆轴扭转时横截面上无正应力,只有垂直于半径方向剪应力
04. 圆轴的扭转解析

在工厂里当看到一套传动装置时,往往可从轴径的 粗细来判断这一组传动轴中的低速轴和高速轴。
§4-1圆轴扭转时所受外力的分析与计算
一、搅拌轴的三项功能 二、n , P, m 之间的关系(重点)
一、搅拌轴的三项功能
1.传递旋转运动 : 将电动机或减速机输出轴的旋转运动传递给搅拌物 料的桨叶。 2.传递扭转力偶矩: 将轴上端作用的驱动力偶传至轴的下端,用以克服 桨叶旋转时遇到的阻力偶;力偶通过轴传递时,其力偶 矩称为扭矩,扭矩属于内力,其值可借助外力偶矩求出; 3.传递功率: 转轴带动桨叶旋转时要克服流体阻力作功,所需功 率也是从转轴的上端输入后,通过轴传递给浆叶的。
(KN*m)
圆轴传递的功率P和转数n为已知时,用上述公式 即可求出该轴外力矩的大小。由上式可以看出: 如轴的功率P一定,转数n越大,则外力矩越小, 反之,转数越低则外力矩越大。 例如:化工设备厂卷制钢板圆筒用的卷板机,工作时滚轴 所需力矩很大,因为功率受到一定的限制,所以只能减 低滚轴的转数n来增大力矩M。由电动机经过一个三级四 轴减速机带动滚轴,此减速机各轴传递的功率可看成是 一样的。因此,转数n高的轴,力矩M就小,轴径就细一 些;转数低的轴,力矩M就大,轴径就粗.
A
解:1)用截面法把所求
各轴截开:
2)分别求各段轴的扭矩: M M 1+ M B = 0
1 2
= -M =-M
B
B
=-350N.m
C
M M
B D
+ M -M
3
C
+ M = 0
2
=0
M
-M
=-700N.m
M
3
= M
D
= 446N.m
二、扭转内力:(扭矩和扭矩图)(续3)
机械基础-圆轴扭转

圆轴扭转使圆轴发生旋转运动, 转动角度和扭矩大小相互关联。
应力分析
圆轴扭转中承受的应力分析是确 保圆轴在运动过程中不会发生破 坏。
圆轴扭转的应用领域
机械传动
圆轴扭转被广泛应用于机械传动系统中,实现能量的传输和转换。
汽车工程
在汽车发动机和变速器中,圆轴扭转起到承载和传输动力的关键作用。
航空航天
航空航天工程中的涡轮机械系统和航空发动机都离不开圆轴扭转。
与圆轴扭转相关的力学概念
弹性模量 剪切应力 扭转角度 Nhomakorabea圆轴材料的弹性变形能力 圆轴扭转引起的应力分布 圆轴扭转的角度变化
圆轴扭转的挑战与解决办法
1
疲劳寿命
圆轴扭转时容易引起疲劳破坏,需采取优化设计和材料选择来提高寿命。
2
动力平衡
圆轴扭转会引起不平衡力,需要进行动平衡设计和校正,减少振动。
3
扭转刚度
圆轴的刚度决定了扭转角度和应力的关系,设计时需考虑刚度的优化。
圆轴扭转的实例和案例分析
风力发电机
风力发电机的转子轴承受着强大 的风力扭转力,充分利用风能。
变速器
汽车变速器中的轴承承载着引擎 输出的扭转力,实现档位切换。
工业机械
各种工业机械设备中都存在圆轴 扭转的应用,如泵、缝纫机等。
结论和启示
结论
圆轴扭转是机械工程中一项重要的运动形式,应用 广泛且具有挑战性。
启示
通过深入了解圆轴扭转的原理和应用,可以优化设 计和解决实际问题。
机械基础-圆轴扭转
圆轴扭转的定义和背景
1 定义
圆轴扭转是指在机械系统中,圆轴受到一对 作用力使得其进行扭转运动。
2 背景
圆轴扭转是机械工程中一项重要的运动形式, 广泛应用于各种机械设备和结构中。
应力分析
圆轴扭转中承受的应力分析是确 保圆轴在运动过程中不会发生破 坏。
圆轴扭转的应用领域
机械传动
圆轴扭转被广泛应用于机械传动系统中,实现能量的传输和转换。
汽车工程
在汽车发动机和变速器中,圆轴扭转起到承载和传输动力的关键作用。
航空航天
航空航天工程中的涡轮机械系统和航空发动机都离不开圆轴扭转。
与圆轴扭转相关的力学概念
弹性模量 剪切应力 扭转角度 Nhomakorabea圆轴材料的弹性变形能力 圆轴扭转引起的应力分布 圆轴扭转的角度变化
圆轴扭转的挑战与解决办法
1
疲劳寿命
圆轴扭转时容易引起疲劳破坏,需采取优化设计和材料选择来提高寿命。
2
动力平衡
圆轴扭转会引起不平衡力,需要进行动平衡设计和校正,减少振动。
3
扭转刚度
圆轴的刚度决定了扭转角度和应力的关系,设计时需考虑刚度的优化。
圆轴扭转的实例和案例分析
风力发电机
风力发电机的转子轴承受着强大 的风力扭转力,充分利用风能。
变速器
汽车变速器中的轴承承载着引擎 输出的扭转力,实现档位切换。
工业机械
各种工业机械设备中都存在圆轴 扭转的应用,如泵、缝纫机等。
结论和启示
结论
圆轴扭转是机械工程中一项重要的运动形式,应用 广泛且具有挑战性。
启示
通过深入了解圆轴扭转的原理和应用,可以优化设 计和解决实际问题。
机械基础-圆轴扭转
圆轴扭转的定义和背景
1 定义
圆轴扭转是指在机械系统中,圆轴受到一对 作用力使得其进行扭转运动。
2 背景
圆轴扭转是机械工程中一项重要的运动形式, 广泛应用于各种机械设备和结构中。
圆轴扭转的受力特点和变形特点

圆轴扭转的受力特点和变形特点
圆轴在受到扭矩作用时,其受力特点和变形特点与直轴不同。
下面我们来详细探讨一下圆轴扭转的受力特点和变形特点。
一、受力特点
在圆轴扭转过程中,受到的力主要是扭矩。
扭矩是使物体产生转动的力,其大小可以用公式T=FT*d来计算,其中T是扭矩,F是力,T是距离,d是轴的直径。
在圆轴扭转时,扭矩会使圆轴上的横截面产生剪切应力,剪切应力的大小与扭矩成正比。
二、变形特点
圆轴在受到扭矩作用时,会产生扭转变形。
这种变形主要表现为圆轴的各个横截面发生相对转动。
在圆轴扭转时,横截面之间的距离保持不变,因此不会出现拉伸或压缩变形。
同时,由于圆轴的刚度较大,所以扭转变形量相对较小。
三、影响圆轴扭转的因素
圆轴的扭转性能受到多种因素的影响,包括材料性质、截面形状、尺寸和边界条件等。
例如,圆轴的材料强度越高,其抵抗扭矩的能力就越强;截面形状和尺寸也会影响圆轴的扭转性能;边界条件如支撑条件和固定方式也会对圆轴的扭转性能产生影响。
四、圆轴扭转的应用
圆轴的扭转性能在机械工程中有着广泛的应用。
例如,在汽车和自行车中,车轴就是一种圆轴,它们需要承受来自轮子和车轮的扭矩。
在设计这些车轴时,需要考虑其受力特点和变形特点,以确保其具有足够的强度和刚度。
此外,在建筑工程和桥梁工程中,钢结构和钢筋混凝土结构的连接节点也需要利用圆轴的扭转性能来传递力和转矩。
工程力学08第八章圆轴的扭转

T
r
A
C
g
df
C O
Bg
D df r
DHale Waihona Puke dxg是微元的直角改变量,即 半径r各处的剪应变。因为
CC= gdx=rdf , 故有:
g rd / dx
df /dx ,称为单位扭转角。
对半径为r的其它各处,可
作类似的分析。
14
1. 变形几何条件
T
A gr B gr
rr
C
df
C O D
D
dx
对半径为r的其它各处,
GA
d
dx
B
r 2CdA T r
gA
df
g
d
/dDxCd fT
O
r/ GIP
t
t ys
---(2) O 11GG g
tma
---(3) x tr r
tor T
---(5)
圆轴扭转切应力公式:
tr
T•Dr
IP
---(4)
I矩PW称,T =为只IP截与求/面r截,I对面P称,圆几为心何W抗的相T扭极关?截惯。面性模量。dxtmtaxm在ax 圆T轴r /表IP面 T处/,W20且T
外力偶
T 内力偶
由平衡方程: T M o
平衡
4
返回主目录
Mo
Mo
T
取左边部分
Mo 假想切面
外力偶
扭矩
由平衡方程:
平衡
Mo
T Mo T
取右边部分 T
T 和T 是同一截面上的内力, 应当有相同的大小和正负。
扭矩
外力偶
平衡
5
扭矩的符号规定:
Mo
圆轴的扭转
第六章 圆轴的扭转
例6-1 求如图所示传动轴1-1截面和2-2截面的扭矩, 并画扭矩图。
解:用截面法求扭矩
1)取1-1截面左侧
T11 M 1.8kN m
2)取2-2截面右侧
=1.8kNm 1 1
=3kNm 2 2
=1.2kNm
1.2kNm
T2 2 M C 1.2kN m
38.4ΜΡa [ ] 40ΜΡa
轴满足 强度条件
4) 刚度校核
Tmax 180 700 32 180 0 max ( / m) 9 4 12 GIp 8010 45 10
1.23
m
[ ] 1.5
m
因轴同时满足刚度条件,所以传动轴是安全的。
扭转强度条件同样可以用来解决三类问题: 强度校核
设计截面尺寸
确定许用载荷
第六章 圆轴的扭转 例6-2 如图所示为阶梯形圆轴,其中实心AB段直 径d1=40mm;BD段为空心部分,外径D =55mm,内 径 d =45mm。轴上A、D、C处为皮带轮,已知主动 轮C输入的外力偶矩为MC=1.8kN· m,从动轮A、D 传递的外力偶矩分别为MA=0.8kN· m,MD=1kN· m, 材料的许用切应力[ ]=80MPa。试校核该轴的强度。 解:1)画扭矩图: 用截面法(或简捷方法) 可作出该阶梯形圆轴的 扭矩图如图所示。
解: 1) 计算外力偶矩
PA M A 9550 n 1168N m
同理
M B 468N m
M C M D 350N m
第六章 圆轴的扭转
2)绘制扭矩图 用截面法求 1-1截面的扭矩
1 2 3
T1 M B 468N m
机械设计基础圆轴扭转

MX 0
M
n
T
0
M
n
T
扭矩Mn、Mn′大小相等、方向相反,是作用力与
反作用力关系。
❖ 扭矩正负号的规定
用右手螺旋定则判断:右手四指绕向表示扭矩绕
轴线方向,则大拇指指向与截面外法线方向一致
时扭矩为正,反之扭矩为负。同一截面的扭矩符 号是一致的。
T ❖外力偶矩正负号的规定
和所有外力的规定一样,
1、计算 外力偶矩
TB
TC
TA
B1 C
2 A
TD 3D
TA
9550 PA n
1592N
•m
TB
TC
9550 PB n
477.5 N • m
TD
9550 PD n
637N
•m
2、计算各截面的T扭B 矩 TC
TA
1-1截面
TD
X
Mn1=TB
=477.5N.m 2- 2截面
③绘制扭矩图
m2
m3
m1
m4
T 9.56 kN m max
BC段为危险截面。 A T
– 4.78
n
B
C
D
6.37
x
–
9.56
课堂练习
3-39(a) 作业
❖3-39(b)
三、圆轴扭转时的应力和变形
(一)圆轴扭转时横截面上的应力
1.扭转试验
等直圆轴试件,在圆轴表面画上若干平行于轴线的 纵向线和垂直于轴线的圆周线,然后在圆轴两端分 别作用一外力偶T,使圆轴发生扭转变形:
M1+ MB= 0 M 1 = -M B =-350N.m M B + M C + M 2 =0 M 2 =-M B -M C =-700N.m
第5章 圆轴的扭转
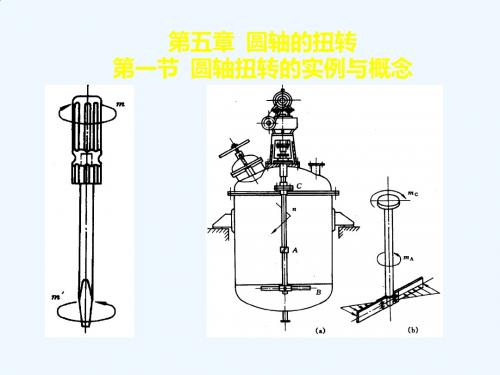
d ( 5 0 1 0 ) I m 6 1 1 0 mO
4 8 4
A
第四节 扭转的强度条件
MT max W
一般: 0 . 5 0 . 6
强度校核、设计截面与确定许可载荷
例5-3 汽车主传动轴内径d=85mm、外径D=90mm,45号钢, [τ]=60MPa,轴受到的最大转矩m=1.5kN.m (1)校核此空心 轴的强度;(2)等强度实心轴直径;(3)求实心轴与空心 轴的质量比。
A C
B
D
实验现象归纳
1 4 2 3
x
Tk
1
4 4
2 3
x
Tk
(1)纵向线转动; (2)圆周线绕轴线转动,但仍在原来的平面内; (3)圆周线大小、形状及两圆周线之间的距离不变。
推论:
① 截面只有剪应力,无正应力,即纯剪切;
② 剪应力方向是沿周边切线方向; ③ 平截面假定。 Tk y
x
Tn
TB
1210
TATBTCTATn2x
Tn
-1590
A
B
C
19 T 9549 1210 Nm A 150 同样 T B =2800Nm, T C =1590Nm
Tn
-2800
x
-1590
第三节 扭转时横截面上的应力
m 关于应力的三个问题:
存在什么应力 应力如何分布 应力如何计算
TK
A m Tn
B
2、空心圆轴 令:d/D=a
J D d 0 . 1 D 1 a 32
4 4 4 4
W D d 0 . 2 D 1 a
4 4 3 4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d
T
G
dx
IP
G
dT
dx IP
d T
dx G IP
max
T R IP
T Wt
Wt
IP R
抗扭截面系数,与截面的大小、 形状、尺寸等有关。
六、公式的适用范围
1、圆轴扭转
2、弹性范围内 max p
的扭矩为负。
.
16
★扭矩图的简便计
算∶
1、自左到右的方向进行;
M1
2、遇到图示外力偶矩,内力扭矩T
的增量为正;
3、遇到图示外力偶矩,内力扭矩T
M2
的增量为负;
4、扭矩图上的突变值等于外力偶矩。
从左开始,向左方向的外力偶矩产生正的扭矩; 从右开始,向右方向的外力偶矩产生正的扭矩。
.
17
例题3
20KN.m
2、扭矩 1216m41.4 2 B
3819.6 m2 A
3 1655.2 4 m3
C
1 T1 m1
m1
m1
2 T1=0
3
4
T2 T2=m1 =2164.4
m2 T3 T3=m1-m2 =-1655.2
m2
m3
T4
.
T3=m1-m2+m132=0
3、作扭矩图
2164.4 m1
B
3819.6 m2
.
1
第四章 圆轴扭转
§4-1 扭转的概念和实例
§4-2 受扭圆杆横截面上的内力
§4-3受扭圆杆的应力和变形
§4-4圆杆受扭时的强度及刚度计算
.
2
§4-1 扭转的概念和实例
一、实例
传动轴
.
3
.
4
传动轴
.
5
二、扭转的概念
受力特点:
构件的两端受相反方向, 作用面垂直于轴线的一对力 偶的作用。(力偶的方向---轴向)
.
23
二、变形几何规律
M
M
x
d
dx
d
R
a
bA
b′ A′
x
c
d
d′
A
A′
dx
ρ x
dx 取一.小段dx圆轴研究之,如上图2示4
d
R
a
bA
b′ A′
x
c
d
d′ dx
d
A
A′
dx
ρ x
外表面上:b→b′
R d
dx
内部A: A→A′
d
dx
变形几何规律
★ d ---单位长度上横截面的相对扭转角
T的方向。
.
26
d
R
a
bA
T
b′ A′
x
c
d
d′ dx
T
τ
.
27
五、静力关系
横截面上内力系合成的结果 内力合力T
x
dA
T
dA
T
T
TdA AGd dx dA
D
G d 2dA dx A
令 IP 2dA 横截面对形心的极惯性矩
仅与图形的面积分布有关而与外界条. 件无关,反映截面性质的量。 28
T
+30KN.m
+10KN.m
x
-30KN.m
.
15
★讨论:
1、完整的T~x 图,包含坐标轴方向、比例尺、大小、单 位、特征点的T值。
2、T~x 图是一条连续的曲线。 3、在集中力偶作用的地方,扭矩图发生突变。 4、突变的数值等于集中力偶的大小,突变的方向由集中力
偶的方向决定。 5、以外法向的力偶产生的扭矩为正,负法向的力偶产生
mx 0 Tm0 Tm
.
9
2、符号规定: T沿截面的外法向为正
TMe ㈩
TMe ㈩
m
x
m
T
T
三、扭矩图: 以横截面所在的轴的位置为横坐标,T的大小
为纵坐标作出的图形-----扭矩图。
意 直观地反映轴上任意位置横截面上的内力--义 扭矩的变化。
.
10
例题1
图示一皮带传动轴,轮子A用皮带直接与原动机连接,轮 子B和C与机床连接。已知轮子A传递的功率为60kW, 轮子B 传递34kW,轴的转速150r/min,略去轴承的摩擦
力,试作出轴的扭矩图。
m1
m2 m3
B
A
C
解:1、外力偶矩
m 295N n4 9 95 1 4 65 9 03 08 .6N 1.m 9
m 195N n4 9 95 1 4 35 9 4 2 01 .4N 6 .m 4
N
26
m 395 . n4 9 95 1 45 9 106 .2N 5 .m 5 11
变形特点:
横截面发生相对的转动 (绕轴转动)
研究对象: 等直杆、圆形截面杆或可近似为等直圆截面杆的构件。
.
6
§4-2 受扭圆杆横截面上的内力
一.外力偶矩 1、直接计算
.
7
2、按输入功率和转速计算
1、承受扭转的轴通常是用来传递功率的,若传输的功率为N千瓦, 转速n转/分,则此轴传递的外力偶矩为:
每秒内做的功: WN10N 0M 0
10KN.m
10KN.m T (KN.m)
+20 +10
.
2.m
20KN.m
20KN.m
40KN.m
T (KN.m) +20
.
40KN.m +40
x
19
例题5
m=2M/a 2M
M
a
a
T
+3M
+M
+M
x
.
20
§4-4 圆轴扭转时的应力
★分析思路:
应力
内力分布
dx
d
★ 同一截面上(选择了参考. 面后), 相同
25
dx
三、物理关系
当
时, G (剪切胡克定律)
剪应力分布规律:
G
d
dx
1)同一截面上, 与 成正比,即 沿半径线线性分布
2)同一截面上,在同一圆周上有相同的大小。
3)从变形可以看出,没有长度的变化,只有相对的转动, 横截面上点沿圆周线位移, 与半径线垂直,且顺着
A
1655.2 m3 C
m1
m2
m3
T +2164.4Nm
x
-1655.2Nm
4、若将轮A和轮B换一个位置,. 则最大扭矩会怎样
13
3819.6 m2 A
m2 T
-3819.6Nm
2164.4 m1
B
1655.2 m3 C
m1
m3
x -1655.2Nm
.
14
例题2
20KN.m
40KN.m
30KN.m
a′
b′
c′
d′
ac、bd代表的是两个横截面
提出假设: 横截面似一刚性平面,在外力偶矩作用下绕轴
转过一定的角度,仍维持为圆截面。
平面假设. 成立!
22
观察到的变形:
a
b
1)平面假设成立
2)轴向无伸缩
c
d
a′
b′
c′
d′
3)纵向线变形后仍为平行直线 4)横截面上同一圆周上所有的点绕轴心转过相同的角度
一、实验观察
静力关系 几何关系 物理关系
实验观察 变形几何规律
ab cd
1)在圆轴的外表面上纵向作平行直线
a
b
2)在圆轴的外表面上横向作平行圆周线
c
d
3)在圆筒的两端加上静载外.力偶矩M,观察变形。 21
3)在圆筒的两端加上静载外力偶矩M,观察变形。
M
M
a′ b′
c′ d′
4)观察变形
a
b
c
d
abcd→a′b ′ c ′ d ′
每秒内做的功还等于:WMMn2NM
60
N1000M2n
60
M(N.m)9549N(KW) n(r/min)
2、若传输的功率为N马力,转速n转/分,则此轴传递的外力偶矩为:
M(N.m)702N 4(马力 )
. n(r/min)
8
二、圆轴扭转内力:-----扭矩T
1、内力: 截面法求内力
m
m
m
x
m
T
T
