2007-2017年(独缺09年)福州大学结构力学考研真题,附部分答案-1
福大结构力学课后习题详细答案..-副本

结构力学(祁皑)课后习题详细答案答案仅供参考第1章1-1分析图示体系的几何组成。
1-1(a)解原体系依次去掉二元体后,得到一个两铰拱(图(a-1))。
因此,原体系为几何不变体系,且有一个多余约束。
1-1 (b)解 原体系依次去掉二元体后,得到一个三角形。
因此,原体系为几何不变体系,且无多余约束。
1-1 (c)(c-2) (c-3)解 原体系依次去掉二元体后,得到一个三角形。
因此,原体系为几何不变体系,且无多余约束。
1-1 (d)(d-1)(d-2)(d-3)解原体系依次去掉二元体后,得到一个悬臂杆,如图(d-1)-(d-3)所示。
因此,原体系为几何不变体系,且无多余约束。
注意:这个题的二元体中有的是变了形的,分析要注意确认。
1-1 (e)解原体系去掉最右边一个二元体后,得到(e-1)所示体系。
在该体系中,阴影所示的刚片与支链杆C组成了一个以C为顶点的二元体,也可以去掉,得到(e-2)所示体系。
在图(e-2)中阴影所示的刚片与基础只用两个链杆连接,很明显,这是一个几何可变体系,缺少一个必要约束。
因此,原体系为几何可变体系,缺少一个必要约束。
1-1 (f)解原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相连,符合几何不变体系的组成规律。
因此,可以将该刚片和相应的约束去掉只分析其余部分。
很明显,余下的部分(图(f-1))是一个几何不变体系,且无多余约束。
因此,原体系为几何不变体系,且无多余约束。
1-1 (g)解原体系中阴影所示的刚片与体系的其它部分用三个链杆相连,符合几何不变体系的组成规律。
因此,可以将该刚片和相应的约束去掉,只分析其余部分。
余下的部分(图(g-1))在去掉一个二元体后,只剩下一个悬臂杆(图(g-2))。
因此,原体系为几何不变体系,且无多余约束。
1-1 (h)解原体系与基础用一个铰和一个支链杆相连,符合几何不变体系的组成规律。
因此,可以只分析余下部分的内部可变性。
这部分(图(h-1))可视为阴影所示的两个刚片用一个杆和一个铰相连,是一个无多余约束几何不变体系。
福州大学结构力学考研真题(3)

福州大学2023年年招收硕士研究生入学考试试卷
招生学院:土木工程学院科目代码:828
考试科目名称(全称):结构力学
简答题
1.简述三铰拱的受力特点及工程适用性。
(12分)
2.试简述下列位移公式的使用范围,并说明理由。
(13分)
3.试简述动力系数中,阻尼对结构自由振动的反应影响。
(20分)
4.试简述动力系数物理意义,单自由度体系中是否有统一的动力系数?为什么?(20分)
第 1 页/共 4 页
5.求下面结构A点的转角。
(20分)
6.使劲法求解下列结构,并校核C点的位移。
a=0.02l,b=0.01l,(30分)
7.用位移法求解下列结构,并对结构举行校核。
(20分)
8.用影响线求Mk ,Fq左Fq 右
第 3 页/共 4 页
9.求下列结构的自振频率。
(15分)。
结构力学试题及答案汇总完整版.

4.图示桁架的零杆数目为:(D)
A. 6;B. 7;C. 8;D. 9。
5.图a结构的最后弯矩图为:(A)
A.图b;B.图c;C.图d;D.都不对。
6.力法方程是沿基本未知量方向的:(C)
A.力的平衡方程;B.位移为零方程;
C.位移协调方程;D.力的平衡及位移为零方程。
图1
2、如图2所示的结构在外力作用下,CD杆D端的剪力 ()
① ②
③ ④
图2
3、如图3所示结构,若支座B产生位移,则该结构将( )
①不产生位移;②产生内力;
③不产生内力;④产生变形。
图3
4、用力法解图4所示结构的未知量个数为()
①5个;
②6个;
39个;
412个;
图4
5、位移法方程的实质是()
①平衡方程;
图5
3、用虚功原理导出计算结构在载荷作用下位移的单位载荷法时,其虚功方程
中的位移和变形是由实际荷载引起的,而作虚功的力是虚功的单位力
及其产生的内力。
4、力法方程就其性质而言,属于位移方程,方程中的载荷项 表
示基本结构在载荷作用下沿方向上的位移。
5、图6所示刚架,假定忽略所有杆件的轴向变形,按位移法求解时,有4
四、.(20分)
(2分) (3分)
力法方程 (2分)
(2分) (2分)
系数: (2分) (2分)
解得: (1分)
最后弯矩图
(4分)
选择其它基本体系可参照以上给分。
五、(20分)
(3分)(2分)
(4分)(2分)MP图(2分)
, , ,(6分)
(1分)
( 1分)最后弯矩图
《结构力学》试题及答案汇总

院(系) 学号 姓名 .密封线内不要答题 密封……………………………………………………………………………………………………………………………………………………结构力学试题答案汇总结构力学课程试题 ( B )卷考 试 成 绩题号 一二三四成绩得分一、选择题(每小题3分,共18分)1. 图 示 体 系 的 几 何 组 成 为 : ( ) A. 几 何 不 变 , 无 多 余 联 系 ; B. 几 何 不 变 , 有 多 余 联 系 ; C. 瞬变 ; D. 常 变 。
2. 静 定 结 构 在 支 座 移 动 时 , 会 产 生 : ( )A. 内 力 ;B. 应 力 ;C. 刚 体 位 移 ;D. 变 形 。
3. 在 径 向 均 布 荷 载 作 用 下 , 三 铰 拱 的 合 理 轴 线 为: ( )A .圆 弧 线 ;B .抛 物 线 ;C .悬 链 线 ;D .正 弦 曲 线 。
4. 图 示 桁 架 的 零 杆 数 目 为 : ( )A. 6;B. 7;C. 8;D. 9。
5. 图 a 结构的最后弯矩图为:()A.图 b; B.图 c ; C.图 d ; D.都不对。
6. 力法方程是沿基本未知量方向的:()A.力的平衡方程;B.位移为零方程;C.位移协调方程; D.力的平衡及位移为零方程。
二、填空题(每题3分,共9分)1.从几何组成上讲,静定和超静定结构都是_________体系,前者_________多余约束而后者_____________多余约束。
2. 图 b 是图 a 结构 ________ 截面的 _______ 影响线。
3. 图示结构 AB 杆 B 端的转动刚度为 ________, 分配系数为________, 传递系数为 _____。
三、简答题(每题5分,共10分)1.静定结构内力分析情况与杆件截面的几何性质、材料物理性质是否相关?为什么?2.影响线横坐标和纵坐标的物理意义是什么?四、计算分析题,写出主要解题步骤(4小题,共63分)1.作图示体系的几何组成分析(说明理由),并求指定杆1和2的轴力。
结构力学练习题及答案讲解
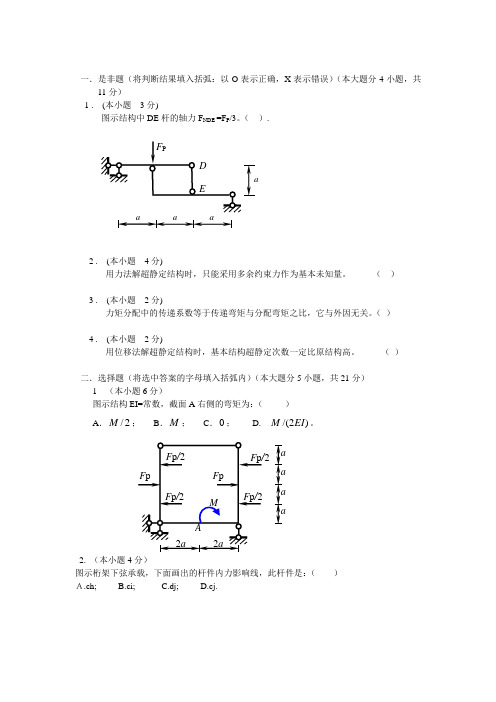
一.是非题(将判断结果填入括弧:以O 表示正确,X 表示错误)(本大题分4小题,共11分)1 . (本小题 3分)图示结构中DE 杆的轴力F NDE =F P /3。
( ).2 . (本小题 4分)用力法解超静定结构时,只能采用多余约束力作为基本未知量。
( )3 . (本小题 2分)力矩分配中的传递系数等于传递弯矩与分配弯矩之比,它与外因无关。
( )4 . (本小题 2分)用位移法解超静定结构时,基本结构超静定次数一定比原结构高。
( )二.选择题(将选中答案的字母填入括弧内)(本大题分5小题,共21分) 1 (本小题6分)图示结构EI=常数,截面A 右侧的弯矩为:( )A .2/M ;B .M ;C .0; D. )2/(EI M 。
2. (本小题4分)图示桁架下弦承载,下面画出的杆件内力影响线,此杆件是:( ) A.ch; B.ci; C.dj;D.cj.23. (本小题 4分)图a 结构的最后弯矩图为:A. 图b;B. 图c;C. 图d;D.都不对。
( )( a) (b) (c) (d)4. (本小题 4分)用图乘法求位移的必要条件之一是: A.单位荷载下的弯矩图为一直线; B.结构可分为等截面直杆段; C.所有杆件EI 为常数且相同; D.结构必须是静定的。
( ) 5. (本小题3分)图示梁A 点的竖向位移为(向下为正):( ) A.F P l 3/(24EI); B. F P l 3/(!6EI); C. 5F P l 3/(96EI); D. 5F P l 3/(48EI).三(本大题 5分)对图示体系进行几何组成分析。
F P=1四(本大题 9分)图示结构B 支座下沉4 mm ,各杆EI=2.0×105 kN ·m 2,用力法计算并作M 图。
五(本大题 11分) 用力矩分配法计算图示结构,并作M 图。
EI=常数。
六(本大题14分)已知图示结构,422.110 kN m ,10 kN/m EI q =⨯⋅=求B 点的水平位移。
福州大学土木工程学院828结构力学考研笔记

福州⼤学⼟⽊⼯程学院828结构⼒学考研笔记历年简答题部分(早年)1、为什么仅⽤静⼒平衡⽅程,即可确定全部反⼒和内⼒的体系是⼏何不变体系,且没有多余约束。
因为静定结构仅有平衡条件即可求出全部反⼒和内⼒;超静定结构仅有平衡条件⽆法求出全部反⼒和内⼒;⼏何可变体系⽆静⼒解答,并且由于静定结构时没有多余约束的,所以仅⽤静⼒平衡⽅程即可确定全部反⼒和内⼒的体系是⼏何不变体系(参考答案)。
2、静定结构受荷载作⽤产⽣内⼒,内⼒⼤⼩与杆件截⾯尺⼨⽆关,为什么?因为静定结构因荷载作⽤⽽产⽣的内⼒仅有平衡条件即可全部求得,因此……3、荷载作⽤在静定多跨梁的附属部分时,基本部分的内⼒⼀般不为零,为什么?因为附属部分是⽀承在基本部分上的,对附属部分⽽⾔,基本部分等同于⽀座,故附属部分有荷载时基本部分内⼒⼀般不为零。
(参考答案)4、⽤⼒法求解结构时,如何对其计算结果进⾏校核?为什么?因为超静定结构的内⼒是通过变形协调条件和平衡条件得出的,因此在对⼒法求解结果进⾏校核时应⾸先校变形协调条件和平衡条件。
①校核变形协调条件:因为基本结构在多余约束⼒和荷载作⽤下的变形与原结构完全⼀致,因此可在基本结构上施加单位⼒,作出单位⼒弯矩图,并与⼒法计算所得的弯矩图图乘,校核计算所得位移与结构的实际位移是否⼀致。
②校核平衡条件:任取结构某⼀部分为隔离体,校核其弯矩、剪⼒、轴⼒是否符合平衡条件。
5、⽤位移法求解结构时,如何对其进⾏计算结果校核,为什么?因为超静定结构的内⼒是通过变形协调条件和平衡条件得出的,因此在对位移法求解结果进⾏校核时应⾸先校变形协调条件和平衡条件。
①校核平衡条件:任取结构某⼀部分为隔离体,校核其弯矩、剪⼒、轴⼒是否符合平衡条件。
②校核变形协调条件:因为在位移法求解过程中已经保证了各杆端位移的协调,所以,变形协调条件⾃然满⾜。
6、为什么实际⼯程中多数结构都是超静定的?①因为超静定结构包含多余约束,万⼀多余约束破坏,结构仍能继续承载,具有较⾼的防御能⼒。
福州大学-考研《结构力学考试样题库》4-静定位移
福州大学-考研《结构力学考试样题库》4-静定位移第四章静定结构位移计算一、是非题1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、用图乘法可求得各种结构在荷载作用下的位移。
5、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
Mk M p21y 1y 2**ωω7、图示桁架各杆EA 相同,结点A 和结点B 的竖向位移均为零。
8、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
aa9、图示简支梁,当P 11=,P 20=时,1点的挠度为0.01653l EI /,2点挠度为0.0773l EI /。
当P 10=,P 21=时,则1点的挠度为0.0213l EI /。
()l10、图示为刚架的虚设力系,按此力系及位移计算公式即可求出杆AC 的转角。
CP11、图示梁AB 在所示荷载作用下的M图面积为ql 3。
lAl /212、图示桁架结点C水平位移不等于零。
13、图示桁架中,结点C 与结点D 的竖向位移相等。
二、选择题1、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;;B.D.M C.=1=1=12、图示结构A 截面转角(设顺时针为正)为:A.22Pa EI / ;B.-Pa EI 2/ ;C.542Pa EI /() ;D.-542Pa EI /() 。
aa3、图示刚架l a >>0 , B 点的水平位移是:A .不定,方向取决于a 的大小;B .向左;C .等于零;D .向右。
4、图示静定多跨粱,当EI 2增大时,D 点挠度:A .不定,取决于EI EI 12;B .减小;C .不变;D .增大。
福州大学考研《结构力学习题集》6-位移法
福州大学考研《结构力学习题集》6-位移法《结构力学》习题集第六章位移法一、是非题1、位移法未知量的数目与结构的超静定9、图示梁之EI=常数,固定端A发生顺,次数有关。
,由此引起铰支端B时针方向之角位移之转角(以顺时针方向为正)是,、位移法的基本结构可以是静定的,也/2 。
2-可以是超静定的。
,B3、位移法典型方程的物理意义反映了原A结构的位移协调条件。
l4、结构按位移法计算时,其典型方程 10、用位移法可求得图示梁B端的竖向的数目与结点位移数目相等。
3qlEI/24位移为。
q5、位移法求解结构内力时如果图为MP零,则自由项一定为零。
R1PELAB l 、超静定结构中杆端弯矩只取决于 6 杆端位移。
,11、图示超静定结构,为 D 点转角 D (顺时针为正),杆长均为 l , i 为常 7、位移法可解超静定结构,也可解静数。
此结构可写出位移法方程定结构。
2 11120iql,,,/。
D8、图示梁之 EI =常数,当两端发生图示角位移时引起梁中点C之竖直位移为(/)38l,(向下)。
PD,,2qCll/2/2二、选择题1、位移法中,将铰接端的角位移、滑动 C. 可以,但不必 ; 支承端的线位移作为基本未知量 : D. 一定条件下可以。
A. 绝对不可 ;B. 必须 ;—— 43 ——《结构力学》习题集MM=Ph/4, =Ph/2 ; C. 2、AB 杆变形如图中虚线所示,则 A 端ACBDMMD. =Ph/2, =Ph/2 。
的杆端弯矩为 : ACBDMiiil,,,426,,,/A. ; ABABABEI=D?CPMiiil,,,426,,,/B. ;ABABABihi2h4Miiil,,,,426,,,/C. ; ABABABBA Miiil,,,,426,,,/D.。
ABABAB6、图示两端固定梁,设 AB 线刚度为 i , ,A、两端截面同时发生图示单位转当 AB B,角时,则杆件端的杆端弯矩为 : AAAB,BA. ; B. 2 ; I iC. 4i ;D. 6i,=1,=1ABAB,,3、图示连续梁,已知 P , l , , , BC( )i 则 :Mii,,44,,A. ; BCBC7、图示刚架用位移法计算时,自由项Mii,,42,,B. ; BCBCR 的值是 : 1PMiPl,,48,/C. ; BCBA. 10 ; B. 26 ; MiPl,,48,/D. 。
结构力学答案(1)
结构力学答案《结构力学》第01章在线测试第一题、单项选择题(每题1分,5道题共5分)1、结构力学的研究对象是 BA、单根杆件B、杆件结构C、板壳结构D、实体结构2、对结构进行强度计算目的是为了保证结构AA、既经济又安全B、不致发生过大的变形C、美观实用D、不发生刚体运动3、对结构进行刚度计算,是为了保证结构 CA、不发生刚体运动B、美观实用C、不致发生过大的变形D、既经济又安全4、固定铰支座有几个约束反力分量? BA、一个B、两个C、三个D、四个5、可动铰支座有几个约束反力分量AA、一个B、两个C、三个D、四个第二题、多项选择题(每题2分,5道题共10分)1、结构的稳定性是指DEA、结构抵抗破坏的能力B、不发生刚体运动的能力C、结构抵抗变形的能力D、结构抵抗失稳的能力E、结构保持原有平衡形式的能力2、下列哪种情况不是平面结构BCDEA、所有杆件的轴线都位于同一平面内,荷载也作用在该平面内B、所有杆件的轴线都位于同一平面内,荷载与该平面垂直C、所有杆件的轴线都位于同一平面内,荷载与该平面平行D、所有杆件的轴线都不位于同一平面内E、荷载不作用在结构的平面内3、下列哪种情况应按空间结构处理ABDEA、所有杆件的轴线都位于同一平面内,荷载与该平面垂直B、所有杆件的轴线都不位于同一平面内C、所有杆件的轴线都位于同一平面内,荷载也作用在该平面内D、所有杆件的轴线都位于同一平面内,荷载与该平面平行E、荷载不作用在结构的平面内4、为了保证结构既经济又安全,要计算结构BA、强度B、刚度C、稳定性D、内力E、位移5、刚结点的约束特点是ABA、约束各杆端不能相对移动B、约束各杆端不能相对转动C、约束的各杆端可沿一个方向相对移动D、约束各杆端可相对转动E、约束各杆端可相对移动第三题、判断题(每题1分,5道题共5分)1、板壳结构的厚度远远小于其它两个尺度。
正确2、实体结构的厚度与其它两个尺度是同一量级。
正确3、为了保证结构既经济又安全,要对结构进行刚度计算。
结构力学(一)试题及答案.docx
结构力学(一)*本节测验题:结构力学的研究对象是A.杆件结构B.板壳结构C.实体结构D.静定结构请选择:r A C B r C r DA本节测验题:不能作为建筑结构使用的是A.无多余约束的几何不变体系B.有多余约束的几何不变体系C.几何不变体系D.几何可变体系请选择:r A r B r C r DD本节测验题:三刚片组成无多余约束的几何不变体系,其联结方式是A.以任意的三个较相联B.以不在一条线上三个较相联C.以三对平行链杆相联D.以三个无穷远处的虚较相联请选择:r A r B r C C DB本节测验题:从一个无多余约束的几何不变体系上去除二元体后得到的新体系是A.无多余约束的几何不变体系B.有多余约束的几何不变体系C.几何可变体系D.几何瞬变体系请选择:r A C B r C C DA 本节测验题:梁上在集中力偶Hl作用处的截面弯矩是A.m/2 (上拉)B.m/2 (下拉)C.m (下拉)D.不确定的请选择:r A r B r C r DD本节测验题:两个简支梁的跨度、荷载、截面尺寸相同但所用材料不同,则两者不同的因素是A.内力B.反力C.应力D.变形请选择:r A C B r C r DD本节测验题:荷载作用在基本梁上,附属梁会产生什么?A.内力B.反力C.位移D.变形请选择:r A r B r C r DC本节测验题:如杆端无集中力偶荷载作用,下列哪些位置杆端弯矩不等于零A.自由端B.较支座杆端C.较节点杆端D.刚结杆端请选择:r A r B r C C DD本节测验题:在弯矩图发生转折处作用有什么外力?A.轴向外力B.横向集中力C.集中力偶D.无外力请选择:r A C B C C C DC本节测验题:桁架计算的截面法所选分离体包含几个节点?A.单个B.最少两个C.最多两个D.任意个请选择:r A C B r C r DD本节测验题:在静水压力荷载作用下,对称三较拱的合理拱轴线是什么曲线?A.抛物线B.圆弧曲线C.悬链线D.双曲线请选择:r A r B r C r DB本节测验题:对于静定结构,改变材料的性质,或改变横截面的形状和尺寸,下列哪一项不会改变?A.内力B.位移C.变形D.应力请选择:r A r B r C r DA本节测验题:在结构中的AB两点加一对等值反向共线的单位力,是求什么位移的虚拟力状态?A.A点位移B.B点位移C.AB两点的相对位移D.AB两截面的相对转角请选择:r A r B C C r DC节测验题:梁和刚架位的位移计算只需要考虑A.扭转变形对位移的影响B.弯曲变形对位移的影响C.轴向变形对位移的影响D.剪切变形对位移的影响请选择:C A C B C C C DB本节测验题:下列那一条不是图乘法求位移的适用条件?A.直杆B.EI为常数C.两个弯矩图至少有一个为直线形D.两个弯矩图都必须是直线形请选择:r A r B r C C DD本节测验题:图乘公式中竖标yOA.必须取在荷载弯矩图中B.可取在任意弯矩图中C.必须取在虚拟的单位弯矩图中D.必须取在直线图形中请选择:r A r B r C r DD*本节测验题:静定结构的支座移动将使其产生A.内力B.位移C.变形D.应力请选择:r A r B C C r D本节测验题:力法的基本未知量是A.支座反力B.多余未知力C.角位移D.独立的结点线位移请选择:r A r B r C r DB本节测验题:力法基本方程的实质是A.平衡条件B.位移条件C.物理条件D.互等定理请选择:r A r B C C r DB本节测验题:在荷载作用下,若将超静定结构各杆刚度同时增大一倍,其各杆内力A.均不变B.均增大一倍C.均减小一倍D.不确定,有的增大,有的减小请选择:C A C B r C C DA本节测验题:温度改变时,若将超静定结构各杆刚度同时增大一倍,则各杆内力A.均不变B.均增大一倍C.均减小一倍D.不确定,有的增大,有的减小请选择:r A r B r C r DB本节测验题:位移法的基本未知量是A.支座反力B.杆端弯矩C.独立的结点位移D.多余未知力请选择:r A C B C C C DC本节测验题:位移法基本方程的实质是A.平衡条件B.位移条件C.物理条件D.互等定理请选择:r A C B r C r DA本节测验题:位移法可以求解A.超静定刚架B.静定刚架C.桁架D.ABC均可请选择:r A r B r C r DD本节测验题:等截面直杆的弯矩传递系数C与下列什么因素有关A.荷载B.线刚度C.材料性质D.远端支承请选择:r A r B C C r DD本节测验题:结点不平衡力矩总是等于A.固端弯矩之和减结点集中力偶B.固端弯矩之和加传递弯矩减结点集中力偶C.传递弯矩D.附加刚臂中的约束力矩请选择: 本节测验题:对称结构在对称荷载作用下,位于对称轴上的截面A.弯矩等于零B.剪力等于零C.轴力等于零D.竖向位移等于零请选择:r A r B C C r DB本节测验题:奇数跨对称结构在反对称荷载作用下,取半边结构时应将对称轴上的截面设置成A.与对称轴重合的支杆B.固定较支座C.定向支座D.固定支座请选择:r A r B r C C DA本节测验题:对于超静定结构,下列说法错误的是A.计算位移时,虚拟单位力可加在任一基本结构上B.只有既满足平衡条件又满足变形条件的计算结果才是正确的C.无荷载就无内力D.内力与各杆刚度有关请选择:r A C B r C C DC*本节测验题:简支梁跨中某截面C剪力影响线是A.一条斜直线B.两段平行线C.两段直线组成的折线D.一条曲线请选择:r A r B r C r DB本节测验题:机动法作静定梁影响线的理论基础是A.虚功互等定理B.位移互等定理C.刚体虚位移原理D.变形体虚功原理请选择:r A r B r C r DC本节测验题:关于多跨静定梁的影响线,下列说法正确的是A.基本部分上某量值的影响线在基本部分上纵标为零B.基本部分上某量值的影响线在附属部分上纵标为零C.附属部分上某量值的影响线在附属部分上纵标为零D.附属部分上某量值的影响线在基本部分上纵标为零请选择:r A r B C C r DD本节测验题:在行列荷载作用下,使量值S取得极值的荷载位置是A.最大荷载位于影响线顶点B.任一荷载位于影响线顶点C.临界荷载位于影响线顶点D.所有荷载位于影响线范围内请选择:C A C B r C C DC本节测验题:下列那个单元的单元刚度矩阵的行列式的值等于零A.简支梁B.一端固定一端較支梁C.悬臂梁D.自由单元请选择:r A r B r C r DD本节测验题:结构动力计算的基本未知量是A.质点位移B.多余未知力C.结点位移D.杆端弯矩请选择:r A r B r C r DA*本节测验题:无阻尼单自由度体系的自由振动方程:y=Clsinwt+C2coswt。
