1011高等数学a(二)试题答案讲义 济南大学
济南大学高等数学下历年考题答案

得f x ( x, x) f x ( x, x) x 2
y( x) -2e 2 x f ( x, x) x 2e 2 x
一阶线性微分方程
P( x) 2
Q( x ) x 2e 2 x
P ( x ) dx
ye
P ( x ) dx
[C Q( x )e
B( x, y )
在 整 个 xoy面 内2 xydx x 2dy是 某 个 函 数 的 全 微 分
取积分路径,如图:
则u( x, y )
2
( x, y)
( 0, 0 )
2
2 xydx x dy
2
2 2
OA
xy dx x ydy xy dx x ydy
2
AB
A( x ,0)
2 xdv 2 ydv 0 (由对称性)
上式 dv
2
0
d
1 rdr 2 dz 0 r 2
1
1
3、计算曲面积分 I x 2 dydz y 2 dzdx ( z x)dxdy ,其中 为抛物面 z
1
) ( x n1 )
n 0
(
1 x ) (1 x ) 2 1 x
1
( x 6 y)dxdy,其中 D 是由 y x
D
y 5x 和 x 1 ,
y 5x
所围成的闭区域.
dx ( x 6 y )dy 0
x
1
5x
y x
0
1
2. ( 2 xy3 y 2 cos x )dx (1 2 y sinx 3 x 2 y 2 )dy ,其中
济南大学2009~2010学年第一学期课程考试试卷(A卷)答案

概念 极限 性质 计算方法
概念 连续 基本结论 性质 初等函数的连续性 闭区间上连续函数的性质
左右极限
第二章主要内容回顾
导数的概念、几何意义 定义求导 导数 求导方法 基本公式、四则运算、复合求导 反函数求导 特殊函数求导 隐函数求导 高阶导数
0
证明至少存在一点 (0,1) ,使得 f ( )(1 ) f ( x)dx
证:
令F ( x) (1 x) f (t )dt
0
x
F ( x) f (t )dt (1 x) f ( x)
0
x
显然,F ( x)在[0,1]上连续,在 0,1)内可导,且 (0) F (1), ( F
原积分
xdf ( x )
2
2
xf ( x)
f ( x)dx
2
4
1
五、解答题(8分)
y f ( x)
的极值。
dy t 2 1 2 0 dx t 1
由参数方程
x t 3 3t 1 3 y t 3t 1
确定,求
f ( x)
3 1 x 3 2 x x
x0 x0
5.设
x ln(1 t an t )dt 0 f ( x) x2 a
2
在原点处连续,则
a
0
lim
x 0
x2 0
ln( tan t )dt 1 x
2
2 x ln( tan | x |) 1 lim x 0 2x
高等数学A(二)(答案及得分详解)

高等数学A (二)带答案一、单项选择题(每小题3分,共30分) 题号 1 2 3 4 5 6 7 8 9 10答案 B B A A D B C C BA 得分1、设三个向量,,a b c 满足关系式0a b c ++= ,则a b ⨯= ( )。
(A) c b ⨯ (B) b c ⨯ (C) a c ⨯ (D) b a ⨯2、函数()22,y x y x f +=在点)2,1(处沿向量→l =( )的方向导数最大。
(A) )2,1( (B) )4,2( (C) )4,4( (D) )2,2(3、函数()y x f ,在点()00,y x 处偏导数都存在且连续是()y x f ,在该点处可微的( )条件。
(A) 充分 (B) 必要 (C) 充分必要 (D) 既不充分也不必要4、空间曲线3,1,1t z tt y t t x =+=+=在对应于1=t 的点处的切线方程是( )。
(A) 12142121-=--=-z y x (B) 121411-=--=z y x (C) 02184=-+-z y x (D) 0284=++-z y x 5、取}01),({22>≤+=x y x y x D ,,则下面二重积分中其值为0的是 ( )。
(A) ()σd y x D ⎰⎰+22 (B) ()σd xy x D⎰⎰+23(C) ()σd y x D ⎰⎰+33 (D) σd y x D ⎰⎰sin cos6、()=+⎰ds y x L22( ),其中L 为圆周222=+y x 。
(A) π2- (B) π24 (C) 238π (D) 17、设曲面∑为上半球面2222x y z R ++=0)z ≥(,曲面1∑是曲面∑第一卦限的部分,则下面等式成立的是( )。
(A) 14xdS xdS ∑∑=⎰⎰⎰⎰(B)14ydS xdS ∑∑=⎰⎰⎰⎰ (C) 14zdS xdS ∑∑=⎰⎰⎰⎰(D) 14xyzdS xyzdS ∑∑=⎰⎰⎰⎰ 8、下列级数中,绝对收敛的是( )。
10-11-2《高等数学A(工科数学分析)》第二学期期末考试试卷(精简版)及参考答案

河南理工大学 2010-2011 学年第 2 学期《工科数学分析》(下)试卷(A 卷)一、填空题(共28分,每小题4分)1.函数xyz z xy u -+=32在点()2,1,1处沿方向l (其方向角分别是00060,45,60)的方向导数 是 9/2 .2.设0 < p < 1,计算级数()∑∞=--1121k k p p k =)20(,22<<-p pp3. 函数())sin(,22y x y x f +=在点)0,0(的泰勒公式(到二阶为止)为()()()2222,y x y x y x f +=++=ρρο4.函数()xx f 3=的幂级数展开式为∑∞=0!3ln n nn x n .5.设()⎰-=22x xxy dy ex F ,则=')(x F ()⎰----+-223522x xxy x x dy ey ex e6.()⎰C ds x =()15532-,其中(C )为抛物线x y =从点()0,0到点()1,1的一段弧。
7.微分方程()02='+''y y ,满足初始条件1,000='===x x y y 的特解为1ln y +=x 。
二、解答题(共50分,每小题10分)1、 设()v u ,Φ具有连续偏导数,函数()y x z ,由隐方程()bz cy az cx --Φ,=0确定,求yz b x z a∂∂+∂∂。
解:将隐方程两边全微分可得:()()()()()0,2121=-⋅Φ'+-⋅Φ'=-⋅Φ'+-⋅Φ'=--Φbdz cdy adz cdx bz cy d az cx d bz cy az cx d ………………………………………………3分 整理得:dy b a c dx b a c dz 212211Φ'+Φ'Φ'+Φ'+Φ'Φ'=……………………………………6分所以,212211,Φ'+Φ'Φ'=∂∂Φ'+Φ'Φ'=∂∂b a c y zb ac x z …………………………………………8分 y zb x z a ∂∂+∂∂=c b a c b b a c a =Φ'+Φ'Φ'+Φ'+Φ'Φ'212211,………………………………………10分2、 判定正项级数∑⎰∞=+1141n n dx x x的敛散性。
0910高等数学A(二)答案

0910高等数学A(二)答案第一篇:0910高等数学A(二)答案济南大学2009~2010学年第二学期课程考试试卷评分标准(含参考答案)A卷课程名称:高等数学A(二)任课教师:张苏梅等一、填空题(每小题3分,共18分)1.yzez-xy;2.y=2x3-x2;3.2xdx+2ydy;π∞(-1)n(2x)2n4.0;5.2;6..12(1-n∑=0(2n)!),(-∞,+∞)二、选择题(每小题3分,共18分)C;D;C;B;A;B.三、计算题(每小题8分,共32分)1.解:∂z∂x=1ycosxy;.....4分∂2z1xxx∂x∂y=-y2cosy+y3siny.....8分2.解:⎰⎰xydσ=⎰2dx⎰xxydy.....4分D0=12⎰20x3dx=2.....8分 3.解:dS=+x2x2+y+y2x2+ydxdy=2dxdy.....2分⎰⎰zdS=⎰⎰x2+y22dxdy.....5分∑Dxy=⎰2πdθ⎰2r2dr=π.....8分 4.解:⎰⎰(x2+y2+z2)dxdy=dxdy=πa4...........8分∑D⎰⎰axy四、应用题(每小题8分,共16分)1.解:由椭球的对称性,不妨设(x,y,z)是该椭球面上位于第Ⅰ卦限的任一点,内接长方体的相邻边长为2x,2y,2z(x,y,z>0),其体积为:V=8xyz构造拉格朗日函数F(x,y,z,λ)=8xyz-λ(x2y2a+b+z2c-1)......4分∂F∂x=8yz-λ2xa2=0令∂F2y∂y=8xz-λb2=0........6分∂F∂z=8xy-λ2zc2=0求得(x,y,z)=⎛a,b,c⎫⎪,V=8xyz=8abc......8分⎝33⎪⎭332.解:Iz=⎰⎰⎰(x2+y2)dv.........3分Ω=⎰2π2430dθ⎰0dr⎰r2rdz.........6分=2π⎰2r3(4-r2)dr=03π.........8分五、(8分)解:因为limana=limn=1,所以收敛半径为1.n→∞n+1n→∞n+1又x=±1时,级数均发散,故级数的收敛域为(-1,1).....3分n=1∑nx∞n=x∑nxn=1∞n-1=x(∑xn)'......6分 n=1∞xx=x()'=,x∈(-1,1).........8分 21-x(1-x)六、(8分)解:① 设u=x2+y2,则∂zx=f'(u);∂xu∂2zx21x2=()f''(u)+f'(u)-3f'(u)........2分 2uu∂xuy21y2同理,2=()f''(u)+f'(u)-3f'(u)uu∂yu由∂2z∂2z∂x2+∂2z∂y2=0⇒f''(u)+1f'(u)=0.....4分 u② 设f'(u)=p,f''(u)=dp,du则原方程化为:dp1dpdu+p=0⇒=-duupu积分得:p=CC,即f'(u)=,........6分 uu由f'(1)=1,得C=1.于是f(u)=ln|u|+C1代入f(1)=0得:C1=0.函数f(u)的表达式为:f(u)=ln|u|.......8分第二篇:1112高等数学B(二)答案济南大学2011~2012学年第二学期课程考试试卷评分标准(含参考答案)A卷课程名称:高等数学B(二)任课教师:一、填空题(每小题2分,共10分)1、2dx+dy,2、-5,3、1,4、⎰10dy⎰1yf(x,y)dx5、1二、选择题(每小题2分,共10分)1、A2、B3、C4、C5、D三、计算题(每小题8分,共40分)1、解:令F=x2+y2+z2-2z,则Fx=2x,Fz=2z-2.....2分∴∂zFx∂x=-xF=z.....4分z1-∂2z∂x(1-z)2+x2∴∂x2=∂x(1-z)=(1-z)3.....8分2、解:⎰⎰(x+6y)dxdy=⎰1dx5x76D0⎰x(x+6y)dy=3.....8分π3、解:⎰⎰+x2+y2dxdy=D⎰2dθ⎰1+r2rdr=π(22-1).....8分4、解:ux(2,1,3)=4,uy(2,1,3)=5,uz(2,1,3)=3 方向lϖ=(3,4,12)cosα=313,cosβ=413,cosγ=12 .....6分∂z∂l=uu68xcosα+ycosβ+uzcosγ=13.....8分5、解:收敛域为(0,2).....2分∞∞令S(x)=∑(n+1)(x-1)n=(1)n+1)'.....6分n=0∑(x-n=0S(x)=(x-12-x)'=1(2-x)2x∈(0,2).....8分四、解答题(每小11分,共33分)ϖ1、解:交线的方向向量为nϖiϖjkϖ=1-4=(-4,-3,-1).....8分2-1-5所求直线方程为x+3y-2z-54=3=1.....11分2、解:令f(x)=xx-1,则f'(x)=-1-x2x(x-1)<0x>1 所以un单调递减且limn→∞un=0∞所以级数∑(-1)nnn=2n-1.....6分n∞由于limn→∞=1,且∑1发散n=2nn∑∞(-1)n所以级数n.....11分n=2n-13、解:旋转曲面方程为z=x2+y2.....3分投影区域D:x2+y2≤1.....5分V=⎰⎰(1-x2-y2)dxdy=⎰2πdθ⎰1π(1-r)rdr=D.....11分五、证明题(每小题7分,共7分)ff(x,0)-f(0,0)x(0,0)=lim证:x→0x=0f(0,0)=limf(x,0)-f(0,0)xx→0x=0所以函数f(x,y)在(0,0)处可导.....3分lim∆z-fx(0,0)∆x-fy(0,0)∆yρ→0ρ=limf(∆x,∆y)∆x∆yρ→0∆x2+∆y2=limρ→0∆x2+∆y2取∆y=k∆x,得极限为k1+k,说明极限不存在所以函数f(x,y),在(0,0)点不可微.....7分第三篇:专升本高等数学(二)成人高考(专升本)高等数学二第一章极限和连续第一节极限[复习考试要求]1.了解极限的概念(对极限定义等形式的描述不作要求)。
高等数学A(二)试卷及答案

高等数学A (二)考试试卷一、 填空题(每小题5分,共25分)1. 设2u 1sin ,2xu e x y x y π-=∂∂∂则在(,)处的值为_________。
2. 改变二次积分10(,)x I dx f x y dy =⎰⎰的积分次序,则I=_______________。
3. 设平面曲线Γ为下半圆周y =22()x y ds Γ+⎰=___________。
4. 若级数1n n u∞=∑的前n 项部分和是:1122(21)n S n =-+,则n u =______________。
5. 设)2,5,3(-=a ,(2,1,4)b =,(1,1,1)c =,若c b a ⊥+μλ,则λ和μ满足 。
二、 计算题(每小题10分,共70分)1. 求由方程xyz =(,)z z x y =在点(1,0,1)-处的全微分。
(10分)2. 设21()x t f x e dx -=⎰,求10()f x dx ⎰。
(10分) 3. 计算xzdxdydz Ω⎰⎰⎰,其中Ω是由平面0,,1z z y y ===以及抛物柱面2y x =所围成的闭区域。
(10分)4. 计算dy xy ydx x L22+⎰,其中积分路径L 是xoy 平面上由点(2,0)A -顺次通过点(0,2)B 、(2,2)C 到点(2,4)D 的折线段。
(10分) 5. 把函数xx f 431)(+=展为1-x 的幂级数,并确定其收敛域。
6. 求点)3,2,1(-关于平面014=-++z y x 的对称点。
(10分)7. 要建造一个表面积为108平方米的长方形敞口水池,尺寸如何才能容积最大.。
(10分)三、证明题(5分)若0lim =∞→n n na ,且∑∞=+-+11])1[(n n n na a n 收敛于常数A ,试证明级数∑∞=1n n a 收敛。
答案课程名称:高等数学A(二) 试卷编号:5一、填空题。
(每小题5分,共25分)1.22e π,2.101(,)y dy f x y dx ⎰⎰,3.π,4.1(21)(21)n n -+, 5. 076=+μλ二、 计算题。
高数A(二)A卷参考答案

学生期末考试试题参考答案及评分标准纸
课程名称
高等数学A(二)
考试班级
05级A类
考试标准用时
120
试卷代号
A
参考答案及评分标准:
一、填空题:(每小题4分,共24分)
1、 2、 3、 4、 5、 6、3
二、选择题:(每小题4分,共16分)
1、D 2、C 3、B 4、C
三、计算重积分:(每小题7分,共14分)
1、 3分
7分
2、 3分
7分
四、计算曲线积分(每小题7分,共14分)
1、 4分
7分
2、 ,
2分
= 4分
7分
五、(本题共有两小题,第1题5分,第2题7分,共12分)
1、 3分
发散5分
2、 2分
命题人
的收敛区域为 3分
5分
7分
六、求解微分方程(每小题7分,共14分)
1、先求对应的齐次方程: ,变量分离可得:
两边积分可得: 是对应的齐次方程的通解3分
再利用常数变易法,设 为原方程的解,代入原方程可得:
为原方程的通解6分
又 即 为原方程满足初始条件的解7分
2、特征方程为 得 所对应的齐次方程的通解为 2分
命题
时间
2006年6月16日
教研室
审核人
审核
时间
年月日
……………………………………………………………………装订线……………………………………………………………………
学生期末考试试题参考答案及评分标准纸
课程名称
高等数学A(二)
济南大学学年学期考试试卷
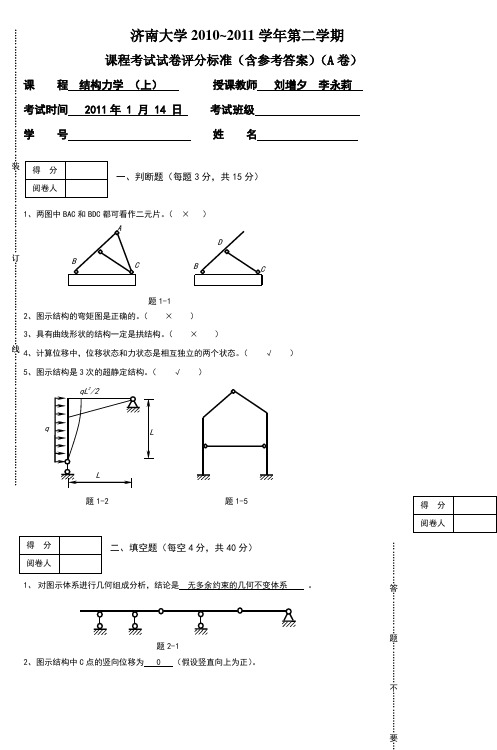
济南大学2010~2011学年第二学期课程考试试卷评分标准(含参考答案)(A 卷)课 程 结构力学 (上) 授课教师 刘增夕 李永莉 考试时间 2011年 1 月 14 日 考试班级 学 号 姓 名一、判断题(每题3分,共15分)1、两图中BAC 和BDC 都可看作二元片。
( × )题1-1 2、图示结构的弯矩图是正确的。
( × ) 3、具有曲线形状的结构一定是拱结构。
( × )4、计算位移中,位移状态和力状态是相互独立的两个状态。
( √ )5、图示结构是3次的超静定结构。
( √ )题1-2题1-5二、填空题(每空4分,共40分)1、 对图示体系进行几何组成分析,结论是 无多余约束的几何不变体系 。
题2-12、图示结构中C 点的竖向位移为 0 (假设竖直向上为正)。
……………答……………题……………不……………要…q2…………………………………………装…………………………订…………………………线…………………………………………3、图示桁架结构的1、2杆的轴力分别为N 1=P 2 ,N 2= 0 。
题2-2 题2-3 4、图示结构的位移法未知量有 3 个。
5、图示结构已知C 点的转角为PL/7i (顺时针),则A 截面的弯矩为 2PL/7 。
题2-4 题2-5三、计算题(13分)作出下列结构的弯矩图。
解:(2分) (2分) (2分)四、计算题(25分) 用力法求解并作出下列超静定结构的弯矩图,EI=常数。
AEL M 图 (3分) …………………………………………装…………………………订…………………………线…H C kN 1H 024224H ,0C C A ==⨯-⨯+=∑M kN1H ,0X A ==∑kN 6V 024V ,0Y A A ==-+=∑解: 原结构可等价与下列两结构的叠加 (2分)图2的弯矩图等于零。
(1分) 计算图1,取半结构,基本体系半结构(3分) 基本体系(2分) (4分) (4分)(6分)五、计算题(23分)写出下列超静定结构位移法典型方程中的各系数,并列出位移法方程。
